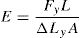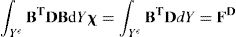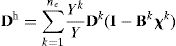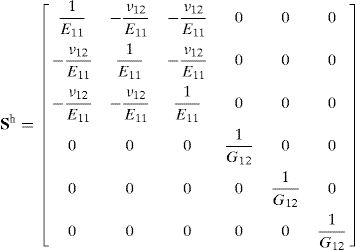Modelling and effective properties prediction of metal foams

Abstract

This work focuses on finding methodologies to describe the effective elastic properties of metal foams. For this purpose, numerical methods and analytical models, were used. Kelvin cells and Weaire–Phelan structures were modelled to represent both open and closed-cell representative unit-cells. These unit-cells were then subjected to different homogenization methods: (i) Far field methods with single freedom constraints, where it was used two different approaches based on the load case. (ii) Asymptotic Expansion Homogenization (AEH) with periodic boundary conditions. The analytical, numerical and experimental results were then compared. The results indicate that the far field methods gave more precise predictions. However, AEH provides more information on the behaviour of the unit-cells. Using this detailed information, it was possible to perform an anisotropy analysis. Furthermore, contrary to the closed-cells, the open-cell numerical methods and analytical models are within the experimental results range.

1

Introduction

Metal foams are a class of materials of increasing interest, that combine a very exciting set of properties that make them interesting for applications in a wide variety of sectors [1]. In order to spread the use of these materials on engineering applications, it is required a detailed understanding of their mechanical properties and behaviour. These properties depend on the characteristics of the base material, such as relative density and morphological parameters (i.e. pore size, type of foam which depend on the manufacturing process used). The relationships between the properties, size of the pores and the foam density have been extensively studied using experimental studies [2,3]. In general, real foams exhibit a high variability in cell sizes and shapes, and wall thickness that influences their elastic properties [4]. An extensive number of uni-axial loading, bending, fatigue experiments were already performed to understand the plastic deformation [5–9]. To properly characterize these heterogeneous materials, it is necessary to complement the experimental studies with numerical and analytical studies. The scope of this work is to define numerical procedures to predict the elastic behaviour of metal foams. First by modelling the representative geometries of the foams, secondly by using numerical analysis software to implement the different homogenization methods and lastly by comparing the predicted values with the analytical models obtained from prior works and experimental results.

2

Numerical method

2.1

Far field method with single freedom constraints

Here the unit-cell behaves as if the strain or stress field arise from the macrostructural problem, often called far field stress or strain. The effective elastic properties of the material are determined by using Hook's law. This method was divided into two approaches based on the type of load case used on the unit-cell. That was, either (i) an imposed force F_y over the surface area A or (ii) a prescribed displacement ΔL_y over the length L, the effective Young's modulus E is given by

The degrees of freedom for three faces of the unitcell are constrained and the displacement in these faces is only tangential, therefore enforcing the condition that a pair of faces must stay parallel throughout the deformation history [10].

2.2

Asymptotic expansion homogenization

To ensure cell-to-cell continuity, the opposite geometrical boundaries of a given cell have to be identical, both for the original and deformed states. The periodicity of the deformed unit-cell in this method is granted by the applying periodic boundary conditions [11].

The microscale problem is solved on two main steps. The first is associated to the calculation of the characteristic displacement field tensor χ. The element strain and stress matrices are given by ¿ = Bu and σ = DBu, respectively where B is the element strain matrix, u is the vector of nodal displacements, and D is the matrix of material properties. Therefore the calculation of the corrector matrix χ[12,13]

where the script e corresponds to element quantities associated with the discretized finite element domain of the unit-cell, namely the body Y^e. The corrector is a matrix on contrary to the case of displacements in conventional elasticity. The second term of Eq. (2) is made of the columns of the load matrix F^D[12,14].

In the second step of the microscale problem solving, the matrix χ is used to correct the homogenized elasticity properties, accounting for the microscale material distribution effect on the volume average. For the AEH approach, the homogenized elasticity matrix D^h correspond to,

where Y^k is the volume of element k, Y the total geometry volume and I the identity matrix. If χ = 0, this equation becomes the classical volume average of the elastic properties of the microscale elements.

The inverse of the constitutive matrix D^h results in the flexibility matrix S^h,

The S₁₁, S₂₂ and S₃₃ components of S^h correspond to the inverse elastic modulli of the material in each orthogonal direction [12].

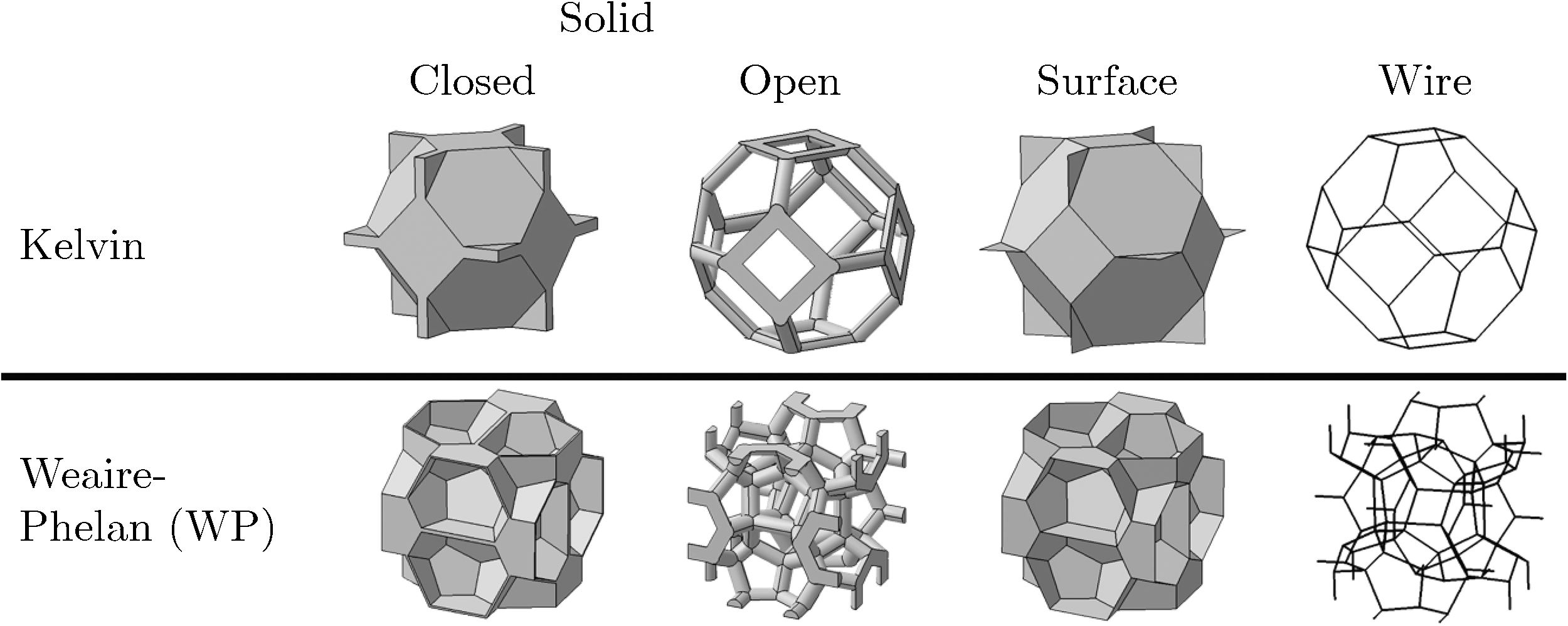
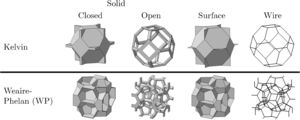
2.3

Modelling cellular materials

When the foam relaxes, tends to a local minimum surface free-energy density, minimizing the surface tension and increasing the surface area per unit volume [15]. The understanding of this process helps the modelling of the representative geometries. To describe the foams geometry one can use: Space-filling polyhedra, Tessellation-based models or image based models which are more accurate representations of the foams. This work uses Space-filling polyhedra as geometrical representation of the foams to characterize the elastic behaviour. The reliability of the unit-cells is usually evaluated by two assumptions, the Plateau's law of equilibrium and the Matzke studies [16–19]. Based on this, the geometries used are, the Kelvin and Weaire–Phelan unit-cells. Fig. 1 shows the modelled geometries used. Even though open-cells foams are not governed by the Plateau's law, it was used the same geometry definition for open and closed-cell foams.

Fig. 1.

The figure compiles all RUCs type used in this work.

The unit-cells were modelled in CATIA V5R15, with the aid of Ken Brakke's Surface Evolver free ware [20]. The far field approaches were applied using NX Nastran as Finite element analysis solver. The AEH simulations were processed in mainFRAN, a user software developed by Oliveira [12,21]. The geometries were modelled using quadratic tetrahedron elements for solids, shell triangular elements with 3 nodes on surfaces and beam elements on wire structures.

To increase the predictions accuracy, the numerical approaches were subjected to: (i) validation; (ii) mesh size refinement; (iii) dependence of the effective properties on the microstructure size. This analysis gave the optimal conditions to proceed with the homogenization approaches. The most relevant results of these studies show that the far field method needs a periodic microstructure to guarantee periodicity. The AEH assure periodicity with one unit-cell, however, it was necessary to define the second phase of the material (void).

3

Results

For each microstructure were defined five different relative densities, distributed between the interval [0.05–0.3]. The predicted effective properties of closed and opencell foams, given by the numerical methods are compared with analytical models obtained from prior works, which are [22–27] for closed-cell foams and [27–32] for open-cell foams. Also, the numerical and analytical predictions are compared with the experimental results from three different works in which the foams were prepared by different manufacturing processes [3–5]. The experimental data is only from closed foams without integer-skin. It was used the AlSi7Mg material for the numerical analysis. The Young's modulus considered was 74 GPa, the density of 2670 kg/m³ and the Poisson's ratio v=0.33.

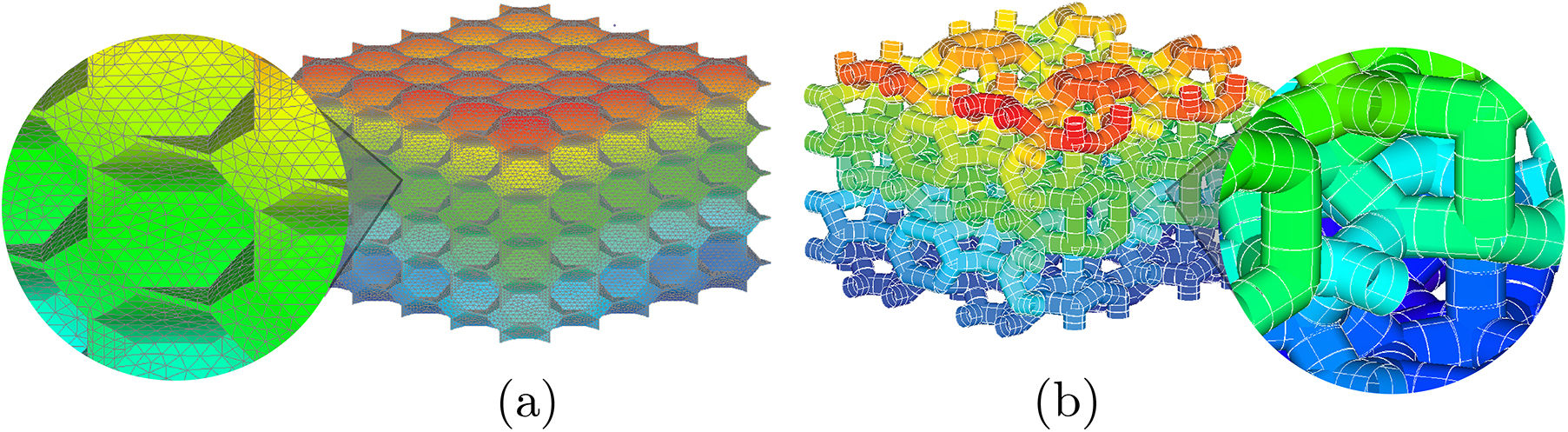
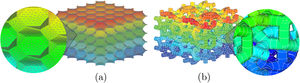
3.1

Far field approaches vs prior results

As expected the results between the two approaches showed similarity, this is further demonstrated in this section. The deformed state of the microstructures when subjected to this approaches is shown in Fig. 2. Due to the use of a uni-axial disturbance the information given by this method is limited.

Fig. 2.

Periodic microstructures deformation when subjected to far field method. (a) Kelvin solid structure, (b) Weaire–Phelan wire structure.

3.1.1

Closed-cell

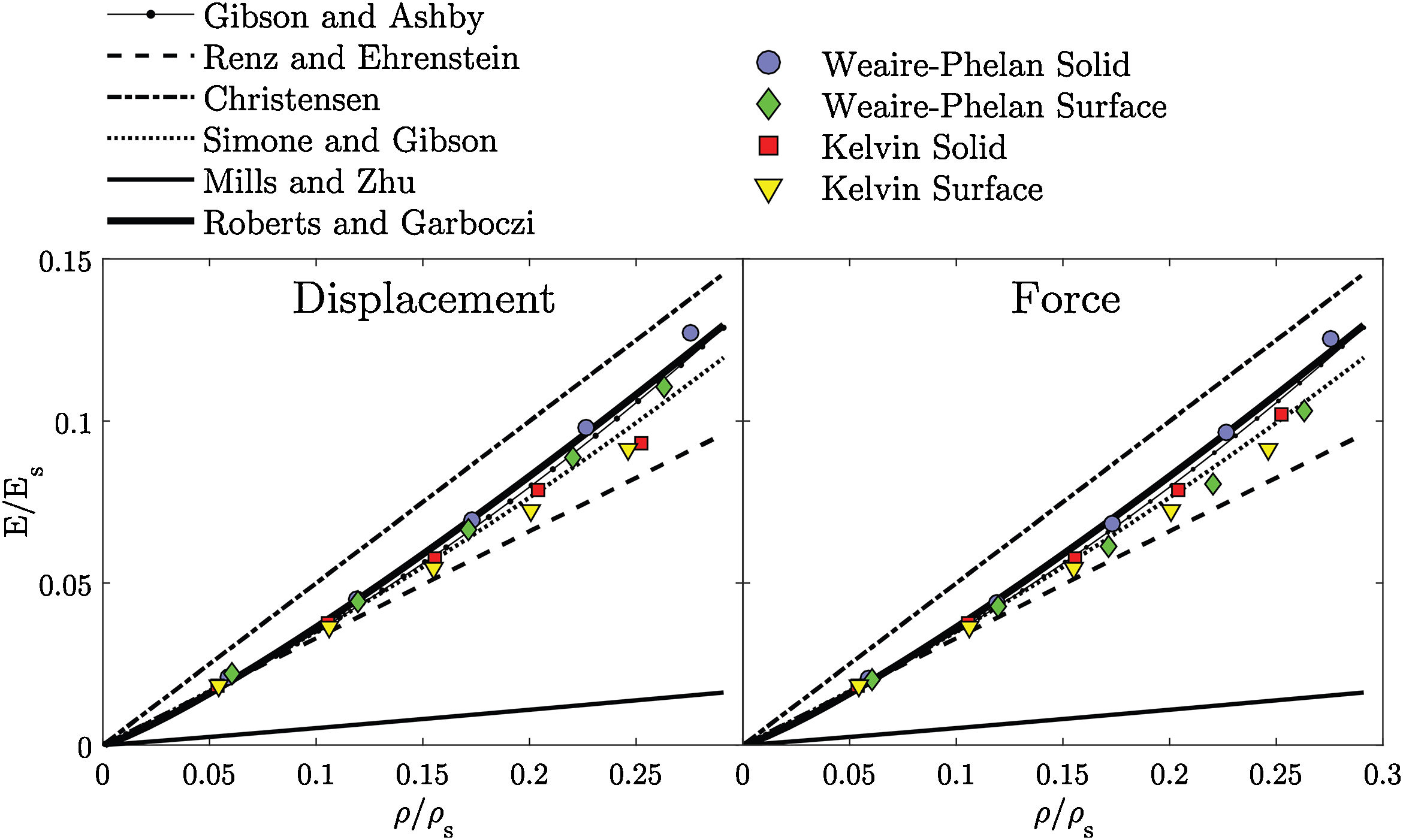
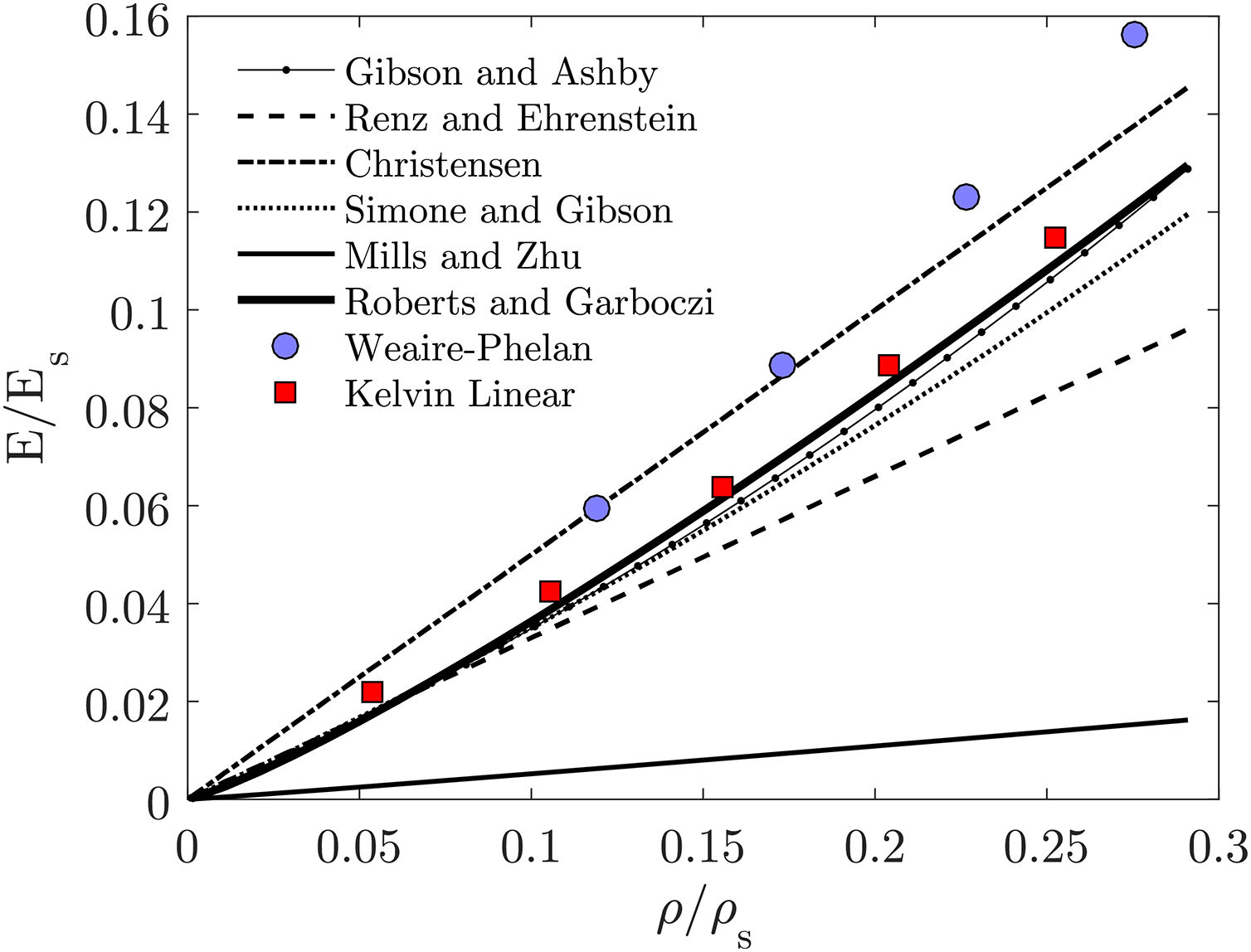
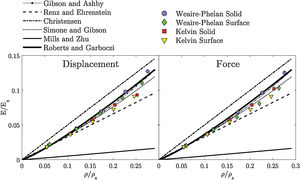
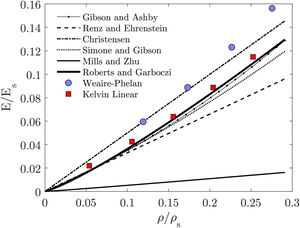
Fig. 3 shows the proximity of the numerical predictions to the analytical models. It is notorious that the numerical results overlap especially with the curves of Simon and Gibson [25], Gibson and Ashby [22] and Roberts and Garboczi [27]. The unconformity of the results obtained by Mills and Zhu [26] is related to the use of representative geometries where the cell walls thickness is 5% of the edge thickness. Comparing the Kelvin with Weaire–Phelan predictions, on one hand it is possible to conclude that for high relative densities the Weaire–Phelan structure is stiffer than the Kelvin. On the other hand for low relative densities the results show that both microstructures have approximately the same stiffness. Also, the surface microstructures are softer than the solid for high relative densities and similar for lower relative densities.

Fig. 3.

Comparison of the far field methods data for closed-cell foams with analytical models.

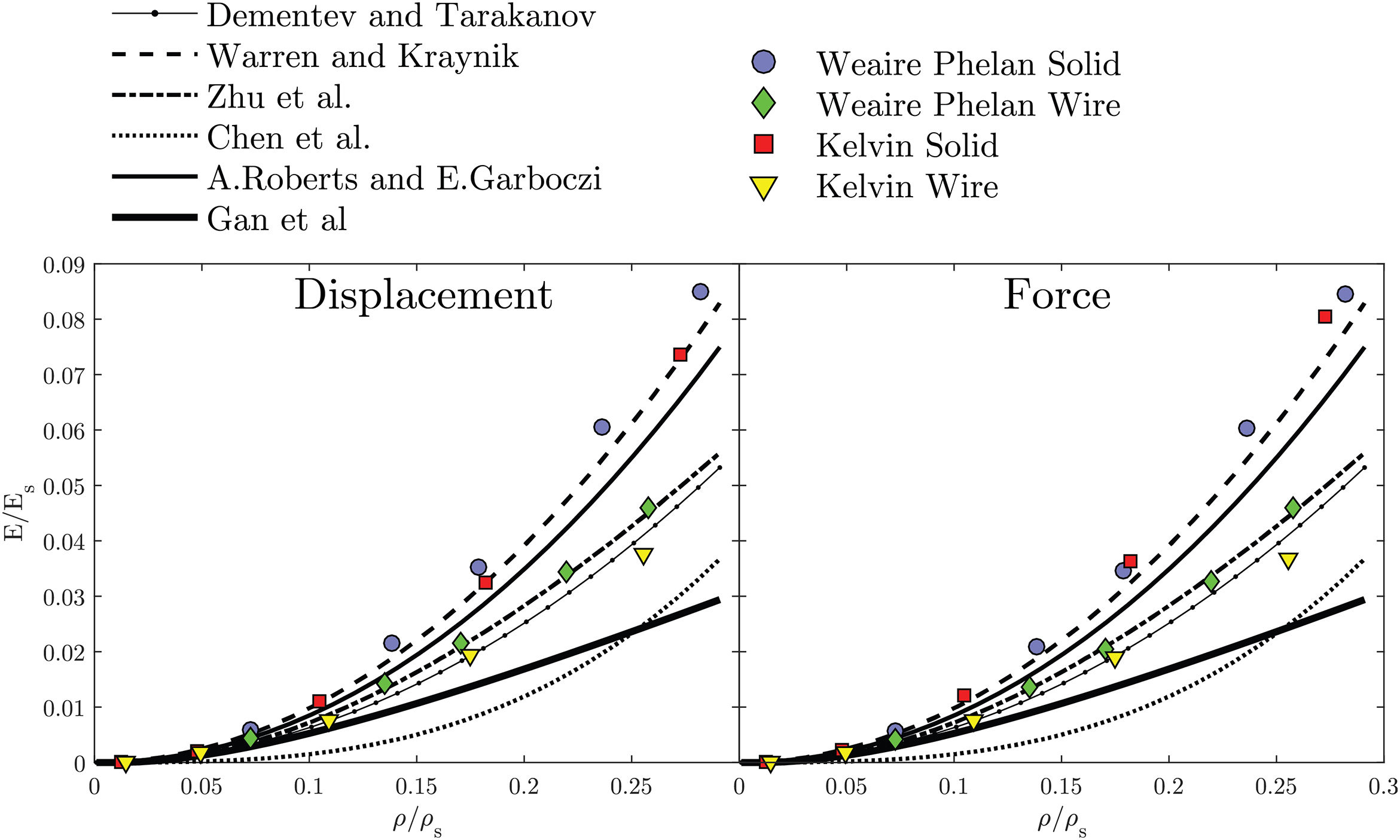
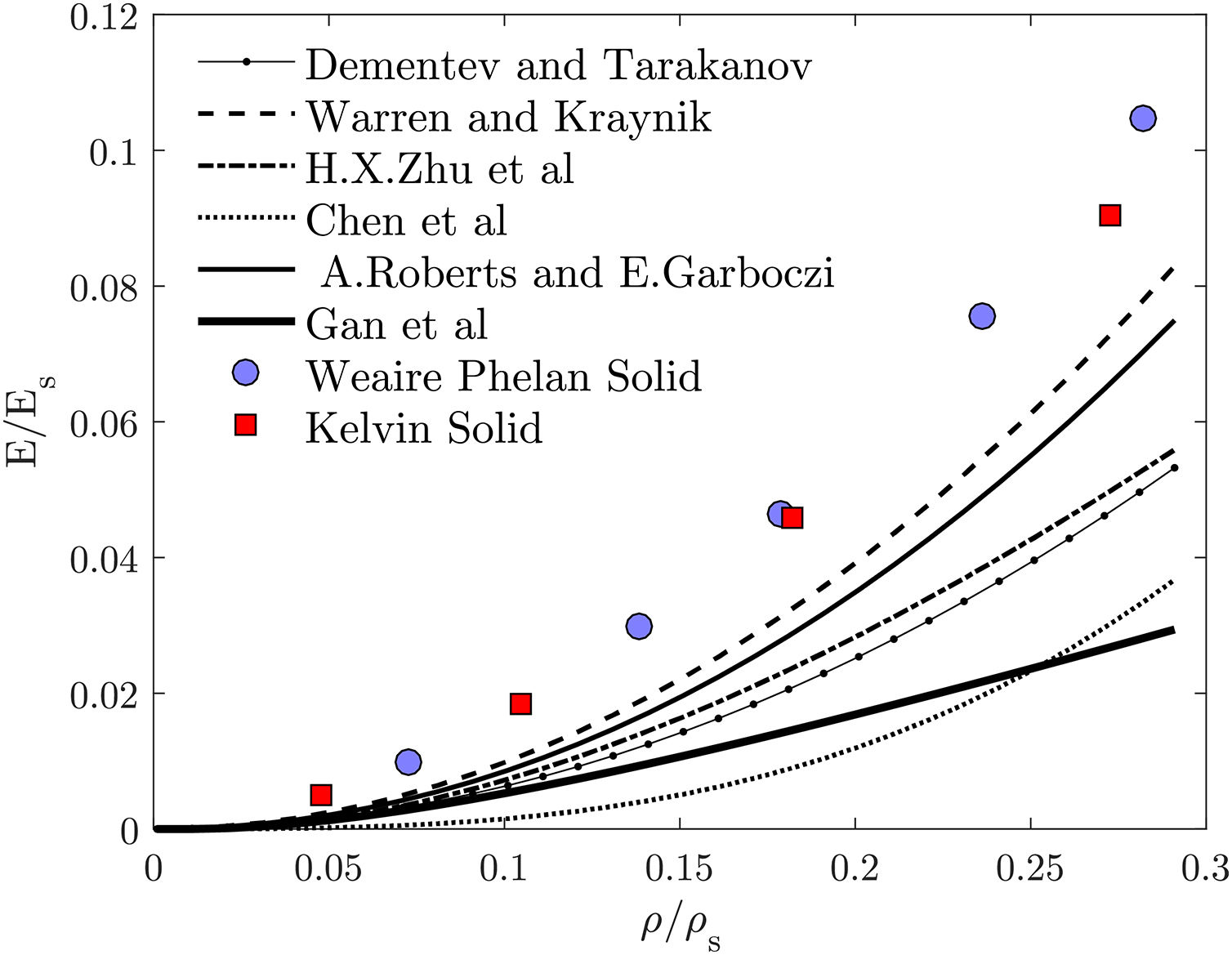
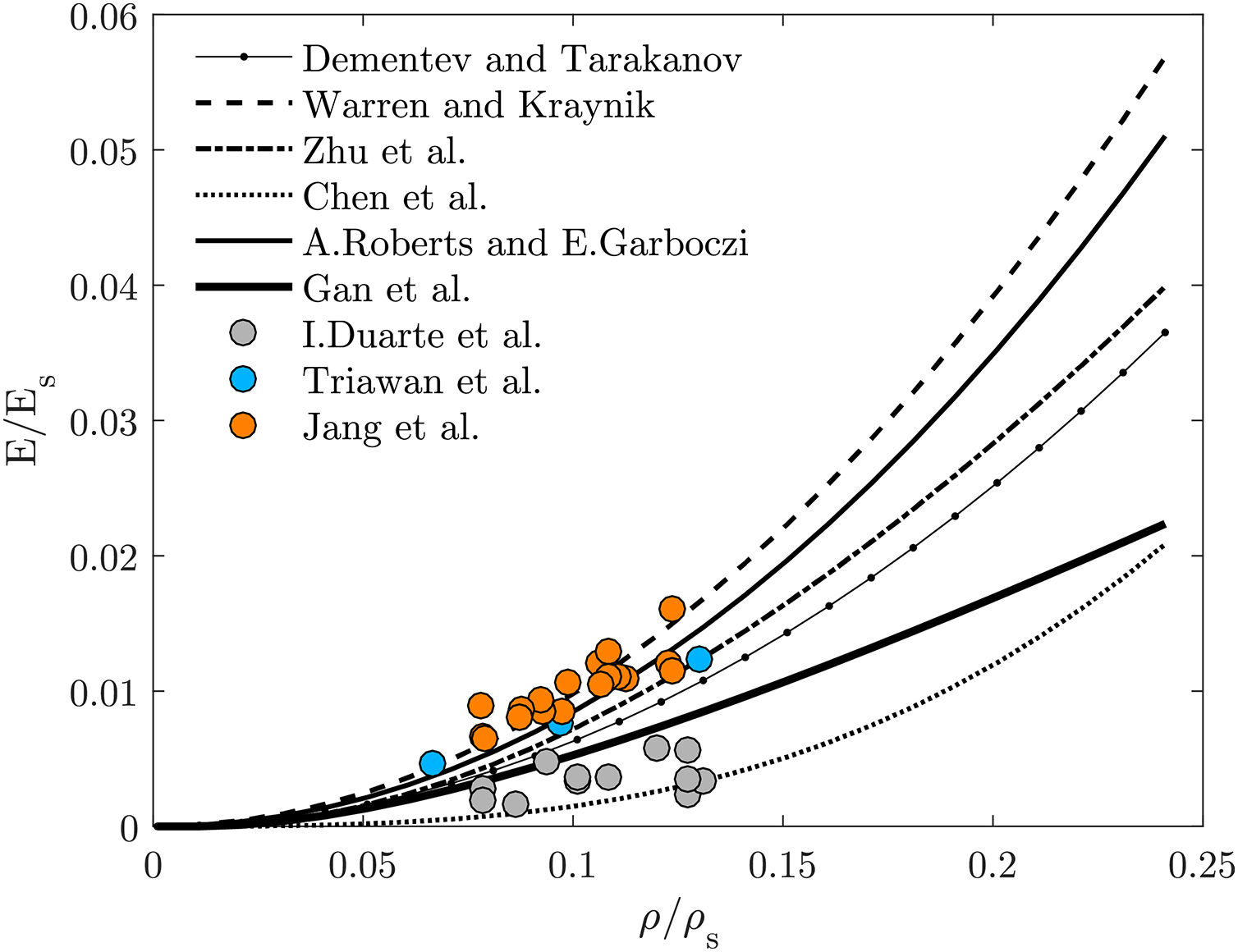
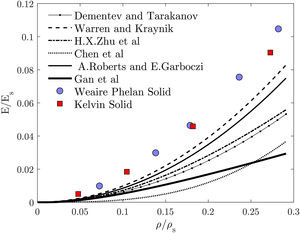
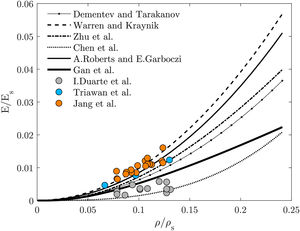
3.1.2

Open-cell

It is apparent in Fig. 4 that the predicted results for the solid microstructures overestimates the Young's modulus when compared to the other estimations. However, these are only around 10% stiffer than the Warren and Kraynik [29] predictions. Wire structures showed better accuracy, which is interesting given the far lower computational effort needed. Kelvin wire predictions are identical to the Dementev and Tarakanov. The explanation may reside in the fact that they also used a tetrakaidecahedra (flat face Kelvin cell) as the representative unit-cell [28]. The results given by the Zhu et al.[30] analytical model are identical to Weaire–Phelan wire microstructures. They used Kelvin cells but considered plateau borders in their approach, which gives stiffer results than using circular cross sections [30,33]. As happened for closed-cell predictions, here the Weaire–Phelan structure is also stiffer than the Kelvin for high relative densities and similar for lower densities. It is noteworthy to point out that open-cell foams exhibits the growth of the Young's modulus with the increasing of the relative density based on a power function, while for closed-cell foams this growth happens linearly.

Fig. 4.

Comparison of the far field methods data for open-cell foams with analytical models.

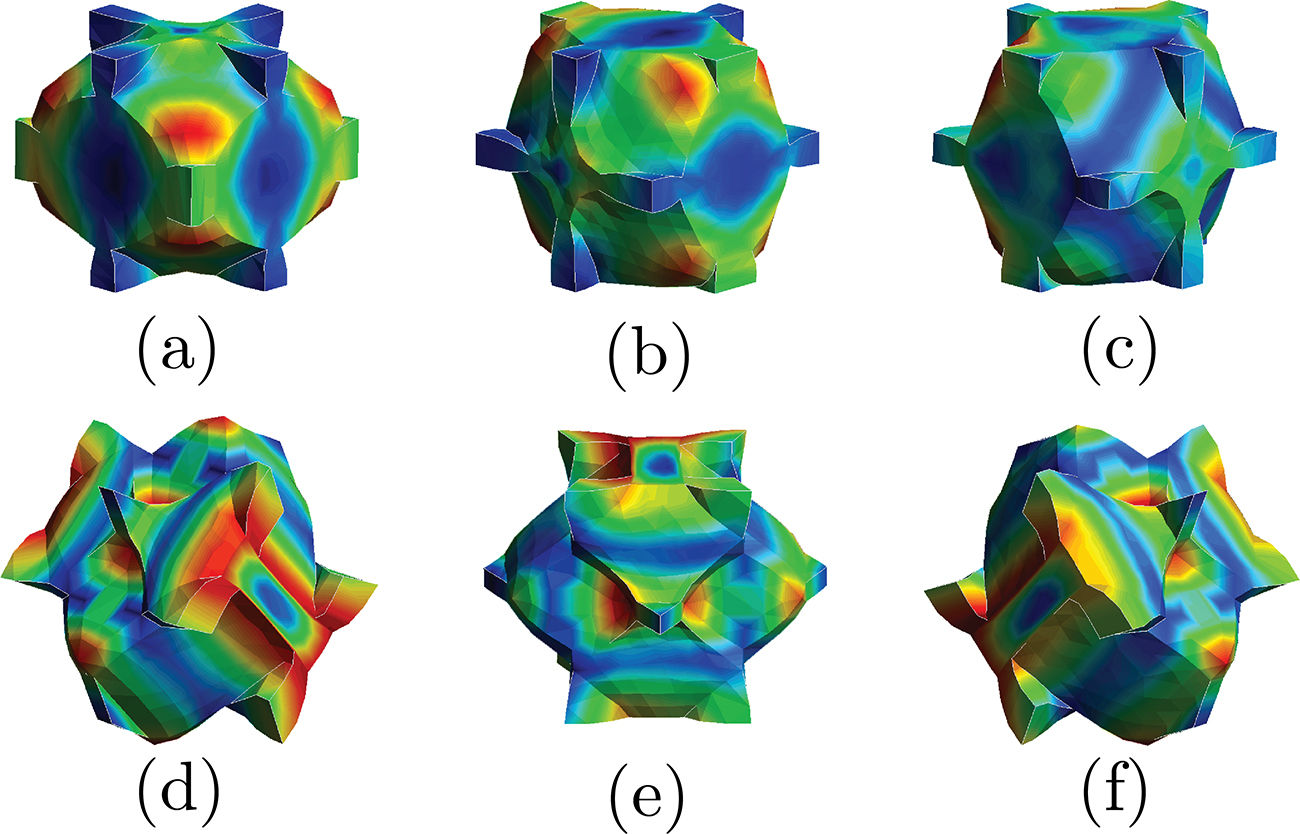
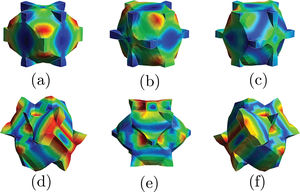
3.2

AEH results vs prior results

The AEH method is strongly dependent on the RUC geometry, so to ensure the convergence of the method it is necessary to have a very well defined geometry. Also, the software used was developed for the study of composite materials with well defined phases using solid finite elements, which means that for this study it was necessary to characterize the void as second phase. This phases were modelled over the existing geometries leading to geometrical imprecisions. The lack of geometrical balance between the two phases, especially for the Weaire–Phelan cells, restricts the utilization of this method to linear elements. This gives place to stiffer and less accurate results because they use less integration points than the quadratic tetrahedral elements. Fig. 5 shows the characteristics displacements of a Kelvin cell when subjected to this method. The second phase it is hidden in order to have a better perception of the information granted.

Fig. 5.

Characteristics displacements for a Kelvin closed-cell RUC, in the normal modes (a) χ_xx, (b) χ_yy and (c) χ_zz and the shear modes (d) χ_xy, (e) χ_yz and (f) χ_xz.

3.2.1

Closed-cell

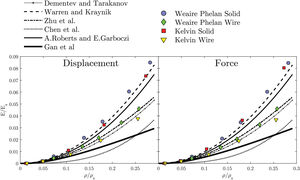
Fig. 6 presents the results using linear elements. These predictions highly overestimate the relative Young's modulus when compared with the analytical models. Also, the difference between the stiffness of Weaire–Phelan and Kelvin cells is larger. In order to improve the results using linear elements it was verified the influence of various convergence parameters of the boundary conditions method used, e.g. the penalty weight, error tolerance. However, the resulting estimations had only little changes on the final results [11].

Fig. 6.

Comparison of the AEH predictions for closed-cell foams with analytical models.

3.2.2

Open-cell

Similarly to what happened for closed-cell, the results for the open-cell RUCs when submitted to AEH are much stiffer when compared to the other results (Fig. 7). Even though the performance of this method for the characterization of the mechanical behaviour of metal foams is not indicated, it provides enough information to know how the Young's modulus is dependent on the orientation.

Fig. 7.

Comparison of the AEH predictions for open-cell foams with analytical models.

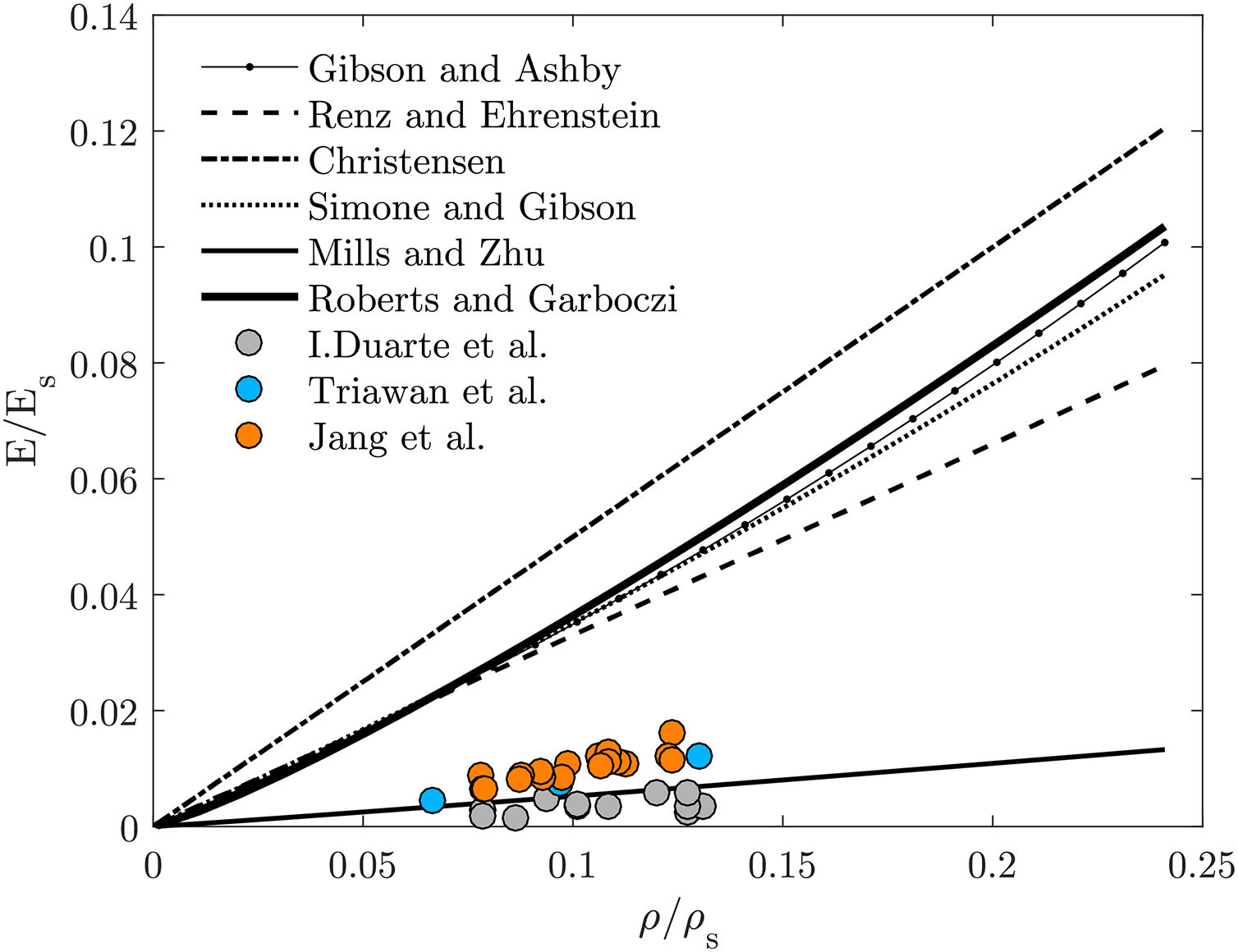
3.3

FEM and prior results vs experimental results

Fig. 8 shows that the closed-cell analytical models, and by resemblance the numerical methods, highly overestimate the value of the relative elastic modulus. Only the Mills and Zhu model compares with the experimental results. Both numerical methods and analytical models presented consider the perfect cells, which means that the microdefects were not taken into account leading to much stiffer structures than real foam. Also if the foams used have most of their material concentrated on the edges or, have cell walls missing, the dominant deformation mechanism in elastic behaviour of this foams becomes edge bending and, in that case, they behave as open-cell foams [4,27].

Fig. 8.

Comparison between closed-foam analytical models and experimental data.

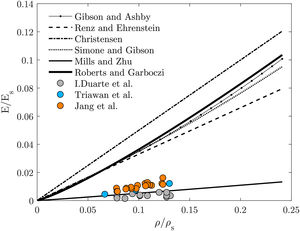
It is possible to observe that the predictions from open-cell models are within the experimental results range (Fig. 9). The curve by Warren and Kraynik [29] is close to Jang [3] and Triawan [5]. The Chen et al. [31] and Gan et al. [32] models are the ones that approximate the most to Duarte et al. [4] experimental results. Still, the curve that is the best fit for experimental results is the closed-cell Mills and Zhu model. These analytical models are simple and easy to apply. Even giving the correct trend of mechanical properties, they appear to be oversimplified, as the Young's modulus only scales with the relative density.

Fig. 9.

Comparison between open-cell foam analytical models and experimental data.

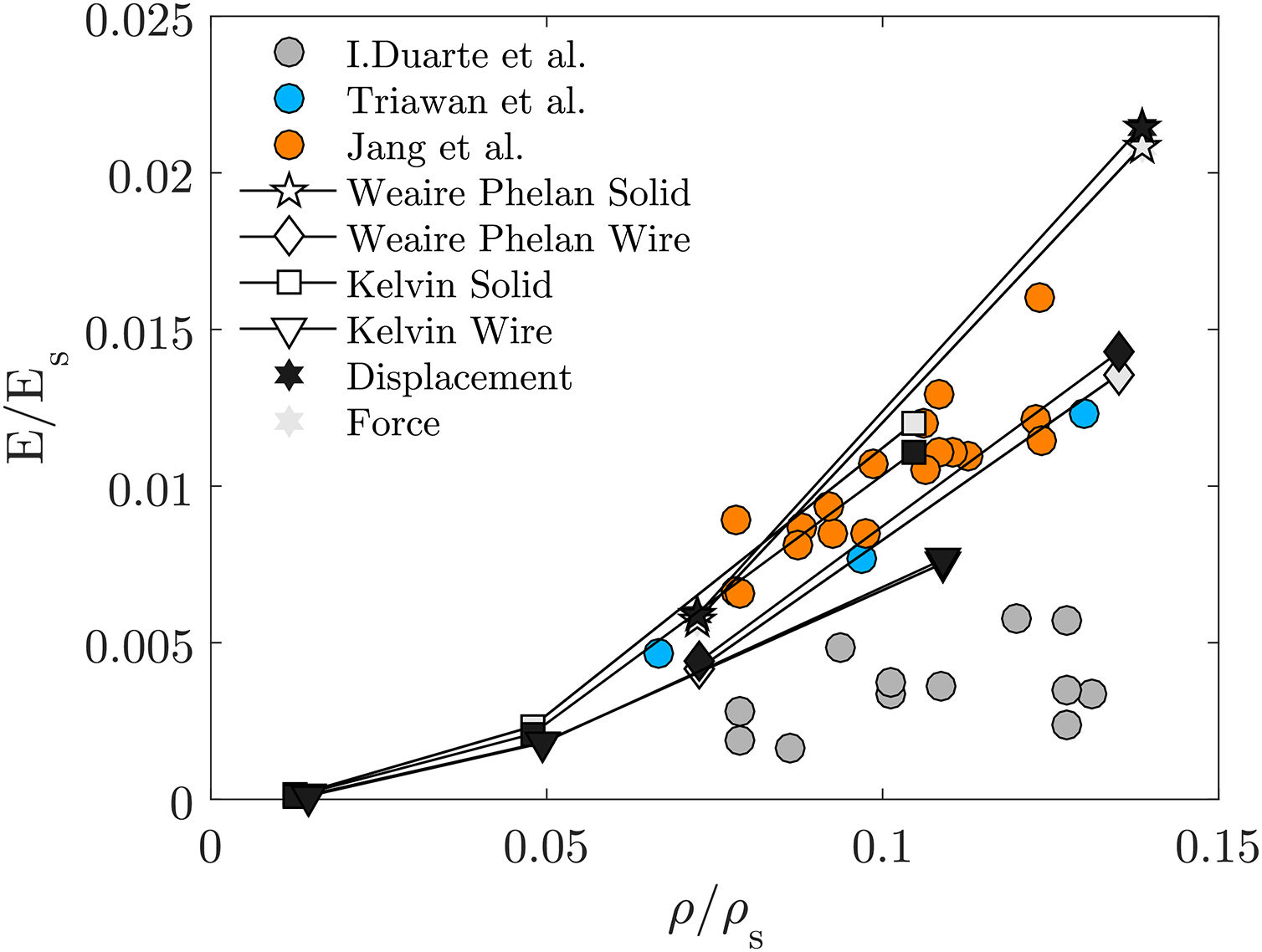
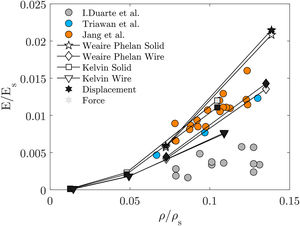
Fig. 10 shows that the numerical predictions are near Jang et al. and Triawan et al. results. However, none of the numerical results are close to the experimental ones measured by Duarte et al. Also, the experimental results are very scattered, even when belonging to the same work, that hinders the elastic behaviour prediction.

Fig. 10.

Comparison between open-cell foam numerical methods and experimental data.

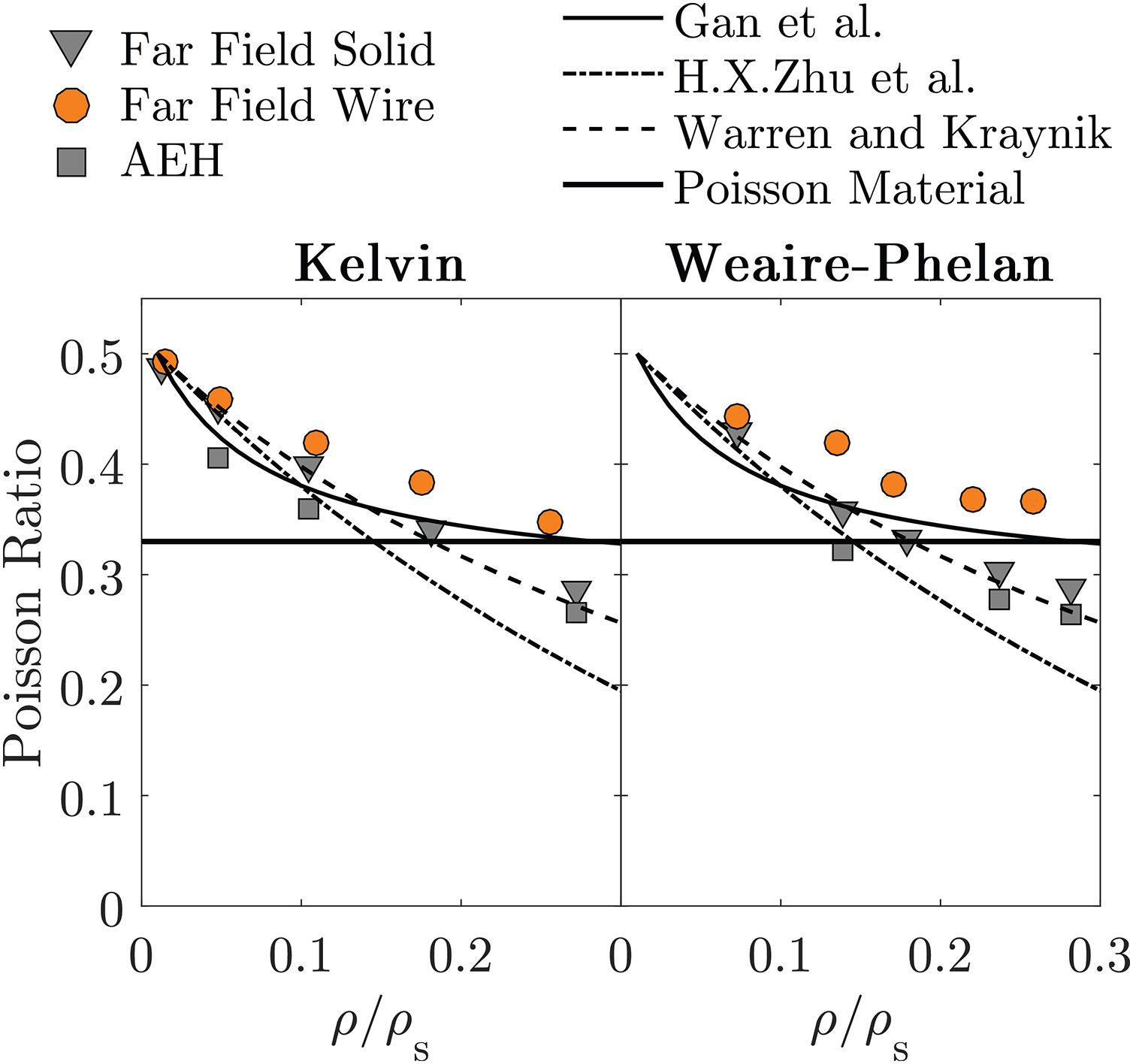
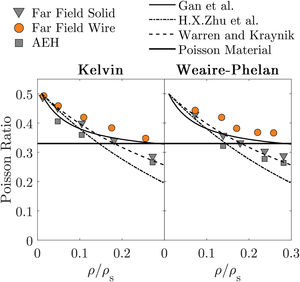
4

Orientation dependence of the Young's Modulus

The closed-cell foams have the Poisson's ratio almost independent of the relative density, having only small variations. Fig. 11 shows that the Poisson's ratio of open-cells shows a large decrease with the increasing of the density. For low relative densities ν ≈ 0.5 which is the highest attainable by an isotropic material. Also means if the structure is uni-axially compressed, the decrease in volume is exactly balanced by the expansion in the perpendicular directions [34]. This nearly incompressible behaviour complies with the analytical models predictions.

Fig. 11.

Predicted Poisson's ratio for open-cell microstructures and comparison with two analytical models.

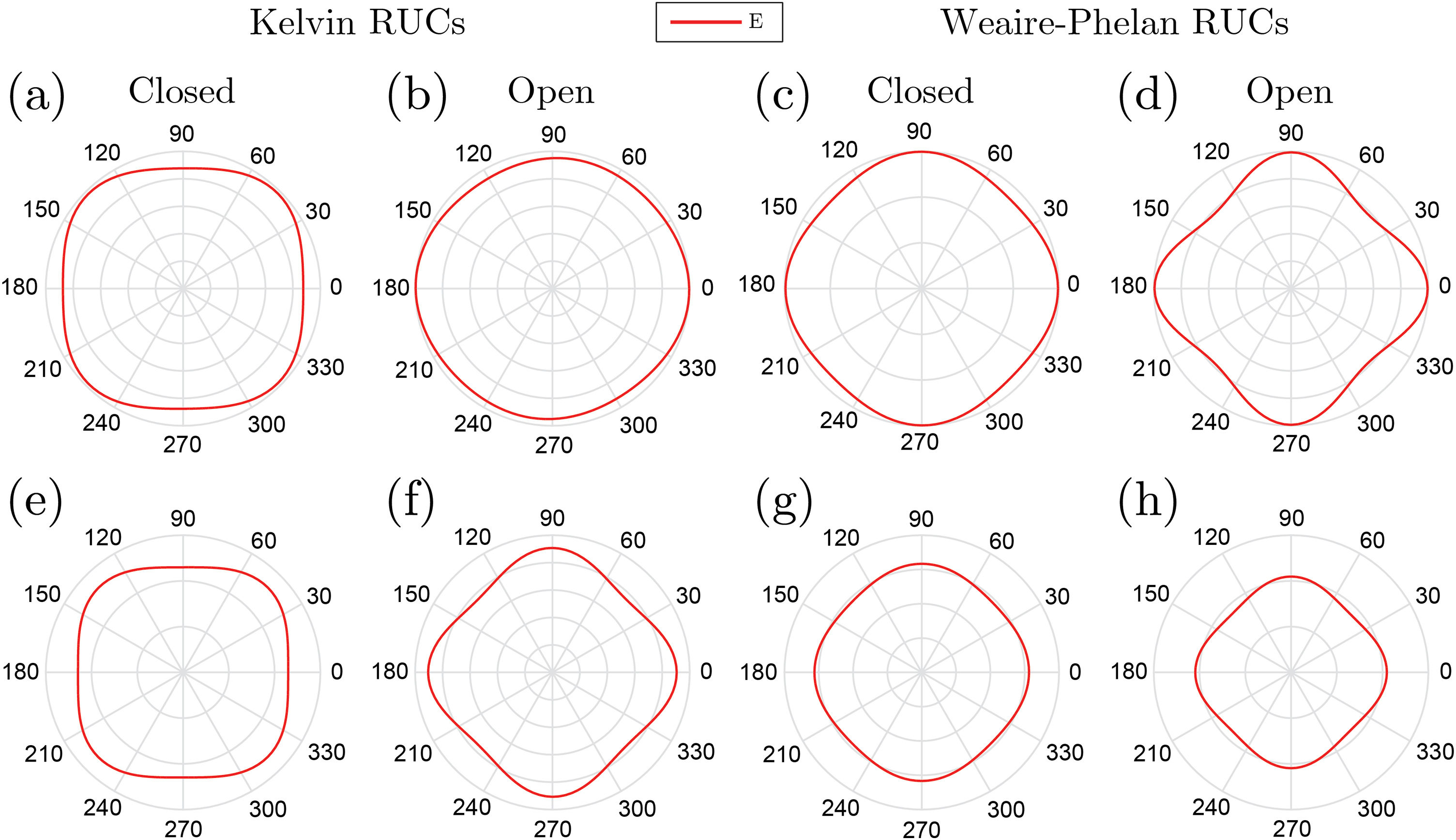
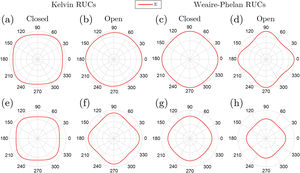
The compliance matrix, given by the AEH method, enables to analyze the anisotropy of the studied RUCs. Fig. 12 reveals how the Young's modulus varies through the representative unit-cells cross-section, from low-density cells and higher density cells. Also, it is shown that these RUCs are orthotropic. These results are close to Daxner et al. [35] where 3D visualization of the direction dependence of Young's modulus, for Kelvin and Weaire–Phelan foam structures of different densities, was also analyzed. However, they only study closed-cell RUCs.

Fig. 12.

Anisotropy maps of the different cells, the maps on the top correspond to the lowest density cell and on the bottom to the highest density cell.

5

Final remarks and conclusion

In this work two homogenization methods were used to predict the effective elastic properties of metal foams: (i) Far field methods with a single freedom constraints, where it was used two approaches related to the type of load used, an imposed displacement and a prescribed force; (ii) asymptotic expansion homogenization. Space-filling polyhedra, Kelvin cells and Weaire–Phelan cells, describing both closed and open-cell foams were subjected to the homogenization methods. The results were compared with analytical models from prior works and experimental results. It was found that the predictions given by far field approaches are identical to some of the analytical models, both for open and closed-cells. However, they provide limited information on anisotropy of the cell. The asymptotic expansion homogenization give this insight but has to be adapted to be used on cellular materials. Comparing the numerical and analytical predictions with the experimental results, it was found that the closed-cell predictions, overestimate the elastic modulus. This is related to the use of perfect cells with no microstructural defects. The open-cell foams, the results indicate that both numerical and analytical predictions are within the experimental results range. The representative unit-cells used are both orthotropic, and it was shown that the Weaire–Phelan cells tend to stiffer results.

Acknowledgements

The authors thank TEMA (Centre for Mechanical Technology and Automation, www.ua.pt/tema) for supporting this work.