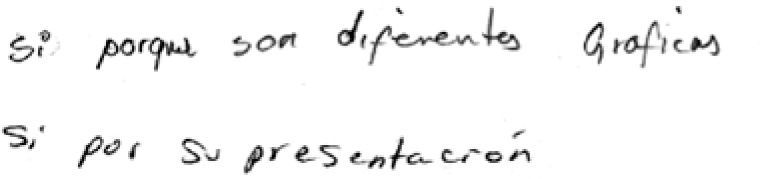Comprensión y razonamiento de profesores de Matemáticas de bachillerato sobre conceptos estadísticos básicos

En el presente artículo se reportan resultados de una investigación con una muestra de 31 profesores mexicanos de bachillerato. El objetivo de la investigación es evaluar la comprensión y razonamiento de dichos profesores sobre diversos conceptos de estadística que forman parte de los programas de estudio. Se utilizó una metodología de tipo mixto para la recopilación de la información. Los resultados muestran que los profesores tienen una comprensión superficial y aislada sobre conceptos estadísticos, como la interpretación y conversión de diversas representaciones gráficas, medidas de tendencia central y medidas de variabilidad. En su razonamiento sobre comparación de distribuciones de datos utilizan pocos conceptos que son clave para describirlas, por lo que el razonamiento de la mayoría de los profesores se ubica en los niveles más bajos del modelo taxonómico SOLO.

This paper presents the results of a study involving 31 high school teachers. The objective of the research is to evaluate the comprehension and knowledge of the said teaching staff regarding diverse statistical concepts that form part of the study programs. The collection of the data was carried out using a mixed methodology. The results show the teachers have only a superficial and isolated understanding of statistical concepts, such as the interpretation and conversion of several graphic representations, or the measurement of key and variable trends. Regarding their knowledge on the comparison of data, they use few of the concepts which are key to describing them, thus meaning the knowledge of the majority of these teachers lies in the lowest levels of the taxonomic model: Structure of the Observed Learning Outcome (SOLO).

Introducción

En los años recientes, el estudio de la estadística se ha convertido en un elemento importante en el desarrollo de competencias para la comprensión e interpretación de información de tipo cuantitativo. Es ahora habitual que las personas tomen decisiones basadas en información numérica referida a encuestas políticas, desempeños educativos, pronósticos económicos, efectividad de medicamentos, entre otros (Ciancetta, 2007). En este mismo sentido, Estrada (2002) resume muy bien la importancia de la estadística, al indicar que este campo del saber ya no es dominio exclusivo de los políticos y científicos; por el contrario, son cada vez más fuertes las voces que reclaman una cultura estadística para todos, la educación del razonamiento estadístico y la necesidad de dotar a todos los ciudadanos de conocimientos básicos sobre herramientas estadísticas en la sociedad de la información. De igual forma, Scheaffer (2000) asegura que el conocimiento de la estadística es esencial, tanto para el buen ciudadano como para el empleado productivo.

Los sistemas educativos han sido sensibles a las necesidades anteriormente descritas, y en muchos países (por ejemplo: NCTM, 2000; NZME, 2006; SEP, 2006) la estadística se encuentra actualmente integrada al currículo de Matemáticas desde el nivel elemental hasta las carreras universitarias. En el caso de México,¹ no obstante que desde la reforma curricular de 1975 se reconoce la necesidad de brindar formación sobre probabilidad y estadística en la educación básica, su incorporación en el nivel medio superior ha sido mucho más lenta; además, su avance no ha sido uniforme en los diversos sistemas de bachillerato que operan en el sistema educativo mexicano (CCHUNAM, 2005; DGETI, 2009).

La incorporación de la estadística en el currículo ha generado interés por los aprendizajes obtenidos por los estudiantes sobre esta materia, de tal forma que investigadores e instituciones de diversos países se han dado a la tarea de elaborar instrumentos de evaluación para medir el aprendizaje y el razonamiento de estudiantes de diversos niveles educativos. Ejemplos de estos instrumentos son la prueba CAOS (Delmas et al., 2007), la prueba SRA (Garfield, 2003), y en el caso de México, el Examen Transversal de Estadística (EXTRA-ES) elaborado por el Centro Nacional de Evaluación para la Educación Superior (CENEVAL). Todo ello ha tenido el propósito de evaluar el impacto de las reformas a los planes de estudio, pero también el de investigar sobre concepciones, dificultades y niveles de razonamiento que permitan comprender mejor el proceso de aprendizaje de la estadística e influir para una mejor enseñanza.

Los resultados de diversas investigaciones han puesto de manifiesto que la estadística es vista por muchos estudiantes y profesores como una materia repleta de fórmulas y procedimientos laboriosos que hay que memorizar para resolver un problema. Esta problemática ha sido resumida por Ben-Zvi y Garfield (2004), de la siguiente manera:

• •

  Los estudiantes igualan a la estadística con las matemáticas, y por tanto, esperan que el énfasis esté en números, cálculos, fórmulas y procedimientos.

• •

  Los estudiantes se sienten desconcertados con el desorden de los datos.

• •

  El contexto en muchos problemas estadísticos puede engañar a los estudiantes, debido a que, con base en su experiencia, creen que es suficiente con dar una respuesta, más que seleccionar un procedimiento estadístico apropiado.

Lo anterior se debe a que, hasta hace poco tiempo, en muchos currículos, el estudio de la estadística era reducido a tareas en las que los estudiantes organizaban un pequeño conjunto de datos, construían gráficas y calculaban algunos estadísticos (por ejemplo: media, mediana, desviación estándar). Este enfoque de enseñanza fomenta el uso y memorización de fórmulas y procedimientos, y poco ayuda al desarrollo del razonamiento y del pensamiento estadístico de los estudiantes. Chance et al. (2004) aseguran que mientras muchos estudiantes pueden ser capaces de realizar los cálculos necesarios, con frecuencia son incapaces de comprender el proceso subyacente o interpretar apropiadamente los resultados de esos cálculos. Por su parte Cobb y McClain (2004) afirman que con frecuencia los estudiantes, en vez de analizar datos, simplemente manipulan números de una manera procedimental. Estos mismos autores indican que en los salones de clase, las actividades realizadas enfatizan procedimientos de cálculo y convencionalismos para hacer gráficas, en vez de crear y manipular gráficas diversas para detectar tendencias y patrones de los datos.

Investigadores y organizaciones que promueven la educación estadística (por ejemplo: Batanero, 2001; Wild y Pfannkuch, 1999; Shaughnessy et al., 1996; Franklin et al., 2005) han hecho diversas propuestas y recomendaciones para mejorar la enseñanza de la estadística en todos los niveles escolares. En dichas propuestas se plantea el diseño de investigaciones para la recolección de datos reales y significativos para los estudiantes; que el análisis de datos haga mayor énfasis en la exploración que en la descripción y la automatización de cálculos y gráficas; y que se hagan preguntas y se desarrollen proyectos reales que puedan ayudar a desarrollar el razonamiento y el pensamiento estadístico de los estudiantes, y a dar un mayor sentido a la importancia de la estadística como ciencia de los datos. Sin embargo, el cambio en la enseñanza de la estadística en las escuelas dependerá, en buena medida, de que los profesores estén convencidos de que la estadística es una de las disciplinas más útiles para sus estudiantes, y de la medida en la cual estén adecuadamente preparados para enseñar la estadística en su nivel respectivo.

De acuerdo con lo anterior, y ante la importancia que está teniendo el conocimiento y razonamiento estadístico en la vida cotidiana y las profesiones, resulta de interés investigar acerca de la comprensión y el razonamiento que los profesores de bachillerato muestran sobre diversos conceptos estadísticos que se contemplan en los programas de estudio actuales, y en qué medida están capacitados para la enseñanza de la estadística de acuerdo a los nuevos enfoques. En este contexto, en el presente trabajo nos hemos planteado las siguientes preguntas de investigación:

• 1.

  ¿Qué tanta confianza tienen los profesores sobre sus conocimientos estadísticos para la enseñanza?

• 2.

  ¿Cuál es la comprensión que los profesores de Matemáticas de bachillerato tienen de diversos conceptos estadísticos que forman parte de un análisis básico de datos?

• 3.

  ¿Cuál es el nivel de razonamiento estadístico exhibido por los profesores al comparar distribuciones de datos, y en qué aspectos de las distribuciones se basan para apoyar sus descripciones y comparaciones?

Marco teórico

El conocimiento estadístico y pedagógico de los profesores de estadística

Para generar un cambio en la enseñanza de la estadística, además de las reformas a los currículos de Matemáticas, es necesario que los profesores conozcan ampliamente el contenido y la pedagogía de la materia (McClain, 2008; Batanero, 2001). Además, los profesores deben comprender cómo aprenden los estudiantes, ser conscientes de dificultades específicas y considerar los medios y recursos adecuados para guiar a los estudiantes hacia la comprensión. Sorto (2006) señala que los profesores deberían tener: a) conocimiento de la materia, conocimiento pedagógico, conocimiento de los estudiantes como aprendices y conocimiento de la evaluación; b) ser capaces de manejar discusiones en clase, establecer una cultura de razonamiento matemático, diseñar y seleccionar tareas, analizar el pensamiento y el desempeño de los estudiantes, y planear la instrucción.

Sin embargo, diversas investigaciones han documentado que muchos profesores poseen un insuficiente conocimiento estadístico para la enseñanza. Por ejemplo, Estrada (2002) reporta que los profesores que participaron en su investigación fueron incapaces de detectar contradicciones en un gráfico de un periódico y de obtener conclusiones de información que requería conocimiento estadístico. Asimismo, Alpízar (2005) observó en su estudio con profesores, que aunque éstos conocían el significado de las medidas de tendencia central, presentaron dificultades al conjeturar acerca de sus propiedades. Por otra parte, tienden a utilizar la media aritmética para caracterizar cualquier conjunto de datos, sin considerar que, por sus condiciones particulares, dicho conjunto admitiría otros promedios que podrían ser más adecuados. Además, cuando se les pidió describir la variabilidad de un conjunto de datos por medio de una medida adecuada, los profesores eligieron a la desviación estándar, sin proporcionar argumentos claros sobre su elección.

En otra investigación, realizada por Ruiz et al. (2007) con futuros profesores españoles, encontraron que una parte importante de los sujetos de estudio no comprendía el concepto de distribución, y el razonamiento sobre variabilidad le resultaba difícil a la mayoría de ellos. También, Arteaga et al. (2012) encontraron en una investigación sobre comprensión de gráficos estadísticos, que futuros profesores de primaria no eran competentes en la interpretación de diversas representaciones gráficas. Por su parte, Inzunsa y Juárez (2007) encontraron un bajo nivel de razonamiento estadístico en un grupo de profesores mexicanos de bachillerato —algunos de ellos con experiencia en la enseñanza de la estadística— tanto en conceptos propios de estadística como en los que tienen que ver con probabilidad. Estos profesores tuvieron dificultades para identificar el promedio adecuado, principalmente porque no pudieron reconocer el contexto de aplicación, aspecto de suma importancia en estadística.

El significado del razonamiento estadístico

El razonamiento estadístico es definido por Garfield (2002) como la manera en la cual las personas razonan con ideas estadísticas y el sentido que le dan a la información estadística, lo cual implica hacer interpretaciones basadas en conjuntos de datos y sus representaciones; el razonamiento estadístico, además, puede implicar conectar un concepto con otro (por ejemplo: tendencia central y variabilidad) y combinar ideas sobre datos y azar. El razonamiento significa comprender, ser capaz de explicar e interpretar resultados de procesos y estudios estadísticos.

Metodología

Los sujetos participantes en el estudio fueron 31 profesores de Matemáticas de bachillerato procedentes de diversas regiones del estado de Sinaloa, los cuales aceptaron participar de forma voluntaria en la investigación. De los 31 profesores participantes, 16 no habían impartido el curso de estadística; sin embargo, fueron incluidos en la muestra porque pertenecen a la academia de Matemáticas en la cual se ubica la materia, y por lo tanto podrían impartirla. La formación profesional de los profesores es variada: predominan los ingenieros civiles e ingenieros químicos; dos son contadores públicos y uno es licenciado en Educación con especialización en Matemáticas. Su edad al momento de la investigación se encontraba entre 30 y 47 años, y su experiencia docente variaba de los 2 a los 25 años de antigüedad.

Los métodos que se utilizaron para responder las preguntas de la investigación corresponden a un enfoque mixto: la parte cuantitativa corresponde a los datos provenientes de las respuestas que los profesores dieron a un conjunto de 33 ítems de opción múltiple; mientras que los datos cualitativos se obtuvieron de las respuestas a tres ítems abiertos. El propósito de estos últimos ítems era evaluar, a un mayor nivel de profundidad, los significados que los profesores otorgaron al proceso de comparación de distribuciones, así como la confianza que ellos mostraron tener en sus conocimientos estadísticos para enseñar la materia.

De los 36 ítems que contemplaba el instrumento de evaluación, 21 fueron seleccionados del cuestionario CAOS (Comprehensive Assessment of Outcomes in Statistics). Dicho cuestionario fue diseñado con el objetivo de atender el desafío que presenta la evaluación en educación estadística, y ha sido validado en varios estudios de investigación. El cuestionario mide resultados básicos en cultura y razonamiento estadístico para un primer curso de estadística a nivel universitario, un nivel muy próximo al grado en el que se imparte la estadística en el bachillerato en México. El criterio principal de selección de los ítems consistió en que permitieran evaluar conceptos que aparecen en el programa de estudios del bachillerato. En Delmas et al. (2007) se hace una reseña amplia sobre la génesis y el desarrollo del proceso de elaboración del cuestionario CAOS y se muestran algunos resultados obtenidos con estudiantes universitarios de Estados Unidos. Otros 12 ítems del instrumento de evaluación fueron tomados del trabajo de Makar (2004) sobre razonamiento estadístico con profesores, y los tres ítems abiertos fueron diseñados por los investigadores. El cuestionario fue aplicado durante algunas sesiones de trabajo con los profesores mientras participaban en un curso sobre la reforma de los planes de estudio del bachillerato.

Para caracterizar el razonamiento estadístico acerca de un concepto o grupo de conceptos definimos categorías que delimitan particularidades de dicho razonamiento, las cuales permiten clasificar por niveles a los sujetos que desarrollan cierta tarea o resuelven un problema estadístico; para ello utilizamos el modelo taxonómico SOLO (Structure of Observed Learning Outcomes) desarrollado por Biggs y Collis (1982), el cual ya ha sido utilizado en otros estudios (por ejemplo: Vizcarra e Inzunsa, 2009; Reading y Reid, 2006) para definir categorías de desarrollo cognitivo de diversos conceptos estadísticos. En el modelo SOLO (Cuadro 1) los conceptos y procesos utilizados por los sujetos al dar respuesta a las preguntas o tareas planteadas se pueden clasificar en un determinado nivel de los cinco niveles que se contemplan.

Cuadro 1.

Descripción de los niveles del modelo SOLO

Nivel	Descripción genérica
Nivel preestructural	Los estudiantes no se enfocan en aspectos relevantes de la tarea que les ha sido planteada. Los conceptos o procesos son utilizados en forma simplista que los conduce a errores. Pueden dejar la tarea sin resolver por falta de comprensión.
Nivel uniestructural	Los estudiantes se enfocan en algún aspecto relevante de la tarea planteada o en alguna etapa de la tarea; realizan alguna conexión de un concepto o proceso con otro. Son capaces de desarrollar procesos simples.
Nivel multiestructural	Los estudiantes se enfocan en más de un aspecto relevante de la tarea, pero no logran integrarlos para obtener una solución correcta.
Nivel relacional	Los estudiantes integran todos los aspectos relevantes de la tarea como un todo coherente con estructura y significado.
Nivel abstracto extendido	Los estudiantes cumplen con las exigencias cognitivas del nivel relacional, pero además son capaces de transferir los conceptos y procesos fuera del contexto en que fueron aprendidos.

Apoyados en el modelo SOLO, algunos autores han establecido marcos para la evaluación del razonamiento sobre aspectos que son de interés para esta investigación, tales como: a) comparación de distribuciones, y b) obtención de inferencias estadísticas informales. Para el análisis de los resultados realizamos una síntesis de dichos marcos y adaptamos un modelo que se muestra en el Cuadro 2.

Cuadro 2.

Descripción de los niveles del modelo SOLO en el razonamiento estadístico

Descripción/comparación
Nivel	Características del nivel
Preestructural (P)	No se refiere a aspectos clave para hacer descripciones o comparaciones de las distribuciones.
Uniestructural (U)	Describe y compara las distribuciones enfocando en un solo aspecto clave de razonamiento (centro, forma, desfase/traslape, dispersión y casos individuales).
Multiestructural (M)	Describe y compara las distribuciones enfocando en más de un aspecto clave de razonamiento, pero sin integrarlos.
Relacional (R)	Describe y compara las distribuciones estableciendo conexiones relacionales entre varios aspectos clave de razonamiento.

Inferencias informales
Nivel	Características del nivel
Preestructural (P)	No plantea ninguna conclusión ni inferencia, o las que plantea no se refieren a aspectos clave de razonamiento de inferencias informales (generalización, datos, conceptos estadísticos, lenguaje probabilístico, muestreo y explicaciones).
Uniestructural (U)	Plantea una conclusión; puede referirse a datos y conceptos estadísticos, pero no generaliza.
Multiestructural (M)	Plantea una conclusión y hace una declaración inferencial (generalización) refiriéndose a otros dos o más aspectos clave, sin lograr integrar lo declarado.
Relacional (R)	Plantea una conclusión y hace una declaración inferencial (generalización) descrita de tal manera que conecta todos los aspectos de una inferencia informal.

Resultados y discusión

Nivel de confianza de los profesores en sus conocimientos estadísticos

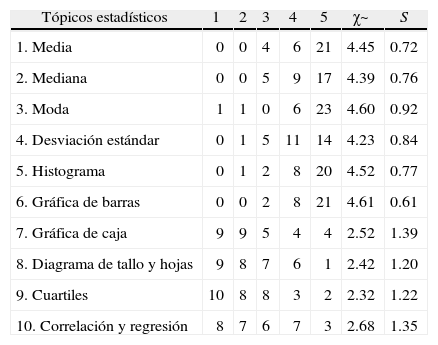
La primera pregunta del cuestionario tenía el propósito de que los profesores realizaran una valoración del nivel de confianza sobre su conocimiento acerca de diversos conceptos estadísticos elementales. La evaluación consistió en seleccionar un valor en una escala de 1 a 5, donde 1 significa conocimiento bajo o nulo y 5 significa conocimiento altamente satisfactorio. Los resultados obtenidos se muestran en la Tabla 1:

Tabla 1.

Nivel de confianza de los profesores sobre conceptos estadísticos elementales

Tópicos estadísticos	1	2	3	4	5	χ~	S
1. Media	0	0	4	6	21	4.45	0.72
2. Mediana	0	0	5	9	17	4.39	0.76
3. Moda	1	1	0	6	23	4.60	0.92
4. Desviación estándar	0	1	5	11	14	4.23	0.84
5. Histograma	0	1	2	8	20	4.52	0.77
6. Gráfica de barras	0	0	2	8	21	4.61	0.61
7. Gráfica de caja	9	9	5	4	4	2.52	1.39
8. Diagrama de tallo y hojas	9	8	7	6	1	2.42	1.20
9. Cuartiles	10	8	8	3	2	2.32	1.22
10. Correlación y regresión	8	7	6	7	3	2.68	1.35

Las mejores puntuaciones corresponden a conceptos básicos y tradicionales de un curso de estadística descriptiva (media, mediana, moda, desviación estándar, histograma y gráfico de barras), lo cual indica que los profesores se sienten capaces de desempeñarse bien en estos temas. En contraste, conceptos como las gráficas de caja, diagramas de tallo y hojas, cuartiles, regresión y correlación, tienen puntuaciones muy bajas, con medias de entre 2.32 y 2.68. Estos conceptos han sido incorporados en tiempos recientes al currículo de estadística del bachillerato; son de suma importancia para implementar un enfoque exploratorio de datos que permita ir más allá de la simple descripción, como se sugiere actualmente en la enseñanza de la estadística.

Nivel de razonamiento estadístico y comprensión mostrada por los profesores

En la Tabla 2 se presenta el propósito de cada uno de los ítems del cuestionario y el porcentaje de respuestas correctas que obtuvieron los profesores. De la pregunta 1 a la 21 corresponden de forma íntegra al cuestionario CAOS;² de la pregunta 22 a la 33 corresponden a las preguntas que fueron tomadas del trabajo de Makar (2004) para complementar la investigación. Las preguntas 34 y 35 son preguntas abiertas, por lo que serán analizadas en forma cualitativa.

Tabla 2.

Propósitos y resultados del cuestionario respondido por los 31 profesores

Pregunta	Resultado de aprendizaje medido	Respuestas correctas	Porcentaje de respuestas correctas
1	Habilidad para describir e interpretar la distribución de una variable mediante un histograma, incluyendo referencias al contexto de los datos.	17	54.8
2	Habilidad para reconocer dos representaciones gráficas diferentes del mismo conjunto de datos (gráfica de caja e histograma).	9	29.0
3	Habilidad para visualizar y relacionar un histograma con la descripción de una variable (distribución sesgada negativamente).	8	25.8
4	Habilidad para visualizar y relacionar un histograma con la descripción de una variable (distribución con forma acampanada).	6	19.4
5	Habilidad para visualizar y relacionar un histograma con la descripción de una variable (distribución uniforme).	11	35.5
6	Comprender que un conjunto de datos cuantitativos se puede expresar gráficamente mediante un histograma con los datos en el eje horizontal y las frecuencias en el eje vertical.	3	9.7
7	Comprender el propósito de aleatoriedad en un experimento.	1	3.2
8	Habilidad para determinar cuál de dos gráficas de caja posee una mayor desviación estándar.	10	32.3
9	Comprender que las gráficas de caja no permiten estimar porcentajes de datos arriba o debajo de algún valor, excepto para los cuartiles.	6	19.4
10	Comprender la interpretación de una mediana en el contexto de gráficas de caja.	8	25.8
11	Habilidad para comparar grupos considerando los promedios y la variabilidad de las distribuciones.	19	61.3
12	Habilidad para comparar grupos considerando los promedios y la variabilidad de las distribuciones.	25	80.6
13	Comprender que comparación de grupos no requiere tamaños de muestras iguales en cada grupo, especialmente si ambos conjuntos de datos son grandes.	21	67.7
14	Habilidad para estimar y comparar correctamente desviaciones estándar para diferentes histogramas. Comprender que desviaciones estándar menores podrían ser para un gráfico con la menor dispersión (típicamente) lejos del centro.	9	29.0
15	Habilidad para estimar correctamente desviaciones estándar para diferentes histogramas. Comprender que desviaciones estándar altas podrían ser para un gráfico con la mayor dispersión (típicamente) lejos del centro.	11	35.5
16	Comprender que estadísticos de muestras pequeñas varían más que estadísticos de muestras grandes.	3	9.7
17	Comprender patrones esperados en variabilidad muestral.	6	19.4
18	Comprender el significado de variabilidad en el contexto de medidas repetidas y en el contexto donde se desea que la variabilidad sea pequeña.	26	83.8
19	Habilidad para relacionar un gráfico de dispersión con una descripción verbal de una relación bivariada.	27	87.7
20	Comprender que una distribución con la mediana más grande es más probable que esté sesgada a la izquierda.	15	48.4
21	Comprender los factores que permiten que una muestra de datos sea generalizada a la población.	19	61.3
22	Habilidad para identificar qué se representa en el eje horizontal de un histograma.	28	90.3
23	Habilidad para identificar qué se representa en el eje vertical de un histograma.	28	90.3
24	Habilidad para hacer uso correcto de la información sobre frecuencias proporcionadas por el histograma y para leer dentro de los datos, a partir de un valor dado.	21	67.7
25	Habilidad para hacer uso correcto de la información sobre frecuencias proporcionadas por el histograma y para leer dentro de los datos.	21	67.7
26	Habilidad para estimar la proporción de un resultado a partir de un histograma.	21	67.7
27	Habilidad para estimar el valor de la mediana a partir de un histograma.	9	29.0
28	Habilidad para estimar el valor de la media a partir de un histograma.	7	22.6
29	Comprender que la variabilidad de un histograma no depende de la irregularidad en la altura de sus barras, sino de la distancia de los datos respecto del centro.	4	12.9
30	Habilidad para identificar si una distribución está sesgada a la izquierda o a la derecha.	5	16.1
31	Comprender las propiedades de las medias y medianas en distribuciones sesgadas.	16	51.6
32	Comprender las propiedades de las medias y medianas en distribuciones sesgadas, y aplicarlas para estimar la proporción de datos que están antes y después de la media.	11	35.5
33	Habilidad para identificar cuál medida del centro y dispersión podrían ser más apropiadas para una distribución que exhibe valores atípicos.	2	6.5

Ítems con alto porcentaje de respuestas correctas

Los resultados de la Tabla 2 indican que 11 de las 33 preguntas fueron contestadas correctamente por más de 60 por ciento de los profesores. Cabe destacar que dentro de estas preguntas se encuentran la 11, 12, 13 y 18, las cuales evalúan la comprensión sobre comparación de grupos de datos; las preguntas 11, 12 y 13 evalúan el razonamiento distribucional para hacer comparaciones entre grupos; y la pregunta 18 mide la comprensión del significado de variabilidad en el contexto de medidas repetidas. Por tanto, y teniendo como base los propósitos del cuestionario CAOS, se podría concluir que los profesores participantes en el estudio tienen buenas intuiciones informales y comprensión acerca de cómo comparar grupos de datos. En el estudio de Delmas et al. (2007) —un referente importante para este estudio— estas preguntas también fueron contestadas correctamente por un porcentaje alto de estudiantes, por lo que estos autores llegaron a la misma conclusión.

Respecto de la pregunta 19, que evalúa la habilidad para relacionar un diagrama de dispersión con una descripción verbal que involucra el coeficiente de correlación, la gráfica fue leída correctamente por 87.1 por ciento de los profesores participantes en este estudio. Este alto porcentaje en un ítem que trata de correlación y regresión puede deberse a que los profesores tienen mucha experiencia con gráficos en el plano cartesiano. En el estudio de Delmas et al. (2007), este ítem fue contestado por 90.5 por ciento de los estudiantes y fue el que obtuvo el porcentaje más alto de respuestas correctas. La pregunta 21, que mide la comprensión de los factores que permiten que una muestra de datos sea generalizable a la población, tuvo 61.3 por ciento de respuestas correctas. Delmas et al. (2007) reportan en su estudio que sólo 26 por ciento de sus estudiantes contestaron correctamente esta pregunta.

Las otras preguntas de alto desempeño son la 22, 23, 24, 25 y 26. Estas preguntas fueron tomadas de un estudio de Makar (2004). Con ellas nos propusimos evaluar la interpretación simple y la lectura de elementos que aparecen en un histograma; específicamente los profesores debían identificar la información que es representada en cada eje y hacer uso correcto de la información sobre frecuencias proporcionada por el histograma. En el caso de los sujetos de estudio de Makar (2004), estas mismas preguntas también estuvieron dentro de las de mejor desempeño, el cual osciló entre 71 y 100 por ciento. Con respecto a la pregunta 26 nos propusimos evaluar la habilidad para leer dentro de los datos y determinar la proporción de datos que caen debajo de un cierto valor. La pregunta fue contestada correctamente por 67.7 por ciento de los profesores.

Preguntas con bajo porcentaje de respuestas correctas

En este grupo de preguntas se ubicaron 15 de las 33 preguntas del cuestionario, las cuales fueron contestadas por menos de 30 por ciento de los profesores. De estas preguntas, nueve tienen que ver con conceptos estadísticos tradicionales (histogramas, distribuciones, media, mediana y desviación estándar), tres corresponden a gráficas de caja, una evalúa la comprensión de la aleatoriedad, y dos evalúan la comprensión de la variación muestral. Los resultados de estas preguntas nos indican que los profesores podrían estar subestimando la complejidad de los conceptos involucrados en estos ítems, dado que al principio habían señalado que se sentían competentes para explicar a sus alumnos varios de estos conceptos.

Análisis de los ítems abiertos

Los dos ítems abiertos que se consideraron en el cuestionario tenían el propósito de evaluar a mayor nivel de profundidad los significados que tenía para los profesores la comparación de dos distribuciones. La razón de elegir este tema reside en que en él confluyen varios conceptos estadísticos, como la tendencia central, la variabilidad, datos extremos y la forma de una distribución. Analizamos las respuestas que los profesores dieron a los dos ítems y las categorizamos en los niveles del modelo SOLO que se describieron en la metodología.

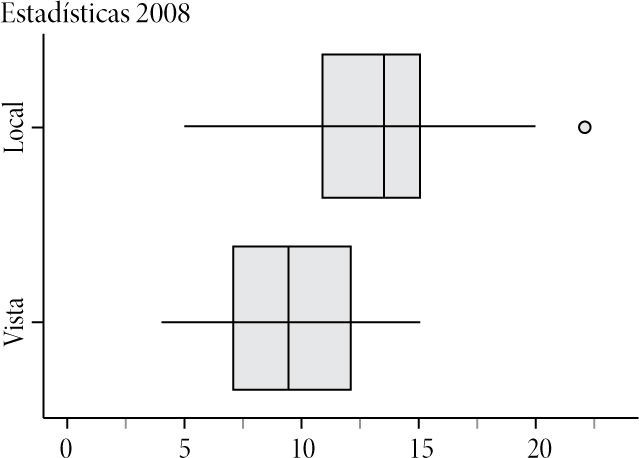
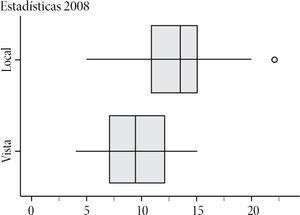
Pregunta 34

Observa los siguientes diagramas de caja. Ellos muestran los puntos ganados, tanto de local como de visita, por todos los equipos de fútbol profesional en el torneo de apertura 2008. ¿Piensas que hay diferencia en los puntos ganados para las dos situaciones descritas? Explica tu respuesta.

Para responder la pregunta planteada se requiere realizar un proceso de descripción/ comparación. Los descriptores y los resultados se muestran en la Tabla 3:

Tabla 3.

Niveles, descriptores y resultados para el proceso descripción/comparación

Descripción/comparación Aspectos clave: centro, dispersión, forma, desfase y traslape, casos individuales		Número de profesores
Nivel	Características del nivel
Preestructural (P)	No se refiere a aspectos clave para hacer descripciones o comparaciones de las distribuciones.	18 (58%)
Uniestructural (U)	Describe y compara las distribuciones enfocando un solo aspecto clave de razonamiento (centro, dispersión, forma, desfase/traslape, casos individuales).	8 (25.8%)
Multiestructural (M)	Describe y compara las distribuciones enfocando en más de un aspecto clave de razonamiento, pero sin integrarlos.	5 (16.2%)
Relacional (R)	Describe y compara las distribuciones estableciendo conexiones relacionales entre varios aspectos clave de razonamiento.	0 (0%)

Algunas respuestas que dieron los profesores en cada nivel se muestran a continuación.

• •

  Nivel preestructural:

  

• •

  Nivel uniestructural:

  

• •

  Nivel multiestructural:

  

Los profesores tuvieron diversas dificultades para razonar adecuadamente al comparar las dos distribuciones mediante los diagramas de caja, como resultado del desconocimiento que tenían de esta representación gráfica. De esta manera, más de la mitad (58 por ciento) se ubicaron en el nivel inferior del modelo SOLO. Además, los aspectos clave (promedios, forma, dispersión, traslape de distribuciones) en los que se apoyaron para realizar la comparación fueron insuficientes y no siempre fueron los más adecuados. Resolver correctamente este ítem requería tener en cuenta la mediana, de manera conjunta, como centro de cada distribución; la variabilidad, los datos atípicos y la forma de la distribución.

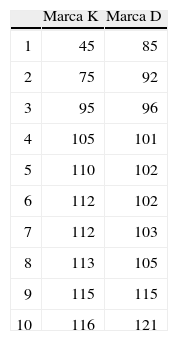
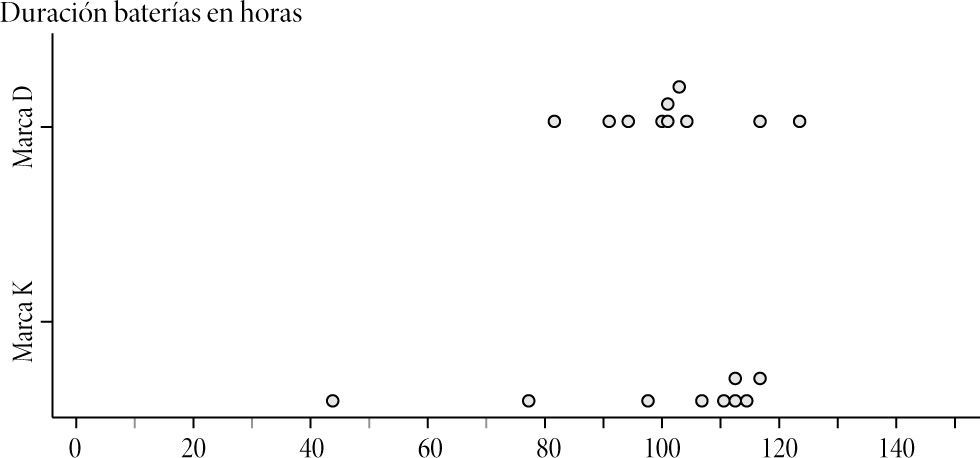
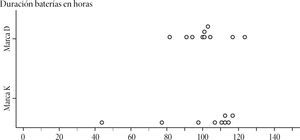
Pregunta 35

Suponga que tiene que hacer un reporte a la revista del consumidor sobre la calidad de dos marcas de baterías. Para ello se le proporcionan los dos conjuntos de datos siguientes, sobre la vida útil de 10 baterías de cada una de las marcas. Argumente con términos estadísticos la calidad de las dos marcas de baterías y cuál recomendaría.

Duración baterías en horas

	Marca K	Marca D
1	45	85
2	75	92
3	95	96
4	105	101
5	110	102
6	112	102
7	112	103
8	113	105
9	115	115
10	116	121

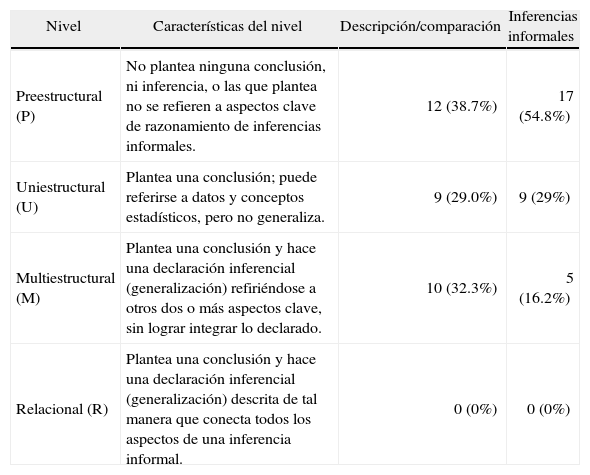
Para responder la pregunta planteada se requiere realizar un proceso informal de inferencia a través de una descripción y comparación de las distribuciones. Por tanto, en estas respuestas podremos evaluar tanto el proceso de descripción/comparación, como el de inferencias informales, descrito anteriormente. Los resultados se muestran en la Tabla 4.

Tabla 4.

Niveles y descriptores para el proceso de inferencias informales

Inferencias informales Aspectos clave: generalización, evidencias, conceptos estadísticos, lenguaje probabilístico, conceptos muestrales, explicación/contexto

Nivel	Características del nivel	Descripción/comparación	Inferencias informales
Preestructural (P)	No plantea ninguna conclusión, ni inferencia, o las que plantea no se refieren a aspectos clave de razonamiento de inferencias informales.	12 (38.7%)	17 (54.8%)
Uniestructural (U)	Plantea una conclusión; puede referirse a datos y conceptos estadísticos, pero no generaliza.	9 (29.0%)	9 (29%)
Multiestructural (M)	Plantea una conclusión y hace una declaración inferencial (generalización) refiriéndose a otros dos o más aspectos clave, sin lograr integrar lo declarado.	10 (32.3%)	5 (16.2%)
Relacional (R)	Plantea una conclusión y hace una declaración inferencial (generalización) descrita de tal manera que conecta todos los aspectos de una inferencia informal.	0 (0%)	0 (0%)

Los resultados nos muestran que los profesores tuvieron un mejor desempeño en este ítem que en el anterior, que contemplaba diagramas de cajas. De esta manera, en el aspecto de descripción y comparación, 10 profesores se ubicaron en el nivel multiestructural, y el resto en los niveles preestructural y uniestructural. En el aspecto de inferencias informales, sólo cinco profesores alcanzaron el nivel multiestructural. Un análisis de los conceptos clave utilizados para realizar las comparaciones muestra en primer lugar a la media aritmética, seguida de los valores máximos y mínimos y de un lenguaje informal de dispersión. Algunas respuestas que dieron los profesores en cada nivel se muestran a continuación:

• •

  Nivel preestructural

  

• •

  Nivel uniestructural

  

• •

  Nivel multiestructural

  

Conclusiones

Los resultados del estudio muestran algunas similitudes con resultados de otras investigaciones donde se han observado dificultades por parte de profesores —o futuros profesores— para razonar adecuadamente con conceptos estadísticos, lo que pone en evidencia que la comprensión de conceptos estadísticos y su razonamiento no son procesos triviales, y que para su desarrollo se requiere poner en juego competencias de mayor nivel cognitivo que agrupar datos, construir gráficas y utilizar fórmulas y procedimientos para resumir datos y obtener resultados, como era característico en el enfoque tradicional de enseñanza de la estadística. Como señala Garfield (2003), el razonamiento implica dar sentido profundo a la información estadística, interpretar adecuadamente los datos y sus diversas representaciones, conectar y relacionar un concepto con otro y combinar ideas sobre datos y azar. En este contexto, los profesores mostraron una comprensión superficial y aislada sobre conceptos estadísticos que son centrales en los nuevos planes de estudio, incluso sobre conceptos que han formado parte del enfoque tradicional de estadística descriptiva, como es el caso de la interpretación de los histogramas, medidas de tendencia central y medidas de variabilidad.

Aun cuando los profesores mostraron mucha confianza en su conocimiento sobre temas tradicionales del currículo de estadística, en los ítems que requerían mostrar razonamiento y comprensión acerca de ellos se identificaron diversas dificultades de interpretación, por lo que se asume que tienen una visión procedimental de dichos conceptos y además subestiman su complejidad. Por ejemplo, en el caso particular de las gráficas, no tuvieron dificultades para leer la información de histogramas, pero sí para visualizar y relacionar un histograma con la descripción de una variable, para estimar el valor de la mediana y de la media a partir de un histograma, y para relacionar la información de un histograma con una gráfica de caja. A su vez, aproximadamente una tercera parte de los profesores mostraron buena comprensión de la desviación estándar, aunque tuvieron dificultad para identificar correctamente la variabilidad en un histograma.

El reconocimiento de los mismos profesores sobre la poca confianza que tenían en su conocimiento sobre conceptos como diagramas de caja, diagramas de tallo y hojas, cuartiles, correlación y regresión, se evidenció en el cuestionario, al ser estos ítems los de más bajo porcentaje de respuestas correctas. Estos conceptos hasta hace poco tiempo no estaban en los planes de estudio del bachillerato y son de mucha importancia para un análisis estadístico de mayor profundidad, como se sugiere en los enfoques actuales de enseñanza.

La comparación de distribuciones de datos constituyó una actividad compleja para los profesores, pues era necesario utilizar y relacionar varios conceptos de forma simultánea para responder adecuadamente a la situación planteada. Los profesores mostraron poco conocimiento sobre la naturaleza implícita en una descripción y comparación de distribuciones, ya que entre diversos conceptos clave que podían utilizar para responder las situaciones planteadas, en muchos casos utilizaron uno o ninguno; destacan la media, el rango y datos atípicos. Como resultado de ello, la mayoría de los profesores se ubicaron en los dos niveles inferiores del modelo taxonómico SOLO.

Aun cuando la muestra de profesores participantes es reducida, los resultados muestran que los profesores en estas condiciones tendrían muchas dificultades para implementar los nuevos enfoques que se exigen en los nuevos planes de estudio. Se requiere profundizar la investigación en muestras más grandes de profesores con mayor experiencia en la enseñanza de la estadística.

Finalmente, es importante señalar que la estadística tiene un doble rol en el currículo de bachillerato: como herramienta metodológica que sirve de apoyo en procesos de investigación que requieren recolección y procesamiento de datos, y como herramienta que permite interpretar adecuadamente información cuantitativa a la que estamos expuestos diariamente en la vida cotidiana; esto es, como elemento que proporciona cultura y razonamiento estadístico. Ante estas exigencias, es grande el desafío que enfrentamos los profesores de estadística, pues esta disciplina, por un lado —al menos en nuestro país— no ha logrado aún el estatus que tienen otras materias, como el álgebra y el cálculo. El cambio en la enseñanza de la estadística en las escuelas dependerá en buena medida de que los profesores estén convencidos de que ésta es una de las disciplinas más útiles para sus estudiantes, y en la medida en la cual estén adecuadamente preparados para enseñarla en su nivel respectivo.