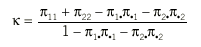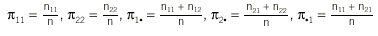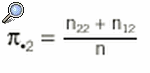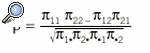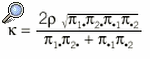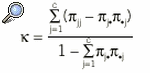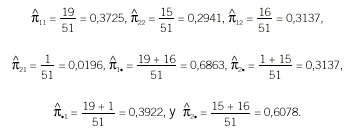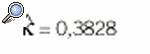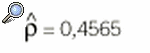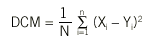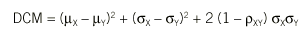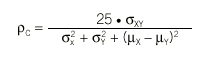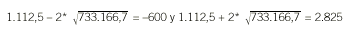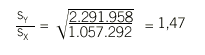Introducción
Garantizar la calidad de los procedimientos de medida es un aspecto fundamental en la investigación biomédica y, en general, en la práctica clínica. Aunque todo el mundo respondería afirmativamente a la pregunta de si la calidad de los datos es un aspecto que debe considerarse siempre, al menos eso nos gusta creer, en realidad es muy común asumir que los procedimientos de medida funcionan razonablemente bien (alguien se debe estar ocupando de ello) y, por tanto, no hay de qué preocuparse. En ámbitos regulados, como es el caso de los ensayos clínicos para el desarrollo de fármacos, la calidad de los datos en general y la de los procedimientos de medida en particular reciben la merecida atención tanto por razones éticas como de eficiencia.
También en la práctica médica la calidad de las medidas es un aspecto básico para conseguir un sistema de salud eficiente. Cuando un médico establece el diagnóstico de un paciente basándose en el resultado obtenido mediante un instrumento de medida, debería estar seguro de que el error de medida es razonablemente pequeño. Las medidas pueden obtenerse a través de algún instrumento cuyos resultados ayuden al profesional en la toma de decisiones (como los resultados analíticos), o mediante observación directa del paciente y evaluación subjetiva por parte del médico (como la puntuación APGAR). Por lo tanto, un método de medida puede ser tanto un instrumento como un evaluador o incluso la combinación de ambos.
Hablar de calidad de los procedimientos de medida equivale a referirse a la magnitud de los errores de medida inherentes al procedimiento, entendiéndose que a mayor calidad de medida menor magnitud de los errores y viceversa. Simplificando, podemos afirmar que existen dos tipos de error de medida: sistemático y aleatorio. El error sistemático es el que se presenta siempre de la misma forma, «sistemáticamente». Por ejemplo, si 5 personas cuyos pesos reales son 49, 63, 78, 81 y 94 kg se pesan con una báscula obteniendo las lecturas 51, 65, 80, 83 y 96 kg, la báscula estaría afectada de error sistemático. En este caso se trataría de un error sistemático constante de +2 kg. En otros casos, el error sistemático puede ser proporcional al valor real (p. ej., errores de +1%, en cuyo caso el valor observado = valor real * 1,01) y también es posible que se den ambos tipos, constante y proporcional, simultáneamente (p. ej., valor observado = valor real *1,01 + 2). A diferencia de lo que ocurre con los errores sistemáticos, los errores aleatorios son impredecibles. Aunque a la larga puedan seguir un patrón conocido, no es posible predecir en qué medida (ni en qué sentido) ocurrirán en una observación concreta.
La presencia de error en las medidas provoca numerosos problemas1, entre los que cabe destacar los errores de clasificación y la atenuación de las asociaciones. Veamos un ejemplo para ilustrar estos 2 problemas. El estudio de las características de las pruebas diagnósticas es un territorio en el que la importancia de los errores de clasificación se pone especialmente de manifiesto. Lo que habitualmente denominamos error de una prueba diagnóstica no es más que un caso particular de error de medida: el estado real del sujeto, si tiene o no la enfermedad sospechada, es la característica que deseamos conocer (medir) y la prueba diagnóstica es el procedimiento de medida que vamos a utilizar. El resultado que obtenemos de aplicar esta prueba diagnóstica es la medida del estado real del sujeto. Imaginemos que en un conjunto de 1.000 individuos se valora la presencia de cierta enfermedad mediante una prueba diagnóstica cuyo resultado es dicotómico (positivo o negativo) y que 100 de estos individuos tienen realmente la enfermedad y los 900 restantes están libres de ella. Por último, supongamos que, como es habitual, el método de diagnóstico está sujeto a error y que la tasa de falsos negativos es del 10% y la de falsos positivos del 20%. Tal como se ilustra en la tabla 1, esto supondría que, de los 100 individuos patológicos, 10 se clasificarían incorrectamente como no patológicos, mientras que de los 900 no patológicos, 180 se considerarían patológicos. Por lo tanto, utilizando el resultado de la prueba diagnóstica como medida del estado real, se consideraría que el número de sujetos patológicos es de 270 en lugar de 100.
Veamos ahora un ejemplo donde el error de medida, en este caso error de diagnóstico o clasificación, induce una atenuación en la asociación con otra variable. Deseamos estudiar la asociación entre la enfermedad y un cierto factor de riesgo. Supongamos ahora que la proporción de enfermos que presentan el factor de riesgo es del 20%, mientras que esta proporción es de sólo el 5% en el grupo no patológico. De igual modo que en el ejemplo anterior, asumiremos que las proporciones se cumplen perfectamente. En primer lugar, estimaremos la asociación utilizando una prueba diagnóstica libre de error y, posteriormente, utilizando la prueba diagnóstica con error de clasificación, comparando los resultados obtenidos en ambas situaciones.
Si se utiliza una prueba libre de error para clasificar a los individuos se observarán 100 individuos con la enfermedad y 900 libre de ella. Si a este número de individuos se le aplica las proporciones relacionadas con el factor de riesgo, se obtendrán las frecuencias representadas en la tabla 2. La asociación entre la enfermedad y el factor de riesgo se medirá mediante la odds ratio (OR); OR = (20 *855)/(45 *80) = 4,75.
Hacemos notar al lector que en esta tabla está implícito el hecho de que estamos midiendo 2 variables: enfermedad y factor de riesgo. Para simplificar el ejemplo asumiremos que el factor de riesgo es una característica que podemos medir sin error.
Ahora repitamos el ejemplo utilizando la prueba diagnóstica con error de clasificación. De los 270 individuos del grupo patológico 90 tienen realmente la enfermedad, mientras que 180 están libres de ella (tabla 1). De esos 90, un 20% presentará el factor de riesgo, es decir, 18. En cambio, de los 180 sólo un 5% tendrá el factor de riesgo, es decir, 9 individuos. Esto supone que de los 270 individuos clasificados como patológicos, un total de 18 + 9 = 27 presenta el factor de riesgo. ¿Qué ocurre con los 730 individuos clasificados como no patológicos? De éstos, 10 tienen la enfermedad, mientras que 720 no (tabla 1). De los 10, un 20% presentará el factor de riesgo, es decir, 2 individuos. De los restantes 720, un 5% tendrá el factor de riesgo, lo que supone 36 sujetos. De este modo, en el grupo de los clasificados como no patológicos, un total de 2 + 36 = 38 individuos presentará el factor de riesgo. Este proceso se resume en la tabla 3.
Ahora la OR adquiere un valor de OR = (27 * 692)/(38 * 243) = 2,02, aproximadamente la mitad del valor obtenido anteriormente, lo que significa que se ha producido una considerable atenuación de la verdadera asociación, subestimación enteramente provocada por el error de medida de la prueba diagnóstica.
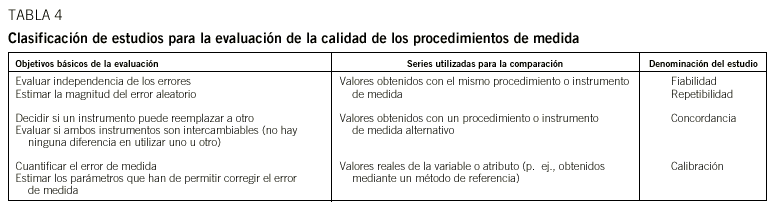
De los resultados mostrados en estos ejemplos se deduce la necesidad de valorar la calidad de cualquier método o procedimiento de medida que utilicemos. Evaluar la calidad del procedimiento o instrumento de medida conlleva analizar comparativamente nuestra serie de mediciones con otras, que pueden ser de distinto origen y características dependiendo de los objetivos planteados en la valoración, tal y como se resume en la tabla 4.
Cualquier comparación entre 2 (o más) series de mediciones es susceptible de ser evaluada en términos de concordancia entre las series, esto es, verificar si ambas concuerdan (son idéntica) o no y en qué grado, aunque el uso de esta denominación indica habitualmente que se están analizando comparativamente 2 instrumentos de medida distintos. En cualquier caso, parece obvio que cuanto menor sea el error de medida en ambas series mayor será la concordancia y viceversa. En el caso extremo y poco realista de 2 series sin error de medida, su concordancia será forzosamente perfecta.
Retomando el esquema de la tabla 4, los estudios de fiabilidad o repetibilidad intentan evaluar cómo concuerdan las medidas obtenidas por un único método o instrumento utilizado de forma repetida. Por ejemplo, podríamos utilizar varias veces un mismo analizador automático para contar el número de CD4, procesando alícuotas de la misma muestra de sangre o podríamos pedir a un mismo médico que evaluase una misma imagen en varias ocasiones. En estos casos, el aspecto que se estaría evaluando es el error de medida del método mediante el estudio de la concordancia intramétodo, de forma que, si las medidas tomadas con el mismo método concuerdan, se puede declarar al método libre de error aleatorio calificándolo de «repetible». En los denominados estudios de concordancia se verifica cómo concuerdan las medidas obtenidas por el método cuya calidad se desea valorar, con las obtenidas por otro método. Por ejemplo, podríamos utilizar 2 analizadores automáticos distintos para contar el número de CD4 de una muestra o podríamos pedir a 2 clínicos que valorasen una misma imagen. En estos casos estaríamos evaluando la concordancia entre métodos de medida, con el objetivo de determinar si los 2 métodos son intercambiables, de forma que sea indiferente utilizar uno u otro. Por último, la calibración de un método de medida es un caso particular de concordancia entre métodos. Este ensayo se realiza cuando se compara un procedimiento de medida con los valores reales de los sujetos. De hecho, el valor real es imposible de determinar y en estos ensayos se comparan 2 métodos de medida, uno de ellos utilizado como método de referencia o patrón (gold standard) para lo que se asume que está libre de error de medida. En este caso, la comparación del método en estudio con el patrón permite estimar los posibles errores, sistemático y aleatorio, del primero. Una vez estimados, cualquier lectura futura obtenida con el método en estudio puede corregirse y quedar exenta de error sistemático. Este ejercicio se conoce como calibración de un método de medida. Lamentablemente, la naturaleza impredecible de los errores aleatorios hace que sea imposible corregirlos, tal como se hace con los errores sistemáticos. Puesto que los errores sistemáticos tienen arreglo (calibrando) y los aleatorios no, ambos tipos de error no son igualmente temibles.
En cualquier caso, la presencia de errores en las medidas es la responsable de que no exista concordancia perfecta entre distintos instrumentos o procedimientos de medida. De hecho, cuanto más error, menos concordancia y viceversa. Así, estudiar la concordancia es una manera de evaluar el error de medida y por ello nos centraremos en ofrecer al lector una panorámica de los métodos más habituales para su estudio.
En general, las técnicas para evaluar la concordancia se pueden clasificar en agregadas y desagregadas. Los procedimientos desagregados evalúan los distintos componentes de la falta de concordancia por separado, mientras los procedimientos agregados valoran la falta de concordancia en global, sin distinguir entre error sistemático y aleatorio. Una medida agregada será útil para una evaluación rápida del grado de concordancia sin entrar en las fuentes de error que causan la falta de concordancia. En cambio, un análisis desagregado analizará más detalladamente las posibles fuentes de error.
Las técnicas utilizadas también variarán según la naturaleza de las variables, dependiendo de si las medidas corresponden a una escala de medida cualitativa o cuantitativa.
Concordancia entre variables cualitativas
Supongamos que un médico realiza habitualmente una clasificación diagnóstica (positiva o negativa) basándose en su particular apreciación de las características de una imagen radiológica. Independientemente de cómo llega a realizar la valoración, el método de medida es el propio médico que estaría realizando medidas en escala nominal (dicotómica). En esta situación podría ser interesante valorar tanto el error de medida del médico (concordancia intramétodo) como la discrepancia en el diagnóstico en relación con otro profesional (concordancia entre métodos). En ambos casos el procedimiento será similar, ya que la primera situación es equivalente a realizar una concordancia entre diferentes mediciones efectuadas con un único método. Veamos la situación en el caso de desear estimar la concordancia entre 2 métodos.
Los datos obtenidos de n pacientes pueden resumirse en una tabla de contingencia 2 * 2 (tabla 5). En principio parece lógico que la concordancia se evalúe mediante la proporción de casos en que los 2 evaluadores coinciden, (n11 + n22)/n, pero se ha de tener en cuenta que parte de esta coincidencia es exclusivamente atribuible al azar. Cohen2 dio la expresión de un índice de concordancia corregido por el efecto del azar y reescalado de forma que tomase un valor máximo de 1. Este índice se conoce como el coeficiente kappa y su expresión es:
donde
y
En caso de concordancia perfecta, el coeficiente tomará el valor 1, y si las valoraciones de los 2 métodos de medida son independientes, el coeficiente será 0.
Como puede observarse, el coeficiente kappa es un procedimiento agregado, ya que mide la concordancia de forma global, sin distinguir entre los componentes de exactitud y precisión.
Si se desea evaluar la concordancia de forma desagregada en error sistemático y error aleatorio, el coeficiente de correlación3 se ha propuesto para medir la asociación (error aleatorio) entre los 2 evaluadores. La expresión del coeficiente de correlación para la tabla 2 *2 es:
donde un valor de 1 indicaría ausencia de error aleatorio. También se ha propuesto3 analizar el error sistemático entre los 2 métodos mediante el estudio de la diferencia entre las proporciones marginales ¼1·, ¼2·, ¼·1, ¼·2. Estas proporciones indican la probabilidad de cada método de realizar un diagnóstico positivo o negativo, considerándose que no existe error sistemático entre evaluadores si ¼1· = ¼·1 y ¼2· = ¼·2. En el caso de una tabla 2 * 2, estas proporciones pueden compararse utilizando una prueba de McNemar4.
Se ha demostrado5 que el coeficiente kappa puede expresarse como:
donde puede observarse que si no existe error sistemático entre observadores, ¼1· = ¼·1 y ¼2· = ¼·2, el coeficiente kappa coincide con *, es decir, la única causa de discordancia es el error aleatorio.
El coeficiente kappa puede ser generalizado para el caso en que la escala de medida tenga más de 2 categorías. En tal caso, la expresión del coeficiente para una escala de medida nominal de c categorías es:
La escala de medida también puede ser ordinal, por ejemplo, una valoración de la evolución de un paciente en la escala «empeora, sigue igual, mejora». En esta situación, es lógico pensar que no debe valorarse igual una discordancia «sigue igual frente a mejora» que una discordancia «empeora frente a mejora», ya que en este último caso la discordancia es más grave. Con el objetivo de tener en cuenta esta gradación de la discordancia se introdujo el coeficiente kappa ponderado6, de forma que se asignan distintos pesos a la discordancias de acuerdo con su magnitud. Por último, se ha demostrado que el coeficiente kappa tiene una gran dependencia de la prevalencia de la enfermedad o característica que se está evaluando, por lo que se ha considerado que no es apropiado comparar coeficientes kappa que se han calculado en poblaciones con distinta prevalencia de la característica en estudio7.
Ejemplo: Se aplican 2 pruebas diagnósticas a un grupo de 51 pacientes cuyos resultados se resumen en la tabla 6. Las estimaciones de las proporciones son:
El coeficiente kappa resultante es:
y su intervalo de confianza del 95% es [0,1292-0,6464]8. El valor del coeficiente es bastante bajo e indica una concordancia débil entre las 2 pruebas.
Si se desea realizar un análisis desagregado, en primer lugar se calcula el coeficiente de correlación:
que indica una asociación débil entre los valores obtenidos con una y otra prueba. Si se comparan las proporciones marginales de las discrepancias mediante una prueba de McNemar se demuestra que son distintas (p < 0,001): la prueba A tiende a dar resultados positivos con mayor frecuencia que la prueba B. Por lo tanto, en este caso la discordancia se debe tanto a error sistemático como a error aleatorio.
Concordancia entre variables cuantitativas
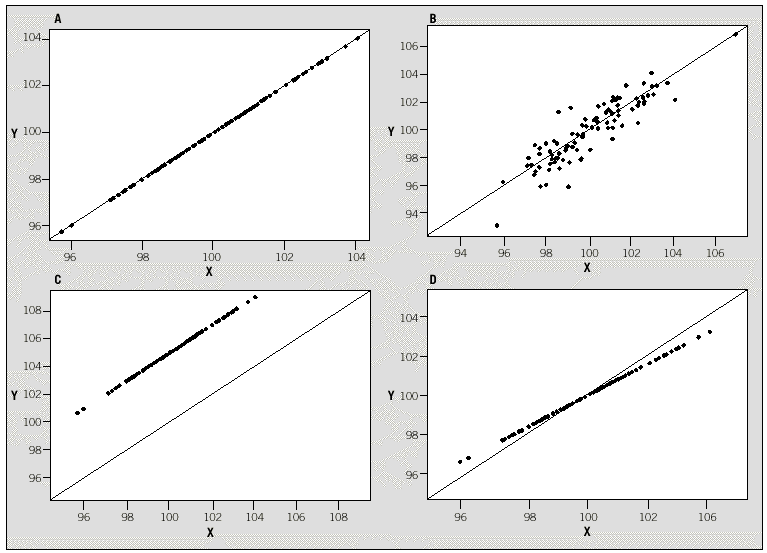
Supongamos que una característica cuantitativa se mide mediante 2 métodos, X e Y, en una serie de N individuos. Una primera aproximación exploratoria sería representar gráficamente los 2 métodos mediante un diagrama de dispersión, donde cada punto representa la pareja de medidas obtenida de cada individuo. Si la concordancia fuera perfecta, todos los puntos se situarían sobre la bisectriz (Y = X), tal como se muestra en la figura 1. En esta situación es fácil ver que la asignación del procedimiento X al eje de abscisas y el de Y al eje de ordenadas es absolutamente arbitraria: se obtendría la misma imagen gráfica en caso de invertir la asignación de los ejes. Observando este gráfico (fig. 1a) es fácil intuir que una medida útil de discordancia podría basarse en la distancia de cada punto a la bisectriz. Se puede demostrar que la media de estas distancias es proporcional a la desviación cuadrática media
Esta medida puede expresarse en función de las medias y las varianzas de los resultados obtenidos con cada método y la correlación entre ambos, del siguiente modo:
donde µX y µY representan las medias de cada método, *X y *Y las desviaciones típicas y *XY el coeficiente de correlación de Pearson.
La concordancia será perfecta cuando DCM = 0, situación que se dará si y sólo si los 3 términos son iguales a cero. Esto implica que haya igualdad de medias (ausencia de error sistemático constante y proporcional), µX = µY , igualdad de desviaciones típicas (ausencia de error sistemático proporcional), *X = *Y, y que la correlación sea perfecta (ausencia de error aleatorio), *XY = 1. Llegados a este punto, es fácil darse cuenta de que la comparación de medias o el cálculo del coeficiente de correlación de Pearson son insuficientes para el estudio de la concordancia. La igualdad de medias tan sólo garantiza que los 2 métodos se centran en el mismo valor, pero en ningún caso que todos sus valores sean iguales. Las figuras 1b y 1d representan situaciones en que hay igualdad de medias, pero los valores no concuerdan. Del mismo modo, un coeficiente de correlación de 1 indica una relación lineal perfecta, es decir, la relación entre los 2 métodos es una recta carente de error aleatorio, pero esta recta no tiene por qué ser la bisectriz (figs. 1c y 1d) y, por tanto, una correlación perfecta no es sinónimo de concordancia perfecta. Además, la diferencia de varianzas ha resultado ser también un componente de la concordancia, y por tanto también debe evaluarse.
Fig. 1. Ejemplos de gráficos de dispersión de las mediciones realizadas por 2 instrumentos de medida.
Existen diferentes procedimientos para determinar la concordancia entre medidas cuantitativas. Entre ellos hemos querido destacar en este artículo el coeficiente de concordancia9 y el método Bland-Altman10, pero existen otros procedimientos ampliamente utilizados, como el coeficiente de correlación intraclase1, estrechamente relacionado con el coeficiente de concordancia, y el modelo de ecuación estructural11. Este último merece una mención especial, ya que es habitual analizar la concordancia entre 2 métodos mediante el ajuste de un modelo de regresión simple Y = * + ßX por el método de mínimos cuadrados, basado en la suposición de que X está libre de error. En general, esta suposición no es razonable y los modelos de ecuaciones estructurales permiten obtener un modelo de relación lineal entre los 2 métodos sin necesidad de hacerla.
Coeficiente de concordancia de Lin
Este coeficiente se definió9 reescalando la desviación cuadrática media entre los métodos de medida de forma que adoptase valores entre 1 y 1. La expresión del coeficiente de concordancia es:
donde *XY representa la covarianza entre los 2 métodos de medida. Este coeficiente toma el valor 1 en caso de concordancia perfecta y el valor 0 en caso de independencia entre los 2 métodos. En teoría, este estadístico puede tomar también valores negativos. Así, *C = 1 indicaría una discordancia perfecta entre los 2 métodos, aunque esta situación resulta inverosímil en un problema real, puesto que los procedimientos X e Y pretenden medir la misma característica.
El coeficiente de concordancia de Lin es una medida agregada, ya que evalúa globalmente la concordancia mediante un único valor. Un análisis desagregado consistiría en evaluar por separado la diferencia de medias, la diferencia de varianzas y el coeficiente de correlación.
Si se desea realizar algún tipo de inferencia sobre este coeficiente, como la construcción de intervalos de confianza o contrastar algún tipo de hipótesis, hay que tener en cuenta que los procedimientos derivados para este fin dan por supuesto que tanto Y como X se distribuyen según una ley normal9.
El coeficiente de concordancia es una medida dependiente de la covarianza entre los métodos y, al igual que en el caso del índice kappa y la prevalencia, no deberían compararse coeficientes de concordancia con covarianzas muy diferentes.
Método Bland-Altman
Con este procedimiento desagregado10,12,13 se pretende determinar si 2 métodos de medida X e Y concuerdan lo suficiente para que puedan declararse intercambiables. Para esto se calcula, para cada individuo, la diferencia entre las medidas obtenidas con los 2 métodos (D = X Y). La media de estas diferencias (xd) representa el error sistemático, mientras que la varianza de estas diferencias (s2d) mide la dispersión del error aleatorio, es decir, la imprecisión. Se ha propuesto utilizar estas 2 medidas para calcular los límites de concordancia del 95% como xd ± 2sd. Estos límites nos informan entre qué diferencias oscilan la mayor parte de las medidas tomadas con los 2 métodos. Naturalmente, corresponde al investigador valorar si estas diferencias son suficientemente pequeñas como para considerar que los 2 métodos sean intercambiables o no.
Por otro lado, para que la media y la varianza de las diferencias sean estimaciones correctas debemos asumir que son constantes a lo largo del rango de medidas, es decir, que la magnitud de la medida no está asociada con un error mayor. Para comprobar esta suposición se puede construir un gráfico de dispersión, representando las diferencias (D) en el eje de ordenadas y la media de las 2 medidas de cada individuo, (X + Y)/2 en el eje de abscisas. La media de las medidas de los 2 métodos puede entenderse como una aproximación al valor real, ya que se estaría atenuando el error de medida de los 2 métodos; de este modo, esta representación gráfica permite observar si existe algún tipo de relación entre la diferencia de los 2 métodos respecto a la magnitud de la medida, es decir, si el error de medida es constante durante el intervalo de valores de la característica que se está midiendo o si, por el contrario, el error se incrementa conforme aumenta el valor real que se quiere medir. Asimismo, es posible representar los límites de concordancia del 95%, con lo que se puede identificar a los individuos más discordantes.
Ejemplo
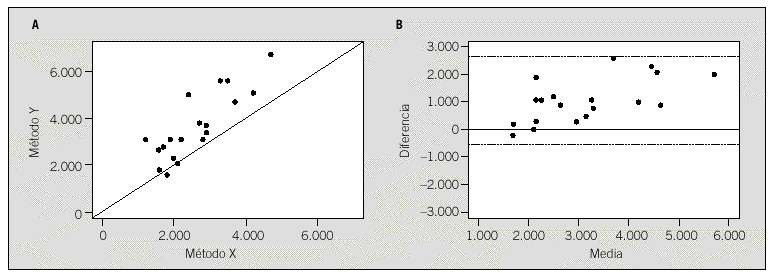
En la tabla 7 se muestran los valores obtenidos por 2 métodos de medida utilizados en 16 sujetos. En la figura 2a se representan las 2 variables en un gráfico de dispersión. En esta figura puede observarse que las medidas no concuerdan, tanto por error sistemático (alejamiento de la bisectriz) como por error aleatorio (dispersión de los puntos alrededor de una recta ideal).
El análisis para evaluar la concordancia se realizará combinando tanto el coeficiente de concordancia de Lin como el método de Bland-Altman, ya que los 2 procedimientos pueden utilizarse paralelamente en el mismo análisis.
Para ello, es necesario obtener las medias y las varianzas de cada método, la covarianza de ambos y la media y la desviación típica de las diferencias. En la tabla 8 se muestran estos valores.
La estimación del coeficiente de concordancia es de 0,5703, con un intervalo de confianza9 del 95% de [0,2892-0,7609], lo que indica un bajo grado de concordancia.
Los límites de concordancia de Bland-Altman son:
Éstos se representan en el gráfico de Bland-Altman de la figura 2b, donde puede observarse que la diferencia entre los 2 métodos tiene una tendencia lineal positiva, esto es, la diferencia se incrementa con la magnitud de la medida. Esto es indicativo de un error sistemático proporcional que se puede estimar mediante el cociente de desviaciones típicas
Este resultado se interpreta del siguiente modo: el método Y toma sistemáticamente valores superiores al método X en una proporción de 1,47. El coeficiente de correlación es de 0,8402, lo que indica un grado de correlación elevado. Por lo tanto, la principal fuente de discordancia entre los 2 métodos es el error sistemático.
Discusión
La calidad de las medidas es fundamental en cualquier ámbito, pero adquiere un especial interés en el campo de las ciencias de la salud14-16, donde continuamente se toman decisiones basadas en mediciones. Esto implica que el acierto en las decisiones depende de la calidad de estas mediciones. Es tentador dar por supuesto que los métodos de medida que utilizamos son buenos y que los resultados que nos proporcionan son correctos y fiables. Si una glucemia en ayunas es de 129 mg/dl se diagnostica al paciente como diabético, pero ¿quién nos asegura que realmente este paciente tiene tal concentración de glucosa en sangre? Es más, si se repite la determinación en otro laboratorio, ¿se obtendrá el mismo resultado? Estas preguntas sólo pueden responderse mediante ensayos de fiabilidad y concordancia de las medidas.
Fig. 2. Gráfico de dispersión y gráfico «diferencia frente a media» relacionados con los instrumentos de medida del ejemplo.
La falta de concordancia puede deberse a dos tipos error: sistemático y aleatorio. Mientras que el error sistemático puede corregirse (por calibración), para disminuir el error aleatorio es necesario estudiar sus posibles causas e intentar controlar algunas de ellas en nuevas versiones más perfeccionadas del método o aparato de medida.