New opportunities for the conceptual design of material-efficient antifunicular structures

Abstract

Non-structural design criteria (e.g., usability, architectural needs, esthetics) may prohibit the selection of purely funicular or anti-funicular shapes. In response to this issue, this paper illustrates the possibility of achieving an axial-only behavior, even if the geometry departs from the ideally bending-free shape. This is achieved by adding forces through an external post-tensioning system, with a layout defined through graphic statics. The paper briefly illustrates examples of this approach and its implementation within a design-driven software where structural performance and geometric variation are embedded within an interactive and parametric working environment.

Resumen

Los criterios de diseño no estructurales (p. ej., funcionalidad, necesidades arquitectónicas o estética) pueden prohibir la selección de formas puramente funiculares o antifuniculares. En respuesta a este problema, este artículo ilustra la posibilidad de lograr un comportamiento axial solamente, aunque la geometría se aparte de la forma idealmente sin flexión. Esto se consigue mediante la adición de fuerzas a través de un sistema de postensado externo, con un diseño definido a través de estática gráfica. El artículo ilustra brevemente ejemplos de este enfoque y su implementación dentro de un software impulsado por el diseño, donde el rendimiento estructural y la variación geométrica están incrustados dentro de un entorno de trabajo interactivo y paramétrico.

1

Introduction

1.1

Motivation

In the design of curved structures, the overall shape, usually decided in conceptual design, is a key contributor to the overall cost and structural efficiency. However, non-structural conditions, such as esthetics, functionality, and geotechnical issues, often prohibit selection of a structurally ideal funicular shape in which only axial forces are activated (the word funicular is independently used for only compression or tension curves). In contrast to a funicular shape, forces may not be able to act in pure tension or compression under self-weight, and bending moments inevitably arise, increasing the structural material required. While in form-finding problems, funicular curves are found from a given set of loads, this research explores the opposite problem: starting from a known geometry, and its related distribution of dead loads, how it is possible to find a system of external loads that, in combination with the existing loads, can convert the starting geometry into a funicular curve.

1.2

Historical background

This study applies the concept of funicularity to curves that are originally not funicular under dead loads, in order to take advantage of the material-efficiency due to a funicular behavior while also allowing for architectural and geometric flexibility. A classical design approach for non-funicular structures is based on the use of bending solutions, in which axial forces and bending coexist, or trusses. In contrast, this study rather explores the possibility of adding external loads on a two-dimensional curve for changing the internal forces distributions, and consequently for improving its structural behavior. An existing example of this concept is represented by the façade of the Pavilion of the Future (Figure 1) built in Seville for the Universal Exposition in 1992, designed by Peter Rice from Ove Arup & Partners [1]. The loadbearing structure of the façade, combining stone and steel, has a semi-circular shape which would require a thick arch size to contain the thrust-line within the thickness. The main design concept takes advantage of the gravity loads generated by roof beams to apply a set of radial equal forces onto the circular arch of the façade, forcing the thrust line to pass closer to the center of the arch.

Figure 1.

Photo of the Pavilion of the Future (1992).

1.3

Research significance

Inspired by this project, this work studies the possibility of achieving an axial-only behavior even if the geometry departs from the ideally funicular bending-free shape.

This paper presents a new design approach, based on graphic statics that shows how bending moments in a two-dimensional geometry can be eliminated by adding forces through an external post-tensioning system.

This results in bending-free structures that provide innovative answers to combined demands on versatility and material optimization. External post-tensioning systems can improve design performance significantly by converting arbitrary curves into geometries that better resist permanent loads with axial forces only; this design philosophy can be implemented to many structural typologies, empowering the designer to control the structural behavior of curved structures.

2

Methodology

2.1

Graphical construction

The theoretical framework is based on the technique of graphic statics, which relates structural geometry and internal forces through reciprocal polygons [2–5]. The concept of the funicular polygon for simply-connected structures (also known as Cremona or Cremona-Maxwell diagram) and force polygon was firstly introduced by Varignon [6], and later extended to analyze trusses and beams. It was the most employed design method until the end of the first third of the 20th century. The virtues of this method for form-finding structures have only been published recently [7–10]. The approach is graphical in the sense that forces are geometrically calculated from the force polygon.

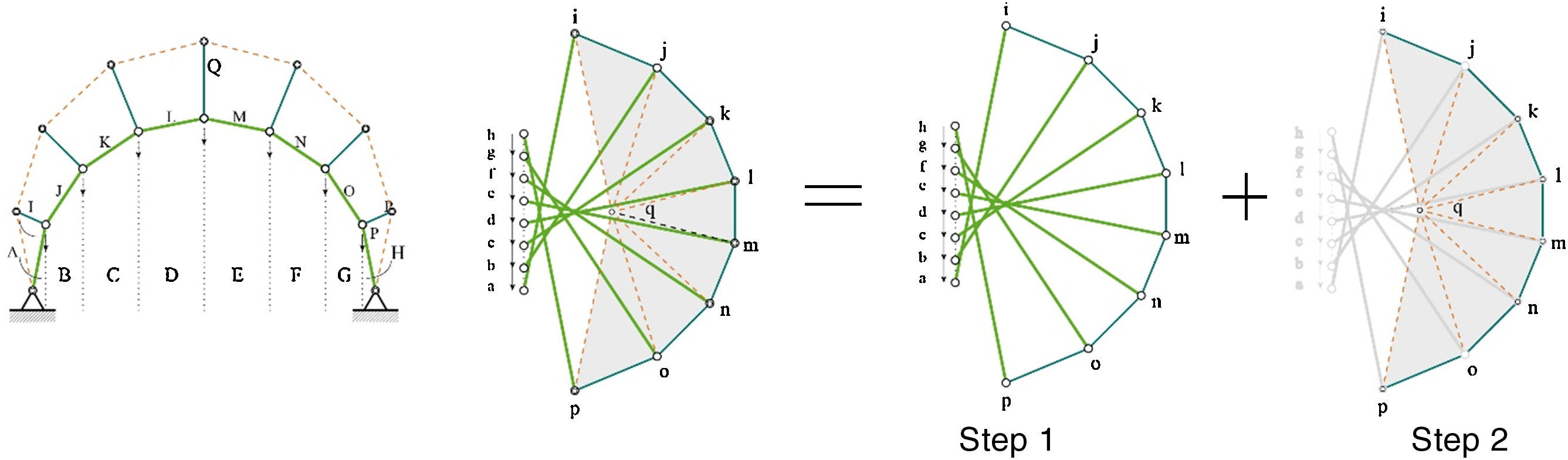
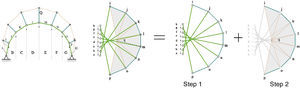
The graphical construction to convert a non-funicular shape into a bending-free one is described in detail in other authors’ papers [11–14]. Here, it is shortened in two main steps, and applied to a circular arch (Figure 2). It consists in:

• •

  Step 1: Definition of the external point forces (blue continuous lines) to be applied to the structure to make it bending-free.

• •

  Step 2: Definition of the post-tensioning system (orange dotted line) for generating the external point loads found in Step 1.

Figure 2.

Graphical construction.

Continuous lines represent compressive elements and forces, respectively, in form and force diagrams; while dotted lines indicate tension elements and forces, respectively, in form and force diagrams.

The graphical procedure allows the identification of an equilibrated geometry where bending moments are eliminated in each polyline vertex, and only axial forces in the cross sections are obtained.

The process starts with a given a curve and its related loads. Yet, the problem is indeterminate: an infinite number of solutions exist to make the starting geometry bending-free. This indeterminacy, which is in-depth studied in the first author's thesis [11], conceptually corresponds to the fact that as infinite axial-only geometries match to a single loading distribution, an infinite sets of loads correspond to a single geometry. Axial forces in the arch and the post-tensioning force applied to the tendon depend on the chosen solution: the smaller the distance between the compressive curve and the post-tensioning system, the higher the forces are in both components. In summary, given a starting geometry, and its related distribution of loads, there are infinite positions of the post-tensioning system for generating the required loads which make the starting shape a bending-free one.

2.2

Implementation

The use of graphic statics for design, as opposed to analysis, has been limited until recently, in part because a variation of the geometry or loads changes the model and the graphical construction, which must be updated, is time-consuming to complete manually. In order to overcome this limitation, a new interactive tool for finding the layout of external post-tensioning systems has been developed. It is interactive in that a change of the geometry of the starting shape results automatically in a new post-tensioning layout in static equilibrium, which is ensured by the dual reciprocity between the force diagram and form polygon. The new tool implemented for this specific research within the Rhinoceros/Grasshopper framework [15,16], is named EXOEquilibrium (it can be downloaded for free sending an email to the first author). Its main features are:

• •

  Geometrical flexibility intended as the possibility to quickly generate, explore and evaluate different alternatives.

• •

  Immediate structural feedback to variation of shape, loads and boundary conditions.

• •

  Graphical output and interactive user experience.

• •

  Parametric environment to better manage data approximations typical in the first design stages.

• •

  Optimization solvers for adjusting variables involved in the conceptual design process.

• •

  Customization for providing the user the possibility to create its own script.

The model definition has four inputs:

• i)

  the geometry of the two-dimensional structure, the number of segment in which the curve should be divided (the curve is transformed in a polyline), the magnitude of permanent loads, and

• ii)

  direction of the struts connecting the compressive curve with the post-tensioning system.

EXOEquilibrium allows users to change parameters involved in the geometry and distribution of loads in order to investigate different structural solutions. As described in the previous section, the problem is indeterminate, so the user can explore the infinite range of equilibrated solutions using some specific parameters. Outputs are represented by internal forces within the base structure, post-tensioning and connecting elements, by reactions and by the layout of the tensioned cable.

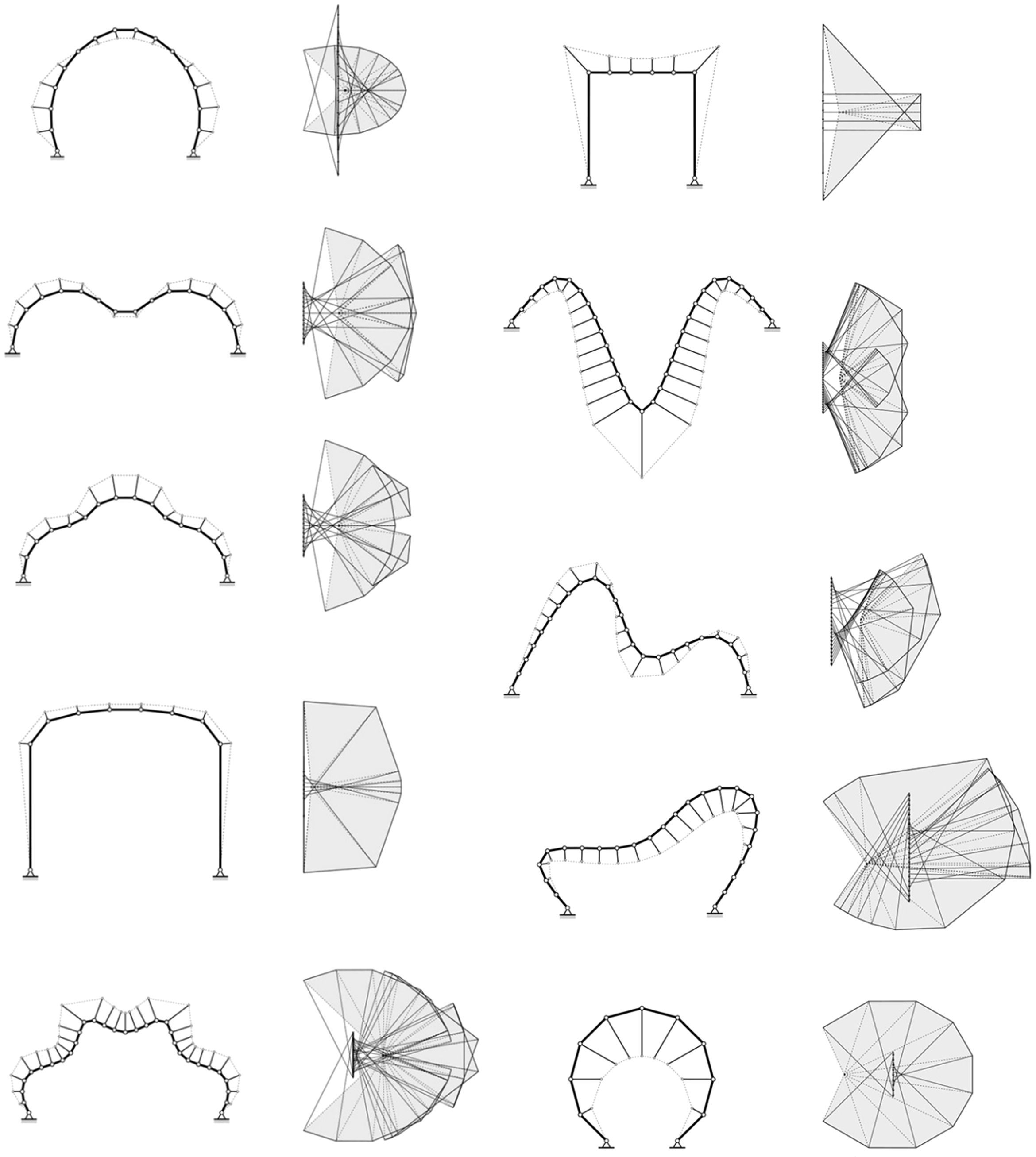
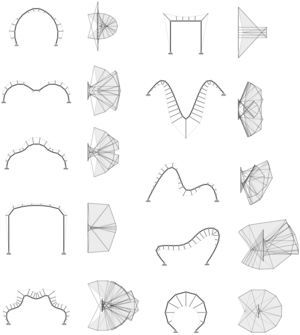
3

Applications

3.1

Design examples: more freedom for creative structural design

EXOEquilibrium enables the interactive exploration of design alternatives for initial non-funicular two-dimensional geometries. Figures 3 illustrates the application of the methodology to arbitrary shapes. The collection of examples, with varying degrees of curvature and both symmetrical and asymmetrical forms, demonstrates the versatility of the methodology and the implemented tool for any two-dimensional geometry. Forces in all structural members can be read in the force diagram, giving to the designer the possibility of evaluating the performance of the whole system consisting of the compressive geometry, the post-tensioning system, and the connecting struts.

Figure 3.

Graphical construction of the external post-tensioning system.

3.2

Design criteria

Given a starting geometry and distribution of loads, the problem can be solved by an infinite number of equilibrated options. A specific part of the research is addressed to illustrate an original procedure that enables the mastery of this infinite domain of solutions by means of specific design criteria related to geotechnical, mechanical and esthetic issues. These design criteria are achieved by manipulating the force diagram, instead of the form diagram, thus equilibrium is always ensured. The main conclusions are:

• •

  The offset (i.e., maximum distance between the compressive geometry and the prestressed cable) plays a key role in optimizing the material-efficiency of the whole structure. Higher offset corresponds to lower material volumes, thus, higher cost-effective structures.

• •

  Design criteria related to the need of having no horizontal thrust (the post-tensioning system, depending on its position, can increase or decrease the total horizontal thrust) or a post-tensioning system always about the compressive geometry (to leave free the inner space) ask for high amount of forces.

Furthermore, several applications of the graphical methodology are described in the other research of the authors [11]. Results point out that:

• •

  The graphical procedure can be applied to a great number of problems, without limitation related to geometry, loads and support position.

• •

  The graphical procedure can be extended to consequent and non-planar structures.

• •

  The graphical approach can be modified to obtain a solution where a constant prestress is achieved in the external post-tensioning system.

• •

  Increasing loads after construction inevitably generate bending moments. An alternative solution would be to employ a responsive structure.

• •

  The implementation of the graphical construction within a parametric tool provides a well-suited environment for the interactive computational exploration of equilibrate solutions within the structural design space.

4

Reduced- and large-scale physical models

4.1

Reduced-scale physical models

Bending-free configurations, obtained with the graphical procedure previously described, have been experimentally validated through reduced-scale models fabricated using a combination of additive manufacturing (3D printing) and laser-cutting [17]. The physical models are composed by three elements:

• •

  Main structure working in compression. It is made of discrete elements printed individually by using a 3D printer.

• •

  Wire. External forces are applied manually by employing a turnbuckle that provides tension to the wire.

• •

  Connecting elements. Main structure and wire are connected by elements made of extruded acrylic and their length is obtained from the graphical construction.

Physical experiments have been carried out with three different shapes: a basket arch, a circular arch and an asymmetrical free-form geometry. Each test was filmed using a high-speed digital video camera proving carefully observation of collapse mechanism and slow-motion videos useful for didactic purposes.

Figure 4, on the top, shows the graphical construction that allows to find the layout of the external prestressed wire and the lengths of connecting elements. Figure 4, on the bottom, illustrates photos taken during the collapse mechanism of the models after cutting the wire. Physical models show that once the post-tensioning force is applied, the non-funicular shapes, made of discrete elements, are stable. This can be considered as a first validation of the approach. Next, once the wire is cut, external forces are removed, there is no way to achieve equilibrium and the structures inevitably collapse. Experimental testing shows that non-funicular structures can be in equilibrium only if external loads are added in a proper way: a wrong position of external forces, or their lack, inevitably entails the collapse of the structure. It is interesting to point out that the starting position of hinges is located in zones in which the distance between thrust line (without external forces) and centroid line is maximum.

Figure 4.

Graphical constructions and collapse sequences of three reduced-scale physical models.

4.2

Large-scale physical models: Paperwave, a Pavilion for the 2015 IASS Symposium

The 2015 IASS Symposium organizers invited universities and/or companies to participate in a contest and exhibition of structurally innovative pavilions. The pavilions had to give a future vision on structural design and innovation and had to be the outcome of excellent structural research. The author, together with other colleagues of the Digital Structures Research Group at Massachusetts Institute of Technology, was involved in this contest. The pavilion proposal was called Paperwave, which is a series of post-tensioned wave forms, constructed nearly entirely of paper. The graphic-statics-based method previously described was used to design the geometry, ensuring that the cardboard boxes in each curved wave are balanced by the tensioned strap and paper tubes, which pull and push the waves into equilibrium. Using low-carbon, inexpensive, and lightweight materials, this pavilion demonstrates the power of structural geometry to achieve creative and high-performing designs.

The main components of the curved waves, which act in compression, have been made from custom-cut corrugated cardboard, assembled on-site into multi-faceted boxes that achieve stiffness through their folding patterns. Compressive or tension connecting post-tensioning systems have been made from cardboard tubes. The post-tensioning system has been achieved with stripes, a relatively strong and stiff material that can be cut and connected with low-tech tools. The use of unconventional and low cost materials has been made possible by the efficiency of the geometric design. The pavilion serves as both a validation and demonstration of method presented in previous sections, expressing the creative freedom and flexibility of designers and the structural performance of the results.

5

Conclusions

Curved structures are characterized by the critical relationship between their geometry and structural behavior, and selecting an appropriate shape in the conceptual design of such structures is important for achieving material-efficiency. However, the set of bending-free geometries are limited and, often, non-structural design criteria (e.g., usability, architectural needs, esthetics, etc.) prohibit the selection of purely funicular or antifunicular shapes.

In response to this issue, this paper studies the possibility of achieving an axial-only behavior even if the geometry departs from the ideally bending-free shape.

This dissertation presents a new design approach, based on graphic statics that shows how bending moments in a two-dimensional geometry can be eliminated by adding forces through an external post-tensioning system. This results in bending-free structures that provide innovative answers to combined demands on versatility and material optimization.

The graphical procedure has been implemented in a free-downloadable design-driven software (EXOEQUILIBRIUM) where structural performance evaluations and geometric variation are embedded within an interactive and parametric working environment. This provides greater versatility in finding new efficient structural configurations during the first design stages, bridging the gap between architectural shaping and structural analysis.

The paper includes the application of the developed graphical procedure to shapes with random curvature and distribution of loads. Furthermore, the effect of different design criteria on the internal force distribution has been analyzed.

The graphical construction has been validated through reduced-scale models which use is informative but also didactic. Finally, the procedure has been employed for the design of Paperwave, a temporary pavilion exhibited during the 2015 IASS Symposium, illustrating the possibilities and trade-offs in funicular explorations for architectural design.

In summary, this work strongly expands the range of possible forms that exhibit a bending-free behavior and, de facto, opens up new possibilities for designs that combine high-performing solutions with architectural freedom.