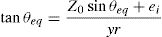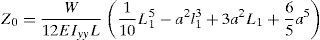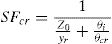Las mejoras tecnológicas de la prefabricación con hormigón han hecho competitivo el uso de vigas prefabricadas de luces cada vez mayores en comparación con otras alternativas. Sin embargo, el peso de las vigas es limitante en las operaciones de izado y transporte, por lo que se tiende a reducir el ancho de las alas, produciendo elementos más propensos a la inestabilidad lateral. En este artículo se describe un caso de estudio real de inestabilidad lateral de una viga pretensada de puente de gran luz y se realiza un estudio paramétrico. Se analizan las actuales provisiones del Código Modelo 2010 y se muestra que pueden resultar inseguras en casos límites.
Improvements in concrete prefabrication technology makes the use of long-span concrete girders more competitive compared to other alternatives. However, the weight of the element is determining factor in transportation and lifting operation costs, hence the width of the flanges tends to be reduced. This results in elements more prone to lateral instability. In this paper, a real case study of lateral instability of a long pre-cast girder is presented. A parametric analysis is carried out to determine the limits of application of the solution. The current provisions of the Model Code 2010 are analysed, and it is shown that they may be insufficient in some limit cases.
Las vigas de hormigón prefabricado se emplean con frecuencia en proyectos constructivos condicionados por la rapidez de construcción y complejidad de hormigonado in-situ. Algunos avances tecnológicos (e.g. mejores hormigones, secciones transversales más eficientes) permiten fabricar elementos de longitudes cada vez mayores y los hacen más competitivos frente a otras soluciones [1]. Como consecuencia, el peso a manipular en cada elemento es mayor, haciendo que los estados de transporte e izado sean limitantes en términos de diseño estructural.
La estrategia más común para permitir alcanzar luces mayores consiste en minimizar el peso del elemento prefabricado mediante la reducción del ancho de las alas. Sin embargo, ello reduce la rigidez del eje débil y la rigidez a torsión, por lo que aumenta el riesgo de inestabilidad lateral. Tradicionalmente, el problema de inestabilidad lateral en las fases de construcción de elementos de hormigón ha recibido poca atención en el proceso de diseño, ya que se consideraba que las secciones son suficientemente compactas y poseen suficiente margen de rigidez lateral. No obstante, recientemente se ha observado un aumento del número y gravedad de los accidentes y daños con vigas prefabricadas esbeltas de hormigón, generando preocupación sobre este problema [2,3].
Los accidentes y daños que se han reportado en la literatura especializada están asociados a excentricidades, en forma de imperfecciones geométricas, que activan el efecto de segundo orden durante ciertas situaciones de carga (izado, transporte y apoyo en elementos elastómeros). El origen de estas excentricidades en vigas prefabricadas incluye [4]: (1) tolerancias de fabricación, (2) variación del posicionamiento lateral del pretensado, (3) fisuración local, (4) fluencia y retracción, (5) soleamiento en una cara lateral, etc. El estudio de la inestabilidad lateral de vigas prefabricadas y la determinación de las magnitudes razonables de las imperfecciones [5] se han mostrado de gran importancia para asegurar la seguridad durante las situaciones transitorias de montaje [2].
Los estudios sobre estabilidad de vigas empezaron en la década de 1950 [6–9]. Probablemente, los estudios analíticos y experimentales de Mast [10,11] sean de los más influyentes en el campo. De hecho, el método propuesto por Mast es la base de las comprobaciones actuales del PCI (2016) [12]. Estos estudios fueron los primeros en considerar el efecto de la imperfección lateral inicial y en proporcionar un factor de seguridad para tener en cuenta la reducción de rigidez debido a la fisuración en esta condición. Posteriormente, otros estudios analíticos y numéricos [13,14] proponen un enfoque más general basados en cálculos complejos. Sin embargo, todos estos modelos asumen linealidad de la respuesta del material y desprecian, por lo tanto, la fisuración.
El objetivo de este artículo es avanzar en el estudio del comportamiento de las vigas de hormigón prefabricado soportadas por cables de izado a través de ganchos de izado. Esta situación resulta ser la más desfavorable ya que no existe, en los puntos de apoyo, ninguna restricción al movimiento de sólido rígido de rotación alrededor de la directriz del elemento. De hecho, la estabilidad se alcanza tras una rotación que genera un contrapeso lateral de los extremos en voladizo que compensa el peso del tramo central.
En el artículo se estudia un caso real de fallo por inestabilidad lateral de una viga prefabricada de 45,6m de luz. Se utiliza la formulación de Mast [10,15] para justificar los fenómenos observados en la realidad. Se realiza un análisis paramétrico y se estudia la sensibilidad, el problema a las variables de diseño. Los resultados cuestionan las previsiones del actual Código Modelo 2010 relativo a los efectos de segundo orden de inestabilidad lateral.
2Análisis del proceso de izadoLos estudios clásicos de inestabilidad lateral asumen la existencia de una restricción al giro lateral en los soportes [15]. El fenómeno se caracteriza por una deformación lateral en la zona central del elemento, produciendo una deformada hacia uno de los lados, lo cual aumenta el momento torsor y, consecuentemente, el giro y la propia deformada lateral. El problema práctico ocurre cuando la deformada no se puede controlar (inestabilidad) o alcanza valores excesivos. Este tipo de inestabilidad es particularmente relevante en vigas metálicas de sección doble-T con baja rigidez a torsión. Las vigas doble-T de hormigón tienen, normalmente, almas más gruesas y alas más anchas, dando lugar a secciones que son entre 100 y 1.000 veces más rígidas a torsión que la contrapartida metálica. Por lo tanto, es razonable asumir que las vigas de hormigón son rígidas a torsión. Esto permite simplificar el problema complejo de acoplamiento torsión-flexión, en un problema gobernado por la flexión lateral.
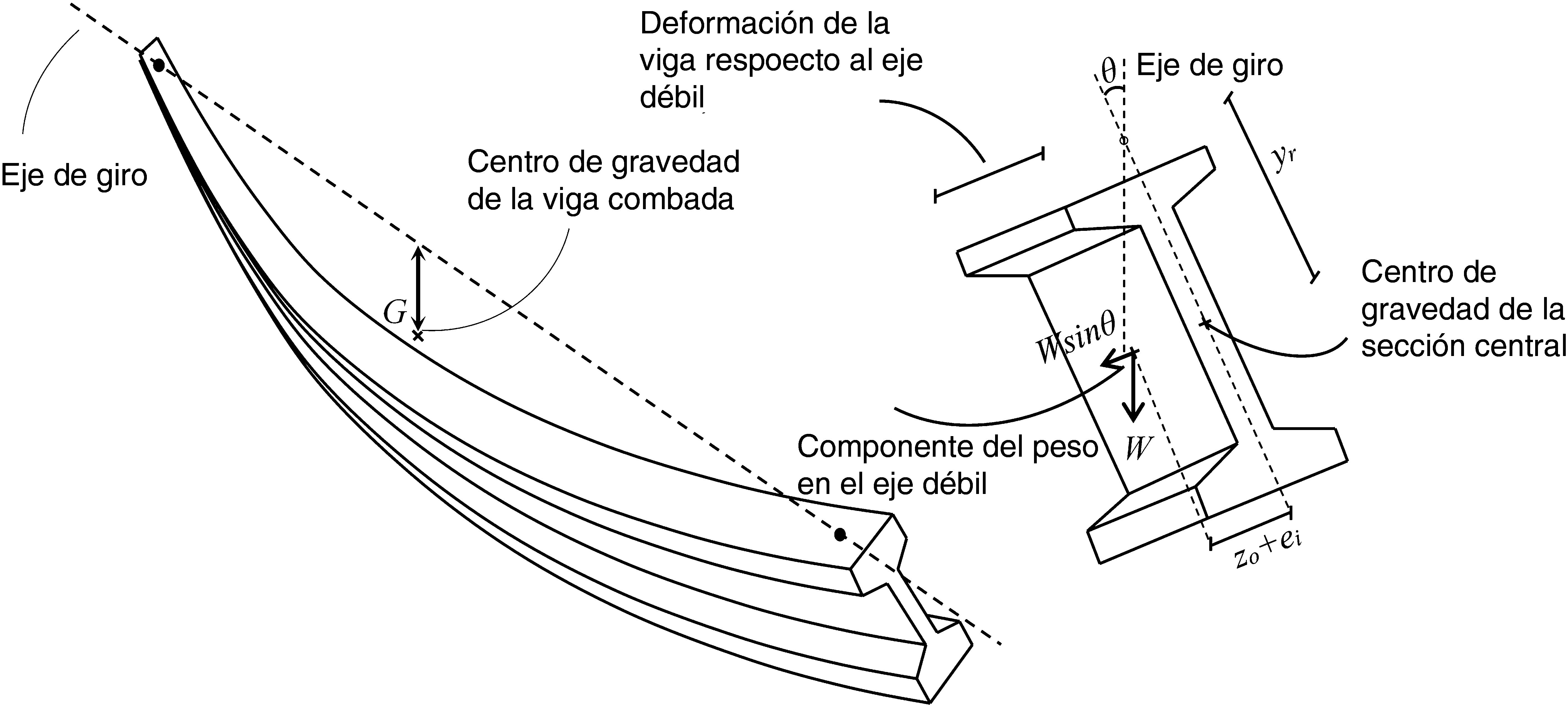
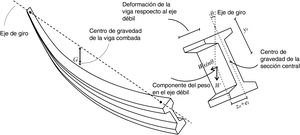
La presencia de imperfecciones laterales (ei) desplaza ligeramente el centro de gravedad (G) hacia uno de los lados de la directriz de la pieza, el cual actúa como eje de rotación (Fig. 1). Consecuentemente, el elemento gira, formando un ángulo θi con el eje vertical. Entonces, una componente del peso (W) se ve aplicado en el eje débil de la sección W sin θ y produce una deformada lateral, la cual desplaza aún más el centro de gravedad (G). Si existe rigidez suficiente en la dirección débil, se alcanza el equilibrio en una inclinación (θeq), superior a la inclinación inicial (θi). Por el contrario, si la rigidez lateral no es suficiente, la deformada lateral y la flexión lateral pueden producir la fisuración del elemento o, incluso, la rotura por flexión lateral.
El ángulo de equilibrio (θeq) puede ser evaluado mediante iteraciones sucesivas usando la ecuación 1. Donde, yr es la altura del punto de eje de giro sobre el centro de gravedad de la sección (G) (Fig. 1), z0 es la deformada lateral, evaluada a la altura de G, debido al peso completo de la viga (W) aplicado en el eje débil.
Los efectos negativos de estabilidad que puede producir la contraflecha de pretensado se pueden tener en cuenta desplazando hacia arriba el centro de gravedad (G) una distancia δG=2/3δP. Donde δP es la contraflecha en el centro luz que se espera durante las operaciones de izado. Por otro lado, se puede calcular z0 mediante la ecuación 2. En ella, L es la luz total del elemento, a es la distancia de los ganchos de izado, desde los extremos de la viga, y L1 es la luz central (L1=L-2a). Así mismo, E es el módulo de deformación del hormigón e Iyy es la inercia en el eje débil.
El margen de seguridad frente a la fisuración (SFcr) viene dado por la ecuación 3. Donde, bajo la hipótesis de viga rígida a torsión, θi=ei/yr y θcr es el ángulo de rotación de la sección de centro luz en el que se espera que ocurra la fisuración. θcr se puede calcular como el ángulo en el que es necesario rotar la sección hasta que aparece una tensión de tracción en el hormigón igual a la resistencia media de tracción (fctm). La subrutina de análisis seccional presentada en [16] ha sido usada para calcular θcr. Nótese que SFcr combina, simultáneamente, los efectos de estabilidad lateral (zo/yr) y los efectos de la flexión lateral en la fisuración (θi/θcr).
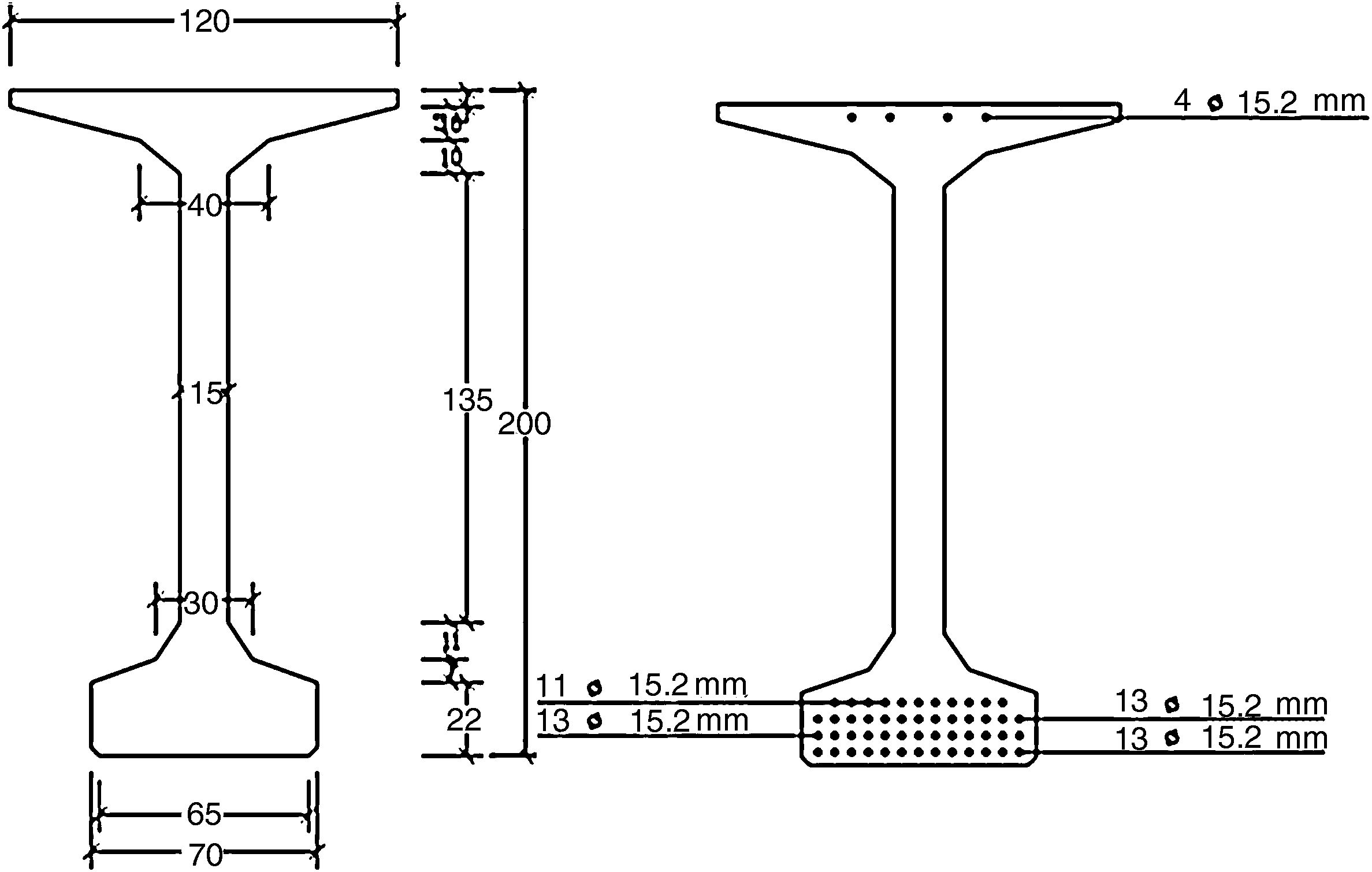
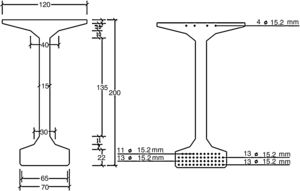
3Caso de estudio3.1IntroducciónEl caso consiste en una viga de puente de 45,6m de longitud, prefabricada, de hormigón pretensado, de sección doble T y geometría prismática (Fig. 2). El área de la sección (Ac) es de 0,58m2, la inercia en los ejes fuerte (Ixx) y débil (Iyy) es 0,325m4 y 0,021m4, respectivamente. La viga fue izada usando ganchos dobles, localizados a 2,0m desde los extremos (a) y a una altura de 0,30m sobre el borde superior de la pieza (Fig. 3). Se usaron dos grúas durante las operaciones de izado para garantizar el alineamiento vertical de los cables de izado (Ψ=0°).
La fuerza de pretensado en el momento de izado (t>28 días) se estimó en Pk=8.514kN (15% de pérdidas). La excentricidad respecto al centro de gravedad de la sección es ep=0,73m. La resistencia del hormigón a los 28 días es de 60MPa. El módulo de deformación y la resistencia media a tracción se estimaron como Ec=34.7GPa y fctm=4.53MPa, respectivamente.
En las inspecciones visuales previas al izado, se detectó una excentricidad de, aproximadamente, 12mm en la posición de los ganchos de izado respecto al eje central de la pieza. Así mismo, se observó una imperfección en la flecha lateral de 90mm. Esta imperfección equivale a L/510, la cual es menor que la tolerancia permitida (L/500) en EN 15050 [17]; por lo tanto, se autorizó el izado de la pieza. Durante la operación, se observó un desplome (Fig. 3) con un dramático incremento del desplazamiento lateral de hasta 300mm, por lo que se bajó la viga y se abortó la operación.
En las inspecciones posteriores, se detectaron fisuras verticales en el ala superior izquierda, donde se esperaban las máximas tensiones de tracción debidas al fenómeno de vuelco lateral. A pesar de que los anchos de fisura observados eran aceptables, la viga no recuperó su forma original, y la flecha lateral permanente superaba L/400, por lo que el elemento fue finalmente rechazado.
3.2Análisis con un modelo de elementos finitosSe llevó a cabo un análisis numérico del proceso de izado de la viga descrita mediante el software DIANA. El modelo estaba compuesto por elementos sólidos isoparamétricos piramidales de 4nodos, con un tamaño máximo de 230mm. Los materiales y sus propiedades se simularon teniendo en cuenta los parámetros definidos en el apartado 3.1. La no lineal geométrica se tuvo en cuenta mediante el método de Lagrange.
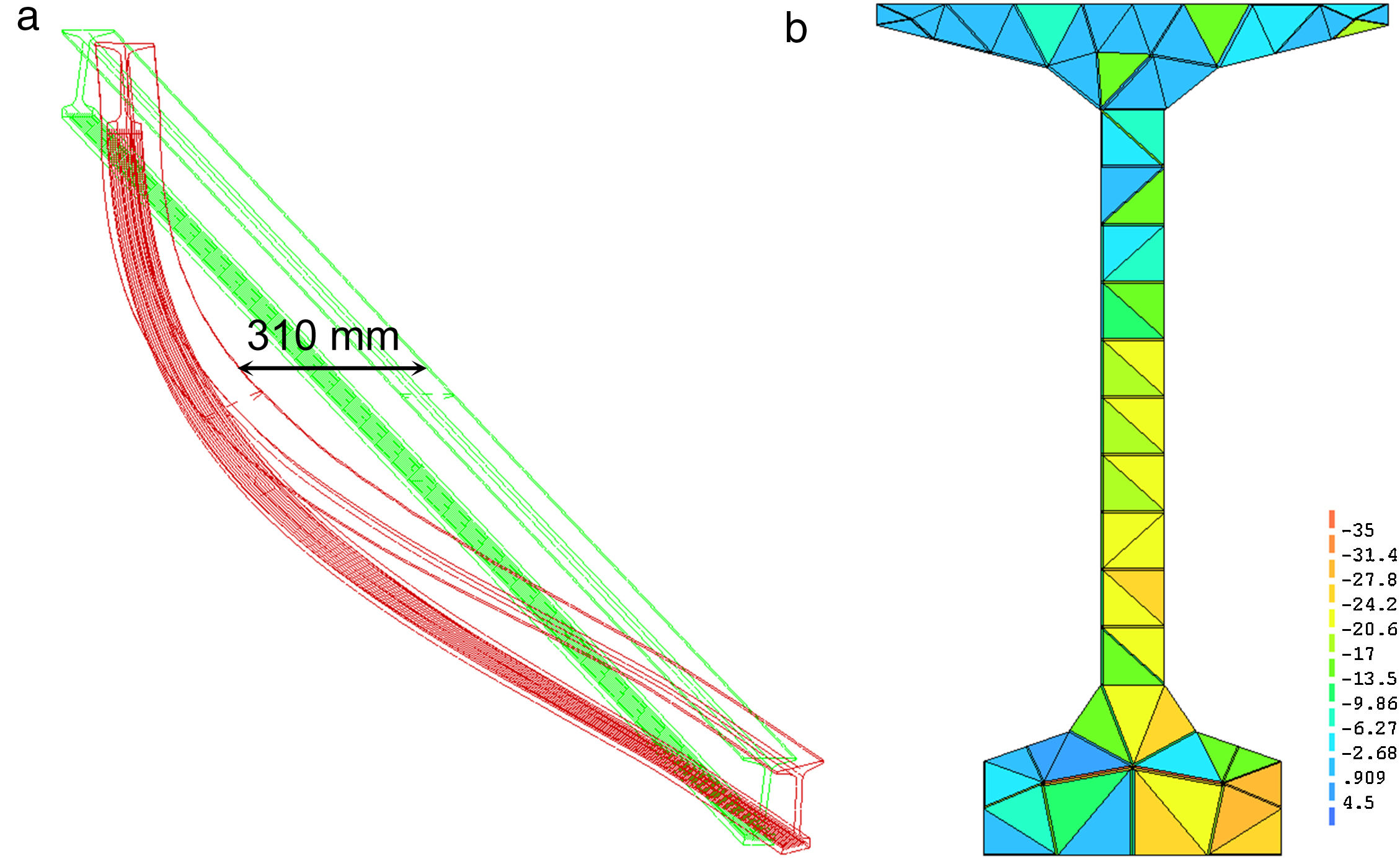
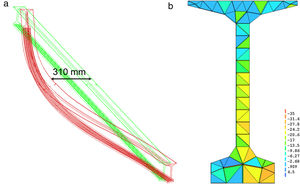
En la figura 4a se presenta la configuración deformada de la viga en fase de izado. La deformación lateral alcanzada por el modelo es de 310mm, ligeramente superior a los 300mm observados en las operaciones reales de izado de la viga. Por tanto, se confirma la tendencia a las grandes deformaciones laterales y a la fisuración de la misma en esta fase transitoria (tensiones superiores a fctm=4,5MPa en el ala superior y parte externa del ala inferior), según la distribución de tensiones en la sección central de la viga (Fig. 4b).
3.3Análisis con el modelo de MastSe realizó un estudio paramétrico considerando el rango de valores de las imperfecciones, usando la formulación de Mast [10,15], tal y como se describió en el apartado anterior. Se consideraron deformaciones iniciales entre L/250 (182mm) y L/1.000 (45,6mm). La excentricidad total del centro de gravedad de la viga (ei) se consideró igual a la flecha lateral, añadiendo una excentricidad lateral de los ganchos de izado (12mm).
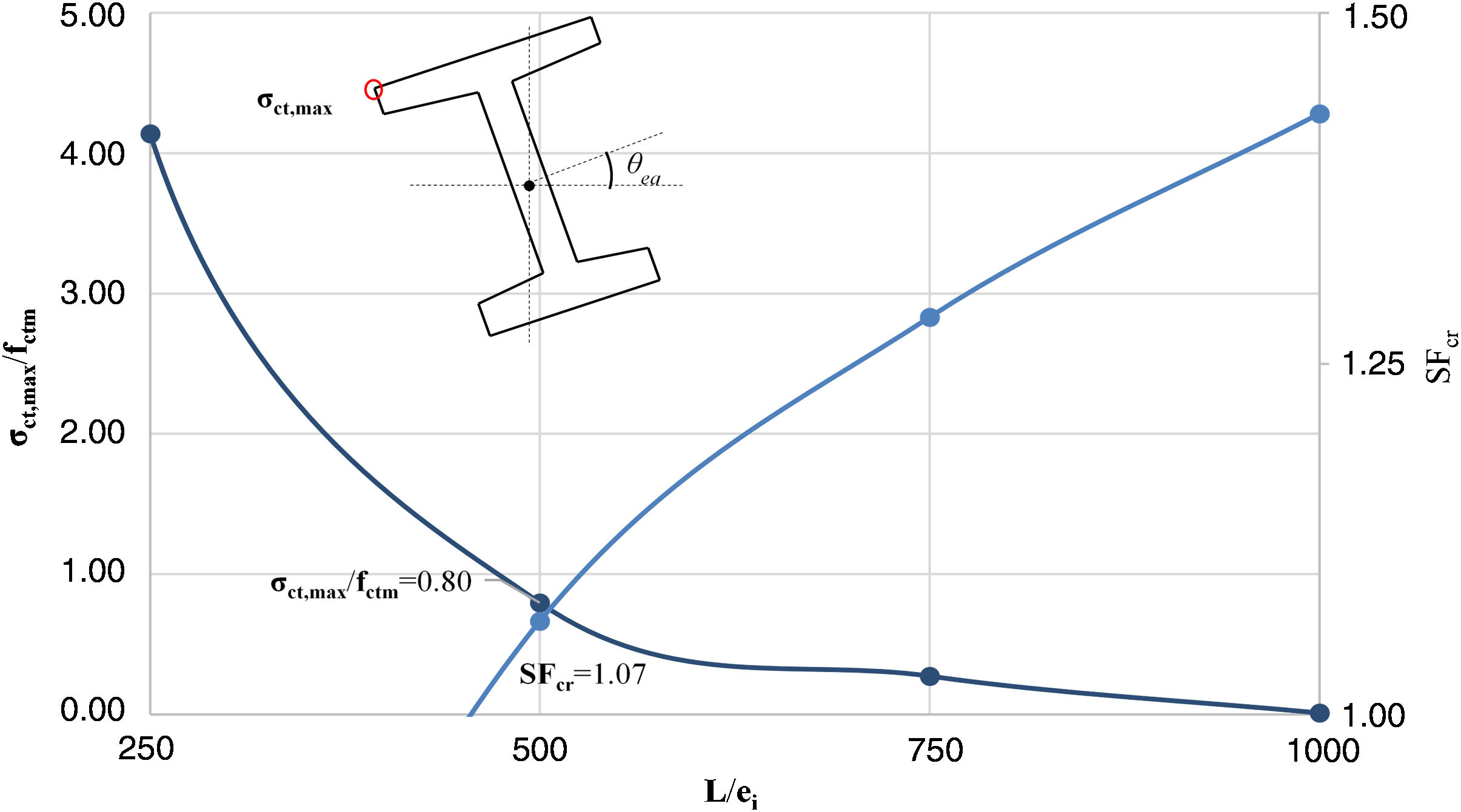
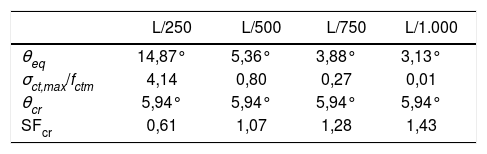
En la tabla 1 se presentan los resultados en términos del ángulo de equilibrio en la sección central (θeq), el ángulo que produce la fisuración (θcr), el ratio tensión máxima de tracción frente a la resistencia media de tracción (σct,max/fctm) y el margen de seguridad frente a la fisuración (SFcr).
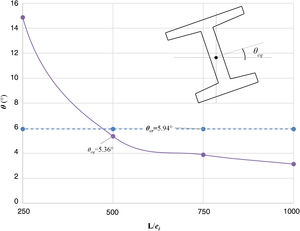
Los resultados de la tabla 1 confirman que la imperfección inicial L/500 (91mm) es suficiente para producir un ángulo de equilibrio θeq=5,36° y SFcr=1,07, el cual satisface las recomendaciones del PCI (2016) (SFcr≥1,00). No obstante, se deduce que la viga es susceptible de fisurar ya que el margen de seguridad está muy cerca del límite.
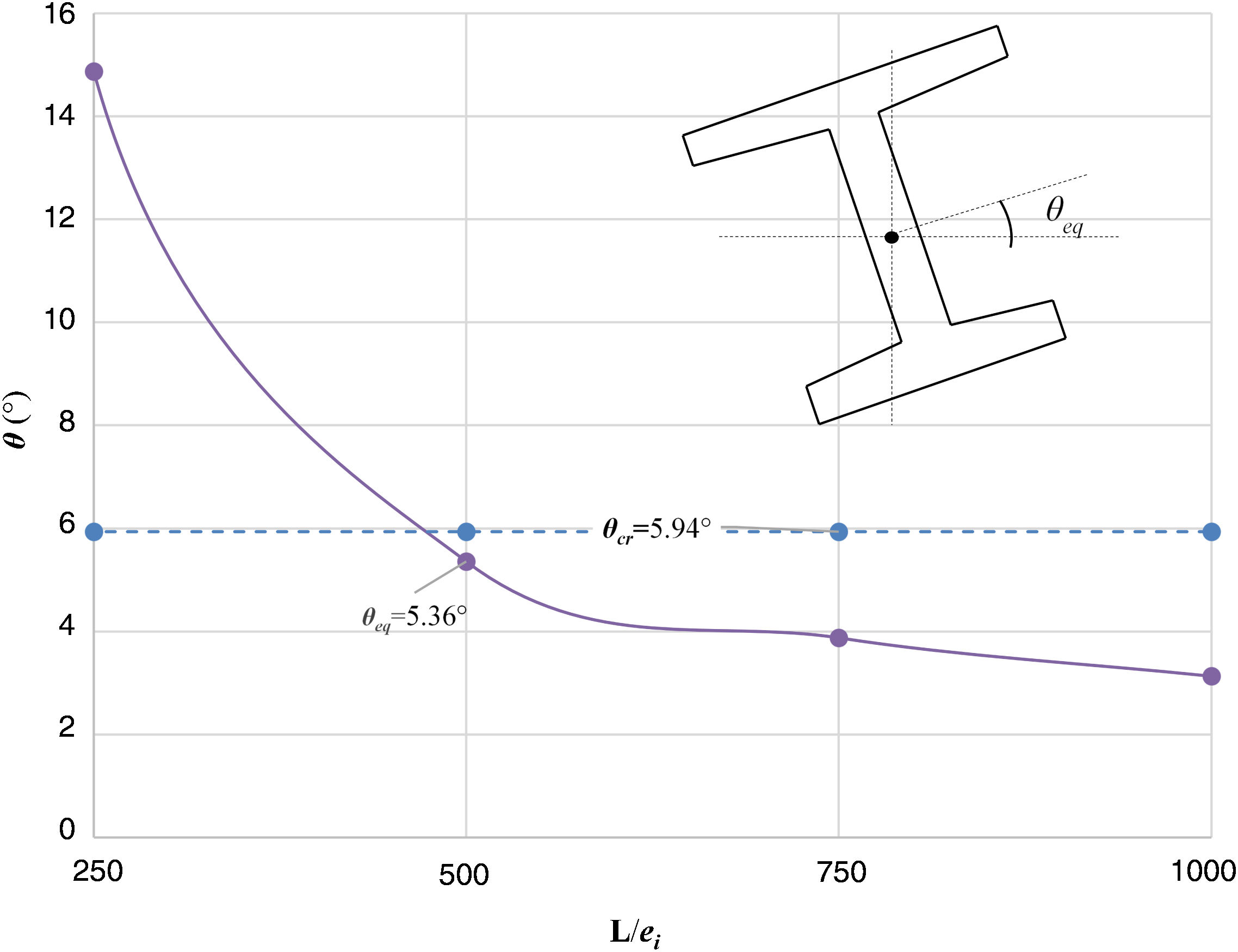
Para profundizar en el análisis, la figura 5 muestra la evolución de θeq y la combadura (L/ei). En la figura 5 se evidencia que θeq es fuertemente dependiente en L/ei. Se observan valores de θeq de entre 3,13° (L/1.000) a 14,87° (L/250). Se debe hacer notar que θeq aumenta exponencialmente para L/ei<600. Así mismo, θcr es casi un 10% mayor que el valor esperado para L/500 (θeq=5,36°). De hecho, se espera que la viga fisure para una imperfección lateral de L/475. Este valor se puede alcanzar fácilmente previamente a las operaciones de izado, debido a fenómenos como gradientes térmicos (radiación solar) acoplados con las deformaciones de retracción y fluencia.
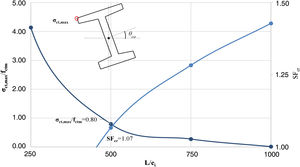
La figura 6 muestra la relación entre el ratio de tensión máxima de tracción y la resistencia media de tracción y el margen de seguridad SFcr en función de L/ei. Se puede observar que σct,max/fctm aumenta exponencialmente con valores L/ei<500. En efecto, para L/500, σct,max está un 20% por encima de fctm y SFcr es de 1,07. Por tanto, el riesgo de fisuración en el ala superior existe. Los resultados y análisis confirman que la configuración de izado hace la viga susceptible a la fisuración y a la inestabilidad lateral.
3.4Comparación con normativasEl Anejo 11 de la Instrucción española EHE-08 [18] establece una tolerancia a la imperfección lateral de L/750, el cual conduce a SFcr>1,25. Por el contrario, el Código Modelo (MC-2010) [19] sugiere, en su sección 7.3.8, que se considera una imperfección lateral de L/300 en el análisis de estabilidad, lo cual no sería aceptable para la viga estudiada, de acuerdo con los resultados presentados. El MC-2010 también sugiere que los efectos de segundo orden pueden ser despreciados si se cumple L/b≤50/(h/b)1/3; siendo b el ancho del ala superior y h la altura de la sección, respectivamente. El caso de estudio aquí presentado cumple esta última condición con L/b=38<50/(h/b)1/3=42. Así pues, se resalta que el cumplimiento de los requisitos en los códigos actuales no garantiza la inexistencia de problemas de inestabilidad lateral.
4ConclusionesEste estudio evidencia que la tendencia actual de usar vigas prefabricadas de hormigón pretensado para luces cada vez mayores, manteniendo la misma sección transversal de los catálogos existentes, aumenta el riesgo de inestabilidad lateral. Es necesario tomar medidas adicionales para evitar este problema.
A pesar de cumplir los requisitos de imperfecciones geométricas de las normativas EN-15050 y MC-2010, el caso de estudio analizado mostró problemas de fisuración y no recobró la deformación inicial después de haber sufrido problemas de inestabilidad lateral durante el izado. El análisis llevado a cabo con las hipótesis descritas en este artículo confirman que existe un margen de seguridad muy pequeño durante el proceso de izado.
Los resultados sugieren que las tolerancias geométricas permitidas y los criterios para determinar la influencia de los efectos de segundo orden que existen en las normativas vigentes deberían ser revisados para tener en cuenta las tendencias actuales en la esbeltez lateral de los elementos. En este sentido, cabe resaltar que el TG 6.5 Puentes Prefabricados de la fib está actualmente proponiendo nuevos requerimientos adaptados a las prácticas actuales de prefabricación con hormigón.
Los autores de esta comunicación quieren agradecer a Don David Fernández-Ordóñez, Dr. Ingeniero de Caminos y actual secretario general de la fib, por las sugerencias aportadas para el desarrollo de este trabajo.