Conformational analysis is one of the significant subjects in the organic chemistry curriculum. Since this subject may be intricate for some beginner students, a concrete model (an activity) has been devised to explain the conformational concepts with an intriguing and simple method. This model is based on geometric shapes (particularly triangles) in which the revolution of each shape on its axis at the centroid (around its vertices and edges) simulates the rotation about a single bond in a molecule. If we take edges as lower energy (more stable) and vertices as higher energy (less stable), this revolution gives a graph almost identical to the actual conformational energy diagram of that molecule. These shapes can also incorporate into the Newman projections to form a tangible representation of these notations. Most of the participants, who got familiar with these newly modified Newman projections, found them beneficial in enhancing the students’ perception of the basic conformational properties of the molecules. Furthermore, searching for a relevant shape to match the right molecule serves as an activity that in addition to being enjoyable can encourage the students to get engaged with the topic. This model is applicable to a large variety of molecules such as the hydrocarbon, aldehyde and ketone molecules, which can also generalize to more functional groups and compounds.
El análisis conformacional es uno de los temas más significativos en la enseñanza de química orgánica. Puesto que este tema puede ser complicado para algunos estudiantes, se propone un modelo concreto (una actividad) con vista a mejorar la percepción para explicar los conceptos conformacionales con un método sencillo y fascinante. Este modelo se basa en formas geométricas (triángulos) en las que el giro de cada triángulo alrededor de su eje (alrededor de sus vértices y bordes) simulará la rotación de la molécula entorno a un enlace sencillo. Si consideramos los bordes y vértices como de baja energía (más estable) y de alta energía (menos estable) respectivamente, el giro dará una gráfica semejante al diagrama de energía conformacional real de la molécula. Además, esta forma geométrica se puede incorporar a las proyecciones de Newman a fin de tener una representación tangible de esta notación. La mayoría de los participantes, que se familiarizaron con esta nueva proyección de Newman modificada, encontraron beneficios en la percepción de los estudiantes sobre las propiedades conformacionales básicas de las moléculas. Asimismo, la búsqueda de una forma geométrica conveniente que corresponda a una determinada molécula sirve como una actividad agradable la cual puede atraer a los estudiantes al tema. Este modelo se aplica a una gran variedad de moléculas incluyendo hidrocarburos, aldehídos y cetonas, y puede generalizarse a otros grupos funcionales y moléculas.
Using a model or a visualization tool for representing the structures and geometries of microscopic molecules as well as their properties is a common practice, which chemists and other scientists use to comprehend the complex behavior of these molecules in a more tangible fashion (Chittleborough & Treagust, 2009; Wu, Krajcik, & Soloway, 2001). An abundant number of papers in the educational literature describe innovative models, visualization materials or activities for this matter (Davis, Leslie, Billington, & Slater, 2010; Palacios & Caballero, 2004; Taherpour, 2005). The model systems will provide roughly the same information compared to the actual systems with much less effort. Also, these models give more reality to the systems that allow the audience to observe at the macroscopic scale, which is crucial for understanding the chemical concepts (Chandrasegaran, Treagust, & Mocerino, 2008). These will make the models as popular tools for teaching, learning and in general, for pedagogical purposes, particularly in chemistry field, which it is difficult to perceive unobservable phenomena for a beginner student. Furthermore, chemistry science is full of three dimensional (3D) objects (especially organic chemistry) that would further emphasize on the use of applicable and appropriate models. Moreover, models and visualization instruments can also exploit as a motivational tool for creating enthusiasm in students to learn faster with more passion.
Stereochemistry and conformational studies in molecules are among the main and probably difficult topics in organic chemistry (Luján-Upton, 2001), especially for beginner students, who have difficulties with imagination and simulations of molecules or other relative shapes in 3D environment. Teaching these subjects also is a wearisome task for many lecturers and other educational practitioners. Since the availability of computational modeling packages, these tasks became much easier, but still owing to some difficulties involved in using these computational software (like handling, steep learning curves for a beginner student and so forth) (Williamson, 2011) they have yet to supersede the traditional education methods completely. The well-established molecular modeling kits (ball-and-stick) are preferred due to their virtues over these computational methods. Nevertheless, the modeling kits also have their own disadvantages. The accessibility of these kits only is restricted to educational environment and not provides a handy tool for most students in different occasions (like exams or other assessments). Owing to the aforementioned limitation in both computational visualizations and molecular modeling tools, most instructors and students still see the regular 2D and pseudo-3D (wedge and dash notation) representations more suitable to utilize under most circumstances (Raiyn & Rayan, 2015). Therefore, although illustrating chemical objects in 3D have great benefits over 2D representations, but a model or an activity, which can be used in the 2D paper without the use of external tool or device is more convenient. This convenience may arise from the fact that students are more familiar with the 2D representations (Pavlinic, Buckley, Burns, & Wright, 2001).
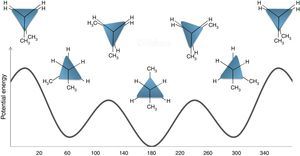
Herein, we devise a model system and an activity (beneficial and intriguing system) for learning and teaching the conformational aspects of some simple molecules such as the alkanes, which can also extend this model to more complex molecules. This strategy (system) converts a 3D phenomenon to more applicable 2D object with the help of stability and instability of geometric shapes (triangles). This conversion has value as it translate one representation (Newman projection) to a perceivable geometric object (triangle). The translation from one representation to another was reported to be an obstacle in learning chemistry (Treagust, Duit, & Nieswandt, 2000). Each of the triangles corresponds to one molecule in which the revolution around the triangle (or other shapes) on its axis imitates the rotation about a single bond in that molecule. This revolution gives the torsional energy (diagram) similar to the real molecules with taking the strains and repulsions into account (torsional barrier). On the basis of this notion, newly modified Newman projections were devised (see the following illustration, Fig. 1) in order to describe the conformational analysis and the affecting factors for beginner students. Additionally, finding a relevant shape to match the correct molecule is like an exercise, which engages the students in the topic and help them to study with more passion. All the rules and concepts are easy to understand even for non-chemistry students, who are interested in stability–instability and conformations of chemical molecules. However, this mainly intended for first year undergraduates who have taken the general or organic chemistry course.
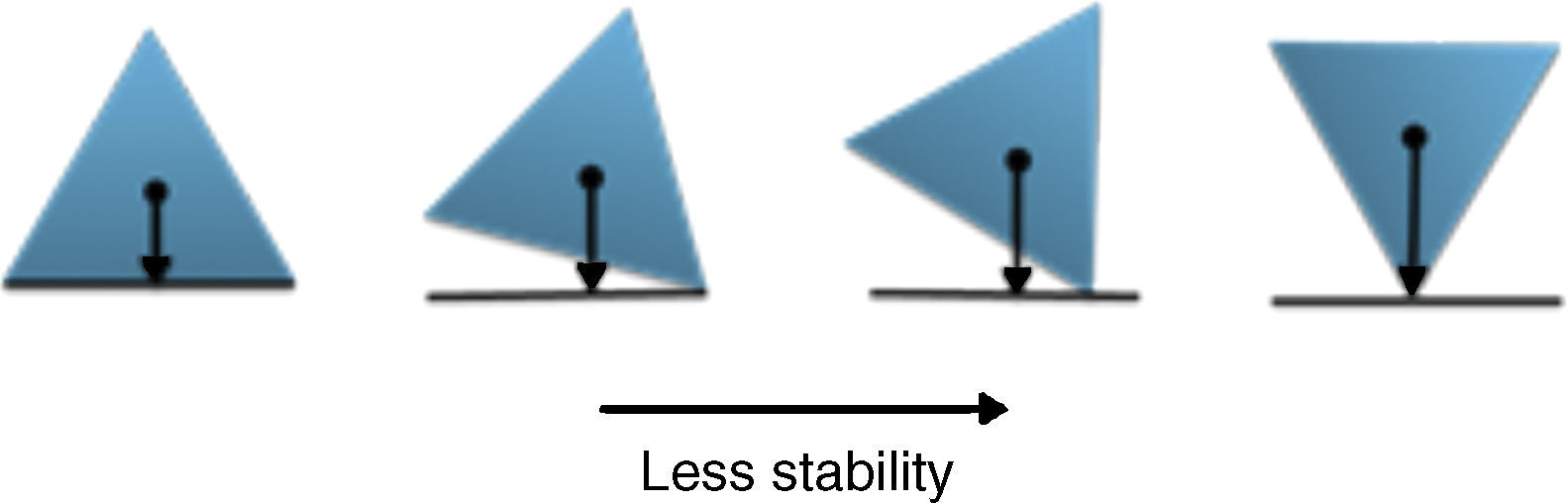
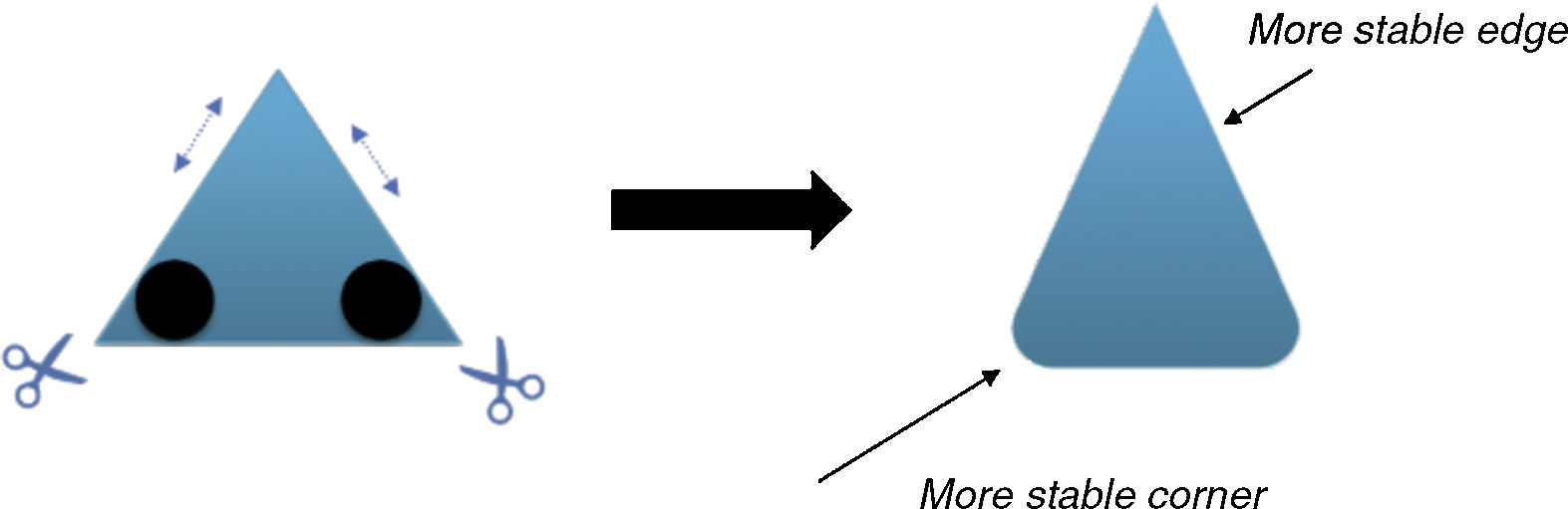
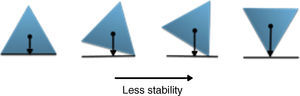
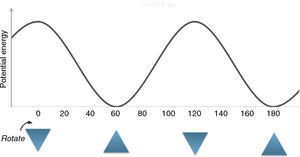
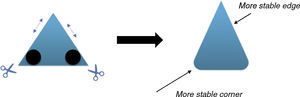
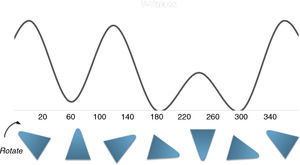
The physical stability of geometric shapesInitially, to get familiar with the concepts of the physical stability in geometric shapes, a brief background has been provided. Although, the physical stability of the shapes in this study is perceptually realizable (Cholewiak, Fleming, & Singh, 2013; Cholewiak, Fleming, & Singh, 2015), but it is recommended to get acquainted with its simple physical background (students may already familiar with this section). As this study primarily copes with triangle shapes, the physical stability explanations were conducted on the equilateral triangle. The center of gravity (COG) of an equilateral triangle is located at its center (centroid, see Fig. 2). There are three factors that influence the stability of the objects (in this case triangle): (i) the position of COG, (ii) the height of the COG from the base (higher is less stable) and (iii) the length of the base (longer is more stable). Since, the position of COG does not alter with revolving, so this factor is constant in this case. The two remaining factors are responsible for the stability of the triangle. As illustrated in Fig. 2, the height of the COG increases from left to right and also the base area reduces. Both of the mentioned changes disfavor the stability of the shape. Therefore, the triangle wants to be on the edges rather than the vertices to increase its stability. Interpretation of the other shapes is similar to this case.
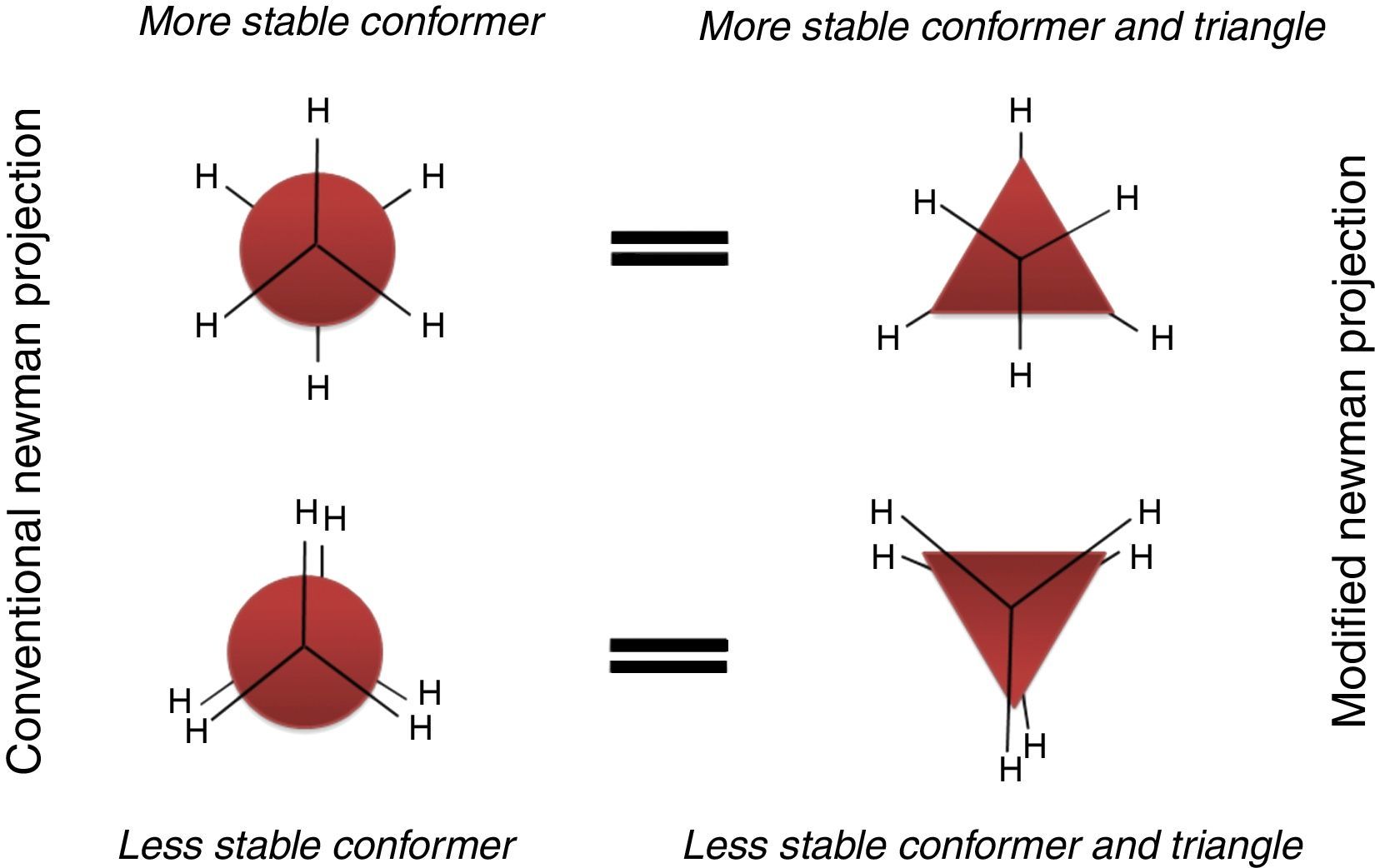
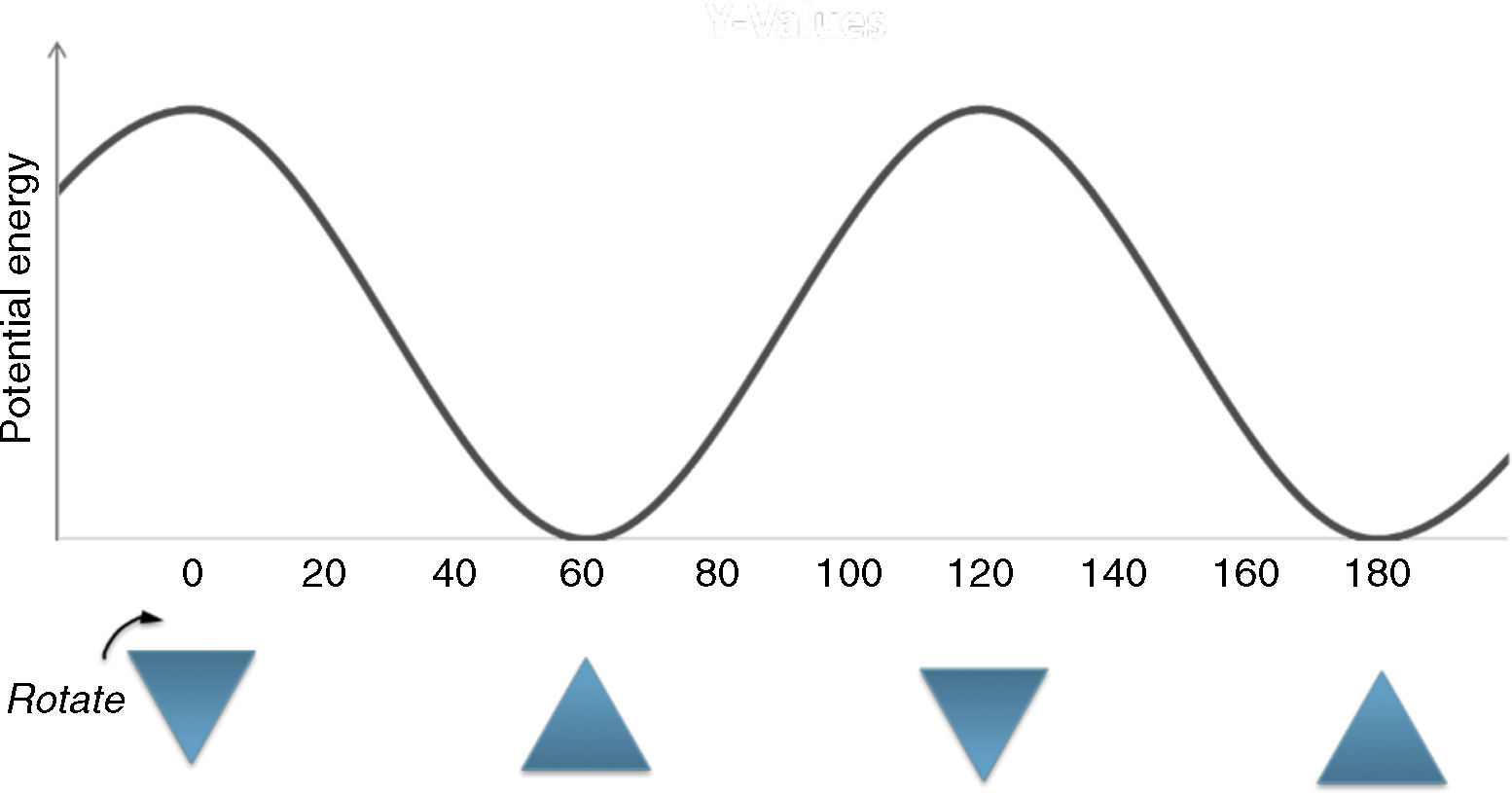
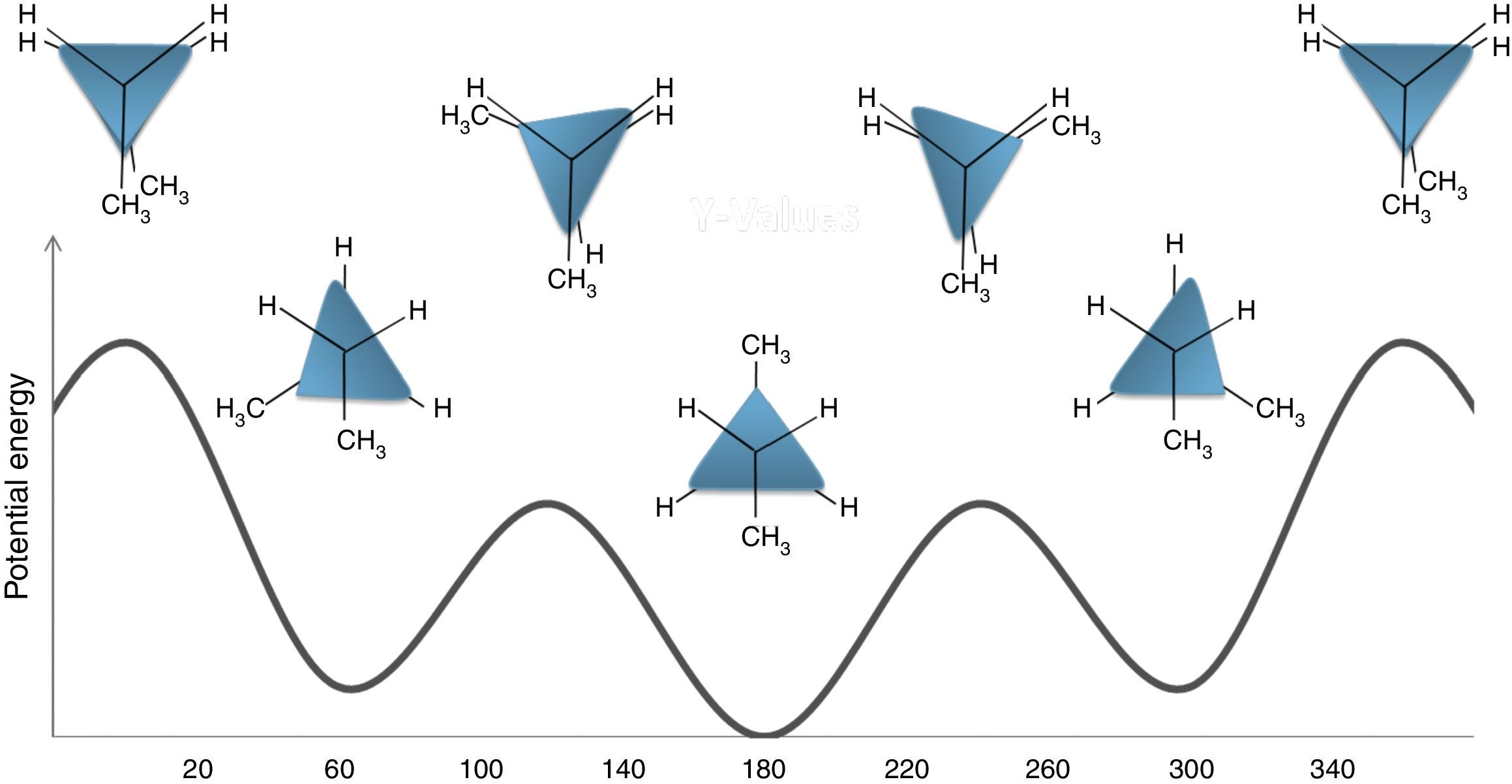
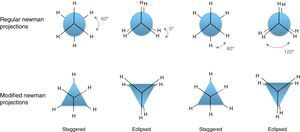
Conformations of the simple alkanesAlkanes conformationally are among the simplest acyclic organic molecules. Methane (CH4) is the simplest form of alkanes. This molecule does not have any carbon–carbon bond, so merely it can exist in one conformation structure (Note: by definition conformation is any of the spatial arrangements of a molecule that can be obtained by rotation of the atoms about a single bond. There is no CC single bond in methane). Recall that, other simple alkane is ethane, which possesses two main conformations; staggered (hydrogens are alternated) and eclipsed (hydrogens are aligned). The staggered conformer is more stable than the other conformer due to the repulsion of electron clouds (two hydrogens), which presents in the eclipsed one. Rotation about carbon–carbon sigma bond in ethane exchanges these conformations (this process is constantly occurring) to each other. One way to demonstrate these conformers is through Newman drawings in which we look straight down the particular carbon–carbon bond to see back and front of the molecule. The front carbon is depicted with a dot that connects three lines to each other and the rear carbon is depicted with a circle.
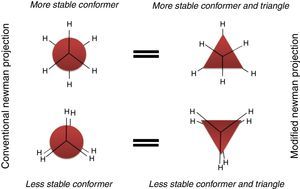
Description of the devised modelA model to explain the ethane conformers and their energy is through the equilateral triangle shape in which a form of the triangle that stands on its edge (stable triangle) represents the more stable staggered conformer, while the other form of triangle (on its vertex) represents the less stable eclipsed conformer. Owing to the equality of all the sides (equilateral triangle) the revolution of the triangle exactly produces the same potential energy (qualitatively) as in ethane molecule. These concepts are evident in Fig. 3.
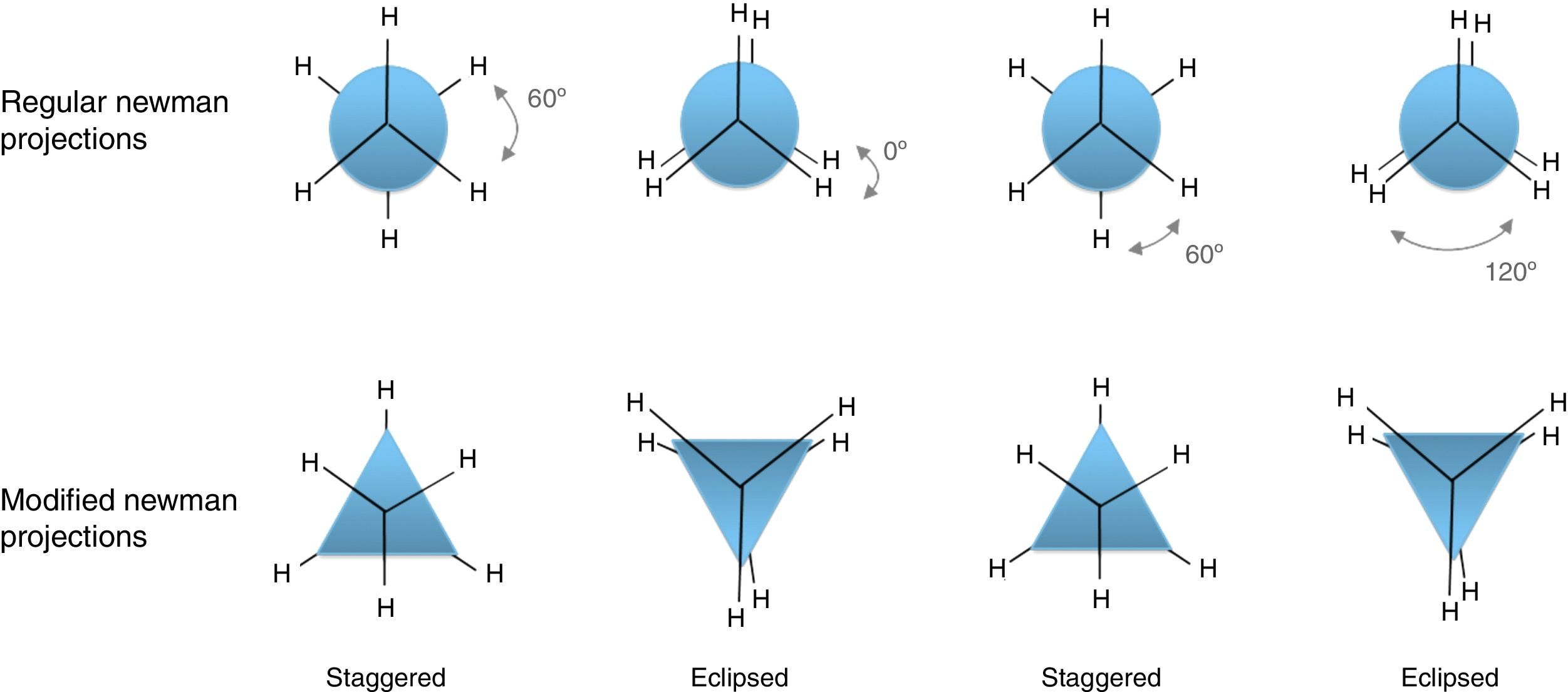
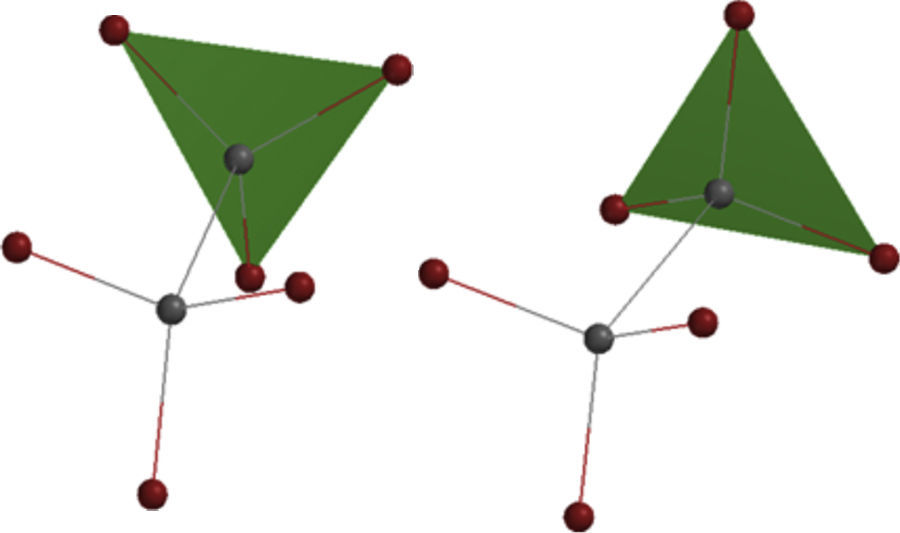
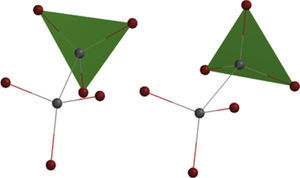
In addition, this model can be merged into the Newman projections (Fig. 4). In this approach, the circle that is drawn in conventional Newman projections as a representation of back carbon (see the conformations of the simple alkanes section) is replaced with this triangle. Although, the triangle is symmetric likewise the circle, but because of the polygon nature of the triangle, the rotation about the bond in modified Newman projections would engender simultaneous alteration of both triangle and the rear hydrogens (substituents) in the direction of rotation (the position of front hydrogens or substituents are considered to be fixed). Thus, if we map the most stable conformer (staggered) on to the most stable shape of the triangle (on its base), the rotation of the molecule gives the inverted triangle and the eclipsed form of the molecule in which both of them are in the unstable form at the same time (it is easier to place the three rear substituents on each corner of the triangle and consider them as a unit, see Fig. 4). Because of this connection between the equilateral triangle and hydrogen substituents in ethane molecule, the conformers of the molecule with their stability can be predicted by just revolving the shape inside the modified Newman projections. So, one glance at the Newman projections of a molecule can reveal the conformational propensity of that molecule. The utilization of triangles could be also justified by considering the fact that the tetrahedral carbon has triangle faces. This fact has been illustrated in Fig. 5 by the help of the Sawhorse projections.
The chief limitation of this new notation is assigning correct and proper shape to the right molecule. To address this issue some rules have been constructed, in order to extend this model to more molecules. These rules are described in the following section. Note that, the provided rules are constructed to be as simple as possible.
Rules and methodologyAs mentioned earlier (physical stability section), the stability of the geometric shapes is associated with two factors (COG position is constant): first, base area or base length and the second is the height of COG. The constructed rules are all based on these two factors and can be rationalized using the same concepts.
- •
Each edge is representative of a stable or meta-stable state.
- •
The length of the edges corresponds to the amount of stability in which the longer length is more stable.
- •
The vertex (corner) of the shapes represents the unstable states (global transition states).
- •
For demonstrating semi-unstable states (local transition states), utilize a circle on the vertex of the shape in which its diameter relates to the stability (longer diameter equals to more stability).
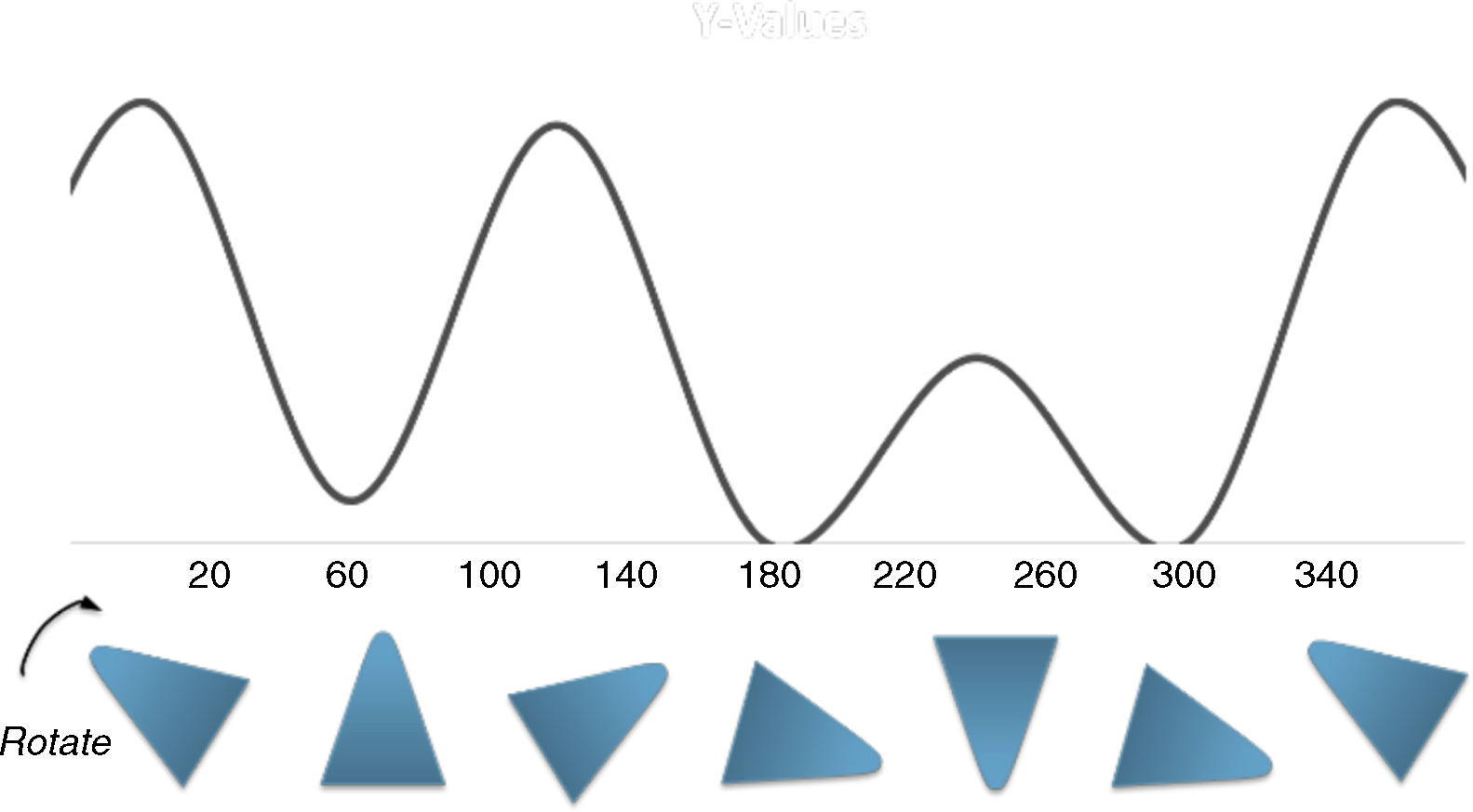
A graphical summary of the stated rules, which show how to employ these rules in geometric shapes were depicted in Fig. 6. These rules can be applied to a large number of molecules to acquire the geometric shape that is consistent with its potential energy diagram.
Conformations of other alkanesThe butane molecule has been selected as a more complex structure to see the validity of the discussed rules. The rotation about the C2 and C3 of this compound gives rise to several (main) conformers. These conformers resemble ethane conformers, but with some differences. Fig. 7 illustrates the potential energy profile for these conformers. This diagram consists of three ground states (GS) and three transition states (TS) in which the GS and TS correspond to staggered and eclipsed conformations, respectively. The most stable GS is a staggered conformer that its two methyl groups are on the opposite sides if we look end-on (look at its Newman projection). This conformation is designated as anti form. The other two GSs (conformers) have the same stability and energy, but have a higher energy with respect to the anti form. These conformers are related to an arrangement called the gauche conformation, which the methyl and hydrogen groups are 60° apart. Similarly, in the TS structures, one of the TSs is also different in stability (least stable conformer) from the other ones. This TS is an eclipsed conformer, which both of its methyl groups are aligned, so this conformer is the most unstable one. This is because of the greater repulsion of methyl groups. Now, to assign a geometric shape to this molecule and to draw the modified Newman projections, from the above rules we anticipated that there should be three edges and three corners (vertices). This is consistent with a triangle shape, which also has three corners and edges. In order to adjust this triangle to the butane energy diagram, we round two corners of the triangle (using two circles with the same diameter) and also enlarge one of its edges to construct an isosceles triangle. The two shorter edges of the isosceles triangle relate to meta-stable gauche conformations and the longer (more stable) one relate to the anti-conformer. Also, the curved corners refer to the semi-unstable and the acute corner of the triangle refers to the least stable conformation. The described shapes are depicted in the potential energy diagram of butane in Fig. 7.
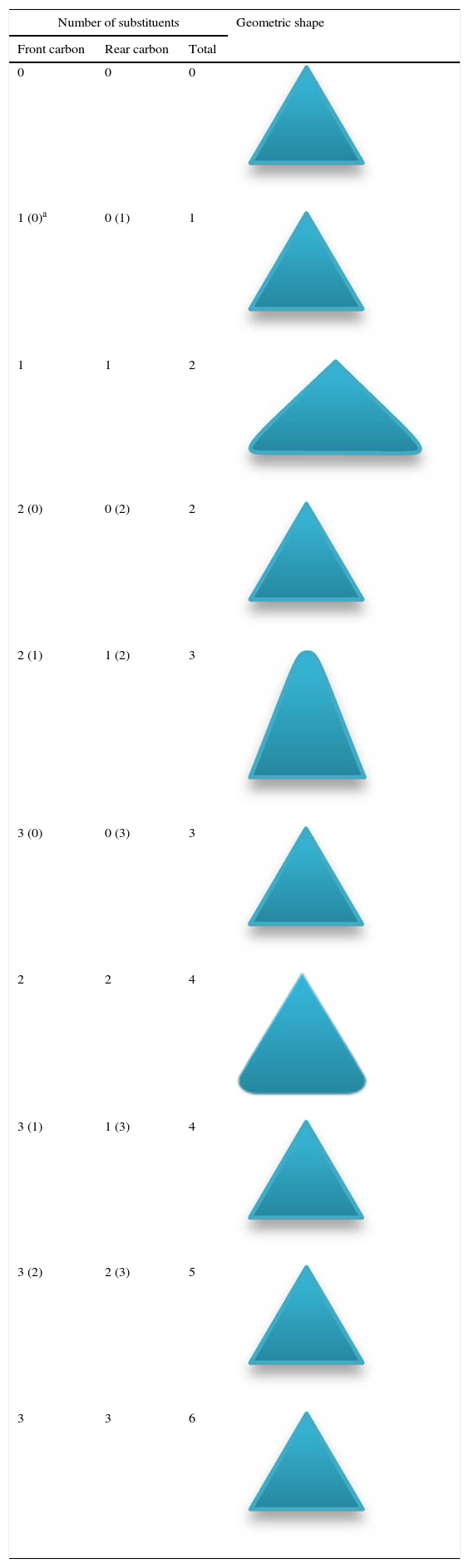
Other alkanes also can be predicted by the remarked rules. Further inspection of the structure and conformation of the alkanes revealed that all the alkanes can be conformationally analyzed by means of only four geometric shapes. This approach can be applied not only to alkanes, but also can estimate the conformations of some other compounds, which have substituents that are approximately similar to the methyl groups. Nevertheless, it merely works qualitatively and not precisely (with some estimations). Table 1 has been drawn to explain which of the shapes pertain to the correct alkane with respect to its number of the substituents. For instance, third row in Table 1 correspond to butane. If we look butane end-on, there is one methyl group attached to the front carbon as well as the rear carbon. In order to make it plainer, several examples were provided in the last section that demonstrate the employment of Table 1 on more complex molecules. The procedure of assigning the correct triangle to the correct molecule (obtaining Table 1) is similar to the butane and previous molecules, which have hitherto been described. Also, it should be mentioned that all the rules presented here are perceptually realizable, so there is no need to instruct these rules in detail. All of the descriptions and rules can be explained in only 5min.
Geometric shapes for predicting alkanes conformations.
| Number of substituents | Geometric shape | ||
|---|---|---|---|
| Front carbon | Rear carbon | Total | |
| 0 | 0 | 0 | |
| 1 (0)a | 0 (1) | 1 | |
| 1 | 1 | 2 | |
| 2 (0) | 0 (2) | 2 | |
| 2 (1) | 1 (2) | 3 | |
| 3 (0) | 0 (3) | 3 | |
| 2 | 2 | 4 | |
| 3 (1) | 1 (3) | 4 | |
| 3 (2) | 2 (3) | 5 | |
| 3 | 3 | 6 | |
These models also can be extended to aldehydes and ketones with some simple modifications, but to be concise, these generalizations are not provided here and are left to the readers as an exercise. However, a brief description has been provided in the Appendix.
Model assessment on more complex moleculesHerein, to become more familiar with the concepts, two examples have been assessed with the implication of this model.
Example 13-Methylhexane – rotation about C3 and C4 bond.
Since, this molecule is classified as an alkane we can use geometric shapes that are given in Table 1 for sketching its energy profile diagram. This structure has one ethyl group attached to C4 and two groups (ethyl and methyl) attached to C3, so the sum of the substituents is 3. From Table 1, two and one (total 3) substituents correspond to the one curved corner isosceles triangle. The quantitative potential energy diagram for this molecule is given in Fig. 8, which is consistent with the proposed geometric shape. Note that, transition energy in 0° and 120° is the same with some estimations (0.2kcalmol−1). This small energy difference is due to the not identical substituents (Me and Et).
Example 21-Chloropropane – rotation about C2–C3.
Owing to the resemblance of the Cl group to the CH3, we can use the same shapes as in alkanes. So, as this molecule has one substituent in each carbon, from Table 1, the geometric shape, which is corresponding to this molecule is the two curved corner triangle. The calculated energy diagram of this molecule demonstrated that it is very similar to what we provided earlier for butane molecule. Thus, the conformation analysis is the same. This consistency transpires the extendibility of this model to alkane-like molecules.
The results of the above examples demonstrated that the constructed model could interpret the energy potential diagram of a more complex molecule, but there are two points that should take into consideration: first, all the geometric shapes, which have been discussed in this study thus far, are all qualitative. Second, with increasing the size of the substituents, the degree of accuracy becomes lower, so these simple shapes may not provide the best results. Thus, all the given information is qualitative and not provides quantitative information.
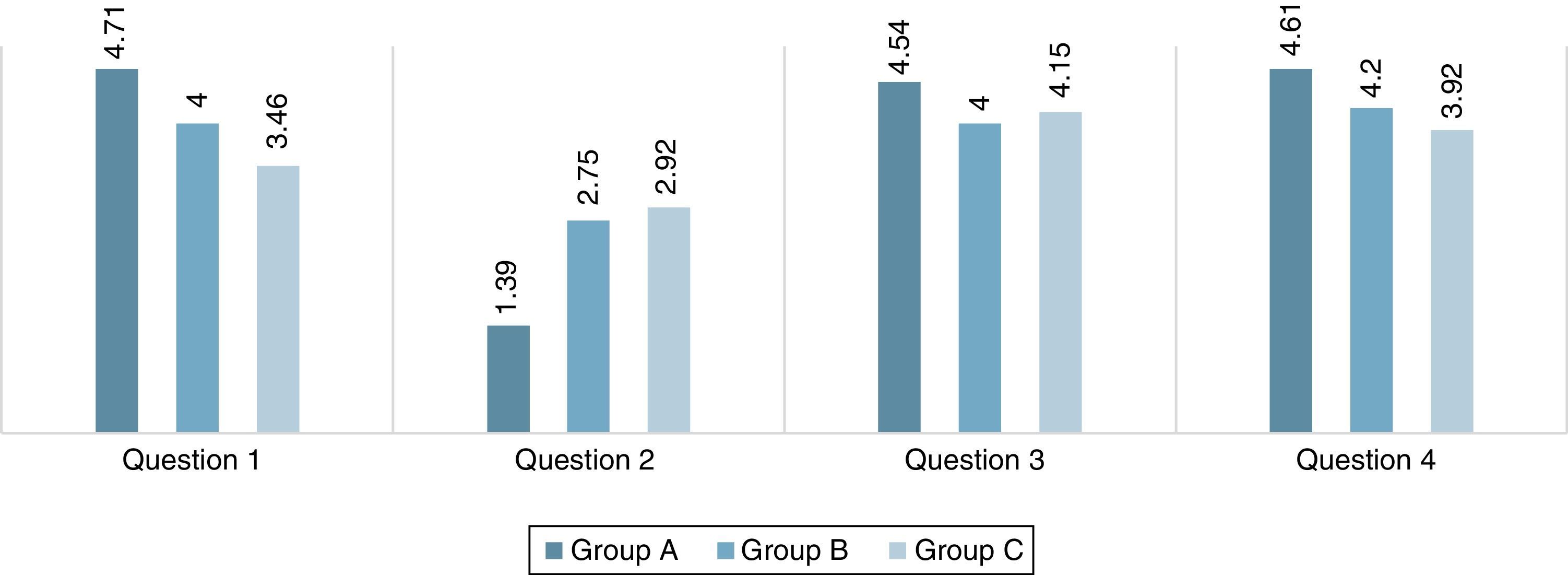
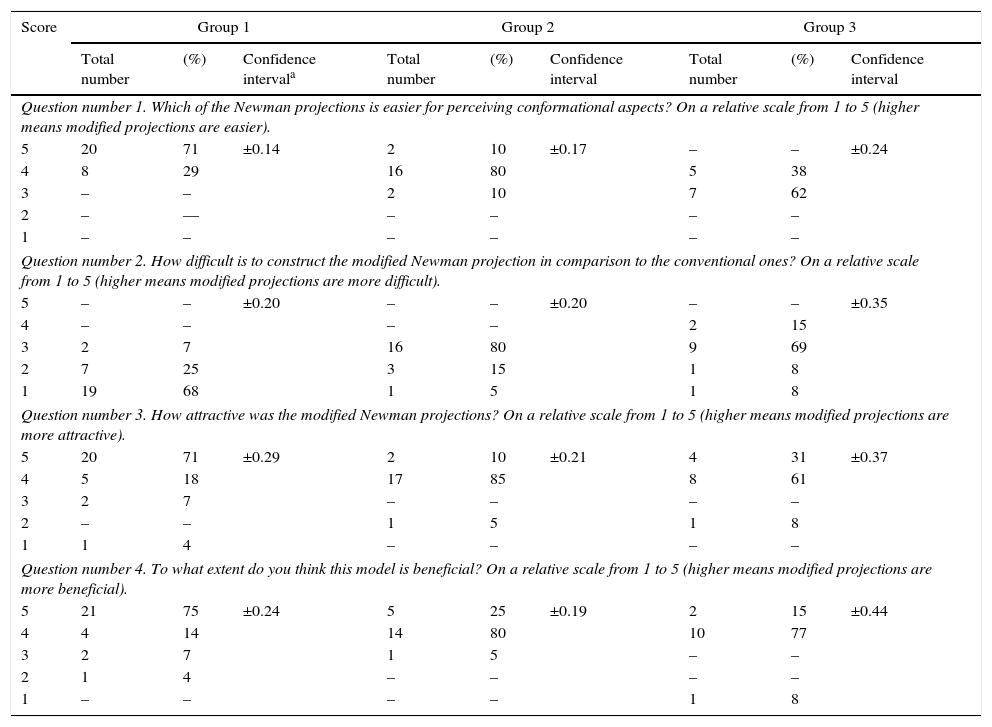
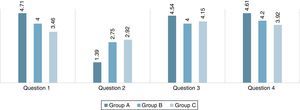
Pedagogical aspects of the modelIn addition to the stated virtues in the introduction section, this model can also be utilized for educational and pedagogical purposes. In order to see the efficacy of the constructed model as a teaching and learning tool in educational purposes, a questionnaire has been distributed to the variety of students, who got familiar with this model earlier. This consists of pupils with no background on the subject (group A, N=28), student with intermediate knowledge (group B, N=20) and upper-level students (graduate student), who have an advanced knowledge (group C, N=13). The questions and the acquired results have been summarized in Table 2 and Fig. 9. As it is illustrated by column chart in this figure, the majority of the group A and B see the model more interesting and easy to construct, on the contrary to the group C, who believes that the construction of this projection is far more complicated than the conventional Newman notions. The reason that group C believes this model is harder to utilize is may due to the fact that this group is much more familiar with the conformational properties of the molecules. Thus, as a result, they are more convenient in using the conventional projections. Furthermore, it should be mentioned that these modified Newman projections have not been meant for simplicity as they may not too simple to construct compared to the conventional notation. They primarily intended as a learning and practicing tool to encourage the students to study the Newman projections, which makes the learning process more enjoyable for them. However, the effectiveness of this model for group A and B demonstrate that these new projections have significant value in learning and teaching basic conformational analysis. Note that, all three groups find these notations very interesting and attractive.
Questionnaire data and statistical analysis.
| Score | Group 1 | Group 2 | Group 3 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Total number | (%) | Confidence intervala | Total number | (%) | Confidence interval | Total number | (%) | Confidence interval | |
| Question number 1. Which of the Newman projections is easier for perceiving conformational aspects? On a relative scale from 1 to 5 (higher means modified projections are easier). | |||||||||
| 5 | 20 | 71 | ±0.14 | 2 | 10 | ±0.17 | – | – | ±0.24 |
| 4 | 8 | 29 | 16 | 80 | 5 | 38 | |||
| 3 | – | – | 2 | 10 | 7 | 62 | |||
| 2 | – | –– | – | – | – | – | |||
| 1 | – | – | – | – | – | – | |||
| Question number 2. How difficult is to construct the modified Newman projection in comparison to the conventional ones? On a relative scale from 1 to 5 (higher means modified projections are more difficult). | |||||||||
| 5 | – | – | ±0.20 | – | – | ±0.20 | – | – | ±0.35 |
| 4 | – | – | – | – | 2 | 15 | |||
| 3 | 2 | 7 | 16 | 80 | 9 | 69 | |||
| 2 | 7 | 25 | 3 | 15 | 1 | 8 | |||
| 1 | 19 | 68 | 1 | 5 | 1 | 8 | |||
| Question number 3. How attractive was the modified Newman projections? On a relative scale from 1 to 5 (higher means modified projections are more attractive). | |||||||||
| 5 | 20 | 71 | ±0.29 | 2 | 10 | ±0.21 | 4 | 31 | ±0.37 |
| 4 | 5 | 18 | 17 | 85 | 8 | 61 | |||
| 3 | 2 | 7 | – | – | – | – | |||
| 2 | – | – | 1 | 5 | 1 | 8 | |||
| 1 | 1 | 4 | – | – | – | – | |||
| Question number 4. To what extent do you think this model is beneficial? On a relative scale from 1 to 5 (higher means modified projections are more beneficial). | |||||||||
| 5 | 21 | 75 | ±0.24 | 5 | 25 | ±0.19 | 2 | 15 | ±0.44 |
| 4 | 4 | 14 | 14 | 80 | 10 | 77 | |||
| 3 | 2 | 7 | 1 | 5 | – | – | |||
| 2 | 1 | 4 | – | – | – | – | |||
| 1 | – | – | – | – | 1 | 8 | |||
Answers to the queries described in Table 2 (the values are reported by taking the mean of all responses).
From the above study we propose three factors, which makes this model as a proper material for educational environments: (i) the better perception of the conformations and stability–instability of the molecules (ii) the increase in motivation and enthusiasm, due to the employment of interactive and more common geometric shapes, which engender more concentration in students on the subject (iii) finding a relevant shape for each conformational diagram is a challenging task and activity, which can encourage the students to get engaged with the topic. Additionally, this model provides a bridge to translate one representation to another (e.g. Sawhorse projections to Newman projections and 2D to 3D translation). As mentioned before the translation from one representation to another is a source of students’ difficulties in learning chemistry (Treagust, Duit, & Nieswandt, 2000; Wu et al., 2001). Finally, this model can also be combined with another hand-held representation such as overhead Newman projections (Silverman & Barbaro, 1999) to provide a tangible way for instructing conformational properties.
ConclusionA model system (an activity) has been devised for conveying the conformational aspects of some simple molecules with interactive and tangible geometric shapes (triangles). These geometric shapes can be used either as an individual tool for teaching conformational properties of molecules or also can be used with the Newman projections to give these representations more reality, which helps the students to interpret them with less difficulty by overcoming translation (between representations) problems. Thus, this model enhanced the students’ ability to make these translations and therefore speeds up the learning process. Since, every model has its own advantages and drawbacks, this model also is not flawless (some adjustments were made to address the issues), but it is significantly efficient for teaching purposes and can be used as a complementary material in this regard. Nevertheless, beyond the pedagogical insights, the newly modified Newman projections are also beneficial owing to the larger data, which we can get from merely a simple notation compared to the conventional representations.
Conflict of interestThe authors declare no conflict of interest.
We would like to express the most sincere appreciation to Professor Avat A. Taherpour for inspiring guidance and encouragements.
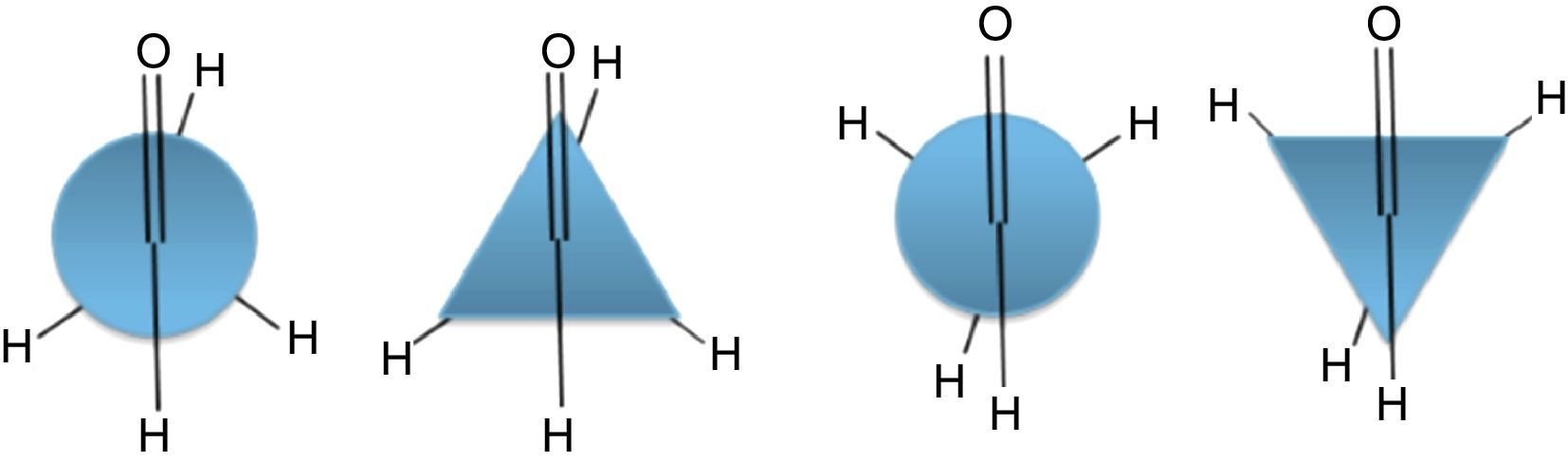
A concise study has been carried out on molecules with carbonyl group to seek the conformations properties of these sort of compounds and to see the suitability of the model.
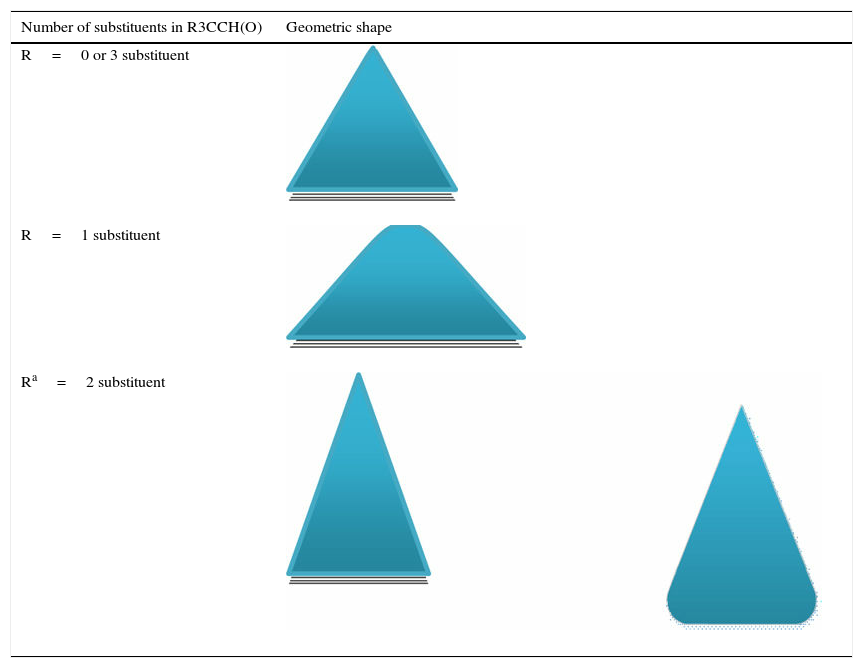
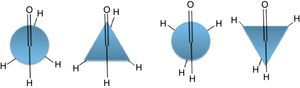
We start our study with consideration of the conformational properties of acetaldehyde molecule. This molecule likewise the ethane molecule has two conformations; eclipsed and bisected (similar to staggered) with regard to rotation about its carbon–carbon bond. Fig. A1 illustrates these conformers with both conventional Newman projections and modified projections. Contrary to the alkanes, which the staggered conformer is the dominant one, in the aldehydes it is the eclipsed conformer that is the favored conformation. This is owing to the reduced repulsion interactions and hyperconjugation. The potential energy diagram of acetaldehyde resembles the ethane molecule that is provided in Fig. 2 of the manuscript. Thus, the lateral triangle can also utilize in this case. To expand the model for other aldehydes a table similar to the previous one (for alkanes) has been provided. The increase in the substituents has been examined and the best geometric shapes that are consistent with the potential energy graph have been offered (Table A1). The given geometric shapes explain the energy profile of all aldehydes with some approximations (qualitatively).
Geometric shapes for predicting aldehyde conformations.
| Number of substituents in R3CCH(O) | Geometric shape |
|---|---|
| R=0 or 3 substituent | |
| R=1 substituent | |
| Ra=2 substituent | |
The conformation of the ketones is somewhat similar to the discussed aldehydes with some differences and can be predicted by small modifications. The existence of more substituents in ketones and also the presence of gauche interactions led to more complex conformers with respect to the aldehydes, which is outside the scope and intention of this study. Those who are interested can apply the same rules and obtain the geometric shapes.
Peer Review under the responsibility of Universidad Nacional Autónoma de México.