El objetivo de este trabajo consistió en el estudio de las diferencias de género en el conocimiento matemático temprano y en sus variables predictoras en 200 alumnos de 5años de edad. Se evaluaron como variables de dominio general: alfabetización emergente, inteligencia fluida, memoria de trabajo y a corto plazo y funciones ejecutivas. Los contrastes estadísticos no arrojaron diferencias significativas entre niños y niñas. El análisis discriminante no mostró un patrón característico en función del género. Sin embargo, el análisis de regresión lineal por pasos indicó que aunque la alfabetización emergente y la inteligencia fluida explicaron la variación en el conocimiento matemático en niños(as), la tercera variable explicativa fue la memoria a corto plazo para las niñas y la memoria de trabajo en niños. Se concluye que las diferencias de género no fueron estadísticamente significativas en relación a las variables predictoras de dominio general y específico en las habilidades matemáticas tempranas.
The main aim of this study was to determine if there were any gender differences in early mathematical knowledge. In order to achieve this, estimated prediction factors were assessed in 200 schoolchildren of 5years-old. Domain-general cognition variables were evaluated, such as fluid intelligence, working memory, short-term memory, executive functions, and early literacy. Statistical contrasts showed no significant differences between boys and girls. Discriminant analysis did not reveal a gender-based characteristic pattern. However, stepwise regression analysis indicated that, although emergent literacy and fluid intelligence explained the variation in early mathematical knowledge for boys and girls, the third explanatory variable was short-term memory for girls, and working memory for boys. The article concludes that gender differences were not statistically different in relation to general and specific domain predictor variables for early maths skills.
Las destrezas matemáticas y cognitivas son un elemento clave para el desarrollo de los países y el crecimiento económico (Hanushek & Woessman, 2008; OECD, 2014; Okan, García-Retamero & Muñoz, 2015; Schrøter-Joensen & Skyt-Nielsen, 2010). La preocupación se acrecienta con base en los resultados obtenidos en los informes PISA (OECD, 2014), donde se manifiestan las dificultades de algunos países europeos para llegar a los niveles promedio en el rendimiento de matemáticas durante el periodo escolar. Estos resultados no pronostican resultados positivos y deben estimular las mejoras en las políticas educativas de los distintos países. Dichas medidas podrían dirigirse a erradicar las diferencias existentes con base en el género entre varones y mujeres; sin embargo, los metaanálisis sobre diferencias de género entre los años ochenta y los noventa promulgaron que estas no eran consistentes en el ámbito matemático y que se relacionaban en mayor medida con aspectos estereotípicos que con la habilidad en el manejo de los números.
Asimismo, en años posteriores se pusieron de manifiesto evidencias a favor de la hipótesis de la similitud de género, que equipara las destrezas de los varones a las de las mujeres en matemáticas (Hyde, Lindberg, Linn, Ellis & Williams, 2008). Posiblemente, debido a que no está confirmada la relación entre el género y la mayor o menor destreza en matemáticas, no se han llevado a cabo medidas oportunas para minimizar estas diferencias. Con respecto a los resultados escolares negativos en matemáticas, la necesidad de tomar medidas enfocadas en el aprendizaje y sus dificultades han promovido el auge de estudios centrados, tanto en las variables que puedan ser determinantes a la hora de establecer diferencias entre estudiantes más o menos competentes en las distintas materias escolares, como en los predictores del aprendizaje de las habilidades académicas básicas.
Es por ello que numerosas investigaciones se han focalizado en el estudio de las variables predictoras del rendimiento matemático, proponiendo líneas de investigación orientadas a profundizar en el conocimiento acerca de estas variables. En un primer lugar se encuentra el estudio de los denominados precursores de dominio general, tales como la memoria de trabajo, la memoria a corto plazo, la velocidad de procesamiento y el nivel de inteligencia, que predicen el rendimiento no solo en matemáticas, sino también en otras materias escolares (Aragón, Navarro, Aguilar & Cerda, 2015; Cirino, 2011; Gullick, Sprute & Temple, 2011; Navarro et al., 2011; Nayfeld, Fuccillo & Greenfield, 2013; Passolunghi & Lanfranchi, 2012; Purpura & Ganley, 2014; Sierra & Ocampo, 2013).
Entre estos predictores la inteligencia general, la memoria a corto plazo, la memoria de trabajo y las funciones ejecutivas se pueden señalar como los más relevantes. Por otro lado, una segunda línea de investigación se basa en el estudio de los precursores de dominio específico de la habilidad matemática, generalmente agrupados bajo el constructo sentido numérico (Geary, Hoard, Nugent & Bailey, 2013; Hannula, Lepola & Lehtinen, 2010; Watts, Duncan, Siegler & Davis-Kean, 2014), entendido como la capacidad basada en la fluidez y la flexibilidad para manipular y comprender los números y las operaciones aritméticas, junto con la destreza para hacer juicios aritméticos derivados de esta comprensión, de manera que constituyan estrategias eficaces en situaciones que requieran el uso de conceptos matemáticos.
Al igual que el análisis de los predictores ha sido objeto de interés, el estudio de las diferencias de género es un hecho también abordado en el ámbito de la investigación en aprendizaje matemático. En esta línea se hallan resultados que no determinan la existencia de diferencias de género en educación infantil ni en educación primaria (Aragón, Delgado, Aguilar, Araújo & Navarro, 2013; Hyde, 2005; Lachance & Mazzocco, 2006; Navarro et al., 2010; Worell & Goodheart, 2006). Por otro lado, aparecen estudios que sí encuentran estas diferencias de género (Dickerson, McIntosh & Valente, 2015; Doris, O’Neill & Sweetman, 2013; Jordan, Kaplan, Nabors-Olah & Locuniak, 2006). En consecuencia, es interesante determinar no solo la posible existencia de diferencias de género a edades en las que se adquieren los aprendizajes matemáticos básicos, sino también conocer si dichos factores que explican las diferencias en el rendimiento matemático se encuentran influenciados o no por el género.
Entre los metaanálisis sobre los patrones cognitivos desplegados por hombres y mujeres de cualquier edad, el trabajo de Hyde (2005) sugiere la hipótesis de la similitud de género, según la cual la ejecución de hombres y mujeres son similares en la mayoría de los dominios cognitivos (habilidades matemáticas, verbales y razonamiento) a cualquier edad. Esta hipótesis se encuentra apoyada por otro reciente metaanálisis (Lindberg, Hyde, Petersen & Linn, 2010). La similitud de género diverge de aquellos modelos que postulan que los hombres y las mujeres (o los niños y las niñas) difieren en alto grado en numerosos dominios psicológicos (Bedard & Cho, 2010; Chen, Chen, Chang, Lee & Chen, 2010; Freeman, 2004; Geiser & Lehmann, 2008; Levine, Vasilyeva, Lourenco, Newcombe & Huttenlocher, 2005; Penner & Paret, 2008).
Por ejemplo, Chen et al. (2010), en un estudio realizado con una amplia muestra de escolares asiáticos de 6 a 17años de edad, señalaron que los niños de los primeros cursos de primaria superaban a las niñas en los dominios cognitivos que se vinculan con el rendimiento matemático. Los factores en los que se encontraron diferencias de género a favor de los varones fueron la capacidad general de aprendizaje, la formación de conceptos, vocabulario, razonamiento verbal, visoespacial y perceptivo y memoria a corto plazo. Sin embargo, las niñas superaron a los niños en la velocidad de procesamiento de la información entre los 6 y los 8años de edad. Estas ventajas a favor de los niños se reducían e incluso eran superadas por las niñas entre los 9 y los 11años. En el mismo estudio, las estudiantes entre los 12 y los 14años comenzaron a sobresalir en habilidades verbales, mientras que los varones las superaban en memoria de trabajo y razonamiento no verbal y numérico. Posteriormente, entre los 15 y los 17años se consolidó la ventaja en las habilidades de tipo verbal en las mujeres adolescentes y en habilidades de tipo no verbal en los varones.
Sin embargo, otro conjunto de investigaciones sugiere la inexistencia de diferencias de género en los primeros años, pero postulan la existencia de una brecha que separa la ejecución de mujeres y varones a favor de estos últimos, y que se situaría en torno a los 9-10años (Fryer & Levitt, 2010; Freeman, 2004; Levine et al., 2005; Robinson & Lubienski, 2011). En esta línea, diversos estudios postulan que las diferencias a favor de los varones irían aumentando de forma paralela a la maduración, desde los primeros cursos de primaria (Husain & Millimet, 2009; Penner & Paret, 2008; Robinson & Lubienski, 2011) hasta hacerse significativas en la adolescencia y en la edad adulta (Bedard & Cho, 2010; Penner & Paret, 2008; Robinson & Lubienski, 2011), en la que permanecerían estables a favor de los varones (Geiser & Lehmann, 2008).
Ante la controversia existente con relación al género, es relevante explorar si existen diferencias en la etapa de transición entre la educación infantil y primaria, especialmente en las habilidades ligadas en mayor medida a las diferencias de género, como son las matemáticas. Asimismo, es procedente analizar si las variables exploradas por la literatura científica predictoras de estas habilidades matemáticas, como son alfabetización emergente, inteligencia fluida, memoria de trabajo, a corto plazo y funciones ejecutivas, se ven influenciadas por el factor género.
MétodoParticipantesLos participantes del presente estudio fueron 200 estudiantes de último curso de educación infantil seleccionados a partir de un muestreo no probabilístico. Sus edades se encontraban entre los 59 y 72 meses (x¿=65.37; dt=3.57). De ellos, 102 fueron niños y 98 niñas. La edad de los niños osciló entre los 59 y los 72meses (x¿=65.51; dt=3.66); en el caso de las niñas fue de entre los 59 y los 71meses (x¿=65.22; dt=3.49).
La evaluación de los estudiantes se realizó con el consentimiento informado de los padres y del alumnado, ajustándose a las normas deontológicas de la investigación con niños. La muestra de estudiantes pertenecía a cuatro centros escolares, de los cuales dos eran públicos y otros dos concertados. Dichos colegios se encontraban en una zona que correspondía al nivel socioeconómico de la clase media española. Del total de la muestra fueron excluidos los alumnos que mostraban necesidades educativas especiales.
Instrumentos• Dígitos en orden directo e inverso (Wechsler, 2005). Para la evaluación de la memoria de trabajo y a corto plazo se empleó la prueba de dígitos (orden directo e inverso) perteneciente a la batería WISC-IV. Por un lado, para la tarea de dígitos en orden directo el evaluado debe repetir series de números enunciadas por el evaluador en el mismo orden en el que han sido mencionados. Esta tarea es útil para la evaluación de la memoria a corto plazo, ya que se almacena una secuencia de dígitos, sin ningún tipo de manipulación. Por otro lado, la tarea en orden inverso sí requiere la manipulación de la información almacenada; en este caso se evaluó la memoria de trabajo verbal. Cada una de las tareas está compuesta de 8 series con 2 intentos cada una. El alfa de Cronbach fue de .78 para la tarea de dígitos en orden directo y de .76 para la tarea de dígitos en orden inverso.
• Get Ready to Read! Screening Tool (Whitehurst & Lonigan, 2003). Esta prueba en su versión computarizada fue empleada para la evaluación de la alfabetización emergente. Concretamente, evalúa la conciencia fonológica (conocimiento de los sonidos de las letras, la segmentación de palabras y las rimas) y el conocimiento del texto escrito (comprensión y discriminación de letras o palabras escritas). Se presentan 20 ítems con cuatro opciones cada uno, entre los que se encuentra la respuesta correcta a la cuestión planteada. Su alfa de Cronbach fue de .78.
• Test de Matrices Progresivas de Raven Color (Raven, 1996). Mediante el uso de esta prueba se valoró el factor g (inteligencia fluida) en los estudiantes que formaron parte de la muestra. Este test implica el establecimiento de relaciones lógicas entre una figura carente de una parte y los posibles patrones que la completan. De este modo se puede evaluar cómo el estudiante otorga sentido a un material desorganizado empleando constructos no verbales que facilitan la comprensión de la estructura compleja presentada. Su alfa de Cronbach fue de .82.
• Animal Stroop (Van der Ven, Kroesbergen, Boom & Leseman, 2012). Para evaluar la inhibición como función ejecutiva, se empleó una tarea en la que se presentaban dibujos de animales formados por el cuerpo de un animal y la cabeza de otro, generando de este modo un efecto de interferencia. El estudiante enunciaba verbalmente el animal al que correspondía el cuerpo, teniendo que inhibir la respuesta automática de nombrar el animal en función de su cabeza. Concretamente, esta prueba presenta 48 ítems de control y 48 de inhibición. El alfa de Cronbach fue de .96.
• Simon Task (Van der Ven et al., 2012). Esta prueba, al igual que la anterior, evaluaba la inhibición, pero en este caso la respuesta en vez de ser verbal era manual, de modo que el alumno debía inhibir la tendencia natural a pulsar la tecla de respuesta en el lugar de presentación del estímulo. Concretamente, se empleó una adaptación de la prueba en la que el evaluado debía presionar una tecla situada a la izquierda en el extremo de un teclado especial tipo RB-730. Dicho teclado disponía de una fila de siete teclas. Las situadas en los extremos coincidían con el color de los personajes, para no causar interferencia adicional ni añadir variables extrañas a la evaluación.
Los evaluados debían pulsar la tecla azul a la izquierda del teclado cuando veían a un ratón en la pantalla, y una tecla situada en el extremo derecho del teclado cuando aparecía un dragón. Los ítems de control se basaban en la presentación de los personajes en el centro de la pantalla, y en la condición de inhibición aparecían en los extremos de la misma; esta condición era congruente cuando coincidía la tecla a pulsar con el lugar de presentación del estímulo, e incongruente cuando no lo hacía. La prueba constaba de 40 ítems de control y 40 de inhibición. El alfa de Cronbach fue de .94.
• Animal Shifting (Van der Ven et al., 2012). La prueba consiste en una presentación de ítems para evaluar la habilidad de shifting del participante utilizando 40 ítems de control y 40 de prueba. Esta prueba se adaptó de modo que en la tarea de shifting se presentaban dos imágenes (un animal y una fruta) de manera simultánea en la pantalla del ordenador. El participante debía nombrar verbalmente solo una de ellas en función del color de fondo de la pantalla. Sin embargo, en la tarea de control se mostraba solo una imagen para nombrar. Su alfa de Cronbach fue de .93.
• Test de Evaluación Matemática Temprana Informatizado [TEMT-i] (Van Luit et al., en prensa). Se empleó una versión computarizada con el fin de evaluar el conocimiento numérico temprano y detectar el alumnado con riesgo de tener Dificultades de Aprendizaje de las Matemáticas (DAM). Esta prueba es de gran utilidad en la transición de educación infantil a primaria para detectar el alumnado que necesita del apoyo necesario para afrontar los nuevos aprendizajes matemáticos, y de este modo adecuar una intervención temprana para poder evitar o prevenir graves dificultades en cursos futuros. Se encuentra destinada a estudiantes entre 4 y 7años, su aplicación es individual y el tiempo de administración es de unos 30min. Consta de dos grupos de subtests compuestos, a su vez, por distintas tareas que contribuyen a la evaluación de conceptos matemáticos tempranos.
En primer lugar, el subtest relacional consta de tareas de comparación, clasificación, correspondencia uno a uno y seriación. Por otro lado, el subtest numérico se compone de tareas de conteo verbal, conteo estructurado, conteo (sin señalar), conocimiento general de los números y estimación. Todas estas variables se evalúan a partir de 45 ítems con una puntuación máxima de 45 puntos (uno por cada ítem correcto). Su alfa de Cronbach fue de .92.
ProcedimientoPara la evaluación de los estudiantes se planificaron 2 sesiones de trabajo llevadas a cabo por psicólogos entrenados para ello. El orden de las sesiones varió de unos alumnos a otros, así como el orden de realización de las pruebas. En una de las sesiones se aplicó la prueba Get Ready to Read para la evaluación de la alfabetización emergente y la prueba TEMT-i para estudiar el conocimiento matemático temprano. En la segunda sesión se aplicaron el resto de pruebas cognitivas para la evaluación de las funciones ejecutivas (animal stroop, simon task y animal shifting), memoria a corto plazo y de trabajo (tarea de dígitos de WISC-IV) y factor g (Raven color). Para las evaluaciones se reservó un lugar en la escuela libre de ruidos y de distracciones, donde se llevaron a cabo las sesiones, dentro del horario escolar.
ResultadosPara el análisis de los datos se recurrió inicialmente al cálculo de los estadísticos descriptivos de las variables consideradas por la literatura especializada como predictoras de dominio general del conocimiento matemático.
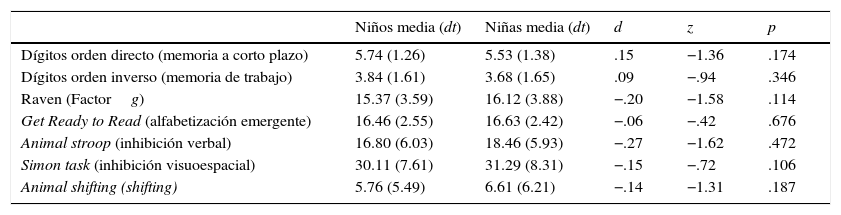
En la tabla 1 se puede observar que los niños fueron superiores a las niñas en memoria a corto plazo y de trabajo. Sin embargo, las niñas fueron superiores en el resto de variables estudiadas. Es decir, factor g, alfabetización emergente y las tres pruebas destinadas a la evaluación de las funciones ejecutivas (shifting, inhibición verbal y visuoespacial).
Media, desviación típica y resultados de la prueba U de Mann-Whitney para las variables predictoras del conocimiento matemático temprano en función del género
| Niños media (dt) | Niñas media (dt) | d | z | p | |
|---|---|---|---|---|---|
| Dígitos orden directo (memoria a corto plazo) | 5.74 (1.26) | 5.53 (1.38) | .15 | −1.36 | .174 |
| Dígitos orden inverso (memoria de trabajo) | 3.84 (1.61) | 3.68 (1.65) | .09 | −.94 | .346 |
| Raven (Factorg) | 15.37 (3.59) | 16.12 (3.88) | −.20 | −1.58 | .114 |
| Get Ready to Read (alfabetización emergente) | 16.46 (2.55) | 16.63 (2.42) | −.06 | −.42 | .676 |
| Animal stroop (inhibición verbal) | 16.80 (6.03) | 18.46 (5.93) | −.27 | −1.62 | .472 |
| Simon task (inhibición visuoespacial) | 30.11 (7.61) | 31.29 (8.31) | −.15 | −.72 | .106 |
| Animal shifting (shifting) | 5.76 (5.49) | 6.61 (6.21) | −.14 | −1.31 | .187 |
Para estudiar si dichas diferencias de género fueron o no significativas se recurrió al contraste estadístico U de Mann-Whitney, cuyos resultados se presentan en la tabla 1; se muestra que las diferencias entre ambos géneros no fueron significativas: en todas las variables se obtuvo un valor de p>.05.
Asimismo, como objetivo del estudio se planteó analizar las diferencias de género en las variables relacionadas con el sentido numérico que han sido identificadas como predictores de dominio específico para las destrezas matemáticas.
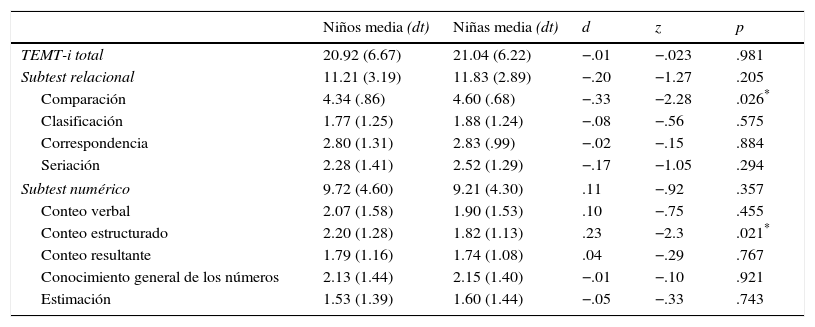
En la tabla 2 se recoge un análisis pormenorizado de los estadísticos descriptivos de los distintos componentes que constituyen las habilidades relacionales y numéricas del conocimiento matemático temprano.
Media y desviación típica y resultados de la prueba U de Mann-Whitney en función del género de las puntuaciones totales de la prueba de evaluación del conocimiento matemático temprano (TEMT-i), de los subtest relacionales, numéricos, y de sus componentes
| Niños media (dt) | Niñas media (dt) | d | z | p | |
|---|---|---|---|---|---|
| TEMT-i total | 20.92 (6.67) | 21.04 (6.22) | −.01 | −.023 | .981 |
| Subtest relacional | 11.21 (3.19) | 11.83 (2.89) | −.20 | −1.27 | .205 |
| Comparación | 4.34 (.86) | 4.60 (.68) | −.33 | −2.28 | .026* |
| Clasificación | 1.77 (1.25) | 1.88 (1.24) | −.08 | −.56 | .575 |
| Correspondencia | 2.80 (1.31) | 2.83 (.99) | −.02 | −.15 | .884 |
| Seriación | 2.28 (1.41) | 2.52 (1.29) | −.17 | −1.05 | .294 |
| Subtest numérico | 9.72 (4.60) | 9.21 (4.30) | .11 | −.92 | .357 |
| Conteo verbal | 2.07 (1.58) | 1.90 (1.53) | .10 | −.75 | .455 |
| Conteo estructurado | 2.20 (1.28) | 1.82 (1.13) | .23 | −2.3 | .021* |
| Conteo resultante | 1.79 (1.16) | 1.74 (1.08) | .04 | −.29 | .767 |
| Conocimiento general de los números | 2.13 (1.44) | 2.15 (1.40) | −.01 | −.10 | .921 |
| Estimación | 1.53 (1.39) | 1.60 (1.44) | −.05 | −.33 | .743 |
Los resultados sitúan a las niñas con mejores puntuaciones en el total del test que evaluaba el conocimiento matemático temprano. Con respecto a los subtests, las niñas fueron superiores en todos los componentes del subtest relacional (comparación, clasificación, correspondencia y seriación). Sin embargo, los niños destacaron en el subtest numérico, siendo superiores a las niñas en conteo verbal, conteo resultante y conteo estructurado; por el contrario, estas fueron ligeramente superiores en conocimiento general de los números y estimación.
Asimismo, se realizó un contraste estadístico para estudiar si las diferencias encontradas fueron significativas. Los resultados únicamente mostraron diferencias significativas (p<.05) en dos tareas: para las niñas en tareas de comparación, y para los niños, en conteo estructurado. Sin embargo, tomando un nivel de confianza del 99% (p<.01) no se hallaron diferencias significativas entre ambos grupos (tabla 2).
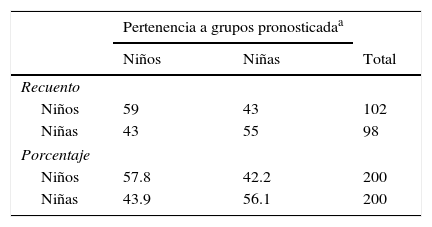
Finalmente se llevó a cabo un análisis discriminante para estudiar si era posible obtener una función capaz de clasificar a los alumnos con base en los valores obtenidos en las distintas variables estudiadas. Esta técnica de análisis estadístico facilitó una clasificación supervisada de vectores de datos numéricos en dos categorías con base en el género, es decir, niños y niñas. El análisis realizado consistía en la obtención de un hiperplano frontera capaz de delimitar ambos grupos de participantes. La distribución obtenida se comparó con los resultados reales y arrojó una matriz de clasificación donde su diagonal representaba los totales o porcentajes de los individuos bien clasificados y donde los elementos extradiagonales representaron los falsos positivos y falsos negativos del procedimiento de clasificación. Los resultados se recogen en la tabla 3.
Resultado del análisis discriminante para predecir la pertenencia de los alumnos en función del género
| Pertenencia a grupos pronosticadaa | |||
|---|---|---|---|
| Niños | Niñas | Total | |
| Recuento | |||
| Niños | 59 | 43 | 102 |
| Niñas | 43 | 55 | 98 |
| Porcentaje | |||
| Niños | 57.8 | 42.2 | 200 |
| Niñas | 43.9 | 56.1 | 200 |
Según los resultados del análisis discriminante, el 57% de los participantes fueron clasificados correctamente en su grupo. Como consecuencia, podemos deducir que no existe un patrón que defina la ejecución del alumnado en las distintas pruebas empleadas con base en el género.
Adicionalmente, se realizó un contraste de igualdad de grupos con base en el estadístico lambda de Wilks y resuelto por una aproximación chi-cuadrado, el cual determinó la aceptación de la hipótesis de igualdad entre los grupos (lambda de Wilks=.955; χ2=8.86; p=.354). La conclusión extraída de dichos resultados fue que las diferencias entre los grupos en función del género no fueron en ningún caso significativas y se corroboraron los resultados anteriormente presentados.
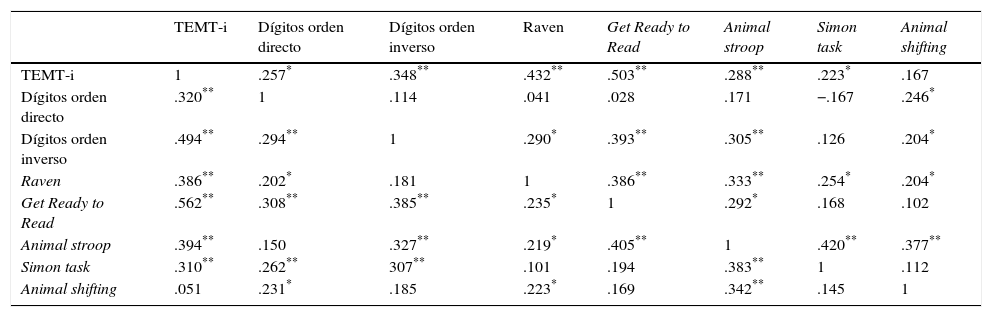
Todas las variables cognitivas de dominio general identificadas por la literatura como predictoras de las habilidades matemáticas tempranas se correlacionaron con los resultados obtenidos en el TEMT-i, exceptuando la medida de inhibición visuoespacial, que no se correlacionó significativamente en el caso de las niñas ni de los niños (tabla 4).
Correlaciones bivariadas entre las variables para las niñas (por encima de la diagonal) y niños (por debajo de la diagonal)
| TEMT-i | Dígitos orden directo | Dígitos orden inverso | Raven | Get Ready to Read | Animal stroop | Simon task | Animal shifting | |
|---|---|---|---|---|---|---|---|---|
| TEMT-i | 1 | .257* | .348** | .432** | .503** | .288** | .223* | .167 |
| Dígitos orden directo | .320** | 1 | .114 | .041 | .028 | .171 | −.167 | .246* |
| Dígitos orden inverso | .494** | .294** | 1 | .290* | .393** | .305** | .126 | .204* |
| Raven | .386** | .202* | .181 | 1 | .386** | .333** | .254* | .204* |
| Get Ready to Read | .562** | .308** | .385** | .235* | 1 | .292* | .168 | .102 |
| Animal stroop | .394** | .150 | .327** | .219* | .405** | 1 | .420** | .377** |
| Simon task | .310** | .262** | 307** | .101 | .194 | .383** | 1 | .112 |
| Animal shifting | .051 | .231* | .185 | .223* | .169 | .342** | .145 | 1 |
Del mismo modo, se realizaron análisis de regresión por pasos para estudiar el peso que presentaban las variables cognitivas estudiadas en la explicación de la variable dependiente, es decir, las habilidades matemáticas tempranas tanto en niños como en niñas.
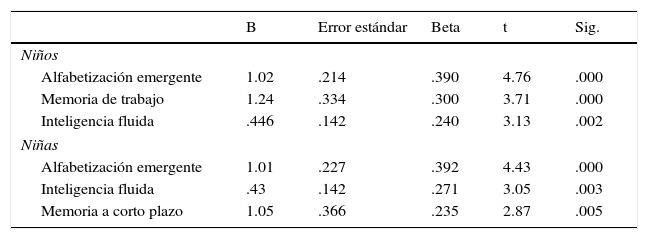
Del análisis de regresión surgieron 3 modelos explicativos, tanto en el caso de los niños como en el de las niñas. El tercer modelo ofreció una mayor capacidad explicativa. Los varones obtuvieron un coeficiente de correlación múltiple de R=.678 y coeficiente de determinación R2=.460 que se ajustaba a R2=.44. En el caso de las niñas el coeficiente de correlación múltiple fue R=.612 y el coeficiente de determinación R2=.375, que se ajustaba a R2=.355. Por un lado, en el caso de las niñas las variables introducidas en el modelo fueron alfabetización emergente (β=.392), inteligencia fluida (β=.271) y memoria a corto plazo (β=.235). Por otro, en el caso de los niños las variables fueron alfabetización emergente (β=.390), memoria de trabajo (β=.300) e inteligencia fluida (β=.240) (tabla 5).
Resultados de los análisis de regresión en función del género
| B | Error estándar | Beta | t | Sig. | |
|---|---|---|---|---|---|
| Niños | |||||
| Alfabetización emergente | 1.02 | .214 | .390 | 4.76 | .000 |
| Memoria de trabajo | 1.24 | .334 | .300 | 3.71 | .000 |
| Inteligencia fluida | .446 | .142 | .240 | 3.13 | .002 |
| Niñas | |||||
| Alfabetización emergente | 1.01 | .227 | .392 | 4.43 | .000 |
| Inteligencia fluida | .43 | .142 | .271 | 3.05 | .003 |
| Memoria a corto plazo | 1.05 | .366 | .235 | 2.87 | .005 |
El presente trabajo pretendió explorar las diferencias de género en el conocimiento matemático temprano a los 5años de edad y en las variables definidas por la literatura como explicativas de estas destrezas matemáticas. Asimismo, se analizaron las diferencias de género de las variables cognitivas en la explicación de las habilidades matemáticas tempranas.
Los resultados descriptivos y los contrastes de hipótesis, así como el análisis discriminante, no arrojaron diferencias significativas entre niños y niñas en las habilidades matemáticas tempranas, ni en las variables cognitivas estudiadas.
En primer lugar, el estudio reflejó ausencia de diferencias de género en el total del test que evaluó las habilidades matemáticas tempranas (TEMT-i). Tampoco se encontraron diferencias en los subtests relacionales y numéricos. Únicamente se encontraron dos grupos de actividades (de las nueve que componen el test) en las que se hallaron diferencias significativas: las de comparación a favor de las niñas y el conteo estructurado a favor de los niños.
Sin embargo, la diferencias dejaban de ser significativas con un nivel de confianza del 99% (p<.01). La literatura especializada apoya los resultados hallados en este trabajo y sugiere que no existen diferencias de género en el desempeño matemático en educación infantil, ni en educación primaria (Aragón et al., 2013; Jordan et al., 2006; Hyde, 2005; Lachance & Mazzocco, 2006; Navarro et al., 2010; Worell & Goodheart, 2006).
En segundo lugar se estudiaron las diferencias existentes entre niños y niñas en las variables cognitivas evaluadas. No se pudieron constatar diferencias de género en memoria de trabajo y a corto plazo a los 5años de edad (Adams, Simmons & Willis, 2015; Bourke & Adams, 2011; Palejwala & Fine, 2015). Con respecto a la alfabetización emergente, aunque las niñas superaron a los niños en estas destrezas, las diferencias no llegaron a ser estadísticamente significativas.
Existen trabajos que defienden que la niñas sobresalen en este aspecto de manera significativa desde la educación infantil (Below, Skinner, Fearrington & Sorrell, 2010) para ir igualándose al inicio de la educación primaria (Robinson & Lubienski, 2011; Husain & Millimet, 2009). Sin embargo, en el presente trabajo a los 5años no se obtuvieron diferencias significativas entre ambos grupos (Gray, Peng, Steward & Thomas, 2004). Por otro lado, a pesar de no ser significativas las diferencias en inteligencia fluida (Keith, Reynolds, Roberts, Winter & Austin, 2011), las niñas fueron superiores a los niños (Palejwala & Fine, 2015). Finalmente, tampoco se encontraron diferencias significativas relacionadas con el género en las funciones ejecutivas evaluadas (Ritter, Perrig, Steinlin & Everts, 2014; Viterbori, Usai, Traverso & de Franchis, 2015).
Resumiendo, los niños obtuvieron puntuaciones superiores en memoria de trabajo y a corto plazo. Sin embargo, las niñas obtuvieron una mejor ejecución en alfabetización emergente, inteligencia fluida, inhibición y shifting. No obstante, ninguna de las diferencias encontradas en las variables analizadas llegó a ser estadísticamente significativa. Los resultados encontrados son similares a los hallados por Hyde et al. (2008), los cuales reflejaron la ausencia de diferencias de género en las habilidades matemáticas entre los grados 2 y 11, apoyando su hipótesis de la similitud de género (Hyde, 2005).
Por otro lado, Chen et al. (2010) demostraron que los niños de los primeros cursos de primaria superaban a las niñas en los dominios cognitivos que se vinculan con el rendimiento matemático. Los factores en los que se encontraron diferencias de género a favor de los varones fueron capacidad general de aprendizaje, formación de conceptos, vocabulario, razonamiento verbal, visuoespacial y perceptivo, y memoria; sin embargo, las niñas superaron a los niños en la velocidad del procesamiento de la información entre los 6 y los 8años de edad (Chen et al., 2010). Estas ventajas a favor de los niños se reducían e incluso eran superadas por las niñas entre los 9 y los 11años. Nuestros resultados se sitúan en la hipótesis de la similitud de género, si bien es cierto que determinados estudios han encontrado diferencias entre niños y niñas en los primeros años que se han ido disipando conforme iban avanzando en edad.
Finalmente, el análisis discriminante mostró que no existía un patrón que explicase la ejecución de los niños y las niñas con base en su género. Sin embargo, el análisis de regresión sí mostró algunas diferencias en el peso que las variables cognitivas presentaban en la explicación de la habilidad matemática temprana entre niños y niñas. A pesar de que, exceptuando la habilidad de shifting, las variables cognitivas estudiadas se correlacionaron significativamente con la habilidad matemática temprana, no todas las variables fueron introducidas en los modelos explicativos. Las funciones ejecutivas no fueron introducidas en el modelo, por ser menos predictivas de las habilidades matemáticas tempranas a los 5años que la memoria de trabajo o a corto plazo (Viterbori et al., 2015).
La diferencia más importante entre los modelos explicativos fue que la memoria a corto plazo formó parte del grupo de variables explicativas en el caso de las niñas (Visu-petra, Cheie & Benga, 2008) y la memoria de trabajo en el caso de los niños (Ganley & Vasilyeva, 2013). La alfabetización emergente y la inteligencia fluida lo fueron tanto en niñas como en niños (Östergren & Träff, 2013; Primi, Ferrao & Almeida, 2010; Purpura, Hume, Sims & Lonigan, 2011). Sabemos que aunque la mayoría de los patrones neurales relacionados con aspectos cognitivos se solapan, el procesamiento neural puede cambiar en función del género, concretamente en la región y en el grado de activación neural.
En este caso estamos hablando de que existen diferencias de procesamiento entre hombres y mujeres desde el punto de vista neurológico (Hill, Laird & Robinson, 2014; Lejbak, Crossley & Vrbancic, 2011). Dentro de estos aspectos cognitivos se encuentran la memoria a corto plazo y la memoria de trabajo y, por tanto, se encuentran implicados su subcomponentes, es decir, las funciones ejecutivas. En el estudio de Kaufman (2007) se evaluó, entre otras variables, la memoria de trabajo y a corto plazo verbal de estudiantes adolescentes (16 y 18años), sin encontrarse diferencias con respecto al rendimiento en dichas habilidades. Por otra parte, el presente trabajo pretendió arrojar luz a la posible diferencia de procesamiento a la hora de enfrentar una tarea matemática, incidiendo en la posibilidad de que en función del género se utilicen distintas estrategias de procesamiento a la hora de resolver tareas de corte matemático (Carr & Davis, 2001).
Con respecto a las limitaciones del estudio y las perspectivas futuras, la presente investigación arrojó diferentes modelos en niños y en niñas en la explicación de la variación en las habilidades matemáticas tempranas. No obstante, las diferencias significativas en las distintas variables estudiadas entre ambos géneros fueron inexistentes a los 5años. Aunque los resultados se encuentran en la línea de la hipótesis de la similitud de género (Hyde, 2005), no puede constatarse la veracidad de la misma y, en consecuencia, la inexistencia de una brecha a favor de los varones desde la educación primaria hasta la edad adulta. Ello se debe a que no se dispone de datos longitudinales que confirmen o no la existencia de esta brecha en años posteriores.
En consecuencia, las futuras líneas de trabajo se centrarán en realizar esos contrastes de datos longitudinales para analizar si la ausencia de estas diferencias continúa con el paso de los años y del progreso escolar. Esta línea es especialmente relevante no solo por la importancia que tiene el dominio de las matemáticas para el desarrollo y el progreso de la sociedad, sino también porque, a pesar de la existencia o no de diferencias de género a nivel cognitivo, existe una importante discrepancia entre el número de hombres y mujeres que cursan estudios técnicos universitarios. Aún estamos lejos de definir cuál puede ser la causa de esa desigualdad, pero esta línea de trabajo puede arrojar luz a la propuesta de medidas de prevención para la completa integración de las mujeres en disciplinas con arraigado contenido matemático.
AgradecimientosTrabajo co-financiado con el proyecto PSI2015-63856-P (MINECO & FEDER).