Introducción
Los meridianos (Jing-Luo) de acupuntura conforman una red antigua y moderna a la vez, que pretende describir el funcionamiento fisiológico del hombre. Antigua debido a la data de su elaboración más primaria, pues el Nei Jing data de, al menos, del año 100 a.C. y moderna en concepción, puesto que el estudio de las redes es algo relativamente reciente. El campo de la medicina complementaria y, en especial, de la medicina tradicional asiática hace uso extensivo de estos conceptos y no debe permanecer apartado de lo que constituye uno de los principales paradigmas de la investigación científica moderna utilizado para estudiar los sistemas complejos, la teoría de redes1,2.
El estudio de la teoría de redes es un fenómeno moderno y ha conocido un rápido incremento en años recientes, pero no es hasta el descubrimiento de los efectos denominados de "mundo pequeño" y la propiedad "libre de escala" que surge el interés por estudiar redes provenientes de los ámbitos biológico, social y tecnológico3,4.
En los 12 años transcurridos hasta la fecha, entre la publicación del trabajo pionero de Watts y Strogatz acerca de la propiedad "mundo pequeño"5 se han creado nuevas herramientas matemáticas y de software, muchas de éstas gratuitas, y áreas como la biología han dado la bienvenida a este paradigma6.
Entonces podríamos preguntarnos, ¿por qué habría de ser de alguna importancia el estudiar la estructura de la red de meridianos y puntos de acupuntura?
Debido a un antiguo principio ampliamente reconocido en la medicina moderna, "la estructura afecta la función". Este trabajo pretende introducir al investigador y al terapeuta tradicional en el estudio de las redes aplicado a la medicina tradicional asiática y producir, además, una caracterización básica de la citada red desde la perspectiva de la teoría de redes y de gráficas.
El estudio de las gráficas ha evolucionado desde el campo de las matemáticas "puras" pasando por la física de los siglos XX y XXI hasta alcanzar la biología y ciencias médicas6. Es el momento de tomar el paso para aquellos dedicados al campo de la medicina complementaria.
En este trabajo se realiza, por primera vez, la caracterización de los canales o meridianos de acupuntura como lo que son realmente, una red.
A pesar de que el campo de la teoría de redes está en desarrollo se puede establecer una serie de parámetros estándar para evaluar una red, de los cuales 3 no pueden ser eludidos3:
La distribución de grado de la red.
El coeficiente de agrupamiento de la red.
La longitud de camino promedio característica de la red.
Obtener estos parámetros y otros es a lo que se llama determinar la topología de la red7. El sistema de meridianos y puntos de acupuntura puede ser fácilmente convertido en símbolos susceptibles de ser analizados por las herramientas de software, basta transformar los puntos de acupuntura y los órganos Zang-Fu en los nodos o vértices de nuestra red, y el recorrido o camino entre un par de puntos o desde un punto hasta un órgano en un arco. Este sencillo cambio de terminología nos brinda las ventajas del enfoque abstracto peculiar a un científico dedicado al estudio de las redes, permitiendo integrar las, a veces, intrigantes indicaciones terapéuticas y efectos de algunos puntos de acupuntura en una visión fisiológica coherente y, además, comprender las peculiares relaciones entre tejidos y órganos propias a la medicina tradicional asiática. Finalmente, el uso de los programas de software de análisis de redes nos permitirá desarrollar la investigación de la medicina complementaria sobre firmes bases científicas, comprobando las informaciones que hemos recibido, corrigiéndolas si es necesario o aumentándolas, en lugar de llevar a la práctica ciegamente estos modelos fisiológicos, los cuales, como podremos ver, nos han llegado de manera incom pleta.
Métodos
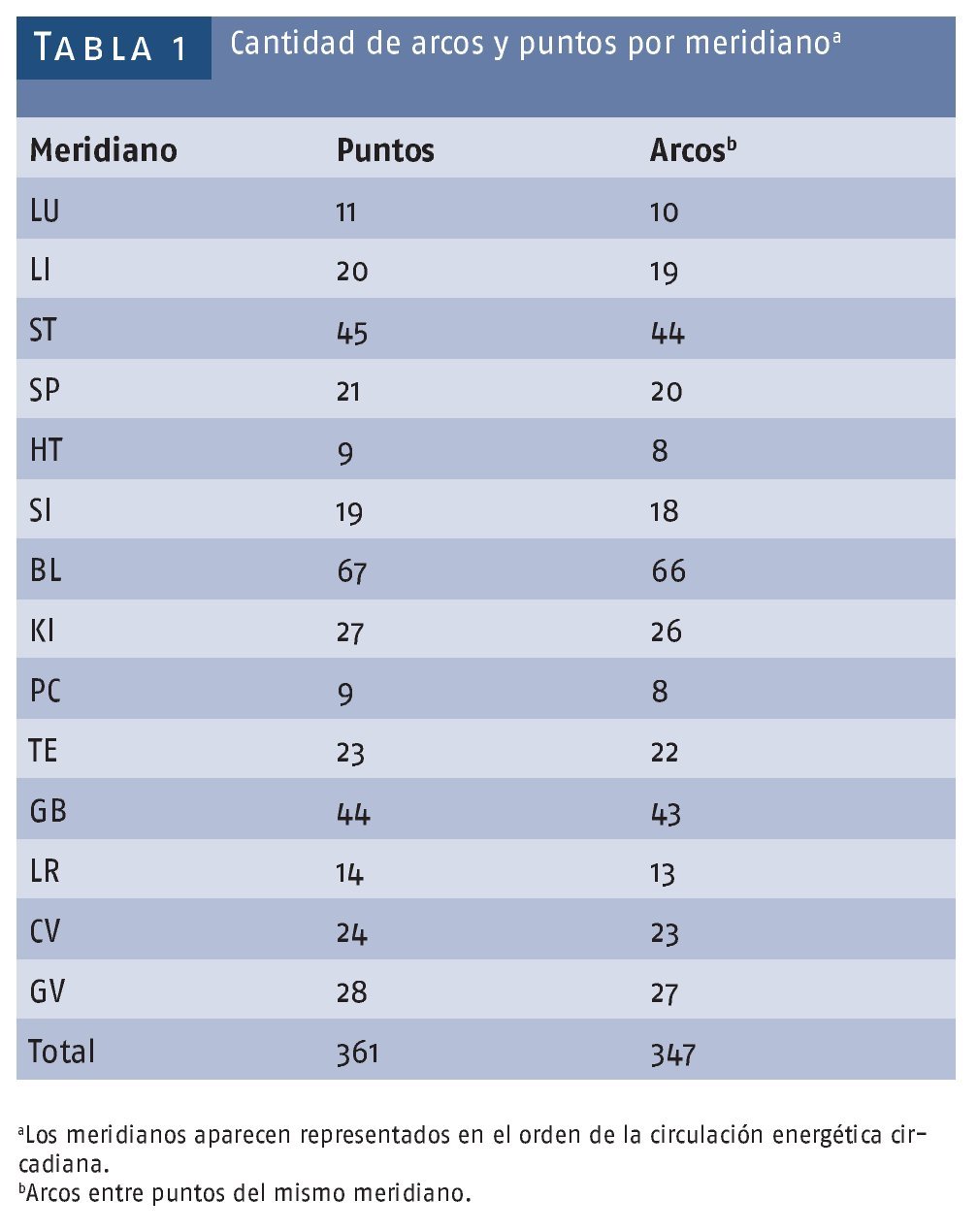
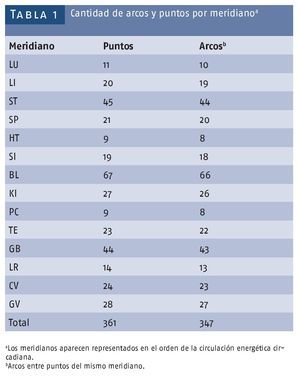
En el Huang Di Nei Jing8 se plantea que existen 365 puntos, aunque en el texto solamente se mencionan 160; sin embargo, si contamos la cantidad de puntos al añadir los puntos pertenecientes a cada uno de los meridianos principales obtenemos solamente 309 (tabla 1), si a estos añadimos los que corresponden a los meridianos Du y Ren alcanzamos un máximo de 361. Como se puede apreciar faltan 4 puntos y no se da ninguna explicación. La cantidad de puntos se ha ido incrementando con el tiempo desde los 160 mencionados en el Nei Jing hasta la cantidad referida actualmente y fijada por Li Xuen Chuan en su trabajo de 1817, el Zhen Jiu Fen Yan8. Para nuestro análisis solamente vamos a considerar los 361 puntos aceptados excluyendo los cerca de 600 puntos extrameridianos9 más los Ashi.
A fin de lograr una representación lo más exacta posible de esta red incluí los puntos pertenecientes a ambos lados del cuerpo doblando, en consecuencia, el número de nodos de la red, ahora 618, también representé el camino profundo de los meridianos por el interior del cuerpo, más los correspondientes meridianos Luo. Los órganos Zang-Fu también fueron representados por medio de nodos (n = 12), así como también algunos otros órganos relacionados con ellos. Cada recorrido de meridiano es representado por medio de arcos que conectan sucesivamente puntos de acupuntura y órganos. En la red, en estudio se representaron además los recorridos de los 8 meridianos extraordinarios (Du, Ren, Chong Mai, Dai Mai, Yang Wei Mai, Yin Wei Mai, Yang Qiao Mai y Yin Qiao Mai). Para lograr una representación gráfica más adecuada se adicionaron varios nodos para permitir bifurcaciones en el recorrido de algunos meridianos, incrementándose el número de nodos a un total de 719. Se puso especial cuidado en los recorridos por el interior del cuerpo y en los cruces de meridianos. Para elaborar la lista se utilizó, en lo fundamental, el libro El gran libro de la medicina China de la autora Ping L10. El graficado de la red, así como el cálculo de la longitud de camino promedio, el diámetro y la intermediación se obtuvieron por medio del software Pajek11, el coeficiente promedio de agrupamiento, el coeficiente de mezclado (assortativity), la distribución de grado y el exponente de escalamiento se calcularon por medio del software Matlab.
Dediquemos un momento a revisar algunos de los conceptos que vamos a utilizar en el presente análisis. En una red, el grado (k) de un nodo es igual alnúmero total de arcos entrantes y salientes de ese nodo. La distribución de grado expresa la probabilidad P(k) de que un nodo seleccionado aleatoriamente tendrá grado k; el coeficiente de agrupamiento (Ca) es un índice de la estructura local y se ha interpretado como una medida de la resistencia y respuesta de la red a los errores aleatorios (si se pierde un nodo, sus vecinos podrían permanecer conectados); la longitud de camino característica (L) de un gráfico es la media de las longitudes de camino entre todos los posibles pares de vértices, y es un indicador de cuán bien integrado que está un grafo y de cuán fácil es transportar información u otras entidades en la red. Una medida relacionada con la longitud de camino es el diámetro,ésta es la longitud de la geodésica más larga del grafico. Otro parámetro es la correlación de grado (Cg), indicador de en qué medida el grado de un nodo está influenciado por otros nodos con los cuales se enlaza. Un parámetro que mide la importancia relativa de un nodo es la intermediación, número de caminos más cortos que pasan por un recorrido o por un nodo, aquí se da en forma de promedio para toda la red y para algunos órganos Zang-Fu relevantes3.
Finalmente, el coeficiente de mezclado es una medida de hasta qué punto los nodos de la red en estudio tienden a conectarse con otros con grado similar (en este caso el coeficiente es positivo) o con otros con grado disimilar (aquí el coeficiente es negativo)12. Ahora ya estamos listos para caracterizar la red de meridianos y puntos de acupuntura.
Resultados
Desde un punto de vista estrictamente matemático, la red de meridianos y puntos de acupuntura es un hipergráfico espacial complejo, porque varios arcos arriban o salen de nodos adyacentes y existen varios arcos paralelos, a pesar de que ningún nodo permanece sin al menos un arco que lo enlace13. También la red en cuestión pertenece al tipo espacial o geográfico, pues la posición de los nodos (puntos de acupuntura y órganos) y las distancias entre éstos es relevante para la evolución y funcionamiento de la red, como lo es para las redes neurales7. Sin embargo, en el presente trabajo no examinaremos las distancias entre nodos.
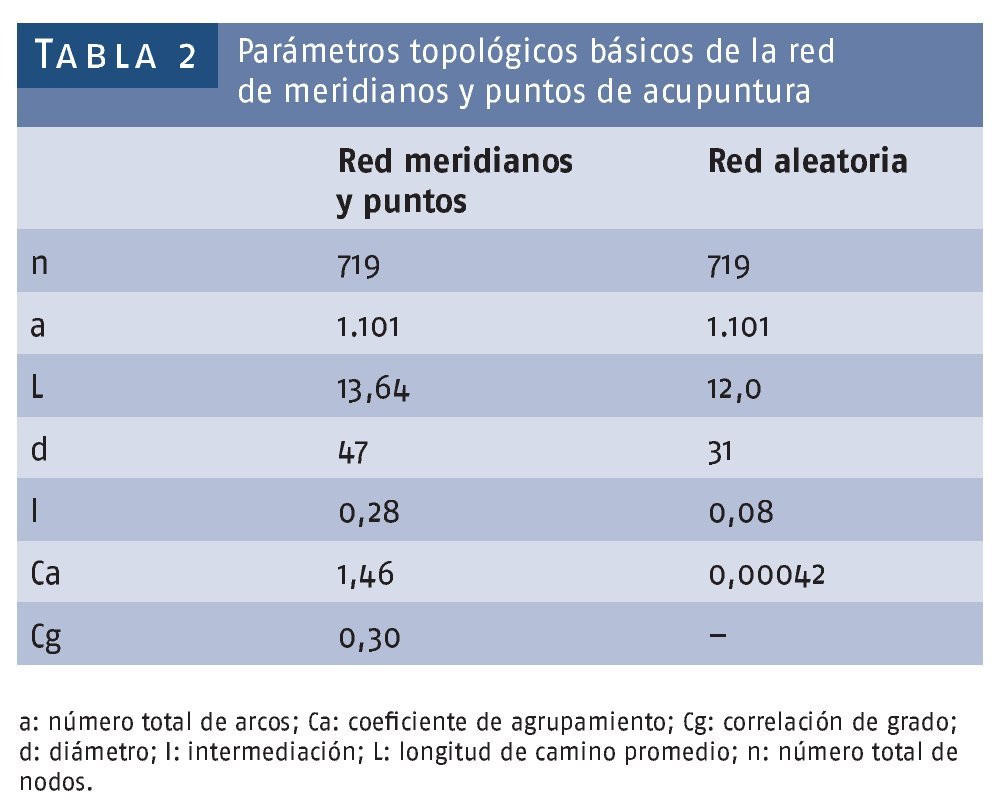
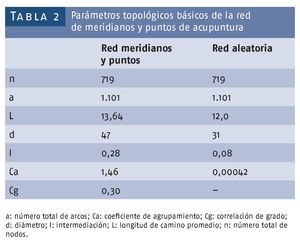
El grado por nodo varió entre 1 y 30, con un promedio de 3, moda en 2 y desviación estándar (σ) de 2,2. Una pregunta relevante es si la red de meridianos y puntos de acupuntura es una red compleja. Una red compleja es una red con una estructura muy complicada14. Debido a esto pudiera parecer trivial mencionar que la red de meridianos y puntos de acupuntura es una red compleja, pues aparece ante nuestra vista como un enmarañamiento complejo de puntos y líneas que recorren el cuerpo humano. Sin embargo, son sus características topológicas las que la definen inequívocamente como una red compleja (tabla 2). Una manera común de estudiar una red es comparar sus características con las de una red equivalente generada aleatoriamente7.
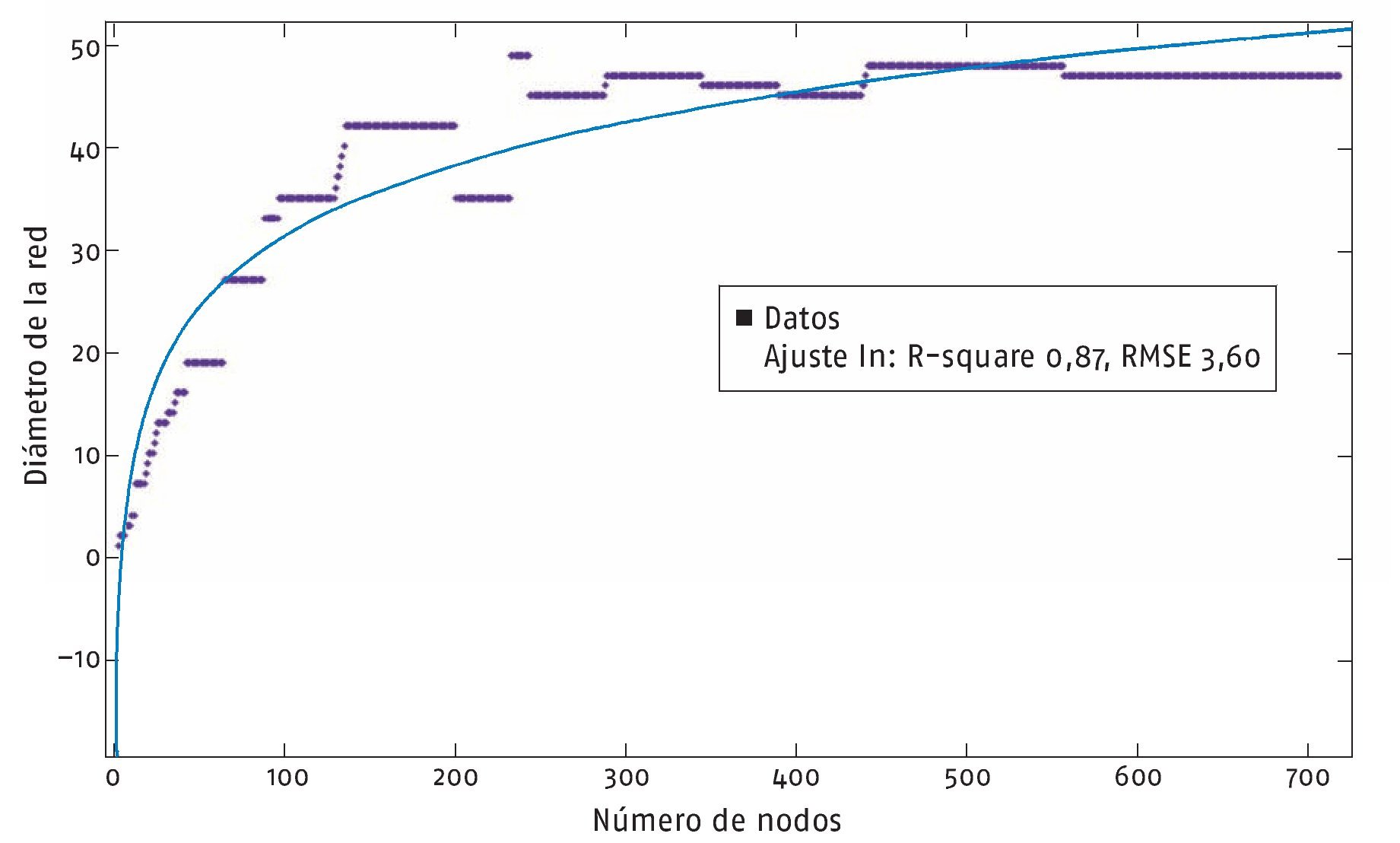
La red de meridianos y puntos de acupuntura tiene un Ca = 1,46, mayor que el de la red aleatoria utilizada para compararla (Ca = 0,00042), esto último nos asegura también que la vecindad local alrededor de cada nodo está bien preservada. Además, el Ca es incluso mayor que el de una red ordenada o rejilla, que es aproximadamente de 0,7513. Al estudiar la red, también es necesario determinar la relación entre su diámetro y el número de nodos, en nuestro caso el diámetro se incrementa logarítmicamente con el número de nodos (fig. 1).
Fig. 1: Incremento del diámetro con el tamaño de la red.
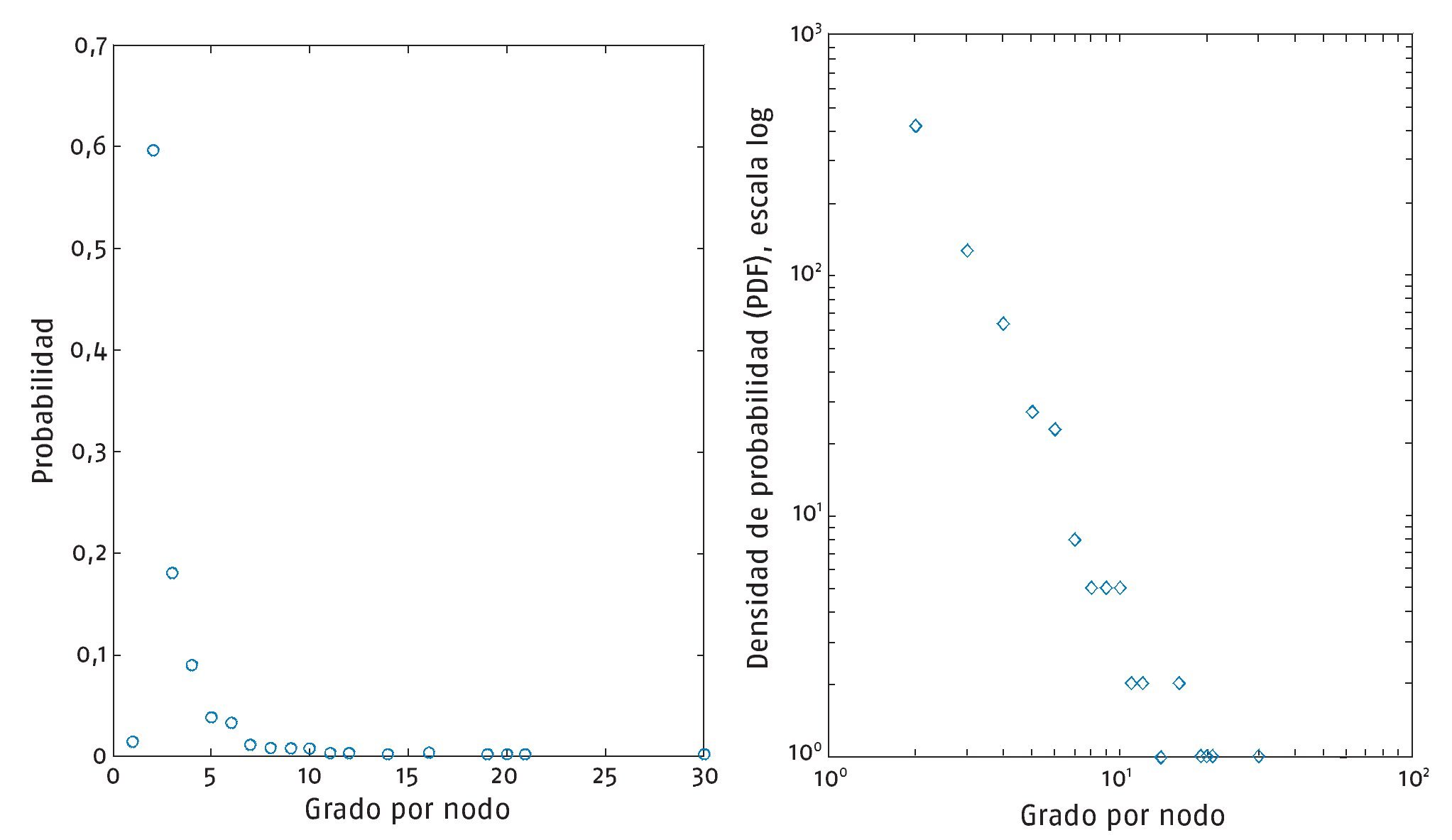
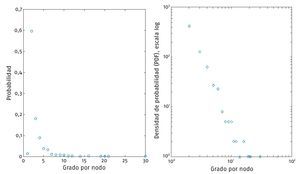
La intermediación promedio de la red es de 0,28, que resulta mayor que la de la red aleatoria de comparación. La distribución de grado de la red (fig. 2) muestra una caídarápida de su cola y en la misma figura el cuadro B permite apreciar una ley de potencia en la génesis de la red, implicando que posee la propiedad «libre de escala».
Fig. 2: Distribución de la probabilidad de grado por nodo. A) Escala linear. B) Densidad de probabilidad, escala log-log.
Los parámetros topológicos básicos de la red de meridianos y puntos de acupuntura se reflejan en la tabla 2.
Discusión
Por su extensión, la red de meridianos y puntos de acupuntura, clasifica entre las medianas, comparable en tamaño con las redes metabólicas; por ejemplo, Escherichia coli tiene una red con 765 nodos, las redes neurales, por ejemplo el nematodo Caenorhabditis elegans con 312 nodos, la red de interacciones mecánicas de las proteínas de Saccharomyces cerevisiae posee 2.115 nodos (detalles adicionales en referencia 13).
Ahora podríamos preguntarnos si la red en estudio cumple alguna de las propiedades de las redes complejas.
La red de meridianos y puntos de acupuntura es una red con propiedades de "mundo pequeño" porque:
Posee un coeficiente de agrupamiento mayor que el de la red de comparación y también que el de una red ordenada.
La relación entre el diámetro de la red y el número de nodos se incrementa logarítmicamente15 (fig. 1). Esta red, también tiene una longitud de camino pequeña (13,64), cercana a la de la red aleatoria, lo que la torna resistente al daño. La intermediación de la red (0,28) es también mayor que la de la red aleatoria, esto indica que en la red existe un número elevado de caminos más cortos entre nodos.
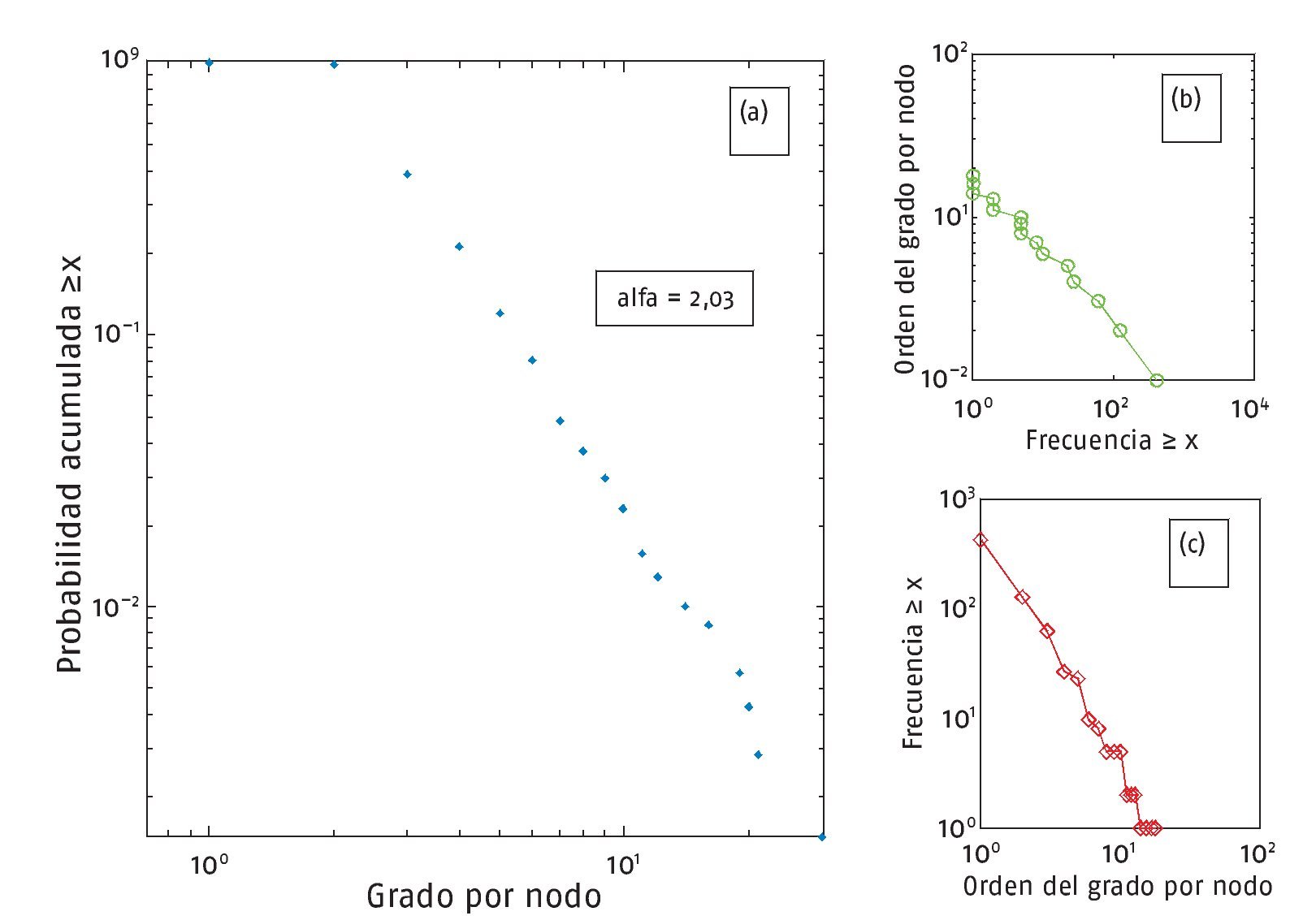
Además, esta red muestra en su distribución de grado unarápida caída en la cola hacia la derecha (fig. 2). En escala logarítmica se puede apreciar mejor este fenómeno, en la figura 2B, esta distribución de los puntos formando una línea recta con pendiente negativa implica que la red tiene además la propiedad «libre de escala». Una forma de hallar si esta propiedad está presente es explorar la distribución acumulada de grado por nodo15. En la figura 3A la ley de potencia es apreciada en la caída en línea recta de la distribución15, implicando en consecuencia que los datos poseen la propiedad "libre de escala". El exponente de incremento o escalamiento se calculó de acuerdo con Jeong et al6 (α = 2,03, con un error de σ de ± 0,03). En la bibliografía acerca de las leyes de potencia uno encuentra habitualmente los gráficos de orden/frecuencia y de Pareto; en la figura 3 se muestran para la red en cuestión y son respectivamente B y C. En aras de la claridad es importante tener presente las diferencias entre ambos tipos de gráficos, en la figura 3A está referido a distribución acumulada de probabilidades, B y C representan frecuencias acumuladas (tener sobre todo en cuenta que entre estos 2 últimos los ejes de coordenadas están invertidos).
Fig. 3: Distribuciones acumuladas de grado por nodo. A) Muestra la distribución acumulada de probabilidad. B) Gráfico número de orden/frecuencia. C) Diagrama de Pareto para los mismos datos.
La red de meridianos y puntos de acupuntura es una red espacial compleja, porque sus características fundamentales no se pueden explicar si la suponemos conectada aleatoriamente. Es también una red "mundo pequeño" y "libre de escala", como la mayor parte de las redes metabólicas de los organismos vivos14. La propiedad "mundo pequeño" nos dice de la red en estudio que es posible conectar 2 nodos por medio de sólo unos pocos enlaces, entre 13 y 14 pasos, lo que se puede plantear también diciendo que los nodos de esta red tienden a enlazarse con otros nodos cercanos. La propiedad "libre de escala" se refiere a la ausencia de un grado por nodo característico7 en la distribución de grado, y nos señala 2 cosas importantes: la primera, que esta red conserva las huellas de un proceso de adhesión preferencial en sus orígenes en el que nodos con alto grado se enlazan a otros de alto grado14, con respecto a esto último se debe tener en cuenta que aunque esta red aparezca como fija en los libros de texto, la red de meridianos y puntos debe seguir un proceso embrionario de desarrollo, en el cual los nodos de mayor grado (órganos Zang-Fu, los "ejes" de la red) aparecen más tempranamente que los demás nodos, de manera similar al de sus contrapartes de la medicina moderna, en un proceso que corre en paralelo al que genera linajes celulares, tejidos y órganos, y además, en segundo lugar, indica la importancia de los nodos ricos en grado ("ejes") que se conectan con aquellos otros más pobres, siendo esta característica la que ofrece robustez a la red frente a fallos accidentales de nodos14,20 debido a que las redes libres de escala no tienen un umbral crítico para su desintegración14. La red tiene un exponente de escalamiento de 2,03, que se encuentra en el rango de todas las redes libres de escala ya estudiadas, que poseen un exponente entre 2 < α < 314, lo que también ocurre con la mayor parte de las leyes de potencia encontradas en la naturaleza16. Como consecuencia de ser este exponente casi igual a 2 emerge una estructura llamada de "eje-rayo"14, con el eje mayor en el centro, en nuestro caso es el órgano Corazón que se encuentra en contacto con una amplia fracción del total de nodos (este nodo recibe 14 entradas y envía 16, en comparación con el punto de acupuntura promedio que envía y recibe 1 conexión).
La red muestra una longitud de camino promedio comparable a la de los circuitos electrónicos y redes de transmisión de energía eléctrica13. Podríamos especular que esto hace a la red eficiente, la eficiencia de una red puede ser calculada, pero no fue objetivo de este trabajo.
El alto Ca ha sido identificado como una señal de topología modular en la mayor parte de las redes, se plantea que tales módulos son una característica fundamental de las redes biológicas19, y varias redes estudiadas los exhiben4. Resulta una tarea pendiente el determinar cuáles están presentes en la red de meridianos y puntos y si corresponden con algún ordenamiento conocido, como por ejemplo el de órganos Zang-Fu con tejidos y otros órganos asociados. Esto podría elevar los conocimientos de fisiología tradicional a un nivel cuantitativo y quizás brindar nuevos agrupamientos que den información relevante.
A pesar de ser ésta una red teóricamente robusta, debido a la propiedad "mundo pequeño", por su alto Ca (ver también referencia 18), podemos notar que las enfermedades se producen y preguntarnos, ¿cuál es la relación entre la patogénesis tradicional y la topología de la red de meridianos y puntos de acupuntura?
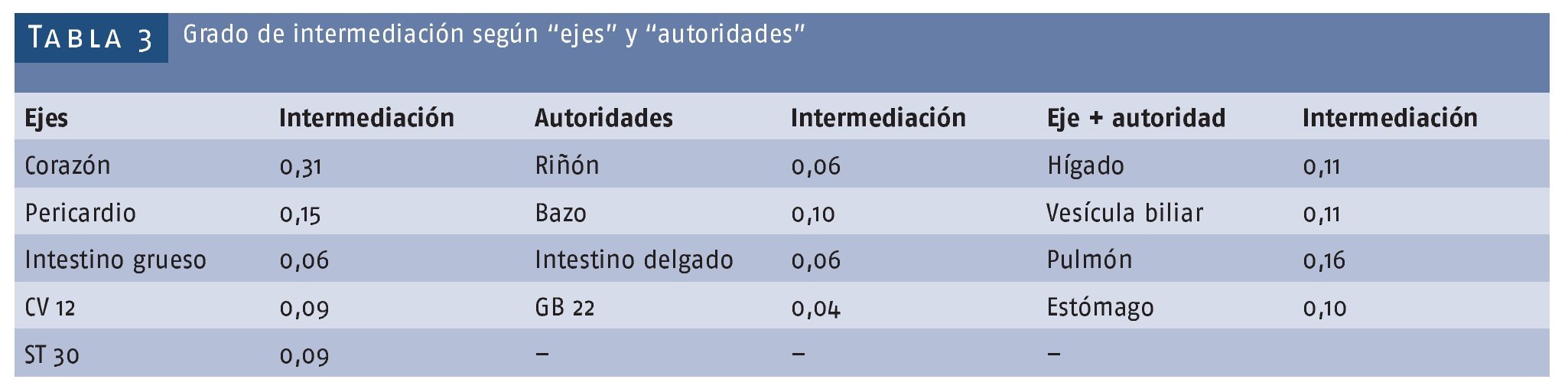
En esta red unos pocos nodos poseen un grado relativamente alto, éstos están situados en la cola de la distribución de probabilidad de grado; sin embargo, se ha planteado que la intermediación resulta mucho más importante al evaluar la importancia de un nodo en la red19. Estos nodos con muchas conexiones se denominan "ejes" porque concentran muchos enlaces y son de gran importancia para mantener la robustez de la red20. Por esto, una lista de los nodos mejor enlazados se obtuvo por medio del software Pajek y se muestra en la tabla 3, junto con la intermediación de cada uno. Hay que señalar que los nodos individuales tienen una intermediación menor que el promedio de la red, con la excepción del órgano Corazón, el nodo con mayor grado e intermediación, lo que resulta coherente con su rol central en la fisiología asiática, donde aparece como el asiento de la conciencia21. Todos los órganos de la tabla reciben significativos enlaces desde la red en comparación con sus aportes, sugiriendo quizás un rol regulatorio o de procesamiento de información que deberá ser especificado en términos modernos, aunque de manera coherente con las funciones tradicionalmente asignadas.
Si alguno de estos órganos o puntos relevantes pierde su funcionalidad esto puede, a su vez, alterar la capacidad de la red para transportar y almacenar información, o traduciendo lo anterior a términos tradicionales: se altera de varias formas la capacidad para transportar energía y sustancias nutritivas, interrumpiendo la capacidad del organismo para responder a los retos o agresiones, algo que constituye el núcleo del concepto tradicional de enfermedad22.
Aún más, tomando una analogía del ámbito de la epidemiología, en la que estos "ejes" juegan un rol tan destacado en la diseminación enfermedades20, podría plantearse que a nivel de organismo estos "ejes" juegan un rol similar al permitir la dispersión de uno o varios de los patógenos tradicionales en el sistema de meridianos y órganos. Tomando otra analogía, esta vez proveniente del campo de las ciencias sociales, se ha propuesto que la cantidad de "poder" informal que un individuo puede esgrimir en una red social es determinable23 y aplicándola de modo comparativo a la fisiología tradicional encontramos que se asemeja a la jerarquía de "poderes" entre los órganos que aparece descrita en el Nei Jing: «el Corazón es como un monarca, que destaca por su intuición y comprensión..."24.
En el contexto de una red social un "eje" es un nodo que emite muchas conexiones y una "autoridad" es un nodo que recibe varias entradas23. En la tabla 3 se muestran los "ejes" y "autoridades" pertenecientes a la red de meridianos y puntos de acupuntura, y podemos apreciar que la metáfora del Nei Jing se mantiene como modelo apropiado de la jerarquía entre los órganos y puntos.
Otras preguntas surgen a colación del rol en la salud y enfermedad de las características topológicas de la red.
¿La propiedad "mundo pequeño" ayuda o entorpece la diseminación de patógenos? Se ha sugerido en modelos epidemiológicos que la propiedad "mundo pequeño" favorece un régimen de dispersión polinómico más que uno exponencial14, esto podría indicar que la topología de la red de meridianos y puntos retarda la progresión del patógeno en el organismo, a pesar de que la propiedad "libre de escala" implica que cualquier tasa de propagación lleva el factor patógeno a la totalidad de la red26. Sabemos, por nuestra práctica clínica, que esto no es así, de modo que se necesitan simulaciones precisas de las energías patógenas tomando los patógenos tradicionales que invaden desde el exterior (Frío, Calor, Humedad, y sus combinaciones) como análogos de los virus epidémicos que permitan determinar cómo esta red los procesa.
¿Será suficiente representar los meridianos, puntos de acupuntura y factores patogénicos para obtener un modelo apropiado de la patogenia asiática? La respuesta es que esto puede representar cómo se comporta este modelo específico, pero no es suficiente para explicar el proceso salud-enfermedad de modo holístico, porque aunque el cerebro aparece en la red y está relativamente bien conectado falta por tomar en cuenta a los factores psicológicos, y además situar y valorar las consecuencias específicas de los patógenos externos.
El diámetro de redes grandes puede ser pequeño, la red www tiene un diámetro de de 1927, mientras que las redes sociales se plantea que tienen un diámetro de aproximadamente 6 (los famosos 6 grados de separación resultado del experimento de Stanley Milgram28), curiosamente la red meridianos y puntos tiene un diámetro que es casi 3 veces el de la www. En este punto es conveniente recordar que el diámetro es solamente el camino más corto de mayor longitud en la red y que la longitud de camino de la www es de l =11,6, muy similar a la de la red de meridianos y puntos (tabla 2)27. Este último planteamiento nos dice que la información puede viajar en nuestra red tan rápido como en la www.
Uno de los parámetros más utilizados, en los análisis contemporáneos de redes, es el coeficiente de mezclado(assortativity) o Cg, este coeficiente nos informa sobre si los nodos de grado elevado de la red tienden a enlazarse con otros nodos de similar grado o no. En nuestro caso, la red muestra una correlación positiva, como la mayor parte de las redes sociales13, mientras que las redes biológicas tienden a tener una correlación negativa, por ejemplo la red neural del C. elegans12. Sin embargo hay una excepción conocida a este fenómeno, la red de contactos de proteínas relacionada con el plegamiento de estas moléculas tiene una correlación positiva29. Pienso, hipotéticamente, que la correlación positiva de la red aquí estudiada puede guardar correspondencia con un carácter "informacional" de la red, en este planteamiento se implica que la red transporta y almacena información.
Debido a que la Cg positiva está asociada a inestabilidad en redes aleatorias y libres de escala30, debería profundizarse este aspecto en futuros estudios.
A pesar de que a muchas redes "mundo pequeño" se les han atribuido propiedades fractales, por ejemplo la www27, y a que la red en estudio manifiesta una distribución de grado en ley de potencia, la dimensión fractal exacta de la red de meridianos y puntos es desconocida. Dado que esta red contiene subsistemas llamados "microsistemas", que en pequeñas áreas de la superficie corporal reflejan la totalidad del organismo (constituyendo pequeñas redes en sí mismos), como: cara, mano y oreja, por citar sólo algunos, el mero hecho de su existencia nos señala que el sistema posee la propiedad fractal de autosemejanza. Si esto se prueba de modo cuantitativo reforzaría la propiedad libre de escala, pues el sistema se refleja a sí mismo en diferentes escalas de medida, y se sabe que la autosimilitud parece implicar la propiedad libre de escala mientras que lo opuesto no es cierto31.
Conclusiones
La red de meridianos y puntos de acupuntura manifiesta ambas propiedades, "mundo pequeño" y "libre de escala". Se confirma el modelo jerárquico de funcionamiento de los órganos Zang-Fu dado en el Nei Jing. Es necesario estudiar en mayor profundidad los "ejes" de mayor intermediación de la red y su rol en la patogenia y fisiología tradicionales. Debido a que el modelo de redes "mundo pequeño" ha permitido predecir eventos extremos como huracanes y terremotos, en el contexto del modelo de la criticalidad autoorganizada, esto abre las puertas a modelar, en la red que nos interesa, fenómenos complejos como: la invasión de patógenos, curaciones o los estratos energéticos.
El empleo de estas herramientas representa un potencial todavía inexplotado con muchos frutos a cosechar, la red se puede "cargar" con valores numéricos afectando a ambos elementos constituyentes, nodos y arcos; podrían servir a este fin valores de voltaje determinados experimentalmente en la piel.
Es el momento de comprobar los paradigmas antiguos, proponer nuevas hipótesis y diseñar medios de diagnóstico. Un nuevo y prometedor campo abre sus puertas a los investigadores.
Agradecimientos
A mi querida esposa Adria, sin cuyo apoyo este trabajo no hubiera sido posible, y al Msc. Román R. Duarte Martell, quien me introdujo en el campo del estudio de redes y sugirió la idea para este estudio.
Dr. Orlando Sánchez Herrera
Policlínico Abel Santamaría, La Habana, Cuba Avda. 21 N.º. 3415 apto. 2 e/34 y 36, Playa, La Habana, Cuba, CP10300
Tel.: 53 53447200
osanchez@infomed.sld.cubeatrizrosales@infomed.sld.cuduarte@inie.cu