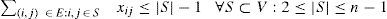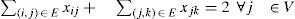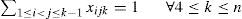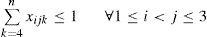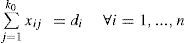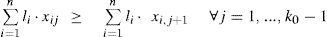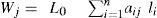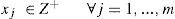En este artículo se presentan los resultados de un análisis computacional que evalúa el impacto de las formulaciones y estrategias de solución sobre el desempeño algorítmico en dos problemas clásicos de optimización: el problema del vendedor viajero y el problema de patrones de corte. Para analizar el desempeño algorítmico de las formulaciones en ambos problemas, se usan tres variables dependientes: calidad de la solución, tiempo de cómputo y número de iteraciones. Los resultados obtenidos sirven de base para elegir el enfoque de solución para cada problema específico. Para el STSP, los resultados demuestran que la formulación como un problema de inserción multietapa es más eficiente que las formulaciones clásicas, al resolver 90.47% de las instancias en comparación a MTZ (76.19%) y DFJ (14.28%). Los resultados para el CSP demuestran que la formulación extendida con variables por patrones es más eficiente que la formulación estándar con desigualdades para romper simetría, cuando la función objetivo modelada corresponde a minimizar la pérdida de material que se produce al realizar el corte de los rollos.
The aim of this article is to perform a computational study to analyze the impact of formulations, and the solution strategy on the algorithmic performance of two classical optimization problems: the traveling salesman problem and the cutting stock problem. In order to assess the algorithmic performance on both problems three dependent variables were used: solution quality, computing time and number of iterations. The results are useful for choosing the solution approach to each specific problem. In the STSP, the results demonstrate that the multistage decision formulation is better than the conventional formulations, by solving 90.47% of the instances compared with MTZ (76.19%) and DFJ (14.28%). The results of the CSP demonstrate that the cutting patterns formulation is better than the standard formulation with symmetry breaking inequalities, when the objective function is to minimize the loss of trim when cutting the rolls.
El problema de patrones de corte (CSP, cutting stock problem) y el problema del vendedor viajero (TSP, travelling salesman problem) son dos de los problemas de optimización combinatoria más estudiados en la literatura. La declaración de ambos problemas es muy simple:
- •
TSP: dado un conjunto de n nodos y las distancias cij para cada par de nodos, encuentre el recorrido de longitud mínima de manera que se visite cada nodo exactamente una sola vez y al final se regrese al nodo inicial.
- •
CSP: dada una lista de n órdenes (demandas), donde cada orden i (i = 1,...,n) requiere di piezas de longitud li a ser cortadas de rollos de longitud estándar L0’ determine el número mínimo de rollos a cortar, de forma que todas las órdenes queden satisfechas sin exceder el largo de cada rollo.
Desde un punto de vista algorítmico ambos problemas son sumamente interesantes debido a su complejidad intrínseca, por lo que el desarrollo de métodos de solución tanto exactos como heurísticos representa un área sumamente fértil para la investigación. En las figuras 1 y 2 se muestran posibles soluciones para una instancia particular de cada problema. La figura 1 muestra un conjunto de soluciones para el recorrido con 5 ciudades en el TSP. Observe que para el TSP simétrico, cuando el número de nodos es igual a n, el número de recorridos (tours) factibles está dado por ½(n - 1)!. La figura 2 muestra dos soluciones factibles para el CSP considerando rollos de longitud igual a 20 y piezas de longitudes 5, 6, 7 y 10 con demandas de 2, 1, 2 y 1 unidades, respectivamente. La parte gris sólida representa el desperdicio del corte. Observe que en esta instancia la solución óptima requiere solo dos rollos.
Desde un punto de vista práctico, ambos problemas surgen en diversas aplicaciones industriales. Por ejemplo, en la manufactura, el problema de programación de tareas en una máquina con cambio de herramental puede formularse como un TSP (González y Ríos, 1999). En la logística, Mar-Ortiz et al. (2011) utilizan TSP como una subrutina incrustada dentro de un algoritmo metaheurístico para resolver un problema complejo de diseño de rutas. Una de las mayores aplicaciones del CSP es en la industria de producción en masa, donde grandes hojas o rollos deben cortarse en trozos más pequeños. Usualmente los rollos son de materiales como papel, acero, vidrio, madera, plástico y textiles. Alp et al. (2006) describen una aplicación del CSP en la industria de la construcción. Se hace referencia a Applegate et al. (2006) para encontrar una descripción de diversas aplicaciones del TSP en la industria y citamos a Dyckhoff (1990) que contiene un listado de aplicaciones del CSP en diversas industrias de producción en masa.
En la literatura es común encontrar diferentes variantes de ambos problemas. Este documento estudia un caso particular de cada problema: el TSP simétrico (STSP, symmetric travel salesman problem), y el CSP unidimensional (1-CSP, one-dimensional cutting stock problem). Gutin y Punnen (2004) presentan un análisis del TSP y sus variantes, y Haessler y Sweeney (1991) dan una descripción de las variantes del CSP y sus procedimientos de solución.
La dificultad computacional del TSP lo ha situado como una fuente para la enseñanza de modelos y algoritmos de programación entera (Pataki, 2003; Lee y Raffensperger, 2006) y combinatoria, debido al reto pedagógico que implica enseñar a resolver el problema. El TSP también da pie a la enseñanza de muchos métodos de la investigación de operaciones, incluyendo los planos de corte (cutting planes), algoritmos aproximados, relajación lagrangeana y el método subgradiente, así como diversos enfoques heurísticos (greedy, k-opt) y metaheurísticos (Búsqueda Tabú, Algoritmos Genéticos).
El principal objetivo de esta investigación consiste en efectuar un estudio computacional para analizar el impacto de las formulaciones, y de la estrategia de solución sobre el desempeño algorítmico en los dos problemas contemplados. El alcance de este estudio para cada problema se describe a continuación:
- •
STSP- El estudio consta de dos partes, en la primera se comparan tres formulaciones diferentes para el STSP: la formulación de Danteig, Fulkerson y Johnson (1954), de aquí en adelante referida como DFJ, la formulación de Miller, Tucker y Zemlin (1960), de aquí en adelante referida como MTZ, y la formulación de Arthanari y Usha (2000) de aquí en adelante referida como ART. Se compararán las tres formulaciones en términos de tamaño y tiempos de cómputo, para derivar algunas conclusiones de interés. La segunda parte del estudio profundiza brevemente en el análisis de la formulación DFJ analizando tres estrategias para su implementación: 1) monolítica, 2) cortes después de solución entera y 3) cortes en el nodo raíz.
- •
1-CSP- El alcance de este análisis consiste en comparar tres formas de abordar el CSP unidimensional con el objetivo de minimizar la pérdida de material: 1) formulación estándar con variables xij, yj’ 2) formulación estándar con desigualdades para romper simetrías y 3) formulación extendida (con variables por patrones), donde se generan variables solo en el nodo raíz del árbol de ramificación y acotamiento (branch-and-bound).
El resto de este documento se organiza de la siguiente manera: la segunda sección describe los modelos matemáticos del STSP y 1-CSP, la tercera describe el estudio computacional y analiza los resultados, por último, la cuarta sección ofrece las conclusiones del estudio.
Formulaciones matemáticasProblema simétrico del vendedor viajeroEl problema simétrico del vendedor viajero (STSP, symmetric traveling salesman problem) requiere la definición de un grafo no dirigido G = (V, E), donde V = {1,..., n} es un conjunto de nodos y E = {(i, j) | 1 ≤ i < j ≤ n} es un conjunto de aristas. Para cada arista (i, j) ∈ E el costo de transitarla cij se conoce. El problema consiste en encontrar el subconjunto de aristas que formen un recorrido de mínima longitud. Un recorrido puede ser denotado como una permutación 〈i1, i2,..., in, i1〉 de los nodos en V.
En el TSP asimétrico se considera la existencia de la variable de decisión xij cuyo valor es 1 si se transita del nodo i al nodo j dentro de la solución, y 0 si no. Sin embargo, para formular el TSP simétrico, se debe notar que la dirección viajada es indistinta (cij = cji), debido a que la dirección no tiene importancia al considerar un grafo con arcos no dirigidos entre cada par de nodos. Así, sea xij ∈ {0, 1} la variable de decisión que indica si la arista (i, j) ∈ E del grafo no dirigido se utiliza o no. La formulación DFJ está dada por:
sujeta a
La función objetivo (1) minimiza la distancia total recorrida. La ecuación (2) establece las condiciones de grado en los nodos. Esta restricción asegura que cada nodo esté contenido en exactamente dos de las aristas seleccionadas. Dicha restricción reemplaza las restricciones de asignación en el TSP asimétrico. La ecuación (3) establece las condiciones de eliminación de subtours, donde S se forma por todos los subconjuntos de V de cardinalidad mayor o igual que 2 nodos. En general esta restricción asegura que dentro de cada subconjunto de nodos de cardinalidad ISI existan ISI – 1 aristas, evitando así la formación de subtours.
Uno de los problemas con la formulación de DFJ es que el número de desigualdades para eliminación de subtours es exponencial. Dado un conjunto de n nodos, el número de desigualdades de eliminación de subtours es del orden de O(2n−1). Por ello, en este documento se describen y comparan tres estrategias de solución dada esta formulación:
- 1)
Monolítica: en la cual se utilizan explícitamente todas las O(2n−1) restricciones de eliminación de subtours.
- 2)
Cortes después de solución entera: se inicia resolviendo el problema entero solo con las restricciones de grado en los nodos, se verifica que la solución sea un recorrido, es decir, que no existan subtours; si los hay, se agrega a la formulación la restricción requerida y se vuelve a resolver. El procedimiento termina cuando se verifica que la solución sea un recorrido.
- 3)
Cortes en el nodo raíz: esta estrategia consta de dos etapas. La primera etapa inicia solo con las restricciones de grado en los nodos, se resuelve la relajación lineal del problema, agregando iterativamente las restricciones de eliminación de subtours conforme se requieren, cuando ninguna restricción de subtour se viola, termina la primera etapa. En la segunda etapa se resuelve el problema entero, iterando como en la estrategia de cortes después de la solución entera.
A diferencia de la formulación anterior, la formulación MTZ requiere un número polinomial de restricciones O(n2). Para ello se utiliza una variable de decisión continua ui ≥ 0 que contabiliza el número de nodos (ciudades) visitadas después de visitar el nodo i. Pese a que la variable ui está definida como continua, la formulación del problema la obliga a tomar valores enteros. La formulación de MTZ está dada por:
sujeta a
Las ecuaciones (1), (2) y (4) son las mismas que en el modelo DFJ. La ecuación (5) remplaza las restricciones de eliminación de subtours (ecuación 3) de la formulación DFJ. La ecuación (6) establece las cotas para la variable ui. Se debe notar que ambas formulaciones, DFJ y MTZ, requieren O(n2) variables binarias. Sin embargo, la estructura poliédrica del modelo DFJ es más entendible, lo que resulta en una relajación lineal más fuerte. El politopo dado por la relajación lineal de la formulación DFJ se llama el politopo de eliminación de subtours (SEP, subtour elimination polytope). El SEP se conoce por ser un politopo más compacto en relación al obtenido por otras formulaciones, en el sentido de que se ajusta estrechamente alrededor del politopo del TSP.
La formulación del STSP como un problema de inserción multietapa (Arthanari y Usha, 2000) es una formulación más compacta que las anteriores. Másaún, Arthanari y Usha (2000) demostraron que el politopo dado por la relajación lineal de dicha formulación es un subconjunto del SEP, cuando se proyecta dentro del espacio de variables del DFJ. La formulación ART para el STSP considera (n - 3) etapas de inserción secuencial de nodos dentro del recorrido inicial T3 =〈1, 2, 3,1〉. Continuando con la nomenclatura anterior, dado un conjun to de nodos V = {1,..., n}. Los nodos 4 a n se insertan secuencialmente entre los nodos del recorrido inicial. Sea xijk ∈ {0,1} la variable de decisión que toma el valor 1 si el nodo k se inserta entre los nodos i y j, para 1 ≤ i < j ≤ k - 1, 4≤ k ≤ n y cero en otro caso. Sea cij el costo de transitar la arista (i, j) ∈ E y sea Ci¡k = cik + cjk - cij. La formulación de ART está dada por:
sujeta a
La función objetivo (7) minimiza el costo total incremental del recorrido obtenido mediante la inserción de los nodos. Debido a que el costo del recorrido inicial (c12 + c13 + c23) es el mismo para cualquier recorrido de una instancia dada, no se incluye en la función objetivo de la formulación. La restricción en la ecuación (8) garantiza que cada nodo de 4 a n quede insertado en una arista. La restricción (9) asegura que como máximo un nodo sea insertado en cada una de las aristas de T3 = 〈1, 2, 3,1〉 La restricción (10) establece que un nodo será insertado dentro de una arista del subtour solo si esa arista se generó por inserciones previas y está disponible. La formulación ART requiere O(n3) variables binarias y O(n2) restricciones.
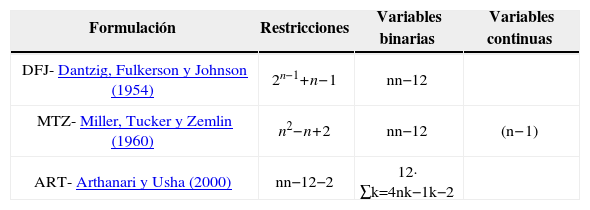
La tabla 1 muestra una comparación del número de variables y restricciones de las tres formulaciones.
Número de variables y restricciones de las formulaciones: DFJ, MTZ y ART
| Formulación | Restricciones | Variables binarias | Variables continuas |
|---|---|---|---|
| DFJ- Dantzig, Fulkerson y Johnson (1954) | 2n−1+n−1 | nn−12 | |
| MTZ- Miller, Tucker y Zemlin (1960) | n2−n+2 | nn−12 | (n−1) |
| ART- Arthanari y Usha (2000) | nn−12−2 | 12· ∑k=4nk−1k−2 |
Considere n tipos de piezas que se van a cortar de rollos de longitud estándar L0. Para cada tipo i = 1,..., n, di denota la demanda y li el largo de cada pieza tipo i, donde l¡ ≤ L0 para cada i. Se supone que el número de rollos es ilimitado, sin embargo, basta considerar k0=∑i=1ndi rollos de largo estándar. Un caso especial en el cual solo una pieza de cada tipo de producto i se ordena, es decir, di = 1 ∀i, se conoce como el problema de empaquetamiento (BPP, bin-packing problem). Sea xij la variable de decisión que representa la cantidad de piezas tipo i (i = 1,..., n) obtenidas del rollo j (j = 1,..., k0), y yi ∈ {0, 1} la variable de decisión que indica si el rollo j se usa o no. Si el objetivo del modelo fuera minimizar el número de rollos usados, la función objetivo estaría dada por: mín ∑j=1ko yj. Sin embargo, para el caso en el que se busca minimizar la pérdida de material o desperdicios del corte, la formulación estándar (CSPml) está dada por:
sujeta a
donde la variable de decisión continua Rj ≥ 0 representa la parte sobrante (pérdida) del rollo j. La ecuación (13) establece que toda la demanda de cada pieza tipo i debe satisfacerse. La ecuación (14) establece que la longitud de cada rollo que se corta, no debe excederse en la obtención de las piezas. Esta formulación requiere O(n2) variables enteras y O(n) variables binarias.
El principal problema de esta formulación, además de contar con una gran cantidad de variables enteras y binarias, consiste en que existen muchas formas de representar una misma solución (k0!), resultando en un problema conocido como multiplicidad de soluciones, mismo que crea simetrías en el árbol de ramificación y acotamiento (por ejemplo, múltiples nodos con la misma solución). Para romper simetrías basta con agregar a la formulación anterior una nueva restricción:
la cual asegura que para cada rollo j, la cantidad de material obtenido de dicho rollo debe ser mayor que lo obtenido en el rollo j+1. El modelo resultante será identificado como CSPm2.
La formulación anterior aún puede mejorarse. Una forma de hacerlo es acotar el conjunto de soluciones, definiendo φ ={conjunto de todos los patrones de corte factibles} (Gilmore y Gomory, 1961). Manteniendo la nomenclatura anterior, donde di es la demanda para las piezas de largo li’ se supone que los rollos (de largo estándar L0) se pueden cortar usando patrones j. Los posibles patrones se denotan por aij, y representan el número de piezas de largo li que se obtienen al aplicar el patrón j. El número de veces que el patrón j se usa está dado por xj. Si se define como Wj el desperdicio cuando se aplica el patrón j en el rollo, tal que:
el CSP que utiliza patrones de corte con el objetivo de minimizar el desperdicio (al cual se refiere de aquí en adelante como CSPm3) está dado por:
sujeta a
Es fácil ver que, en general, el número de patrones de corte requeridos es muy grande, por lo que en lugar de enumerar todos los posibles patrones de corte j, se puede comenzar con un pequeño conjunto de patrones iniciales y resolver utilizando un enfoque de generación de columnas (Wolsey, 1998). Este conjunto inicial puede crearse de dos formas: la más básica consiste en indicar que para cada pieza de largo li se requiere un rollo completo; por otro lado, un conjunto inicial más avanzado de patrones se forma indicando que de un rollo se obtienen ⌊L0/li⌋ piezas de largo l¡. En general, los patrones de corte iniciales proveen una solución factible inicial de baja calidad, la cual mejora conforme se desarrolla el algoritmo. Para ejemplificar, considere una instancia con 4 tipos de piezas con li = [30 50 70 25] y di = [1 2 2 1] y rollos de L0 = 100. Si inicialmente se declaran los patrones: {<0, [1 0 0 0]> <1, [0 1 0 0]> <2, [0 0 1 0]> <3, [0 0 0 1]>} (con ¿j Wj. = 70 + 100 + 60 + 75 = 305). Se esperaría que el procedimiento generara al menos los siguientes patrones: {<4, [1 0 1 0]> <5, [0 2 0 0]> <6, [0 0 1 1]>} (con ¿j Wj = 0 + 0 + 5 = 5). Con lo cual se minimizaría el desperdicio total.
Para encontrar un nuevo patrón que añadir al conjunto de columnas bajo consideración, se debe observar el costo reducido ój de la columna xj. El subproblema para encontrar el posible patrón de corte con el costo reducido más negativo está dado por:
En los últimos años, se han realizado esfuerzos para atacar el 1-CSP por medio de programación lineal basada en el algoritmo de ramificación y precio (branch-and-pricé), que combina el algoritmo de ramificación y poda con generación de columnas; y mediante planos de corte de propósito general del tipo Chvátal-Gomory. Belov y Scheithauer (2006) propusieron una combinación de ambos enfoques donde cada nodo del árbol de ramificación y precio se refuerza mediante cortes Chvátal-Gomory y cortes MIP de Gomory.
Estudio computacionalEn esta sección presentamos los resultados experimentales obtenidos. Las formulaciones y estrategias de solución se implementaron en IDE OPL Studio, y ILOG CPLEX v.12.2 se utilizó como el motor de optimización. Todos los experimentos se realizaron en una PC Acer Aspire 5530 con procesador AMD Athlon X2 Dual Core de 1.9 GHz y 2 GB de memoria RAM. Para el estudio computacional del STSP se utilizaron 21 de las instancias geométricas del TSPLIB1. Por su parte, para el 1-CSP se utilizaron 188 instancias agrupadas en tres conjuntos: sDATO, sDATl y hard282. Para todos los experimentos se estableció un tiempo límite de 1 hora, reportando la mejor solución encontrada hasta el momento. Para comparar la eficiencia de las formulaciones y estrategias utilizadas, para cada instancia se calculó la desviación (DEV) respecto a la mejor solución encontrada (BEST): DEV = ((ZSOL − ZBEST)/ ZBEST) × 100, la cual estima la calidad de la solución, se analiza el tiempo de cómputo y número de iteraciones.
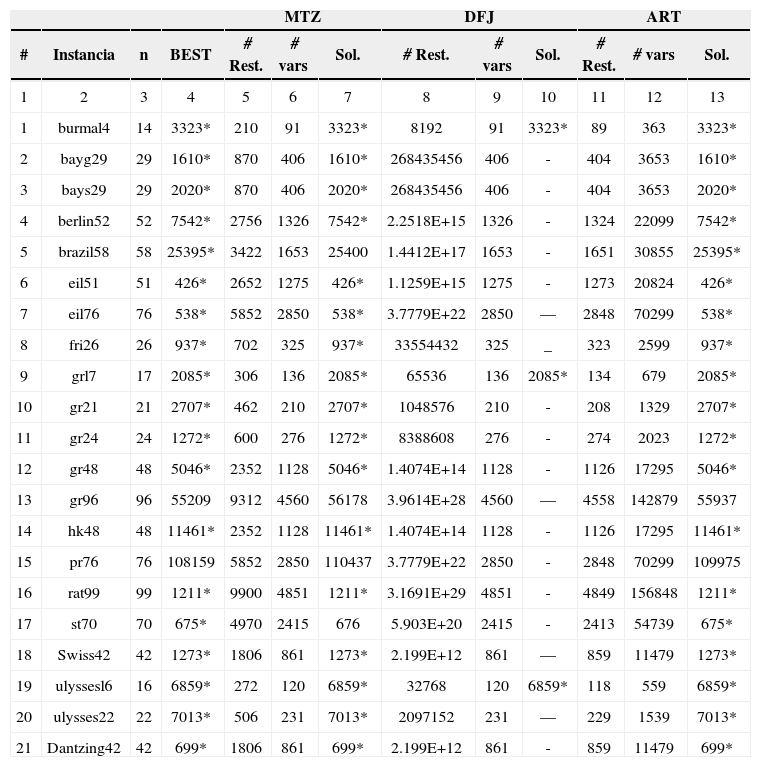
Estudio del STSPExperimento 1– Comparación MTZ, DFJ y ART. En este primer experimento, se comparan las formulaciones DFJ, MTZ y ART. La tabla 2 muestra los resultados obtenidos al comparar las tres formulaciones en 21 de las instancias geométricas del TSPLIB. La columna 2 indica el nombre de la instancia conforme a la nomenclatura del TSPLIB, la columna 3 indica el número de ciudades contempladas en la instancia (n), mientras que la columna 4 indica para cada instancia la mejor solución reportada (BEST) en el TSPLIB. De las columnas 5 a 7 se encuentran el número de restricciones, variables binarias y solución encontradas con la formulación MTZ. El resto de las columnas indican lo propio para las formulaciones DFJ y ART, respectivamente. En negritas se identifica la mejor solución encontrada hasta el momento. Cuando esta corresponde a la solución óptima, se identifica con un (*). Cuando en el tiempo establecido de computo no fue posible encontrar una solución factible, en la casilla correspondiente se observa un guión“–”.
Comparación de las formulaciones DFJ, MTZy ART en relación al número de restricciones, número de variables binarias y solución encontrada
| MTZ | DFJ | ART | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| # | Instancia | n | BEST | # Rest. | # vars | Sol. | # Rest. | # vars | Sol. | # Rest. | # vars | Sol. |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 1 | burmal4 | 14 | 3323* | 210 | 91 | 3323* | 8192 | 91 | 3323* | 89 | 363 | 3323* |
| 2 | bayg29 | 29 | 1610* | 870 | 406 | 1610* | 268435456 | 406 | - | 404 | 3653 | 1610* |
| 3 | bays29 | 29 | 2020* | 870 | 406 | 2020* | 268435456 | 406 | - | 404 | 3653 | 2020* |
| 4 | berlin52 | 52 | 7542* | 2756 | 1326 | 7542* | 2.2518E+15 | 1326 | - | 1324 | 22099 | 7542* |
| 5 | brazil58 | 58 | 25395* | 3422 | 1653 | 25400 | 1.4412E+17 | 1653 | - | 1651 | 30855 | 25395* |
| 6 | eil51 | 51 | 426* | 2652 | 1275 | 426* | 1.1259E+15 | 1275 | - | 1273 | 20824 | 426* |
| 7 | eil76 | 76 | 538* | 5852 | 2850 | 538* | 3.7779E+22 | 2850 | — | 2848 | 70299 | 538* |
| 8 | fri26 | 26 | 937* | 702 | 325 | 937* | 33554432 | 325 | _ | 323 | 2599 | 937* |
| 9 | grl7 | 17 | 2085* | 306 | 136 | 2085* | 65536 | 136 | 2085* | 134 | 679 | 2085* |
| 10 | gr21 | 21 | 2707* | 462 | 210 | 2707* | 1048576 | 210 | - | 208 | 1329 | 2707* |
| 11 | gr24 | 24 | 1272* | 600 | 276 | 1272* | 8388608 | 276 | - | 274 | 2023 | 1272* |
| 12 | gr48 | 48 | 5046* | 2352 | 1128 | 5046* | 1.4074E+14 | 1128 | - | 1126 | 17295 | 5046* |
| 13 | gr96 | 96 | 55209 | 9312 | 4560 | 56178 | 3.9614E+28 | 4560 | — | 4558 | 142879 | 55937 |
| 14 | hk48 | 48 | 11461* | 2352 | 1128 | 11461* | 1.4074E+14 | 1128 | - | 1126 | 17295 | 11461* |
| 15 | pr76 | 76 | 108159 | 5852 | 2850 | 110437 | 3.7779E+22 | 2850 | - | 2848 | 70299 | 109975 |
| 16 | rat99 | 99 | 1211* | 9900 | 4851 | 1211* | 3.1691E+29 | 4851 | - | 4849 | 156848 | 1211* |
| 17 | st70 | 70 | 675* | 4970 | 2415 | 676 | 5.903E+20 | 2415 | - | 2413 | 54739 | 675* |
| 18 | Swiss42 | 42 | 1273* | 1806 | 861 | 1273* | 2.199E+12 | 861 | — | 859 | 11479 | 1273* |
| 19 | ulyssesl6 | 16 | 6859* | 272 | 120 | 6859* | 32768 | 120 | 6859* | 118 | 559 | 6859* |
| 20 | ulysses22 | 22 | 7013* | 506 | 231 | 7013* | 2097152 | 231 | — | 229 | 1539 | 7013* |
| 21 | Dantzing42 | 42 | 699* | 1806 | 861 | 699* | 2.199E+12 | 861 | - | 859 | 11479 | 699* |
Del análisis de la tabla 2 se derivan las siguientes conclusiones: la formulación MTZ fue capaz de encontrar la solución óptima en 16 de las 21 instancias utilizadas (76.19%), en un tiempo promedio de 46.87 segundos. Para los casos en los que no se logró la solución óptima, el DEV promedio alcanzó 0.80%. Pese a que en la instancia más grande rat99 (n = 99) se llegó a la solución óptima, la instancia pr76 (n = 76) obtuvo un DEV de 2.10%. La formulación DFJ solo fue factible para 3 de las 21 instancias con (n ≤ 17), en los tres casos se alcanzó la solución óptima en un tiempo promedio de 14.33 segundos. La formulación ART fue capaz de encontrar la solución óptima en 19 de las 21 instancias utilizadas (90.47%), en un tiempo promedio de 42.71 segundos. Cuando ART no logró la solución óptima, el DEV promedio fue 1.60%. Por lo que la formulación ART sobresale sobre las otras dos formulaciones en términos de calidad de la solución y tiempo de cómputo.
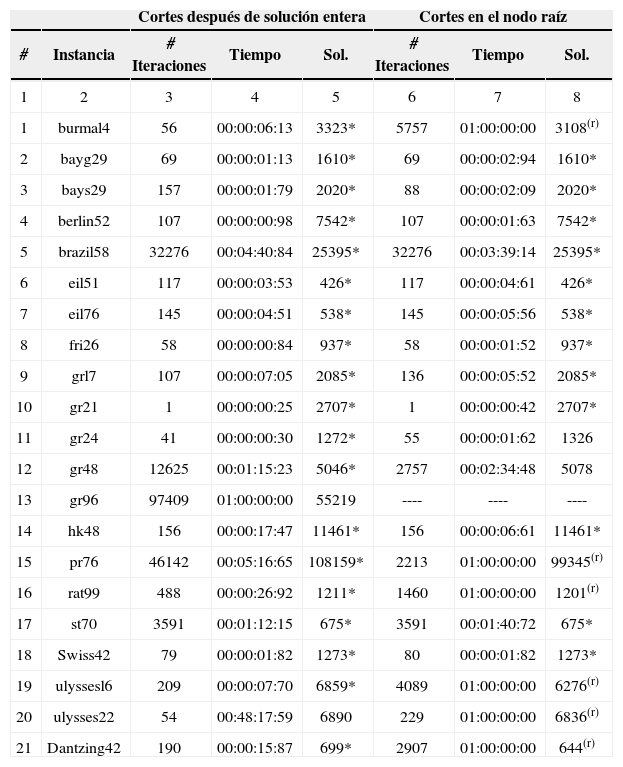
Experimento 2– Comparación de tres estrategias para resolver DFJ. La estrategia monolítica ya se implementó en el experimento anterior. Sin embargo, sus resultados se comparan con los obtenidos mediante las estrategias de cortes después de la solución entera y cortes en el nodo raíz. La tabla 3 muestra los resultados obtenidos en ambas estrategias. Las columnas 3, 4 y 5 muestran respectivamente el número de iteraciones requeridas, el tiempo para alcanzar la solución y la solución obtenida al implementar la estrategia de cortes después de solución entera. Por su parte, las columnas 6, 7 y 8 hacen lo correspondiente para la estrategia de cortes en el nodo raíz. En negritas se identifica la mejor solución encontrada hasta el momento. Cuando esta corresponde a la solución óptima, se identifica con un (*). Cuando la computadora se quedó sin memoria tanto el tiempo como la solución se identifican por un guión “–”. Cuando al terminar el tiempo límite, la estrategia de cortes en el nodo raíz, aún está iterando en la relajación lineal, la solución reportada corresponde al de la última iteración y se identifica como (r).
Resultados de las estrategias: corte después de solución entera y cortes en el nodo raíz
| Cortes después de solución entera | Cortes en el nodo raíz | ||||||
|---|---|---|---|---|---|---|---|
| # | Instancia | # Iteraciones | Tiempo | Sol. | # Iteraciones | Tiempo | Sol. |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 1 | burmal4 | 56 | 00:00:06:13 | 3323* | 5757 | 01:00:00:00 | 3108(r) |
| 2 | bayg29 | 69 | 00:00:01:13 | 1610* | 69 | 00:00:02:94 | 1610* |
| 3 | bays29 | 157 | 00:00:01:79 | 2020* | 88 | 00:00:02:09 | 2020* |
| 4 | berlin52 | 107 | 00:00:00:98 | 7542* | 107 | 00:00:01:63 | 7542* |
| 5 | brazil58 | 32276 | 00:04:40:84 | 25395* | 32276 | 00:03:39:14 | 25395* |
| 6 | eil51 | 117 | 00:00:03:53 | 426* | 117 | 00:00:04:61 | 426* |
| 7 | eil76 | 145 | 00:00:04:51 | 538* | 145 | 00:00:05:56 | 538* |
| 8 | fri26 | 58 | 00:00:00:84 | 937* | 58 | 00:00:01:52 | 937* |
| 9 | grl7 | 107 | 00:00:07:05 | 2085* | 136 | 00:00:05:52 | 2085* |
| 10 | gr21 | 1 | 00:00:00:25 | 2707* | 1 | 00:00:00:42 | 2707* |
| 11 | gr24 | 41 | 00:00:00:30 | 1272* | 55 | 00:00:01:62 | 1326 |
| 12 | gr48 | 12625 | 00:01:15:23 | 5046* | 2757 | 00:02:34:48 | 5078 |
| 13 | gr96 | 97409 | 01:00:00:00 | 55219 | ---- | ---- | ---- |
| 14 | hk48 | 156 | 00:00:17:47 | 11461* | 156 | 00:00:06:61 | 11461* |
| 15 | pr76 | 46142 | 00:05:16:65 | 108159* | 2213 | 01:00:00:00 | 99345(r) |
| 16 | rat99 | 488 | 00:00:26:92 | 1211* | 1460 | 01:00:00:00 | 1201(r) |
| 17 | st70 | 3591 | 00:01:12:15 | 675* | 3591 | 00:01:40:72 | 675* |
| 18 | Swiss42 | 79 | 00:00:01:82 | 1273* | 80 | 00:00:01:82 | 1273* |
| 19 | ulyssesl6 | 209 | 00:00:07:70 | 6859* | 4089 | 01:00:00:00 | 6276(r) |
| 20 | ulysses22 | 54 | 00:48:17:59 | 6890 | 229 | 01:00:00:00 | 6836(r) |
| 21 | Dantzing42 | 190 | 00:00:15:87 | 699* | 2907 | 01:00:00:00 | 644(r) |
Del análisis conjunto de ambos experimentos se obtienen las siguientes conclusiones: la estrategia de cortes después de la solución entera parece ser la mejor forma de atacar los problemas del STSP, al ser capaz de alcanzar la solución óptima en 19 de las 21 instancias consideradas (90.47%), en un tiempo promedio de 99 segundos. Pese a que la estrategia de cortes en el nodo raíz no corrió el tiempo suficiente en todos las instancias, esta fue capaz de encontrar la solución óptima para dos de las instancias en que el MTZ no pudo. En algunas instancias como la brazil58, grl7 ó hk48, la estrategia de cortes en el nodo raíz, llegó a la solución óptima en menos tiempo que cualquier otra estrategia. Por ello, en ciertos casos puede ser una estrategia sumamente eficiente si se deja correr por un tiempo suficientemente largo. Debido a que ambas formulaciones (MTZ y DFJ) requieren el mismo número de variables binarias (vea formulaciones en la sección del problema simétrico del vendedor viajero), la complejidad del problema está en relación con el número de restricciones. Sin embargo, se debe notar que para la estrategia de cortes después de solución entera, el número de iteraciones corresponde al número de cortes implementados, es decir, al número de restricciones de eliminación de subtours efectivamente requeridas.
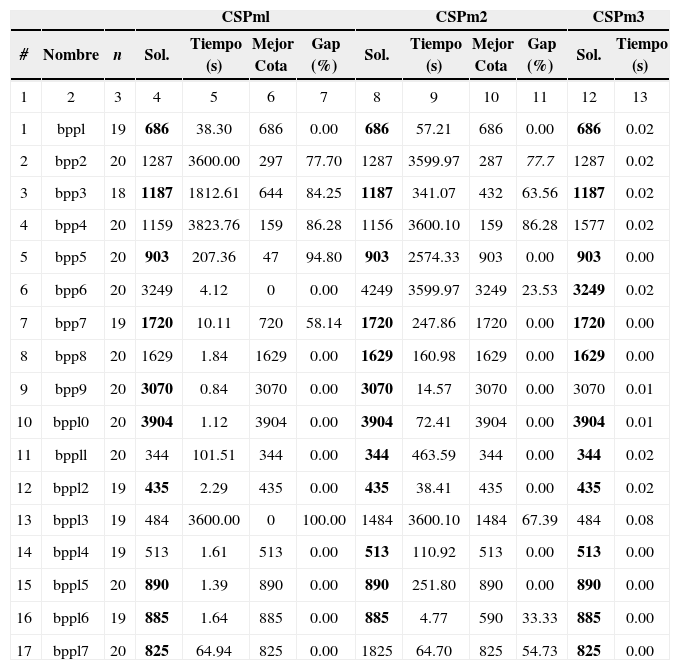
Estudio del 1-CSPPara el estudio del 1-CSP se comparan los tres modelos CSPml, CSPm2 y CSPm3 en términos de calidad de las soluciones y tiempo necesario para resolver las instancias de los tres conjuntos. Por cuestiones de espacio, la tabla 4 muestra los resultados obtenidos al comparar las tres formulaciones en las primeros 17 instancias del conjunto sDAT0. La columna 2 indica el nombre de la instancia, la columna 3 indica el número de tipos de piezas en la instancia (n), las columnas 4,5,6 y 7 indican para cada instancia la solución alcanzada, el tiempo requerido para tal solución, la mejor cota encontrada y el gap porcentual para CSPml. El resto de las columnas hacen lo propio para CSPm2 y CSPm3.
Parte del conjunto de instancias sDAT0 para el 1-CSP
| CSPml | CSPm2 | CSPm3 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| # | Nombre | n | Sol. | Tiempo (s) | Mejor Cota | Gap (%) | Sol. | Tiempo (s) | Mejor Cota | Gap (%) | Sol. | Tiempo (s) |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 1 | bppl | 19 | 686 | 38.30 | 686 | 0.00 | 686 | 57.21 | 686 | 0.00 | 686 | 0.02 |
| 2 | bpp2 | 20 | 1287 | 3600.00 | 297 | 77.70 | 1287 | 3599.97 | 287 | 77.7 | 1287 | 0.02 |
| 3 | bpp3 | 18 | 1187 | 1812.61 | 644 | 84.25 | 1187 | 341.07 | 432 | 63.56 | 1187 | 0.02 |
| 4 | bpp4 | 20 | 1159 | 3823.76 | 159 | 86.28 | 1156 | 3600.10 | 159 | 86.28 | 1577 | 0.02 |
| 5 | bpp5 | 20 | 903 | 207.36 | 47 | 94.80 | 903 | 2574.33 | 903 | 0.00 | 903 | 0.00 |
| 6 | bpp6 | 20 | 3249 | 4.12 | 0 | 0.00 | 4249 | 3599.97 | 3249 | 23.53 | 3249 | 0.02 |
| 7 | bpp7 | 19 | 1720 | 10.11 | 720 | 58.14 | 1720 | 247.86 | 1720 | 0.00 | 1720 | 0.00 |
| 8 | bpp8 | 20 | 1629 | 1.84 | 1629 | 0.00 | 1629 | 160.98 | 1629 | 0.00 | 1629 | 0.00 |
| 9 | bpp9 | 20 | 3070 | 0.84 | 3070 | 0.00 | 3070 | 14.57 | 3070 | 0.00 | 3070 | 0.01 |
| 10 | bppl0 | 20 | 3904 | 1.12 | 3904 | 0.00 | 3904 | 72.41 | 3904 | 0.00 | 3904 | 0.01 |
| 11 | bppll | 20 | 344 | 101.51 | 344 | 0.00 | 344 | 463.59 | 344 | 0.00 | 344 | 0.02 |
| 12 | bppl2 | 19 | 435 | 2.29 | 435 | 0.00 | 435 | 38.41 | 435 | 0.00 | 435 | 0.02 |
| 13 | bppl3 | 19 | 484 | 3600.00 | 0 | 100.00 | 1484 | 3600.10 | 1484 | 67.39 | 484 | 0.08 |
| 14 | bppl4 | 19 | 513 | 1.61 | 513 | 0.00 | 513 | 110.92 | 513 | 0.00 | 513 | 0.00 |
| 15 | bppl5 | 20 | 890 | 1.39 | 890 | 0.00 | 890 | 251.80 | 890 | 0.00 | 890 | 0.00 |
| 16 | bppl6 | 19 | 885 | 1.64 | 885 | 0.00 | 885 | 4.77 | 590 | 33.33 | 885 | 0.00 |
| 17 | bppl7 | 20 | 825 | 64.94 | 825 | 0.00 | 1825 | 64.70 | 825 | 54.73 | 825 | 0.00 |
Del análisis experimental en los tres conjuntos de instancias se derivan las siguientes conclusiones: el modelo CSPml requirió un tiempo promedio de 569.13 segundos y la exploración de 300,170 nodos en el árbol de ramificación y acotamiento en promedio, el gap promedio fue 22.14%. El CSPm2 requirió (en promedio) un poco más de tiempo 1021.15, pero el gap promedio bajó 16.5%. El conjunto sDATl parece ser el más difícil de los tres conjuntos de instancias, donde el número de piezas va desde 231 a 246. En las instancias sDATl y hard28 el CSPm2 parece enfrentar dificultades, pues en algunos de ellos los 3600 segundos no son suficientes para encontrar una solución factible. El CSPm3 utiliza patrones de corte, pero debido a que el número de estos puede ser muy grande, se utiliza la estrategia de iniciar con un subconjunto de estos patrones, y posteriormente generar patrones de corte más adecuados en el nodo raíz del árbol de ramificación y acotamiento, para finalmente resolver el problema como un modelo entero.
ConclusionesPara un mismo problema pueden existir diversas formulaciones. Con frecuencia, esas formulaciones difieren en términos de su conjunto de variables y restricciones. Esto implica que si una formulación resulta compleja computacionalmente hablando, puede reformularse utilizando un conjunto diferente de variables. Además, dada una formulación, se pueden identificar varias estrategias de solución como las descritas para la formulación DFJ. En este artículo se presentan los resultados de un análisis computacional que evalúa el impacto de las formulaciones y estrategias de solución sobre el desempeño algorítmico en dos problemas clásicos de optimización: el problema simétrico del vendedor viajero y el problema unidimensional de patrones de corte. Para analizar el desempeño algorítmico de las formulaciones, se utilizan tres variables dependientes: calidad de la solución, tiempo de cómputo y número de iteraciones.
Para el STSP se analizaron tres formulaciones: DFJ, MTZ y ART. La formulación ART sobresale ante las otras dos formulaciones en términos de calidad de la solución, tiempo de cómputo y número de iteraciones. Por otro lado, la formulación DFJ es estrictamente mejor que las otras dos formulaciones, en el sentido de que se ajusta estrechamente alrededor del politopo del TSP. La formulación DFJ requiere un número exponencial de restricciones, por lo que solo es factible para instancias pequeñas (n ≤ 17). Sin embargo, se ha demostrado que se requiere solo un número polinomial de estas restricciones en cualquier caso; por lo que se analizaron dos estrategias más, en las cuales iterativamente se van añadiendo las restricciones conforme se necesitan: cortes después de solución entera y cortes en el nodo raíz. El estudio computacional demuestra que la estrategia de cortes después de solución entera ofrece mejores resultados en relación con los tres métodos y aún mejores que la formulación MTZ y ART.
Para el 1-CSP la función objetivo modelada fue minimizar la pérdida de material que se produce al realizar el corte de los rollos. Se analizaron tres formulaciones: la formulación estándar con variables xij y yj (CSPml), la formulación estándar con desigualdades para romper simetría (CSPm2) y la formulación extendida con variables por patrones (CSPm3). El CSPml es ineficiente en el sentido de contar con muchas variables enteras y binarias, y de contener muchas soluciones simétricas, lo cual provoca que el problema sea extremadamente difícil de resolver por medio de algoritmos de tipo ramificación y acotamiento. De las 188 instancias analizadas fue posible resolver 172 (91%), estableciendo un tiempo de cómputo límite de 1 hora. La formulación CSPm2 resuelve el problema causado por la simetría, alcanzando a resolver todos las instancias del conjunto sDATO, pero encontrando problemas al resolver los conjuntos sDATl y hard28. Finalmente CSPm3 fue capaz de correr sin problemas en los tres conjuntos de datos.
Ingeniero industrial y de sistemas por la Universidad Autónoma de Tamaulipas. Maestra en ciencias con especialidad en sistemas de calidad y productividad por el Tecnológico de Monterrey. Actualmente cursa el doctorado en ciencias de ingeniería en la Universidad de Santiago de Chile. Es profesor de tiempo completo en la Facultad de Ingeniería de la Universidad Autónoma de Tamaulipas, donde imparte cursos de logística, cadenas de suministro, y gestión de operaciones. Ha participado en varios congresos internacionales de especialidad como ponente y es coautora de 2 capítulos de libro relacionados con supply chain management, decision support systems, optimización y simulación.
Citación estilo Chicago Gracia, María D., Julio Mar-Ortiz, Oscar Laureano-Casanova. Análisis computacional de los problemas del vendedor viajero y patrones de corte. Ingeniería Investigación y Tecnología, XVI, 01 (2015): 59-70. Citación estilo ISO 690 Gracia M.D., Mar-Ortiz J., Laureano-Casanova O. Análisis computacional de los problemas del vendedor viajero y patrones de corte. Ingeniería Investigación y Tecnología, volumen XVI (número 1), enero-marzo 2015: 59-70.
Profesor de tiempo completo en la Facultad de Ingeniería de la Universidad Autónoma de Tamaulipas, México. Líder del grupo disciplinar en productividad y optimización, y asesor facultativo del capítulo estudiantil 970 del HE. Es doctor en ingeniería industrial con especialidad en investigación de operaciones, y maestro en ciencias con especialidad en sistemas de calidad y productividad. Miembro del Sistema Nacional de Investigadores a nivel candidato, y perfil PRO-MEP. Sus investigaciones han sido publicadas en revistas científicas como: el Journal of the Operational Research Society, Journal of Heuristics, European Journal of Industrial Engineering, Computación y Sistemas.
Profesor de tiempo completo en la Facultad de Ingeniería de la Universidad Autónoma de Tamaulipas, México. Integrante del grupo disciplinar en productividad y optimización. Doctor en ingeniería de procesos y sistemas por la Universidad de Valladolid, España. Miembro de la IAENG. Sus investigaciones han sido publicadas en: el Lecture Notes in Engineering and Computer Science. Actualmente es coordinador de la maestría en administración industrial, en el departamento de Posgrado e Investigación de la Facultad de Ingeniería.