Using the Origin of Chemical Ideas to Enhance an Understanding of the Chemistry of Air: Issues and Challenges for including mathematics in the teaching and learning of chemistry

Abstract

This paper describes some of the mathematical components of a narrative constructed for firstyear tertiary chemistry students to celebrate the International Year of Chemistry in 2011. The narrative is entitled, “Making Good Use of the Air Around Us”, and deals with the origin of our understanding of the physical and chemical properties of air largely through the work of Robert Boyle and Antoine Lavoisier. The paper argues for the importance of mathematics not only as a skill but as a language for the teaching and learning of chemistry and indicates that our efforts to have mathematicians and chemists work together on curriculum issues need to be re-energized if we are to enhance our understanding of such a progressive discipline as chemistry.

Resumen

Este artículo describe algunos de los componentes matemáticos de una narración construida para el primer año de estudiantes universitarios, para celebrar el Año Internacional de la Química en 2011. El título de la narración es: “Haciendo buen uso del aire alrededor de nosotros”, y tiene que ver con el origen de nuestro entendimiento de las propiedades físicas y químicas del aire, a través del trabajo de Robert Boyle y Antoine Lavoisier. El trabajo argumenta sobre la importancia de las matemáticas no sólo como una habilidad, sino como un lenguaje para la enseñanza y el aprendizaje de la química, y nos indica que nuestros esfuerzos de poner a matemáticos y químicos a trabajar juntos en aspectos del currículo necesita ser vigorizado en el futuro si es que deseamos mejorar nuestra comprensión de una disciplina progresiva como lo es la química.

Introduction

It will be nearly twenty years since the very first volume of the journal, Science & Education, dedicated to promoting the use of the history and philosophy of science in science teaching, was published. I have been perusing the first editorial written by the editor, Michael Matthews, and pondering what our successes have been and what our failures have been over this period. In 1992, one of the major aims of the journal was expressed in the editorial as follows (Matthews, 1992, p. 2).

One major division that Science & Education seeks to overcome is that between researchers in mathematics education and researchers in science education. Seldom, particularly in the Anglo world, do these two groups meet or read each others’ work… The history and philosophy of science and mathematics are interwoven disciplines, they are a natural vehicle for bringing the two communities together. Many problems in science education have their origin in the quantitative side of science, and many problems in mathematics education have their origin in the supposed irrelevance of mathematical formalism… The mathematizing of science is one of the central features of modern science, as is the making practical of modern mathematics.

The extent to which the journal has been successful in bringing the science and mathematics communities together can be gleaned from the wording of the subtitle of the journal. In 1992, the subtitle read, “Contributions from History, Philosophy and Sociology of Science and Mathematics”, which encompassed very much the aims of the editorial staff at the time. In 2011, the subtitle has changed to read, “Contributions from History, Philosophy and Sociology of Science and Education”. Does the change in subtitle mean that the battle for integrating science and mathematics in science teaching has been lost? While the journal still attracts articles from mathematicians and mathematics educators, there is a real sense that much work is still required in taking seriously the role of mathematics in science teaching and learning and this includes chemistry education. Given this state of affairs one must ask the question as to why there appears to have been a lack of engagement between the two communities. I think there are possibly three contributing reasons for this.

Firstly, statements defining the Nature of Science often do not refer to mathematics. This is the case, for example, for the fourteen consensus statements on the Nature of Science compiled by McComas, Almazroa and Clough (1998). There may be a number of reasons as to why this is the case but among them is most certainly the view that mathematics is a skill or a tool for probing nature rather than a language that is endemic to nature itself, albeit in an idealized form. Curriculum documents such as the Cambridge International O-level (University of Cambridge, 2011a) and A-level Chemistry syllabi (University of Cambridge, 2011b) specify a list of mathematical skills required for completing chemistry at this level but do not suggest any deeper meaning for the mathematics used. Rohrlich (1987, p. 13) reminds us that, “The mathematical formulation of a theory introduces mathematics as a kind of ‘language’. Concepts are characterized by mathematical symbols and are manipulated as such… A purely verbal account of reality would suffer badly under the ambiguity of everyday language, the variation in denotative as well as the connotative meanings of words causing considerable difficulties”. The challenge for chemistry educators is to continue to seek ways of making such mathematical formulations accessible to students because any attempt at understanding nature demands it. This is reflected in the preface to the ninth edition of Atkins’ Physical Chemistry: “The concern expressed in previous editions about the level of mathematical ability has not evaporated, of course, and we have developed further our strategies for showing the absolute centrality of mathematics to physical chemistry and to make it accessible… We have kept in mind the struggling student, and have tried to provide help at every turn” (Atkins & De Paula, 2010, pp. vii-viii).

Secondly, mathematics is often associated with algorithmic problem solving as opposed to what is considered to be the more appropriate conceptual problem solving. What often characterises algorithmic problem solving is, “the emphasis on remembering and using facts and mathematical formulas, without trying to embed these in a rich framework of qualitative knowledge” (Reif, 1983, p. 952); “a recipe book acquaintance with a number of mathematical techniques… often used on an ad-hoc basis” (Stenhouse, 1985, p. 21); and a “sea of meaninglessness… where formulae and equations are recited but few people know what they mean” (Matthews, 1992, pp. 11-12). The challenge is how to nurture the mathematical content of science in a way that enhances concepts and speaks to the grand narrative of nature. In this paper I attempt to show how an historical approach to the chemistry of air uses mathematics in a way that is foundational to modern applications of the properties of air and draws a balance between mathematics as a tool or algorithm and as a language.

Thirdly, mathematics is often seen as beyond the reach of many students leading them to detest science. Sichau (2000, p. 389) observes that, “Thermodynamics is unpopular among the majority of students. Many students have an abhorrence of it, especially of the mathematics involved”. This has led to attempts by textbook authors and curriculum developers to construct chemistry and physics courses with minimal mathematics involved giving the impression that mathematics after all is not central to science anyway. As it turns out, the function of mathematics in science is a rather complex one. Some associate mathematics only with the theoretical side of science, or what Hottecke (2000) calls intellectual work, and experiment with the practical side of science. Such a suggestion implies that experimental work is non-mathematical and non-intellectual and I would suggest that this is an extreme view to take as far as chemistry education is concerned. There is also a view that mathematics cleansed chemistry from “the very messy business of actually doing experiments” (Sichau, 2000, p. 390) by making it “more elegant, abstract, and concise” (Callen, 1960, p.viii). The opposing view is that mathematics destroyed chemistry because, “by its even greater abstract treatment of phenomena [it] led to the vanishing of substances” (Gingras, 2001, p. 385). Henry Armstrong felt compelled to attack physical chemistry as a discipline because of its preoccupation with numerical data and mathematics. He believed “we have to recover this [chemical feeling] or chemistry will be imperilled” (Armstrong, 1928, p. 51). In this paper I illustrate one approach to the chemistry of air that is cognisant of the importance of mathematics to chemistry and which embeds mathematics into an analysis of a set of historical experimental results that emphasizes mathematics as a language and a tool.

Recently I have written two narratives under the general title, “Making Good Use of the Air Around Us” for first-year undergraduate chemistry students. Part A deals with the physical properties of air and Part B deals with the chemical properties of air. Part A focuses on the work of Robert Boyle and Part B on the work of Antoine Lavoisier. The narratives try to deal with mathematics in a creative way and deal with two key historical experiments which are foundational to two current applications of the chemistry; hot-air balloons and car air bags. The motivation for writing the narratives was partly to celebrate the International Year of Chemistry and to search for new ways of making mathematics in chemistry more attractive for students. What follows here are some examples of the mathematical tasks presented in the narratives for the physical and chemical properties of air.

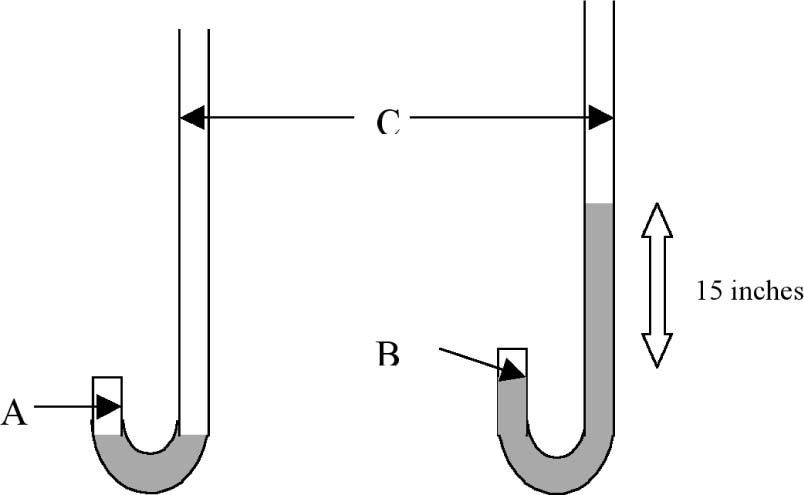
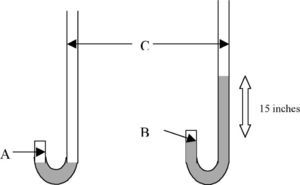
The Physical Properties of Air

Students are presented with the results of Boyle's “J” tube experiment of 1662 as shown in Table 1.

Table 1.

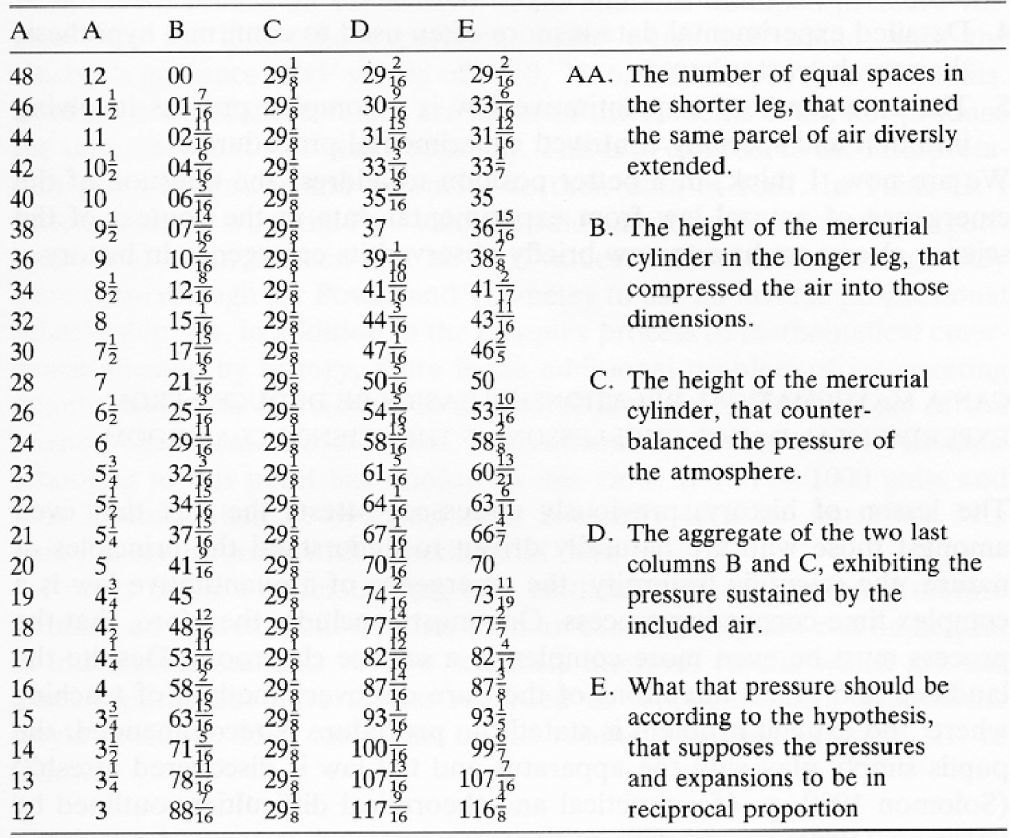
Boyle's 1662 results for the compression of air showing the volume of trapped air (A columns-different units) and its associated pressure (D) obtained with the J tube (Boyle, 1662).

These results were obtained with a piece of glass apparatus in the shape of the letter “J” with a short and long arm as shown in Figure 1. Boyle kept adding mercury to the open side or long arm of the J tube until he had the enclosed air in the short arm supporting a much greater height of mercury than 29 inches, the characteristic height supported by one atmosphere of pressure. He made careful measurements of the pressure of the enclosed air and the volume of the enclosed air space and published his results in 1662. Boyle knew from previous work done by British scientists Power and Towneley that the pressure (spring) and volume (space occupied) of enclosed air could be inversely proportional to each other (de Berg, 1995a). Notice how he used his results to check this hypothesis in Table 1. In column E, Boyle calculated what the pressure of enclosed air should be if pressure and volume were in reciprocal (inverse) proportion to each other and this was compared with the experimental results in column D. Both columns labelled A are measures of volume but in different units.

Figure 1.

J-tube apparatus.

We know from studies conducted as far back as the 1970's that students have difficulty with proportional reasoning (Karplus & Karplus, 1972) and will often attempt to solve a problem using a form of mathematical reasoning other than proportional reasoning (de Berg, 1995b). We also know that complete reliance on mathematical equations as algorithms in science teaching does not enhance understanding (de Berg, 1995b). Consequently, with these facts in mind, I have attempted to help students understand the data in Table 1 by asking them to do tasks such as the following after having reminded them that one way of thinking about inverse or reciprocal proportion is that if you double one of the variables then the other variable should halve in value.

Task 1: Illustrate this doubling-halving principle by selecting two sets of data from Table 1 (use the first column A for volume and column D for pressure). Is inverse proportion consistent with this data? Clearly show your calculations.

Students are reminded that inverse proportion also means that if you triple one of the variables then the other variable should be reduced to one third of its original value.

Task 2: Illustrate this (tripling-one third) principle by selecting two sets of data from Table 1 (use the first column A for volume and column D for pressure). Is inverse proportion consistent with this data? Clearly show your calculations.

While Boyle expressed the inverse proportion relationship in words in 1662 (pressures and expansions are in reciprocal proportions), Wilhelm Ostwald (1902) expressed the relationship algebraically at the beginning of the twentieth century in the form, p₁v₁ = p₂v₂. Now, is there any advantage in representing a law using the symbols of mathematics, that is, using algebraic mathematical expressions?

Task 3: One advantage is that the laws of mathematics can be used to rearrange a mathematical expression to generate a new expression. Rearrange the expression, p₁v₁ = p₂v₂, to get an expression for v₂.

Task 4: See if you can determine how Boyle calculated the value 99 in column E. For this purpose use the first column of A values and the first row of values as a reference. Clearly show your calculations.

In 1902 Ostwald also represented the pressure-volume law graphically. Is there any advantage in representing a law graphically?

Task 5: Place the values in column A (first column)(volume) and column D (pressure) from Table 1 in an Excel spreadsheet and ask Excel to plot pressure against volume. Express column D values in decimal notation to the first decimal place. Place V values on the left-hand side of the P values, highlight V and P values, tick the chart wizard, choose scatter plot, give a title, label x and y axes, tick finish, highlight the graph, print the graph and attach here. Name one advantage of expressing this pressure-volume law graphically.

Task 6: On the Excel spreadsheet create a column of reciprocal volume values (1/V) and plot pressure against reciprocal volume (1/V). Place (1/V) values on the left-hand side of the P values and follow the guidance given above in Task 5. Print off your graph and attach here. What do you notice about the graph and what does this mean about the relationship between P and (1/V)?

Students typically say that there is a straight line relationship between P and 1/V but have difficulty saying that P is directly proportional to 1/V. The significance of the line passing through the origin is not always appreciated either as an ingredient of direct proportionality.

Task 7: What does the slope of the graph in Task 6 represent? [Hint: Right click on one of the points on the graph and ask for a trendline, format the trendline to get an equation of y against x. In Excel create a column of (P×V) values. What do you observe?]

To complete Task 7 students often need to be reminded of the form of the equation for a straight line so they can identify the slope with the value of (P×V).

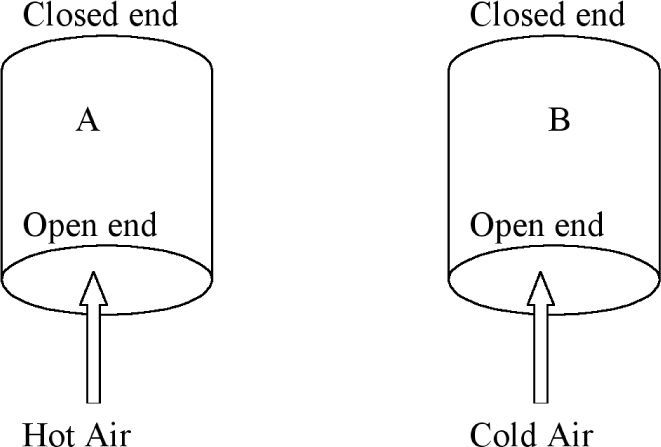
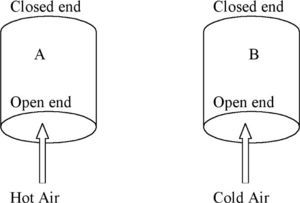
Students are then introduced to the ideal gas equation where the product (P×V) equals (nRT) where R is the gas constant, T is the absolute temperature, and n is the amount of gas expressed in moles. Whilst students are given examples which resemble algorithmic substitution, they are also encouraged to use semi-quantitative reasoning with the ideal gas equation. This is done in the following task which is a preparation for understanding the operation of a hot air balloon. Consider two containers, A and B, of the same volume open to the atmosphere as shown in Figure 2. Hot air is blown into one and cold air into the other.

Task 8: How would the amount of air (n_A) contained in the volume of A and the amount of air (n_B) contained in the volume of B in Figure 2 compare if the air pressure is the same in both volumes and equal to the external air pressure? Explain how you arrive at your answer by making use of the ideal gas equation, PV = nRT.

Figure 2.

Cold air and hot air exercise.

Students are not used to engaging in this type of reasoning with mathematical equations and yet it is one strategy that can dilute the impact of algorithmic substitution. The process can continue with Tasks 9 and 10 as an approach towards understanding how a hot air balloon works.

Task 9: Use your knowledge of chemistry, particularly the formula for the number of moles in terms of mass, to compare the mass of air (m_A) contained in the volume of A to the mass of air (m_B) contained in the volume of B.

Task 10: Now show how you can compare the density of air in A to the density of air in B, given that density is defined as mass per unit volume (d = m/v).

After completing Task 10 students are asked to use the internet to determine the major components of a hot air balloon and are asked to describe how such a balloon works. Three tasks lead up to a task which involves substitution of values into the ideal gas equation but the exercise is not just a blind, non-thinking substitution. It is designed to check a value for the density of air pertinent to a hot air balloon given on the website. The four tasks related to the website now follow.

Task 11: Who was the first to fly a hot air balloon and in what year ?

Task 12: What is the volume of air contained inside a hot air balloon to enable it to lift?

Task 13: What is the density of air inside a hot air balloon at 20°C and at 120°C? (obtained from the website)

Task 14: Are the values listed in Task 13 consistent with the ideal gas equation given the average molar mass of air as 28.97 g mol^–1 and an atmospheric pressure of 101,300 pascals? [Use P = (d/M)RT as the appropriate form of the gas equation and use R = 8.314 J K^–1 mol^–1].

Task 14 involves the accurate processing of units for the quantities in the ideal gas equation and students initially struggle with this process. However, thinking about units dilutes the mechanical nature of mathematical problem solving and enhances the understanding necessary to interpret the quantities in an equation. We will now look at some numerical and mathematical ideas related to the chemical properties of air. The emphasis here will be on the importance of units of measurement.

The Chemical Properties of Air

The focus of this narrative is to seek an answer to the question, “How did we learn that air consists largely of two elements, oxygen and nitrogen?” Now this is not a trivial problem. In 1789 the French chemist Lavoisier did an ingenious experiment (Lavoisier, 1789, pp. 16-18). A diagram of his apparatus is shown in Figure 3 and what follows is the narrative as presented to students.

Figure 3.

Lavoisier's apparatus for studying the role of air in chemical reactions.

The diagram shows a glass retort (curved shaped vessel) with one end containing mercury and sitting on the top of a furnace and the other end submerged in mercury and sticking up out of the mercury inside a bell jar containing a fixed amount of air. Lavoisier gently heated 4 ounces of mercury in the retort over 12 days at which time he noticed a red scale form on the mercury and the volume of air decrease from 50 cubic inches to 42 cubic inches. He would have noticed the mercury inside the bell jar rise as the air pressure inside dropped due to reaction with the retort mercury. Now the gas left in the bell jar was shown not to support combustion because a flame was quickly extinguished when placed in this gas. The gas did not support life as animals placed in it died in a very short time. The gas had the same properties as the gas that was left after Joseph Priestley burned charcoal in a fixed volume of air and removed the fixed air (carbon dioxide) formed in the process with alkali solution. Priestley had called this gas, phlogisticated air; Carl Scheele, a Swedish chemist, had called it foul air; and Lavoisier called it azote (no life). The name, nitrogen, was given to the gas in 1790 by Chaptal. Now it took a little while for chemists to realise that this gas was an element but as it never seemed to lose weight in its chemical reactions it was increasingly believed to be an element.

Now when the red-speckled mercury or red calx (which was actually red mercuric oxide) was placed in a smaller retort and heated very strongly over a furnace Lavoisier observed a gas coming off which he collected over water. He obtained 8 cubic inches of gas which matched the difference in his earlier experiment between the volume of initial air (50 cubic inches) and air left (42 cubic inches). He inferred that the air used up in his experiment was the same as the air produced on heating the red calx. This enabled him to perform further tests on the air that was used up and the air that was left behind. He found that the air that was used up supported combustion, that is, a candle burned very brightly in this air. The air that was left behind did not support combustion, that is, a burning candle was extinguished in this air. Tests like this supported the belief that air consisted predominantly of two parts, one that supported combustion and one that did not support combustion. The gas produced by heating the red calx was the same gas that Priestley and Scheele had earlier discovered because it was shown to support combustion in that things burnt more brightly in this gas than in common air and it supported life. Priestley had found that a mouse had lived twice as long in this gas as in common air. Priestley called the gas dephlogisticated air; Scheele called it fire air; and Lavoisier eventually called it oxygen (acid producer). When Lavoisier added this gas to the azote (nitrogen) left in the bell-jar from the first part of the experiment neither heat nor light was used or evolved so Lavoisier thought that this was good evidence that air was a mixture of these two gases, nitrogen and oxygen.

Lavoisier later tells us in his description of the experiment that 45 grains of the red calx (mercuric oxide) were obtained after 12 days. Now in your science studies you are going to have to learn to appreciate how important units of measurement are in science. These 45 grains represented a French unit of measurement for mass in the 18^th century. Lavoisier was responsible for developing the balance for measuring masses in chemistry. But how many grams would 45 grains represent? To answer this question we need to consult conversion tables. It turns out that 1 grain is equivalent to 53.11 mg and 1 cubic inch (French) is equivalent to 19.836 cm³.

Task 15: What was the mass in grams of mercuric oxide (HgO) (red calx) produced in Lavoisier's experiment?

Task 16: Write down a balanced chemical equation for the reaction between mercury and oxygen to produce mercuric oxide. Use subscripts (s, l, g) to indicate state.

Now looking back on Lavoisier's experiment from the 21st century point of view we can calculate how many cubic inches of oxygen would have been required to produce 45 grains of red calx theoretically and compare this volume with the volume he maintains he got experimentally (8 cubic inches). From your answer in Task 15 you can calculate the number of moles of calx (HgO) and from your answer in Task 16, the number of moles of oxygen required. Once you have this you can use the ideal gas law [PV = nRT] to determine the number of cubic metres of oxygen required and then by using the conversion work out the number of French cubic inches required. To do this calculation you will have to assume a temperature say of 25°C and an atmospheric pressure of say 101,300 pascals. Do your calculation with a gas constant R value of 8.314 J K^–1 mol^–1.

Task 17: Use the guidance above to determine how many cubic inches (French) of oxygen would theoretically have been required to produce 45 grains of red calx (mercuric oxide).

Task 18: Deviations from the experimental volume could be due to our assumptions of temperature and atmospheric pressure. The deviation could also be due to an inaccurate measurement of the mass of calx (HgO) produced. Considering these three variables separately what changes to temperature, atmospheric pressure, and amount of calx would bring the theoretical volume closer to the experimental volume [8 cu.in]?

Task 18 can prove rather demanding for students but it does show how important mathematical equations are in addressing such semi-quantitative questions. The narrative moves on to compare Lavoisier's values for the composition of air with the currently accepted ones; the discovery of argon; the function of an electron ionization mass spectrometer; the phlogiston model of combustion; and finally a discussion of how the air bag works in a motor vehicle, including a calculation of the mass of sodium azide required to produce 67 L of nitrogen at 1 atm pressure and 200°C, the volume sufficient to fill an air bag.

Conclusion

This paper has attempted to show how history of chemistry and mathematics can combine to potentially enhance a student's understanding of how chemical ideas developed and how they are pertinent in understanding the technological devices used in our current world, a theme of importance during the International Year of Chemistry. Describing chemistry and its associated mathematics in the form of a narrative has great potential for engaging our students with the subject of chemistry. Peter Watson's (2009, p. 463) review of twentieth century intellectual development includes this challenging statement:

Neil Postman drew my attention to the fact that at the beginning of our century William James said that any subject, treated historically, can become a humanity. You can give humanistic value to almost anything by treating it historically. Geology, economics and mechanics are humanities when taught with reference to the successive achievements of the geniuses to which these sciences owe their being. Not taught thus, literature remains grammar, art a catalogue, history a list of dates, and natural science a sheet of formulas and weights and measures… The story is so overwhelming that I believe it can provide, or begin to provide, an antidote to some of the problems that have plagued our educational institutions in recent years.

While a narrative does not necessarily involve history, in a subject like chemistry narrative, history, and epistemology are intimately linked with mathematics acting like a thread holding the pieces together. In this paper I have shown how mathematics acts as a language, albeit an ideal language spoken by air in the form of the gas law. Mathematics is also a skill that enables us to find new information using the laws of algebra. It is my contention that we portray a disintegrated chemistry if we exclude mathematics from its teaching and learning.