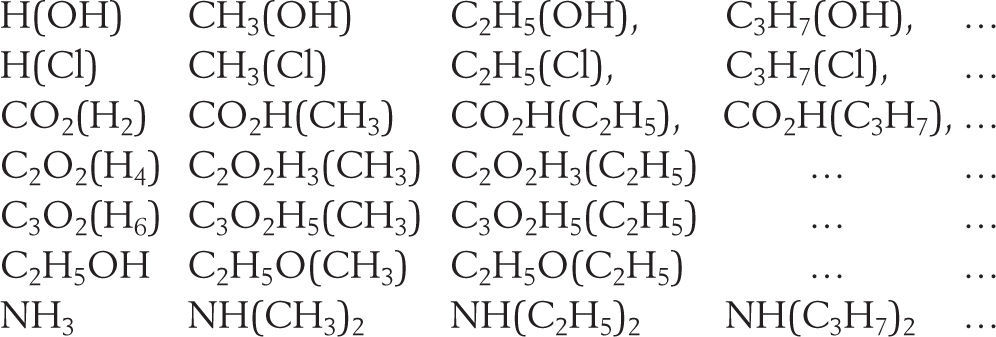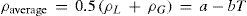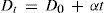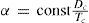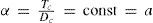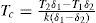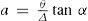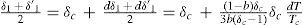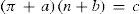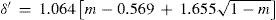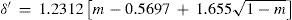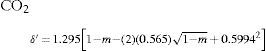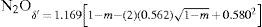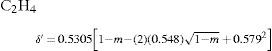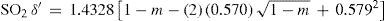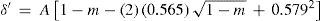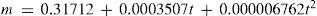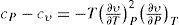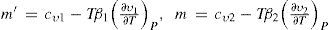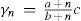Émile Ovide Joseph Mathias. Thermodynamics of saturated fluids

Abstract

Émile Ovide Joseph Mathias (1861-1942) was a multifaceted scientist who started his activities in the area of thermodynamics and then switched to magnetic phenomena and electrical phenomena in the atmosphere. He collaborated with Cailletet in the development of methods for measuring and correlating the density of liquefied gases and their saturated vapors. His name is particularly known for the so-called law of rectilinear diameters that allows an easy determination of the critical volume.

Resumen

Émile Ovide Joseph Mathias (1861-1942) fue un científico multifacético que comenzó sus actividades en el campo de la termodinámica y luego se dedicó al magnetismo terrestre para terminar estudiando fenómenos eléctricos en la atmósfera. Colaboró con Louis Cailletet en el desarrollo de métodos para medir y correlacionar la densidad de gases licuados y sus vapores saturados. Su nombre es particularmente conocido por la llamada ley de los diámetros rectilíneos, que permite determinar fácilmente el volumen crítico.

Life and career

Very little information is available about the life, family, and career of Émile Ovide Joseph Mathias (1861-1942). The mayor sources are the eulogy read by Charles Maurain (1871-1967) at the March 25, 1942, session of the Académie des Sciences (Maurain, 1942) and the summary of his scientific work that Mathias prepared on the occasion of his candidacy to the Académie des Sciences (Mathias, 1926b).

Émile Mathias was born in Paris on August 15, 1861 and passed away at Clermont-Ferrand on March 7, 1942. He received a Bourse (scholarship) de License (1882) and a Boursier de Agrégation from the Faculty of Sciences of Paris (1884). In 1885, after graduation, he was appointed agrégé des Sciences Physiques et Naturelles at the Lycée de Lorient and then promoted to professor. In the same year he became Préparateur au Laboratoire d'Enseignement de la Physique at the Sorbonne, directed by Edmond Marie Bouty (1846-1922), but worked primarily with Louis Paul Cailletet (1831-1913) at the École Normale, who was then doing his famous researches on gas liquefaction (Wisniak, 2003b). At the Sorbonne laboratories he developed a method for measuring the heat of vaporization of liquefied gases using a calorimetric procedure at constant temperature, which allowed making measurements under specified conditions and with high accuracy (Mathias, 1889b). This research led to his doctoral thesis (Mathias, 1890c). Between 1889 and 1891 he served as Professor (1^e Chair) at the Lycée de Marseille and after being awarded his degree of Docteur ès Sciences Physiques (1890) he was appointed Maitre de conférences at the Faculty of Sciences of Toulouse, followed by promotions to Chargé d'un Cours Complementaire (1892) and Professeur Titulaire de Physique (1895). In 1910 he was appointed Professor of Physics at the Faculty of Sciences of Clermont (1910), Dean of the Faculty (1912-1919), and then Honorary Dean in 1919.

Mathias collaborated with Cailletet in the development of methods for measuring and correlating the densities of liquefied gases and their saturated vapors. This work led in 1886 to the discovery of the law of rectilinear diameters. These measurements, not necessarily executed up to the critical temperature, allowed constructing the saturation curve and the rectilinear diameter, whose intersection yields a very precise determination of the critical density (Mathias, 1904). Later on, Mathias showed that for certain substances the law of rectilinear diameters was only an approximation (Maurain, 1942).

At Toulouse Mathias continued his work on the calorimetry of liquefied gases, measuring their specific heat and heat of vaporization. Afterwards he studied the application of the law of corresponding states at conditions near the critical point and showed that although the law was not applicable in a general way its verification was more satisfactory when considering groups of substances conveniently structured (Maurain, 1942).

In 1909, following conversations held with Heike Kamerlingh Onnes (1853-1926, 1913 Nobel Prize for Physics) at the First International Congress on Cold, Mathias began a long experimental program with the scientists at the Cryogenic Laboratory at Leyden on the measurement of the density of the saturated vapor and liquid phases of substances having low critical temperature and simple molecular structure (such as the permanent and noble gases) and the possible validity of the law of corresponding diameters. A few years before Lord Rayleigh (John William Strutt, 1842-1919) and William Ramsay (1852-1916) had discovered and isolated the noble gases (Wisniak, 2007a) and Onnes (Wisniak, 2003a) had discovered superconductivity and succeeded in liquefying helium. These studies led to a series of publications about oxygen (Mathias and Onnes, 1922), argon (Mathias, Onnes and Crommerlin, 1922a), nitrogen (Mathias, Onnes and Crommerlin, 1922b), hydrogen (Mathias, Crommerlin, and Onnes, 1922b), neon (Mathias Crommerlin, and Onnes, 1922a), helium (Mathias, Crommerlin, Onnes, and Swallow, 1926), ethylene (Mathias, Crommerlin, and Watts, 1926), CO (Mathias et al., 1932ab) and krypton (Mathias et al., 1937abc). His findings indicated that although for most of these substances the diameters were not rectilinear, the method was very satisfactory for the determination of their critical density.

From 1893 on Mathias was charged with the direction of the meteorological and magnetic Services of the Toulouse Observatory, directed by Benjamin Baillaud (1848-1934). There he organized the service and afterwards the magnetic measurements at the central station. Mathias himself made measurements in more than 170 stations (Mathias, 1897). He then studied the representation of the data acquired using different magnetic elements and simple equations in terms of the latitude and longitude, which could be considered as a regular distribution of the magnetic field in a small region. He extended this representation procedure to the ensemble of the French magnetic network established by Moreaux (Mathias, 1929-1931). He summarized his experience in a book about terrestrial magnetism (Mathias, 1907a; Maurain, 1942).

Mathias also became interested in meteorology and after the sudden death of Bernard Brunhes (1867-1910) he succeeded him as director of the Observatory of Puy-de-Dôme and as professor at the University of Clermont-Ferrand. From here on, his activities centered on the physics of the earth. Under his suggestion and the auspices of the French Committee of Geodetics and Geophysics, a new French magnetic network was established (1922-1926), which eventually comprised over 1300 stations (Maurain, 1942).

Mathias paid large importance to the study of atmospheric electricity, established the measurement of the conductivity and the electric field at the summit of Puy-de-Dôme, and directed the publication of a treatise of atmospheric and telluric electricity (Mathias and Bosler, 1924). His studies of lightning and thunderbolt led to many publications particularly about the different forms of thunderbolts and about the nature of the fulminating matter brought into play to interpret certain phenomena (Mathias, 1922ab; 1925ab; 1926a; 1928; 1932ab; 1933; 1935ab; Maurain, 1942).

During the First World War Mathias organized the observatory of the plain and a hospital to which he and his wife devoted much time, after the death of their eldest son in the battlefield (Maurain, 1942).

Besides his academic activities, Mathias occupied many public offices, among them, correspondent of the Ministry of Public Instruction (1911); member of the French committee of Geodesy and Geophysics (1920); member of the Conseil de Perfectionnement de l'Institut de Physique du Globe de la Université de Paris (1921); non resident member of the Committee of Historical and Scientific Works (1919); Secretary of the 6^th Section (Terrestrial Magnetism and Atmospheric Electricity) of the French Committee of Geodesy and Geophysics (1927); member of the committee of the French Central Bureau of Terrestrial Magnetism (1927); and member of the commission of the Répertoire de Bibliographie Scientifique (1924). He was elected corresponding member of the Société Royale de Sciences de Liège (1899) and of the Institut (1919), and foreign member of the Société Hollandaise des Sciences de Harlem (1920). In 1897 the International Exposition of Brussels awarded him a merit diploma and in 1907 the Institut the Gastón Planté Prize.

Scientific contribution

Here we will describe and comment Mathias's contributions in the area of thermodynamics.

Law of rectilinear diameter

In 1886 Cailletet and Mathias (Cailletet and Mathias, 1886) reported that they had constructed a very simple apparatus to measure the density of the saturated vapor and liquid phases of a pure compound as it approaches its critical point. A plot of their experimental results of the density of N₂O (–20.6° to +24°C), ethylene (–21° to +6.2°C), and CO₂ (–34° to +22°C), showed that the mean density of both phases decreased linearly with the temperature and that the straight line drawn through the middle point of the chords was inclined with respect to the abscissa axis and went through the critical point. They suggested employing this fact to determine the critical temperature and density of a gas, using measurements below the critical point. Thus they reported that the critical density of the three gases studied was 0.46 for CO₂, 0.41 for N₂O, and 0.22 g/cm³ for ethylene. This work was considered quite an achievement because of the experimental difficulties involved in measuring the critical volume accurately. Cailletet and Mathias believed that their method yielded the value of the critical volume within 1% of the real one.

This finding is known today as the Cailletet-Mathias law of the rectilinear diameters, expressed as follows:

where ρ_L and ρ_G are the densities of the saturated liquid and gas phase, respectively, and T the absolute temperature. An alternative expression of the law is

where D_t and D₀ are the means of the densities at t° and 0°C, respectively, and α is the slope of the straight line passing through these means.

If the rectilinear diameter line is extrapolated to the absolute zero, ρ will be half the density of the liquid if it could exist at the absolute zero, since the density of the vapor is then zero. In this way it was found (Davies, 1912) that the ratio of the critical volume to the volume at the absolute zero is between 3.6 and 4.

Cailletet's and Mathias publication was followed by another one reporting the measurement of the density of very pure sulfur dioxide in the range 6.6° to +156°C, done in order to extend the limits of the critical temperature measured (Cailletet and Mathias, 1887). Their results indicated that the liquid phase disappeared at 156°C, a temperature slightly above the critical one reported by Zaionchevskii (Zaionchevskii, 1882). Using the rectilinear diameter procedure they estimated the critical density of SO₂ as 0.520 g/cm³ (the value accepted today is 0.525 g/cm³).

In a following work (Mathias, 1892a), Mathias wrote that Émile Hilaire Amagat (1841-1915) had confirmed that the law of rectilinear diameters was also valid for carbon dioxide (Amagat, 1892), and that the results of Sidney Young (1857-1937) (Young, 1891ab) for twelve widely different substances, covering the very large temperature ranges of 300° and 325°C from the critical temperature, could also be seen as the definite proof of the validity of the law. An important general consequence was that the curves giving the densities of the saturated liquid and of the saturated vapor with temperature, converged smoothly to a common limit, located at the critical temperature. In other words, at the critical point the system was homogeneous and not heterogeneous, as some had previously claimed.

In 1892 Mathias and Young (Mathias, 1892ab; Young, 1892; 1900ab) demonstrated independently that if van der Waals' principle of corresponding states is correct, then the value of α should be directly proportional to the critical densities and inversely proportional to the absolute temperatures, that is, for any substance:

or

Mathias then discussed the methods available, notably that of Thomas Edward Thorpe (1845-1925) and Arthur William Rücker (1848-1915) (Thorpe and Rücker, 1884), for evaluating the critical temperature for the cases where it had not been measured directly. Thorpe and Wicker suggested that the critical temperature could be estimated according to

where δ₁ and δ₂ are the densities at the temperatures T₁ and T₂, respectively, and k a parameter that they believed to be 1.995 for all substances.

According to Mathias if in Thorpe and Rücker's formula k took the value 2 then a became equal to 1 and allowed determining both the critical density and the critical temperature by a geometrical method. However, in most cases the value of k was different from 2 and that of a different from 1, making the geometrical method inapplicable. Mathias also showed that when the temperature was far from the critical one the density of a liquid tended to the value three times that of its critical density (Mathias, 1892a).

In a previous work Mathias had shown (Mathias, 1892b) that calling y the ordinate of a diameter relative to T = mθ the absolute temperature, –tanα its angular coefficient, Δ the critical temperature and θ the absolute critical temperature, then the following relation was true (Mathias, 1900):

where a = θ tan α / Δ.

According to Young (Young, 1900a) the law of Cailletet and Mathias had been found to hold good for a considerable number of substances from the boiling-point up to the critical point, and Mathias, making the very natural assumption that the law may be relied upon at lower temperatures, had calculated the value of a from the mean densities below the boiling point. All these arguments, coupled with his own research on the critical density, led Young (Young, 1900ab) to undertake a careful examination of the data that he had measured for thirty substances (Young, 1891ab, 1892) and to investigate in more detail the ability of the law of rectilinear diameters to predict the critical density more accurately that by direct measurement of the critical volume. In every case, except the alcohols, he calculated the critical densities using the method of Cailletet and Mathias for the temperature range between the normal boiling point and the critical temperature. Although the deviations from the formula D_t =D₀ + αt were sometimes considerably, there did not appear to be any definite tendency for curvature and Young attributed the deviations to the experimental error (Young, 1900ab).

Young found that if the rectilinear diameter was traced on the plane T_r-P_r (reduced temperature-reduced pressure) it coincided exactly with the one drawn in the plane T-P. He also proved that this was true for acetic acid (rectilinear diameter) and for methanol (curvilinear diameter). Mathias used following thermodynamic arguments to prove the truth of Young's conclusion (Mathias, 1893a).

As mentioned before, parameter a, whose constancy is a necessary and sufficient condition for the law of rectilinear diameters to obey the principle of corresponding states, is given by the relation (Mathias, 1899ab)

where θ and Δ are the absolute temperature and critical density, respectively, and α is the angular coefficient of the diameter. To determine the value of a it is sufficient to know the location of the summit K of the curve of the density and the value of α. These parameters can be determined by measuring the density of the liquid at different temperatures below or near the normal boiling temperature, the critical temperature, the variation of the vapor pressure with temperature, and the vapor density of the substance. Mathias's experiments showed that α can be very different from unity and simple gases like oxygen, nitrogen, chlorine and bromine, have the smallest values of α (Mathias, 1899ab).

Mathias then returned to the answer that consists in measuring directly one of the unknowns Δ, θ, or a. He used Rudolph Knietsh's (1854-1906) extensive experimental data on the densities of chlorine (Knietsch, 1890) to obtain tanα = 0.0010756, a = 0.7675, and Δ = 0.58719. Afterwards he determined the values of a for more than 30 substances and concluded that this parameter was not constant, it varied from 0.68 for nitrogen to 1.09 for ethyl propionate thus showing that the principle of the corresponding states did not apply to the rectilinear diameters (Mathias, 1900).

Since its presentation in 1886 until today, the law of rectilinear diameters has been, directly or indirectly, the subject of many publications. Some of them are illustrated in what follows.

Philippe-Auguste Guye (1862-1922) developed a method for calculating the molecular weight at the critical point, which was particularly applicable to compounds like water and methanol that deviated more pronouncedly from relations that had been derived previously (Guye, 1890; 1894). This procedure led Guye to conclude that methanol at its critical point seemed to exist as a dimer. William Ramsay (1852-1916) and John Shields (1818-1879) (Ramsay and Shields, 1893) studied the molecular complexity of 55 different liquids and found that most of them had the same degree of polymerization in the liquid and vapor phases. For compounds such as methanol, fatty acids, acetone, propionitrile, nitroethane, and water, the phenomenon of polymerization was particularly strong and the degree of polymerization decreased with increased temperature. Another interesting finding was that the ratio of the critical density, determined by the law of rectilinear diameter of Cailletet and Mathias, to the density calculated using the ideal gas law, was about 3.85 for a large variety of substances (i.e. halobenzenes, carbon tetrachloride, diethyl ether, and many methyl and ethyl fatty esters). Further investigation by Young (Young, 1900a) had demonstrated that at low temperatures the law of the rectilinear diameter failed to be true for substances known to polymerize like water, methanol, ethanol, and propanol, but continued to be true for acetic acid. To Guye this observation meant that the presence of polymerized molecules was not a sufficient condition for curving of the diameter. Analysis of the available information indicated that although water and the lower alcohols were strongly polymerized in the liquid phase, this was not true for the vapor phase; at temperatures approaching that of boiling the density of the vapor was slightly larger than that predicted by the ideal gas law. At higher temperatures both densities became essentially identical. Acetic acid behaved different; Ramsay and Young (Ramsay and Young, 1886) had found it to be strongly polymerized in the vapor phase. Guye concluded that the law of rectilinear diameter was true for simple liquids and for those in which both phases were polymerized to more or less the same degree. Bending of the diameter was then a clear demonstration that the liquid phase had a higher degree of polymerization than that of the vapor phase (Wisniak, 2007b).

Henry Eyring (1901-1981) used his theory of holes to explain the rectilinear diameter law (Eyring, 1936). In a system composed of a pure substance in vapor-liquid equilibrium, there is a continuous exchange of material between the two phases. Using statistical arguments Eyring proved that it required the same energy to make a hole in a liquid of a size, which would just accommodate a single molecule, as it did to vaporize one molecule without leaving a hole. That is, it took the same amount of energy for a hole the size of a molecule to detach itself from the empty space above a liquid and pass into the liquid as it did for a molecule to detach itself from the liquid and pass into the empty space. Since both processes took place in both phases it could be assumed as a first approximation that association or dissociation would not affect the distribution ratio of holes between the phases. In that case, at the critical temperature we should have exactly as much matter in one cubic centimeter of otherwise empty space as we have holes in one cubic centimeter of matter. The plot of the average density of both phases against the temperature would produce a line almost parallel the temperature axis, the density increasing slightly as the temperature decreased. Hence, the average temperature of the two phases should be nearly independent of the vapor pressure (or the temperature). Since the law of rectilinear diameters stated that a plot of average density was a straight line somewhat inclined with respect to the temperature axis, it could thus be said that it followed from the statistical mechanical consideration of holes (Eyring, 1936).

The possibility that the law of rectilinear diameters may be violated has been discussed in several theoretical papers. Goldstein et al., (Goldstein et al., 1987), for example, proved that the plot of the values of the saturated densities of mercury, rubidium, and cesium, exhibits a noticeably nonlinear behavior. Ross and Hensel (Ross and Hensel, 1996) used mercury as the prototype substance to show that a two-state van der Waals model, which introduces compositional fluctuations, leads to an asymmetry in the calculated coexistence curve.

A semi-theoretical deduction of the law of rectilinear diameter was given by Karpen (Karpen, 1923) by assuming that the liquid and vapour phases are not separated by an ideal surface (of negligible thickness) but by a thin transfer layer of thickness h where the total pressure varies gradually from the pressure P₁ of the liquid to P₂, the pressure of the vapor. The molecular exchange (diffusion) between the liquid and the vapour takes place through this layer. All the molecules located in the layer are subject to a Laplacian attraction that changes their relative velocities between two successive collisions. The change in velocity is only local, the average square velocity (of which depends the temperature) remaining constant. Thus he derived the following equation for the vicinity of the critical point we have

where δ1,δ′1, are the densities of the saturated liquid and saturated vapor respectively at temperature T, δc the critical density at temperature T_c, b the covolume, and dδ1,dδ′1 the increase in density caused by a decrease dT in the temperature. Equation (8) is the law of rectilinear diameters.

Homologue series

One additional area of study was related to the variation of the critical properties in series of homologues substances derived by substitution of a hydrogen atom by the radicals methyl, ethyl, propyl, etc. In his first publication on the subject (Mathias, 1892b) Mathias showed that the critical densities (Δ) of a homologue series varied according to a continuous function of the molecular mass of the compound. A plot of Δ as against the value of n as abscissa (where n is the number of carbon atoms of the radical substituting a hydrogen atom) for the different series studied, was a net of regular curves each presenting an asymptote parallel to the abscissa axis. In a following publication Mathias (Mathias, 1893b) showed that the same result was obtained for the reduced critical pressure (π) of at least the following homologue series:

Except for the di-substituted ammonias, it was possible to go from one curve to the other by a simple linear substitution of the form π′ = απ+β where α and β are numerical constants that can have a zero value (Mathias, 1893b). Within the experimental precision, the curves of the critical pressure could be approximated by arches of equilateral hyperbola having asymptotes parallel to the abscissa axis and thus be represented by the general equation:

where a, b, and c were numerical constants varying from one substance to another.

Density of the liquid

According to Mathias, there was little information available of the variation of this property near the critical point. In particular, the experiences of Cailletet and Mathias (Cailletet and Mathias, 1886) on liquid carbon dioxide in the temperature range –34° – +21°C and those of Gustave Adolf Blümcke on the same substance between 0° – 30°C, had shown that the reduced densities δ′ were well represented by the equation:

where m = T/T_c is the reduced temperature. This was the translation, using the van der Waals' notation of corresponding states, of an empirical equation that Mathias and Cailletet, had reported previously. Similarly, the density of liquid sulfur dioxide between 90°-156°C (critical temperature) could be represented with an approximation better than 1/300, by the relation

having the same structure as the previous one and thus justifying the principle of corresponding states. This conclusion was strengthened by the fact that the coefficients 1.064 and 1.2312 in these formulae were well proportional to the critical densities of CO₂ (0.45 g/cm³) and SO₂ (0.520 g/cm³). If instead of considering the above formulae, the experimental data were taken, it was found that the deviation between the theoretical and experimental values followed a regular course and grew as it got away from the critical temperature. For temperatures far away from the critical one, the theorem was no longer applicable. Without that, all substances possess, like water, a maximum density in the liquid state (Mathias, 1891ab).

Density of saturated vapors near the critical point had been reported only for CO₂, N₂O, ethylene, and SO₂ in an interval of 60°C from the critical temperature by Cailletet and Mathias (Cailletet and Mathias, 1886), and correlated by the following empirical relations:

Inspection of eqs 28-30 shows that the terms in parenthesis are identical functions on m reflecting again the principle of corresponding states. Hence, Mathias assumed that the density of the saturated vapor of sulfur dioxide would be given by an equation of the same structure; Mathias was able to do so, for the temperature range of 75°-156°C:

On the basis of these results Mathias suggested that the density of a saturated vapor in the vicinity of its critical temperature should be given by the following general empirical equation having only one parameter:

ignoring the negligible variation of the numerical constants. In order to determine the value of A it is necessary to know only the critical density of the substance in question (Mathias, 1891ab).

Properties of the saturated state

In the introduction of his thesis Mathias wrote that a saturated liquid is completely known from a calorimetric view point when the following quantities are known as a function of the temperature: (a) heat of vaporization, internal and external, (b) specific heat of the saturated liquid, and (c) specific heat of the saturated vapor (Mathias, 1890c). This was the justification of his extensive study of the above properties (Mathias, 1888a; 1890bc, 1894b; 1896ab).

Heat of vaporization

According to Mathias, liquefied gases had been hardly studied from a quantitative viewpoint because of the difficult in preparing them in a high degree of purity and liquefying them in sufficient amount. The experimental methods available for measuring the heat of vaporization were limited to working either at atmospheric pressure or at the fusion temperature of ice. Henri-Victor Regnault (1810-1878) had designed a double water and flow calorimeter capable of working at higher temperatures (Regnault, 1871) but requiring a very complicated method of calculation and some doubtful assumptions (for example, the constancy of the water temperature) (Mathias, 1888a; 1890abc). In order to improve the precision of Regnault's method Mathias developed a new calorimeter capable of operating at constant temperature by compensating on line the cooling of the water (caused by the vaporization of the liquefied gas), with a continuous heat source (the heat developed by the dilution with water of a known weight of concentrated sulphuric acid). Thus, his apparatus not only assured measurement of the heat of vaporization at a given temperature but also changing the latter within a wide range of values (Mathias, 1890abc). In his doctoral thesis Mathias described in detail the measurement of the heat of dilution of sulfuric acid, the vaporization of the liquefied gas and calculation of the corresponding heat of vaporization, the quantitative results for liquid sulfur dioxide, CO₂, and N₂O, as well as data about the specific heat of the specific heat of the saturated vapors.

Mathias concluded that for the three substances studied, the heat of vaporization decreased constantly. The decrease for SO₂ was essentially linear, while for CO₂ and N₂O it decreased rapidly with increased temperature and could be represented by a second-degree function on the temperature. At the critical point of the gas, the heat of vaporization was essentially zero, and the tangent to the curve λ = f(t) was perpendicular to the abscissa axis. As a consequence of these results, the specific heat of the saturated vapor was negative near the critical point, increasing indefinitely in absolute value. Mathias believed that the specific heat presented a maximum value and two possible inflection points (Mathias, 1890abc).

Specific heat

An important question was to determine the actual variation of the specific heat at constant pressure of a saturated liquid with temperature. It was known that this property increased with temperature but the information about its value at the critical temperature was conflictive. Some scientists believed that the specific heat of a liquid increased indefinitely in absolute value, remaining positive, while that of a gas, in the same conditions, was infinitely large and negative (Mathias, 1894ab).

Mathias made a series of very careful and detailed measurements of the specific heat of liquid sulfur dioxide in the temperature range 32.3° to 155.5°C and concluded that its specific heat m at constant pressure (cal/g°C) was always positive, increased monotonously with temperature, and could be represented well by the equation (Mathias, 1894a)

where t is the temperature in °C.

To answer the question theoretically Mathias started from the following equation giving the difference in specific heats for any pure substance (derived from the TdS equations) (Mathias, 1892b; Smith and Van Ness, 2005):

Defining β = ∂υ∂TP/∂υ∂PT and letting the indexes 1 and 2 refer to the saturated vapor and saturated liquid, respectively, the specific heats at constant pressure of the saturated vapor (m’) and of the saturated liquid (m) are expressed by the following equations:

According to Pierre Duhem (1861-1916), c_v tends to finite positive values as the state of the substance approaches the critical state. Since (∂v₁/∂T)_P and (∂v₂/∂T)_P at the critical temperature become infinitely large and of the same order, it follows that (1) the specific heat m’ of the saturated vapor is infinitely large and negative at the critical temperature, and (2) the specific heat m of the liquid is infinitely large and positive, so that their ratio m’/m tends to –1 (Mathias, 1896a).

In another work, Mathias considered the possibility of developing an analytical description of the specific heat of saline solutions (acids, bases, salts) as a function of the concentration. Little information was available so as to generate simple and general expressions (Mathias, 1888bc; 1889a). Mathias then proposed the following general empirical relation, applicable to aqueous and non-aqueous solutions and valid when the specific heat did not present a maximum value (as, for example, solutions of water–alcohol) (Mathias, 1889a):

where γ_n and c is the specific heat of the solution and of the solvent in cal/g°C, respectively, n the number of equivalents of solvent per equivalent of solute, and a and b constants. In principle, only two measurements are necessary for determining the values of the constants. Mathias then reported the values of a and b for 80 different substances, among them chlorides, bromides, iodides, nitrates, sulfates, chromates, carbonates, phosphates, arsenates, pyrophosphates, metaphosphates, acetates, oxalates, bases, and organic substances such as tartaric acid, and sugar. The equation was found to predict the specific heat within 1/1000 odf the experimental one. Only the data for zinc chloride could not be fit by the equation, fact that Mathias attributed to the fact that aqueous solution of this salt tended to deposit zinc oxychloride when diluted in water (Mathias, 1889a).

Equation 35 is easy to interpret. Assuming that e is the equivalent of the solvent and writing γ₀= ac/b and E = eb, eq 35 can be written:

from where it can be said that Woestyn's law is applicable to a diluted solution (n ≥ 25) and everything occurs like if the solute has acquired a new equivalent (E) and a new specific heat in the liquid state (γ₀), both independent of the degree of dilution (Mathias, 1888bc).