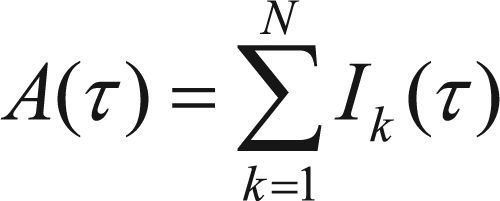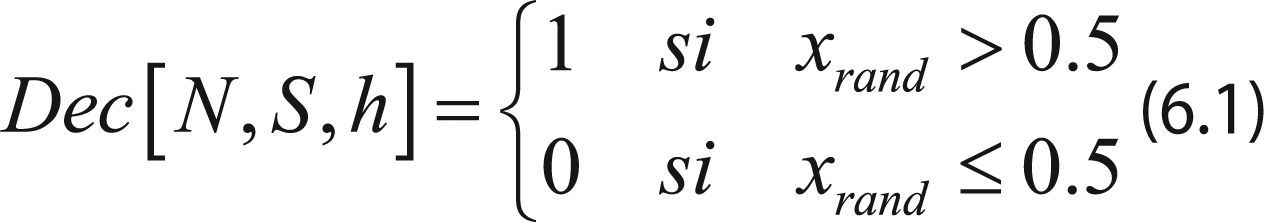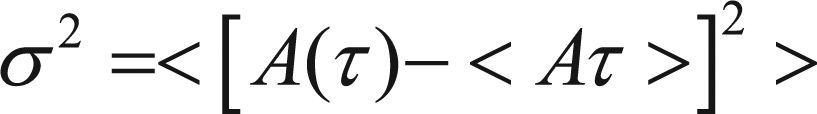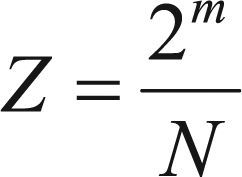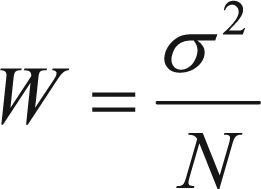El presente trabajo considera el problema de decisión planteado por el economista Brian Arthur del bar “El Farol”[1]. A partir de él se desarrolló el algoritmo computacional que simula el problema de decisión en el que incurren un número grande de agentes racionales, mejor conocido como el juego de minorías. El juego de minorías resulta ser un problema de teoría de juego que exhibe la competencia en el tiempo que existe entre agentes racionales adaptativos. La complejidad que caracteriza al problema surge del hecho de que los gentes no interactúan directamente entre sí, sino a través de un entorno cerrado común creado por ellos mismos. Además de reproducir los resultados más citados del mismo, simulamos un conjunto de “juegos mixtos” con el fin de contrastar diferentes memorias para así determinar con cuál de ellas los agentes que participan en el juego obtienen un mejor desempeño o mejores ganancias a través del tiempo. Así también, estudiamos sus propiedades estadísticas, más específicamente, la distribución estadística que las ganancias de los jugadores exhiben en el tiempo.
The present paper considers the decision problem of the bar “El Farol”, posed by the economist Brian Arthur. From which the computational algorithm that simulates the decision problem with a large number of rational agents was developed, best known as the game of minorities. The game of minorities turns out to be a problem of game theory that exhibits the time competition that exists between adaptive rational agents. The complexity that characterizes the problem arises from the fact that people do not interact directly with each other, but through a common closed environment created by themselves. In addition to reproducing the most cited results of the same, we simulate a set of “mixed games” in order to contrast different memories to determine in which of them the agents involved in the game get better performance or better gains over time. So we study their statistical properties, more specifically, the statistical distribution that players’ earnings exhibit over time.
El “juego de minorías” surge del famoso problema del bar “El Farol” ubicado en Santa Fe, nuevo México. La anécdota del bar “El Farol” de la que se generaliza el juego se plantea la pregunta, considerando que el bar es un espacio fijo y de dimensiones modestas, de qué tan satisfactoria puede ser una velada en él cuando la mayoría de las personas asisten al mismo. Evidentemente, si el lugar está repleto la velada no será nada grata y convendrá mejor quedarse en casa o acudir a otro sitio. Por el contrario, si el lugar no está repleto, será buena elección ir al bar.
En ese sentido, el problema del bar el “El Farol” consiste en saber cuántos deciden ir al bar para así poder tomar una decisión. Sin embargó, lo anterior es imposible de saber, por consiguiente, no existe una manera a priori de saber si al bar asistirá una minoría o una mayoría para entonces decidir ir o no ir. Cuando la mayoría decidió ir al bar, la mejor elección que cualquier asistente en el bar pudo haber tomado era la de no haber asistido, mientras que cuando una minoría asistió, la elección que proveía la mayor satisfacción era la de asistir al bar.
En términos del bar “El Farol”, la manera en que casa asistente toma su decisión, tomando en cuenta que ninguno le comunica a los demás acerca de ella y que la única información en común que tienen a sus disposición para consultar es el historial del número de asistentes al bar en semanas pasadas, consiste en tratar de deducir el comportamiento y la decisión que los demás pueden llegar a tomar acerca de ir o no ir al bar. Al respecto, en los mercados financieros se suele considerar la hipótesis de los mercados eficientes (emh), que establece que un mercado es eficiente si:
- 1.
Todos los agentes son racionales y siempre tratarán de maximizar su ganancia.
- 2.
La información está disponible para todos los agentes y los precios reflejan toda la información existente.
- 3.
No hay costos de transacción.
En la realidad, aun cuando hoy en día el uso de las computadoras facilita en mucho la obtención y acceso de la información, no siempre se tiene acceso a toda. Lo anterior hace que los agentes traten con información parcial o incompleta. De ahí que la emh contempla 3 acepciones: la débil, la semifuerte y la fuerte. Sin embargo, aun cuando los individuos no se enfrentan a un problema de acceso a la información, el principal problema tiene que ver con la asunción del comportamiento racional y deductivo sobre los agentes. Como se desarrolla en[2], en la práctica los humanos no pueden lidiar o hacer frente a un exceso de información (completa o no), lo que implica que su racionalidad queda delimitada o rebasada por el grueso de información que tiene a su disposición y que su capacidad de análisis puede llegar a procesar, con ello su capacidad de hacer elecciones “óptimas” se torna más hacia elecciones “satisfactorias”. En ese sentido, en lugar de tomar decisiones deductivas, los humanos se comportan más como inductivos, esto es, constantemente se encuentran construyendo nuevas hipótesis que prueban, siendo algunas desechadas y otras no debido a su grado de efectividad, con ello el reconocimiento de patrones o decisiones se torna más hacia una toma de decisión más inductiva.
Supongamos, sin embargo, que una sola persona tiene un don para la deducción. Él no puede nunca tomar una decisión racional, porque otras personas no se comportan racionalmente. Por lo tanto, la mayoría de los problemas en la economía están mal planteados, y la racionalidad limitada, ante tales restricciones, la inducción es más adecuada que la racionalidad para resolverlos.
En el problema del bar es justo este tipo de racionalidad con la que se asume los agentes del juego toman sus decisiones. En el “juego de minorías” la única información relevante, y que está totalmente disponible para cada uno de los agentes que conforman el sistema, es la asistencia pasada en el bar (i.e. attendance), la cual puede no ser suficiente para tomar una decisión racional; por otro lado, se asume que los agentes no se conocen, por lo cual no pueden intercambiar información entre ellos. Aunado de esto, ellos no pueden estar completamente seguros si los otros se comportaran de forma racional.
Más allá de la abstracción y pérdida de tiempo que algunos les podría parecer, el problema del bar “El Farol” es uno de esos que se inscribe en el terreno de los sistemas complejos, en particular esta nueva tendencia académica-científica que pertenece a la complejidad y que comúnmente se alude a ella como Econofísica.
La Econofísica[3] aplica el formalismo de la Física Estadística en la descripción de los sistemas financieros. Comúnmente cuando uno estudia los sistemas económicos es posible tener una apreciación de la esfera macro y micro. Sin embargo, es casi imposible tener un algoritmo o relación matemática que describa el comportamiento e interacción de cada una de las partes que constituye el sistema económico total. Conceptos propios de la Física Estadística como dinámica estocástica, transiciones de fase, correlaciones de corto y largo alcance, procesos de Levy, por solo mencionar algunos, parece ser que permiten, aun cuando no se tiene una apreciación certera del comportamiento de cada individuo que conforma el sistema económico, un entendimiento en mayor alcance que el que ofrece el ortodoxo del comportamiento global de los sistemas económicos de acuerdo a su naturaleza compleja.
El problema del bar “El Farol” se puede reinterpretar, formalmente, en términos de este nuevo enfoque Econofísico, como aquel que se presenta en los mercados financieros cuando un número grande de individuos se encuentra ante la decisión de comprar una acción. En el caso de los mercados financieros se puede considerar al precio como una cantidad macroscópica que fluctúa como resultado de las interacciones entre los agentes.
Desde el terreno de los mercados financieros la forma en la que el precio de una acción se fija muchas de las veces implica un desarrollo matemático arduo e ingenioso para resolver la ecuación diferencial estocástica que determina el precio, otra posibilidad sería la de modelar el comportamiento de los agentes a un precio definido y con ello mostrar la interacción que hay entre el comportamiento de los individuos y las propiedades macroscópicas que de tales interacciones emergen.
Considerando esta última alternativa, lo que procede a continuación es la definición y modelación del “juego de minorías” desde su acepción más simple y con ello la caracterización estadísticas de los agentes del juego, posteriormente introducimos una variante del “juego de minorías”: los “juegos mixtos”, con los cuales se pretende acotar la memoria “óptima” para los agentes que participan en el juego.
2El juego de minoríasEl “juego de minorías” es un modelo de características adaptativas que estudia la dinámica en el tiempo de la toma de decisiones en un conjunto considerablemente grande de individuos que forman parte del mismo sistema.
La formación original del problema del “juego de minorías” fue desarrollado por D. Challet y Y. C. Zhang [4]. En el presente trabajo contextualizamos el juego de minorías en un escenario financiero, donde cada uno de los individuos debe tomar una decisión de dos únicas posibles: invertir o no invertir. Cada agente que participa en el juego tiene a su disposición un conjunto de estrategias, que bien podrían asociarse a los esquemas mentales o reglas de comportamiento que ellos utilizan para hacer una elección. Cada una de estas estrategiastiene un score que evoluciona en el tiempo, lo cual les provee las cualidades adaptativas a los agentes, con base a lo que les sugiere su estrategia con mayor score es que los agentes deciden si invierten o no invierten.
Para cada paso de tiempo del juego hay un segmento de los individuos que si su decisión es la que la minoría eligió entonces obtendrá un peso de ganancia, mientras que aquellos que su decisión resulta ser la que toma la mayoría pierde un peso. En ese sentido la decisión menos numerosa es la ganadora, de ahí el nombre del juego. El juego asume que cada individuo del sistema decide tomando en cuenta el attendance de las semanas pasadas en conjunto con la información contenida en sus estrategias de decisión, y que no hay información que se filtre acerca de ellas entre los jugadores, en ese sentido es un problema iterado del dilema del prisionero de la teoría de juegos. Cada estrategia del conjunto de estrategias de cada jugador que predice la decisión de la minoría en cada paso de tiempo es valorada en un peso más, en caso contrario pierde valor en un peso.
El número de datos pasados del attendance que cada individuo que participa en el juego puede recordar es una variable que en el juego se denomina memoria. La memoria es la variable que le provee las características adaptativas al juego. Una vez que se fija el tamaño de la memoria y que se tiene el nuevo dato del attendance, la memoria elimina el dato más pasado del attendancee incorpora el más reciente, actualizándose así para cada paso del tiempo y quedando el tamaño de la memoria en el que fue fijado al inicio del juego.
3Formulación del juego de minorías: la memoria, las historias y las estrategiasEl sistema está constituido por N individuos. Cada uno de los individuos posee un conjunto de S ≥2 estrategias, de las cuales puede hacer uso para tomar su decisión en cada paso de tiempo acerca de invertir o no invertir.
Cada estrategia de cada individuo está constituida por un cierto número h de historias. El tamaño de historias que definen a las distintas estrategias de los agentes que participan en el “juego de minorías” depende del valor de la memoria que se elige inicialmente.
En el problema original se asigna un valor común para todos los jugadores. La mayoría de los artículos que tratan el problema eligen el valor de m = 2, del mismo modo lo hacemos nosotros. Lo anterior tiene que ver con que, además de ser el caso más sencillo tanto en términos de comprensión del problema como en términos de cálculo computacional, el juego ya exhibe sus propiedades de inductividad en la toma de decisiones y adaptabilidad de la estrategia. Sin embargo, para algunas simulaciones y obtención de resultados variamos dicho parámetro.
La forma en la que la memoria determina el tamaño de las historias de una estrategia es de gran importancia para la comprensión del juego. En términos de las estrategias, cada historia sugiere una decisión que puede ser invertir o no invertir.
Para efectos de la modelación hicimos una identificación binaria del par de decisiones posibles de las siguiente forma: invertir → 1 y no invertir → 0. Si pensamos a la memoria como un conjunto de cajas en las que se puede colocar 2 cosas, en este caso 1 o 0, cuando se fija m= 3, tendremos tres cajas;en cada caja se pueden colocar o 1 o 0, por tanto el número total de historias en este caso sería 23 = 8. De esta forma, las posibles longitudes de historias de cada estrategia están dadas como 2m, esto es, h = 0, 1, 2, 3,…, (2m - 1).
Una estrategia queda definida cuando se ha fijado el valor de la memoria, el cual, como hemos visto más arriba, determina el tamaño de historias de la estrategia, y, además, cada estrategia a final de cuentas le sugiere a cada jugador si invierte o no invierte. Entonces podemos definir una estrategia como una función que va del conjunto {0, 1,…, 2m– 1} → {0, 1}. Por tanto el número total de estrategias es de 22m. A continuación mostramos cómo está constituida una estrategia para el caso en que m= 3.
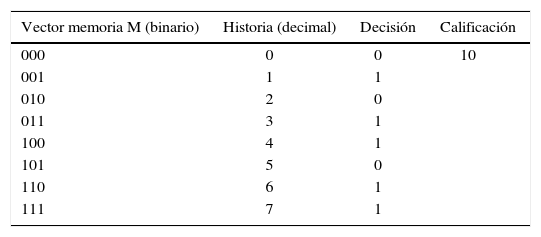
En la tabla 1 tenemos que al ser m = 2,nuestra estrategia tendrá 8 historias. Es decir, hay 8 formas distintas de decir invertir o no invertir, de acuerdo a cada historia de esta estrategia en particular, además le hemos etiquetado su score,que representa el “valor monetario” de dicha estrategia. Como detallaremos a continuación, el hecho de que en todo paso de tiempo cada participante del juego puede calificar cada una de sus estrategias de decisión, independientemente de que haya o no usado esa estrategia en particular para tomar su decisión, le brinda la sistema características adaptativas. En otras palabras, los agentes siempre están adaptándose al mejor escenario financiero con base es su estrategia más exitosa.
| Vector memoria M (binario) | Historia (decimal) | Decisión | Calificación |
|---|---|---|---|
| 000 | 0 | 0 | 10 |
| 001 | 1 | 1 | |
| 010 | 2 | 0 | |
| 011 | 3 | 1 | |
| 100 | 4 | 1 | |
| 101 | 5 | 0 | |
| 110 | 6 | 1 | |
| 111 | 7 | 1 |
La columna 1 de la tabla se refiere al vector memoria, que es el total de posibles permutaciones de los elementos 1 y 0 dado m. la segunda es la relación entre binario y decimal del total de historias de la estrategia. La columna 3 es la decisión que implica cada historia de la estrategia. Por último, la columna 4 muestra el puntaje o score de esta estrategia en particular.
Supongamos que cada individuo que participa en el juego de minorías posee una memoria de m= 3 y un total de 5 estrategias, esto implica que tendrá a su disposición 5 estrategias como la que se mostró en la sección anterior, con la única diferencia de que la columna de decisiones será diferente en cada una de ellas, así como la calificación de ellas.
La estrategia más exitosa Smax es aquella que tiene la mayor calificación en cada paso de tiempo. Recordemos que cada estrategia S de cada jugador gana un punto (i.e. payoff) en cada paso de tiempo τ siempre y cuando la decisión de la historia h en cuestión que sugiere cada estrategia sea la decisión que eligió la minoría de los N individuos para el paso de tiempo actual, en caso contrario se les resta un punto. La decisión correcta (DC) o decisión de la minoría se determina en cada paso de tiempo τ del juego, una vez que se contabilizan las decisiones de cada uno de los agentes, es decir, cuantos eligieron invertir y cuantos eligieron no invertir.
El attendance A(τ) contabiliza la decisión que tomo cada uno de los jugadores de la siguiente forma:
donde Ik(τ) es la decisión, 1 o 0, que el k-ésimo individuo elige de su estrategia más exitosa al tiempo τ. Por ejemplo, si tenemos un juego en el que N = 101 y τ = 2 y al final 51 de los agentes eligen invertir (1) y los restantes 50 eligieron no invertir (0), tenemos que, de acuerdo a (4.1), el valor del attendance será A(2) = 51. Como veremos mλs adelante, a partir de la variable A(τ) podemos determinar la decisión de la minoría en cada paso de tiempo.5Vector calificaciones, vector ganancia y vector memoriaEl vector de calificaciones es una matriz de N x S en el que se contabiliza el historial de la calificación de la S-ésima estrategia del N-ésimo jugador en cada paso del tiempo. En términos de notación lo identificamos como C˜alN,S y al igual que las estrategias, en cada paso de tiempo se le suma (o resta) un punto (i.e. ganancia) en cada paso de tiempo se le suma (o resta) un punto (i.e. ganancia) a cada uno de los N individuos que conforman el sistema y que su decisión tomada corresponde (no corresponde) con la de la minoría. En ese sentido, G˜alN,S contabiliza la ganancia o pérdida de cada agente que participa en el juego en cada paso de tiempo.
Por otro lado, el vector memoria es una cadena binaria de longitud m. Supongamos que se establece para un juego que el tamaño de la memoria sea de 3 pasos, en ese caso se tiene el siguiente arreglo:
De la tabla 2 observamos que al fijar m,el tamaño del vector M→ queda inmediatamente definido y con ello tenemos 2m formas distintas en una misma estrategia de decidir invertir o no invertir. Como al inicio del juego alguna de las entradas de M→ es elegida de manera aleatoria, será este componente el que fija la condición inicial de la decisión financiera que cada jugador debe de tomar en el tiempo inicial τ= 1.
6Inicializacion y dinámica del juego de minoríasLos partidos que definen al juego de minorías son: N, S y m. Una vez elegidos los valores de los parámetros se crea la matriz tridimensional booleana1:
donde x es un número pseudoaleatorio que está en el intervalo [0,1]. La matriz en (6.1) define la decisión financiera: invertir o no invertir, de cada agente, en cada historia, de cada una de sus estrategias. La decisión que corresponde a cada historia de cada estrategia inicialmente se elige de manera aleatoria; sin embargo, cada que se inicia un nuevo juego la matriz en (6.1) es diferente. Una vez que fueron asignado los valores para las variables principales del juego, se inicializan los vectores C˜alN,S=0 y G˜alN,S=0.En τ= 1 se elige de forma aleatoria la configuración inicial del vector memoria, una vez que se tiene el vector memoria M, según sea el paso m, se mapea la historia que implica dicho vector y, por tanto, cada uno de los individuos consulta cada una de las estrategias y elige la decisión que le sugiere su estrategia más exitosa. Puesto que en τ= 1 la calificación de cada una de las estrategias S de cada uno de los individuos es cero, entonces cada uno de los individuos elige por simplicidad su primera estrategia, ya que le es indiferente elegir de entre el total de sus estrategias si todas inicialmente valen cero. Para el final del tiempo τ= 1, puesto que ya todos los individuos que participan en el juego han tomado su elección financiera, tendremos que la decisión correcta puede haber sido 1 o 0. ¿De qué depende cual sea la decisión correcta? Como lo referimos más arriba, simplemente del hecho de que haya elegido la minoría de los N agentes. Si la minoría eligió 1, la decisión correcta es 1, de lo contrario, es 0.
Haciendo uso de la ecuación (6.1) podemos determinar cuál fue la decisión que tomo la minoría de la siguiente manera:
Para mostrar el uso de (6.2), por ejemplo, consideramos el caso más sencillo en el que tenemos un juego donde el número de participantes es N = 5. Los posibles escenarios que podrían presentarse serían:
- a)
Todos los individuos deciden invertir. En otras palabras todos los agentes eligen 1, por tanto la decisión correcta en dicho paso de tiempo era elegir no invertir, esto es, elegir 0. De presentarse tal escenario tendríamos que (2*A(τ) – N) = 5 > 0 de ahí entonces que la decisión correcta sea DC = 0.
- b)
Todos los jugadores deciden no invertir. En tal caso todos los individuos eligen 0, y tendremos que (2*A(τ) - N) = -5 < 0, por tanto la decisión correcta era DC = 1.
- c)
Tres de los 5 jugadores deciden invertir mientras que los dos restantes deciden no invertir, entonces la decisión que toma la minoría es no invertir. En tal caso tendremos que (2*A(τ) - N) = 1 > 0, por tanto DC = 0.
- d)
d)Tres de los 5 jugadores deciden no invertir y los 2 restantes deciden invertir. En tal caso tendremos que (2*A(τ) - N) = -1 < 0, por tanto la decisión correcta era DC = 1.
Finalmente, la forma en que se actualiza la memoria para los siguientes pasos de tiempo en los que se desarrolla el juego consiste en tomar en cuenta la decisión correcta en cada paso de tiempo. Por ejemplo, si m= 3 y en el tiempo τ= 1 el elemento que se elige del vector M→ de acuerdo a la tabla 2, es el 101, y asumiendo que en dicho paso de tiempo DC = 1, entonces el nuevo elemento del vector M→ al tiempo τ = 2 será 011, así para cada paso del juego.
Una vez que se tiene el nuevo elemento del vector memoria para el tiempo τ+ 1, entonces el juego de minorías es un proceso iterativo en el que las condiciones anteriores descritas se deben cumplir en cada paso de tiempo.
7Resultado del juego de minoríasLa primera parte del desarrollo del modelo se centró principalmente en reproducir los resultados más citados en la literatura acerca del juego de minorías, de tal forma que estos sirvieran para calibrar y dar consistencia a nuestro código y simulaciones y así fundamentar los resultados propios acerca de la distribución que exhiben las ganancias de los jugadores, así como los resultados que se refieren a los “juegos mixtos”.
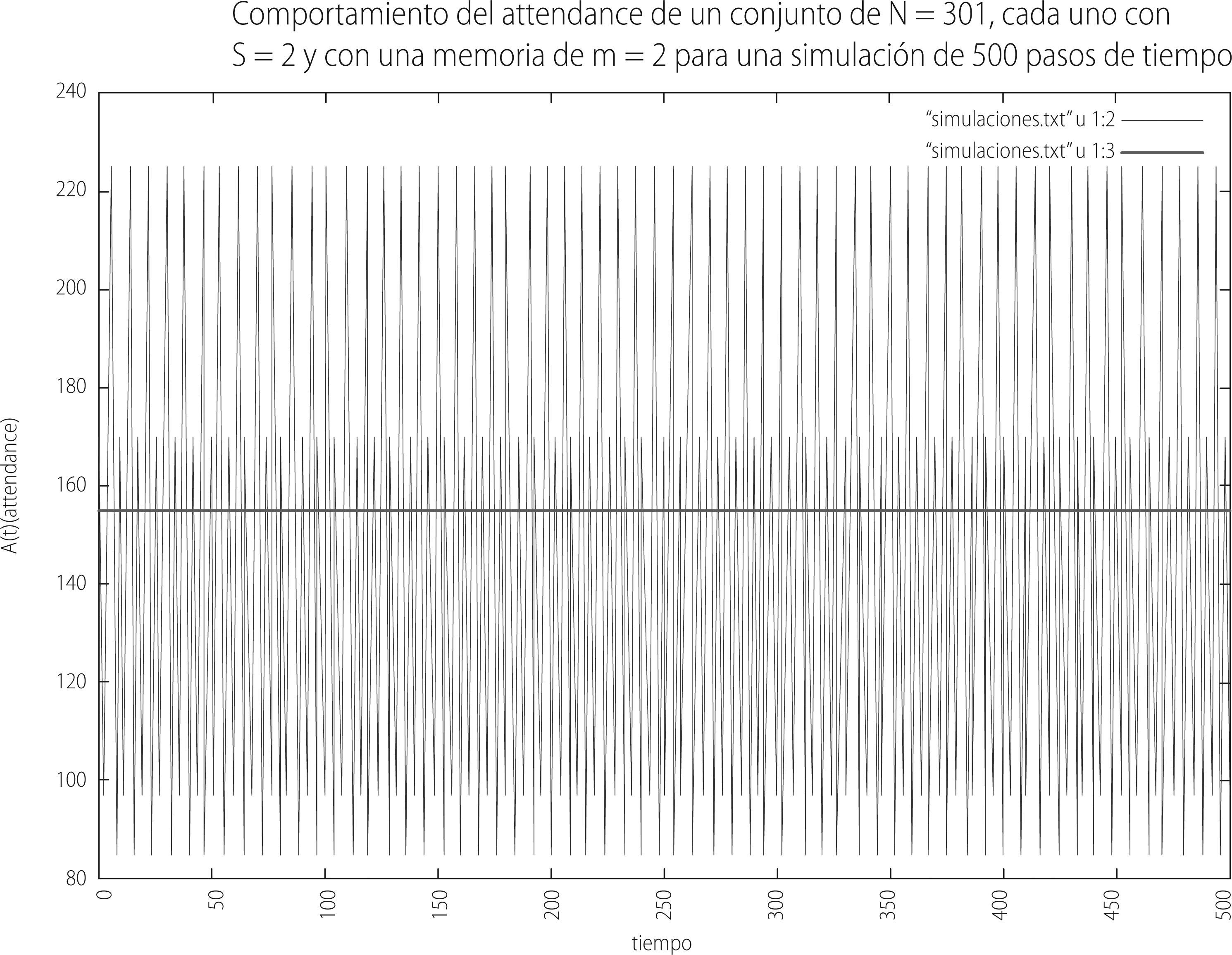
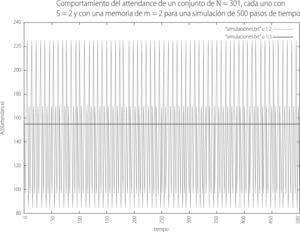
AttendanceEl termino attendance,como se vio en la sección 4, es la variable que en el juego está relacionada con la suma de las decisiones que cada agente que participa en el juego toma en el tiempo: invertir (1) o no invertir (0). La variable attendance ayuda a determinar la decisión que la minoría tomó al consultar su estrategia más exitosa en cada paso de tiempo. A partir de nuestro modelo pudimos obtener los siguientes resultados que muestran el attendance para un juego en el que los parámetros principales se fijaron de acuerdo a [5], con N = 301 y 500 pasos de tiempo.
La gráfica 1 exhibe la suma total para cada tiempo de las decisiones que cada uno de los 301 jugadores toma durante los 500 pasos de tiempo. Observemos que, en efecto, el valor promedio en torno al que oscila el attendancese encuentra en 155 (línea verde), que prácticamente viene siendo el 50 por ciento del total de agentes que participan en el juego.
Además, considerando que las decisiones que se toman en el juego son simétricas y con la misma probabilidad de que sucedan, es de esperar que
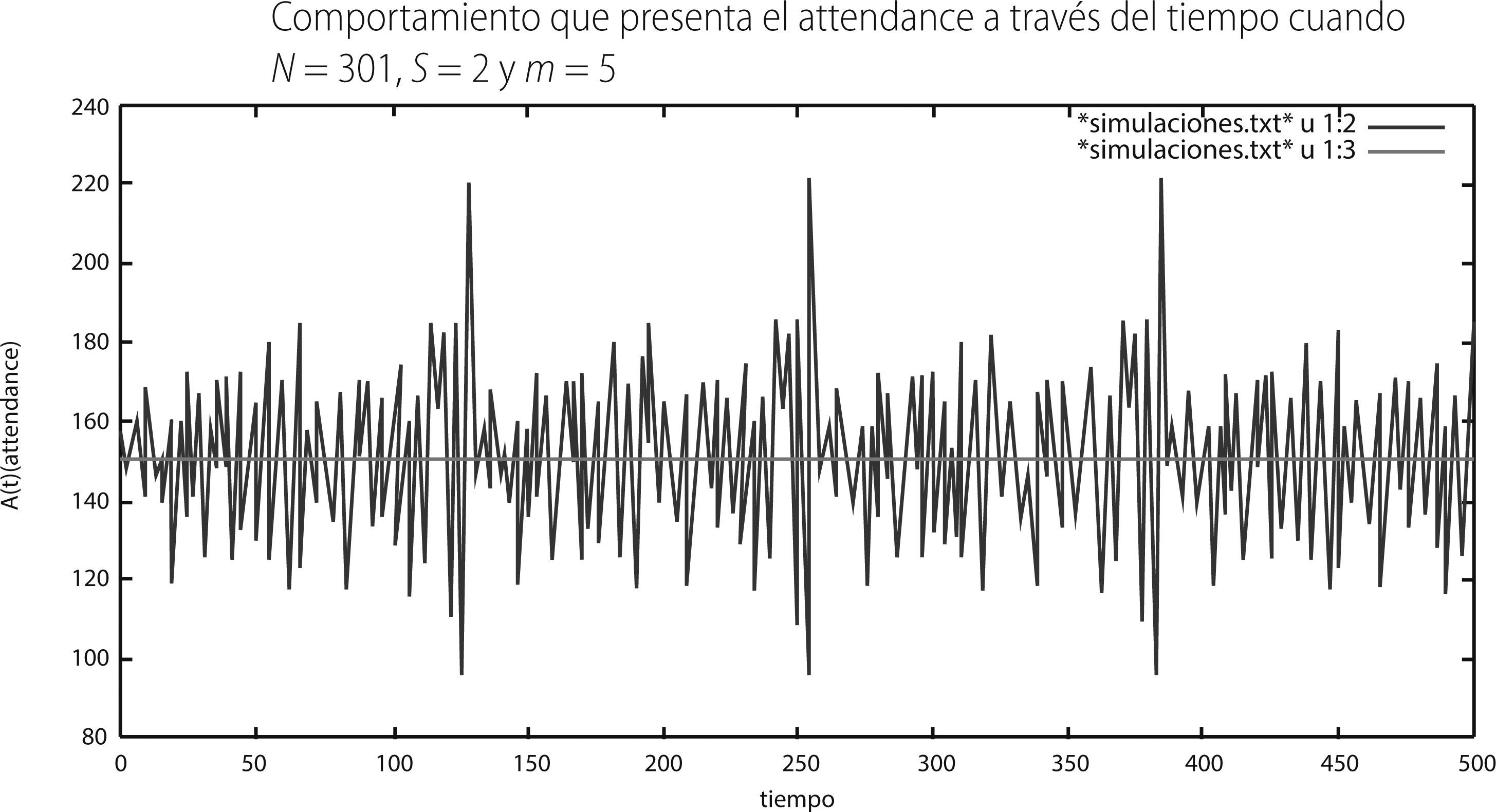
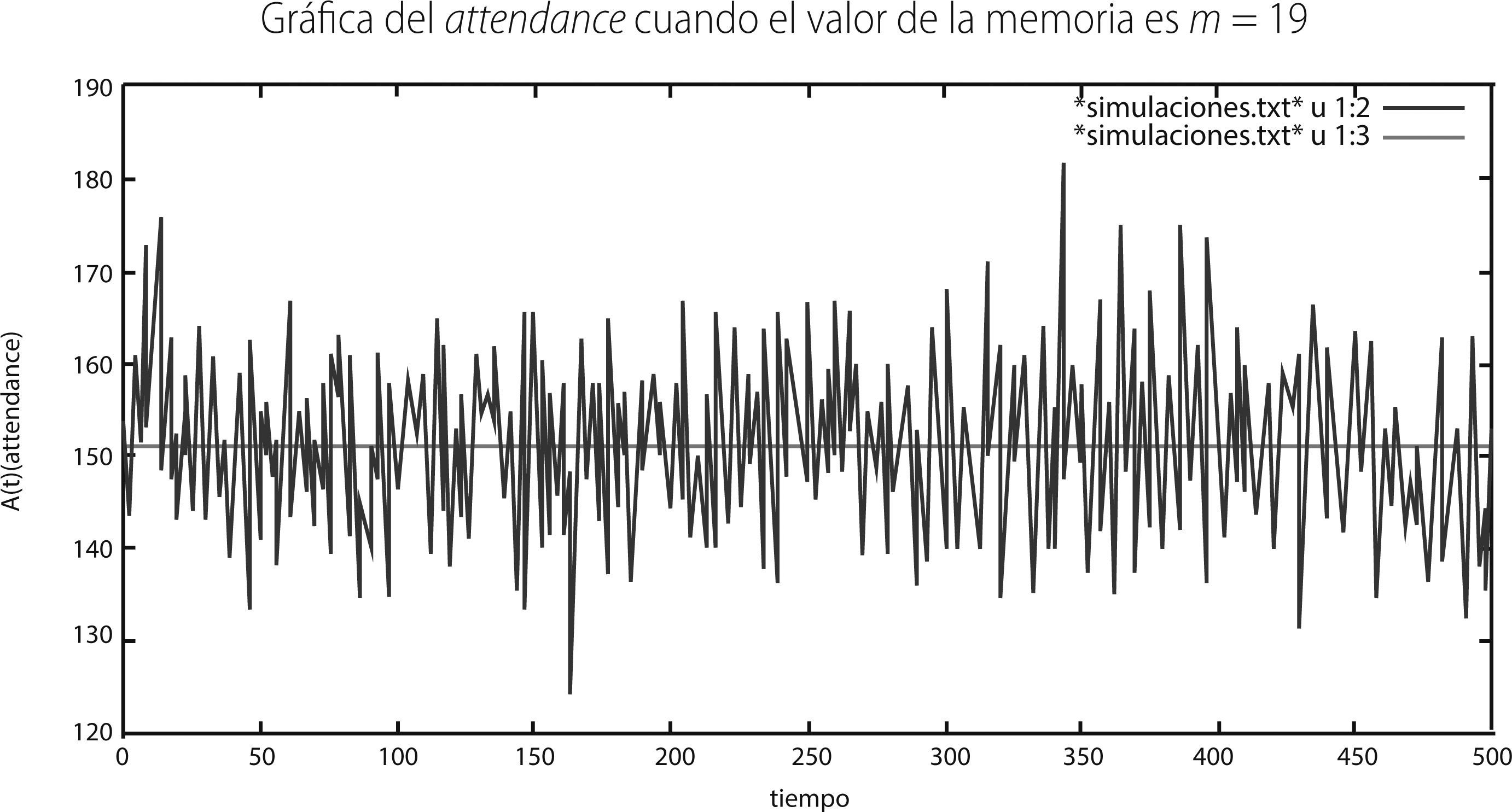
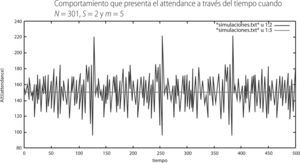
Puesto que el número total de agentes N se elige por convención como impar, la parte minoritaria siempre puede determinarse, con lo cual se observa que el número de agentes que ganan en el juego siempre es menor al número de agentes que pierden en el juego, lo que implica que el juego de minorías es un juego de suma negativa. A continuación presentamos la misma gráfica manteniendo constantes los parámetros N y S, pero ahora el valor de la memoria se fija en m = 5 y m = 19.
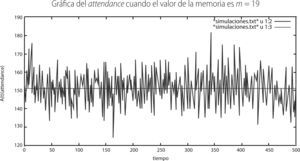
De las tres gráficas anteriores se puede observar que a medida que aumenta el tamaño de la memoria en el juego, el rango o amplitud de las oscilaciones que registra el attendance parece disminuir.
Observamos el comportamiento de cada una de ellas. La gráfica con m = 2 presenta un patrón de fluctuaciones periódicas que barren aproximadamente el intervalo {90, 220} y con una promedio de 155.006. La gráfica que simula un juego con memoria de m = 5 muestra que las fluctuaciones más importantes se dan en el intervalo entre {110, 190} y con un promedio de 150.738. Hay que notar que cuando m = 5 las fluctuaciones siguen siendo periódicas pero un poco más intrincadas. Finalmente, la gráfica con m = 19 presenta fluctuaciones que barren el intervalo {120,170} y un promedio de 150.938. Entonces es característico del juego de minorías que a medida que aumenta la memoria en el juego, el rango de las fluctuaciones que exhibe el attendance disminuyen. En otras palabras, pareciera ser que, en una primera impresión, a medida que la memoria que pueden retener los individuos es mayor, entonces éstos deciden de manera más eficiente su decisión financiera en los pasos de tiempo posteriores.
Fluctuaciones del sistema y transición de faseLa volatilidad es otro resultado que la literatura [5–8] en el juego de minorías presenta para caracterizar la dinámica que exhibe el sistema. En términos estadísticos, la volatilidad es la varianza σ2, y determina el grado de dispersión que presenta la suma de las variables aleatorias (i.e. attendance) con respecto a la medida de las mismas en cada paso de tiempo. Más formalmente podemos definir la volatilidad de la siguiente manera:
donde A(τ) es el attendance y <Aτ> es la media del attendance al tiempo T. Como antes, en (7.1) <…> representa en promedio en el tiempo, mientras que <…> representa el promedio con respecto a las realizaciones.La forma en la que se obtiene la volatilidad del juego de minorías implica realizar procesos del juego que conlleven un gran número de realizaciones. Además, que cada realización del juego se desarrolla en un número de pasos de tiempo lo suficientemente largos para poder tomar promedios con respecto al número total de pasos de tiempo, y, finalmente, tomar promedios con respecto al número total de realizaciones del juego. En cuanto a la volatilidad del sistema, en [9] se encontró que el comportamiento macroscópico que exhibe el juego de minorías no depende de forma independiente de los parámetros N y m, sino de la combinación de ambos mediante la relación:
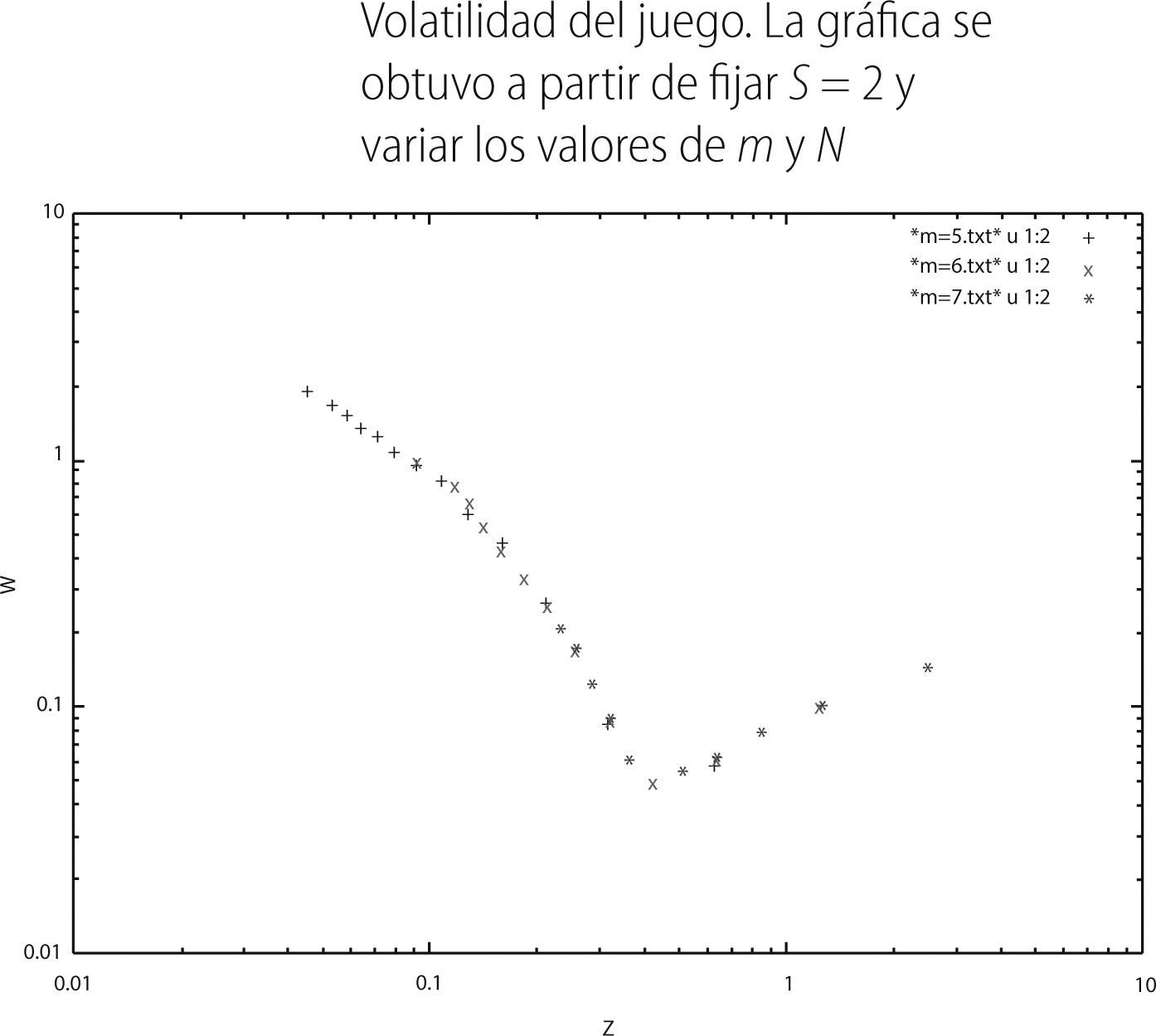
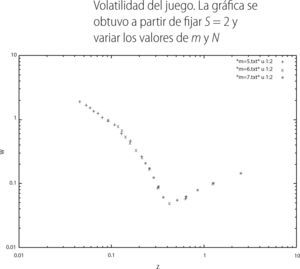
La cantidad anterior es denominada parámetro de control y es la variable que representa la abscisa del eje coordenado en la gráfica de la volatilidad. Por lo que respecta a la ordenada o volatilidad del sistema, está definida como:
Observemos que la gráfica anterior se compone de tres colores en el que cada uno se refiere a un valor específico de la memoria que se eligió en las simulaciones. Se tomó m = 5, m = 6 y m = 7, con un valor en las estrategias de S = 2 en cada uno de los tres juegos. Elegimos S = 2 ya que para ese valor de la memoria es en donde el sistema presenta la mínima varianza, con el valor de Zc= 0.42. Dicho valor está en concordancia con el que se reporta en [6,10]. La gráfica de volatilidad se obtuvo a partir realizar un conjunto de simulaciones fijando cada uno de los valores de la memoria antes mencionados y se varió el parámetro N de cincuenta en cincuenta, empezando por en N = 51 y terminando hasta N = 651.
En la gráfica 4 podemos observar que cuando Z es pequeño la volatilidad W del juego es grande. A medida que Z va aumentando, la volatilidad del juego va disminuyendo. En este caso el sistema entre en una región en la cual los agentes que participan en el juego están decidiendo de una manera más “eficiente” que de la forma azarosa. Posteriormente la volatilidad del sistema alcanza un valor mínimo, también denominado valor crítico o Zc. Finalmente, una vez que el sistema llega al punto mínimo Zc la volatilidad del sistema vuelve a aumentar, teniendo asintóticamente a 1.2
En términos del sistema, como es referido [11], las transiciones de fase que exhibe el juego de minorías son 3:
- a)
Fase impredecible o sobrepoblada (Z< 0.1). Es la región en la que Z<Zc. En esta región las fluctuaciones del sistema son grandes, además de que el comportamiento colectivo de los agentes que participan en el juego es mucho peor que si estuvieran decidiendo de manera azarosa. En esta región el tamaño del grupo perdedor es mucho más grande que la N2.
- b)
Punto de transición de fase (Z = Zc). Es la región en la que para valores intermedios de Z la volatilidad llega a su punto mínimo Zc. Cuando el sistema entra en esta región las fluctuaciones del sistema se van reduciendo hasta llegar a su valor más bajo. En esta región pareciera como si los agentes de alguna forma se coordinaran para ser más predictivos en su toma de decisiones en cada paso de tiempo. En esta región intermedia el tamaño del grupo perdedor es más próximo a N2, que es el mínimo posible para el lado perdedor del juego.
- c)
Fase asimétrica o poco sobrepoblada. Comienza a partir del punto en el que Z>Zc. En términos del sistema implica una transición de fase en la que la manera de tomar cada agente su decisión financiera se torna más hacia el lado azaroso, lo que en parte se debe de a que como en esta región de la gráfica del número de estrategias supera por mucho al número de agentes que participa en el juego. En términos de la información que tienen a su disposición los agentes para tomar su decisión, al ser ésta demasiada, éstos de alguna forma no saben cómo hacer uso de ella de forma racional, entonces sus decisiones se tornan más aleatorias, lo que propicia que las fluctuaciones del sistema comiencen a aumentar teniendo asintóticamente el valor de 1.
Para terminar con el conjunto de resultados más importantes que caracterizan al “juego de minorías”, pasemos a revisar la forma estadística y geometría en la que se desarrolla la dinámica y ganancia que obtienen los participantes en el juego.
Desde el punto de vista financiero, el payoff es la manera de representar la ganancia que cualquier agente obtiene una vez que se decidió cual es la decisión financiera que es merecedora de obtener un punto y, por el contrario, cual es la opción que implica la pérdida de un punto en aquellos individuos que eligieron de acuerdo a la mayoría.
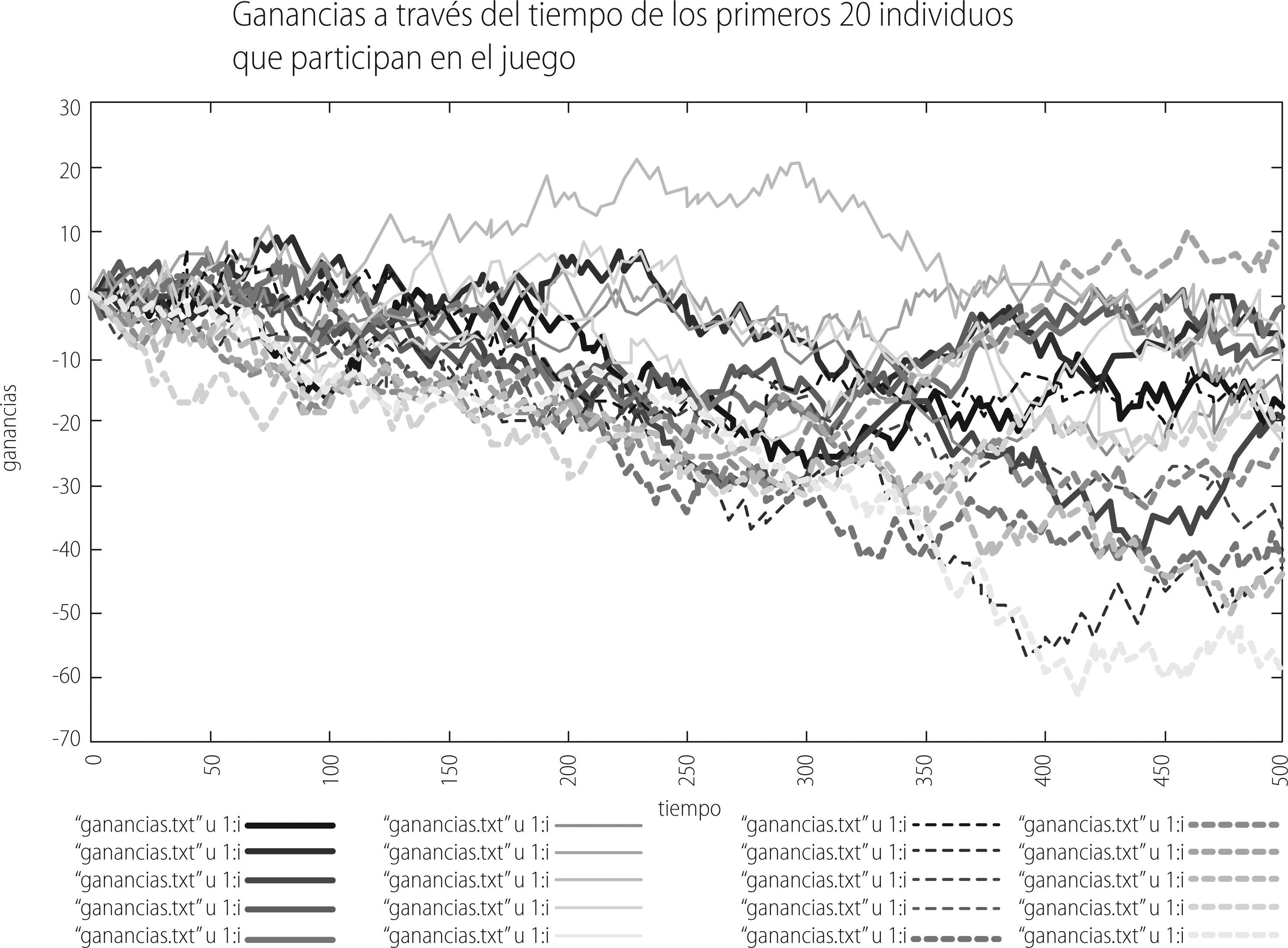
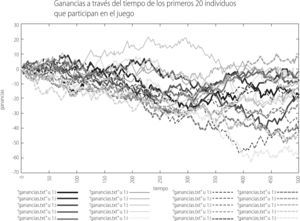
Como se mencionó más arriba, la manera en que cada individuo toma su decisión de invertir o no invertir es a partir de consultar la cadena histórica de eventos exitosos que han sucedido en el pasado y que le sugiere su estrategia más exitosa según sea la memoria que se fija en el juego. Sin embargo, el que hay tomado dicha acción no asegura en lo absoluto que tal decisión vaya a redituarle una ganancia, ya que como antes referimos ello depende del comportamiento colectivo de los participantes en el juego. El hecho de que en todo paso de tiempo cada participante en el juego pueda calificar el grueso de las estrategias que tienen a su disposición, independientemente de que haya o no usado esa estrategia en particular para tomar su decisión, le brinda al “juego de minorías” las características de ser un juego adaptativo. Es decir los jugadores siempre están tratando de adaptarse a su mejor escenario financiero. A continuación presentaremos la gráfica que da muestra simulación se obtiene para una simulación de 500 pasos de tiempo.
La gráfica 5 muestra la trayectoria a través de tiempo del “payoff” de los primeros 20 individuos que participan en el juego. Podemos observar que para algunos sus ganancias oscilan alrededor del cero, para otros se van haciendo infinitamente negativas, y solo para algunos infinitamente positivas [14]. También se puede apreciar que la dinámica colectiva del payoff exhibe las características geométricas de una caminata aleatoria o también denominada movimiento browniano [15]
8Simulaciones de juegos mixtosEn la presente sección concentramos nuestro análisis en investigar cómo es que influye la memoria en la distribución de las ganancias que exhiben los agentes que participan en el juego a través del tiempo. De forma que trataremos de averiguar e identificar si existe algún valor en la memoria que sea mejor que otro cuando se simula un juego en el que hay dos clases de jugadores, cada uno con diferente valor en su memoria. A continuación simulamos un conjunto de juegos “mixtos” en el que el total de jugadores N que participan en cada uno de ellos se divide en dos bandos, Nm′ y Nm, con memorias m′ y m, respectivamente.
En ese sentido el total de individuos que participan en cada juego es la suma N = Nm′+Nm, con la distinción anterior tenemos como objetivo percibir qué bando es el que gana más y qué bando es el que pierde más en el tiempo, de acuerdo a los valores correspondientes a su memoria.
El tema de la memoria ha sido ya discutido por varios autores y los enfoques al respecto han sido varios y diversos. Algunos han argumentado que la memoria no es relevante en el juego y otros, por el contrario, que si es relevante. Por ejemplo en [16] se muestra numéricamente que la forma de la curva de volatilidad del sistema (Figura 4) no cambia cuando una cadena aleatoria del tamaño m se elige para cada uno de los próximos pasos de tiempo de la simulación. Por otro lado en [17] se aborda lo relevante que es la memoria en la fase simétrica (Z<Zc) del sistema.
La manera en que nosotros tratamos de investigar la forma en que la memoria puede influir en los agentes obedece a una motivación más directa y cuantitativa. Pretendemos investigar el desempeño histórico del “payoff” (exitoso o no exitoso) que pueden tener un grupo de individuos que pertenecen a un diferente grupo cuando compiten en un mismo juego, donde cada grupo posee un valor diferente en el tamaño de su memoria. De hecho, hasta ahora ninguno de los artículos citados estudia las siguientes cuestiones: ¿Qué pasa cuando compiten un par de grupos en el juego, en el que cada uno posee una memoria diferente en su conjunto de estrategias? ¿Implicará esto algún beneficio para alguno de los grupos o será indiferente? Para dar respuesta a estas preguntas simulamos distintos juegos mixtos en los que se fijó S= 2 para ambos bandos.
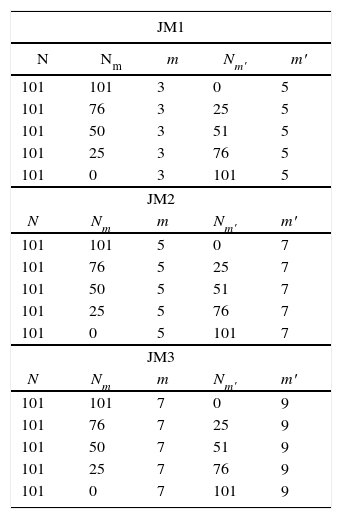
Consideraciones del juego mixtoPuesto que el objetivo principal de los resultados que a continuación presentaremos es el de determinar y comparar la distribución temporal que presentan las ganancias de los bandos que conforman el juego mixto, así como sus valores promedios a lo largo del tiempo y la varianza de los mismos, las simulaciones al respecto fueron desarrolladas un total de 600 realizaciones y cada realización consistió en 9 200 pasos de tiempo. Como al final deseamos obtener la distribución estadística del “payoff” que caracteriza a cada bando de acuerdo al valor de su memoria, determinamos realizar nuestro muestro estadístico para el conjunto de tiempos que son potencia de dos y que están comprendidos en los 9 200 pasos de tiempo que abarca cada juego. A continuación mostramos las características de los 3 juegos mixtos que hemos simulado.
Configuración gráfica de los 3 juegos mixtos simulados
| JM1 | ||||
|---|---|---|---|---|
| N | Nm | m | Nm′ | m′ |
| 101 | 101 | 3 | 0 | 5 |
| 101 | 76 | 3 | 25 | 5 |
| 101 | 50 | 3 | 51 | 5 |
| 101 | 25 | 3 | 76 | 5 |
| 101 | 0 | 3 | 101 | 5 |
| JM2 | ||||
| N | Nm | m | Nm′ | m′ |
| 101 | 101 | 5 | 0 | 7 |
| 101 | 76 | 5 | 25 | 7 |
| 101 | 50 | 5 | 51 | 7 |
| 101 | 25 | 5 | 76 | 7 |
| 101 | 0 | 5 | 101 | 7 |
| JM3 | ||||
| N | Nm | m | Nm′ | m′ |
| 101 | 101 | 7 | 0 | 9 |
| 101 | 76 | 7 | 25 | 9 |
| 101 | 50 | 7 | 51 | 9 |
| 101 | 25 | 7 | 76 | 9 |
| 101 | 0 | 7 | 101 | 9 |
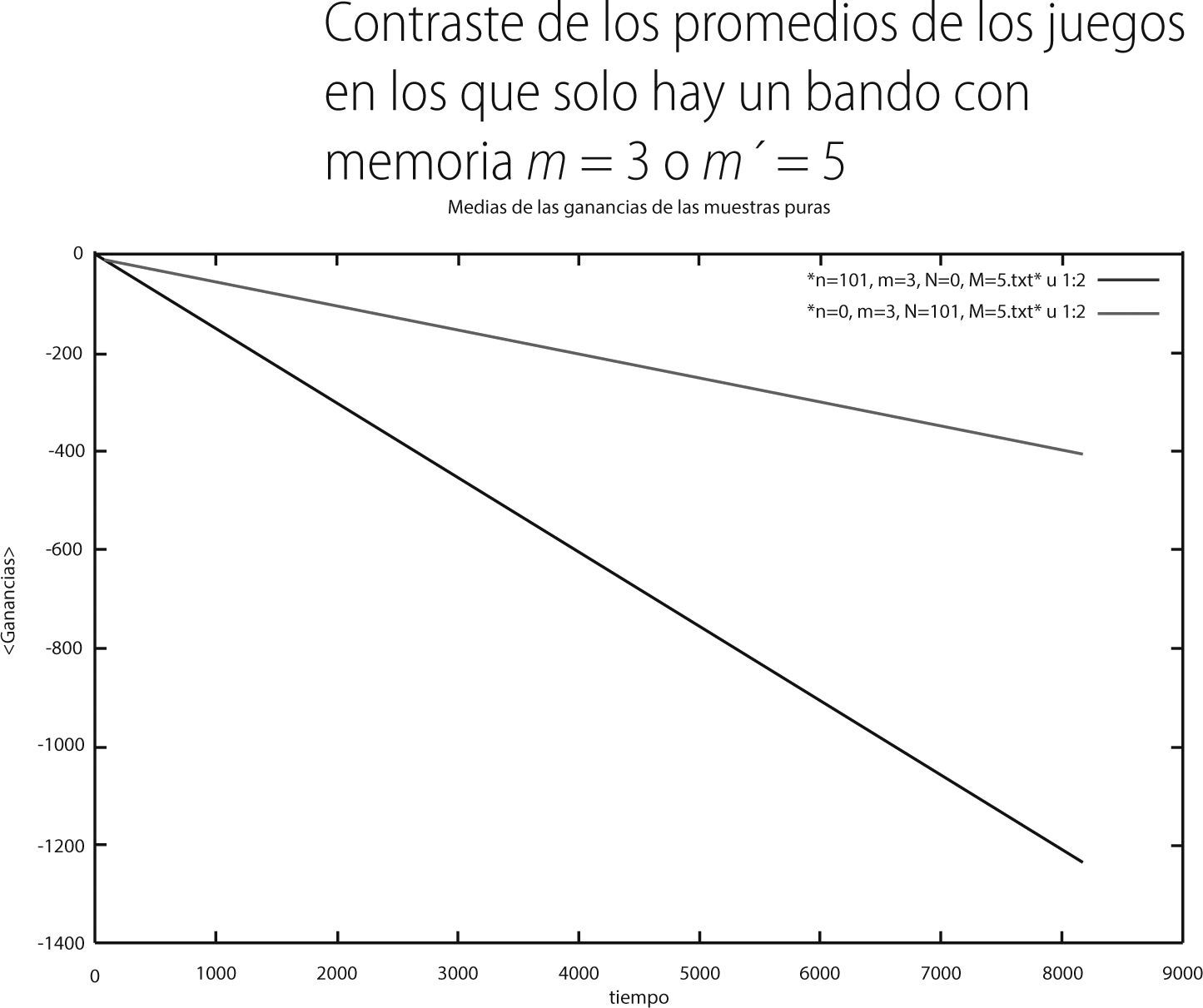
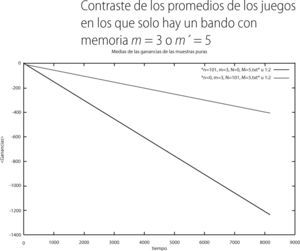
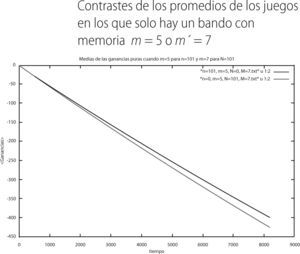
En esta sección presentamos los resultados que obtuvimos en cada uno de los 3 juegos mixtos con referencia a los casos en que solo hay un bando con su respectiva memoria, tales resultados los hemos denominado como muestras puras. Los promedios de las ganancias para los casos puros del primer juego mixto (i.e. solo un bando) son los siguientes:
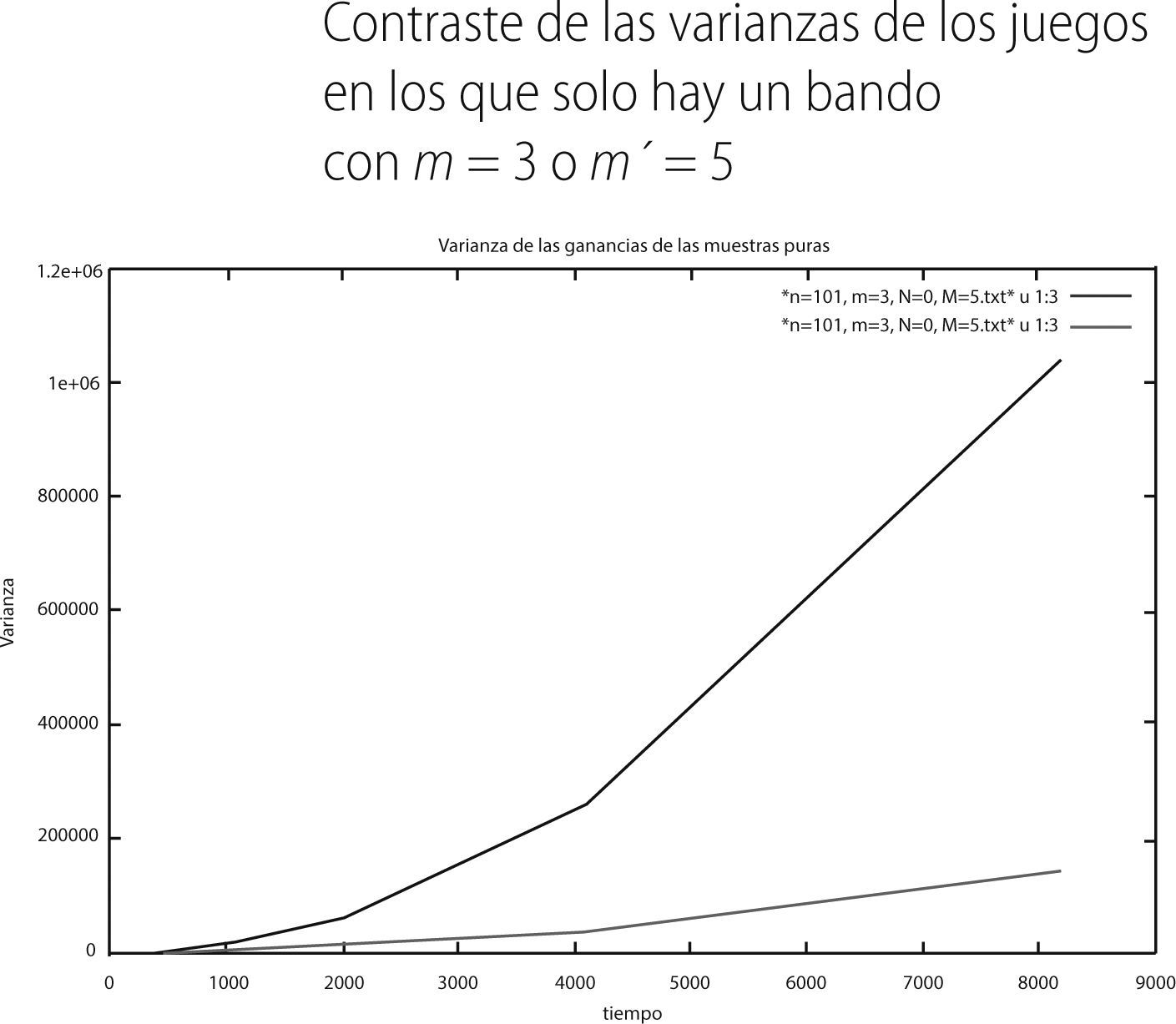
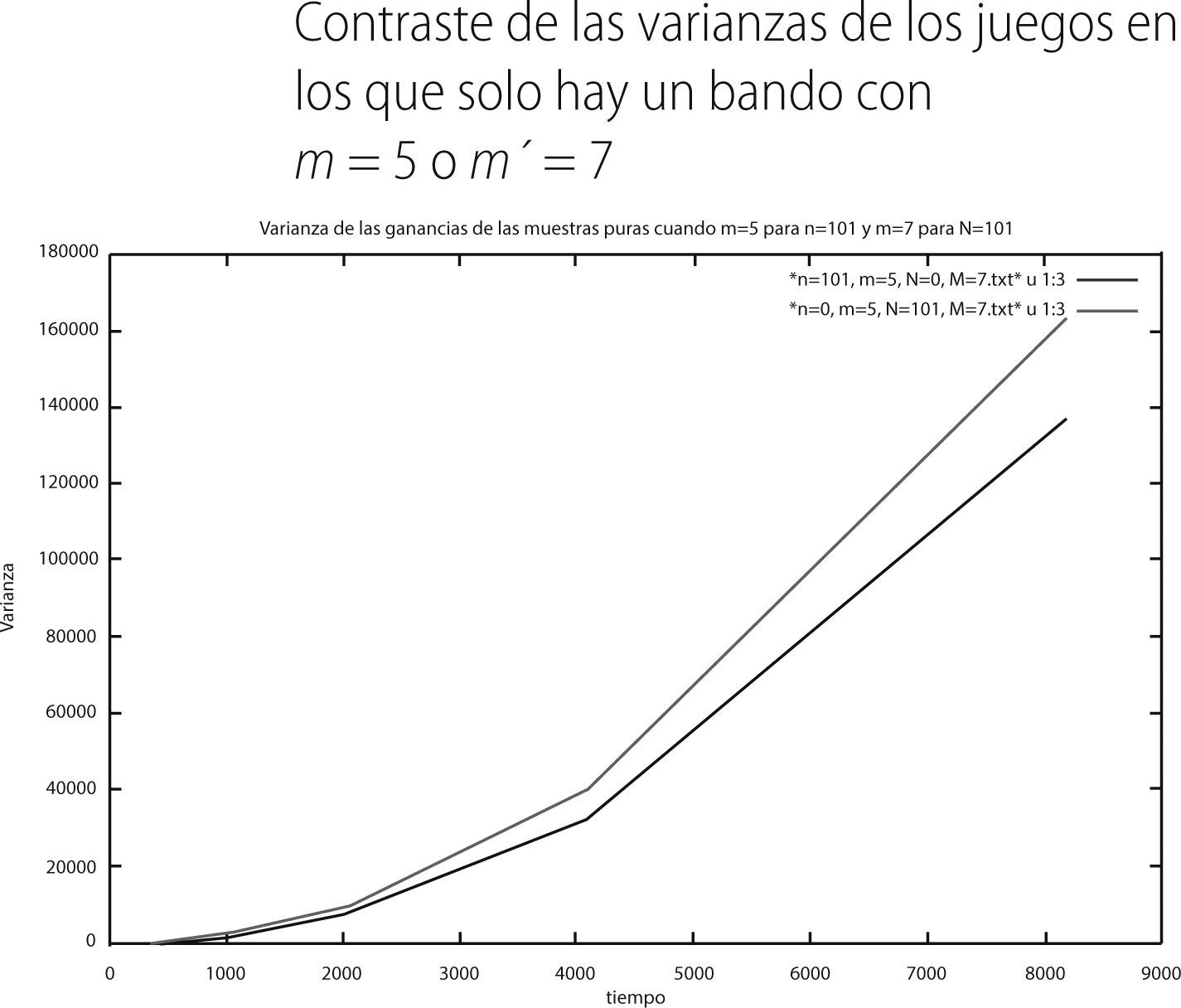
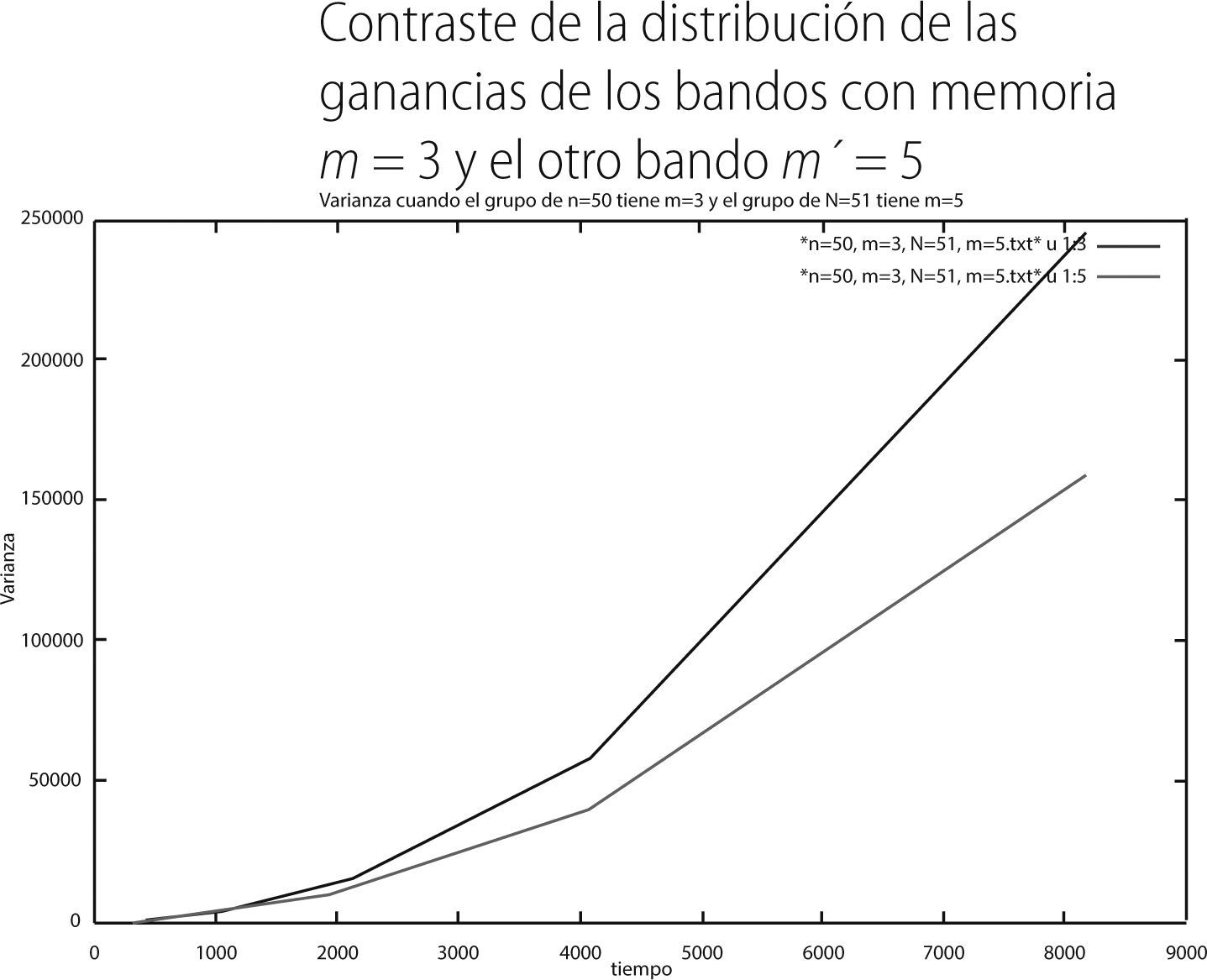
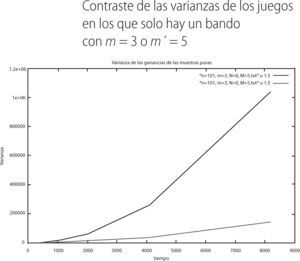
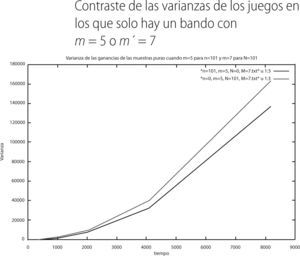
Como podemos apreciar en la gráfica 6, los individuos con memoria m′ = 5 exhiben promedios menos negativos (línea verde) que aquellos que tienen una memoria de m = 3 (línea roja). Ahora presentamos la varianza que presenta cada bando:
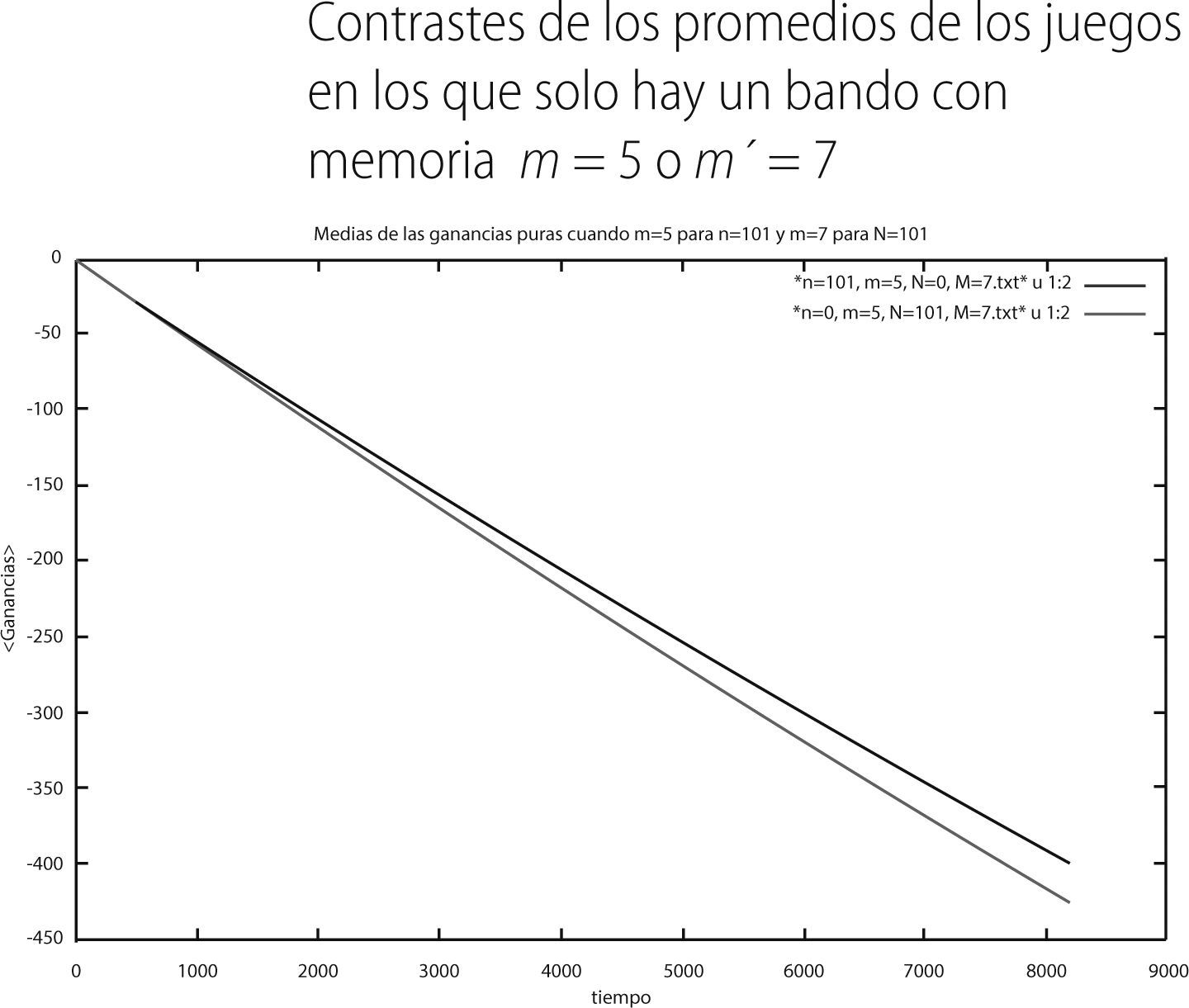
Como se puede percibir, la varianza en el grupo con memoria 3 (línea roja) siempre es mayor a la varianza del grupo de memorias 5 (línea verde). Por lo que respecta a los resultados de las muestras puras del segundo juego mixto, el promedio y la varianza en el tiempo fueron las siguientes:
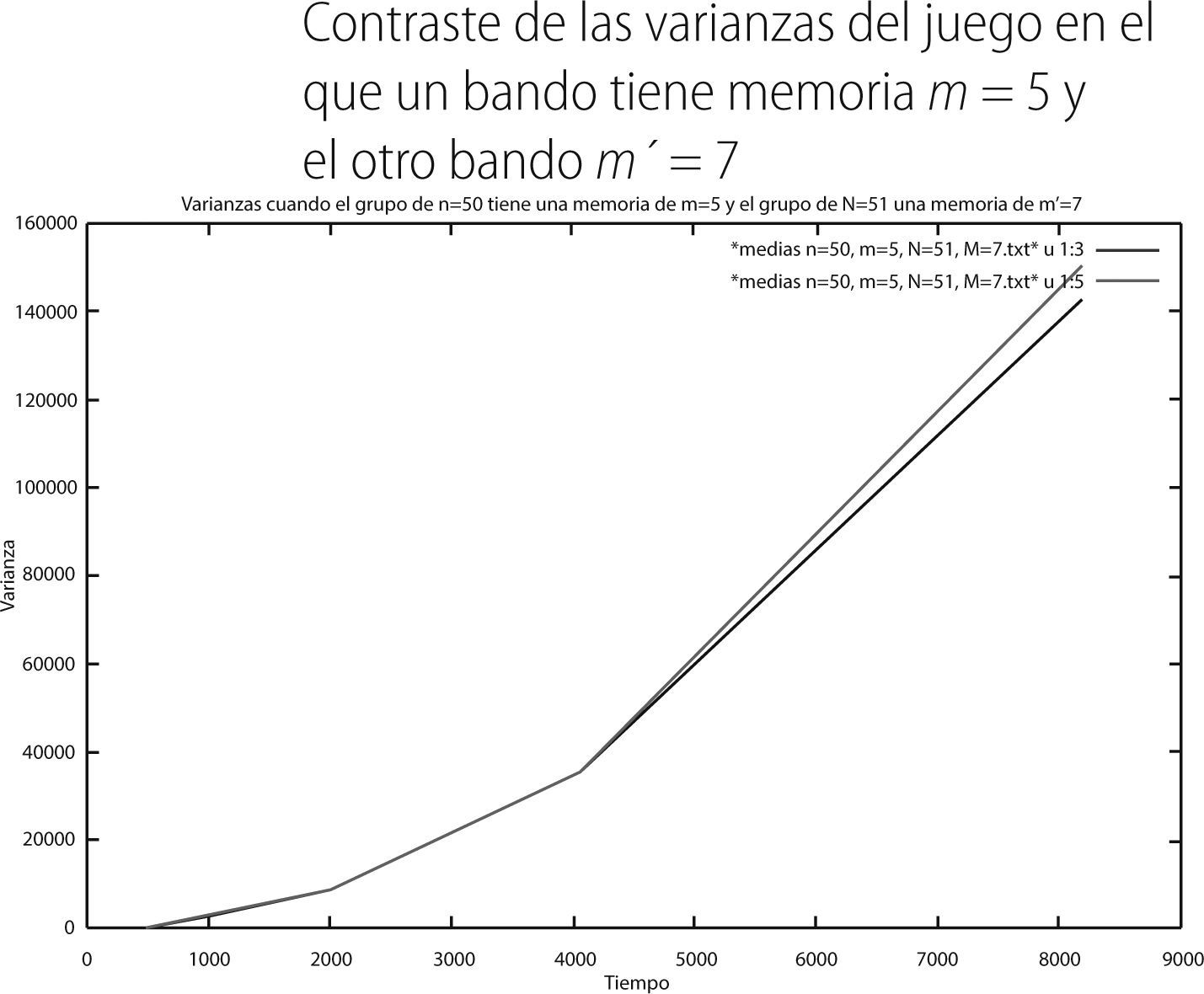
Mientras que el comportamiento de las varianzas en el tiempo fue:
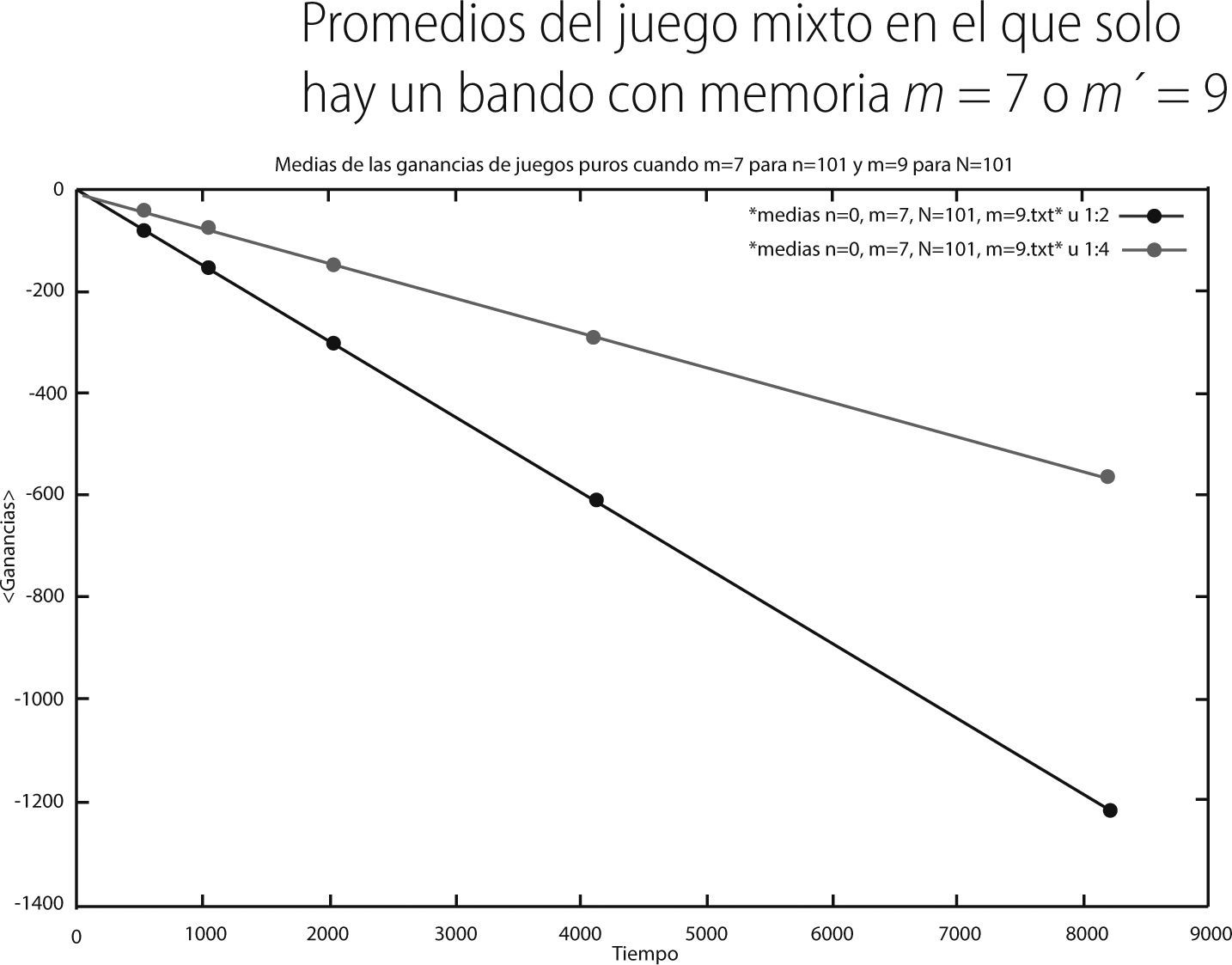
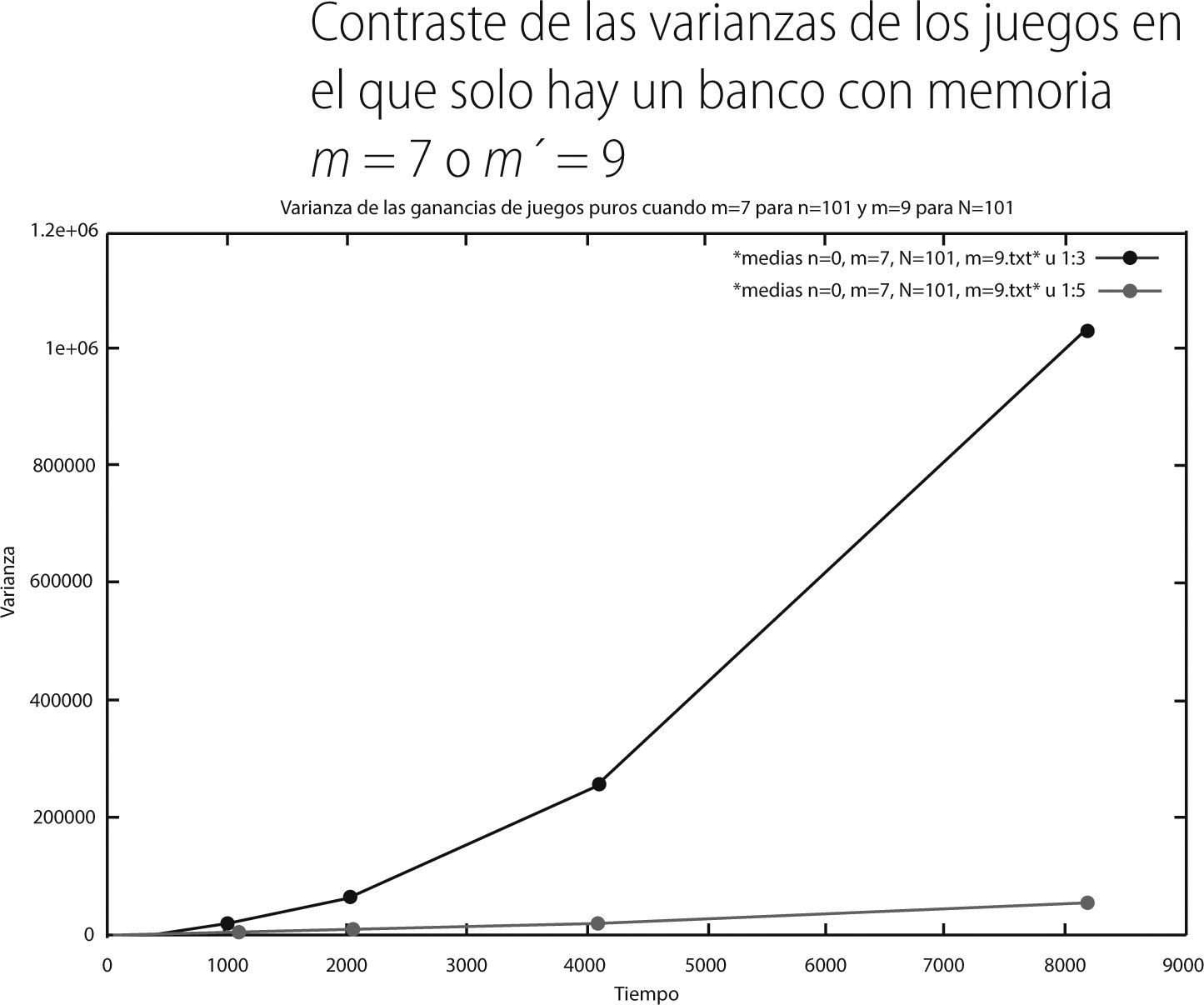
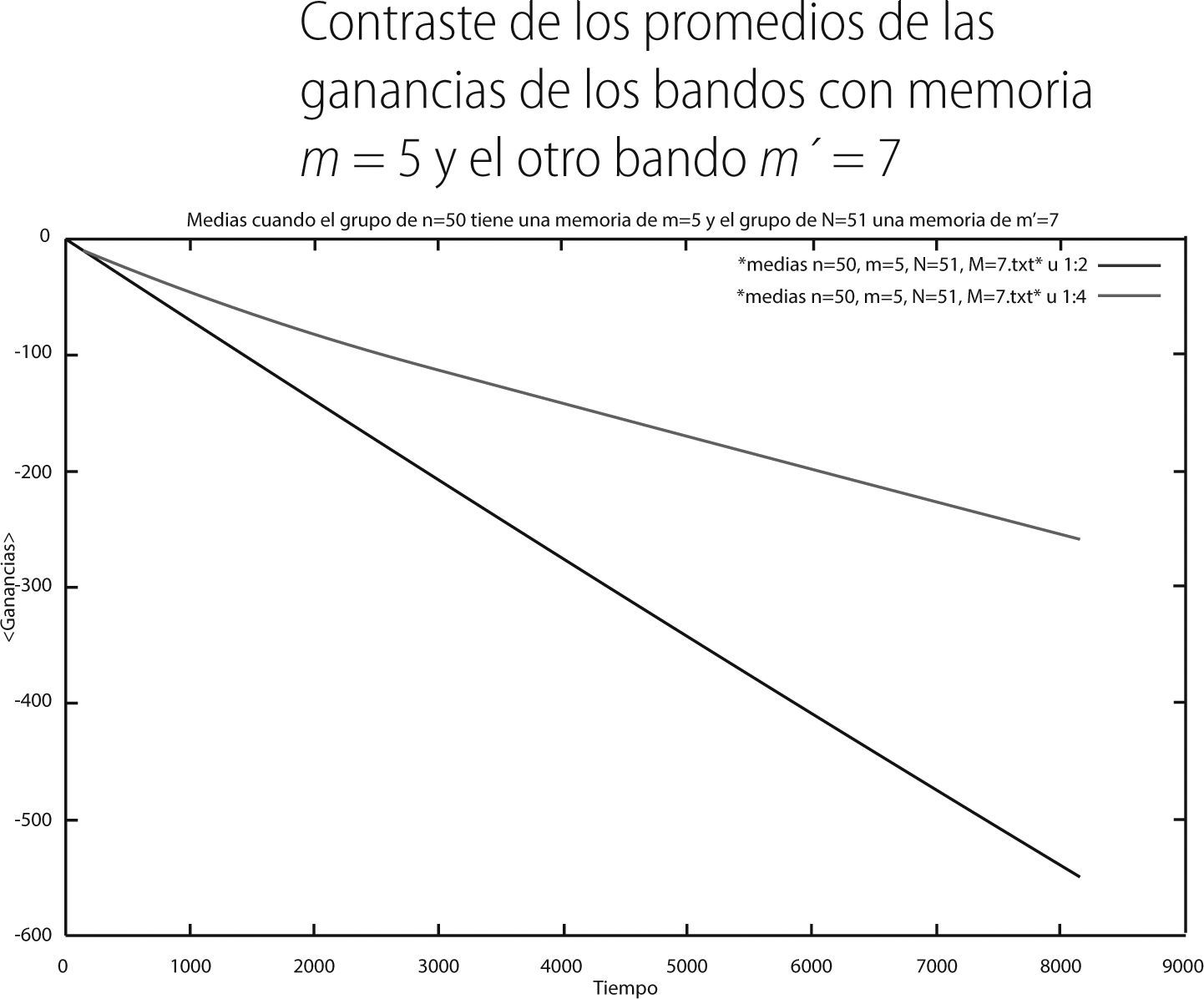
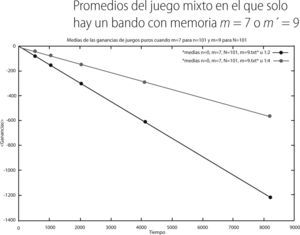
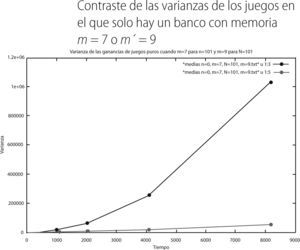
De las gráficas 8 y 9 se puede observar que el bando con memoria m = 5 (curva en rojo) presenta un promedio de sus ganancias en el tiempo menos negativas que el bando con memoria m′ = 7 (curva en verde). En concordancia con esto la varianza de dicho bando es menor que la varianza del bando con memoria m′= 7. Finalmente, para el último juego mixto los promedios y varianzas en el tiempo fueron:
De las gráficas 10 y 11 observamos que en este caso es el grupo con memorias 9 (curva verde) es el que tiene valores promedio menos negativos en sus ganancias que aquellos que pertenecen al bando con memoria 7 (curva roja), con lo cual la varianza del grupo con memoria nueve es menos volátil que la del grupo con memoria siete. Hasta aquí, con los resultados anteriores y de acuerdo a las muestras puras, parece ser que el valor de la memoria que provee de menos perdida a los agentes que participan en el juego están entre m = 5 o m = 9.
Al respecto, como se sugirió en la introducción, el hecho de que algunos agentes tengan una ventaja para tomar su decisión en términos de la información de que disponen acerca de una acción o firma en particular con respecto a otros, parece no ser tan clara de acuerdo a nuestros resultados anteriores. A continuación corroboraremos estos resultados con los resultados que obtuvimos de las simulaciones de los juegos mixtos.
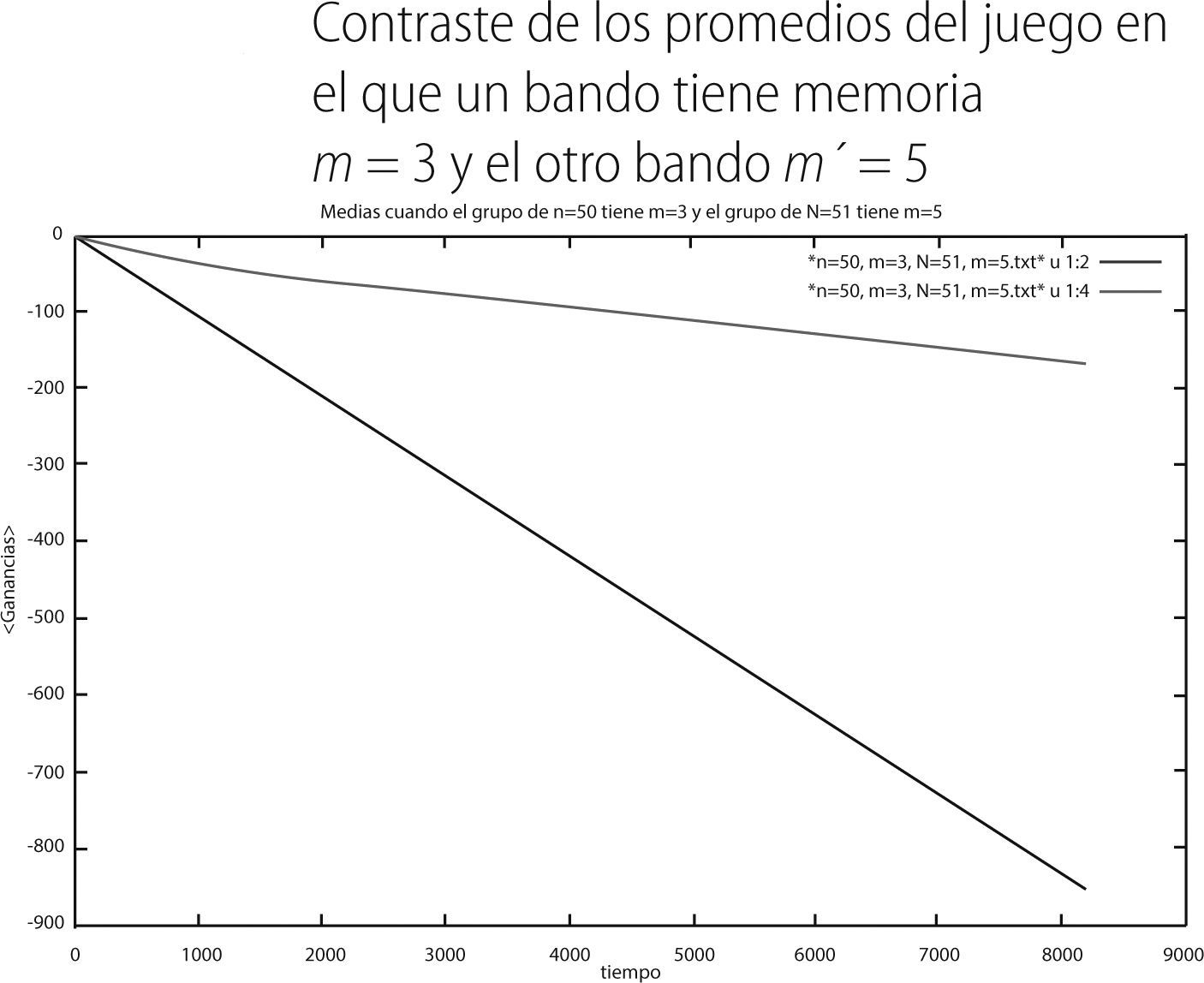
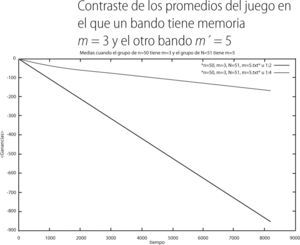
Resultados juegos mixtosEn esta sección presentamos los resultados de los juegos mixtos considerados, la configuración que elegimos estudiar fue aquella en el que Nm= 50 y Nm′= 51, para valores en la memoria de m = 3, 5, 7 versus m′ = 5, 7, 9. Elegimos esta configuración ya que consideramos que en ella la competencia entre bandos es lo suficientemente pareja para poder percibir los efectos de la memoria en cada uno de ellos y su historial en las ganancias de cada bando. Los promedios de las ganancias que presentan los agentes cuando participan en el mismo juego, pero un bando tiene una memoria de 3 y el otro bando una memoria de 5 son:
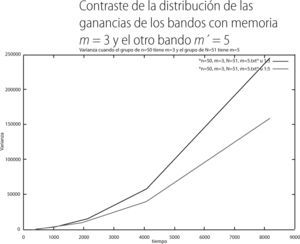
Mientras que las varianzas fueron:
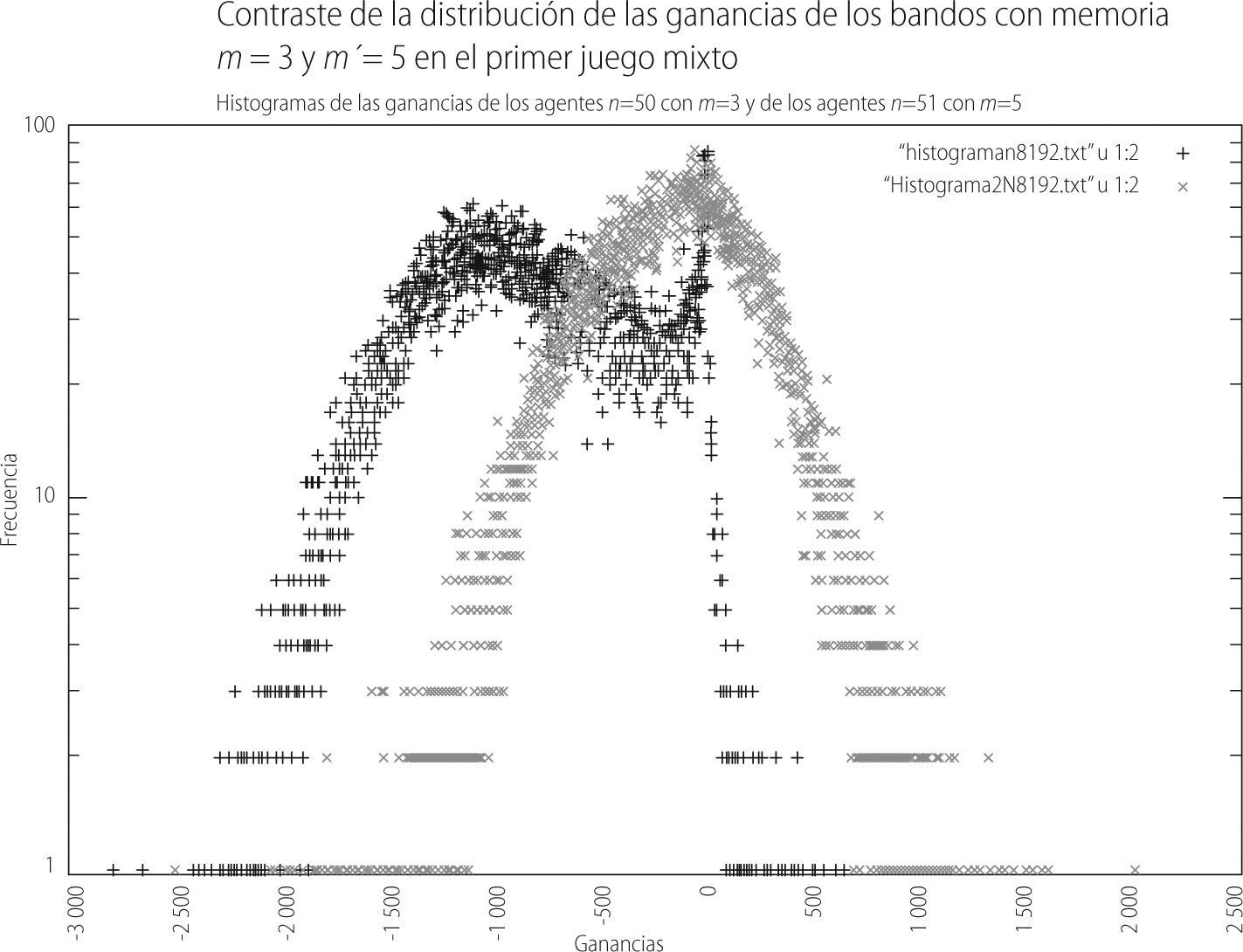
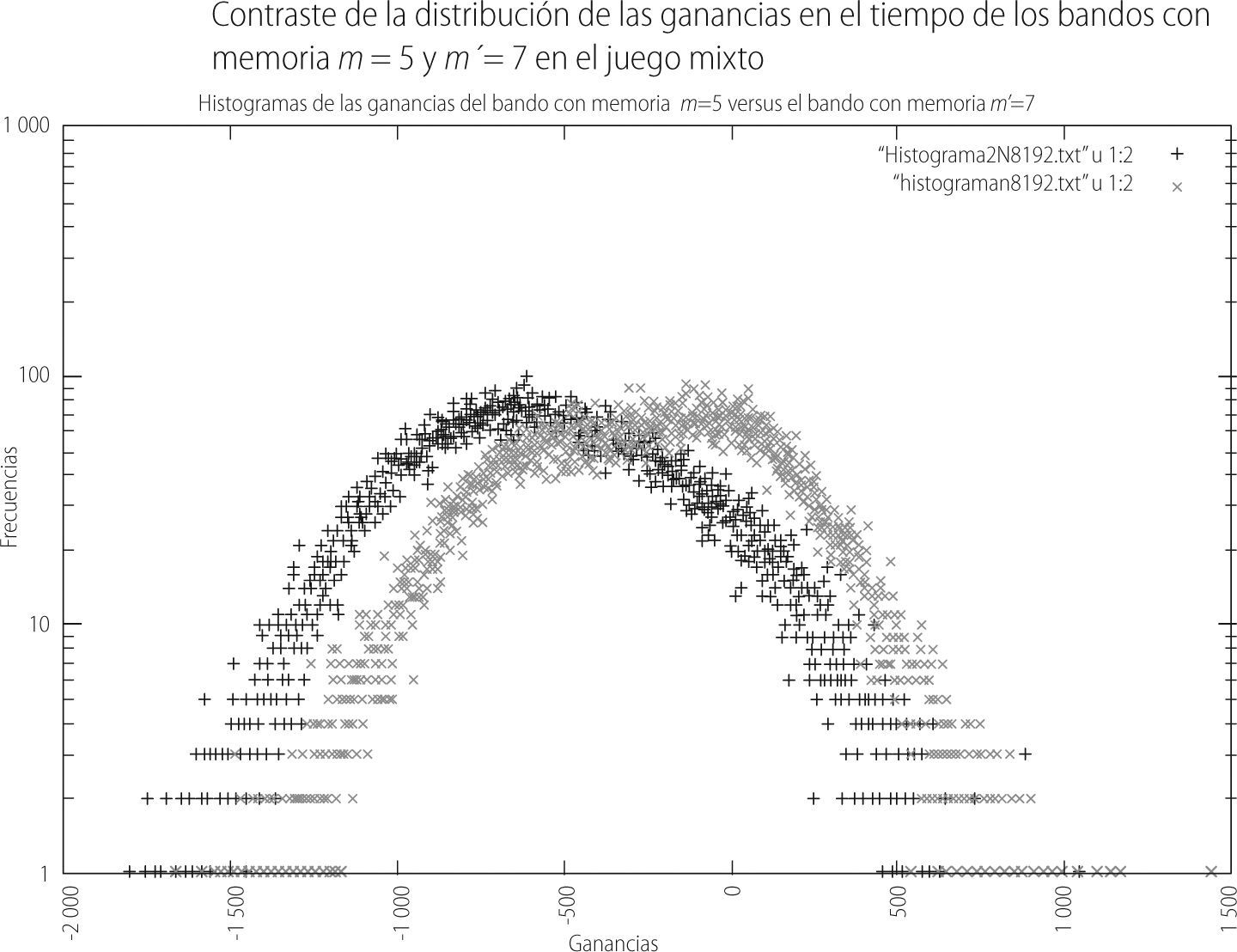
Por otro lado, podríamos preguntarnos cómo es la forma de la distribución de las ganancias en el tiempo de cada bando en este juego mixto, lo cual puede observarse en el siguiente resultado:
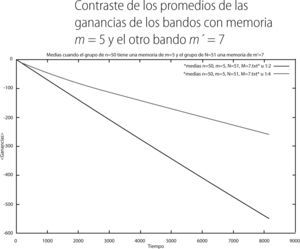
De la gráfica 14 se observa que los individuos con memoria 5 (histograma en verde) pierden menos que aquellos a los que se les asignó una memoria de 7 (histograma rojo). Ahora mostramos las mismas gráficas de la misma configuración del juego mixto pero para el caso en que las memorias del juego en uno de los bandos es m = 5 y para el otro grupo de m′ = 7. Los promedios de este juego mixto son las siguientes:
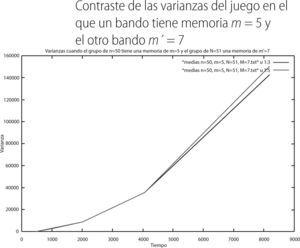
Por lo que se refiere a las varianzas de este segundo juego mixto y la distribución de las ganancias en el tiempo de cada bando son:
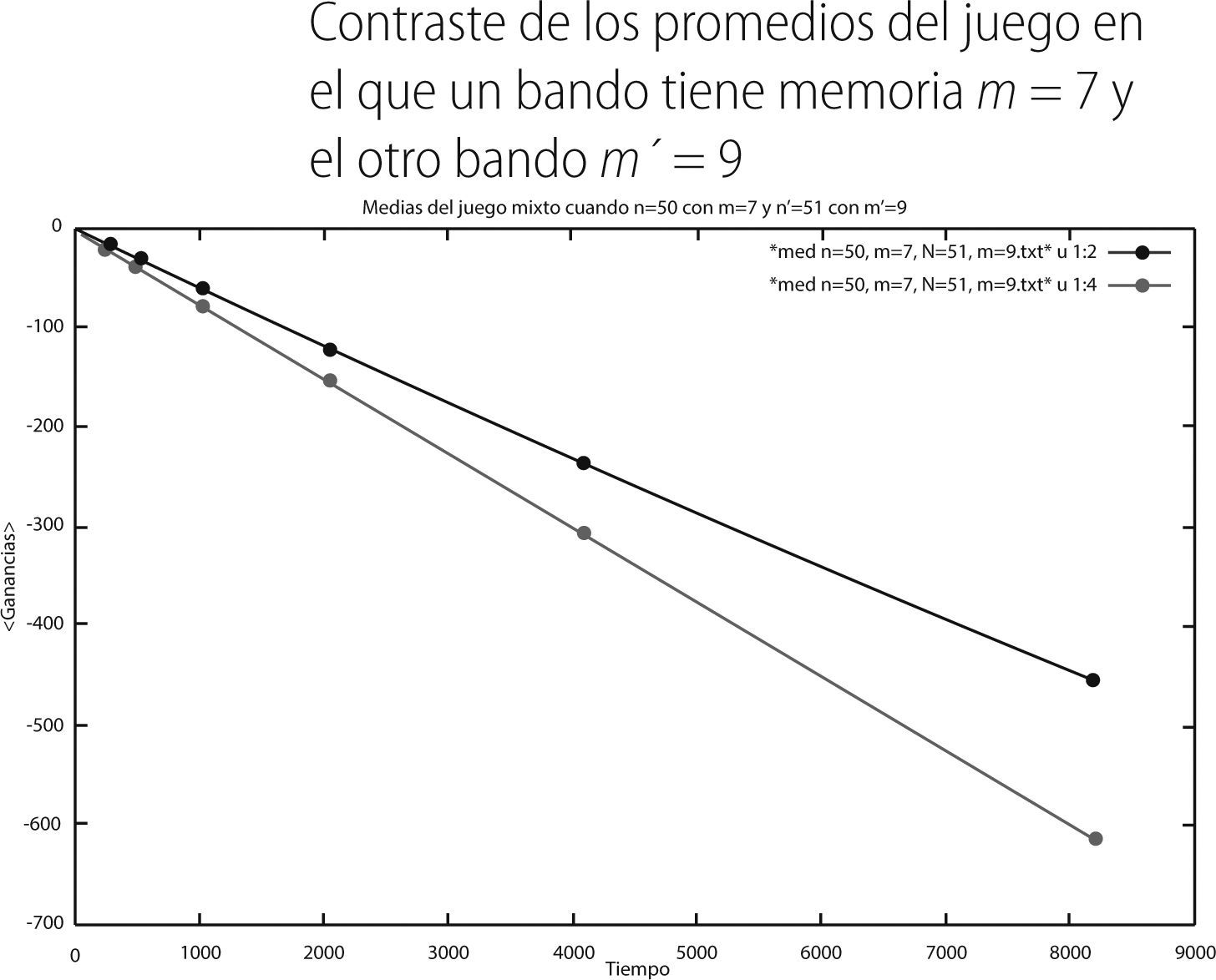
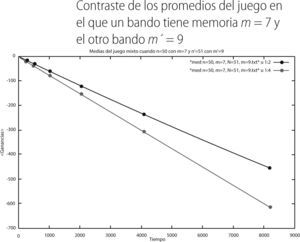
Finalmente, presentamos los resultados del último juego mixto que simulamos en el que el bandoNm= 50 tiene una memoria de m = 7 y el bando Nm′ = 51 tiene una memoria de m′= 9.
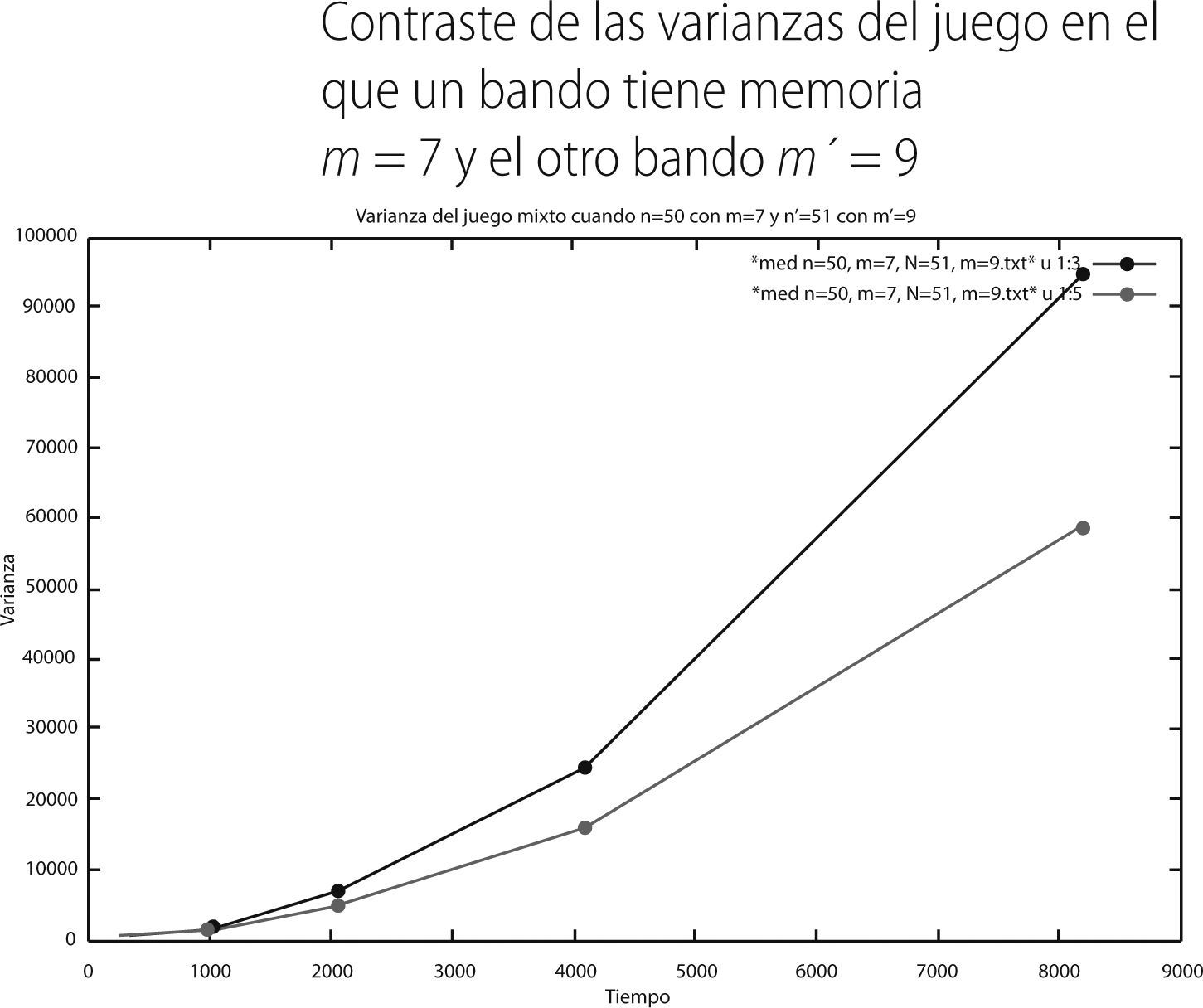
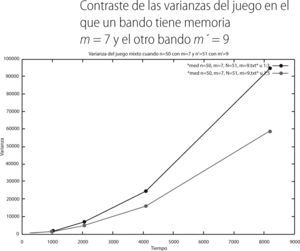
Las varianzas de este último juego mixto fueron las siguientes:
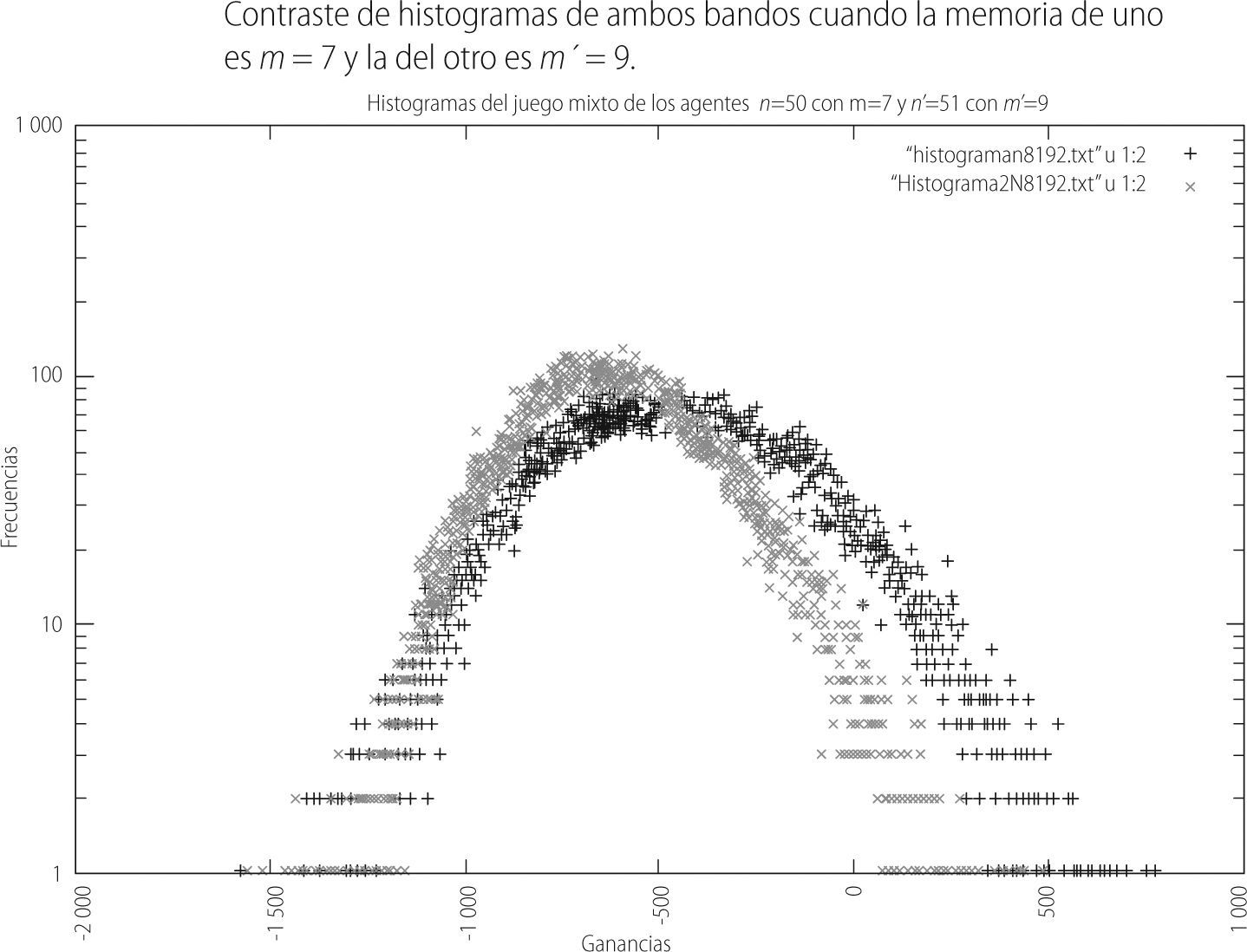
Por último, el contraste de la distribución de las ganancias en el tiempo para ambos bandos en este juego mixto fue:
9Discusión de resultadosLa primera parte de los resultados de los “juegos mixtos” presentados se refieren a los casos en el que no hay competencia entre “bandos” y el total de individuos, N = 101, que participan en el juego poseen una memoria de m = 3, 5, 7 y 9, respectivamente. También nos hemos referido a estos como los “juegos puros”. De tales resultados hemos podido corroborar que, al menos en este caso, el valor de la memoria que provee de menores pérdidas al conjunto de jugadores que participan es cuando se les asigna una memoria de m = 5, ya que pare este valor en la memoria es cuando se tiene el valor menos negativo en el promedio de las ganancias a través del tiempo, siendo este de -398.005 en el tiempo 8,192 de las simulación, de acuerdo a la gráfica 8. En segundo lugar, el valor de la memoria que resulta en menores pérdidas para los agentes que participan en el juego de minorías es m = 9 (-565.533), de acuerdo a la gráfica 10.
Por lo que respecta a los resultados en los que se simuló la competencia entre dos bandos, uno con 50 individuos y el otro con 51 individuos, donde a cada uno de estos bandos se les asignó un tamaño de memoria diferente en el juego. También nos hemos referido a ellos como “juegos mixtos”.
Del primer juego mixto, en el que a uno de los bandos se le asignó una memoria de m = 3 y al otro una memoria m = 5, tuvimos que el promedio en el tiempo 8,192 del bando con memoria m = 3 fue de -852.4 y la del bando con memoria m = 5 fue de -167.204, de acuerdo a la gráfica 12. Así también, de acuerdo a la gráfica 14, la cual contrasta la distribución de las ganancias de los bandos, se puede observar que el histograma del grupo con m= 3 tiene como extremos los valores de -2,500 y 500. Mientras que el histograma del bando con memoria m = 5 tiene por extremo los valores de -2,000 y 1,500. Por tanto, en este juego mixto es el grupo de jugadores con memoria m = 5 el que pierde menos en el “juego de minorías” a través del tiempo.
Para el segundo juego mixto obtuvimos que el promedio del bando con memoria 5 fue de -259.733 en el tiempo 8,192 de la simulación, mientras que la del bando con memoria 7 fue de -550.244, lo cual se puede apreciar en la gráfica 15. De acuerdo a esto, y como se puede apreciar en la gráfica 17, observamos que los extremos de la distribución de las ganancias del bando con memoria m = 5 son -1,500 y 1,000, respectivamente. Por lo que se refiere al bando con memoria m = 7 tenemos que los extremos son de -1,700 y 600. De esto se puede concluir que es el bando con memoria m = 5 el que pierde menos en el “juego de minorías”
Finalmente el último juego mixto simulado fue en el que a un bando se le asignó una memoria de m = 7 y al otro bando una memoria de m = 9. De los resultados presentados en la última sección tenemos que el promedio del bando con m = 7 en el tiempo 8,192 fue de -454.948, mientras que la del bando con m = 9 fue de -611.634, de acuerdo a la gráfica 18. Por otro lado, de la gráfica 20 podemos observar, aún cuando es muy poca la diferencia entre ambos histogramas, que el bando con memoria m = 7 tiene por extremos -1,500 y 700 (curva en rojo). Mientras que el bando con memoria m = 9 tiene como extremo a -1,500 y 500 (curva en verde), respectivamente. De lo anterior podemos decir que, a diferencia de los otros dos juegos, este último resulta ser el más competitivo, sin embargo, el bando con memoria m = 7 pierde un poco menos que el bando con memoria m= 9.
En el presente trabajo nos hemos dedicado, en primera instancia, en reproducir los resultados más representativos del modelo del “juego de minorías” para así concentrarnos en el estudio estadístico de la variable memoria, así como la distribución de las ganancias de los agentes que participan en el juego. El “juego de minorías” es solo un problema más de teoría de juegos, en el que el comportamiento macro del fenómeno puede ser analizado y simulado mediante las técnicas de la física estadística. Este tipo de problemas es uno de los muchos que hoy en día, debido a sus características, se adhiere al nuevo enfoque de los sistemas complejos y, en particular, a la Econofísica.
A diferencia de los enfoques abordados en la literatura y el estado del arte del problema del “juego de minorías”, en nuestra investigación diseñamos un conjunto de “juegos mixtos” en los que la motivación principal fue la de investigar la variable memoria, y con ello la capacidad de razonamiento deductivo a la hora de tomar una decisión por agentes racionales. De acuerdo a los resultados obtenidos, aun cuando el dotar de mayor memoria a un conjunto de individuos del juego implica proveer a éstos de una mejor capacidad para almacenar un número mayor de las decisiones exitosas del pasado (i.e. información), parece ser que esto no provee de ninguna ventaja a éstos a la hora de tomar la decisión correcta que les beneficie económicamente.
Como hemos podido observar en nuestros resultados presentados en los diferentes juegos mixtos simulados, parece ser que el valor de la memoria que garantiza menores pérdidas a los participantes en el “juego de minorías” es cuando se les asigna una memoria de m = 5. En términos del contexto financiero en el que hemos enmarcado el problema, la decisión de comprar o no comprar una acción de un individuo con mayor información de la acción versus otro con menos información de la misma, de acuerdo a nuestras simulaciones, no resulta ni en una mejor toma de decisión para el agente racional ni en un beneficio económico extra. Por el contrario, parece corroborarse el hecho de que los agentes racionales maximizadores de su utilidad tiene una límite para digerir cantidades de información y usarla de manera eficiente y efectiva, aunado a ello es que su toma de decisión se vuelve más inductiva que deductiva.
Es importante referir que, desde el punto de vista aplicativo, así como justificativo, es gracias al teorema del límite central y el enfoque del caminante aleatorio que nuestras simulaciones tienen y toman sentido. Así también, hemos podido corroborar la aplicación de tales conceptos a la simulación de carácter económico-financiero, destacando el uso de la modelación científica. Un resultado del mismo hecho es que hemos podido determinar que la distribución estadística que gobierna al “juego de minorías”, específicamente las ganancias de los agentes, es la distribución normal. En cuanto a la aportación de nuestros resultados esperaríamos que sirva como referencia para posteriores enfoques que se dediquen a discutir más variantes del juego de minorías. Así también, que la metodología y enfoque sea una referencia (al mismo tiempo que una motivación) más para posteriores investigaciones de problemas económicos que puedan ser modelados desde un enfoque no convencional y desde su realidad compleja.
Profesor de asignatura de métodos cuantitativos fe unam. Sus líneas de investigación son econofísica, sistemas complejos, economía de los recursos naturales y estadística aplicada.
Una matriz booleana es una matriz cuyas componentes o entradas son ceros y unos.
Con respecto al límite de tomar una decisión de forma siempre azarosa, si consideramos a la decisión que toman los agentes como una variable aleatoria independiente e idénticamente distribuida (v.a.i.i.d), podemos asumir que la distribución estadística de dicho fenómeno se rige por una distribución binomial Bin(n, p), con p = 1/2. De ahí que σ2/N = 1.