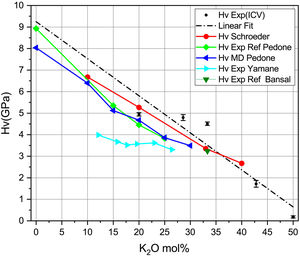
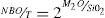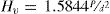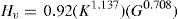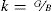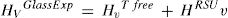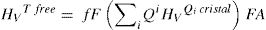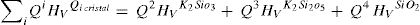En este trabajo se presenta un estudio en el que se aplica la teoría funcional de densidad (DFT), utilizando el software CASTEP, para cristales de silicato (K2SiO3, K2Si2O5 y K2Si4O9) y de óxido de silicio (cuarzo). La densidad de estados (DOS) de estos silicatos muestra que los dos tipos de átomos de oxígeno, puente (BO) y no puente (NBO), tienen una distribución electrónica significativamente diferente en los orbitales 2p y 2s, debido a un ambiente químico inmediato diferente. Esto lleva a un desplazamiento a energías menores de las bandas de valencia s y p de la densidad de estados parcial (PDOS) del NBO de alrededor de 2 eV respecto de la PDOS del BO. En el cristal de menor contenido en K2O (K2Si4O9), se incrementan los enlaces covalentes Si-O debido a la transferencia de carga electrónica del orbital 4s del átomo de potasio al NBO, y de este NBO al átomo de silicio y, finalmente, a todos los átomos del tetraedro, lo que permite mejorar la fuerza de enlace del sistema. Este hecho resulta en que el material final tenga una mayor resistencia mecánica. Por otro lado, en el K2Si2O5 (el cual posee un NBO por tetraedro) el enlace Si-O es más débil con respecto al del K2Si4O9, tendencia que se acentúa en el K2SiO3 (que posee dos NBO por tetraedro). Esta misma tendencia sigue la dureza Vickers calculada teóricamente. Este estudio se ha aplicado a vidrios de silicato de potasio obtenidos experimentalmente y se han comparado varias propiedades mecánicas con las teóricas de los respectivos cristales de igual composición química. Los NBO tanto de cristales como de vidrios se han cuantificado a partir de las unidades estructurales Qn. Se ha observado que las propiedades mecánicas de los vidrios no pueden ser explicadas únicamente por las contribuciones de los tetraedros libres unidos por el vértice y caracterizados por sus BO y NBO como función de la concentración en K2O, es decir por los Qn. Esto es debido a que la DFT de CASTEP para sistemas cristalinos considera todo orden de interacción. Por ello es necesario utilizar estructuras a alcance intermedio, denominadas como unidades estructurales rígidas (RSU). La contribución de los tetraedros libres se ha calculado usando la dureza Vickers del cristal y un factor de apantallamiento por la pérdida de la interacción de medio y largo alcance. En el trabajo se explica el comportamiento de la dureza Vickers y módulo de Young de vidrios de SiO2-K2O en un amplio rango de composiciones molares.
In this work, a study is presented in which the density functional theory (DFT) is applied, using the CASTEP software, for crystals of silicate (K2SiO3, K2Si2O5 and K2Si4O9) and of silicon oxide (quartz). The Density of State (DOS) of these silicates shows that the two types of oxygen atoms, bridging (BO) and non-bridging (NBO), have a significantly different electron distribution in the 2p and 2s orbitals, due to a different and close chemical environment. This leads to a displacement to lower energies (around 2 eV) of the s and p valence bands of the partial density state (PDOS) of the NBO regarding the PDOS of the BO. In the crystal with the lowest K2O concentration (K2Si4O9), the covalent Si-O bonds are increased due to the electronic charge transfer of the 4s orbital from the potassium atom to the NBO, and from this NBO to the silicon atom and, finally, to all the atoms of the tetrahedron, which allows to improve the bond strength of the whole system. This fact results in the final material having a higher mechanical resistance. On the other hand, in K2Si2O5 (which has one NBO per tetrahedron) the Si-O bond is weaker compared to K2Si4O9, a tendency that is highlighted in K2SiO3 (which has two NBOs per tetrahedron). This same trend follows the theoretically calculated Vickers hardness. This study has been applied to experimentally obtained potassium silicate glasses and several mechanical properties have been compared with the theoretical properties of the respective crystals of similar chemical composition. The NBO of both crystals and glasses have been quantified from the Qn structural units. It has been observed that the glass mechanical properties cannot be only explained by the contributions of the free tetrahedral joined by the vertice and characterized by their BO and NBO as a function of the concentration in K2O, that is by Qn. This is because CASTEP's DFT theory for crystalline systems considers every order of interaction. Therefore, it is necessary to use intermediate-range structures called rigid structural units (RSUs). The contribution of free tetrahedral has been calculated using the Vickers hardness of the crystal and a screening factor for the loss of medium and long range interactions. This work explains the behaviour of the Vickers hardness and Young's modulus of SiO2-K2O glasses in a wide range of molar compositions.
Es bien conocido que varios factores determinan la dureza de un material, o lo que es lo mismo, su habilidad para resistir a ser indentado por otro material. Estos factores dependen del nivel o escala que se considere, es decir escala atómica o escala molecular. Así, a escala atómica la dureza es dependiente de la fuerza, la distancia y de la densidad de enlaces (poseer una alta densidad de enlaces aumenta la dureza), densidad electrónica de valencia (a mayor densidad mayor resistencia) y direccionalidad del enlace (presencia de orbitales d o f), así como de la densidad atómica [1]. A escala molecular, la resistencia depende de la dimensionalidad de la red y de la topología estructural, es decir de la presencia de anillos, cadenas, superestructuras atómicas, etc. [2]. Asimismo, la resistencia mecánica determinada por el módulo de volumen (B), el cual caracteriza la incompresibilidad del material, está también relacionada con la densidad electrónica de valencia. En este mismo sentido, el módulo de cizalladura (G) que a su vez caracteriza la resistencia al cambio de forma a volumen constante. Cuanto más grande es G, mayor capacidad para resistir fuerzas de cizalladura y está igualmente relacionado con la fuerza de los enlaces. Ambos módulos, B y G, están relacionados con la microdureza del material, y por lo tanto, con la fuerza de los enlaces presentes en el mismo. Debido a la importancia de las constantes elásticas de la mayoría de los materiales y de su relación con las diferentes aplicaciones de los mismos, es posible encontrar multitud de artículos en los que se resumen los valores obtenidos tanto para cristales y vidrios, en general [2–4], como para vidrios de silicatos de potasio, en particular [5–7].
El cálculo de las propiedades mecánicas de los materiales vítreos, a partir de su estructura atómica, se basa en la composición química de éstos y en considerarlos como cristales iónicos. Según estas consideraciones, se calculan dichas propiedades a partir de la densidad de empaquetamiento atómico, de la densidad de la energía de enlace o energía de disociación por unidad de volumen de cada constituyente en el vidrio y de su concentración molar. Una de las primeras aproximaciones fue la de Makishima y Mackenzie [8], si bien en los últimos años se han desarrollado métodos basados en la dinámica molecular con muy buenos resultados. Por otro lado, a escala molecular, los procedimientos se basan en la teoría de las restricciones topológicas que considera la presencia de anillos, cadenas, superestructuras atómicas, y otras similares en la estructura vítrea y que dichas estructuras son las que determinan la resistencia mecánica del vidrio. En las últimas décadas, estas dos teorías, la dinámica molecular y la teoría de las restricciones topológicas, han permitido obtener valores teóricos de las constantes elásticas y de la dureza Vickers en este tipo de materiales [9,10]. Mediante dinámica molecular, Pedone et al. [11] han calculado los valores teóricos de los módulos elásticos para silicatos de Li, Na y K y han comparado dichos resultados con los valores experimentales, obteniendo muy buena coincidencia. Por otro lado, la teoría de las restricciones topológicas, según el modelo propuesto por Sidebottom [12] basado en las diferentes unidades estructurales existentes en el vidrio, o el modelo propuesto por Mauro [13], K. Yang [14] y Phillips [15], basado en ángulos y distancias de enlace, permite predecir las principales propiedades de vidrios, en particular la dureza Vickers, en función de su composición y de la temperatura [16]. Es necesario tener en cuenta que la teoría de las restricciones topológicas es una herramienta transcendente para el desarrollo de vidrios y posibles nuevas aplicaciones de los mismos.
En las dos teorías mencionadas se considera que la estructura vítrea corresponde al modelo descrito por Zachariasen [17], quien propuso que el vidrio puede describirse como una red aleatoria, pero continua, en la que no tiene lugar el orden a medio y largo alcance y en la que existen oxígenos puente (BO) y oxígenos no puente (NBO), siendo los primeros aquellos donde los átomos de oxígeno actúan como puentes entre átomos del catión formador (Si, B, P, Ge, etc.), mientras que en los segundos los átomos de oxígeno no unen a los átomos del correspondiente catión. Así, en un vidrio formado solamente por SiO2 existirán tetraedros de SiO4 unidos entre sí por los cuatro vértices, con lo que la conectividad será de cuatro. La incorporación de elementos alcalinos a una red de tetraedros de SiO4 provoca la rotura de los enlaces Si-O-Si, es decir la rotura de los BO, para formar NBO con lo que la conectividad se verá reducida. El valor de la conectividad es fundamental para describir la red vítrea y, por lo tanto, sus propiedades elásticas [18,19]. La disminución de la conectividad se produce por la rotura de los enlaces T-O (T = átomo tetracoordinado) y que, en el caso del SiO2, puede ocurrir en cualquiera de los cuatro enlaces del átomo de Si, hecho que se ha observado utilizando la resonancia magnética nuclear de Si29[20]. Mediante esta técnica se han propuesto diferentes especies Qn, siendo Q el tetraedro SiO4 y n el número de BO. Así, las especies Q4, Q3, Q2, Q1 y Q0 corresponderían a un átomo de Si con 4, 3, 2, 1 y 0 BO, respectivamente, o lo que es lo mismo 0, 1, 2, 3 y 4 NBO. En una estructura vítrea, el número de NBO que existe en una red formada por cationes tetracoordinados (como es el Si en el caso de los vidrios de silicato) se puede calcular según la expresión:
Siendo T la concentración de los átomos tetracoordinados formadores de red y M el catión modificador de red (Li, Na, K, etc.). Sin embargo, mediante otras técnicas experimentales, como son las espectroscopías Raman, IR, XANES, etc., se ha comprobado que la estructura del vidrio no sólo puede representarse mediante las especies Qn, sino que existen también otras estructuras o superestructuras, como son los anillos de tres, cuatro y seis miembros, o los supertetraedros, anillos unidos por caras, cadenas, etc [21,22]. Dado que las propiedades de los vidrios son muy dependientes de sus características estructurales, es necesario conocer éstas para poder predecir las primeras.
En el trabajo que aquí presentamos se muestra cómo la teoría funcional de densidad (DFT) utilizada para cristales puede dar resultados comparables a las dos teorías anteriormente mencionadas y que abren una nueva vía para el estudio de la estructura del vidrio. De acuerdo con los trabajos de Ching et al. [23] y Tang et al. [24], los cuales utilizan la DFT para estudiar cristales de silicatos de Li y Na, en este trabajo nosotros hemos aplicado la DFT para estudiar cristales de silicato de potasio utilizando el método ab initio del software CASTEP [25]. Teniendo en cuenta que en estos sistemas cristalinos de Si y K también existen enlaces BO y NBO con el mismo software, hemos determinado sus estructuras electrónicas y sus constantes elásticas y hemos comparado los resultados con las medidas experimentales de vidrios con composiciones químicas similares, intentando establecer diferencias entre cristales y vidrios, pues en ambos existen tanto BO como NBO. Para los cristales, al utilizar la aproximación DFT es posible conocer y determinar su estructura, densidad electrónica, estructura de bandas, muchas otras propiedades o características como espectros Raman e IR, UV-vis, etc.; los resultados obtenidos en este estudio nos servirán de base para intentar predecir las propiedades de los vidrios, ya que éstos poseen estructuras intrínsecamente complejas. No obstante, y como se mostrará más adelante, no solamente las unidades Qn son necesarias para predecir las propiedades mecánicas de los vidrios, sino que también ha sido necesario incorporar las diferentes estructuras de alcance intermedio (anillos, supertetraedros, tetraedros unidos por una arista, etc.) para obtener una buena coincidencia con los valores experimentales, es decir, para obtener un buen resultado deben ser aplicadas ambas teorías, las relacionadas con la escala atómica y las relacionadas con la escala molecular.
Una de las ventajas de los sistemas cristalinos de silicato es que los orbitales de valencia de todos los átomos son sólo s y p, es decir, son sistemas simples que pueden ser utilizados para su estudio mediante DFT. Así, desde hace tiempo se está llevando a cabo un estudio sistemático, tanto de vidrios como de cristales de silicato, basado en que ambos materiales poseen características comunes en cuanto a interacciones a corto y medio alcance. En este sentido cabe destacar los estudios realizados que utilizan las técnicas XPS, RMN Si29, IR y Raman tanto para vidrios como para cristales de silicato [26–29].
El estudio de materiales de silicatos de potasio (ya sea vidrios o cristales) se desarrolla en nuestro grupo de investigación para conocer su posible aplicación como vidrios fertilizantes (VF) en la agricultura industrial. Los silicatos de potasio son constituyentes importantes de los VF. Una de las ventajas de usar el VF es la posibilidad de modular su velocidad de disolución, según la necesidad de nutrientes que requieren las plantas [30]. Hay dos formas de modular la disolución del VF, una es variando el contenido de las especies Qn, y la otra es la incorporación de otros óxidos de los elementos Ca, Mg, Al, B, P, entre otros. Para entender el comportamiento tanto de las especies Qn como del resto de los óxidos incorporados a los VF, en este primer trabajo realizaremos un estudio teórico sobre el sistema más sencillo, el silicato de potasio.
Como primera etapa aplicaremos el cálculo ab initio, dentro de la teoría DF, para explorar la estructura electrónica de los silicatos de potasio cristalinos y, a partir de los resultados obtenidos, se evaluarán las constantes elásticas de los cristales de silicato. Estas propiedades se compararán con los datos experimentales obtenidos para los vidrios de silicato de potasio con composiciones químicas similares. A pesar de que el origen de la dureza no es totalmente comprendido, en este trabajo presentamos resultados teóricos de la estructura electrónica y dureza de cristales de silicatos de potasio, junto con las medidas y los resultados experimentales de Hv y módulo de Young (E) de los vidrios correspondientes.
ExperimentalFusión de vidrios. Medidas de microdureza y módulo de elasticidadLas muestras de vidrio utilizadas en este estudio fueron obtenidas usando reactivos químicos de grado para análisis (cuarzo y carbonato de potasio). Para ello, una vez pesadas, se mezclaron en un mezclador-agitador Túrbula® durante 60 minutos y posteriormente fueron fundidas en un crisol de platino a una temperatura de 1.400°C en un horno eléctrico durante dos horas. Los vidrios fundidos fueron vertidos en un molde metálico caliente y posteriormente las muestras sólidas fueron recocidas a 580°C durante dos horas y enfriadas lentamente hasta temperatura ambiente. Las muestras de vidrio recocido fueron mantenidas en un desecador hasta posterior estudio. Se prepararon cinco muestras variando la composición de sílice y óxido de potasio, según xK2O-(100-x)SiO2 con x = 20, 30, 40 y 50. Las composiciones se analizaron mediante fluorescencia de rayos X, encontrándose variaciones muy pequeñas de la composición respecto a las teóricas.
Las medidas de microdureza Vickers (Hv) y módulo de elasticidad se realizaron con un nano-indentador UMT-2 (Bruker, Alemania), utilizando una punta Vickers. Este equipo se calibra con un cristal de cuarzo cuya microdureza es de 14.63 GPa en la dirección (0001). Las muestras de vidrio fueron pulidas con papel de SiC y diamante hasta obtener una superficie especular y se guardaron a vacío y a 50°C para evitar adsorción de agua o CO2 ambiental. Las medidas se realizaron con una carga (P) de 1 N durante 10 segundos. Al menos 10 medidas fueron realizadas para cada muestra hasta obtener un error inferior a +/- 0.2 GPa en Hv. Los valores de Hv se obtuvieron a partir de la ecuación:
siendo d el valor medio de las diagonales de indentación, en mm.
Por otro lado, el módulo de elasticidad se obtuvo mediante el método de Oliver y Pharr a partir de la curva carga-desplazamiento durante cada indentación [31]. Dado que los valores de Hv y E determinados mediante la técnica de indentación son dependientes del tipo de punta (Vickers, Knoop, etc.), carga y tiempos utilizados, los valores obtenidos en este trabajo se compararán con los recogidos en la bibliografía para condiciones experimentales similares.
Cálculo DFTEn este trabajo hemos usado el software CASTEP de Materials Studio versión 2017 R2, para estudiar tres sistemas cristalinos de silicato de potasio. Los datos de la estructura de estos cristales de silicato corresponden a los de los ficheros CIF de Inorganic Cristal Structure Database (ICSD), con referencia ICSD 3121 para K2Si4O9, 280480 para K2Si2O5 y 201163 para K2SiO3. En todos los casos se usó la optimización geométrica con la opción ultra-fina (energy cutoff 830 eV y pseudopotenciales que conservan la normalización) y el potencial de canje y correlación de la aproximación del gradiente generalizado de Perdew-Burke-Ernzerhof (GGA-PBE) (5). La tolerancia del ciclo autoconsistente fue de 5 x 10-7 eV/átomo. Para los tres sistemas cristalinos de silicato de potasio se usaron los orbitales de valencia del K (3s2, 3p6, 4s1), Si (3s2, 3p2) y O (2s2, 2p4). Asimismo, para el cálculo de las constantes elásticas se ha usado la opción ultra-fina, con un número de etapas de tensión de seis. Además, como los materiales obtenidos son sólidos, se ha utilizado el potencial de canje y correlación GGA-PBESOL, ya que es un procedimiento mejorado del funcional PBE para sólidos. Las constantes elásticas de un material describen su respuesta a una tensión aplicada y estas constantes elásticas lineales forman una matriz simétrica 6 x 6. El método para calcular la matriz de constantes elásticas consiste en aplicar una deformación homogénea en el material y calcular la tensión resultante, manteniendo fija la celda unidad. Este método se conoce como primeros principios.
En el nivel de desarrollo de la teoría existen modelos macroscópicos que relacionan los coeficientes elásticos con la dureza del material [3]. La dureza Vickers (en GPa), se evalúa con el software CASTEP usando la relación:
Siendo B el módulo de volumen del policristal, G el módulo de cizalladura y k el módulo de Pugh. Usando los valores de las constantes elásticas (en GPa) para materiales policristalinos y aplicando el método de Hill, que usa el promedio de los valores obtenidos por los métodos de Voigt y Reuss [32], la ecuación Eq 2 permite obtener valores de dureza muy próximos a los datos experimentales de cualquier material policristalino.
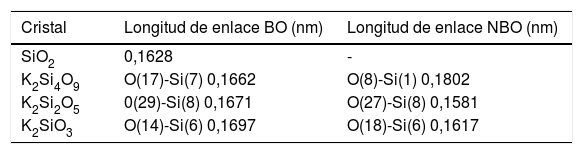
Resultados and discusiónSistemas cristalinosEl software CASTEP de Materials Studio (el cual usa una base de ondas planas) aplica la técnica de Sanchez-Portal [33] para obtener una base LCAO (linear combination of atomic orbitals) y así conocer la carga en el átomo, la distancia de enlace, los ángulos entre átomos, entre otros, lo cual permite hacer un análisis de la población en los sistemas másicos usando el formalismo desarrollado por Mulliken [34,35]. Utilizando este software y los ficheros CIF mencionados anteriormente, se han obtenido los valores de las distancias de enlace para los BO y los NBO de los sistemas cristalinos estudiados. Estos resultados se recogen en la tabla 1 para una serie de átomos de la celda unidad de cada sistema. En esta tabla 1, los números indicados en cada átomo corresponden a la posición de cada uno de ellos en la red analizada. A partir de estos datos, se ha llevado a cabo el análisis de la población electrónica del citado software y de la estructura electrónica para cada sistema. Valores similares han sido utilizados por Pedone et al. [11] para calcular las constantes elásticas de vidrios de silicatos alcalinos.
Distancias de enlace en cristales de silicato de potasio. O(x)-Si(y), indica la distancia entre el átomo de oxígeno en posición x y el átomo de silicio en posición y
| Cristal | Longitud de enlace BO (nm) | Longitud de enlace NBO (nm) |
|---|---|---|
| SiO2 | 0,1628 | - |
| K2Si4O9 | O(17)-Si(7) 0,1662 | O(8)-Si(1) 0,1802 |
| K2Si2O5 | 0(29)-Si(8) 0,1671 | O(27)-Si(8) 0,1581 |
| K2SiO3 | O(14)-Si(6) 0,1697 | O(18)-Si(6) 0,1617 |
Éste es el sistema más simétrico de los tres estudiados poseyendo una relación de NBO/T = 0.5 [36]. Las cargas Mulliken de los átomos de K, Si y O se recogen en la tabla 2, pudiendo comprobarse que el K pierde 1,12e (toda la carga del orbital 4s), quedando en estado iónico. La carga del Si octaédrico es de 1,93e y la del tetraédrico es de 1,92e. El NBO tiene una carga de -1.09e y el BO una de -1,13e, siendo por ello el BO más electronegativo (0,04e de diferencia). Los NBO interaccionan con el K recibiendo la carga transferida del orbital 4s para luego transferirla al átomo de silicio, que se queda con una parte y el resto la distribuye a todos los BO restantes del tetraedro. Además, según la tabla 1, la mayor distancia de enlace Si-O en el NBO (0,1802 nm) se explica por la menor carga electrónica disponible en el octaedro (debida al Si) por enlace (1,93e/6 = 0,321e), respecto al tetraedro (1,92e/4 = 0,48e), lo cual hace que la distancia de enlace del BO sea menor (0,1662 nm).
Distribución de la valencia electrónica por el método de Mulliken
| Cristal | Átomo | Carga (e) |
|---|---|---|
| SiO2 | SiO | 2,38-1,19 |
| K2Si4O9 | K(1)Si(1) (octaedro)Si(7) (tetraedro)O(8) (NBO)O(17) (BO) | 1,121,931,92-1,09-1,13 |
| K2Si2O5 | K(7)Si(8)O(27) (NBO)O(29) (BO) | 1,031,89-1,11-1,13 |
| K2SiO3 | K(12)Si(6)O(18) (NBO)O(14) (BO) | 0,741,72-1,08-1,10 |
En este sistema, a pesar de que hay 15 tipos de átomos de oxígeno en la celda primitiva (definidas por la cercanía con los átomos de potasio), tomamos como referencia un tetraedro, pues las cargas son muy parecidas. Las cargas Mulliken de los átomos de K, Si y O para este sistema también se recogen en la tabla 2. La carga disponible para los enlaces en el Si ha disminuido respecto al K2Si4O9 (de 1,92e a 1,89e). A menor carga positiva en el Si, menor interacción coulombiana con los oxígenos del tetraedro y, por tanto, menor enlace covalente. La carga electrónica del orbital 4s de los átomos de K (el cual ha perdido 1,03e) es transferida a los NBO de forma similar al caso anterior. Los NBO tienen una carga de -1,11e y los BO de -1,13e. La distancia de enlace del BO es 0,1671 nm, que es un valor mayor que la distancia de enlace del NBO (0,1581 nm). Esto se explica porque, a pesar de que la carga del BO es ligeramente mayor, el NBO sólo enlaza covalentemente a un átomo de silicio y usa toda su carga disponible en este enlace, siendo por ello mayor la interacción coulombiana con la carga positiva del Si en el tetraedro y menor la distancia de enlace. El BO enlaza dos átomos de silicio (comparte su carga electrónica en dos enlaces covalentes), a la vez que el enlace del NBO con los átomos de potasio es ahora de carácter iónico.
Sistema K2SiO3Este sistema está compuesto por cadenas de tres tetraedros con igual número de NBO y BO (dos por cada tetraedro). En este cristal hay nueve tipos diferentes de átomos de oxígeno, por lo que nos centraremos en uno de ellos para el análisis de carga. La carga en el potasio es 0,74e, siendo por ello casi iónico. La carga en el Si es de 1,72e (0,43e por cada enlace), valor que es menor que los de los dos sistemas anteriores. La carga en el NBO es de -1,08e y en el BO es de -1,10e. Como en el caso del K2Si2O5, el NBO tiene distancia de enlace (0,1617 nm) más corta que el BO (0,1697 nm), por lo que su explicación es la descrita anteriormente.
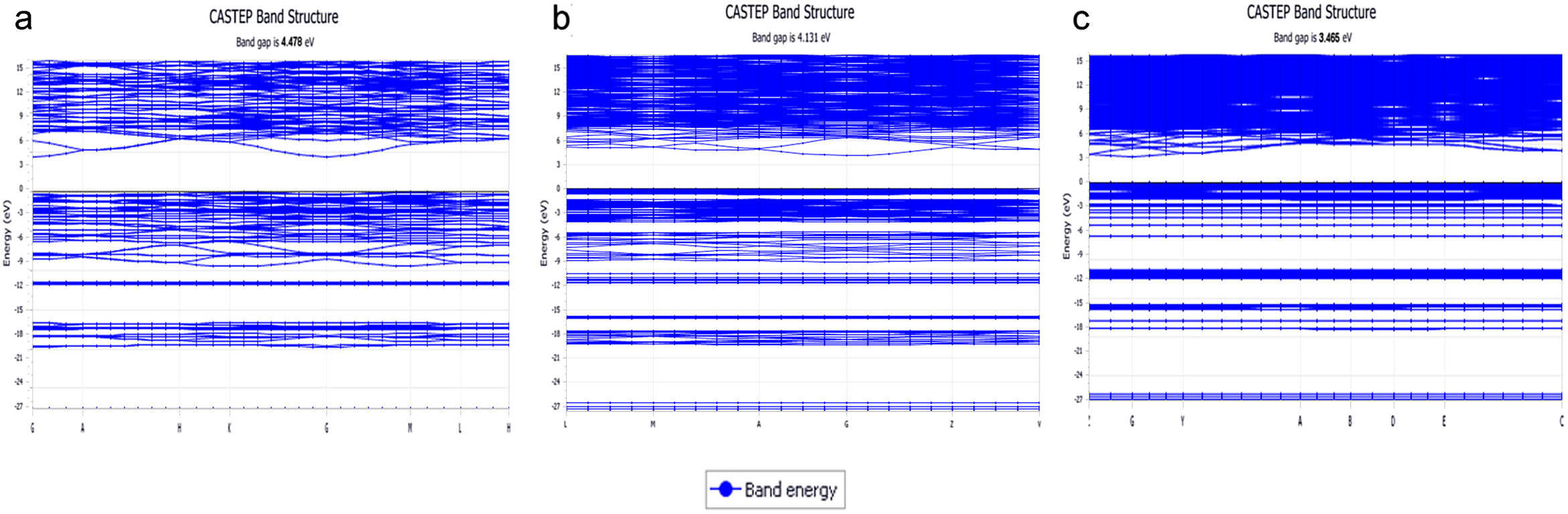
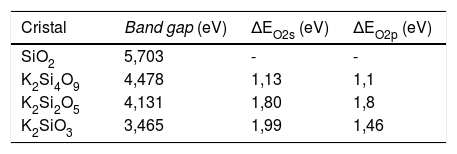
Estructura electrónica de los sistemasEn la fig. 1 se muestran las estructuras de bandas obtenidas para los tres sistemas cristalinos en donde se pueden apreciar los band-gap para cada sistema. En la tabla 3 se muestran los valores del band-gap (eV) para estos tres sistemas, así como los desplazamientos de la densidad de estados de los NBO y BO para las bandas s y p. En esta tabla 3, los valores de ΔEO2s y ΔEO2p corresponden a los desplazamientos de los máximos de la densidad de estados de los NBO respecto a los BO para las bandas s y p, respectivamente. El valor experimental del band gap para el cristal de cuarzo es 8,8 -11,15 eV, si bien correcciones adicionales en la teoría, permiten obtener valores de band gap entre 9,8-10,1 eV [37]. Según los valores del band-gap, se puede comprobar que estos sistemas poseen naturaleza aislante y, además, se observa que el band-gap decrece con el aumento del óxido de potasio en la composición del cristal.
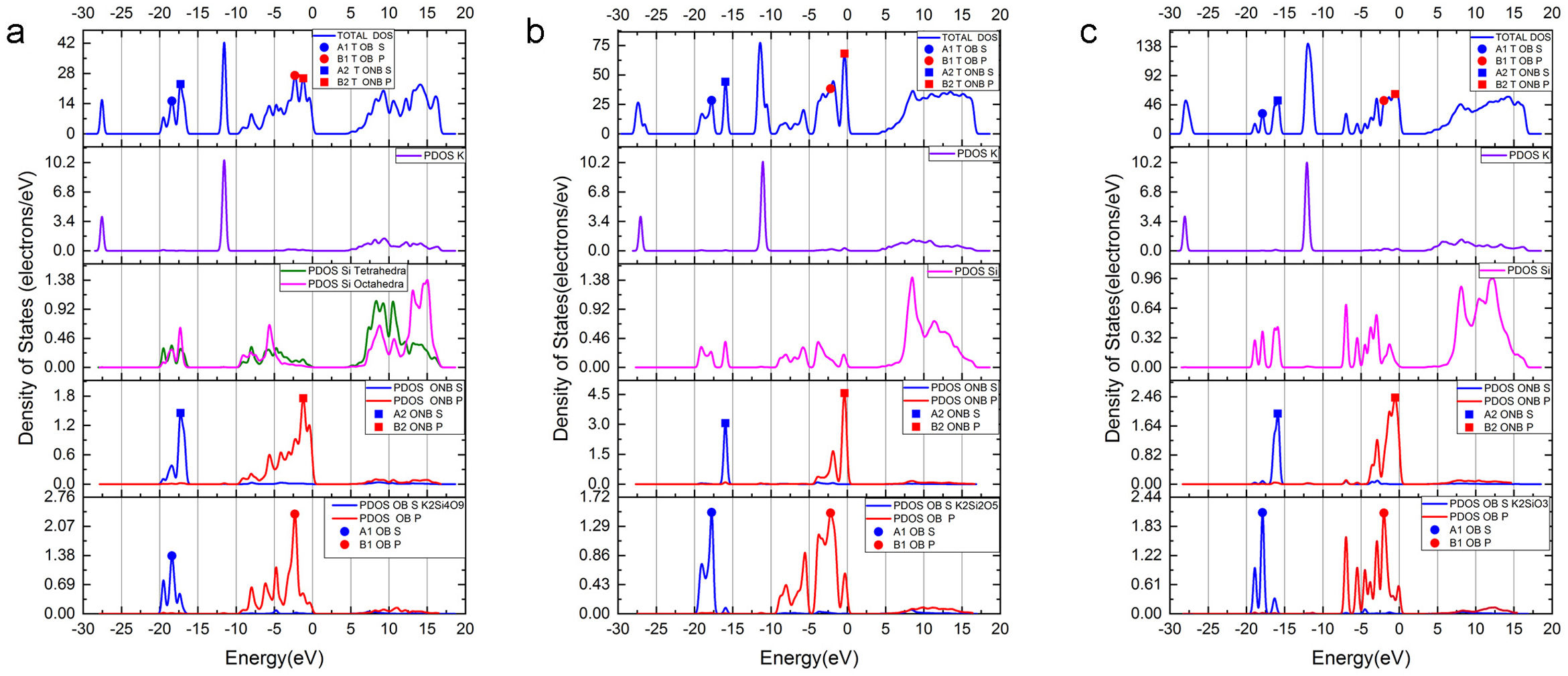
Para los tres sistemas cristalinos estudiados, en los tetraedros el enlace covalente se produce a través de la hibridación de los orbitales Si 3s y Si 3p (orbital híbrido sp3), los cuales forman con los orbitales O 2pz enlaces σ. Estos estados se ubican a la misma energía en la DOS (densidad de estados), indicando la compartición electrónica del enlace covalente. Para el sistema K2Si4O9, la fig. 2 a muestra la densidad de estados total (TDOS) y la densidad de estados parcial (PDOS) para K, Si y O, bien sean NBO o BO. La banda de valencia (VB) superior (entre -13 y 0 eV) está compuesta principalmente de O 2p, Si 3p y K 4s3p, mientras que la VB inferior (entre -30 y -13eV) lo está por O 2s, Si 3s3p y K 3s, observándose que la VB inferior del K 3s aparece muy localizada alrededor de -27.5 eV. La PDOS del oxígeno, ya sea de un NBO como de un BO, muestra una densidad electrónica diferente. Para este caso del K2Si4O9 en la PDOS, los máximos de las bandas 2s y 2p del NBO están desplazados a menores energías (más cerca de la energía de Fermi, 0 eV.), 1,13 eV en el caso de la banda 2s, y 1,1 eV en el caso de las bandas 2p. En la analogía atómica, el desplazamiento a energías menos negativas del pico máximo de la PDOS de NBO respecto BO indica que los niveles de los orbitales 2s y 2p del NBO (y también el orbital 1s) están menos atraídos por el núcleo, es decir tienen una energía de enlace menor que los niveles BO, resultado que está de acuerdo con los datos experimentales obtenidos por XPS para el O 1s[36,38,39].
a) TDOS para el sistema cristalino K2Si4O9 en la parte superior. Hacia abajo las DOS de K, Si, y de NBO y OB. La posición del máximo de la banda s de BO se muestra indicada (A1); b) TDOS para el sistema cristalino K2Si2O5 en la parte superior. Hacia bajo la DOS del K, Si, NBO y BO; c) TDOS para el sistema cristalino K2SiO3 en la parte superior. Hacia abajo la DOS para el K, Si, NBO y BO. El máximo correspondiente a la banda s de NBO se muestra indicado (A2). Para los máximos de la banda p OB (B1) se usa un círculo y NBO (B2) un cuadrado. La posición en energía se detalla en la tabla 4.
En el caso del K2Si2O5, cuyas TDOS y PDOS se muestran en la fig. 2 b, las bandas 2s y 2p de los NBO siguen la misma tendencia que para el K2Si4O9, pero están más localizadas en energía que las de los BO. En este caso, el desplazamiento de las bandas 2s y 2p es de 1,80 eV. Finalmente, para el cristal de K2SiO3, cuyas TDOS y PDOS se muestran en la fig. 2 c, el desplazamiento hacia menores energías de las bandas 2s y 2p es de 1,99 eV y 1,46 eV, respectivamente. Igual que en el caso anterior, las bandas s y p de los NBO están más localizadas en un menor intervalo de energías que las correspondientes del BO, pues como puede observarse para la banda s, los intervalos de eV están entre -20 a -16 eV (es decir 4 eV) para los BO, mientras que para los NBO están entre -17 y -15 (sólo 2 eV), y lo mismo sucede para la banda p (aunque está desplazada a mayor eV respecto a la s). En la fig. 2 se han marcado las posiciones de los máximos de energía (eV) para los NBO y BO de los tres sistemas estudiados. Estos valores de energías se recogen en la tabla 4.
Posición de los picos en la densidad de estados (DOS)
| Cristal | Nombre | Posición del pico máximo (eV) | Tipo de átomo de O | Orbital |
|---|---|---|---|---|
| K2Si4O9 | A1A2B1B2 | -18,39-17,26-2,31-1,21 | BONBOBONBO | 2s2s2p2p |
| K2Si2O5 | A1A2B1B2 | -17,77-15,97-2,18-0,38 | BONBOBONBO | 2s2s2p2p |
| K2SiO3 | A1A2B1B2 | -17,89-15,90-2,00-0,54 | BONBOBONBO | 2s2s2p2p |
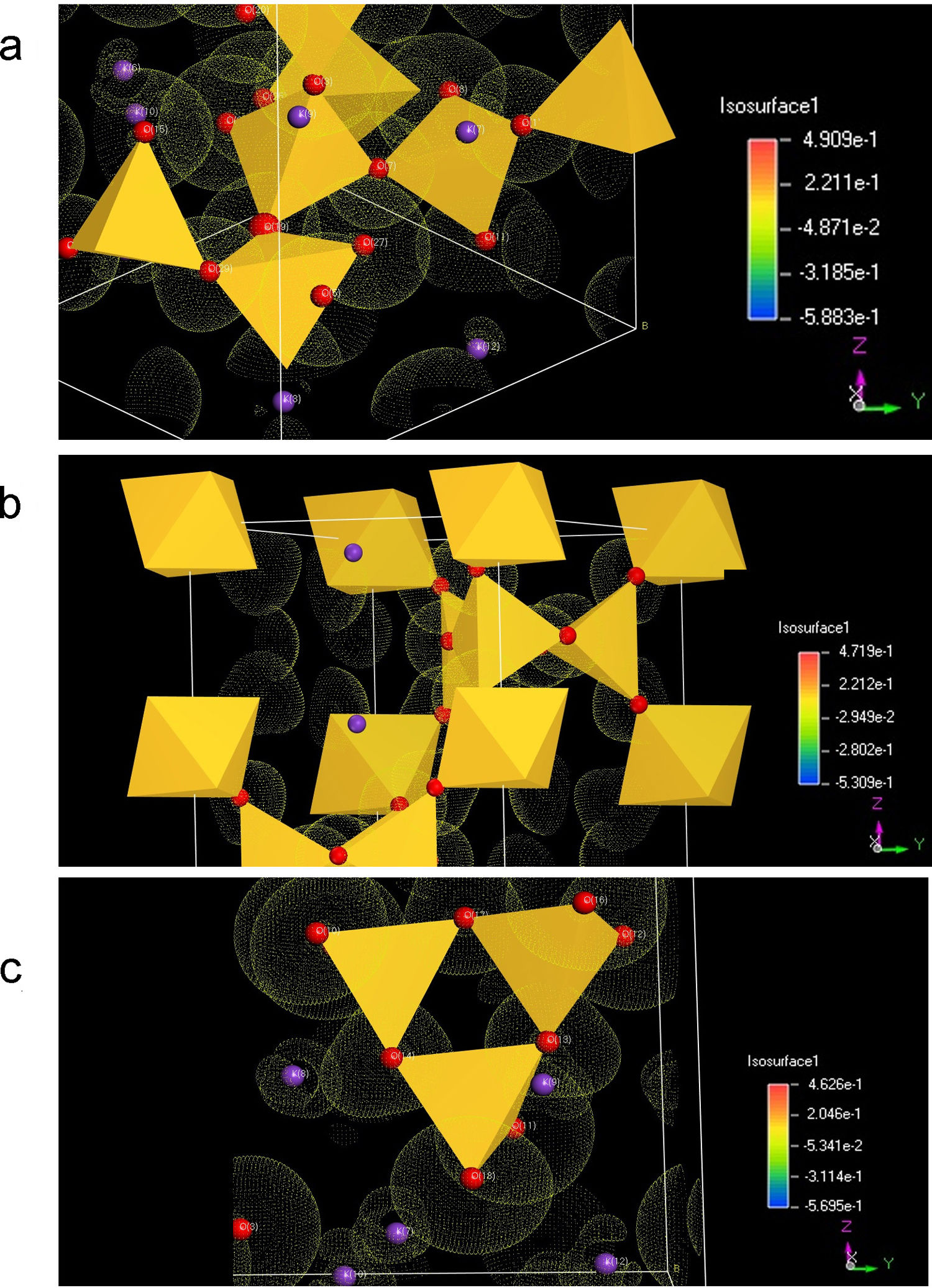
Con base en los resultados de los apartados anteriores, en la fig. 3 se muestran las diferentes de densidades electrónicas para los tres sistemas cristalinos estudiados. En ellas se puede observar que la distribución electrónica es diferente en los BO respecto a los NBO, a la vez que los átomos de K tienen interacción preferente con los NBO, aunque la nube electrónica también solapa con los BO, es decir que existe cierto nivel de interacción entre ellos. Respecto al sistema K2Si2O5 que se muestra en la fig. 3 b, se observa que la nube electrónica asociada a los NBO es bastante esférica. Y, finalmente, en el sistema K2SiO3 (fig. 3 c) se observa que el NBO posee simetría esférica, mientras que el BO posee una forma distorsionada de la densidad electrónica. A su vez, los átomos de K solapan con los NBO.
Los resultados mostrados en la fig. 3 están de acuerdo a con lo descrito por Nesbitt et. al. [38] para materiales de silicato de sodio. Estos autores estudiaron la transferencia de electrones 3s desde los átomos de Na a los NBO para dar lugar a Na+ y NBO-, y encontraron que se producía una transferencia razonable desde una perspectiva del enlace iónico para producir octetos estables en los núcleos de Na y O (configuración de gas noble). A su vez, utilizando la técnica XPS, Zakaznova-Herzog et al. [39,40] estudiaron la banda de valencia tanto en olivinos como en piroxenos y confirmaron la transferencia casi completa de los electrones del orbital s del metal a los orbitales 2p del O. En este sentido en silicatos de potasio Nesbitt, et al. [38] también emplearon la teoría del enlace de valencia y la hibridación de orbitales atómicos para proponer un mecanismo de deslocalización de la carga sobre el tetraedro de Si. Esto significa que el electrón 4s del átomo de K se transfiere a un orbital de valencia 2p de un NBO, aumentando la densidad de electrones sobre este NBO y, también parte de la carga transferida se redistribuye al Si y a los otros átomos de BO a través de los cuatro orbitales de hibridación sp3 (hibridación de los orbitales Si 3s y los 3 orbitales 3p).
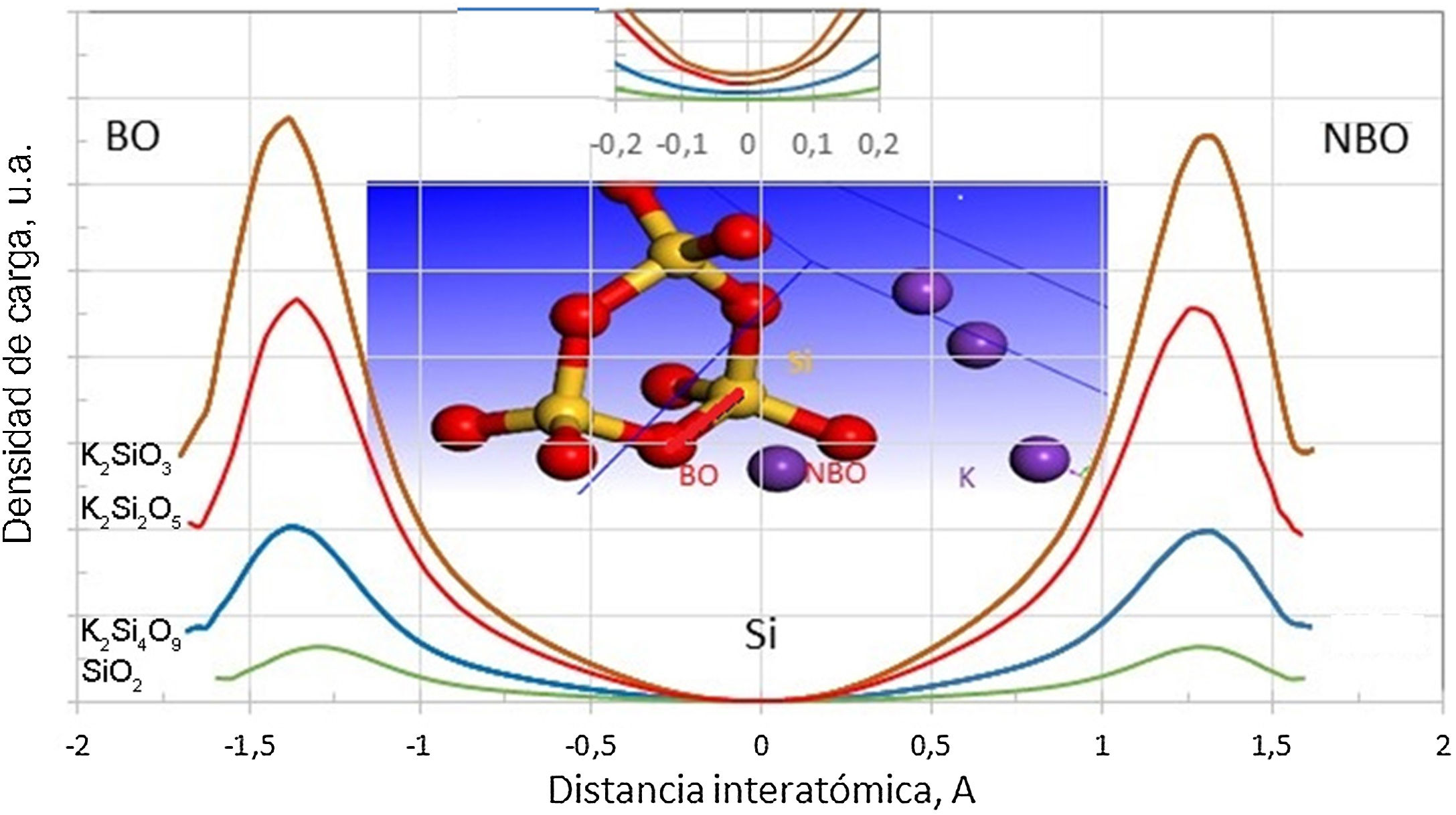
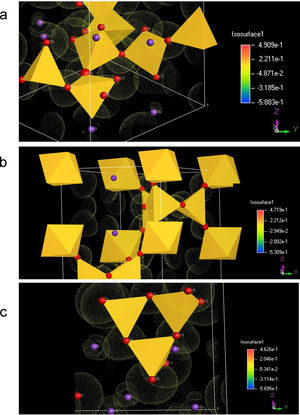
Esta redistribución de carga para los silicatos de potasio estudiados en este trabajo se puede observar en la fig. 4, en la que se muestra el perfil de distribución de carga de electrones de valencia a lo largo de la dirección de enlace BO-Si-NBO. La carga neta sobre el catión Si es 2,38e para el cuarzo y decreciente para los demás sistemas. La carga electronica, por lo tanto, es menor sobre el Si del cuarzo, como lo muestra el recuadro insertado de la fig. 4. A mayor contenido de K, mayor será la carga redistribuida sobre los átomos del tetraedro conformado por BO, Si y NBO. Una mayor densidad electrónica de valencia hace que el átomo central (Si) llegue a ser menos positivo, lo que disminuye las fuerzas de interacción coulómbicas entre los átomos de Si y O, debilitando el enlace Si-O. En la fig. 4 también se puede apreciar que la distancia atómica de la unión covalente de Si-BO es mayor cuanto mayor es el contenido de K2O en el silicato.
Una vez analizadas las estructuras electrónicas para los tres sistemas estudiados, es posible calcular, a partir de ellas, las diferentes constantes elásticas de los correspondientes materiales. El número de estas constantes generalmente depende de las propiedades de simetría de la clase de cristal. El programa CASTEP obtiene los valores de las constantes elásticas, sometiendo a la celda cristalina un número apropiado de patrones de deformación y, posteriormente, optimiza y ajusta la energía total asociada con cada patrón de deformación [25]. Teniendo en cuenta que el K2SiO3 y K2Si2O5 poseen estructuras monoclínicas y el K2Si4O9 hexagonal, es posible obtener 13 y nueve constantes Cij para las estructuras monoclínica y hexagonal, respectivamente. Estas constantes elásticas se resumen en la tabla 5. Valores similares han sido obtenidos por Plucinski et al. para vidrios de silicato, en los que la densidad y el factor de empaquetamiento estructural pueden ser descritos de forma adecuada a modelos simulados [19].
Constantes elásticas para los cristales de silicato de potasio
| Especie | Cij(GPa) | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| C11 | C12 | C13 | C15 | C22 | C23 | C25 | C33 | C35 | C44 | C46 | C55 | C66 | |
| K2SiO3 | 82,9 | 24,4 | 26,4 | -9,2 | 58,5 | 26,6 | 1,12 | 66,5 | 1,3 | 17,7 | 1,5 | 15,2 | 16,0 |
| K2Si2O5 | 69,5 | 26,8 | 22,0 | 7,9 | 91,6 | 20,6 | 3,4 | 83,5 | 10,1 | 27,8 | 3,7 | 30,2 | 34,2 |
| K2Si4O9 | 162,3 | 28,7 | 53,1 | 162,3 | 53,1 | 259,6 | 43,1 | 43,1 | 66,8 | ||||
Para el cristal hexagonal, las cinco constantes elásticas Cij (C11, C12, C13, C33 y C44) deben satisfacer las siguientes desigualdades: C11 > 0, (C11-C12) > 0, C44 > 0 y (C11 + C12) C33 – 2 C212) > 0, hecho que indica que este cristal es mecánicamente estable. En este sentido, la matriz de constantes elásticas obtenidas para el K2Si2O5 y K2Si4O9 (tabla 5) tiene valores positivos, hecho que prueba que, tal y como se ha mencionado anteriormente, ambos materiales poseen estructuras mecánicamente estables. Sin embargo, en la matriz de constantes elásticas del K2SiO3, C15 es negative, indicando que el K2SiO3 podría ser en cierto grado inestable mecánicamente.
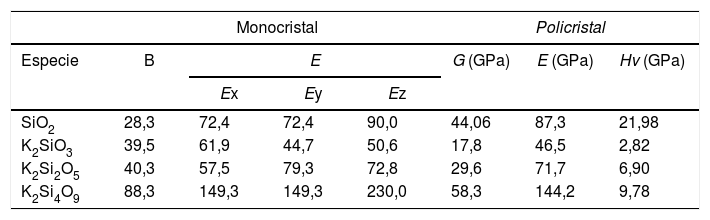
Las constantes elásticas (C11 o C33) están relacionadas con la resistencia de la dirección a o c en la compresión lineal. Para el K2Si4O9, C33 es mayor que C11, lo que implica que el eje c es menos compresible que el eje a. Un mayor valor de la constante elástica C44 significa una mayor capacidad para resistir la deformación de cizalladura. Además, la constante elástica C44 también es un parámetro importante que controla indirectamente la dureza del material. Los valores de los módulos de B, E y G se calculan a partir de estas constantes elásticas y se recogen en la tabla 6. El K2Si4O9 tiene el mayor C44 y, además, tiene los mayores valores de los módulos B y G, por lo que presenta una mayor dureza respecto a los otros cristales de silicato.
Módulos B (GPa), E (GPa), G (GPa) y dureza Hv (GPa) para sistemas cristalinos obtenidos mediante DFT
| Monocristal | Policristal | ||||||
|---|---|---|---|---|---|---|---|
| Especie | B | E | G (GPa) | E (GPa) | Hv (GPa) | ||
| Ex | Ey | Ez | |||||
| SiO2 | 28,3 | 72,4 | 72,4 | 90,0 | 44,06 | 87,3 | 21,98 |
| K2SiO3 | 39,5 | 61,9 | 44,7 | 50,6 | 17,8 | 46,5 | 2,82 |
| K2Si2O5 | 40,3 | 57,5 | 79,3 | 72,8 | 29,6 | 71,7 | 6,90 |
| K2Si4O9 | 88,3 | 149,3 | 149,3 | 230,0 | 58,3 | 144,2 | 9,78 |
Como se muestra en la tabla 6, el módulo B calculado para el K2SiO3, K2Si2O5 y K2Si4O9 es 39,5 GPa, 40,3 GPa y 88,3 GPa, respectivamente. Los valores obtenidos de B indican que el K2SiO3 (B = 39,5 GPa) es más compresible que el K2Si4O9 (B = 88,3 GPa). Dado que las estructuras monoclínica y hexagonal tienen una simetría inferior, en comparación con la estructura cúbica, los módulos E de los silicatos estudiados presentan anisotropía en los planos x-y, y-z y x-z, por lo que los valores de E calculados a lo largo de los ejes x, y, z son diferentes. Para el K2Si4O9 es 57,5, 79,3 y 72,8 GPa a lo largo de los ejes x, y, z, respectivamente, mientras que para el K2Si4O9 es 149,3, 149,3 y 230 GPa, respectivamente.
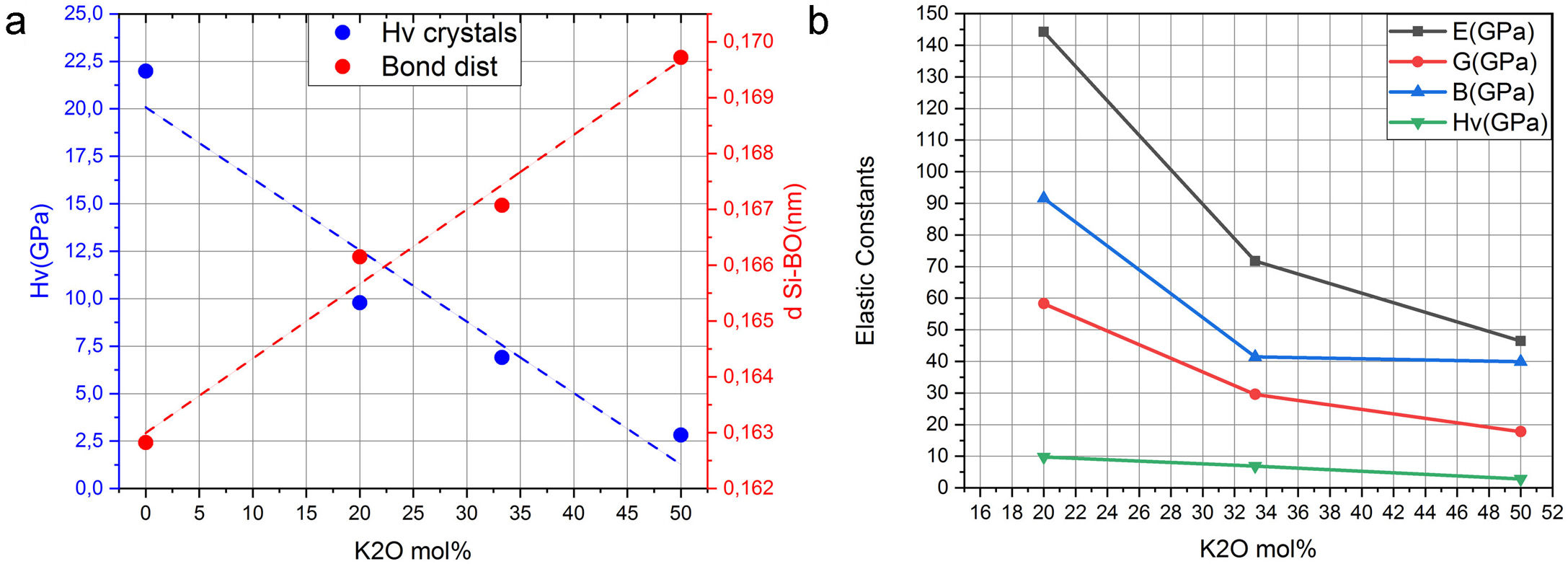
Es bien conocido que en el enlace covalente Si-O son los BO los que fundamentalmente definen la fuerza de los sistemas cristalinos de silicato de potasio. Este hecho puede comprobarse a partir de los datos recogidos en la tabla 2, en la que los valores de la carga en el Si tetraédrico disminuyen al aumentar el contenido en K. Además, en la tabla 1 se muestran los valores de las distancias de los enlaces Si-O para los NBO y BO, observándose que para los BO dichas distancias tienden a aumentar con el contenido en K. Ambos factores, carga y distancia de enlace, determinan la dureza del material. Mediante el software CASTEP es posible predecir los valores de la resistencia (Hv, B, E y G) de un material para una estructura cristalina determinada. Los resultados obtenidos para los sistemas estudiados en este trabajo se muestran en la fig. 5, donde se puede apreciar que al aumentar la distancia de enlace Si-O, la cual a su vez aumenta con el contenido en K, da lugar a una disminución tanto Hv como de los módulos B, E y G del material, es decir que, a mayor fuerza del enlace covalente, menor distancia de enlace Si-BO y mayor es la resistencia mecánica del material. A su vez se puede observar en la fig. 5 b que al aumentar el contenido en K2O disminuyen las propiedades mecánicas (Hv, G, E y B) del material, hecho que está correlacionado con el aumento de los NBO, como se ha demostrado anteriormente
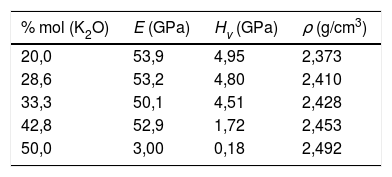
Sistemas vítreosConstantes elásticasUna vez analizados los sistemas cristalinos por el procedimiento DFT y habiendo calculado la relación entre su composición química y los NBO (o lo que es lo mismo, Qn) presentes en dichos sistemas y las distintas propiedades mecánicas de los mismos, el paso siguiente ha sido la comparación con vidrios y, en concreto, con vidrios de silicato de potasio. Los valores de Hv medidos experimentalmente para las muestras de vidrio de silicato de potasio estudiadas se recogen en la tabla 7. Se puede comprobar que al aumentar el contenido de K2O en la composición del vidrio, la microdureza disminuye de 4,95 a 0,18 GPa, aunque a 33,3% mol de K2O se observa un ligero incremento hasta 5,00 GPa. Valores similares han sido obtenidos por otros autores, bien sea de forma experimental [5] o de forma teórica, utilizando dinámica molecular [11].
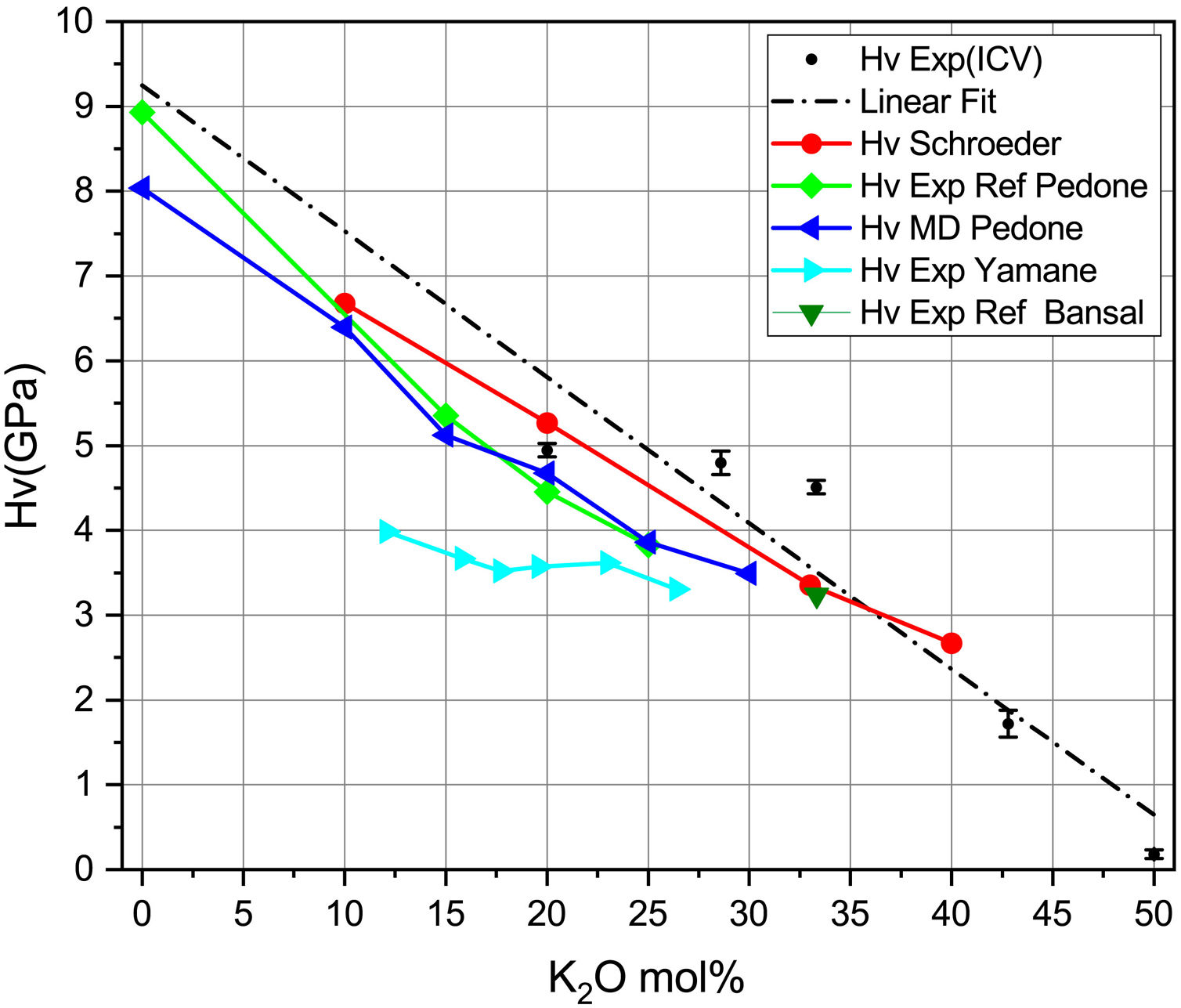
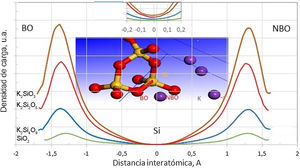
En la fig. 6 se representan los valores experimentales y teóricos para vidrios de silicato de potasio obtenidos a partir de diferentes publicaciones, junto con los obtenidos en este trabajo (tabla 7). En la fig. 6 se presentan, como puntos marcados con HV exp, las medidas experimentales y, en línea de puntos (linear fit), su ajuste lineal. Se presenta también la dureza Vickers calculada con la Eq 2 y los datos experimentales de las constantes elásticas de Schroeder [5] (HV Schroeder), los datos experimentales de las constantes elásticas según Pedone [11] (HV Exp Ref Pedone) y sus módulos elásticos calculados por dinámica molecular y la dureza calculada con la Eq 2. (HV MD Pedone), los Hv experimentales de Yamane [41] (HV Exp Yamane) y los Hv experimentales referidos en el libro de Bansal [6] (HV Exp Ref Bansal). Se puede comprobar cómo los resultados son bastante similares entre los diferentes trabajos, ya sean teóricos o experimentales, lo que corrobora la posibilidad del cálculo de las propiedades mecánicas mediante métodos teóricos.
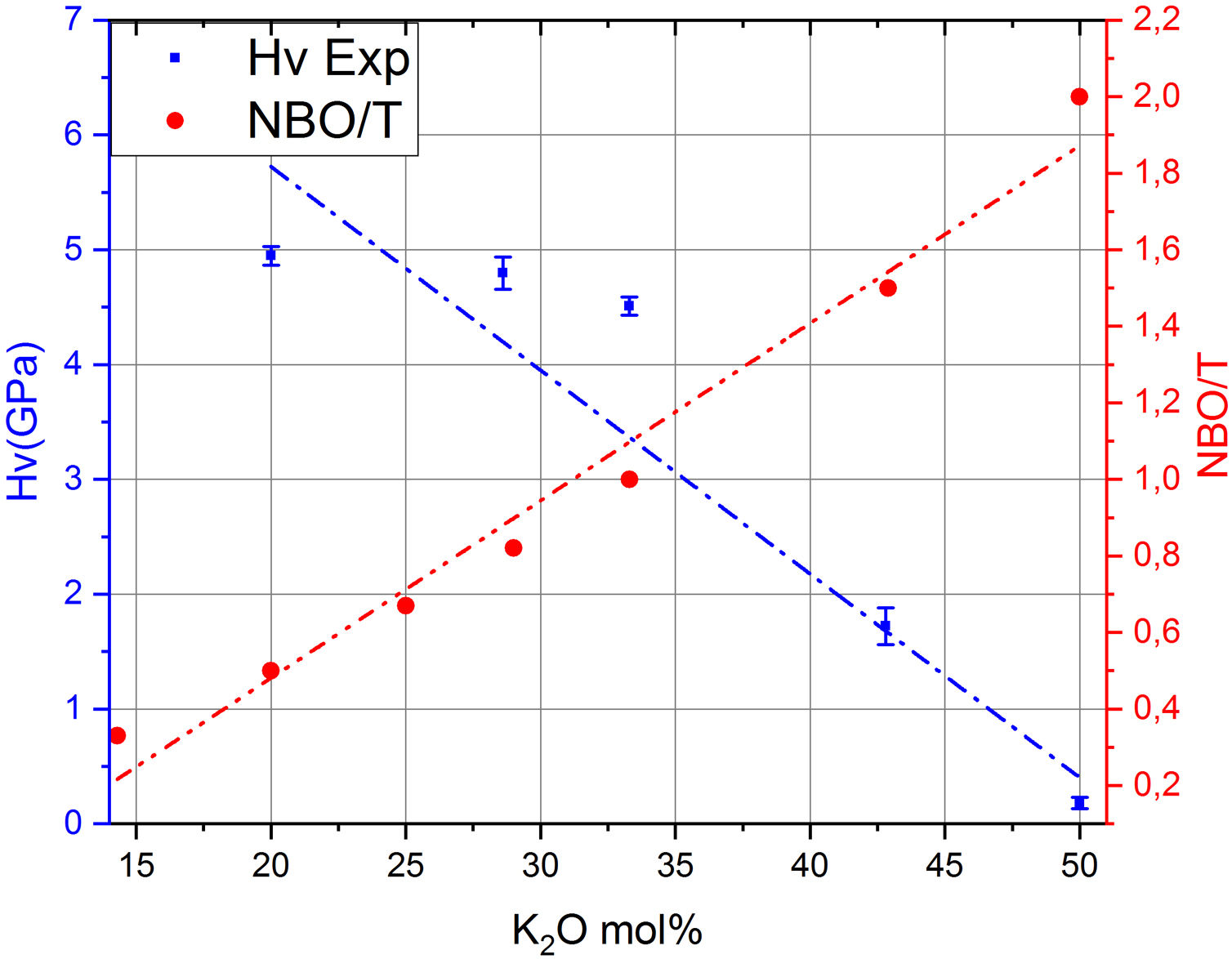
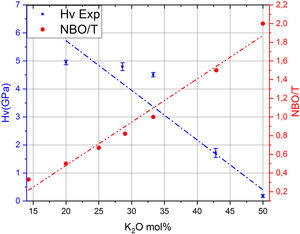
Por otro lado, en la fig. 7 se muestran los valores de Hv en función del contenido en K2O y de los correspondientes NBO para los vidrios obtenidos en este trabajo, pudiéndose observar que la relación NBO/T es un parámetro muy útil para predecir cualitativamente la microdureza de los vidrios de silicato. Así, se puede comprobar que la adición del óxido modificador K al vidrio aumenta la relación NBO/T es decir, disminuye el grado de polimerización o conectividad de la red de vidrio debido a la ruptura de los enlaces Si-O-Si y, dado que los enlaces covalentes Si-O-Si constituyen los enlaces más fuertes en el vidrio de silicato, la fuerza de enlace promedio disminuye cuando NBO/T aumenta, los enlaces se debilitan y las uniones Si-BO aumentan en distancia y, todo esto en conjunto explica la disminución de Hv observada en los vidrios estudiados. No obstante, es preciso tener en cuenta los trabajos de Smedskjaer et al. [9], quienes indican que esta correlación entre NBO/T y Hv no es válida para todos los sistemas de vidrio de silicato, especialmente cuando hay presentes varios elementos modificadores.
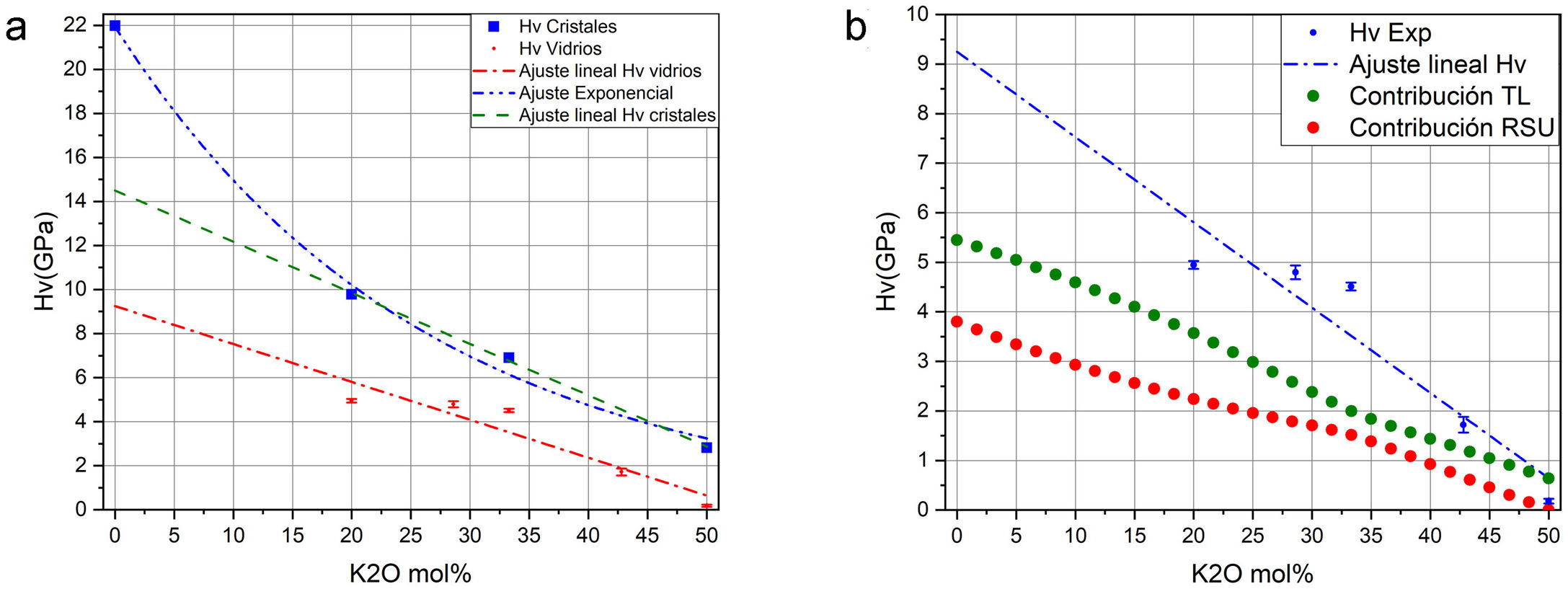
Como se puede observar en la fig. 7, la cantidad de NBO influye directamente en la resistencia del vidrio. Dado que, tanto para materiales cristalinos como para vidrios, la cantidad de NBO puede ser calculada mediante la Eq 1, para un mismo contenido en óxido alcalino en un vidrio o en un cristal, la concentración de NBO debe ser la misma ya que ésta depende de la concentración del óxido alcalino. Tal y como se indicó anteriormente, los NBO pueden ser descritos por las distintas unidades estructurales Qn (n = 0-3), presentes en la estructura vítrea o cristalina; sin embargo, mediante RMN Si29 se observó que mientras los cristales de silicatos típicamente contienen sólo una especie Qn (Q2 y Q3 para los cristales de metasilicato y disilicato de potasio, respectivamente) [42,43], en el caso de sus vidrios correspondientes, es decir con el mismo contenido en óxido alcalino, los vidrios contienen una mezcla de especies Qn, mayoritariamente de Q2 para el vidrio de 50% mol K2O y de Q3 para el de 33,3% mol de K2O [20]. Esta diferencia entre cristales y vidrios se ha comprobado en diferentes trabajos como los de Anlin et al. [43] y Kalampounias [44], los cuales utilizaron la espectroscopía Raman para estudiar los modos de vibración de las unidades estructurales de los cristales de silicato de potasio (metasilicato y disilicato) y de sus correspondientes vidrios. En dichos trabajos encontraron que las diferentes unidades estructurales Qn de los cristales coexisten en los vidrios de silicato. También en los mismos estudios observaron que los modos de tensión en Raman (entre 900 y 1.100 cm-1) de los enlaces de corto alcance Si-O del cristal coinciden con los de su vidrio correspondiente, con un ligero desplazamiento y ensanchamiento de las bandas de vibración debido al desorden estructural a medio y largo alcance existente en el vidrio. Por otro lado, en diferentes publicaciones que han utilizado la RMN Si29 se dan las concentraciones de especies Qn para vidrios de silicato de sodio o potasio, en función del contenido en alcalino [5,20,36] y se ha comprobado que la concentración de dichas especies coincide con las predicciones realizadas mediante mecánica estadística y dinámica molecular [9]. En la fig. 8 a, se representa Hv en función del contenido en K2O, tanto para cristales de SiO2-K2O (según los cálculos realizados mediante DFT mostrados en la fig. 5a) como para los vidrios obtenidos en este trabajo. Aunque la concentración de NBO, tanto en los cristales como en los vidrios es la misma, sin embargo, y como era de esperar, se observa una gran diferencia entre dichos valores, pero también se aprecia que la evolución de Hv es similar para ambos tipos de materiales. En un principio, esta diferencia entre los valores de Hv de cristales y vidrio se atribuyó la no existencia del orden a medio y largo alcance de los vidrios, y que por lo tanto, dicha diferencia podría ser calculada a partir de aproximaciones basadas en propiedades de la escala atómica, es decir propiedades de los átomos y sus enlaces (energía de enlace, ángulo de enlace, densidad de empaquetamiento, etc.) [8,45]; sin embargo, se ha comprobado que es necesario incluir otras propiedades basadas en la escala molecular como son la presencia de anillos y otras superestructuras. Estos nuevos tipos de unidades estructurales han sido consideradas por Sidebottom [12] como formadoras de un orden de alcance intermedio (IRO) existente en el vidrio y que por ello deben ser tenidas en cuenta para los cálculos de las propiedades mecánicas del mismo.
La presencia de estos tipos de unidades estructurales se basa en resultados obtenidos con diferentes técnicas de análisis como las espectroscopías Raman, IR y RMN-Si29. Así, mediante espectroscopía Raman, Anlin et al. [43], entre otros, mostraron que en el intervalo de bajas frecuencias (entre 200 y 650 cm-1), las bandas de los espectros presentaban variaciones asociadas con la flexión del enlace Si-O-Si y con la formación de anillos de tres o cuatro tetraedros de Si (es decir, existe orden a alcance intermedio), a la vez que también encontraron que existía una amplia distribución de longitudes y ángulos de enlace y que éstos tenían una dependencia con la historia térmica de cada vidrio. Simakin et al., utilizando la espectroscopía IR, describieron la existencia de anillos de tres, cuatro y seis miembros [22] y McMillan et al. [21] utilizando RMN-Si29 propusieron, además, la existencia de supertetraedros, cadenas de tetraedros y anillos unidos por caras. Todas estas superestructuras existentes en un orden de alcance intermedio han sido clasificadas por Sidebottom dentro de un grupo denominado como unidades estructurales rígidas (RSU) que, junto con los tetraedros libres de SiO4 (free tetrahedra) conformarían la estructura general vítrea [46]. A partir de estas consideraciones, las diferencias existentes entre los valores de Hv de cristales y vidrios observadas en la fig. 8 a tienen que ser debidas a las citadas superestructuras existentes en el vidrio. En este sentido se puede considerar que:
Es decir, la dureza Vickers de los vidrios, HVGlassExp, medida experimentalmente, es suma de la contribución a la dureza Vickers de los tetraedros libres, HVTFree, más la contribución de la dureza Vickers de las RSUs, HVRSU. Los tetraedros libres son todas las unidades SiO4 existentes en el vidrio, las cuales tienen diferentes NBO y, por lo tanto, Qn, en función de la concentración del óxido alcalino y que puede ser calculada a partir de la Eq 1.
Según los resultados obtenidos para cristales utilizando DFT y la relación entre los Qn y la microdureza (fig. 5), es posible calcular la contribución a la dureza Vickers que está asociada con los tetraedros libres, es decir:
Donde fF es la fracción de tetraedros libres en el vidrio para cada composición molar, cuyos valores están dados por diferentes autores [20] y FA es el factor que relaciona los valores de Hv calculados y los Hv experimentales. A partir de la Eq 4 es posible despejar HvRSU para obtener la contribución de las superestructuras a la microdureza del vidrio y en la fig. 8 b se muestran los resultados obtenidos. En estos cálculos hay que tener en cuenta el valor de HvTfree, ya que dicho valor influye directamente en los resultados obtenidos. Los valores de HvTfree para el cuarzo varían desde 21.9 GPa, según los cálculos teóricos del programa CASTEP, a 16.7 GPa o 13.9 GPa, según el plano del cristal de cuarzo medido experimentalmente [47]. Teniendo en cuenta estas consideraciones, y tras un análisis detallado de todos los posibles valores de Hv del cuarzo encontrados en la bibliografía, es difícil definir un valor único para la HvTfree. Sin embargo, en este trabajo se ha elegido 16.31 GPa como el valor más adecuado, que es prácticamente el promedio de todos los valores anteriormente mencionados y que es el que se obtiene a partir de los datos que proporciona R. Bechmann [48]. Para confirmar la validez de este valor elegido, se ha realizado la extrapolación mediante ajuste lineal de los puntos teóricos obtenidos con el CASTEP para cristales de SiO2-K2O cuando la concentración de K2O es nula (es decir, un cristal de SiO2) y el valor obtenido es 14.50 GPa, tal como se muestra en la fig. 8 a.
En la fig. 8 b se muestra la variación de la microdureza de los vidrios estudiados y las contribuciones a dicha microdureza, tanto de los tetraedros libres (orden a corto alcance) como de las unidades RSU. Puede comprobarse cómo los tetraedros libres contribuyen más que las unidades RSU a la microdureza del vidrio, si bien a partir de una concentración alrededor del 33% de óxido modificador (K2O en este estudio) ambas contribuciones son muy parecidas, aunque siempre la correspondiente a la de los tetraedros libres es superior. Todos estos estudios sirven para corroborar que para materiales de vidrio, la dureza está relacionada con su estructura [34]. Dado que hay pocos trabajos que hayan intentado relacionar las propiedades de los cristales con las de los vidrios correspondientes, el aporte de nuestro trabajo es que se emplean resultados experimentales determinados en vidrios y cristales de silicato y mostramos que las propiedades de los cristales contribuyen a explicar la dureza Vickers de los vidrios.
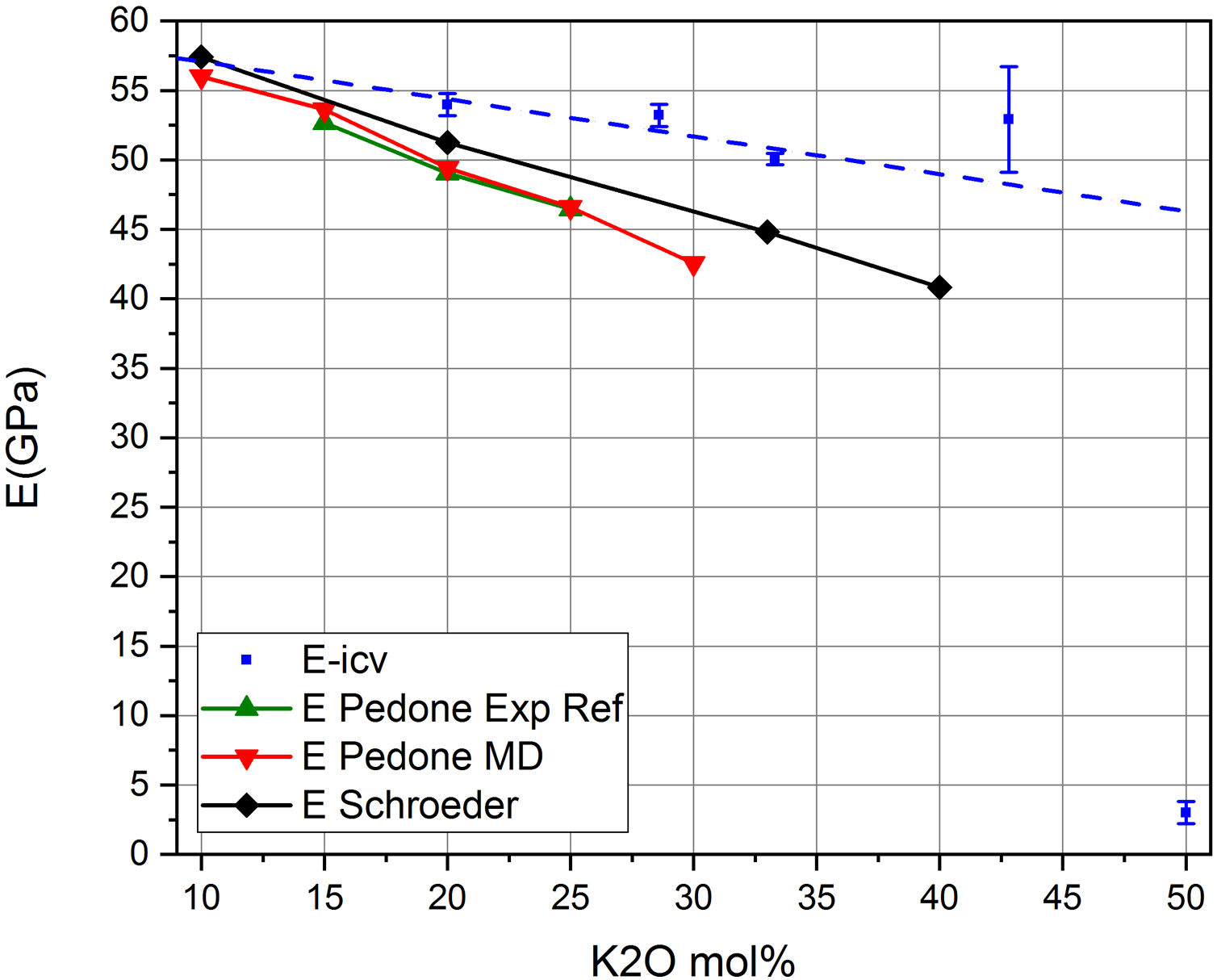
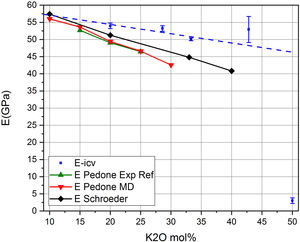
Finalmente, en la fig. 9 se muestra la relación entre el módulo E y el contenido en alcalino en el vidrio, y por lo tanto, con sus valores de NBO y de Qn. Se muestran las medidas experimentales obtenidas en los vidrios preparados, E-icv, las medidas recogidas en los trabajos de Schroeder [5] (E-Schroeder), la referencia experimental de Pedone [11] (E-Pedone Exp Eef) y el valor teórico calculado por la dinámica molecular de Pedone [11] (E-Pedone MD). También se muestra la contribución al módulo E, tanto de los tetraedros libres como de las RSU. Puede comprobarse que esta relación similar obtenida para sistemas cristalinos (fig. 5 b) y que la variación observada es análoga a la mostrada en las fig. 7 y fig. 8 a para sistemas vítreos, es decir que en todos los casos, a medida que aumenta el contenido en NBO, en el vidrio disminuye el módulo elástico. Por otro lado, aplicando las ecuaciones Eq 4 a Eq 6, pero en este caso para el módulo E es posible calcular las correspondientes contribuciones de los tetraedros libres y de las unidades RSU, observándose que mientras que la contribución de los tetraedros libres disminuye, la de las unidades RSU aumenta con la concentración de K2O en el vidrio.
ConclusionesEn este trabajo se ha demostrado que realizando un estudio basado en primeros principios con el software CASTEP de Materials Studio y usando el funcional GGA-PBE permite el cálculo de la estructura electrónica de cristales de silicato de potasio. La magnitud del enlace covalente Si-BO define la fuerza de los sistemas cristalinos de silicato de potasio, disminuyendo al aumentar el contenido de óxido de potasio. El software CASTEP se ha usado para calcular las constantes elásticas de estos materiales cristalinos. A mayor contenido de óxido de potasio, mayor es la distancia de enlace Si-BO, lo que disminuye la fuerza del enlace covalente en los tetraedros, y por tanto un menor módulo de Young y menor dureza Vickers.
Para los vidrios de silicatos de potasio, las medidas experimentales del módulo de Young y de la dureza Vickers muestran la misma tendencia que para los cristales respecto a la variación con el contenido de K2O, esto es, que a mayor contenido de K2O menor es el módulo de Young y la dureza. En el silicato de potasio, la presencia de este óxido despolimeriza la red de sílice, por lo que al aumentar el contenido de K2O se incrementa la formación de NBO, disminuyendo por tanto la conectividad de la red y su correspondiente dureza Vickers.
Las interacciones de corto alcance en cristales y vidrios son similares, esto significa que los comportamientos de la carga atómica y las distancias de enlace Si-O calculadas para los cristales se conserven en los vidrios. Sin embargo, al aplicar estos cálculos a la estructura de los vidrios estudiados se comprueba que suponiendo una estructura basada en tetraedros libres (con sus NBO y respectivas Qn), es decir asumiendo un orden a corto alcance, los valores de las propiedades mecánicas son inferiores a lo esperado. De esta forma ha sido necesario incorporar nuevas superestructuras (estructuras no rígidas) para que los valores experimentales coincidieran con los teóricos. Estas superestructuras son consideradas como un orden a alcance intermedio y en ellas tiene lugar una amplia distribución de los ángulos Si-O-Si y O-Si-O, formación de anillos de tres y cuatro tetraedros y otros tipos de superestructuras. El método mostrado en este trabajo hace posible el uso de la estructura cristalina, mucho más sencilla, para evaluar las interacciones de corto alcance, la carga electrónica y su redistribución en el sistema, esencial para comprender las propiedades mecánicas de cristales y ayudar a comprender la estructura de los vidrios y, entre ellas la dureza Vickers.