The kinetics of the thermally induced glass / crystal phase transformation of chalcogenide glasses plays an important role in determining their candidacy for optical phase change memory applications. The rate of crystallization and the corresponding activation energy are the two crucial kinetic parameters that reflect the durability and quality (i.e., storage properties) of phase change materials. This script deals with metal-induced effects on thermally regulated non-isothermal crystallization in a new glass alloy of Se-Te-Sn using calorimetric measurements. The elements Antimony (Sb), Cadmium (Cd) and Indium (In) have been used as structural modifiers for this purpose. The crystallization and glass transition kinetics of these glass alloys have been investigated by thermal analysis of several kinetic parameters such as the parameter of order n, the maximum crystallization temperature Tc, the crystallization rate K and the consequent activation energy Ec). A DSC is used in non-isothermal mode for the present studies. The values of the activation energy Ec are determined using the data obtained from the displacement of the exothermic peaks of crystallization in non-isothermal DSC plots at various heating rates. The role of the additives Sb, Cd and In in the variation in the rate of crystallization K of and the Avrami index (n) for each glass alloy is also examined. Detailed thermal analysis of the kinetic data confirms the superiority of Cd over the other two additives (In and Sb) for optimization of the kinetic properties of the main SeTeSn glass.
La cinética de la transformación de fase vidrio/cristal inducida térmicamente de los vidrios calcogenuros desempeña un papel importante en la determinación de su candidatura para las aplicaciones de memoria óptica de cambio de fase. La tasa de cristalización y la energía de activación correspondiente son los dos parámetros cinéticos cruciales que reflejan la durabilidad y la calidad (es decir, las propiedades de almacenamiento) de los materiales de cambio de fase.
El presente guión trata de los efectos inducidos por metales sobre la cristalización no isotérmica regulada térmicamente en una nueva aleación vítrea de Se-Te-Sn, utilizando mediciones calorimétricas. Los elementos antimonio (Sb), cadmio (Cd) e indio (In) se han empleado como modificadores estructurales para este propósito. La cinética de cristalización y transición vítrea de estas aleaciones de vidrio se ha investigado mediante el análisis térmico de varios parámetros cinéticos como el de orden n, la temperatura máxima de cristalización (Tc), la velocidad de cristalización (K) y la energía de activación consiguiente (Ec). Se usa un DSC en modo no isotérmico para los presentes estudios. Los valores de la energía de activación Ec se determinan utilizando los datos obtenidos del desplazamiento de los picos exotérmicos de cristalización en gráficos de DSC no isotérmicos a diversas velocidades de calentamiento. También se examina el papel de los aditivos Sb, Cd e In en la variación en la K y el índice de Avrami (n) para cada aleación vítrea. El análisis térmico detallado de los datos cinéticos confirma la superioridad del Cd sobre los otros dos aditivos (In y Sb) para la optimización de las propiedades cinéticas del vidrio principal Se-Te-Sn.
The phase change effects in chalcogenide glasses (ChGs) are attractive for scientific and technological applications in the area of optoelectronics [1–4]. The structural changes that take place in the course of the amorphous-to-crystal transition are an interesting issue in modern physics. In this regard, the devitrification process should be slow to obtain high-class chalcogenide glasses because of their wide applications in the fabrication of optical fibers, waveguides, and optical elements and lenses. On the other hand, it should be fast during the erasing process in phase-change optical recording in CDs and DVDs [2,3]. Thus, the study of crystallization kinetics of newly developed multi-component glasses has become a basic requirement for their use in the expertise behind the device fabrication like phase change optical and electrical memories [4].
The atomic arrangements behind the phase-change mechanism in phase change materials based on ChGs are still uncertain. This is a serious hindrance to their utilization with full competency [5]. Crystallization kinetics plays an important role to help in this direction. A systematic understanding of the crystallization kinetics might also contribute to the breakthrough of novel and future materials. In particular, the awareness of kinematic of crystallization helps us in understanding the character of the concerned mechanisms. Also, it might endow with information about the crystalline framework, forecasts of devitrification behavior under incredible or unique experimental conditions. Moreover, proper knowledge of the mechanism involved in devitrification also reveals the functioning of specific elements in the molecular arrangements. This allows us the well-planned and efficient tailoring of innovative materials. In literature, various papers on the physical properties of various binary Se-Te and ternary SeTeM glassy semiconducting alloys are available [6–12]. Tripathi and Kumar studied the role of Cd, In, and Sb additives on the photoconductivity of glassy Se80Te20 alloy [6]. They observed that photosensitivity decreases after the incorporation of cadmium, indium, and antimony in the parent binary glass. The photosensitivity also decreases quite significantly after the amorphous films of binary Se80Te20 alloy and ternary Se80Te10In10 and Se80Te10Sb10 alloys are crystallized. Nevertheless, the photosensitivity rises after the crystallization of the Se80Te10Cd10 alloy. Chandel et al. studied thermally activated a.c. conduction in SeTeM (M=Cd, In, Sb) glasses for lower concentration (0.5 atomic weight percentage) and higher concentration (10 atomic weight percentage) of Cd, In, and Sb [7,8]. They found that the electrical properties are changed significantly for higher concentrations. In various reports [9–12], it was also observed that a phase reversal appears in the increasing/decreasing trend of different physical properties of Se80−xTe20Mx (M=Cd, In, Sb) at 10 atomic weight percentage. Chandel and Mehta [13] also observed that when Cd, In and Sb are incorporated in Se80Te20 glass then thermo-mechanical properties are varied significantly after incorporation of Cd, In, and Sb additives. They also found a correlation between Mohs hardness of Cd, In, and Sb and Vickers hardness of Se80Te10M10 (M=Cd, In, Sb) alloys [13]. Therefore, we have used Cd, In, and Sb additives for the present studies and choose 10 atomic weight percentage as their concentration.
Hereof, thermal analysis by using differential scanning calorimeter is the most fundamental technique for achieving that level of scientific ability during the thermal characterization of ChGs. Kinetic analysis of glassy materials using the DSC technique involves the thermal analysis of a variety of kinetic properties. To reveal the information about such kinetic properties in ChGs, we deal with the corresponding kinetic temperatures of vitrification and devitrification. Some examples are the kinetic temperatures, the corresponding activation energies, and the pre-exponential factor. We use the combination of these parameters and formalism of the kinetic model (here JMA model) as a tool to check their candidature for potential applications.
The glass-formation region of tin-based binary and ternary chalcogenide glasses is very narrow and corresponds to a small amount of tin in the alloys. Recently, Georgieva et al. [14] reported the effect of amorphous to crystalline phase transformation on both optical and electrical parameters of thin-film samples of Se–Te–Sn. Further, Kaur et al. [15] investigated the kinematics of crystallization on the bulk glassy samples of the Se80−xTe20Snx system. Kumar et al. [16] used two different approaches for the alteration of optical characterization of some alloys of Se–Te system by using their amorphous films. In the first approach, they incorporated Sn as a modifier for modifying the optical parameter. In the second approach, they exposed the amorphous thin films by irradiation of swift heavy ions. The role of tin in changing the electrical properties of parent binary Se85Te15 glass was reported by Sharma et al. [17,18]. Saraswat et al. reported the bandgap studies on amorphous films of the ternary Se–Te–Sn system [19]. The results of surface conductivity measurement on Sn containing Se–Te binary alloys were reported by Solanki et al. [20]. Kinematics of glass transition and crystallization of Sn containing Se-Te binary alloys was reported by Kumar et al. [21,22]. They [21,22] found that the kinetics of glass transition and crystallization of Se80Te20 glass is affected significantly after the addition of Sn.
The general observation of these studies is that most of the Tin containing ChGs have the drawback of low electronic conductivity, extreme volume expansion, and rigorous accumulation during the cyclic route. These facts appreciably hamper their practical applications. To resolve these issues, the most effective strategy is the incorporation of the foreign element in ternary Se–Te–Sn systems. A lot of fundamental work is already reported in the literature on the crystallization kinetics of the ternary system of Se-Te with Sn as a foreign element. However, the thermal characterization of novel quaternary glasses of this system is not resolved.
In the above thorough literature survey, we have noticed that the effect of foreign elements on a variety of physical and chemical properties in binary and ternary alloys of Selenium rich glasses has been studied by different research groups by altering the concentration but no serious effort has been done to investigate crystallization kinetics in multi-component (ternary and quaternary) alloys by changing the additives in a ternary parent glass for a fixed composition. Currently, a series of papers have been reported in the last decade to understand the outcome of different metallic additives on various physical properties of the Se–Te–Sn system [23–26] after their inclusion and then changing their composition. Sharma et al. [23] observed that the specific Heat in Multi-component glasses of Se–Te–Sn–Pb is changed appreciably after the addition of lead as the fourth element in the parent Se–Te–Sn system. Sharma and Mehta [24] reported that the incorporation of Pb can also enhance the dielectric relaxation and thermally activated a.c. conduction in the Se–Te–Sn system. Pal et al. [25] studied glass/crystal phase transition in the Se–Te–Sn–Ge system and found that Ge plays a significant role to control the kinematics of glass transition and crystallization of Se78Te20Sn2 glass. Srivastava et al. [26] found that the glass transition temperature decreases slightly with the increase in silver concentration due to the reduction in the cohesive energy of the glass matrix.
Keeping in mind this fact, we have used a different approach in the present work i.e., we have fixed the composition and varied the foreign element. We have executed a systematic experiment for thermal analysis of the crystallization kinetics in Sn containing Se-Te parent alloy before and after the inclusion of Sb, In, Cd additives. Such results are useful to understand the “metal-induced effects” for a fixed concentration (here 10 atomic weight percentage %).
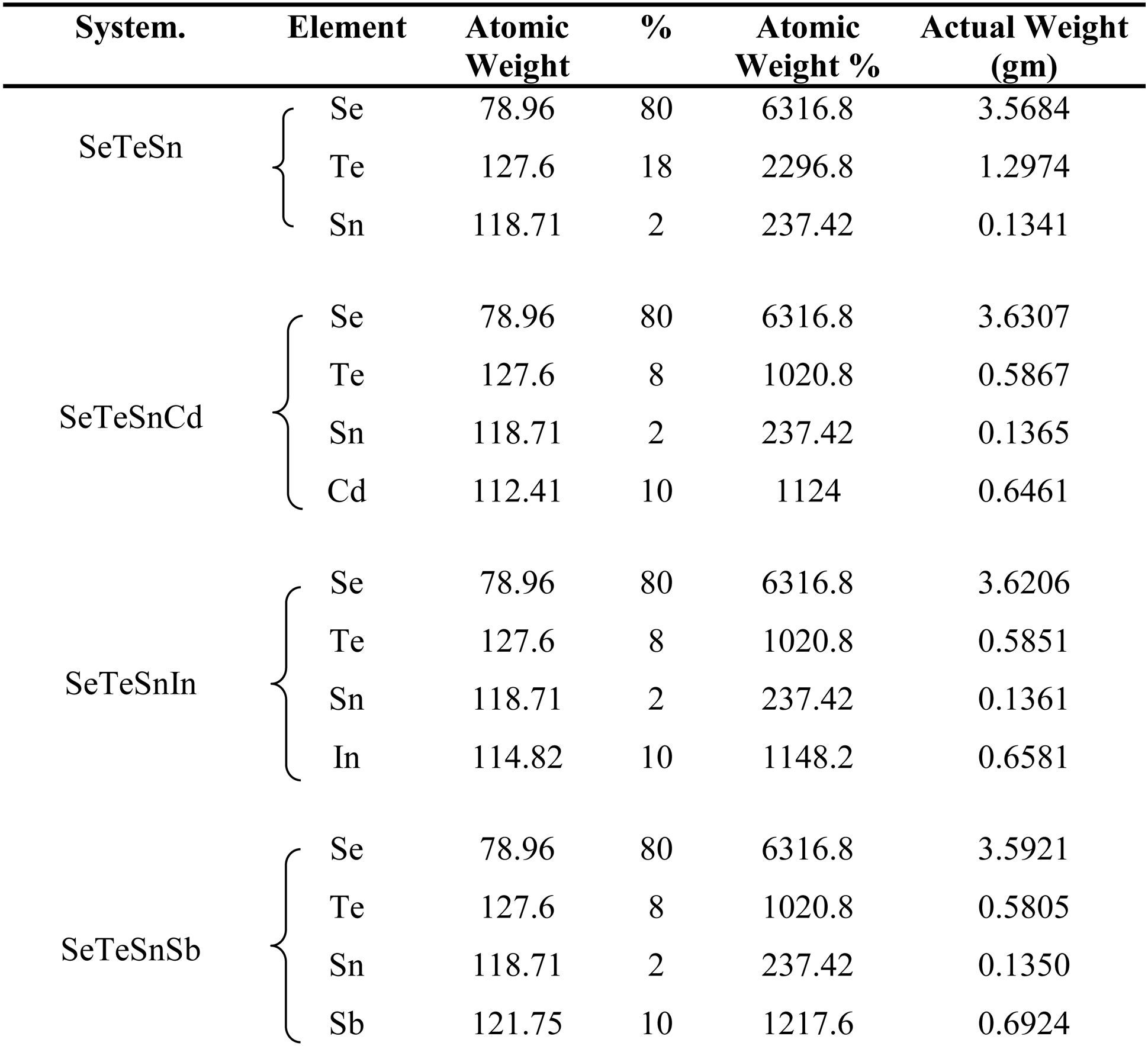
ExperimentalThe source materials (i.e., Sn containing Se-Te parent alloy and its quaternary alloys having dopants Sb, In, Cd) were synthesized by direct retort of highly pure elemental Se, Te, Sn, Sb, In, Cd. The melt-quench approach was used for this purpose. The atomic weight percentages of elements in each alloy are described in Table 1. Weighing of the desired amounts of the constituent elements was done according to their atomic-weight percentages and after then each sample was sealed in a quartz ampoule under a high vacuum (∼1μ-Torr). Each sealed ampoule containing the materials was kept inside an organized furnace to raise the temperature to a fixed and high temperature (> m.p. of the constituents of the ampoule). The holding time in the furnace was 10h and each ampoule was rotated frequently to inter-mix the constituents. This step is necessary for maintaining the homogeneity of the final product. The tubes were then dipped rapidly in ice water to achieve glasses. The surface morphology of quenched samples was investigated using Scanning Electron Microscope (SEM) (Model: Quanta 200F). Fig. 1 shows the SEM pictures of all samples. From these micro-pictures, it is revealed that there is no sign of any kind of crystal growth. This indicates the glassy character of quenched samples.
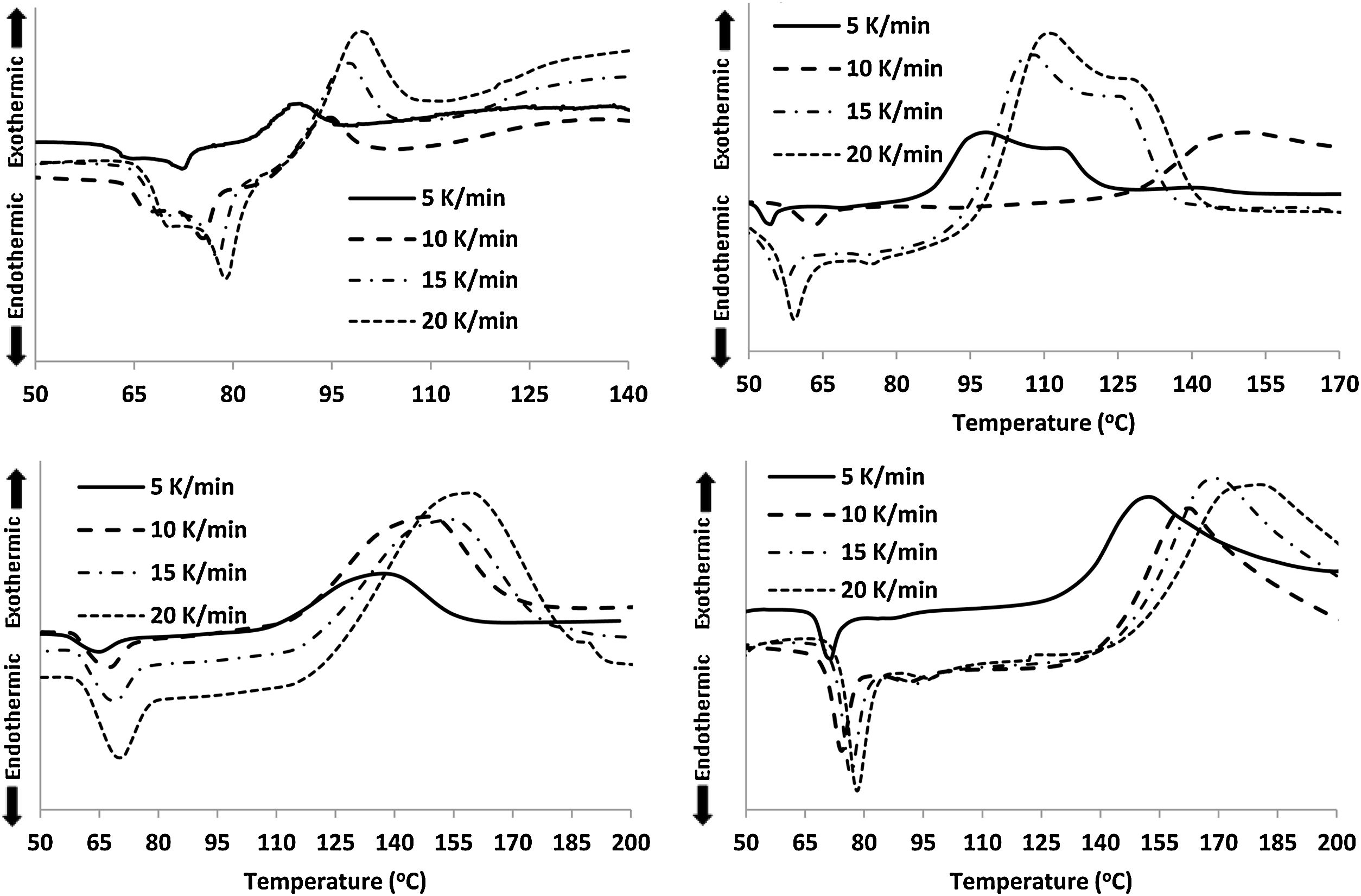
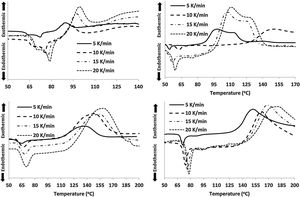
For the thermal analysis of each sample, we employed a state of art Differential scanning calorimetry (TA Instruments, Model: Q20 MDSC) to note-down the caloric signs under non-isothermal conditions. About 5–10mg of the crushed sample was enclosed in an aluminum pan, and then the pan was heated in the DSC cell at different heating rates. The changes in heat flow were measured under an N2 atmosphere at a constant flow rate (∼40mL). Each DSC scan, (see Fig. 2) at different heating rates (5, 10, 15, 20K/min), showed a distinct endothermic and exothermic peak at the glass transition and crystallization temperature Tg and Tc respectively as the indicators of the homogeneousness of the samples. This is a fundamental condition to utilize ChGs as phase-change materials in the optical recording memory. The appearance of distinct glass transition peaks also confirms the glassy nature of as-prepared samples. Thus, the results of DSC patterns of the present samples are in good agreement with that of SEM images.
Results and discussionsThe crystallization temperature has a vital contribution to the understanding of the crystallization of different types of amorphous semiconductors and semiconducting glasses [27–32]. The values of Tc for all the samples at diverse heating rates are given in Table 2. This table reveals that Tc is increased after the replacements of Te atoms by Sb, Cd and In additives in parent glassy alloy. The increasing sequence of crystallization temperature (Tc) is (Se–Te–Sn)<(Se–Te–Sn–Cd)<(Se–Te–Sn–In)<(Se–Te–Sn–Sb). This rising order can be explained in terms of the rate of crystallization. The rate of crystallization can be expressed by following the Arrhenius equation:
Peak crystallization temperature (Tc/°C) and the peak value of the rate of crystallization (Kp/min−1) for glassy Se–Te–Sn and Se–Te–Sn–M (M=Sb, In, Cd) alloys at different heating rates.
| Heating rate (β) (K/min) | Se–Te–Sn | SeTeSnCd | SeTeSnIn | SeTeSnSb | ||||
|---|---|---|---|---|---|---|---|---|
| Tc (°C) | Kp (min−1) | Tc (°C) | Kp (min−1) | Tc (°C) | Kp (min−1) | Tc (°C) | Kp (min−1) | |
| 5 | 90.2 | 0.8 | 98.2 | 0.5 | 137.4 | 0.3 | 152.5 | 0.2 |
| 10 | 94.7 | 1.5 | 103.7 | 1.0 | 148.9 | 0.6 | 162.5 | 0.5 |
| 15 | 97.4 | 2.2 | 107.6 | 1.5 | 154.8 | 0.9 | 168.9 | 0.7 |
| 20 | 99.4 | 2.9 | 111.1 | 2.0 | 159.1 | 1.1 | 180.6 | 0.8 |
Here, Ec represents the activation energy involved in devitrification. Here R is the universal gas constant while K0 denotes the pre-factor corresponding to the rate constant.
Gao and Wang [33] developed the following relation using the JMA equation to determine the crystallization reaction rate constant (Kp) is expressed as:
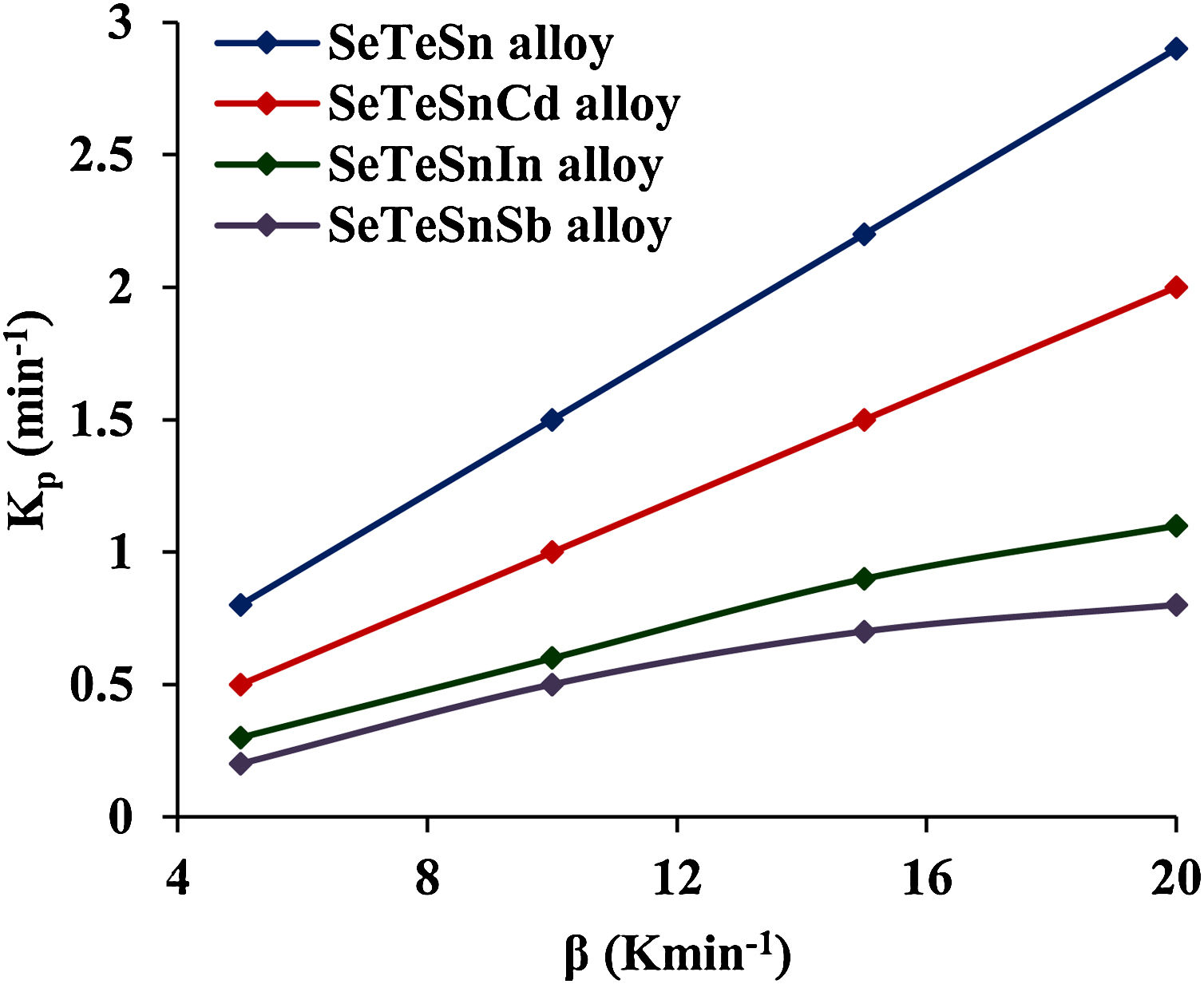
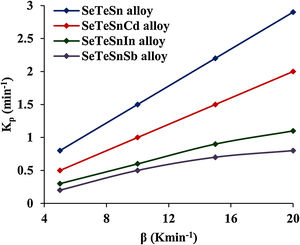
This parameter provides knowledge about the morphology of crystal growth in glassy alloys. Here, Kp signifies the value of K at temperature Tc corresponding to the crystallization peak for an invariable heating rate. The values of Kp for glassy Se–Te–Sn and Se–Te–Sn–M (M=Sb, In, Cd) alloys are also given in Table 2. One can realize easily that the rising order of Kp in present glasses is just contrary to that of temperature Tc corresponding to the crystallization peak. This indicates that the crystallization of glassy alloys having a lower rate of crystallization starts at a higher temperature.
When we incorporate additives (Sb, In, Cd) in parent Se–Te–Sn, the increasing sequences of three kinetic parameters Tc, ln K, and Kp in quaternary glasses are as follows:
- •
(Tc)Cd<(Tc)In<(Tc)Sb
- •
(ln K)Sb<(ln K)In<(ln K)Cd
- •
(Kp)Sb<(Kp)In<(Kp)Cd.
These increasing sequences of the above three kinetic parameters clearly show that the higher the value of K(T) or Kp, the greater the speed of crystallization and hence lower the crystallization temperature in both glassy systems. Fig. 3 shows the variation of Kp with β for quaternary Se–Te–Sn–M (M=Sb, In, Cd) alloys. From this plot, one can understand that the increasing sequence of Kp is the same in both systems for all heating rates and it is highest in the case of Cadmium containing quaternary glass.
Kissinger [34] proposed that the observed shift in the value of crystallization peaks with heating rate variation can be expressed as in terms of the following correlation between Tc and β:
Similar relations were derived by another researcher [35–37] by using the traditional JMA model which show the following correlations between Tc and β:
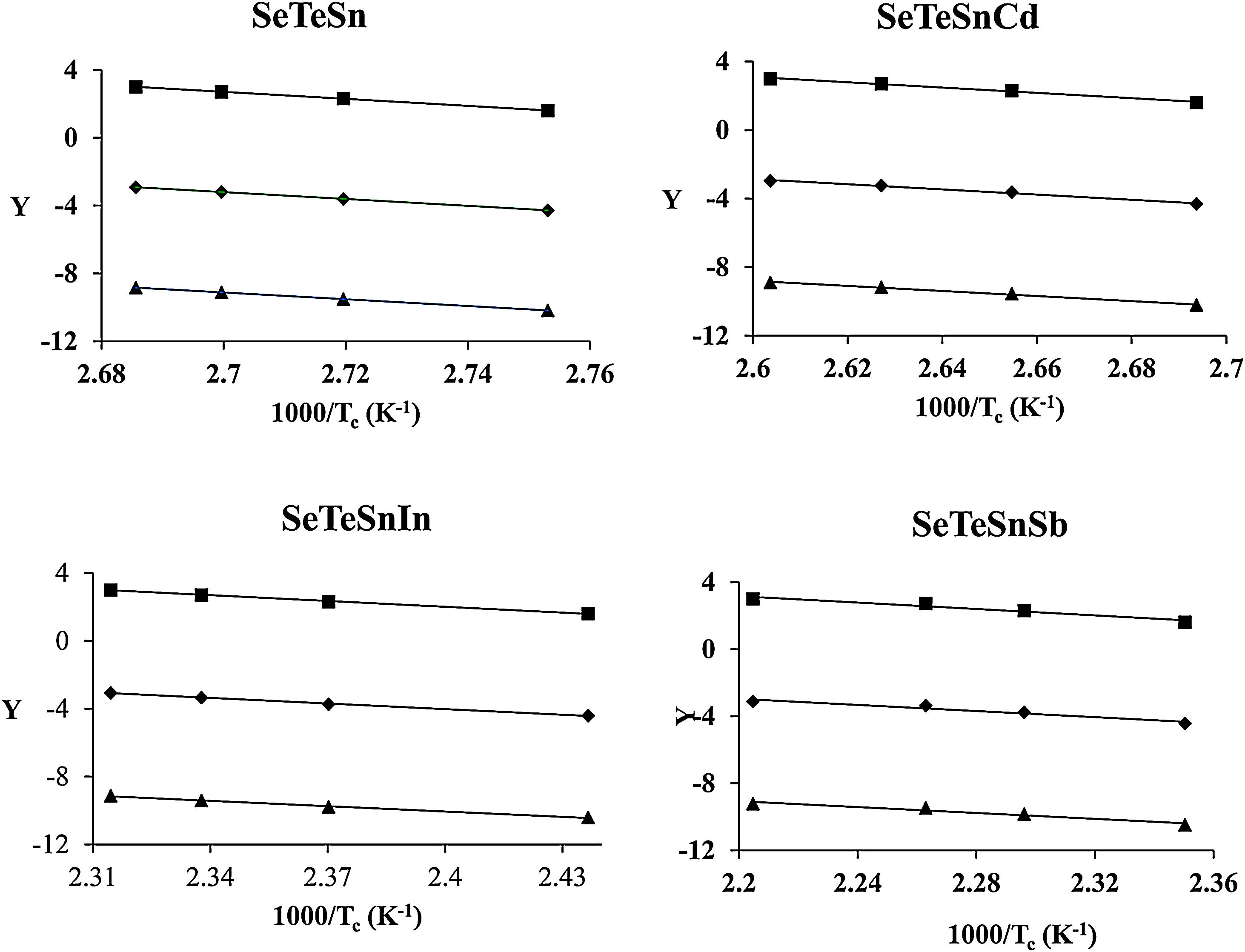
The determination of Ec values of different samples is possible by plotting linear curves of ln (β/Tc2), ln (β/Tc2) and ln (β/Tc2) against 1/Tc in Eqs. (3)–(5) respectively.
The plots of ln (β/Tc2), ln β, and ln (β/Tc) against 1000/Tc are shown in Fig. 4. The determination of the Ec values of different samples was done by knowing the values of the slopes of such plots. The values are tabulated in Table 3. From this table, it is clear that the activation energy of crystallization of parent Se80Te18Sn2 glass is reduced after the inclusion of the foreign elements. The reduction in the value of Ec can be revealed by considering the mean atomic volume of the present alloys. It is generally observed in chalcogenide glasses that the crystallization temperature is linked with the progression of the crystal nucleation and their growth and this controls the re-crystallization of nearly all glasses. The number of nuclei formed, along with their critical size, from the amorphous phase to the crystalline one, depends on the activation energy. In the present glassy system, the foreign elements have been entered in the glass matrix of parent alloy at cost of Te. The atomic volume (20.5cm3/mol) of Te is higher than the atomic volumes (>20.5cm3/mol) of Sb, In, and Cd. Thus, it is reasonable to expect that there is a need for less activation energy to initiate crystallization in an alloy having low atomic volume. In the devitrification of the present parent glass, the larger size of Te atoms causes the rise in the potential barrier and delays the diffusion. As a result, in parent glass, the value of Ec is reduced when we substitute foreign elements having atoms of larger radii as compared to replaced atoms of Te. Consequently, a lower energy barrier is required to conquer the diffusion of atoms and corresponding atomic relocation during the devitrification in quaternary glasses [38].
Activation energy of crystallization for glassy Se–Te–Sn and Se–Te–Sn–M (M=Sb, In, Cd) alloys.
| Non-isothermal method | Ec (kJ/mol) | |||
|---|---|---|---|---|
| Se–Te–Sn | SeTeSnCd | SeTeSnIn | SeTeSnSb | |
| Kissinger method | 164.6 | 122.3 | 87.1 | 72.6 |
| Augis–Bennett method | 167.7 | 125.5 | 90.6 | 76.2 |
| Matusita–Sakka method | 170.7 | 128.6 | 94.1 | 79.9 |
| Average value | 167.7 | 125.5 | 90.6 | 76.2 |
Obtaining the values of the crystallization activation energy and corresponding pre-factor from Eq. (5), we have determined the values of the crystallization rate. Table 4 tabulates the values of ln K at diverse temperatures lying in the crystallization range for the present samples. This table points out that K is decreased with rising in temperature and its value is highest for glassy SeTeSnCd alloy. Further, we noticed an interesting observation that the increasing order of rate constant ln K in the present glasses is similar to that of its peak value Kp.
Rate constant ln K (T) for glassy Se–Te–Sn and Se–Te–Sn–M (M=Sb, In, Cd) alloys in the crystallization region at a particular temperature.
| Se–Te–Sn | SeTeSnCd | SeTeSnIn | SeTeSnSb | ||||
|---|---|---|---|---|---|---|---|
| T (K) | lnK (min−1) | T (K) | lnK (min−1) | T (K) | lnK (min−1) | T (K) | lnK (min−1) |
| 361 | 3.6×1046 | 361 | 9.6×1033 | 413 | 1.2×1021 | 413 | 1.3×1017 |
| 366 | 1.6×1046 | 366 | 5.5×1033 | 423 | 6.3×1020 | 423 | 7.8×1016 |
| 371 | 8.0×1045 | 371 | 3.0×1033 | 433 | 3.5×1020 | 433 | 4.7×1016 |
To determine the Avrami index, the following correlation between the crystallization fraction α at a particular temperature and the uniform heating rate β is used [39]:
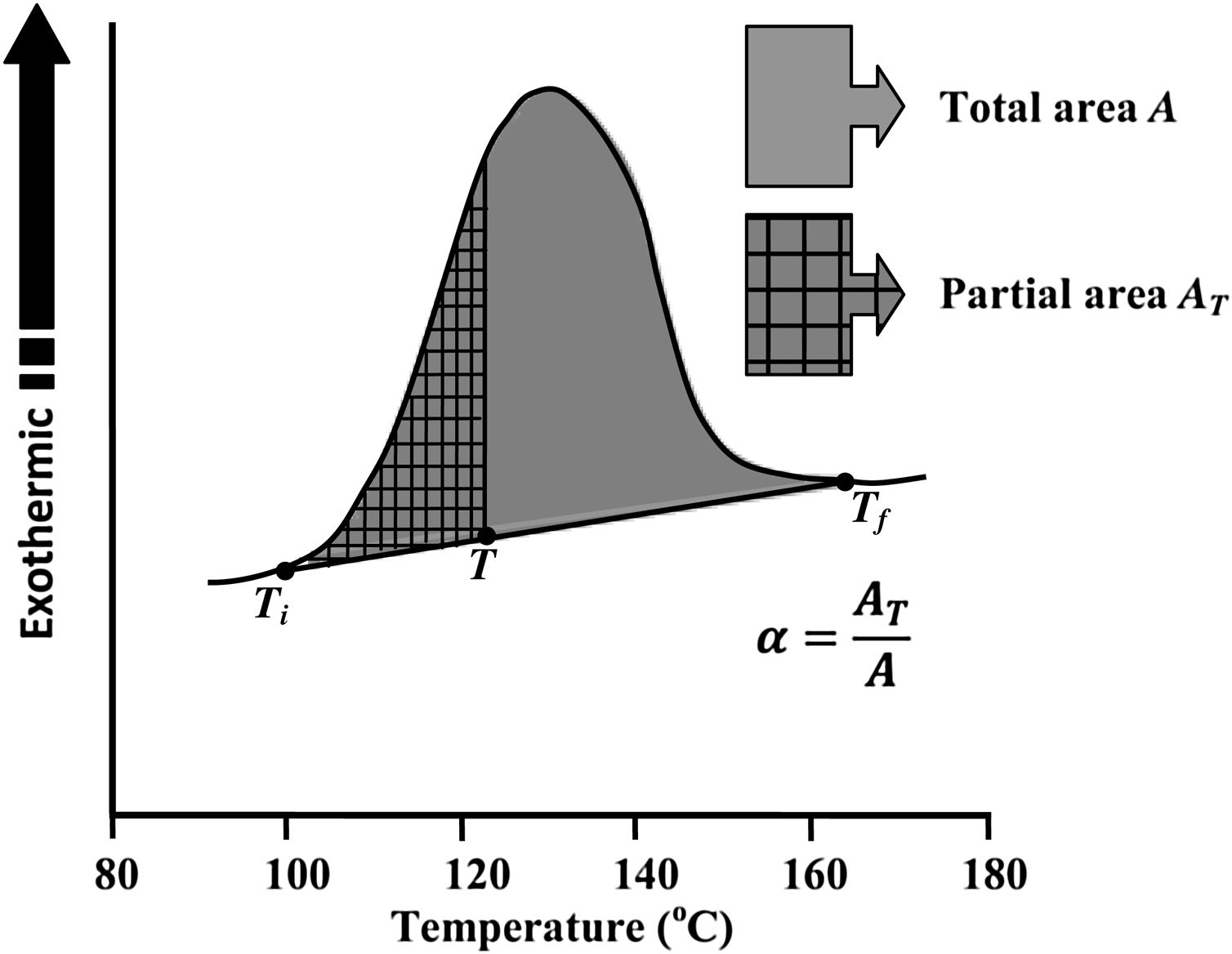
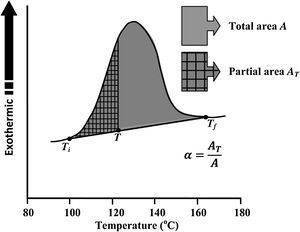
Avrami index (n) can be evaluated from this equation from the slope of ln [ln(1−α)−1] versus ln β curves plotted at different values of temperature T lying in the crystallization range. At a particular temperature T, the crystallization fraction ‘α’ is evaluated from the following relation.
Here, A is the entire area of the crystallization peak having the starting temperature Ti where it starts (i.e. the devitrification is initiated) and the final temperature Tf where it terminates (i.e. the crystallization is completed). The partial area of the exothermic peak corresponding to a temperature T denoted by AT and it lies between Ti and T (see Fig. 5).
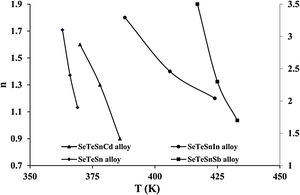
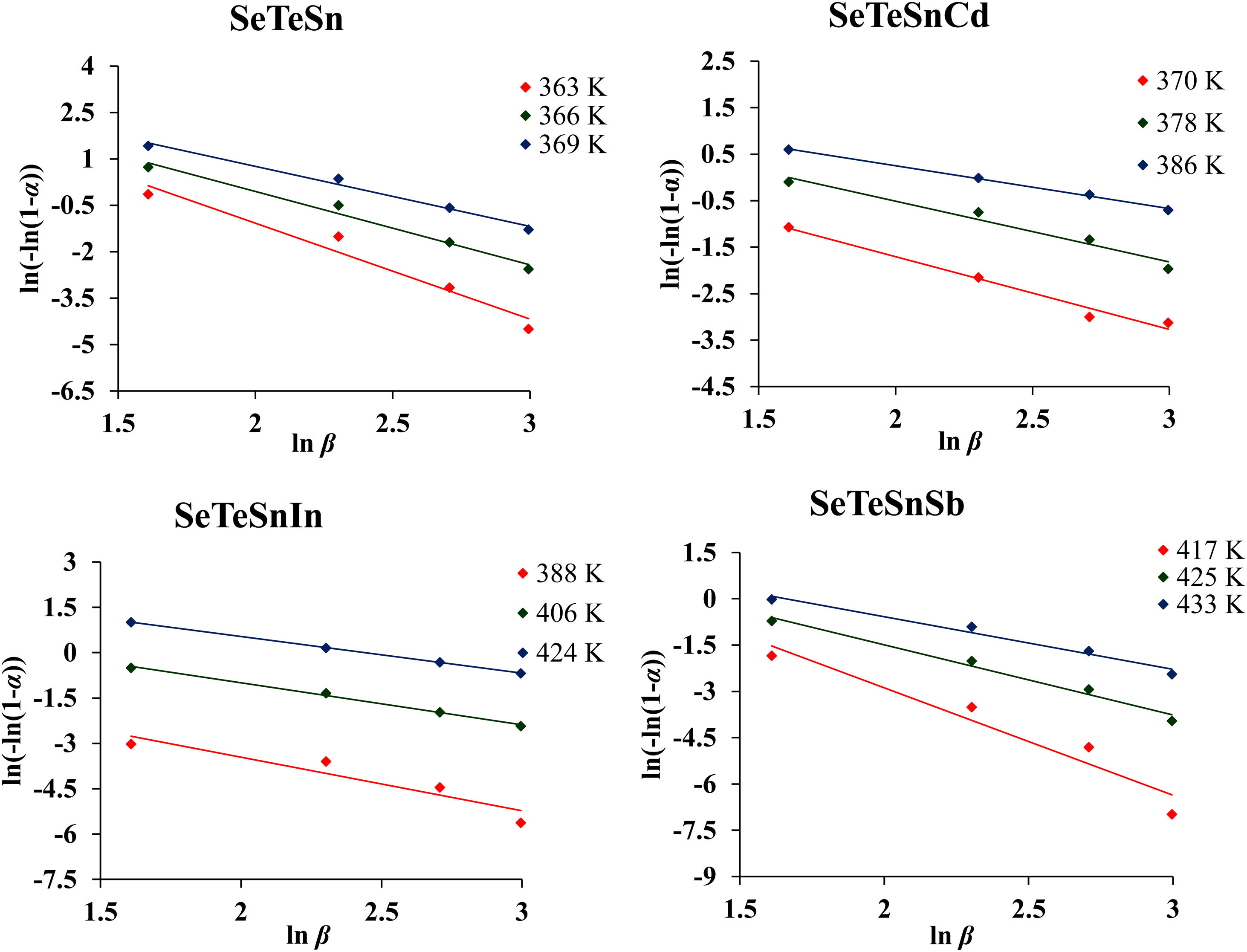
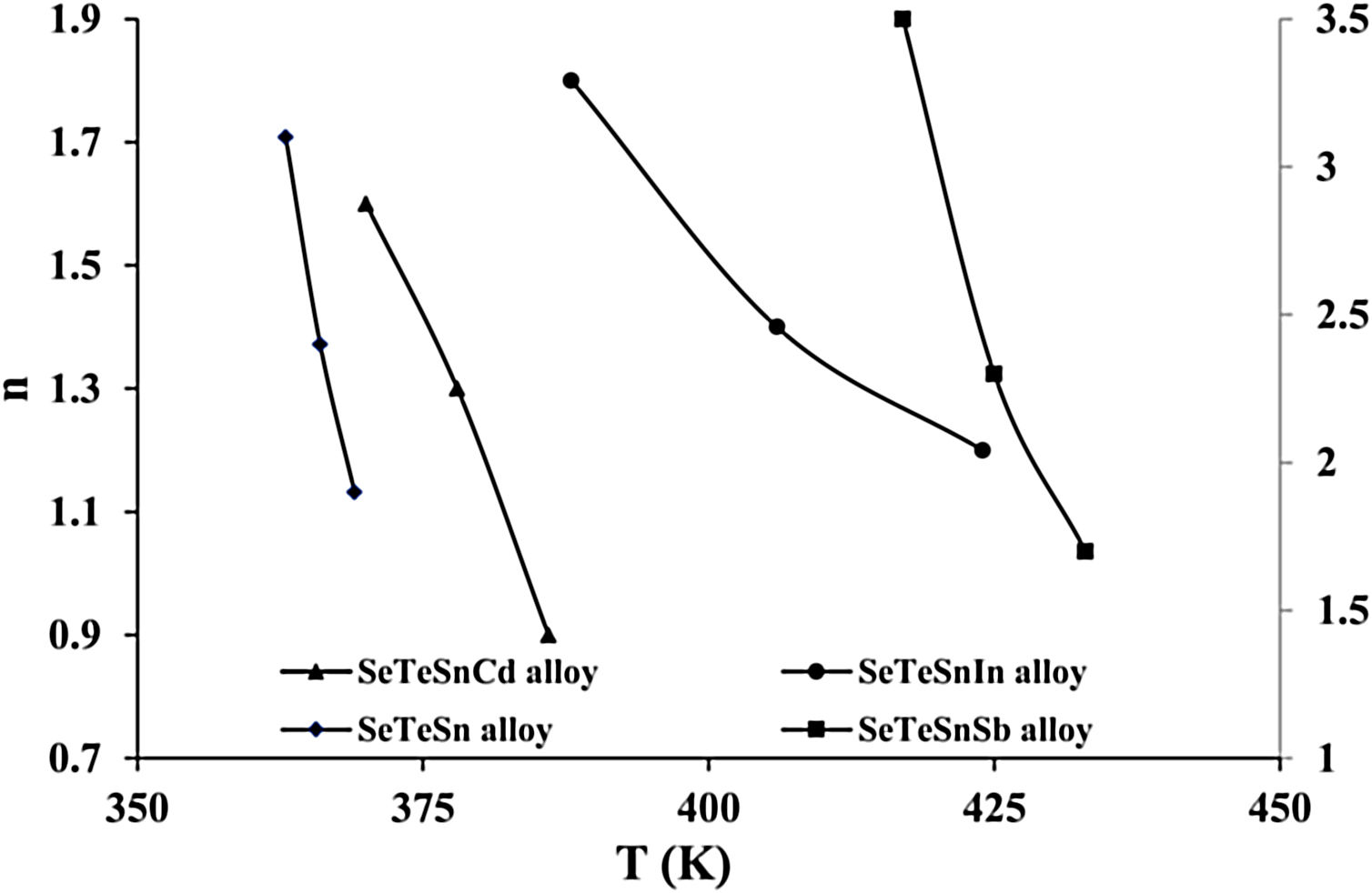
For diverse values of T in the crystallization range, the plots of ln [ln(1−α)−1] versus ln β are shown in Fig. 6 for glassy SeTeSn and SeTeSnM alloys. The values of n are listed in Table 5 for all glassy alloys. The temperature dependence of n is shown in Fig. 7. These plots indicate that there is a significant reduction in “n” values with the rising temperature. Thus, the increase in the crystallization fraction α with rising temperature in ChGs is a clear indication of this fact [40,41].
We already pointed out that both nucleation and growth play a key role in controlling the re-crystallization. [42]. According to this model, the maximum value that α may attain is unity. The falling tendency in the values of n, therefore, reveals the reduction in the rate of nucleation because of its saturation. Similar results have been observed in numerous second-generation glasses (i.e., ternary systems of ChGs) [25–30].
The mean value of n comes out to be almost 2.5 for ternary SeTeSn alloy and quaternary SeTeSnSb alloy, which shows that the crystallization mechanism in these glasses is bi-dimensional (both two-dimensional and three-dimensional) in these samples. However, the average value of n for quaternary SeTeSnCd and quaternary SeTeSnIn alloys is between 1 and 2. This indicates that the crystal geometry growth is bi-dimensional (both one-dimensional and two-dimensional) in these samples.
ConclusionsKinematic studies of non-isothermal crystallization on parent SeTeSn glass and elements Antimony (Sb), Cadmium (Cd), and Indium (In) containing quaternary SeTeSnM glasses indicate that values of crystallization temperatures (Tc) are decreased after incorporation of atoms of a foreign element in parent SeTeSn alloy. This is clarified by shifting the peak value of the rate constant of crystallization. The drop off in Ec values after the addition of these additives in the present ternary alloy is explained in terms of reduced mean atomic volume of quaternary alloys. The crystallization mechanism of parent SeTeSn alloy remains unaffected for Sb incorporation. However, it changes from one kind of bi-dimensional (two-dimensional and three-dimensional) growth to another type of bi-dimensional (one-dimensional and two-dimensional) growth after the addition of Cd and In additives. The general observation is that the extreme values for the different kinetic parameters are obtained in glassy SeTeSnCd alloy. This shows that the insertion of Cd in parent glass SeTeSn affects more efficiently its crystallization mechanism as compared to the other two additives (Sb and In).
The author (A. Dahshan) extends his appreciation to the Deanship of Scientific Research at King Khalid University for the financial support through the research groups program under grant number (R.G.P2/113/41). NM is grateful to the Council of Scientific and Industrial Research (CSIR), New Delhi, India for providing financial assistance under a major Project (Scheme no. 03(1453)/19/EMR-II).








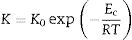
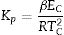

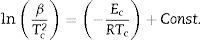
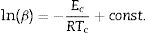
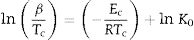
![Plots of ln (β) vs 103/Tc, ln (β/Tc) vs 103/Tc and ln (β/Tc2) vs 103/Tc for glassy Se–Te–Sn and Se–Te–Sn–M (M=Sb, In, Cd) alloys [ Kissinger method, ♦ Augis–Benett method, and ■ Matusita–Sakka method]. Plots of ln (β) vs 103/Tc, ln (β/Tc) vs 103/Tc and ln (β/Tc2) vs 103/Tc for glassy Se–Te–Sn and Se–Te–Sn–M (M=Sb, In, Cd) alloys [ Kissinger method, ♦ Augis–Benett method, and ■ Matusita–Sakka method].](https://static.elsevier.es/multimedia/03663175/0000006100000004/v1_202207290548/S0366317521000121/v1_202207290548/en/main.assets/thumbnail/gr4.jpeg?xkr=ue/ImdikoIMrsJoerZ+w96p5LBcBpyJTqfwgorxm+Ow=)
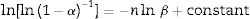
![Plots of ln [−ln (1−α)] with ln β for a-Se80Te18Sn2 and a-Se80Te8Sn2M10 (M=Cd, In, Sb) alloys. Plots of ln [−ln (1−α)] with ln β for a-Se80Te18Sn2 and a-Se80Te8Sn2M10 (M=Cd, In, Sb) alloys.](https://static.elsevier.es/multimedia/03663175/0000006100000004/v1_202207290548/S0366317521000121/v1_202207290548/en/main.assets/thumbnail/gr6.jpeg?xkr=ue/ImdikoIMrsJoerZ+w96p5LBcBpyJTqfwgorxm+Ow=)