Modeling the booster vaccine effect on new COVID-19 variant management employs the Atangana-Baleanu-Caputo fractional derivative operator together with the Laplace-Adomian decomposition method

Abstract

Introduction

New COVID-19 variants create worldwide health difficulties that call for effective control methods including booster vaccinations. The risk factors associated with new COVID-19 variants include enhanced transmission capabilities together with escape from immune responses and more severe disease manifestations which requires advanced vaccination measures. The developed mathematical model assesses how effectively booster vaccines help stop new COVID-19 variants from transmitting between people. Environmental variables that measure both public vaccine acceptance levels and widespread awareness levels integrated with the model to determine their roles in disease propagation rates. The research introduces fractional calculus to examine disease progress as well as booster vaccination effectiveness in stopping outbreaks.

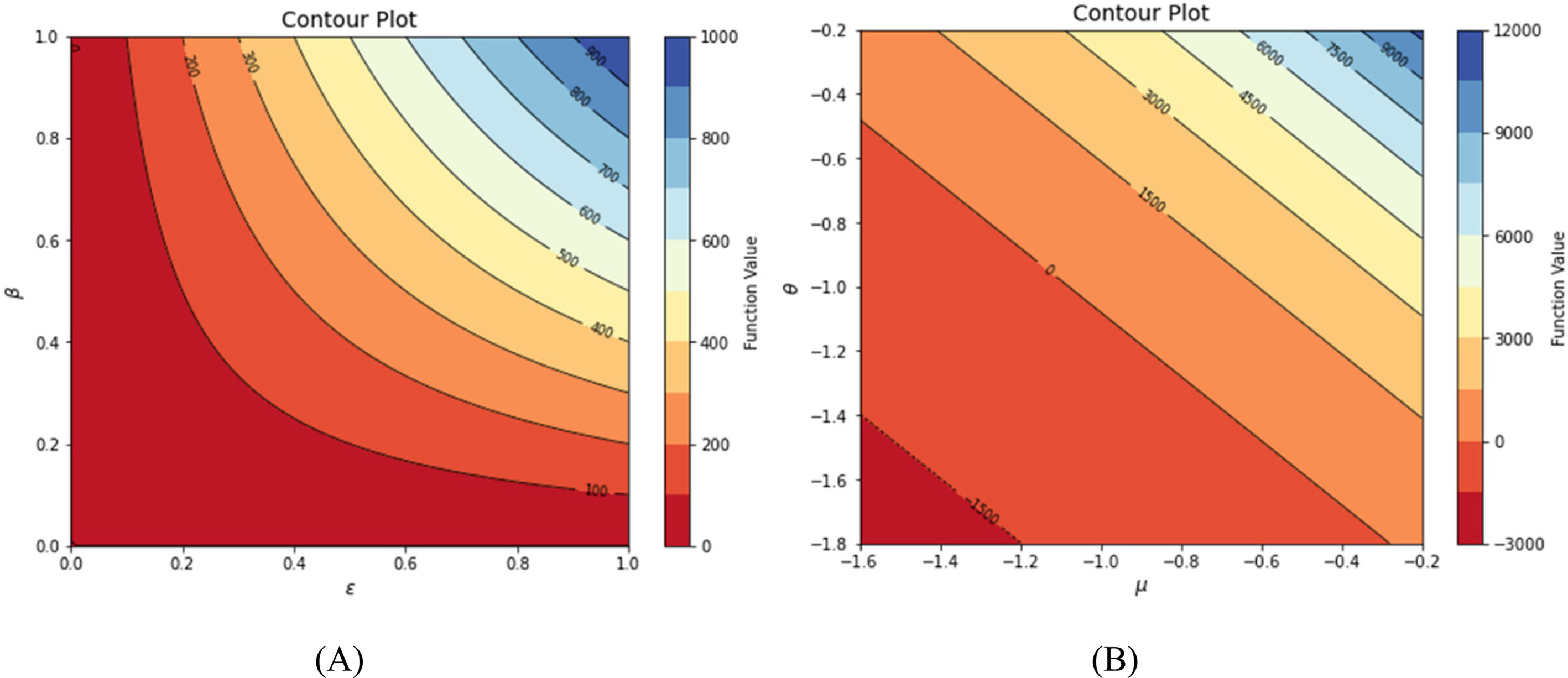
Methods

This research establishes a fractional mathematical model to evaluate how booster vaccinations affect the spread of new COVID-19 variants. The stability evaluations and determination of basic reproduction number (R0) through next-generation matrix method form the basis of operational analysis for the model. Sensitivity analysis evaluates the effects that variable modifications have on disease outbreak controls. Evaluating complex fractional differential equations requires the analytical solutions derived by employing the Laplace-Adomian Decomposition Method (LADM). The solution approach provides accurate insights into equilibrium points as well as stability patterns together with control measures of disease transmission through vaccination strategies.

Results

Numerical data confirms the success of booster vaccination strategies because they lower transmission rates of infections and manage disease spread. Boosted vaccination rates lead to substantial decline in the basic reproduction number (R0) thus reducing disease transmission across the population. Sensitivity analysis shows how vaccine acceptance together with public awareness directly affects the maximum results achievable through booster doses. Success rates of vaccination programs heavily depend on behavioral elements which include vaccine hesitancy together with social perceptions about immunizations. The study demonstrates how vaccinating people alongside education programs leads to superior transmission control which supports long-lasting mitigation tactics.

Conclusion

The research evidence shows that booster vaccinations play a critical role in containing new COVID-19 variant spread. The research enables a full disease dynamics understanding through its integrated fractional-order model with behavioral components so it delivers effective vaccination optimization recommendations. Public health measures together with transmission control improve when people become more aware of vaccines. This developed model provides both scientific fundamentals for behavioral approaches in disease modeling and operational guidance to policy makers who need to create efficient vaccination programs. Booster vaccinations used together with awareness-raising programs establish a strong framework to manage the impact of new COVID-19 variants along with other infectious diseases.

Resumen

Introducción

Las nuevas variantes de COVID-19 crean dificultades sanitarias a nivel mundial, que exigen métodos de control efectivo, incluyendo las vacunaciones de refuerzo. Los factores de riesgo asociados a las nuevas variantes de COVID-19 incluyen la mejora de las capacidades de transmisión junto al escape de las respuestas inmunitarias, así como más manifestaciones graves de la enfermedad que requieren medidas de vacunación avanzadas. El modelo matemático desarrollado evalúa el modo en que las vacunas de refuerzo ayudan a frenar la transmisión de las nuevas variantes de la COVID-19 entre las personas. Las variables ambientales que miden tanto los niveles de aceptación pública de la vacuna como los niveles de concienciación generalizada integrados con el modelo para determinar sus roles en la tasa de propagación de la enfermedad. La investigación introduce el cálculo fraccional para examinar el progreso de la enfermedad, así como la efectividad de la vacunación de refuerzo de cara a parar los brotes.

Métodos

Este estudio establece un modelo matemático fraccional para evaluar el modo en que las vacunaciones de refuerzo afectan a la propagación de las nuevas variantes de la COVID-19. Las evaluaciones de la estabilidad y la determinación del número básico de reproducción (R0) a través de un método matricial de nueva generación establecen la base del análisis operacional para el modelo. El análisis de sensibilidad evalúa los efectos que tienen las modificaciones variables en los controles de los brotes de la enfermedad. Evaluar las ecuaciones diferenciales complejas requiere las soluciones analíticas derivadas, utilizando LADM (Laplace-Adomian Decomposition Method). El enfoque de la solución aporta perspectivas precisas a los puntos de equilibrio, así como patrones de estabilidad, junto con medidas de control de la transmisión, mediante estrategias de vacunación.

Resultados

Los datos numéricos confirman el éxito de las estrategias de la vacunación de refuerzo, dado que reducen las tasas de transmisión de las infecciones y manejan la propagación de la enfermedad. Las tasas de la vacunación de refuerzo conducen a una reducción sustancial del número básico de reproducción (R0), disminuyendo así la transmisión de la enfermedad entre la población. El análisis de sensibilidad muestra el modo en que la aceptación de la vacuna, sumado a la concienciación pública, afecta directamente a los resultados máximos alcanzables mediante las dosis de refuerzo. Las tasas de éxito de los programas de vacunación dependen grandemente de los elementos conductuales, que incluyen la indecisión sobre la vacuna junto con las percepciones sociales acerca de las inmunizaciones. El estudio demuestra el modo en que la vacunación de las personas, junto con los programas educativos, conduce a un control superior de la transmisión que respalda las tácticas de mitigación a largo plazo.

Conclusión

La evidencia de la investigación muestra que las vacunaciones de refuerzo juegan un papel esencial en la contención de la propagación de las nuevas variantes de la COVID-19. La investigación permite comprender plenamente la dinámica de la enfermedad a través de su modelo de orden fraccional integrado con componentes conductuales, por lo que aporta recomendaciones de vacunación efectivas. Las medidas sanitarias públicas, junto con el control de la transmisión, mejoran el momento en que las personas adquieren más consciencia sobre las vacunas. Este modelo desarrollado proporciona tanto fundamentos científicos para los enfoques conductuales en la modelación de la enfermedad como una guía operativa para los formuladores de políticas, que necesitan crear programas de vacunación eficaz. Las vacunaciones de refuerzo, utilizadas junto con programas que susciten la concienciación, establecen un marco sólido para gestionar el impacto de las nuevas variantes de la COVID-19, junto con otras enfermedades infecciosas.