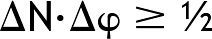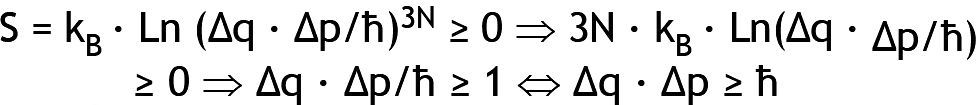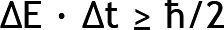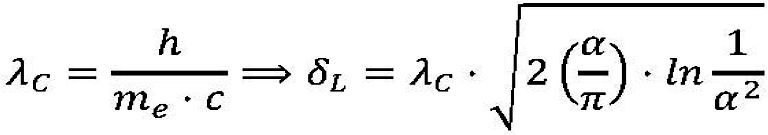Dentro del marco de la teoría cuántica, analizamos la sugerencia original de Samuel Hahnemann acerca de la existencia de una fuerza dinámica inmaterial para explicar la homeopatía. Basándonos en la teoría cuántica de campos y el concepto de los dominios de coherencia 2D, proponemos un modelo plausible de acción de los remedios homeopáticos que permite tratar el concepto de la memoria del agua y la transferencia de información a través de las señales electromagnéticas, dentro de un marco científico cuantitativo y riguroso. Este punto de vista cuántico-mecánico apunta al papel esencial que juegan las membranas lipídicas, un componente universal de cualquier organismo vivo. Los intentos de asimilar la homeopatía a un mero efecto placebo, y las tentativas de bloquear la financiación de la investigación sobre los remedios homeopáticos deberían contemplarse como una actitud conservadora que emana de la adhesión a una filosofía materialista basada en las leyes físicas clásicas. Es el momento de que los médicos y biólogos se percaten de que la física cuántica se aplica a todas las escalas, otorgando a la homeopatía sus credenciales como enfoque médico racional de curación de las personas.
The original suggestion of Samuel Hahnemann of the existence of an immaterial dynamical force for explaining homeopathy is analyzed within the frame of quantum theory. Based on quantum field theory and the concept of 2D coherence domains, a plausible model of action of homeopathic remedies is proposed allowing to discuss the concept of water memory and information transfer through electromagnetic signals within a scientific rigorous quantitative frame. This quantum-mechanical viewpoint points to the crucial role played by lipidic membranes, a universal component of any living system. Attempts to assimilate homeopathy to a mere placebo effect and trials to block research funding on homeopathic remedies should be viewed as a conservative attitude stemming from a sticking to a materialistic philosophy based upon classical physics laws. Time is now ripe for physicians and biologists to realize that quantum physics applies at all scales, giving to homeopathy its credentials as a rational medical approach for healing people.
Desde su introducción en 1810 por Samuel Hahnemann1, la homeopatía ha sido siempre objeto de profundas controversias (fig. 1). El principal motivo parece radicar en el postulado de que cuanto menor sea la dosis de un remedio dado, mayor será su acción terapéutica sobre el cuerpo. Por tanto, dicho principio contradice directamente los postulados del materialismo, que defienden que cualquier cosa está hecha de partículas materiales, y que el efecto debería ser directamente proporcional a la causa que ha producido dicho efecto. Una consecuencia directa para la medicina de dicho punto de vista materialista es el principio de contraria contrarii curantur, el credo de cualquier enfoque alopático para la curación de la enfermedad. Básicamente, frente a una patología dada, los remedios alopáticos tratan de aniquilar la causa primitiva, utilizando dosis medibles de fármacos. Por contra, el credo homeopático se basa en el principio de similia similibus curantur, donde la única indicación de un remedio es seleccionar aquel que comparta la totalidad de los síntomas con la enfermedad.
La homeopatía fue diseñada originalmente como una medicina racional basada únicamente en los síntomas observables, y no en las diversas teorías que pretendían que era posible penetrar en el cuerpo a través de líneas especulativas del pensamiento, a fin de descubrir las causas y la esencia de las diferentes enfermedades.
Cuando se utiliza una sustancia que provoca los mismos síntomas de la enfermedad, se hace obligatorio utilizarla de manera altamente diluida. Lo extraño es que cuanto mayor es la dilución mayor parece la actividad terapéutica, siempre que el remedio haya sido correctamente seleccionado a partir del principio de similitud. En particular, las diluciones que exceden de mucho el límite de Avogadro son utilizadas de manera rutinaria en homeopatía, lo cual exige una explicación científica que no puede basarse en las cantidades medibles del agente terapéutico, como en el caso de la medicina alopática. Esta falta de explicación científica sobre el modus operandi del remedio homeopático es el principal motivo del considerable escepticismo alcanzado por la comunidad alopática frente a las prácticas homeopáticas. A fin de explicar los efectos reales de los remedios homeopáticos, Hahnemann se vio obligado a invocar a la existencia de una fuerza dinámica inmaterial, cuya fortaleza se incrementa a medida que disminuyen las fuerzas fisicoquímicas debido a la dilución. Su gran idea fue descartar las propiedades materiales, de cara a guardar únicamente las propiedades terapéuticas, exaltando la virtud dinámica de los remedios homeopáticos a través de la trituración y la sucusión.
Por tanto, el objetivo básico de la homeopatía es eliminar todos los síntomas de la enfermedad, al provocar una respuesta curativa en el propio organismo. Por ello, no es el fármaco el que cura, sino el propio organismo el que —gracias a la información “patogénica” recibida por la medicina— puede encontrar la vía hacia la recuperación. En lenguaje moderno, un medicamento homeopático permite que el cuerpo evolucione desde un patrón dinámico representativo de un estado de la enfermedad a otro patrón dinámico más en línea con la salubridad. Es el organismo entero, a través de su complejo metabolismo que incluye la modulación de la expresión génica, el que reacciona a una información patogénica responsable del estado de enfermedad que proviene tanto del exterior como del interior del cuerpo. Como ambos tipos de información patogénica compiten por los mismos canales de expresión conducentes a los mismos síntomas, uno de ellos debería ganar, y el otro está obligado a retirarse. Debido a la alta dilución, la información patogénica procedente del exterior es normalmente más activa que la información que se enraíza en el interior del cuerpo. Por tanto, siempre que se elija correctamente el factor de dilución, el cuerpo sigue expresando los mismos síntomas, sintonizándose ahora con el remedio homeopático procedente del exterior. Una vez que esta sintonización es perfecta, la vieja información patogénica enraizada en el cuerpo se borra. Lo único que hay que realizar a continuación es interrumpir el tratamiento homeopático, lo cual conducirá automáticamente a la desaparición simultánea y total de todos los síntomas. Como un estado de enfermedad viene definido normalmente por un conjunto total de síntomas, la eliminación de estos significa que el cuerpo está definitivamente curado de la enfermedad correspondiente. Cuanto mayor sea la similitud de los síntomas entre el remedio homeopático y la enfermedad, mejor será la sintonización, y más rápida la recuperación del estado de salubridad.
Teniendo en cuenta este mecanismo de acción, debería resultar obvio que el peor modo de sanar sería administrar una sustancia no diluida que no comparta síntomas comunes con la enfermedad. En tal caso, en lugar de que el cuerpo compita con los mismos canales de expresión, ambas informaciones patogénicas cuentan con sus propios canales, lo cual añade estrés externo al interno ya presente. Esta sobrecarga corporal puede eliminar temporalmente uno o dos de los antiguos síntomas, a expensas de una serie de síntomas nuevos que pueden ser más invalidantes que los síntomas previos. Además, una vez que se elimina el remedio, los antiguos síntomas suelen volver a aparecer, aunque ahora de manera más degradada, lo que conlleva una mayor dificultad de recuperación de la salud.
De hecho, una característica sorprendente del enfoque homeopático es su alineación con el modo de pensamiento cuántico. Por tanto, recordemos que a principios del siglo xx los médicos se enfrentaron al comportamiento problemático de los electrones, que giraban alrededor del núcleo del átomo. Polarizados por el modo de pensamiento clásico, en términos de trayectorias bien definidas, sus pensamientos se basaron en el concepto de las órbitas electrónicas alrededor del núcleo, en total analogía con el concepto de las órbitas planetarias alrededor del sol. Pero una de las características enigmáticas fue que las transiciones electrónicas entre las diferentes órbitas eran responsables de la emisión de ondas electromagnéticas por parte de los átomos, mientras que el movimiento electrónico alrededor de la misma órbita no aporta emisión de luz alguna. Esto contradijo completamente la teoría electromagnética de Maxwell, que establecía que las ondas electromagnéticas se emitirían tan pronto como la carga eléctrica se moviera, en la misma órbita o no. A fin de resolver el enigma, un joven médico alemán llamado Werner Heisenberg propuso un modo revolucionario de pensamiento al establecer que las órbitas electrónicas no tenían realidad física. Ateniéndose a una postura filosófica positivista, argumentó que un átomo no debería caracterizarse por su contenido material (órbitas electrónicas alrededor de los núcleos), sino por la única cosa que podía observarse realmente: un conjunto completo de frecuencias electromagnéticas inmateriales. Basándose en esta brillante idea, fue el primero en desarrollar un marco mecánico cuántico coherente para explicar las propiedades atómicas basadas en las matrices transcendentales no conmutadas. El punto clave era considerar la matriz en su conjunto, y no los elementos individuales, para describir el movimiento electrónico, que no era observable por principio. Básicamente, ¿cómo sabemos que los átomos contienen electrones? Simplemente porque somos capaces de diseccionarlos, mediante un proceso denominado ionización. Pero, en cuanto contemos con un átomo neutro unificado, no dispondremos de medios para saber si existen electrones en su interior. Lo único que podemos observar es la serie de frecuencias electromagnéticas que el átomo es capaz de emitir, una vez excitado. Inferimos la existencia de electrones en el interior de un átomo porque podemos observarlos cuando están en el exterior. Esto es simplemente una inferencia lógica que no se basa en modo alguno en la observación.
Ahora, debemos tener claro que esta idea de definición de la realidad mediante una realidad inmaterial indivisible fue invocada por Hahnemann un siglo antes que Heisenberg. Y, con anterioridad a Hahnemann, existían diversas escuelas médicas que pretendían saber cómo funcionaba el cuerpo humano. Dicho conocimiento era una consecuencia de la disección de cadáveres, y no se basaba definitivamente en la observación de los cuerpos vivos. Hahnemann fue el primero en resaltar el hecho de que, por principio, era imposible saber realmente el modo de funcionamiento de un organismo vivo; del mismo modo en que, un siglo más tarde, Heisenberg fue el primero en resaltar que era imposible observar una órbita atómica2. Lo único que podemos aprender de un organismo vivo es una serie de síntomas que definen tanto estados de enfermedad como de salud. Un síntoma aislado no tiene significado alguno en sí mismo, ya que la realidad biológica reside en una serie de síntomas más o menos entrelazados. Cuando se conoce el conjunto completo de los síntomas, se conoce la enfermedad. De igual modo, si se conoce la serie completa de frecuencias electromagnéticas, se conoce el átomo. El conocimiento de una frecuencia única no permite la identificación del átomo y, de manera análoga, el conocimiento de un único síntoma no significa que sepamos cuál es la enfermedad. Este entramado en el organismo vivo impide su análisis como si se tratara de una máquina mecánica con partes interactivas bien definidas. Por ejemplo, cuando movemos la pierna: ¿estamos seguros de que únicamente se mueve esta y no el cuerpo entero? De hecho, el único modo de asegurarnos de que solo se mueve la pierna es arrancarla del cuerpo. Esta incapacidad de dividir algo en dos partes separadas es una mera consecuencia de las partes entrelazadas. Se trata claramente de una propiedad cuántica que se aplica tanto a los átomos como a los organismos vivos.
Por tanto, el entrelazamiento está enraizado en lo más profundo de la doctrina homeopática; lo cual fue claramente reconocido por Hahnemann hace más de dos siglos en su obra Organon, un término que significa instrumento: un método práctico y no un sistema de pensamientos. De nuevo, esta postura puramente epistemológica de Hahnemann con relación al tratamiento de las enfermedades se adapta perfectamente a la interpretación de Copenhague de la mecánica cuántica. Este es el motivo por el cual cualquier intento de comprender la homeopatía y los efectos de las altas diluciones, sin una base mecánica cuántica, está condenado al fracaso. Si la mecánica clásica es el lenguaje natural de los partidarios de la alopatía, la mecánica cuántica constituye el lenguaje natural de la homeopatía. Este es uno de los motivos principales del gran enfrentamiento entre los dos enfoques médicos. Lamentablemente para la homeopatía, los principios de la mecánica cuántica son no deterministas en esencia: en contraposición a la naturaleza determinista clara de los principios físicos clásicos. Por tanto, es fácil presentar las explicaciones mecanicistas detalladas en cuanto a la acción del tratamiento alopático, mientras que la acción de la homeopatía se basa en una reacción no predecible del organismo vivo, que implica una fuerza dinámica inmaterial.
Por ello, el primer paso que permite la comprensión del modo en que puede actuar la homeopatía es la familiarización con los principios de la mecánica cuántica. Lógicamente, esto se deriva del hecho de que la mecánica cuántica utiliza números complejos no observables que combinan una longitud con un ángulo de fase, y números reales no observables que tienen únicamente una longitud. Por tanto, en la raíz de cualquier mundo cuántico hallamos cosas materiales que son observables y ondas inmateriales que no lo son pero que, en cualquier caso, contienen toda la información necesaria para predecir qué cosas son materiales y qué cosas no. De manera similar, en homeopatía contamos con organismos vivos materiales con sus síntomas observables y transferencias de información inmaterial que, aunque no son directamente observables, rigen de cualquier modo el estado de enfermedad o salud del ente vivo.
La mecánica cuántica para los biólogos¿Quién no ha oído hablar o ha leído la famosa frase de Richard Feyman acerca de la mecánica cuántica?: “Creo que puedo afirmar con seguridad que nadie comprende la mecánica cuántica”3. ¿Se trataba simplemente de un chiste de un hombre jocoso o de una verdad profunda acerca del modo de actuación de la naturaleza? Nadie lo sabe, pero hay pistas en la literatura científica que indican que se trataba realmente de un chiste. La primera pista viene dada por una serie de documentos interesantes publicados en los años cuarenta por una pareja de matemáticos franceses4–7. La primera conclusión que puede extraerse de dichos documentos es que la mecánica cuántica podría definirse mediante una simple frase compuesta por muy pocas palabras: “No existe variable de estado”. Cualquier formalismo cuántico está plenamente enraizado en este simple principio.
A fin de comprender el modo en que las normas cuánticas surgen de esta simple frase, debemos considerar que, si todas las cantidades físicas son teóricamente medibles de manera simultánea, debería existir una variable de estado. Lo que se denomina variable de estado es una variable de la que pueden derivarse el resto de variables. Este es el planteamiento de la mecánica clásica. A su vez, si existen cantidades no medibles de manera simultánea, no puede existir variable de estado. Este es el planteamiento de la mecánica cuántica. La ausencia de variable de estado aporta una incertidumbre esencial, y significa que existen por derecho dos cantidades que no son simultáneamente observables o medibles.
Dicha incertidumbre implica que algunas predicciones son propensas a errores fundamentales y, por tanto, deberían expresarse en términos de probabilidades. Por ello, considerando para una cantidad física A la totalidad de predicciones ciertas (X1, X2,…, Xn) se debería considerar por principio cualquier predicción X como combinación lineal X = c1·X1 + c2·X2 +…+ cn·Xn (principio de descomposición espectral). Por tanto, la probabilidad de observar el elemento Xi es una función arbitraria f(ci) del coeficiente asociado ci. Si además el requisito posterior es que la función desconocida f fuera la misma para cualquier descomposición espectral, es posible demostrar que debería ser de modo que f(x·y) = f(x)·f(y), donde x e y son números complejos, es decir, números que tienen tanto una magnitud r como una fase φ: z = r·exp(i·φ). El siguiente requisito de que f sea una función continua conduce a la única solución aceptable: f(x) = |x|k, donde k > 06. Por último, utilizando una versión generalizada del teorema de Pitágoras, fue posible demostrar que solo son posibles dos valores de k: k = 1 (existencia de una variable de estado, lógica de Boole) y k = 2 (sin variable de estado, sin lógica de Boole)8. Para este último caso, la probabilidad de observar un elemento determinado viene dada por el cuadrado del coeficiente complejo correspondiente en la superposición lineal, una de los postulados básicos de la teoría cuántica8.
El siguiente paso es introducir las dos cantidades básicas que no pueden medirse simultáneamente. Como estamos buscando una teoría cuántica para los sistemas macroscópicos de alta densidad, tales como los organismos vivos, el número de cuantos N disponibles surge como variable esencial. Si se permiten ciertas fluctuaciones ΔN en el número de cuantos, puede demostrarse que la variable conjugada es necesariamente la fase cuántica φ con una relación de incertidumbre fundamental9:
El punto esencial aquí es que solo se incluyen los números puros sin unidades. Esto significa que dicha relación de incertidumbre es una invariable de escala, es decir, que la mecánica cuántica es el modo correcto de pensamiento a cualquier escala, atómica o macroscópica. La implicación es que no existe distinción fundamental entre el observador y el sistema observado, entre el sistema cuántico y el clásico. Aquí, el modo clásico de pensamiento se obtiene cuando puede determinarse con certidumbre el número total de cuantos; es decir, cuando ΔN = 0. La consecuencia es que la fase φ es, por tanto, una variable aleatoria que cambia de modo completamente arbitrario de un cuanto a otro (incoherencia). Pero, si el número total de cuantos no se conoce con certidumbre, la fase cuántica puede adoptar un valor bien definido (Δφ → 0) cuando ΔN → +∞. Esta situación describe un régimen cuántico que se observa rutinariamente a escala macroscópica en los fenómenos ferromagnéticos, ferroeléctricos, de superconductividad y superfluidez, por ejemplo. El cuanto tiene aquí el significado de una apariencia coherente colectiva de muchos organismos que no puede explicarse al considerar únicamente los pares de cuantos interactivos.
Se trata de la coherencia cuántica típica de situaciones de alta densidad que es pertinente en el agua en estado líquido9 y, por supuesto, en un organismo vivo10. Más importantemente, no puede observarse en casos diluidos (ΔN → 0). El punto interesante es que un “cuanto” no es necesariamente una partícula elemental, sino que puede ser un ion, una molécula, una proteína, una célula o incluso un ave o un pez. Esto quiere decir que un cuanto es cualquier cosa que pueda considerarse a una escala dada como una unidad conjunta, y no separable en partes más pequeñas. Por ejemplo, en homeopatía, se considera un cuanto al organismo vivo en su conjunto en estado salubre. Para dejar claro el argumento, hablemos de aves, considerando no una única ave sino una bandada (fig. 2). ¿Se han percatado de que cuando es posible contar con exactitud el número de aves de la bandada (caso diluido) el movimiento de cada ave parece errático e impredecible? Pero, por encima de un cierto número de aves por unidad de volumen, se hace imposible hacer el recuento de manera individual (ΔN > 0) y, como consecuencia, surge un comportamiento colectivo por encima de cierto umbral crítico. Ahora la bandada se mueve con un comportamiento colectivo maravilloso, coherente y suave, en lugar de errático y aleatorio. Lo mismo se aplica, por supuesto, a los bancos de peces.
Estos ejemplos muestran que la invarianza de escala de la relación (1) asociada a la existencia de los operadores de la creación y la destrucción en las teorías cuánticas de campos9 es una realidad tangible a todas las escalas, siempre que nos enfrentemos a una situación de alta densidad. De hecho, puede demostrarse que cualquier sistema cuántico podría mostrar globalmente un comportamiento clásico, con una trayectoria predecible computable acorde al principio de acción mínima11. En otras palabras, la mecánica clásica es simplemente una aproximación de la mecánica cuántica cuando surge la coherencia de fase.
Pero también conocemos a partir de la termodinámica que cualquier macroestado M, tanto en equilibrio como no, tiene entropía no mecánica S(M) = kB · log W(M), donde W(M) es el espacio de fase (posición, momentos) volumen compatible con un conjunto de macrovariables que permiten definir con precisión el macroestado. Como demuestra Edwin Thompson Jaynes, la segunda ley que establece que S(inicial) ≤ S(final) se deriva directamente del teorema de Liouville, que expresa que la condición necesaria de un cambio de un macroestado Mi a otro macroestado Mf puede ser reproducible por cualquier observador capaz de controlar únicamente el conjunto de las macrovariables que definen el macroestado M12.
A fin de establecer un nexo equitativo entre la entropía y la mecánica cuántica, consideremos un conjunto N de partículas de masa m incluidas en un cubo de borde L en contacto térmico con un baño térmico que fija el número de microestados (posiciones q y momentos asociados p) que son accesibles para este conjunto. Debido al movimiento de Brown, cualquier partícula tiene igual probabilidad de ser hallada en cualquier localización en el volumen V = L3 que conduce a una incertidumbre en la posición Δq = L a lo largo de las direcciones x-, y- o z. Por tanto, el número de los estados de posición debería ser Wq ∝ VN = (Δq)3N. Por otro lado, la teoría cinética de los gases nos aporta la densidad de probabilidad de observar una velocidad dada v a una temperatura T con una profundidad a media altura que mide la incertidumbre Δv en el conocimiento de las velocidades moleculares. Por tanto, el número de estados dinámicos correspondientes a una propagación Δp = m · Δv, debería ser Wp ∝ (Δp)3N. Por ello, el número total de estados en el espacio de fase debería ser W ∝ Wq · Wp ∝ (Δq · Δp)3N, con una constante de proporcionalidad universal que debería tener la dimensión de una acción mecánica a fin de garantizar que W sea un número sin dimensión. Identificando esta constante de proporcionalidad con la constante de Planck ħ, y teniendo en cuenta que S ≥ 0, se deriva que:
A diferencia de (1) que se aplica a cualquier escala, este segundo tipo de relación de incertidumbre impone que los átomos deberían tener un tamaño característico cercano a 0,1nm. Además, no depende de N, el número total de partículas idénticas que puede ser tan elevado como la constante de Avogadro. En su lugar, debido al valor muy pequeño de la constante de Planck, nos aporta la ilusión de un mundo cuántico que existe a escala muy pequeña que no puede ser directamente experimentado por nuestros sentidos macroscópicos. Esto proviene del hecho de que, históricamente hablando (2), se derivó anteriormente (1).
De hecho, deberíamos darnos cuenta de que (2) se trata simplemente de un caso especial (1) en el límite de la dilución infinita (N → 1 ⇒ ΔN → 0 and Δφ → +∞). Esto podría demostrarse fácilmente al comprobar que ħ es un cuanto de acción, que permite contemplar cualquier tipo de energía E como pulsación ω = Δφ/Δt, con arreglo a la relación de Planck-Einstein: E = ħ · ω. Aquí, se espera que un conjunto N de cuantos no distinguibles tenga una energía total E = N·ħ·ω; lo que significa que cualquier incertidumbre ΔN en el número de cuantos ΔN se traduciría en una incertidumbre correspondiente en la energía ΔE = ΔN · ħ · ω. Por tanto, la relación de incertidumbre fundamental ΔN·Δφ ≥ ½ puede volver a enunciarse como (ΔE/ħ · ω) · (ω · Δt) ≥ ½, conducente a:
Un punto esencial que se pasa a menudo por alto en la literatura de la mecánica cuántica es que el tiempo de incertidumbre t que aparece en (3) no es definitivamente el tiempo t utilizado en las transformaciones de Lorentz, o el tiempo t que rige la ecuación dependiente del tiempo de Schrödinger. Según muestra su definición, Δt = Δφ/ω, corresponde a un tiempo “interno” íntimamente asociado a la rotación de un vector de fase enclavado en el objeto cuántico. Por tanto corresponde a una vida útil intrínseca, si se prefiere, al tiempo “adecuado” de la teoría de la relatividad. De manera similar, la energía E que aparece en (3) no constituye el valor propio de un operador hamiltoniano, sino en su lugar una energía interna termodinámica asociada a un conjunto de cuantos indistinguibles. Por tanto, no existe necesidad de invocar la existencia de un operador de tiempo conjugado al operador hamiltoniano para justificar (3). La relación (3) es simplemente una reformulación de (1) utilizando la energía total y la vida útil en lugar de un número de cuantos y una fase cuántica. Los operadores no conmutados responsables de (3) son simplemente el operador de número y el operador de fase de las teorías cuánticas de campo, en lo que se refiere a (1).
Ahora, en el caso de una partícula simple libre (N = 1) de masa m y de la velocidad v, tendríamos E = p2/2m o ΔE = p · Δp/m, donde p = m · v es el momento asociado. La formulación de v = p/m = Δq/Δt, conduce a Δt = m · Δq/p y la relación ΔE · Δt ≥ ħ/2 se convierte en (p · Δp/m) · (m·Δq/p) = Δp · Δq ≥ ħ/2. Esto refleja claramente que (2) está de hecho arraigada en (1) o (3), debiendo considerarse una aproximación a la dilución infinita de las teorías cuánticas de campo. Al igual que con la energía, debemos tener en cuenta el hecho de que ħ es un cuanto de acción, que permite la asociación a cualquier valor del momento p de un vector de onda característico k = p/ħ, con arreglo a la relación de Broglie-Schrödinger. Esto significa que tanto las ecuaciones de Schrödinger como las de Dirac deberán considerarse una aproximación a la dilución infinita de las teorías cuánticas de campo aplicadas a un objeto cuántico individual (N = 1) aislado de otros objetos similares.
Como (1) y (3) se aplican a situaciones de alta densidad, se hace obligatorio no ignorar las excitaciones virtuales procedentes del vacío entre los objetos cuánticos que son responsables de los desplazamientos de los niveles energéticos en los átomos de Lamb13 o de la incidencia de fuerzas de atracción entre las placas conductoras (efecto de Casimir)14. A fin de comprender esta importancia del vacío, volvamos a la explicación cuántica de la estabilidad atómica. Básicamente, basándonos en (2), resulta que es posible aportar un elevado momento Δp al electrón tan pronto como Δq sea demasiado pequeño. Este es el efecto cuántico que impide que los electrones colapsen contra los núcleos, según la predicción de la física clásica. Demostremos ahora que trasladarnos a (3) nos permite obtener una percepción más profunda de lo que ocurre realmente cuando el electrón se acerca demasiado al núcleo.
Por tanto, la naturaleza relativista de la electrodinámica cuántica permite la creación de materia y/o radiación a partir del vacío, así como su destrucción dentro del mismo, lo que crea una equivalencia de facto entre los conceptos de energía y vacío. De manera específica, cuanto más reducimos la escala de la observación espaciotemporal más se posibilita la tenencia de una masa M o una energía E = M · c2. El electrón y su antipartícula, el positrón, constituyen las partículas con menor masa por naturaleza, pero aun así una debe tener una energía de al menos 1,02 MeV para crear un par electrón-positrón. Esto se hace posible en cuanto el tamaño de este vacío se sitúa en el orden de 0,1 pm, puesto que ħ · c ≈ 197 MeV · fm. Por tanto, cualquier electrón que se aproxime a 1fm del núcleo atómico se encontrará con un par virtual electrón-positrón. El electrón no alcanzará nunca el núcleo, ya que se desintegra al encontrarse con el positrón virtual, liberando el electrón asociado; lo que a su vez se convierte en observable, con energía cinética en exceso que es ampliamente suficiente para escapar de la atracción de Coulomb. Todo esto tiene lugar a una escala temporal del orden de attosegundos, dejando al observador potencial con la ilusión de un electrón permanente que se escapa “milagrosamente” de la atracción de Coulomb del núcleo.
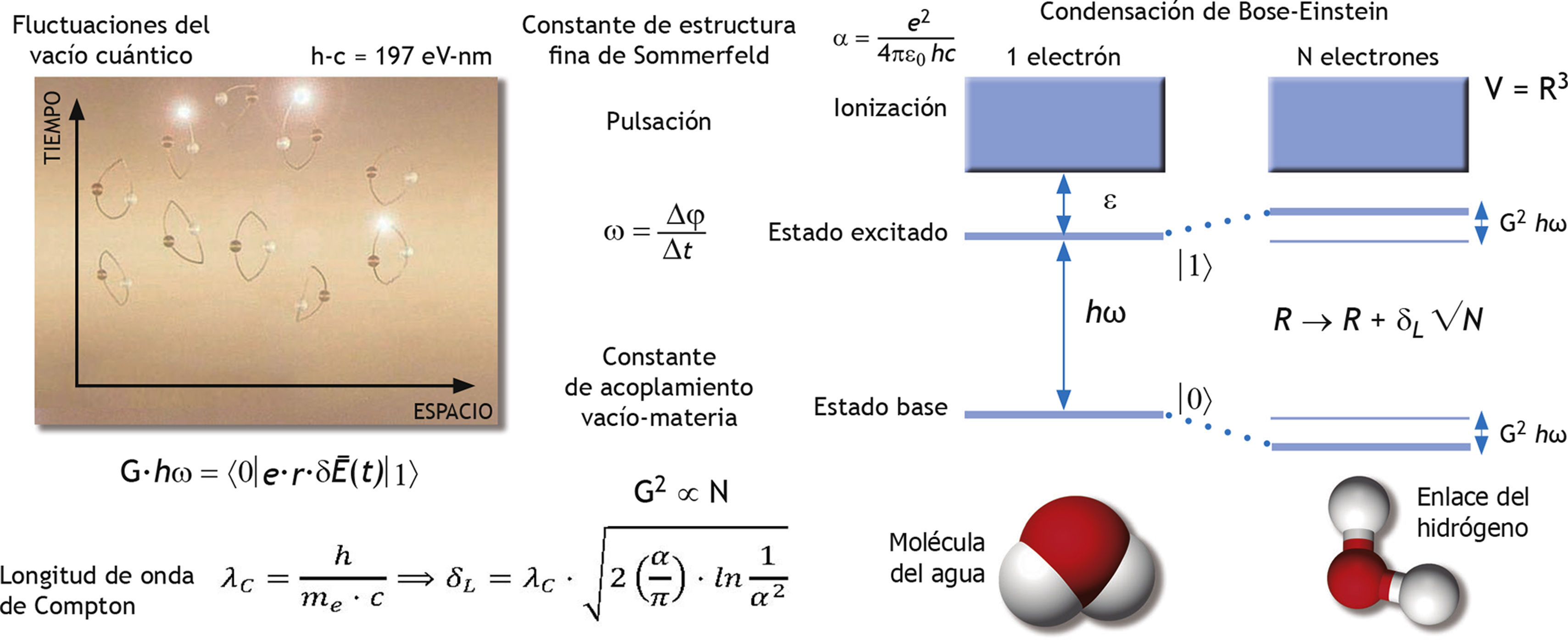
Este mecanismo funciona bien debido a la imposibilidad de distinguir dos electrones. Por tanto, a nivel de campo cuántico, se puede argumentar que los electrones que rodean el núcleo son creados y destruidos permanentemente por el vacío atómico. De media, cualquier núcleo que incluya Z protones estará siempre rodeado de Z electrones; pero estos electrones no son definitivamente partículas permanentes, sino entidades bastante efímeras que aportan la ilusión de corpúsculos indestructibles debido a su carácter indistinguible, ligado a nuestra incapacidad de diferenciar entre un electrón que surge del vacío y otro que desaparece casi simultáneamente en el mismo vacío. La prueba de que esta extraña imagen de la estabilidad atómica es correcta proviene de la existencia de los desplazamientos de Lamb, la evidencia irrefutable de esta participación activa del vacío en la energía de enlace entre los electrones y los núcleos. Por tanto, puede demostrarse que al “comerse” su vacío, los átomos incrementan su tamaño mediante una pequeña cantidad universal δL que depende únicamente de la constante de estructura fina α de Sommerfeld y de la longitud de onda λC de Compton, calculada a partir de la masa en reposo me del electrón15:
Ahora, la invarianza de escala de (1) garantiza que este mecanismo no se limita a la interacción entre los electrones y los protones en los átomos. También explica la atracción de Van der Waals entre las moléculas y, más importantemente, el enlace del hidrógeno en las moléculas del agua (véase sección siguiente). El vacío cuántico es probablemente responsable también del increíble poder catalítico de las enzimas en biología, que son capaces de realizar —a temperatura y presión ambientes, y con elevado rendimiento— reacciones químicas que son bastante difíciles de lograr en un recipiente. Como ħ · c ≈ 197eV · nm, resulta que un vacío de 1nm es capaz de generar fotones de rayos X con una energía cercana a 200eV, que ningún enlace químico es capaz de resistir. Por ello, una enzima que utilice cavidades nanométricas consigue lograr, a temperatura y presión ambientes, reacciones químicas que son imposibles a escala macroscópica. El secreto radica simplemente en el control de las fluctuaciones naturales del vacío cuántico.
Obviamente, en lo que se refiere a las interacciones de Van der Waals, no existe necesidad de invocar en tal caso la creación-destrucción de los pares de electrones/positrones responsables del enlace químico covalente. Aquí, la creación/destrucción de fotones carentes de masa procedentes del vacío, una situación que demanda mucha menos energía, es responsable de la adherencia entre moléculas de Van der Waals.
Por tanto, debido a (3), cualquier molécula se halla permanentemente rodeada de un campo virtual de fotones que emergen del interior y exterior del vacío que los rodea. Cuando dos moléculas se acercan lo suficientemente, sus campos virtuales fotónicos respectivos se solapan; rompiendo la simetría esférica de las moléculas aisladas. Debido a esta rotura de la simetría, los fotones virtuales con una longitud de onda superior a la distancia intermolecular quedan excluidos del espacio entre las dos moléculas, lo que fuerza su adhesión. Por ello, a nivel cuántico de campos, la atracción de Van der Waals deberá considerarse un tipo de interacción de agotamiento que implica a los fotones virtuales en lugar de las partículas de la materia.
Este maravilloso mecanismo de adhesión universal, que amalgama materia y vacío, se mantiene normalmente oculto al invocar el enlace químico para la escala atómica y las capacidades de polarización atómicas, o constantes de Hamaker para la escala molecular. El principal problema de llevar a cabo dicha mascarada es sustituir el efecto cuántico de muchos cuerpos que incluyen fotones con una energía de entre 0 y varios cientos de eV, por una interacción entre dos cuerpos con unas pocas eV para enlaces químicos, y unos pocos meV para los enlaces de Van der Waals. Esta aproximación bastante drástica funciona bien únicamente para situaciones de dilución, descomponiéndose completamente en cuanto la densidad se hace superior a un valor crítico, con elevada dependencia del número de electrones y núcleos implicados en la interacción. En tales casos, uno se ve obligado a invocar a los denominados “efectos específicos” para explicar los hechos experimentales. Dichos efectos específicos son, de hecho, únicamente el precio a pagar por separar la materia del vacío circundante.
Nueva visión del aguaUna de las primeras sustancias que se beneficia de un tratamiento cuántico completo, incluyendo el vacío, es el agua. Se han publicado muchos datos9,16, por lo que únicamente reportaremos aquí las conclusiones. El principal resultado es que el enlace del hidrógeno entre las moléculas de agua deberá considerarse un enlace coherente de Van der Waals. Por coherente entendemos aquí que las moléculas y el vacío del agua se funden a través de un campo electromagnético interno que se obtiene del vacío, atrapado en los denominados “dominios de coherencia”.
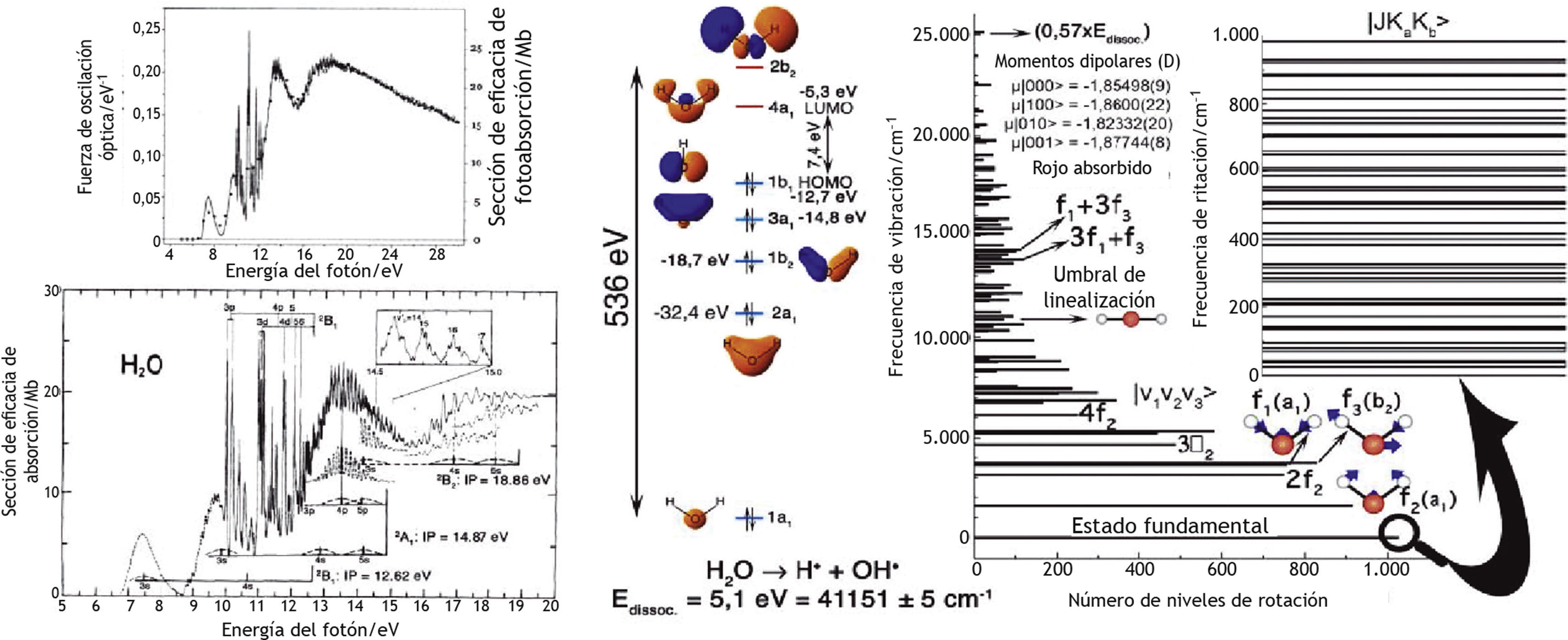
La función de este campo electromagnético interno es llevar a cabo excitaciones virtuales de las moléculas del agua hacia un nivel de Rydberg localizado en los átomos del oxígeno situados 0,5eV por debajo de su umbral de ionización (ca. 12,6eV). Como ocurre siempre en los enfoques del campo cuántico, deberán tenerse en cuenta todas las vías posibles conducentes a este nivel localizado. Esto significa una excitación directa en el estado base y en las transiciones indirectas a través de otros niveles discretos (adición), así como en cualquier nivel energético localizado en el continuum (integral). Por tanto, las propiedades del agua se rigen mediante fuerzas osciladoras que abarcan todo el espectro de excitación protónica (0-200eV) y no una única excitación HOMO-LUMO, o un potencial de ionización único.
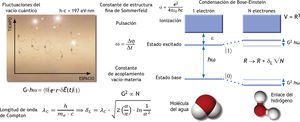
Como estas excitaciones electromagnéticas provienen del vacío interno de las moléculas del agua, y no del exterior, constituyen necesariamente excitaciones virtuales; es decir, de manera que ΔE · Δt < ħ/2, con fotones que adquieren una masa negativa a fin de permanecer atrapados entre las moléculas del agua. La principal consecuencia observable de esta mezcla coherente interna pero invisible de materia, radiación y vacío es la apertura de una brecha de coherencia no clásica que obliga a las moléculas del agua a adherirse entre ellas, de manera más eficiente que una mera atracción de Van der Waals, que implica únicamente una rotura de simetría. En este caso, existe tanto rotura de simetría como condensación de Bose-Einstein de los fotones virtuales que se intercambian constantemente entre las moléculas del agua (fig. 3). Esta aparición de la coherencia de fase cuántica entre la materia y la radiación se enmascara normalmente como “enlace del hidrógeno”, a fin de reducir el problema entre muchos organismos a una interacción específica entre dos cuerpos.
Principios físicos tras la formación de los dominios de coherencia del agua. La absorción de fotones virtuales que emergen continuamente del vacío cuántico dentro de un ensamblaje de N electrones pertenecientes a las moléculas del agua transforma su forma, desde una estructura trigonal a una tetrahédrica con un incremento de tamaño del volumen total que se rige por la constante universal δL función de la longitud de onda de Compton del electrón λC y de la constante de estructura fina α de Sommerfeld. Dependiendo de la constante de acoplamiento G entre la materia y los campos electromagnéticos de punto cero a través de un estado excitado localizado bajo el umbral de ionización de la molécula del agua, podría abrirse una brecha de coherencia fusionando las moléculas del agua y los fotones en un dominio de coherencia. Esta condensación cuántica de Bose-Einstein es denominada enlace del hidrógeno por parte de químicos y biólogos.
Este enmascaramiento explica por qué es tan difícil definir claramente cuál es la naturaleza real del enlace del hidrógeno, existiendo mucha confusión latente alrededor de su naturaleza putativa covalente frente a la naturaleza electroestática17. De hecho, se trata de un debate completamente inútil; ya que se trata de capturar a través de una ecuación de Schrödinger, o a través de una interacción de Coulomb, que se aplican rigurosamente a una molécula individual infinitamente diluida, un fenómeno que aúna varios millones de moléculas indistinguibles.
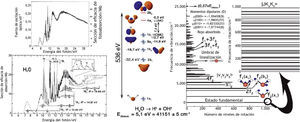
Por tanto, un dominio de coherencia se compone de una gran cantidad de moléculas de agua densamente compactas que muestran un comportamiento colectivo coherente, al igual que una bandada densamente compacta de aves en el cielo se comporta como una entidad inseparable autónoma. El tamaño de estos dominios coherentes viene fijado por la brecha energética existente entre el estado base y el estado excitado perseguido. Para el agua, esta brecha es de alrededor de 12eV, correspondiente a una longitud de onda fotónica de alrededor de 100nm. De este tratamiento cuántico pleno se deduce que el agua en fase líquida deberá considerarse un medio nanoestructurado y no un líquido aleatorio homogéneo. Lamentablemente, dicha predicción teórica parece estar en completo desacuerdo con las mediciones NMR18,19 o de difusión de neutrones20,21, que en su lugar apuntan a una estructura homogénea por debajo de la escala molecular, en forma de red vacilante de enlaces del hidrógeno.
De hecho, otras mediciones espectroscópicas tales como IR22,23, Raman24, absorción25 o difusión de rayos x26–28 (pero véase Clark et al29 para refutación) precisan realmente un modelo de dos estados para el agua en fase líquida, respaldando la visión del dominio de coherencia. Esta falta de acuerdo entre los científicos que trabajan en el campo del agua es uno de los motivos principales de por qué la hipótesis sobre dominios de coherencia se sigue considerando con sospecha. Recientemente, el nuevo modelo cuántico ha clarificado la situación, demostrando que los dominios de coherencia no pueden formarse en sistemas 3D uniformes, tales como el agua pura en fase líquida, debido al hecho de que el número mínimo de electrones necesarios para alcanzar la estabilidad en 3D es muy superior al número de átomos N, por lo que dicha estabilidad no puede lograrse30. Sin embargo, el modelo no admite la aparición de estructuras coherentes en la superficie de los volúmenes mesoscópicos existentes. Esto significa que los dominios coherentes del agua pueden producirse en agua en fase líquida a granel, siempre que estén presentes nanoburbujas u otros coloides.
De ahí que deberán considerarse seriamente los efectos cuánticos procedentes de las fluctuaciones del vacío, conducentes a la formación de dominios coherentes, antes de hacer tentativas sobre el modelado de las propiedades del agua en fase líquida. Ignorar la influencia del vacío y de la estructura de los dominios de coherencia en presencia de nanoburbujas conllevaría resultados contradictorios y controvertidos, reportados en publicaciones pasadas, donde el estatus exacto de los gases disueltos no ha sido estudiado.
Conviene resaltar que los conceptos tales como átomos, iones, moléculas y enlaces constituyen modos convencionales de pensamiento que sustituyen al acoplamiento convencional materia/vacío a través del intercambio de fotones virtuales, mediante cosas más tangibles con un tamaño o longitud característicos (radios atómicos o iónicos, así como longitudes de enlaces). Una longitud característica mide, de hecho, el rango espacial donde existe la coherencia de fase cuántica entre los núcleos y electrones. A esta longitud característica se asocia automáticamente una frecuencia característica f = ΔE/h, que se rige por la profundidad de la brecha de coherencia ΔE que se crea cuando la materia, el vacío y los fotones permanecen confinados juntos, oscilando en fase a esta frecuencia característica f. Conviene resaltar que dicha frecuencia se vuelve a desplazar sistemáticamente en relación a las frecuencias f’ = c/λ de las excitaciones virtuales que son responsables de la aparición de la coherencia. En el agua, por ejemplo, son las excitaciones virtuales en el dominio UV (ΔE ≈ 12eV, λ ≈ 100nm, f’ ≈ 3 PHz) las que dan lugar al enlazamiento del hidrógeno que implica intercambios fotónicos virtuales a nivel de los infrarrojos medios (ΔE ≈ 200 meV, f ≈ 39 THz, λ ≈ 10μm) entre las moléculas del agua.
Por tanto, consideremos un electrón perteneciente a una molécula de agua dada, tomando un fotón virtual de energía ΔE del vacío. De acuerdo a (3), la vida útil máxima Δt de este fotón virtual viene dada mediante Δt ≈ ħ/ΔE. Durante este tiempo, el fotón virtual es capaz de propagarse a una distancia máxima Δx ≈ c/Δt, portando un momento Δp ≈ ħ/Δx hacia otro electrón perteneciente a la molécula de agua vecina. Por tanto, la fuerza existente entre el emisor y el absorbedor viene dada mediante: f = Δp/Δt ≈ ħ · c/(Δx)2. Introduciendo ahora la constante de estructura fina α sin dimensión de Sommerfeld, que mide el acoplamiento del fotón virtual a otras partículas virtuales del vacío que pueden encontrarse durante la distancia Δx recorrida en el vacío (fig. 3) origina una fuerza f = α · ħ · c/(Δx)2. Se trata simplemente de la fuerza de Coulomb clásica entre dos electrones pertenecientes a dos moléculas de agua que están lo suficientemente cerca para emitir y absorber un fotón virtual durante la ventana de tiempo enmarcada por las relaciones de incertidumbre cuántico-mecánicas. Al promediar este tipo de interacciones electromagnéticas entre todos los electrones y todas las moléculas del agua en un dominio de coherencia, se explica la aparición de una interacción específica denominada “enlazamiento del hidrógeno”.
Esto explica por supuesto por qué el agua —a pesar de su peso molecular bastante bajo— es un líquido y no un gas, al igual que explica por qué su densidad se incrementa al calentar el líquido desde T ≈ 230K a T = 4°C31. El punto clave tras esta denominada “anomalía de densidad” es la participación activa del vacío físico a través de las interacciones electrónicas de muchos organismos que no pueden reducirse a meras interacciones directas entre los objetos ficticios denominados “moléculas del agua”. La realidad cuántica física que reside en el agua en estado líquido se asemeja, por tanto, a un electrón libre no homogéneo y altamente correlacionado estabilizado por los núcleos atómicos en las distancias dos o tres veces mayores en magnitud al tamaño característico del objeto molecular. Este comportamiento colectivo de largo alcance es una característica típica de la aparición de coherencia cuántica entre las nubes de electrones.
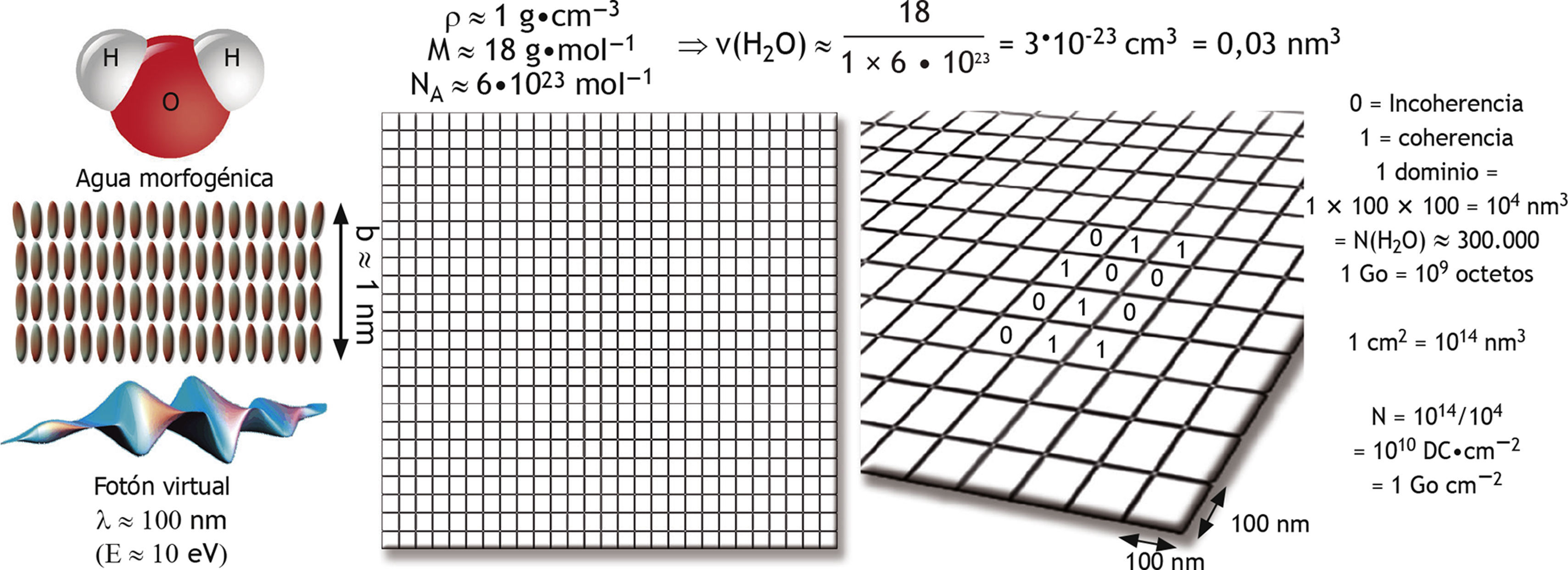
Comprensión de los efectos de la alta diluciónEstamos ahora en situación de debatir qué ocurre cuando una solución concentrada se diluye por debajo del umbral de Avogadro. De hecho, hablando en términos de mecánica cuántica, no existe dilución alguna porque la densidad en cada paso sigue siendo la de un líquido. La única cosa que ocurre al diluir un soluto es que se sustituye la coherencia cuántica regida por el soluto por otra coherencia cuántica regida por el agua. En otras palabras, cuando la concentración del soluto es elevada, la concentración del dominio de coherencia del agua es baja. Una vez diluida, la concentración del soluto disminuye; lo que significa que la concentración del dominio de coherencia del agua aumenta. Cuanto mayor es la dilución del soluto, mayor es el número de dominios de coherencia del agua. Como se refleja en la figura 4, para una energía de excitación ħω ≈ 10eV, un dominio de coherencia reúne en torno a 300.000 moléculas de agua, aunándolas como objeto cuántico único que comparte una fase cuántica definida con un campo electromagnético interno de infrarrojos fluctuante.
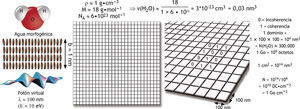
El agua morfogénica es un término genérico que cubre todos los casos en los que las moléculas del agua adoptan una estructura 2D de 4 mono-capas, a fin de hidratar cualquier materia orgánica e inorgánica. El acoplamiento con los fotones virtuales con una longitud de onda de alrededor de 100nm, que permite alcanzar un estado excitado localizado a 10eV por encima de la energía de estado base de las moléculas del agua, define un mosaico de dominios de coherencia que reúnen unas 300.000 moléculas de agua y son capaces de retener alrededor de 1 Go · cm–2 de información.
Es dicho objeto cuántico el que podría manipularse durante la dilución. Dependiendo de la naturaleza química del soluto, deberá establecerse una partición característica dada entre este, el dominio de coherencia y el resto de moléculas de agua que permanecen en un estado incoherente. Conviene destacar que las moléculas de agua en este estado incoherente comparten necesariamente la misma extensión espacial (alrededor de 100nm) que las moléculas de agua en un estado coherente. La diferencia reside en el estado incoherente: la atracción entre las moléculas de agua conlleva una interacción de Van der Waals que es mucho más débil que el enlazamiento del hidrógeno. Otra consecuencia es que la densidad del agua incoherente es poco mayor que la del agua coherente como en este último caso, ya que las moléculas de agua son un poco mayores debido a su acoplamiento con el vacío cuántico.
Esta organización supramolecular de las moléculas de agua en dominios de coherencia tiene algunas consecuencias importantes. En primer lugar, como los dominios de coherencia no pueden ser tridimensionales, no pueden observarse en el agua pura en fase líquida. A fin de autoorganizarse, debe estar presente otra sustancia que no sea agua. Para el agua en fase líquida, los mejores candidatos son las nanoburbujas y/o nanopartículas de gas. Esto explica obviamente la importancia de la sucusión en los preparados homeopáticos. Sin la agitación rigurosa del líquido, la incorporación de gases atmosféricos como las nanoburbujas no sería eficiente. De igual modo, la dispersión de partículas coloidales nanométricas procedentes, bien del preparado (lactosa), o bien de las paredes del contenedor, no sería posible. El hecho es que los nanoobjetos sistemáticamente detectados en cualquier dilución homeopática confirman plenamente esta perspectiva.
Como los dominios de coherencia se ensamblan a las moléculas de agua a través de los fotones virtuales, se deduce que el agua debería ser altamente sensible a los campos electromagnéticos en ciertos rangos de frecuencia (principalmente ultravioletas e infrarrojos lejanos). Además, como los electrones forman plasma atrapado coherente, los dominios de coherencia pueden comportarse como pequeños magnetos, haciendo también que el agua sea altamente sensible a las ondas de radio. Esto explica claramente los efectos bien documentados de los campos magnéticos y las ondas de radio en la cristalización, deterioro, crecimiento de biopelículas, etc. Y, por cierto, esto podría explicar los grandes incrementos de las patologías degenerativas crónicas que podrían estar inducidas por la niebla electromagnética que se están produciendo sin límite en la actualidad. También se deduce que los preparados homeopáticos deberían realizarse en un lugar donde se haya controlado cuidadosamente cualquier campo de fuerza electromagnética.
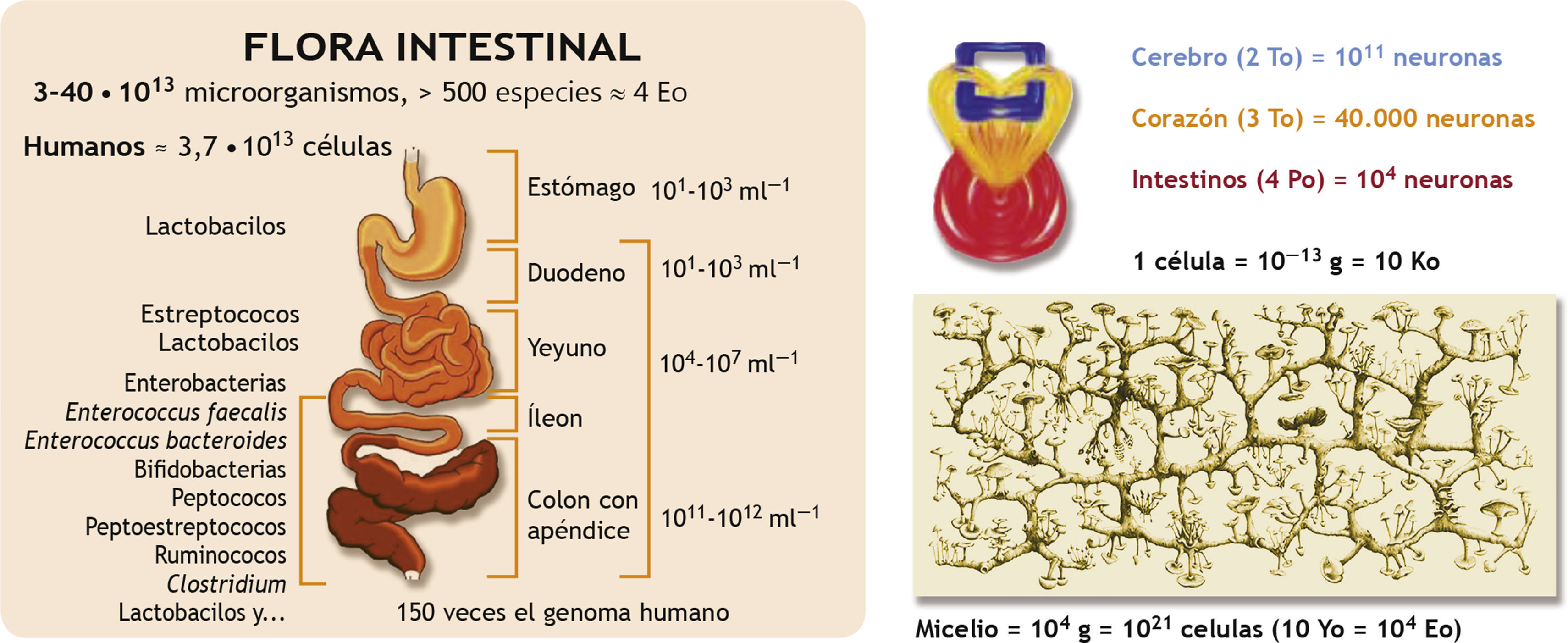
Consideremos ahora cómo se podría dejar una impronta en el agua de una información proveniente de un soluto. Una primera posibilidad sería una estructura de mosaico, donde el dominio de coherencia se alternara con dominios de incoherencia de tamaño aproximadamente igual. La cifra xx aporta una representación esquemática de esta hipótesis, en la que se podría asignar el número “1” a un dominio de coherencia y el número “0” a un dominio incoherente. Ello transforma el agua en un conjunto de bits que podría memorizar cierta información. A fin de evaluar la cantidad de información que podría almacenarse en este agua morfogénica, podríamos suponer una estructura de 4 capas de moléculas de agua, originando un grosor de capa de b ≈ 1nm (fig. 4). Entonces se deduce que un centímetro cuadrado de agua morfogénica podría albergar alrededor de 1 Go de información. A fin de comprender el significado de esta cifra, supongamos que una célula rodeada por su bicapa lipídica tiene un área de alrededor de 500μm2. Como la membrana consta de dos lados, cada centímetro cuadrado es capaz de albergar 2 Go de información, originando una capacidad de almacenamiento de 500 × 10–8 × 2 × 109 octetos ≈ 10.000 octetos = 10 ko por célula. Como seres humanos, nuestro organismo contiene alrededor de 3,7 × 1013 células; lo cual significa que el cuerpo entero tiene una capacidad de almacenamiento de 3,7 × 1013 × 104 ≈ 4 × 1017 octetos = 400 Po (1 Po = 106 Go = 1015 octetos). Teniendo en cuenta que 5min de vídeo H.264 (formato MP4) se corresponden con 4 Go de datos, el cuerpo humano es capaz de memorizar a través de su membrana 5 108min de vídeo H.264. Como el año contiene alrededor de 525.600min, un cuerpo humano puede constituir un disco duro con un almacenamiento de 951 años de vídeo H.264. De forma alternativa, debemos considerar que, al menos, 109 bits por segundo procedentes de nuestro entorno alcanzan nuestro cuerpo. Con nuestra capacidad de almacenamiento de 400 Po en las membranas, esto se traduce en 3,2 × 109 s ≈ 100 años de vida humana, ya que 1 año ≈ 3,1 × 107 s. Por tanto, un organismo humano tiene la capacidad de memorizar esta interacción con el entorno durante la totalidad de su vida biológica.
La clasificación de los tres órganos principales capaces de mostrar actividad neuronal puede resultar también de interés (fig. 5). La clasificación con arreglo al número de neuronas arroja el siguiente resultado: cerebro (≈ 1011 neuronas), intestino (≈ 108 neuronas) y corazón (≈ 40.000 neuronas). Clasificaremos ahora estos 3 órganos con arreglo a la capacidad de almacenamiento de las membranas. Para el cerebro, con 146.000 neuronas por metro cuadrado, obtenemos alrededor de 1 m2 para 1011 neuronas, es decir, una capacidad de almacenamiento de 2 × 109 × 104 = 2 × 1013 octetos = 20 To. Para el corazón, formado por 3 billones de células que suponen un área de 500μm2 por célula, obtenemos una capacidad de almacenamiento de 3 × 109 × 104 = 3 × 1013 octetos = 30 To. Por último, el área intestinal, con alrededor de 200 m2 = 2 × 106cm2, resulta ganadora con sus 2 × 109 × 2 × 106 = 4 × 1015 octetos = 4 Po de capacidad de almacenamiento.
Cabe resaltar que la capacidad de memorización de información en la capa morfogénica del agua que rodea cualquier membrana lipídica no se limita a los seres humanos. Cualquier célula viva tiene la capacidad de hacerlo. En particular, se sabe que un ser humano almacena en su intestino hasta 4 × 1014 bacterias (fig. 5), lo que supone una capacidad de almacenamiento de 4 × 1014 × 104 = 4 × 1018 octetos = 4 Eo. Pero la mayor memoria desplegada por un único organismo se halla en los micelios, algunos de ellos con edades de 1.500 años, capaces de alcanzar una masa de 100 toneladas correspondientes a alrededor de 1021 células que se traducen en una capacidad de memoria de 10 yotta-octetos, es decir, un billón de Po. Estas consideraciones podrían ayudar a asimilar que los seres vivos son capaces de almacenar gran cantidad de información dentro del agua morfogénica que rodea a sus membranas lipídicas. A través de nuestra agua morfogénica, estamos constantemente comiendo y bebiendo no solo materia, sino también una gran cantidad de información inmaterial. A través de la circulación constante —y del intercambio de información dentro de nuestro organismo— cualquier parte de este se halla entrelazada con otras, dando lugar a un cuanto o a una fuerza dinámica inmaterial utilizando el vocabulario de Hahnemann.
Si la capacidad de memorizar información es esencial para cualquier ser vivo, la capacidad de procesarla y transferirla no es menos crucial. El modo más obvio de procesar y transmitir información es depender de los campos electromagnéticos que son capaces de viajar a velocidades cercanas a la velocidad de la luz. Como se muestra en la figura 3, muy en el interior de un dominio de coherencia del agua, existe un campo electromagnético asociado a cualquier transición electrónica entre el estado base de las moléculas del agua hacia un estado excitado con una pulsación de ω, de manera de ΔE = ħ · ω. Esto significa que cualquier dominio de coherencia porta una onda electromagnética monocromática cuya frecuencia f = ω/2π se rige por la energía del estado excitado implicado en la transición electrónica. Cambiar esta energía de excitación significa cambiar la frecuencia asociada. Entonces, un resultado bien conocido del análisis de Fourier es que cualquier tipo de señales complejas debe contemplarse como una suma de ondas monocromáticas. Esto significa que cualquier tipo de señal electromagnética, aun cuando pudiera generarse una de ellas altamente compleja si se dispusiera de suficientes dominios de coherencia, podría codificar su propia frecuencia, ligeramente diferente del resto.
Como se muestra en la figura 6, una única molécula de agua se caracteriza por millones de niveles energéticos excitados, dependiendo del estado exacto de electro-vibro-rotación de la molécula. Dado que cuanto mayor sea la dilución mayor será el número de dominios de coherencia, no es sorprendente que sea mayor la capacidad de codificar un espectro electromagnético de un ADN completo, un fármaco complejo e incluso un órgano, planta o árbol completos. De este análisis riguroso se deduce que cualquier remedio homeopático puede contar, a través de sus dominios de coherencia constitutivos en 2D, una impronta electromagnética inmaterial que crece en complejidad a medida que se incrementa la dilución. En este sentido, traspasar de largo el límite de Avogadro no debería contemplarse como un problema, y pretender que los preparados homeopáticos no contienen nada es únicamente la consecuencia de una actitud corta de miras que se centra solo en la materia dentro de un marco de pensamiento no cuántico. Teniendo en cuenta el hecho obvio de que nuestro universo está hecho de materia y radiaciones regidas por las reglas cuántico-mecánicas en todas las escalas, permiten que la homeopatía merezca unas credenciales científicas.
Espectro energético de una molécula de agua con arreglo a la mecánica cuántica. Cada nivel energético aquí mostrado podría utilizarse como el estado excitado asumido en la Figura 3. Se deduce que una serie de dominios de coherencia del agua es capaz de almacenar cualquier tipo de señal electromagnética, fuera cual fuere su complejidad.
Dentro del marco conceptual de pensamiento aquí presentado, la acción de dosis ultrabajas debería considerarse una alternativa terapéutica real que no “viola” ningún conocimiento científico, sino que, en su lugar, lleva a cabo una acción específica que se halla al nivel de las más elevadas sensibilidades y complejidades biológicas. Más específicamente, no debería sorprender que los remedios homeopáticos pudieran conectar o desconectar algunos genes importantes, iniciando una cascada de acciones genéticas para corregir la expresión génica que se ha vuelto errónea, y que ha producido el trastorno o la enfermedad32,33. Se deduce que el sistema inmune, los mecanismos de la inflamación y los leucocitos se hallan dentro de los objetivos de los efectos homeopáticos. Los esfuerzos por excluir a la homeopatía de la práctica médica racional34 carecen por tanto de sentido35. Lo que es peor, tratar de bloquear la financiación para la investigación homeopática sobre la base de que la homeopatía = placebo, debería considerarse una actitud criminal. En homeopatía, la capacidad de autocuración del organismo se explota a plena capacidad, evitando plenamente los efectos secundarios: un problema que plaga la práctica alopática. Como actualmente la mayoría de enfermedades constituyen procesos multifactoriales, la homeopatía, con su enfoque multifacético vinculado a la posibilidad de utilizar diluciones ultraelevadas, debería considerarse una respuesta viable a enfermedades complejas (tales como diabetes, esquizofrenia, cáncer o aterosclerosis) que implican cientos de variantes genómicas que interactúan entre ellas, al igual que con los factores medioambientales. De forma más general, considerando que todo está entrelazado, el pensamiento cuántico-mecánico se hace obligatorio a la hora de analizar los seres biológicos vivos. Este es el reto al que se enfrenta cualquier médico o biólogo que desee realmente curar a las personas de sus enfermedades.