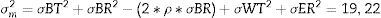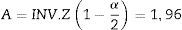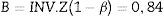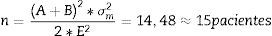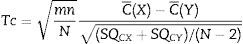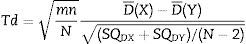Ensayo clínico cruzado y aleatorizado para comparar 2 modelos farmacocinéticos de propofol usando índices de entropía

Resumen

Introducción

Hay 2 modelos farmacocinéticos diferentes para la administración de la anestesia total intravenosa con propofol (Marsh y Schnider); las diferencias entre los parámetros podrían tener algún impacto sobre la profundidad anestésica.

Objetivo

Comparar la variabilidad de la profundidad anestésica durante administración de infusión de propofol con los modelos de Marsh y Schnider para determinar si hay diferencias significativas que sugieran que uno de los modelos es superior en lograr una profundidad anestésica más estable y predecible.

Métodos

Estudio clínico cruzado, controlado y aleatorizado llevado a cabo en 16 pacientes programados para cirugía ambulatoria de ortopedia. Los pacientes fueron asignados aleatoriamente a: a) infusión controlada por objetivo de propofol con el modelo de Marsh a una concentración objetivo en sitio de efecto de 2,5 ug/ml durante 20 min, 20 min de periodo de lavado, seguido de infusión de propofol con modelo de Schnider a la misma concentración objetivo; o b) la secuencia inversa. La diferencia en variabilidad de profundidad anestésica fue evaluada mediante la comparación de registros de índices de entropía con una prueba «t» no pareada.

Resultados

No se encontró evidencia de diferencias significativas de la varianza media en los índices de entropía espectral asociada a los modelos (valor de p: 0,57 para entropía de estado; valor de p: 0,51 para entropía de respuesta).

Conclusión

El estudio sugiere que ambos modelos son equivalentes en términos de estabilidad de profundidad anestésica. Es importante continuar estudiando la eficacia de los modelos en diferentes tipos de población, dado que su comportamiento según características individuales de los pacientes o variables, como costo-efectividad, podrían inclinar la balanza.

Abstract

Introduction

There are two different pharmacokinetic models (Marsh and Schnider) for the administration of total intravenous anesthesia with propofol, the parameter differences could have some impact over the depth of anesthesia.

Objective

to determine if there is a significant difference in the variability of depth of anesthesia suggesting that one model is superior in achieving a more stable and predictable depth of anesthesia during surgery.

Methods

a cross-over clinical trial was conducted on 16 healthy patients programmed for upper or lower limb ambulatory orthopedic surgery. Patients were randomly assigned to i) effect site target controlled infusion of propofol with Marsh model at a target concentration of 2,5 μg/ml for 20 minutes, a 20 minute washout, then propofol was administered with Schnider model at the same effect site target for the reminder of the surgery, or ii) the reverse sequence. Differences in variability of depth of anesthesia, were assessed by comparing records of spectral entropy indices during surgery through an unpaired t-test.

Results

there was no evidence of significant difference in the mean variances of either spectral entropy indices between the two models (P-value: 0.57 for State Entropy, P-value: 0.51 for Response Entropy).

Conclusion

the study suggests that both pharmacokinetic models are equivalent in terms of stability of depth of anesthesia. It is important to keep testing determinants of the efficacy of the models in different types of population because their behavior according to individual characteristics of patients or variables such as cost-effectiveness could end up tilting the scale.

Introducción

En la actualidad existen múltiples agentes anestésicos eficaces, tanto inhalatorios como intravenosos. Ambos tipos permiten una valoración detallada y una recuperación rápida con buen perfil de seguridad. No obstante, la anestesia total intravenosa ha venido demostrando posibles ventajas con respecto a las técnicas inhalatorias, no solo en la seguridad durante la cirugía y el bienestar postoperatorio, sino también en términos de la conveniencia de esta técnica de administración en algunas circunstancias específicas (intervención en la vía aérea, neuroanestesia) y otros asuntos como el impacto medioambiental. Por estas razones, la anestesia total intravenosa ha ganado popularidad en la práctica clínica, y su uso se ha generalizado especialmente desde la introducción del propofol^1–4.

Hay 2 modelos farmacocinéticos para la administración de la anestesia total intravenosa (TIVA) con propofol, los modelos de Marsh y Schnider, que toman en cuenta las interacciones entre los compartimentos corporales para modificar la velocidad de la infusión y, en teoría, mantener una concentración plasmática constante⁵. Aunque no existe evidencia de diferencias clínicas importantes entre ambos modelos, tampoco está claro cuál de los 2 puede predecir con mayor precisión las concentraciones en plasma. Es evidente que los modelos difieren en los cálculos de los volúmenes de los compartimentos, así como en la velocidad de difusión entre los mismos, lo que resulta en diferencias significativas en la dosis total de propofol administrada, la velocidad de infusión y, por ende, en la estimación de las concentraciones plasmáticas y en el sitio de efecto⁶, diferencias que pueden tener un impacto sobre la profundidad anestésica. La tabla 1, presenta las respectivas ecuaciones para cada modelo implementado en la bomba de infusión BBraun Space⁷, los parámetros correspondientes son: V1, volumen de distribución para el compartimento central; V2, V3, volumen de distribución para los compartimentos periféricos rápidos y lentos; k10, constante de velocidad para la tasa de eliminación; k12, k13, constante de velocidad del compartimento central a los compartimentos periféricos; k21, k31, constantes de velocidad de compartimentos periféricos al compartimento central.

Tabla 1.

Parámetros del modelo; modelo Marsh con peso; modelo Schnider con edad, peso, altura y masa corporal magra (LBM)

Parámetro	Modelo Marsh	Modelo Schnider
V1	0,0228 L/kg	4,27 L
V2	0.463 L/kg	18,9-0,391*(edad-53) L
V3	2.893 L/kg	238 L
k10	0,119	0,443 + 0,0107*(peso-77)-0,0159*(LBM-59) + 0,0062*(altura-177)
k12	0,112	0,302-0,0056*(edad-53)
k13	0,042	0,196
k21	0,055	[1,29-0,024*(edad-53)]/(18.9-0,391*(edad-53)
k31	0,0033	0,0035
keo	0,26	0,456

Fuente: Marsh et al.⁸; Schnider et al.⁹.

Hasta ahora no existe un estándar de oro para medir cuantitativamente el estado de consciencia y la profundidad anestésica. Normalmente la monitorización de las mismas se basa en el criterio del anestesiólogo, quien a su vez se basa en las variables de actividad autonómica, ciclos respiratorios y tamaño de la pupila¹⁰. Sin embargo, ha habido un progreso importante en el análisis de las señales electroencefalográficas con técnicas como el índice biespectral (BIS)¹¹ y los índices de entropía espectral (M-Entropy)¹², que han demostrado una buena correlación con los niveles de sedación clínicamente evaluados en las diferentes etapas de la anestesia^13,14. El módulo M-Entropy, particularmente el índice de entropía de respuesta, fue considerado como un mejor predictor de la respuesta del paciente a estímulos dolorosos que el BIS¹⁵. Es por esta razón que la medición de la entropía puede considerarse como un indicador indirecto de la profundidad anestésica y permite un tipo de monitorización capaz de detectar variaciones, incluso en el mismo plano de la anestesia, lo que la hace la herramienta ideal para evaluar dinámica y cuantitativamente las repercusiones reales de las diferencias observadas entre los 2 modelos farmacocinéticos para la administración de la anestesia con propofol.

Esta investigación tiene como objetivo describir la variabilidad de la profundidad anestésica de acuerdo con M-Entropy en pacientes ASA I programados para cirugía ortopédica ambulatoria de miembros superiores o inferiores durante la administración de los modelos farmacocinéticos Marsh y Schneider. Esta variabilidad es usada para determinar si existe una diferencia significativa entre ambos modelos que sugiera que uno es superior en alcanzar una profundidad anestésica más estable y predecible durante la cirugía.

Métodos

El ensayo clínico cruzado, controlado y uniformemente diseñado fue aprobado por el comité de ética de la Clínica Universidad de la Sabana (CUS). Se llevaron a cabo ensayos experimentales con el equipo de cirugía involucrado en los procedimientos para buscar homogeneidad en los criterios y la gestión de todo el personal involucrado. El estudio se realizó de febrero a julio de 2015, y se registró en el sitio Web: www.clinicaltrials.gov, con el número de identificación: ECC001-2015. Dieciséis pacientes con edades comprendidas entre los 18 y los 65 años fueron incluidos en el estudio, todos con al menos 8 h de ayuno, que no habían tomado previamente medicamentos con acción en el sistema nervioso central o en el sistema nervioso autónomo (benzodiacepinas, bloqueadores beta, antagonistas del calcio, alfa 2 agonistas); sin dificultades comunicativas o auditivas; no alérgicos al proporfol; con evaluación preanestésica (por médico y enfermera) por el departamento de Anestesiología de la CUS; con clasificación ASA I; programados para cirugía ortopédica ambulatoria de miembros superiores e inferiores; quienes requerían anestesia regional por bloqueo de nervio guiada por ecografía combinada con anestesia general. Con todos los pacientes se firmó y se verificó el consentimiento informado (para cirugía, anestesia e inclusión en la investigación), se realizó la lista de chequeo y se revisaron la presión de oxígeno adecuada, los vaporizadores de anestesia conectados, el sistema de respiración asegurado y ensamblado correctamente, el tanque de oxígeno de urgencia, el estado adecuado de flujómetros, circuitos, válvulas unidireccionales, válvulas de alivio de presión, contenedor de absorbente de CO₂ y, finalmente, el funcionamiento adecuado del ventilador y los monitores. Se implementó «La lista de seguridad quirúrgica: cirugías seguras salvan vidas». Se inició la monitorización con electrocardiografía, presión sanguínea no invasiva, oximetría de pulso, capnografía y entropía. Se aseguraron la impedancia adecuada del electrodo y la lectura fiable del monitor (Datex/Ohmeda).

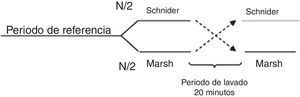
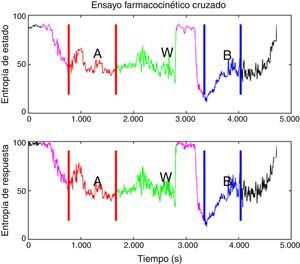
Todos los pacientes fueron premedicados con 0,03 mg/kg de midazolam por vía intravenosa y 2 μg/kg de fentanilo; el área se preparó con clorhexidina de forma estéril. El nervio se localizó usando aguja de estimulación, estimulador nervioso y línea de extensión (ref. 5194.103 30°-21 G-L 100 mm, Locoplex^®). Para el miembro inferior se usó una corriente avanzada de 1,2 mA, hasta que se logró la respuesta del nervio a 0,5 mA para localizar los nervios obturador y femoral utilizando un abordaje anterior y el nervio ciático con un abordaje posterior. Con el miembro superior se realizó un procedimiento similar con abordaje supraclavicular o axilar para el bloqueo nervioso. Se infundió 20 ml de anestésico local sobre cada nervio, usando levobupivacaína al 0,375% sin epinefrina y lidocaína al 1% con dosis ajustada al peso, sin alcanzar una dosis máxima de 150 mg de levobupivacaína y 5 mg/kg de lidocaína. Se confirmó ausencia de dolor, parestesia, disestesia e infusión difícil durante la administración del anestésico local. Adicionalmente, la posición de la aguja fue evaluada mediante guía ecográfica. Para asegurar la aleatorización se generó una lista equilibrada de valores 0 y 1, usando la función de aleatorización de Matlab (The Mathworks Inc., Massachusetts, EE. UU.) versión 2015a¹⁶, donde 0 significaba iniciar con el modelo Marsh y 1 iniciar con el modelo Schnider. A continuación, la recopilación de datos digitales de entropía de estado (SE) y entropía de respuesta (RE) se realiza cada 5 seg usando el software de adquisición de comunicación en serie de Datex/Ohmeda collect^TM para posterior procesamiento en Matlab. Los índices M-Entropy se registraron durante un período de referencia de 4 min sin propofol, luego se le informaba al anestesiólogo con qué modelo iniciar el procedimiento de acuerdo con el orden generado por la lista. Se usó una técnica de TIVA a través de infusión controlada a objetivo (TCI) con bomba de infusión de laboratorios B Braun⁷. La inducción se realizó con 5 ng/ml de remifentanilo (Ultiva, modelo Minto), y después de 3 min se inició una infusión de propofol-lipuro al 1% con una concentración objetivo en el sitio efecto de 2,5 μg/ml con los modelos Marsh o Schnider. Un bolo adicional de 1 mg/kg de propofol se administró para la colocación de la máscara laríngea. La TCI con propofol se administró por un periodo de 20 min desde el inicio de la cirugía (periodo A), después del cual se suspendió por 20 min de periodo de lavado (W). A continuación se configuró y se reinició la infusión de propofol con el modelo farmacocinético restante hasta el final de la cirugía (periodo B). W se estableció por observación de los niveles en plasma estimados por la bomba de infusión durante los ensayos experimentales (fig. 1).

Figura 1.

Diseño cruzado.

Fuente: Modificado de Wellek et al.¹⁷.

El tamaño de la muestra se determinó usando los parámetros que se muestran en la tabla 2. Se usó la ecuación 1 para la integración de las varianzas¹⁸.

Tabla 2.

Parámetros para calcular el tamaño de la muestra

Parámetro	Descripción	Valor
σBT	Desviación estándar de los pacientes en el mismo grupo de tratamiento	10,0
σBR	Desviación estándar de los pacientes del grupo de referencia	10,0
ρ	Correlación entre pacientes de los grupos de tratamiento y control	1,0
σWT	Error estándar (dentro del paciente) del grupo de tratamiento	3,1
σWR	Error estándar (dentro del paciente) del grupo de referencia	3,1

Fuente: datos de los ensayos experimentales en la CUS.

Fuente: Siyasinghe y Sooriyarachchi¹⁸.

Teniendo en cuenta el error tipo i (α = 0,05) y una potencia del 80% (β = 0,2) para determinar una diferencia esperada en valores de entropía entre los grupos de E = 10 unidades, los parámetros de la distribución de probabilidad normal estándar A (Ec.2) y B (Ec.3) se determinaron usando Matlab 2015a¹⁶

Luego el cálculo del tamaño de la muestra es (Ec.4)

Fuente: Siyasinghe y Sooriyarachchi¹⁸.

Para el análisis estadístico se promediaron las varianzas resultantes de cada paciente a partir de los periodos asociados con los modelos farmacocinéticos. Se realizó e implementó una prueba «t» no pareada (Ec.5) para confirmar la ausencia del efecto de arrastre entre periodos de acuerdo con Wellek y Blettner¹⁷.

Fuente: Wellek et al.¹⁷.

Donde: m: número de pacientes en el grupo Marsh-Schnider; n: número de pacientes en el grupo Schnider-Marsh; N: número total de pacientes; C¯(X): media de la suma de las varianzas en el grupo Marsh-Schnider; C¯(Y): media de la suma de las varianzas en el grupo Schnider-Marsh; SQ_CX: [C₁(X)- C¯ (X)]² + ...+ [C_m(X)- C¯ (X)]²; SQ_CY: [C₁(Y)- C¯ (Y)]² +...+ [C_n(Y)- C¯ (Y)]²

A continuación se evaluaron las diferencias entre los modelos. Se calculó la significación estadística usando una prueba «t» no pareada, esta vez comparando la media de las diferencias de las varianzas de los índices de entropía para cada modelo en cada paciente, como se muestra en la ecuación 6:

Fuente: Wellek et al.¹⁷.

Donde: D¯(X): media de las diferencias de las varianzas en el grupo Marsh-Schnider; D¯(Y): media de las diferencias de las varianzas en el grupo Schnider-Marsh.

Por último, se calculó la potencia post-hoc (1-β) como una función de los diferentes grados de la media de diferencia de varianzas (δ)¹⁹. El procesamiento de datos y las pruebas estadísticas se realizaron con una función desarrollada en Matlab (analisis_pk.m) que toma como argumentos de entrada los tiempos registrados durante la recolección de datos y las series de M-entropy para calcular la varianza de cada periodo, luego se aplicaron pruebas estadísticas.

Resultados

Ocho pacientes fueron asignados inicialmente a cada grupo y se sometieron a la intervención descrita. Se excluyeron los datos de 2 de los pacientes debido a que el tiempo de duración de la cirugía no fue suficiente para completar el diseño del estudio. Las características demográficas de la población estudiada se presentan en la tabla 3, organizadas de acuerdo a los grupos asociados con cada modelo farmacocinético (tabla 4).

Tabla 3.

Descripción demográfica

Marsh-Schnider, n = 7				Schnider-Marsh, n = 7
	Edad	Sexo	Peso	Edad	Sexo	Peso
Media	34	M:5	66,71	32	M:4	67
Desviación	11,57	F:2	9,92	13,50	F:3	11,80

Fuente: Información de los pacientes recopilada en la CUS.

Tabla 4.

Diferencias de las varianzas

Entropía de respuesta, n = 7			Entropía de estado, n = 7
	M-S	S-M	M-S	S-M
Mediana-Q2	24,93	10,29	33,66	21,89
Desviación	29,44	23,16	40,85	39,60

Fuente: Diferencias de las varianzas calculadas con la información de los pacientes recopilada en la CUS.

Se definieron los periodos de análisis para cada modelo farmacocinético; la figura 2 muestra el diseño experimental aplicado a uno de los pacientes. Posteriormente, se determinó la varianza de los índices de M-Entropy de Datex-Ohmeda (SE, RE) para cada periodo en los 2 grupos del estudio. La mediana de las varianzas y la desviación estándar respectiva para SE en el periodo Marsh fue 31,12 ± 25,01 y en el periodo Schnider 21,97 ± 36,76; para RE fue 30,54 ± 49,24 en el periodo Marsh y 43,97 ± 50,34 en el periodo Schnider.

Figura 2.

Diseño experimental aplicado al paciente 6 (inducción con el modelo Schnider, 72 kg, 1,64 m, 58 años, sexo femenino). En morado está el tiempo delta, que se define como el tiempo entre el inicio de la infusión de propofol con el primer modelo hasta el manejo de la vía aérea. Este tiempo tiene el propósito de que los datos procesados pertenezcan a un paciente anestesiado, no a un paciente despierto o en secuencia de transición. A. Es el primer periodo, en rojo, definido como el tiempo entre el manejo de la vía aérea hasta el final de la infusión de propofol con el primer modelo. B. Es el segundo periodo de tiempo entre el inicio de la infusión con el modelo restante en la secuencia hasta el final de la infusión, en azul, excluyendo el tiempo delta inicial. W. Es el periodo de lavado que ocurre del final de primer periodo al inicio de la infusión de propofol con el modelo restante, en verde.

Fuente: gráfica producida por los autores usando Matlab 2015a.

Pre-test de efecto de arrastre

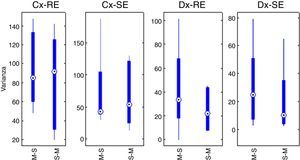
Con la suma de las varianzas de cada grupo se realizó el pretest de efecto de arrastre entre periodos. El efecto acumulativo se reporta en forma de: mediana ± desviación estándar. Para SE y secuencia Marsh-Schnider SE-C(X) = 42,80 ± 57,14, para secuencia Schnider-Marsh SE-C(Y) = 53,70 ± 48,52. Efecto acumulativo de RE-C(X) = 84,89 ± 39,63 y RE-C(Y) = 91,93 ± 48,90. La figura 3 muestra el diagrama de caja del efecto acumulativo de cada grupo en las series RE y SE (Cx-RE, Cx-SE). No hay evidencia de efecto de arrastre significativo entre periodos, prueba «t» pareada a 2 colas para SE (valor p = 0,54, T = 0,63) y RE (valor p = 0,92, T = –0,10).

Figura 3.

Diagramas de cajas de los efectos acumulativos (Cx-RE, Cx-SE) y las diferencias en los efectos (Dx-RE, Dx-SE); M-S representa grupo de secuencia Mars-Schnider y S-M grupo de secuencia Schnider-Marsh.

Fuente: gráfica producida por los autores usando 2015a.

Prueba estadística de las diferencias

Se obtuvieron las diferencias de las varianzas para cada periodo en ambos grupos (tabla 4. La figura 3 también muestra los diagramas de cajas de las diferencias entre los periodos relacionados con cada índice Datex-Ohmeda (Dx-SE, Dx-RE).

El estadístico Td. (ecuación 2) se calculó para detectar diferencias significativas entre las series de SE y RE entre los 2 modelos farmacocinéticos, no se encontraron diferencias significativas en la varianza media de los índices de entropía entre los modelos farmacocinéticos Marsh y Schnider, prueba «t» pareada a 2 colas para SE (valor p = 0,57, T = –0,58) y RE (valor p = 0,51, T = –0,68).

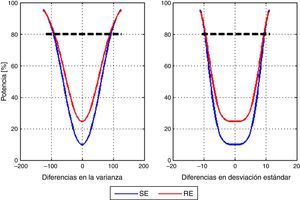
Por último, se calculó la potencia post-hoc del estudio para detectar diferencias entre la varianza media de los modelos con la entropía de estado y la entropía de respuesta. Se usó un vector que parte de –125 a 125 con pasos de incremento de a 2,5 unidades de la varianza. La figura 4 muestra la curva de potencia correspondiente a las diferencias en la media de la varianza y la media de la variación estándar. En el caso particular de una diferencia de 100 unidades de varianza se tiene que 10 unidades de desviación estándar corresponden a una potencia de 84,66% para SE y de 85,99% para RE.

Figura 4.

Curva de potencia post-hoc para SE (azul) y RE (rojo).

Fuente: gráfica producida por los autores usando Matlab 2015a.

Discusión

Hasta donde saben los autores no se han encontrado estudios que evaluaran la variabilidad media de la anestesia general en relación con el modelo farmacocinético usado durante la anestesia total intravenosa con propofol. Este fue un factor inicial limitante para determinar el tamaño de la muestra, y fue necesario usar valores estimados para los parámetros de los resultados de las pruebas piloto. El diseño cruzado permite un tamaño de muestra reducido porque cada sujeto es su propio control, lo que disminuye la variabilidad interindividual y el efecto de covariables como el peso, la edad y la estatura. No se consideró necesario mantener el estudio a doble ciego, ya que ninguno de los modelos es un «estándar de atención», lo que significa que no existe una expectativa por parte del anestesiólogo sobre los resultados. Adicionalmente, el proceso se estandarizó para que no fuera implementado ningún manejo suplementario; de esta manera, la dosificación de las infusiones fue controlada por la bomba de infusión, de acuerdo con los modelos farmacocinéticos, y se proporcionó un manejo analgésico estándar. En relación con el posible sesgo de cointervenciones el modelo farmacocinético inicial fue revelado al anestesiólogo justo antes del inicio de la inducción y después del bloqueo del nervio para la anestesia regional. Finalmente, se midió la respuesta a la intervención. y se registró de forma automatizada sin mediación del anestesiólogo. Además, los índices de entropía espectral (SE, RE) son puntos finales obtenidos a partir de información objetiva que los hace menos susceptibles al sesgo.

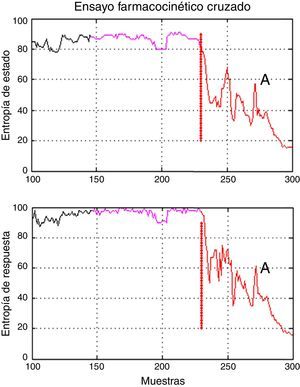
Hubo un periodo de intervención con valores atípicos de la varianza en el paciente 3 (inducción con el modelo Marsh, 60 kg, 1,72 m, 22 años, sexo masculino). La inspección adicional de las gráficas de las series de entropía reveló una brecha temporal en los índices en relación con la evaluación clínica (colocación de vía aérea); por tanto, la definición de los tiempos para el periodo A incluyó valores de entropía asociados con un paciente despierto (fig. 5), lo que produce en dichos casos valores atípicos de varianza. Los datos que excedieron el umbral estadístico definido por cuartiles [Q3 + 3*(Q3-Q1)] fueron considerados atípicos inicialmente, y se excluyeron del análisis estadístico, pero se decidió no descartar la información que los valores atípicos pueden proporcionar; los datos marcados como atípicos fueron incluidos en este análisis.

Figura 5.

Brecha temporal en los índices de entropía observados en el paciente 3 del grupo Marsh-Schnider. Muestra que el periodo A incluye valores de entropía de estado y entropía de respuesta asociados con un paciente despierto y la transición a un plano anestésico adecuado entre 40 y 60. El tiempo delta, en morado, y A, en rojo, corresponden al primer periodo de la secuencia de modelos.

Fuente: gráfica producida por los autores usando Matlab 2015a.

La varianza mediana y la respectiva desviación estándar en todo el conjunto de datos para SE en el periodo Marsh fue 27,93 ± 78,97, en el periodo Schnider fue 20,26 ± 39,45; para RE en el periodo Marsh fue 34,01 ± 123,08, y en el periodo Schnider fue 36,03 ± 60,59. Se observó un incremento en la desviación estándar del conjunto de datos correspondiente al periodo Marsh, aunque no se encontraron diferencias significativas entre los modelos farmacocinéticos (p > 0,05). Resultó interesante notar que los valores atípicos produjeron un mayor impacto en el grupo que inició el procedimiento con el modelo Marsh. Esto podría estar relacionado con la diferencia entre el parámetro farmacodinámico Keo. El menor valor usado en el modelo Marsh (0,26 min⁻¹) en este estudio pudo ocasionar una estimación errónea de la concentración en el sitio de efecto, conduciendo a una incorrecta estimación de la dosis de propofol. Usamos la concentración objetivo en sitio de efecto. Se ha sugerido que si el modelo Marsh se usa en modo objetivo con sitio de efecto debería ser usado con un valor keo más rápido de 1,2 min^-1 recomendado por Struys et al.^6,20.

El tiempo de lavado estimado puede considerarse suficiente para que el fármaco administrado durante el periodo A no afecte los resultados del periodo B. Aunque el uso de remifentanilo puede modificar la profundidad anestésica, el presente estudio se centra en analizar la variación de los índices de entropía y no en su valor medio. Por lo tanto, se considera una administración constante durante toda la intervención y en cada paciente para no afectar los resultados del estudio.

No se encontró información sobre el valor de la varianza que pudiera considerarse clínicamente significativo. Además, no se encontraron diferencias estadísticamente significativas entre los modelos de ninguno de los índices de entropía estudiados. Sin embargo, considerando el rango del plano anestésico adecuado para los índices (40-60)¹² puede deducirse que un valor de la varianza por debajo de 100 se podría tolerar, porque a pesar de las fluctuaciones permanecería en un rango adecuado. El análisis de datos mostró una potencia del 80% para detectar diferencias de 100 unidades de varianza entre los modelos para el índice de entropía de estado, lo que significa que, incluso si existe una diferencia, la variabilidad media real de la profundidad anestésica entre ambos modelos probablemente no es suficiente para definir la superioridad clara de un modelo en el ámbito clínico.

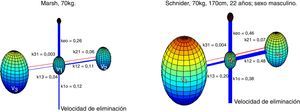
Absalom et al. afirman en su artículo que la infusión de propofol controlada por el modelo Marsh incrementa el uso de propofol en comparación con el modelo Schnider. Los autores destacan que la cuestión importante no es qué modelo proporciona la dosis del fármaco más grande o más pequeña, sino cuál produce la predicción más acertada de las concentraciones plasmaticas y en sitio de efecto. La figura 6 presenta una visualización 3D de los modelos de múltiples compartimentos para propofol en un paciente (70 kg, 170 cm, 25 años; sexo masculino) programado en el software de Matlab. Cada compartimento se representa con esferas de acuerdo con sus volúmenes respectivos. Un enlace más grueso entre los compartimentos representa una constante de velocidad más alta y, por lo tanto, una circulación más rápida de propofol entre los compartimentos. Las líneas azules representan parámetros de velocidad desde el compartimento central V1 hacia los compartimentos periféricos V2, V3, y la tasa de eliminación o aclaramiento. Los enlaces rojos representan los parámetros de velocidad de los compartimientos periféricos hacia V1.

Figura 6.

Representación 3 D de los modelos de Marsh y Schnider para propofol basados en parámetros farmacocinéticos publicados^8,9. El modelo Marsh, v1 = 15,96 L, v2 = 32,41 L, v3 = 202,51 L. El modelo Schnider, v1 = 4,27 L, v2 = 31,02 L, v3 = 238 L.

Fuente: gráfica producida por los autores usando Matlab 2015a

Aunque no existe evidencia significativa de la variabilidad de la profundidad anestésica proporcionada por estos modelos, se observaron diferencias marcadas en las constantes de velocidad. En términos generales, se proporciona una circulación más rápida de propofol entre los compartimentos en el modelo farmacocinético Schinder. La línea azul más gruesa, asociada con Keo en el modelo Schinder, propone una circulación más rápida de propofol desde el plasma hacia el sitio de efecto. Los parámetros v1, v3, k13, k31 son fijos. El compartimento v2 es inversamente proporcional a la edad. La constante de velocidad de eliminación varía de manera compleja con el peso, la estatura y la masa corporal magra. El modelo Marsh considera las mismas constantes de velocidad para todo tipo de pacientes, los volúmenes de los compartimentos son proporcionales al peso y se ha demostrado que infravalora la concentración plasmática de propofol en los adultos mayores²¹. Este hecho y los datos encontrados en el presente estudio apuntan hacia una posible ventaja del modelo Schnider, que ajusta los parámetros de acuerdo a la edad del paciente, su estatura, su masa magra y el sexo.

El desarrollo de modelos farmacocinéticos^3,4 no incluyó pacientes con obesidad severa. En el caso de un paciente de 96 kg, 1,70 m, 22 años y de sexo masculino la única diferencia en el modelo Schnider sería un incremento en la constante de velocidad de eliminación; el modelo de Marsh consideraría compartimentos de mayor tamaño pero las mismas constantes de velocidad entre compartimentos y aclaramiento. Es importante seguir realizando pruebas en diferentes tipos de población porque el comportamiento de acuerdo con características individuales, como el paciente con obesidad severa o variables como costo-efectividad podrían inclinar la balanza.

Responsabilidades éticas

Protección de personas y animales

Los autores declaran que los procedimientos seguidos se conformaron a las normas éticas del comité de experimentación humana responsable y de acuerdo con la Asociación Médica Mundial y la Declaración de Helsinki.

Confidencialidad de los datos

Los autores declaran que han seguido los protocolos de su centro de trabajo sobre la publicación de datos de pacientes.

Derecho a la privacidad y consentimiento informado

Los autores han obtenido el consentimiento informado de los pacientes y/o sujetos referidos en el artículo. Este documento obra en poder del autor de correspondencia.

Financiamiento

El presente estudio fue financiado por la Sociedad Colombiana de Anestesia y Reanimación, en la modalidad concurso de propuestas de investigación.

Conflicto de intereses

Los autores declaran no tener ningún conflicto de intereses.