La introducción de las secuencias potenciadas en difusión ha supuesto una revolución para la detección y caracterización de la patología del sistema nervioso central. Sin embargo, en numerosas ocasiones, la valoración de dichos estudios se limita a una estimación cualitativa. Además, la complejidad fisiopatológica de las distintas entidades que afectan al sistema nervioso central no siempre puede ser correctamente explicada por los modelos clásicos. El desarrollo de nuevo modelos para el análisis de las secuencias de difusión aporta numerosos parámetros que podrían permitir un abordaje cuantitativo tanto desde el punto de vista del diagnóstico como pronóstico, así como para llevar a cabo la monitorización terapéutica, y podrían ser considerados como potenciales biomarcadores de salud y enfermedad. Realizamos por este motivo una actualización que incluye las bases físicas de los estudios de difusión y tensor de difusión, sus modelos de análisis avanzado (IVIM y Kurtosis) y la significación biológica de los parámetros derivados.
The introduction of diffusion-weighted sequences has revolutionized the detection and characterization of central nervous system (CNS) disease. Nevertheless, the assessment of diffusion studies of the CNS is often limited to qualitative estimation. Moreover, the pathophysiological complexity of the different entities that affect the CNS cannot always be correctly explained through classical models. The development of new models for the analysis of diffusion sequences provides numerous parameters that enable a quantitative approach to both diagnosis and prognosis as well as to monitoring the response to treatment; these parameters can be considered potential biomarkers of health and disease. In this update, we review the physical bases underlying diffusion studies and diffusion tensor imaging, advanced models for their analysis (intravoxel coherent motion and kurtosis), and the biological significance of the parameters derived.
Las secuencias de resonancia magnética potenciadas en difusión (DWI, Diffusion Weighted Imaging) son capaces de estimar, de manera no invasiva, el movimiento de las moléculas de agua en un medio biológico1. Los estudios basados en difusión permiten valorar cualitativa y cuantitativamente dicho grado de movimiento, y aportan información anatómica y funcional de los tejidos.
El diseño de la secuencia de difusión se ha ido perfeccionando gracias a múltiples mejoras técnicas. De esta forma se ha conseguido reducir los tiempos de adquisición y artefactos, mejorando la relación señal-ruido. Otras optimizaciones técnicas de la secuencia de DWI han permitido el desarrollo del tensor de difusión (DTI, Diffusion Tensor Imaging), herramienta que ha supuesto una revolución en la valoración de la sustancia blanca en el sistema nervioso central (SNC).
La secuencia DWI ha demostrado una gran utilidad para el estudio de patología del SNC. Sin embargo, las bases físicas de dicha secuencia no han variado prácticamente en los últimos 20 años. Es por eso por lo que el campo de mejora se está centrando hoy día más en la fase de análisis e interpretación de los datos obtenidos que en la propia adquisición.
Pequeñas modificaciones en el proceso de adquisición, pero sobre todo el uso de diferentes modelos matemáticos y biológicos de análisis de la caída de la intensidad de señal, están permitiendo comprender de manera más exacta los procesos fisiopatológicos que ocurren en el SNC.
Dichos modelos de análisis nos permitirán obtener como resultado múltiples parámetros derivados con la potencial utilidad de ser usados como biomarcadores. En esta actualización se lleva a cabo un repaso con un enfoque didáctico de las bases físicas de los modelos convencionales de DWI y DTI, y se profundiza en los nuevos modelos de análisis basados en los estudios de movimiento incoherente intravóxel (IVIM) y Kurtosis. Se detallará el origen y significado biológico de los distintos parámetros derivados de estos modelos de análisis, así como las posibles aplicaciones clínicas de estos.
Bases físicas y adquisición de la secuencia clásica de DWI y DTILa secuencia clásica de difusión se basa en la aplicación de dos gradientes de difusión idénticos en magnitud y duración sobre una secuencia spin-eco (SE). Mejores técnicas han permitido desarrollar secuencias basadas en turbo spin-eco (TSE) y, especialmente, la más extendida hoy en día, la difusión eco-planar (EPI)2.
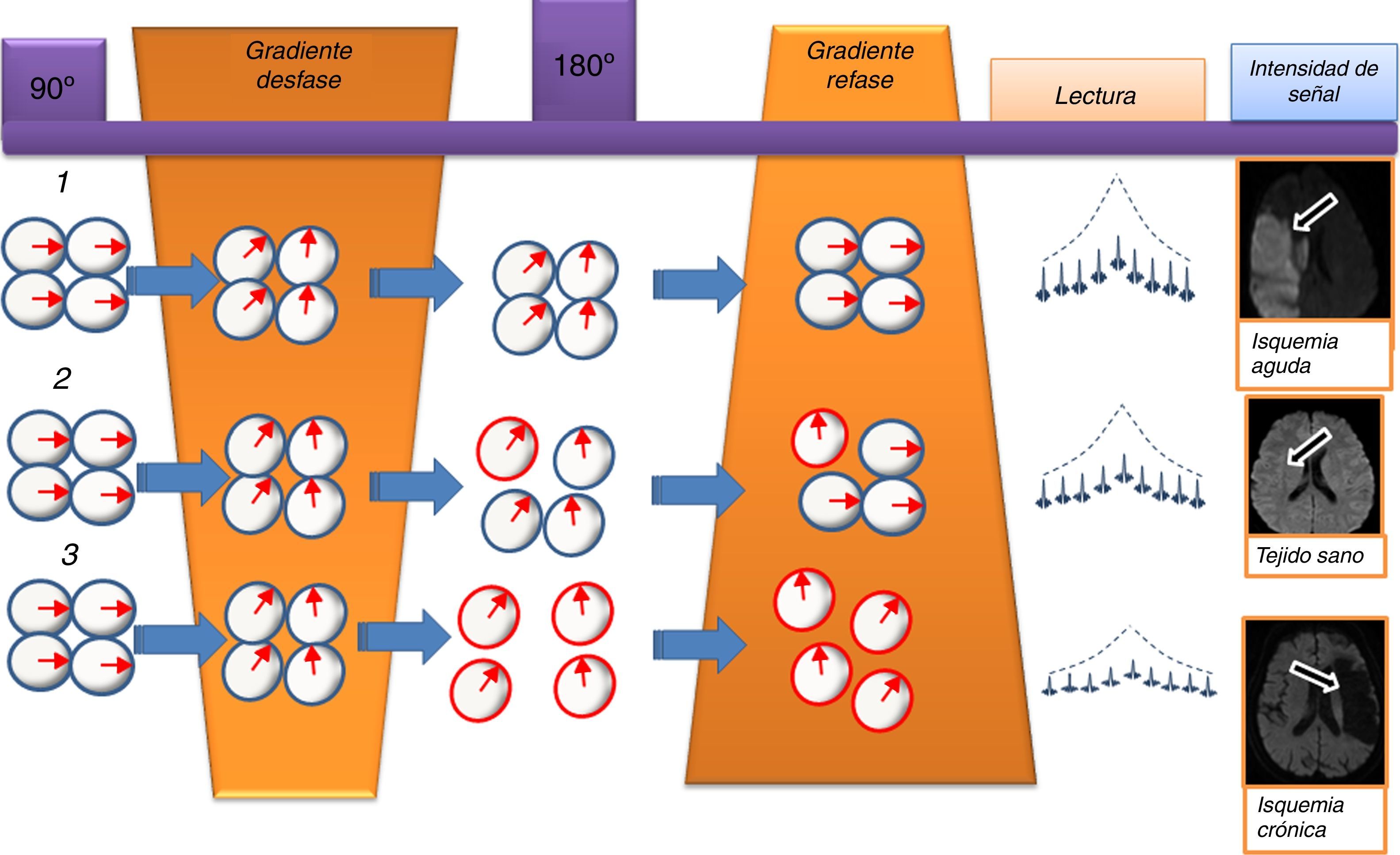
El primer gradiente aplicado desfasará las moléculas de agua y, transcurrido un determinado espacio de tiempo, el segundo gradiente refasará dichas moléculas en la misma proporción que fueron desfasadas. Aquellas moléculas que se mantengan estacionarias, tras el segundo gradiente recuperarán por completo su estado inicial energético, lo cual se traducirá en una alta intensidad de señal en valores b altos de la secuencia de difusión, fenómeno que se denomina “restricción de la difusión”. Por otra parte, las moléculas que experimenten movimiento en el tiempo transcurrido entre ambos gradientes perderán su posición y no podrán recuperarla por completo, con lo cual su estado energético será menor y tendrá lugar una atenuación de su intensidad de señal de manera proporcional al grado de movimiento, lo que se denomina “difusión libre o facilitada”3. De esta forma, las secuencias DWI son capaces de diferenciar entre los distintos tejidos bándose en la libertad de movimiento del agua en su interior (fig. 1).
Esquema de la secuencia de difusión. 1) Aquellas moléculas que presentan movimiento limitado o no experimentan movimiento en el tiempo transcurrido entre los dos gradientes de difusión (el de desfase y el de refase) conservarán su nivel energético al final de la secuencia, ya que recuperan completamente su fase y por lo tanto asociarán una alta intensidad de señal en valores b altos como es el caso de la isquemia en fase aguda, en la que el edema citotóxico conlleva un descenso en el espacio extracelular que dificulta el movimiento de las moléculas de agua a dicho nivel. 2) En el tejido normal existe un cierto grado fisiológico de libertad de movimiento de las moléculas de agua en el espacio extracelular que se corresponde con un nivel de intensidad de señal intermedio. 3) En el caso del sistema ventricular o de las lesiones isquémicas crónicas, existe un desplazamiento completo de las moléculas de agua entre los dos gradientes de la secuencia de difusión, lo que supone una pérdida completa de su fase e intensidad de señal en los valores b altos.
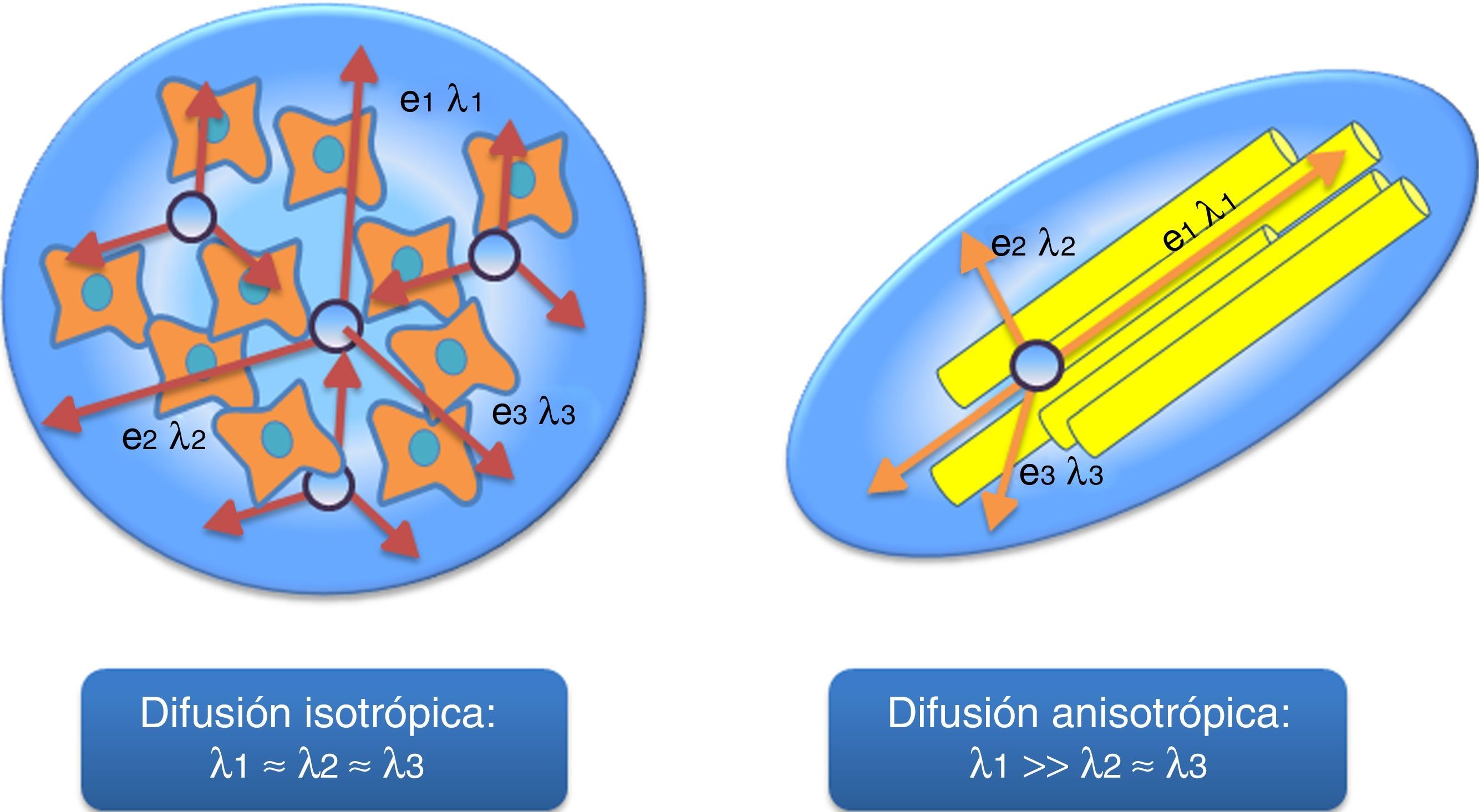
La difusión se puede considerar como isotrópica o anisotrópica en función de la dirección de movimiento del agua4. La difusión isotrópica es aquella en la que el movimiento del agua ocurre con igual probabilidad en todas las direcciones del espacio, esté o no limitado. La difusión anisotrópica es aquella en la que existe una dirección dominante de movimiento del agua en un determinado tejido, normalmente condicionado por la existencia de barreras anatómicas y fisiológicas. Este es el caso del movimiento del agua dentro de los axones y entre las vainas de mielina, en las cuales la dirección dominante de movimiento tendrá lugar a lo largo del eje mayor del axón (fig. 2). Para el estudio de la difusión anisotrópica se ha desarrollado, como una optimización técnica de la secuencia de DWI, el tensor de difusión (DTI)5.
Tipos principales de movimiento del agua en los tejidos. Se considerará difusión isotrópica cuando no exista una dirección dominante del movimiento del agua en el espacio extracelular, esté limitada o no. Hablaremos de difusión anisotrópica cuando exista una dirección dominante del movimiento del agua en los tejidos, como ocurre en los haces de fibras de sustancia blanca. En el caso de la difusión isotrópica no encontraremos diferencias significativas entre la magnitud de los 3 eigenvectors principales (λ1 ≈ λ2 ≈ λ3). Si existe una difusión anisotrópica del agua, encontraremos una dirección dominante axial del movimiento del agua a lo largo del eje mayor del axón (λ1 >> λ2 ≈ λ3) con respecto a los 2 eigenvectors menores (perpendiculares). Estos vectores son la base de los principales parámetros derivados de los estudios de DTI (DA: difusividad axial; DR: difusividad radial; FA: fracción de anisotropía; MD: difusividad media).
El DTI se basa en la aplicación de gradientes de difusión en múltiples direcciones ortogonales del espacio (al menos 6). De esta forma, nos permite valorar la movilidad de las moléculas del agua en cada dirección y detectar si existe una dirección dominante de la difusión. Desde el punto de vista matemático se genera una matriz 3 × 3 que permitirá diagonalizar la dirección dominante en cada plano del espacio representada por un vector (eigenvector) que tendrá una determinada magnitud (eigenvalue)3.
Uno de los valores añadidos del DTI es la realización de estudios de tractografía6. La tractografía se basa en la representación tridimensional de los haces de sustancia blanca a través de la determinación de la dirección dominante de movimiento del agua en cada vóxel.
Bases físicas y análisis de modelos avanzados de DWI: IVIM y KurtosisPese al salto cualitativo y cuantitativo que ha supuesto el desarrollo e implementación en la práctica radiológica y clínica diaria de las secuencias DWI y DTI, numerosos estudios han puesto de manifiesto que los procesos fisiológicos y patológicos que subyacen en los tejidos son mucho más complejos de lo que parecían a priori7–9.
La comparación de estudios in vivo e in vitro ha llegado a determinar que existe una alta complejidad basada en la presencia de varios compartimentos a nivel tisular (intracelular, extracelular e intravascular) que hace que los modelos clásicos de adquisición y análisis de la difusión resulten en ocasiones insuficientes para explicar la fisiopatología del SNC.
Para estudiar dichos compartimentos y los procesos biológicos que ocurren en ellos, podemos intervenir tanto en el proceso de adquisición como en el análisis de los datos obtenidos. Partiendo básicamente de la misma secuencia clásica de difusión modificaremos el número de valores b adquiridos y su magnitud, lo que nos permitirá, en una segunda fase, obtener un modelo de análisis de la caída de señal más preciso.
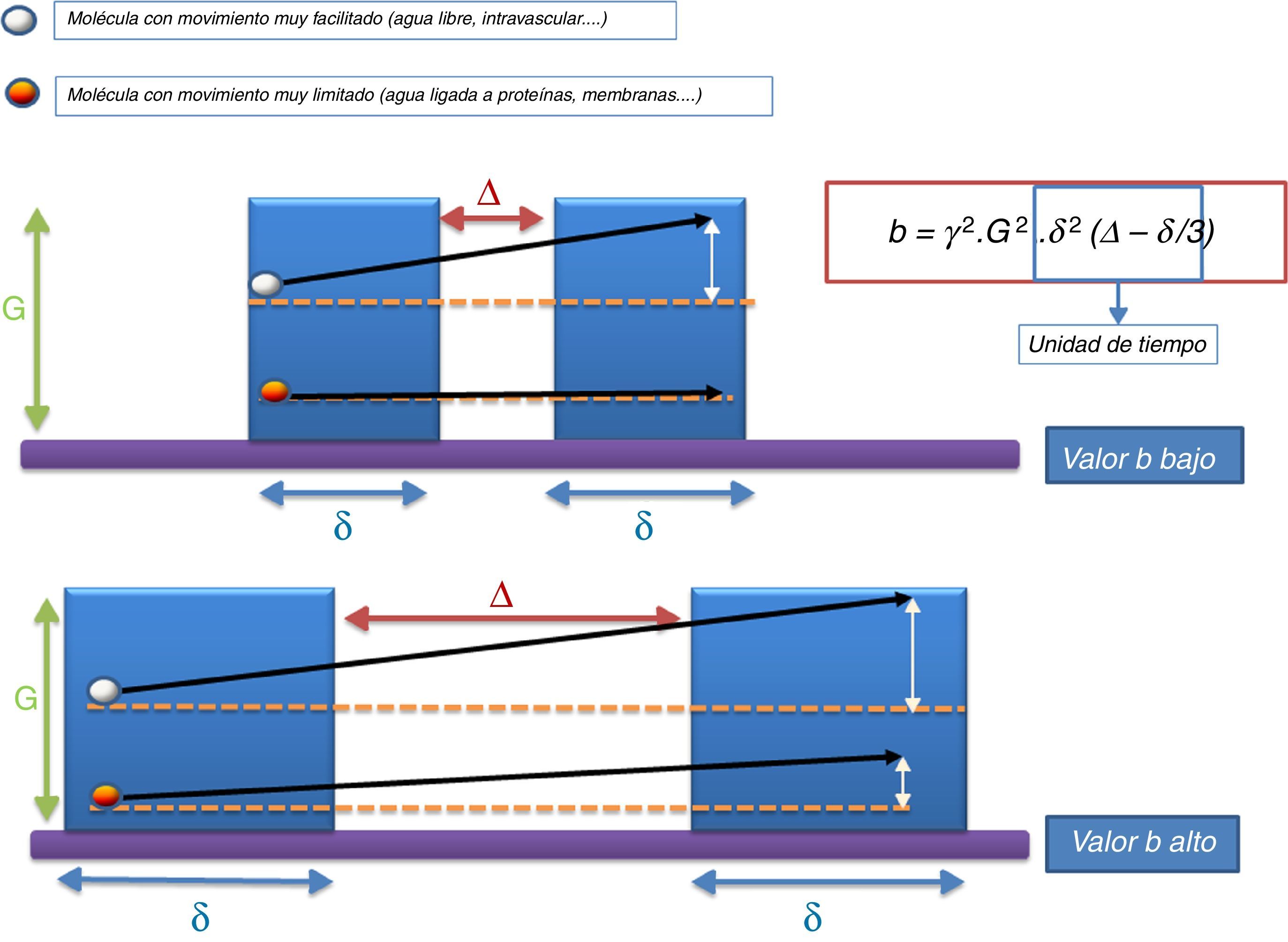
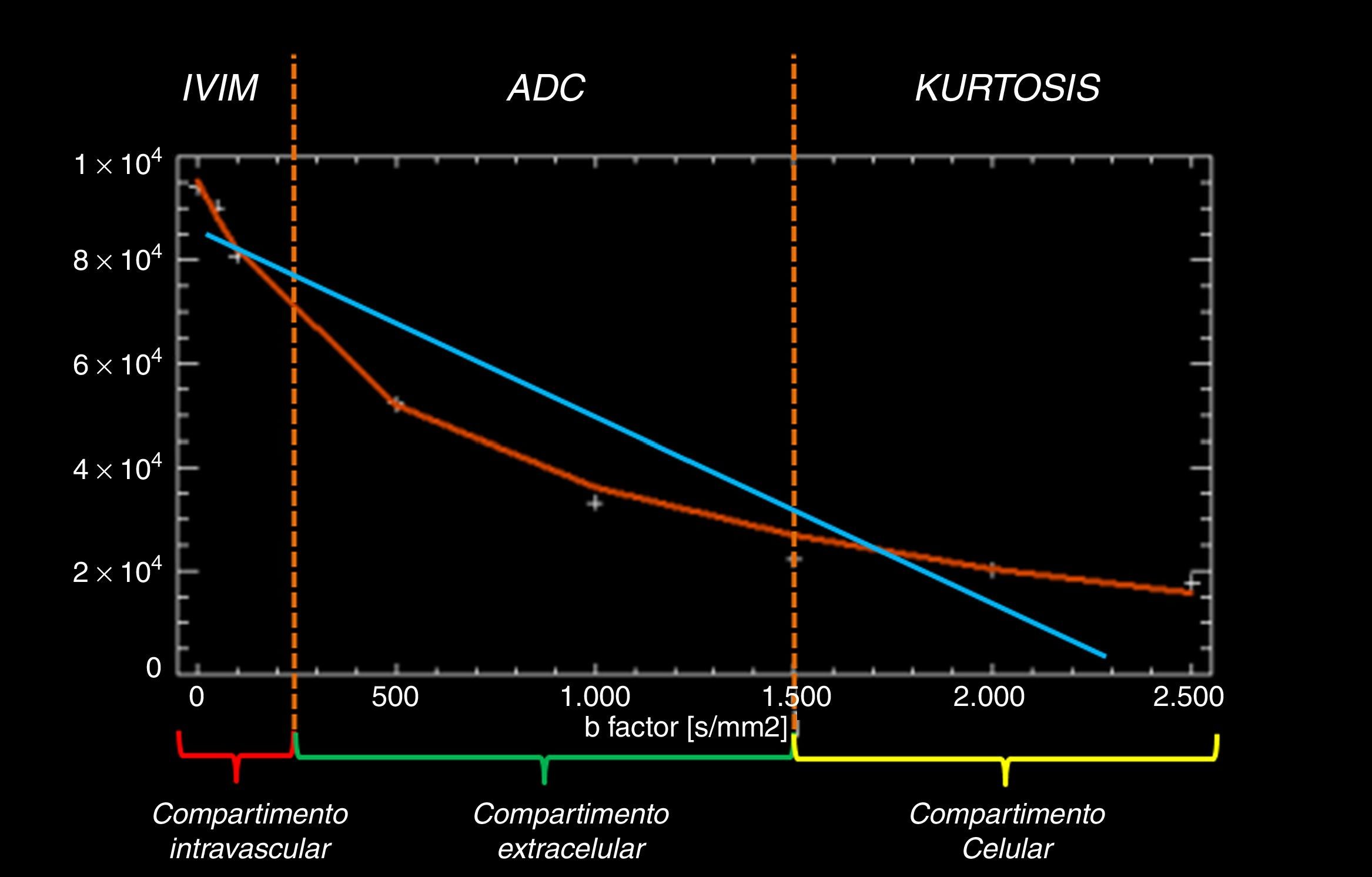
La selección y ponderación de los valores b es el punto clave en el desarrollo de estos nuevos modelos de análisis, por lo que consideramos necesario recordar brevemente el significado físico y biológico de dicho parámetro. El valor b viene determinado por el coeficiente giromagnético (γ), la intensidad del campo magnético (G), la codificación de la amplitud del pulso de los gradientes (δ) y el tiempo transcurrido entre ambos gradientes (Δ) siguiendo la fórmula b=γ2· G2· δ2(Δ-δ/3). La intensidad del campo generalmente no se modifica en los de estudios de difusión. Sin embargo, la amplitud de los gradientes y el tiempo transcurrido entre ellos sí es modificable, lo cual nos lleva al concepto de valores b bajos y valores b altos10 (fig. 3).
Significación biológica de los valores b bajos y altos. Un valor b bajo implica que el gradiente de difusión se aplica durante poco tiempo y que, además, transcurre escaso tiempo entre ambos gradientes. Esto supone que si una molécula de agua experimenta un movimiento muy lento, transcurrido ese breve espacio de tiempo no seremos capaces de demostrar dicho desplazamiento, por lo que no experimentará pérdida de señal. Por el contrario, si una molécula experimenta un movimiento muy rápido, bastará con aplicar valores b bajos para demostrar su cambio de posición y, por tanto, su pérdida de señal. Sin embargo, en el caso de valores b altos (>1000-2000 s/mm2), aquellas moléculas que apenas experimentaban movimiento son estudiadas con un amplio tiempo entre ambos gradientes, por lo que transcurrido dicho tiempo sí seremos capaces de detectar alguna variación en su posición, lo que se reflejará en pérdida parcial de su intensidad de señal.
Los valores b bajos son la clave del modelo IVIM, el cual es capaz de valorar, gracias al uso de múltiples valores b por debajo de 150 s/mm2, el movimiento aleatorio (incoherente) del agua en el interior de la red capilar en un determinado vóxel (compartimento intravascular)1. Los valores b altos son la base del modelo de Kurtosis, el cual es capaz de determinar el movimiento, muy limitado, del agua ligada a membranas celulares (compartimentro intracelular y extracelular) (fig. 4).
Modelos de caída de intensidad de señal de la secuencia de difusión. La adquisición de valores b por debajo de 150 s/mm2 y por encima de 1500 s/mm2 permite obtener una curva de caída de intensidad de señal (curva roja) que refleja un modelo multicompartimental exponencial más ajustado a la realidad que el modelo monocompartimental clásico, lineal (línea azul). Para valores b bajos existe una caída pronunciada de la intensidad de señal (primera parte de la curva roja) debido al rápido desfase de las moléculas de agua en el interior del espacio intravascular. Para valores b intermedios existe una caída mantenida de la intensidad de señal que refleja el comportamiento del agua en el espacio extracelular, paralelo a la caída hipotética de intensidad de señal del modelo monocompartimental (línea azul). Para valores b altos se objetiva una menor caída de la intensidad de señal que la esperada según el modelo monocompartimental, lo que refleja la interacción de las moléculas de agua a nivel celular con las membranas. Este análisis se realiza a través de herramientas de posproceso que permiten ajustar la caída de intensidad de señal para cada valor b y de esta forma conocer el estado de cada compartimento a través de una sola adquisición.
El modelo IVIM se basa en la consideración de dos compartimentos principales dentro de un mismo vóxel de tejido: el extracelular y el intravascular1. Esta aproximación permite, en un solo estudio, conocer de forma independiente del grado de celularidad de un tejido, su coeficiente real de difusión (D), y estimar la vascularización de un tejido a través de D*, que se corresponde con la pseudodifusión, es decir, la medida de la difusión en ese compartimento vascular (un tipo de movimiento aleatorio que se ajusta igualmente al estudio clásico de difusión). Además, f, un parámetro derivado de D*, representa la fracción de perfusión o el porcentaje de moléculas moviéndose dentro de los capilares en un determinado vóxel11.
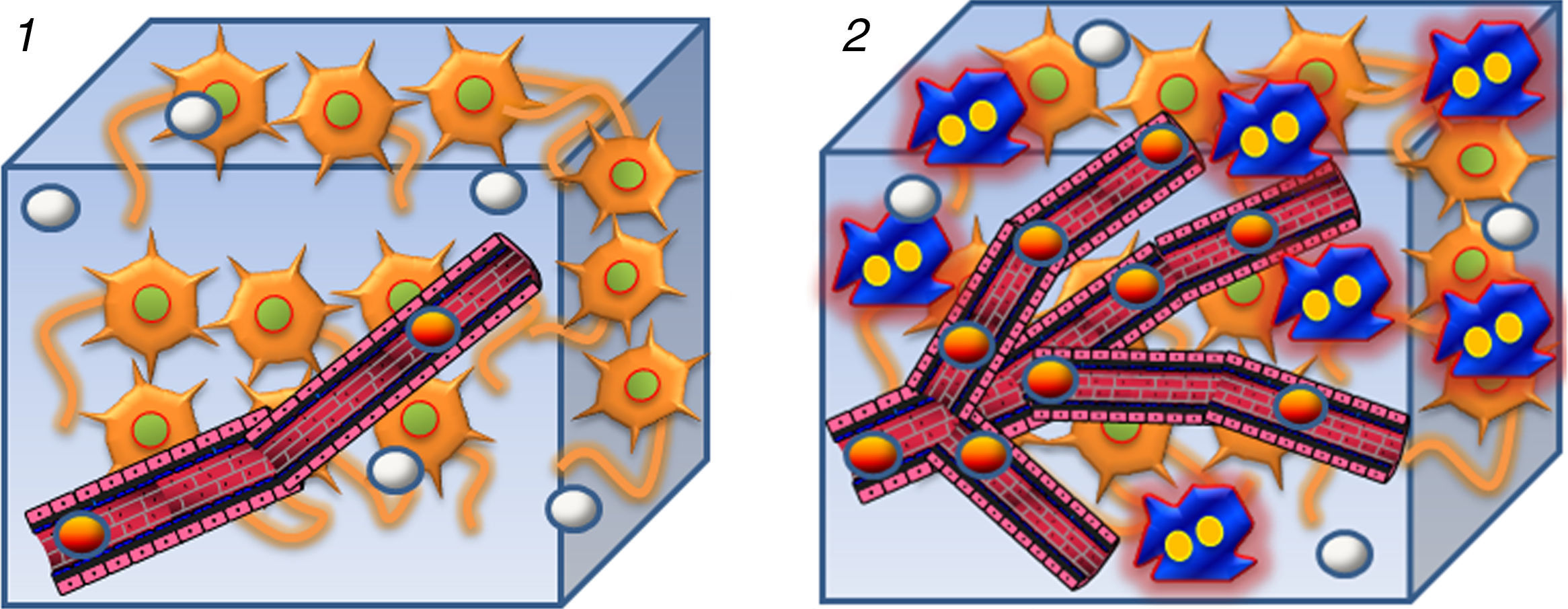
Se ha demostrado que los valores de ADC obtenidos mediante la secuencia de difusión clásica difieren entre las muestras in vivo e in vitro12. Los valores de ADC de los tejidos in vivo pueden presentar cifras más elevadas que los datos in vitro. De ahí la nomenclatura de aparente, ya que no es una medida exacta del grado de difusión de las moléculas en los tejidos. La diferencia entre ambas medidas se ha atribuido a la existencia de otro tipo de movimiento sobreañadido que interfiere en la medición del ADC esperable. Dicho movimiento es el que tiene lugar en el compartimento intravascular. El movimiento de las moléculas en el interior de los capilares hace que exista la posibilidad de cometer una sobrestimación de los valores de ADC cuando se valoran tejidos biológicos in vivo13 (fig. 5).
IVIM. En los tejidos sanos (1), el movimiento del agua en el espacio extracelular se ve ligeramente influenciado por la presencia de movimiento del agua en el compartimento intravascular, por lo que se pueden encontrar valores de ADC iguales o ligeramente por encima de los valores de difusividad pura (D). En el caso de patología tumoral del sistema nervioso central (2), pese a objetivarse una diminución del espacio extracelular debido al incremento en el número de células tumorales, los valores de ADC pueden verse aumentados por la contribución del movimiento del agua en el espacio intravascular (ADC > D). Dicho componente capilar suele encontrarse aumentado en lesiones de alto grado debido al fenómeno de neoangiogénesis tumoral. El modelo IVIM permite la correcta caracterización de las lesiones tumorales, evitando la influencia del componente vascular, el cual a su vez puede ser estimado sin necesidad de usar contraste intravenoso.
Mediante la aplicación de valores b por debajo de 150 s/mm2 se consigue desfasar, es decir, anular la contribución a la intensidad de señal de dicho movimiento más rápido intravascular. El valor verdadero del coeficiente de difusión se estimará, pues, usando valores b por encima de 150 s/mm2, para evitar dicha contaminación14.
KurtosisEl análisis convencional de la caída de intensidad de señal de la DWI considera que existe un movimiento aleatorio de las moléculas de agua en un determinado tejido. La probabilidad de que un protón difunda en una determinada dirección viene determinada por una función tipo Gauss, y existe una desviación estándar en torno a los valores de ADC.
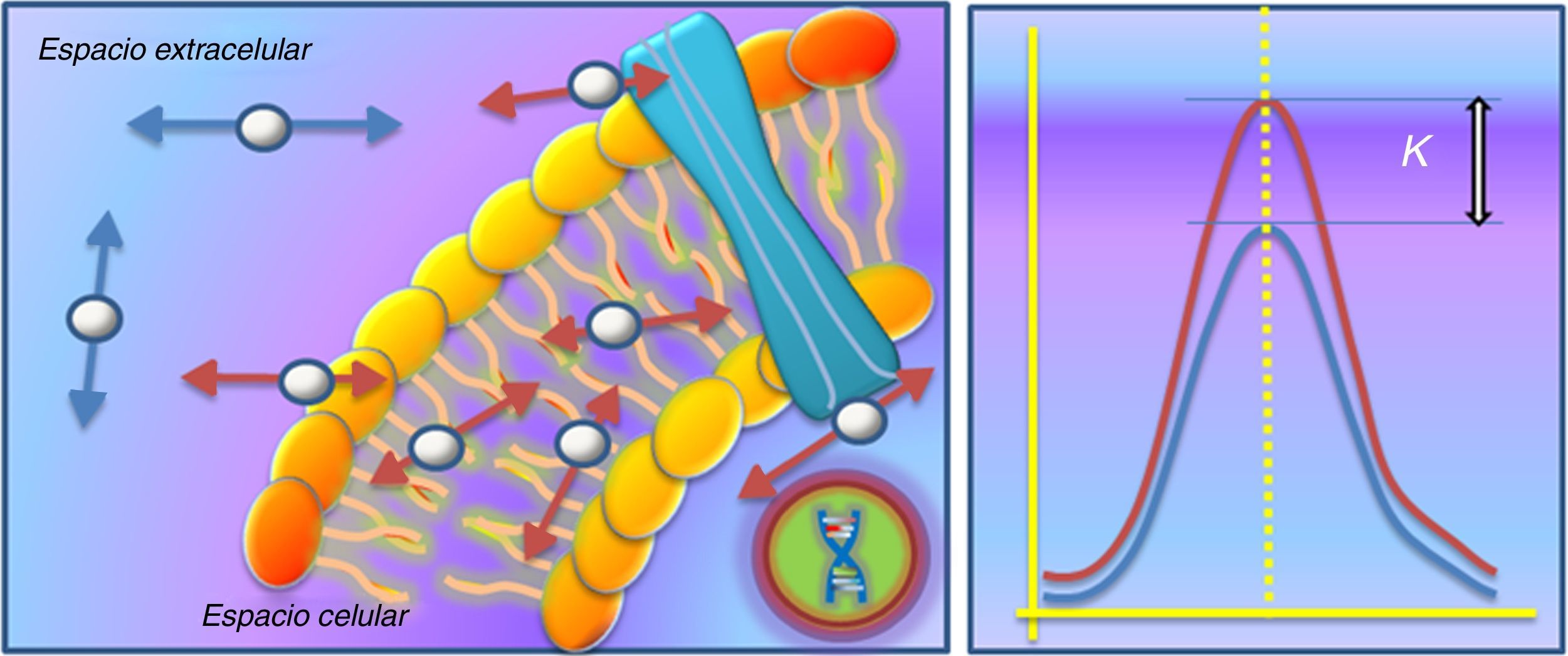
Sin embargo, se ha demostrado que la presencia de barreras fisiológicas como las membranas celulares, o incluso las de las propias organelas, limitan esa aleatoriedad del movimiento. El agua no difunde con igual libertad o con igual grado de restricción en todas las direcciones. Este movimiento del agua ligada a las membranas puede ser estudiado mediante la Kurtosis, la cual considera que existe una distribución no gaussiana de la difusión15 (fig. 6). El concepto de Kurtosis, importado del mundo de la estadística, hace referencia al grado de concentración que muestran los valores en torno a la zona central de la distribución, que es igual a 0 en el caso de la distribución gaussiana (normal) y mostrará valores por encima de 0 cuando los valores obtenidos no sigan una distribución gaussiana.
Kurtosis. La interacción de las moléculas de agua con las membranas celulares sigue una distribución no gaussiana (flechas rojas) que se aleja de la distribución normal del movimiento de las moléculas de agua en el espacio extracelular (flechas azules). La Kurtosis refleja la diferencia de dicha distribución no gaussiana con respecto a la distribución normal, que será mayor cuanto más heterogéneo sea el tejido a estudiar.
Para poder detectar ese desplazamiento del agua ligada a las membranas, que se trata de un movimiento muy lento del agua, es necesaria la aplicación de valores b muy altos (>2000 s/mm2)16.
Este modelo de análisis nos permite estimar la heterogeneidad o complejidad de los tejidos, ya que nos aproxima al grado de interacción del agua con las membranas biológicas, algo que va más allá de la “simple” restricción del movimiento del agua en el espacio extracelular. Diversos estudios han demostrado que, a igualdad de valores ADC en distintos tejidos, es decir, tejidos que aparentemente presentan el mismo grado de restricción de la difusión, la estimación de la Kurtosis permite diferenciar entre ellos17. Cuanto más se aleje un tejido de la distribución normal, mayor será su Kurtosis, su complejidad15.
Parámetros derivados de DWI y DTILos parámetros derivados de los estudios de DWI y DTI nos permiten evaluar desde el punto de vista cuantitativo distintos procesos fisiopatológicos, de una manera más exacta y con una mayor precisión diagnóstica. Muchos de estos parámetros se encuentran todavía en fase de validación clínica debido a que no se ha logrado todavía una estandarización global de los protocolos de adquisición y análisis de las secuencias de difusión, aparte de las limitaciones técnicas inherentes a la secuencia de difusión, como son una mayor sensibilidad a los artefactos por movimiento o susceptibilidad magnética. Por ello es fundamental conocer el significado biológico de estos parámetros como punto de partida para poner en marcha futuros estudios y poder contribuir a dicha validación.
Para que puedan ser considerados como biomarcadores, dichos parámetros tienen que cumplir una serie de requisitos, entre los que destacan su fiabilidad, reproducibilidad, capacidad de reflejar una característica de un tejido de manera cuantitativa, indicando la existencia de un proceso fisiológico o patológico subyacente con una determinada relevancia clínica18. Estos parámetros, que se desglosan a continuación, vienen resumidos en la tabla 1.
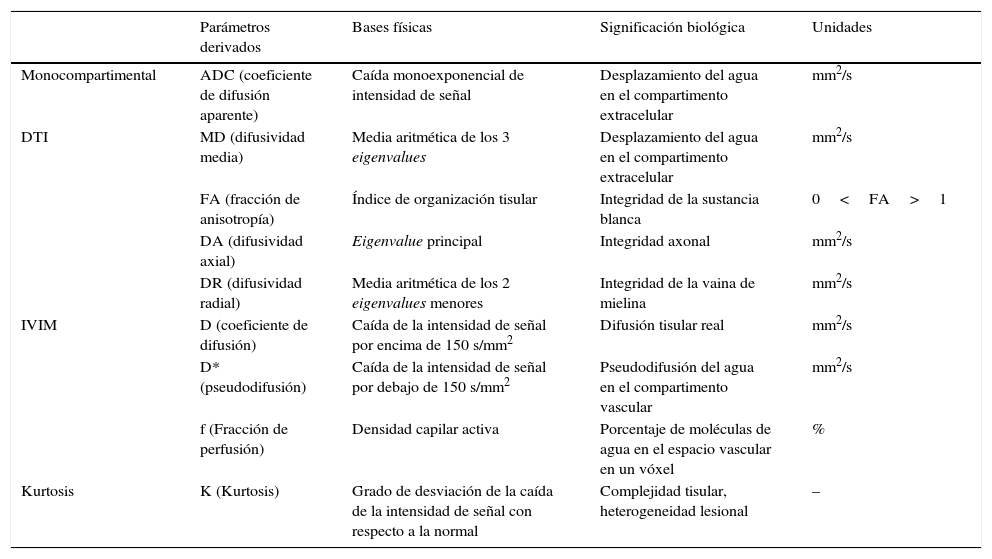
Parámetros derivados del análisis básico y avanzado del estudio de difusión y DTI
| Parámetros derivados | Bases físicas | Significación biológica | Unidades | |
|---|---|---|---|---|
| Monocompartimental | ADC (coeficiente de difusión aparente) | Caída monoexponencial de intensidad de señal | Desplazamiento del agua en el compartimento extracelular | mm2/s |
| DTI | MD (difusividad media) | Media aritmética de los 3 eigenvalues | Desplazamiento del agua en el compartimento extracelular | mm2/s |
| FA (fracción de anisotropía) | Índice de organización tisular | Integridad de la sustancia blanca | 0<FA>1 | |
| DA (difusividad axial) | Eigenvalue principal | Integridad axonal | mm2/s | |
| DR (difusividad radial) | Media aritmética de los 2 eigenvalues menores | Integridad de la vaina de mielina | mm2/s | |
| IVIM | D (coeficiente de difusión) | Caída de la intensidad de señal por encima de 150 s/mm2 | Difusión tisular real | mm2/s |
| D* (pseudodifusión) | Caída de la intensidad de señal por debajo de 150 s/mm2 | Pseudodifusión del agua en el compartimento vascular | mm2/s | |
| f (Fracción de perfusión) | Densidad capilar activa | Porcentaje de moléculas de agua en el espacio vascular en un vóxel | % | |
| Kurtosis | K (Kurtosis) | Grado de desviación de la caída de la intensidad de señal con respecto a la normal | Complejidad tisular, heterogeneidad lesional | – |
El ADC es el parámetro más extendido derivado de la adquisición de la secuencia convencional de difusión, y es capaz de estimar el grado de restricción del movimiento del agua en el espacio extracelular. Dichos valores de ADC se verán reducidos en aquellas situaciones en las que disminuya el espacio extracelular debido a un aumento del número o tamaño de las células (edema citotóxico).
Para calcular el ADC es necesario como mínimo la participación de dos valores b, normalmente el 0 y el valor b más alto (1000-1500 s/mm2 en SNC). El ADC nos permite corregir la influencia del efecto T2 sobre la difusión y confirmar si la hiperintensidad de un determinado tejido para los valores b más altos se debe a verdadera restricción de la difusión (en cuyo caso los valores ADC serán bajos) o por el contrario nos encontramos ante un efecto de brillo-T2 (que asociará valores altos de ADC).
Hay que recordar que el ADC es un valor aparente, ya que no solo mide la difusión del agua extracelular en los tejidos, sino que se ve influenciado por otros movimientos como el respiratorio, cardíaco, vascular, líquido cefalorraquídeo o secreciones. El ADC tiene una ventaja principal sobre todos los demás parámetros que iremos describiendo, su amplia disponibilidad19.
La principal aplicación clínica de la secuencia de difusión convencional y del ADC en el SNC es la detección y caracterización de patología isquémica. El grado de restricción de la difusión permite establecer con gran precisión el tiempo de evolución de los ictus isquémicos20.
Los estudios de difusión también han permitido mejorar la caracterización de lesiones tumorales. Numerosas publicaciones han demostrado que aquellos tumores con valores más bajos de ADC presentan una mayor celularidad, lo que se correlaciona con un mayor grado de agresividad tumoral21. De igual forma, los valores de ADC pueden servir para monitorizar la respuesta al tratamiento de estos tumores, apreciándose un incremento de valores ADC en aquellos que respondan al tratamiento debido a fenómenos de necrosis22. A través de los valores ADC podemos predecir la respuesta al tratamiento, ya que se ha demostrado que lesiones con valores más bajos de ADC previos al tratamiento presentan una respuesta más positiva a este que aquellas con valores ADC más elevados, que normalmente asocian áreas necróticas, con menor aporte capilar y peor oxigenadas, que disminuyen la efectividad del tratamiento tanto de quimioterapia como de radioterapia23 (fig. 7).
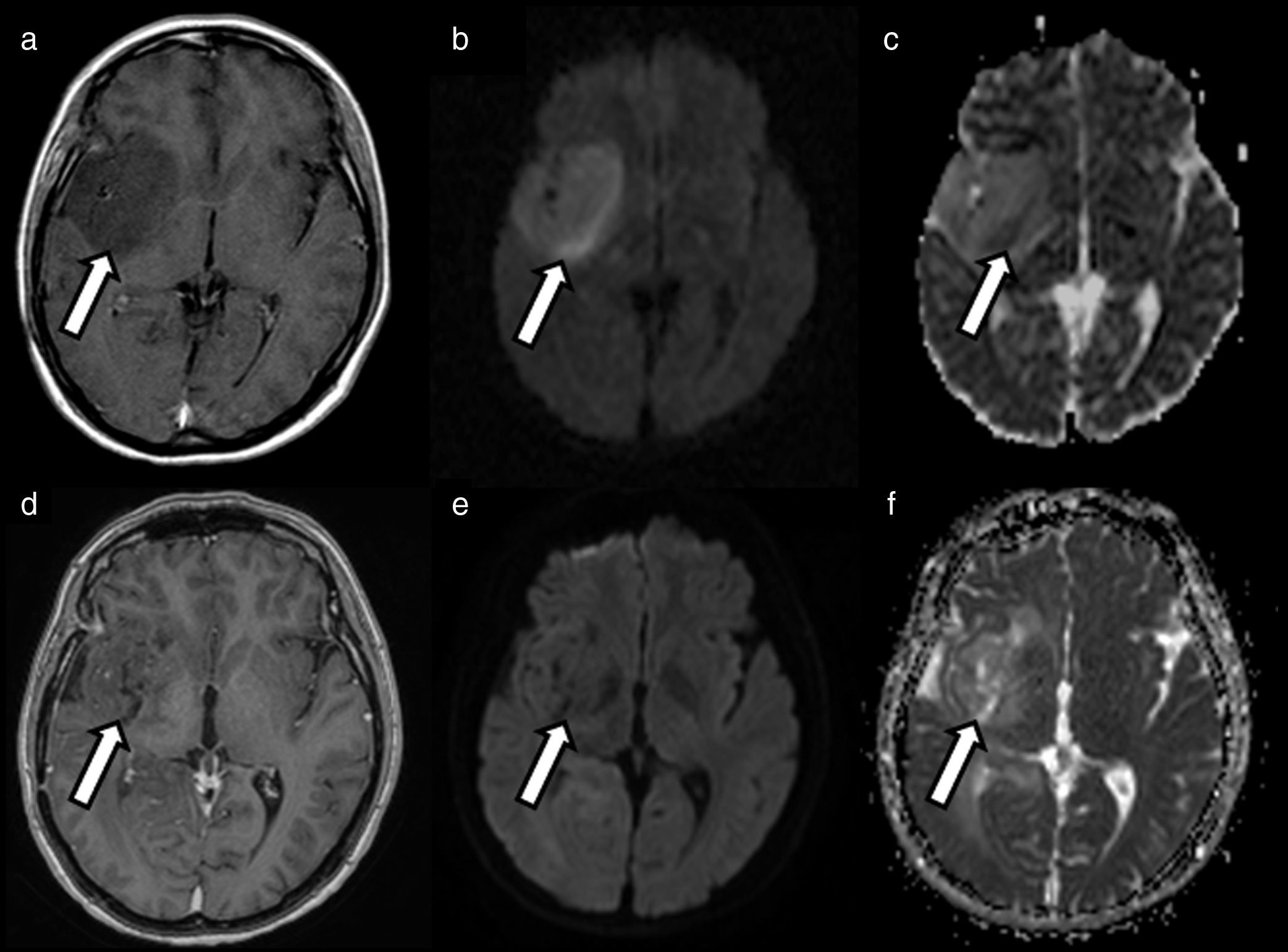
Predicción de respuesta a tratamiento y monitorización. Paciente de 56 años que muestra lesión insular derecha con biopsia de astrocitoma de grado III de la OMS. En el estudio previo a tratamiento (enero 2015) se identifica lesión infiltrativa sin realce aparente en el estudio con contraste (a) que muestra áreas de marcada restricción de la difusión (b) con valores de ADC de 0,6×10−3 mm2/s (c) compatible con áreas hipercelulares. El paciente fue sometido a radioterapia, y se objetivó una reducción de la masa tumoral (d), así como menor grado de restricción de la difusión con incremento en los valores de ADC 1,5×10−3 mm2/s (f) compatible con adecuada respuesta al tratamiento debido a muerte celular. El estudio de difusión permite en este caso tanto predecir una respuesta favorable al tratamiento como confirmar dicha evolución adecuada.
El uso de ADC permite valorar la patología infecciosa intracraneal, como es el caso de los abscesos, en los que la difusión ayuda al diagnóstico diferencial con otro tipo de lesiones necróticas con realce periférico como son las metástasis. En el interior de los abscesos, la presencia de detritus, restos celulares y de microorganismos condicionan una muy importante restricción de la difusión, aunque no siempre este hallazgo es específico de los abscesos y puede existir solapamiento con determinados subtipos histológicos de metástasis en el SNC24,25.
Parámetros derivados de las secuencias de DTILos estudios de DTI permiten obtener un mayor número de parámetros, la mayoría de ellos de gran utilidad para la valoración de sustancia blanca. El más conocido es la fracción de anisotropía (FA, Fractional Anisotropy), que refleja el grado de anisotropía de un tejido, es decir, cómo de dominante es la dirección del movimiento del agua en un determinado vóxel, y varía desde 1 (máxima anisotropía) hasta 0 (máxima isotropía). La FA puede ser considerada como un biomarcador de integridad axonal, ya que posee una alta sensibilidad en la valoración de patología de sustancia blanca, y se ve alterada (generalmente disminuida) prácticamente en cualquier proceso que la afecte; sin embargo, y por el mismo motivo, su especificidad no es la deseable26.
La dirección dominante en cada plano del espacio viene marcada por los eigenvectors, los cuales poseen un valor, una magnitud conocida como eigenvalues, que se expresa, al igual que el ADC, en mm2/s. El valor medio de los 3 eigenvalues principales se conoce como difusividad media (MD, Mean Diffusivity), y podría ser considerado como una medida más exacta del ADC, ya que tiene en cuenta las tres direcciones principales de movimiento del agua, con comportamiento similar al ADC en los distintos escenarios clínicos.
Otros dos parámetros derivados del DTI son la difusividad axial (DA) y la radial (DR). La DA refleja el movimiento de las moléculas de agua en la dirección longitudinal, dominante del axón, y coincide con el eigenvalue principal. Dicha medida será normalmente elevada, ya que como recordamos, la difusividad en dicho eje se encuentra facilitada. La DA nos permitirá valorar la integridad de conducción del axón o la existencia de una lesión a nivel de la neurona principal (que alteraría el flujo axonal por un mecanismo similar al de la degeneración valeriana).
La DR es la expresión de la media aritmética de los otros 2 eigenvalues menores, aquellos que tienen disposición perpendicular al eigenvalue principal. La difusividad en el plano radial se verá condicionada por la existencia de las vainas de mielina7. Son estas características biológicas las que hacen de la DR un adecuado parámetro para valorar la integridad de la mielina, probablemente el más específico de los derivados del DTI en la actualidad. La pérdida de mielina provocará un aumento de la DR, ya que las moléculas encontrarán menos dificultad para desplazarse en dicho plano transversal19. (fig. 8).
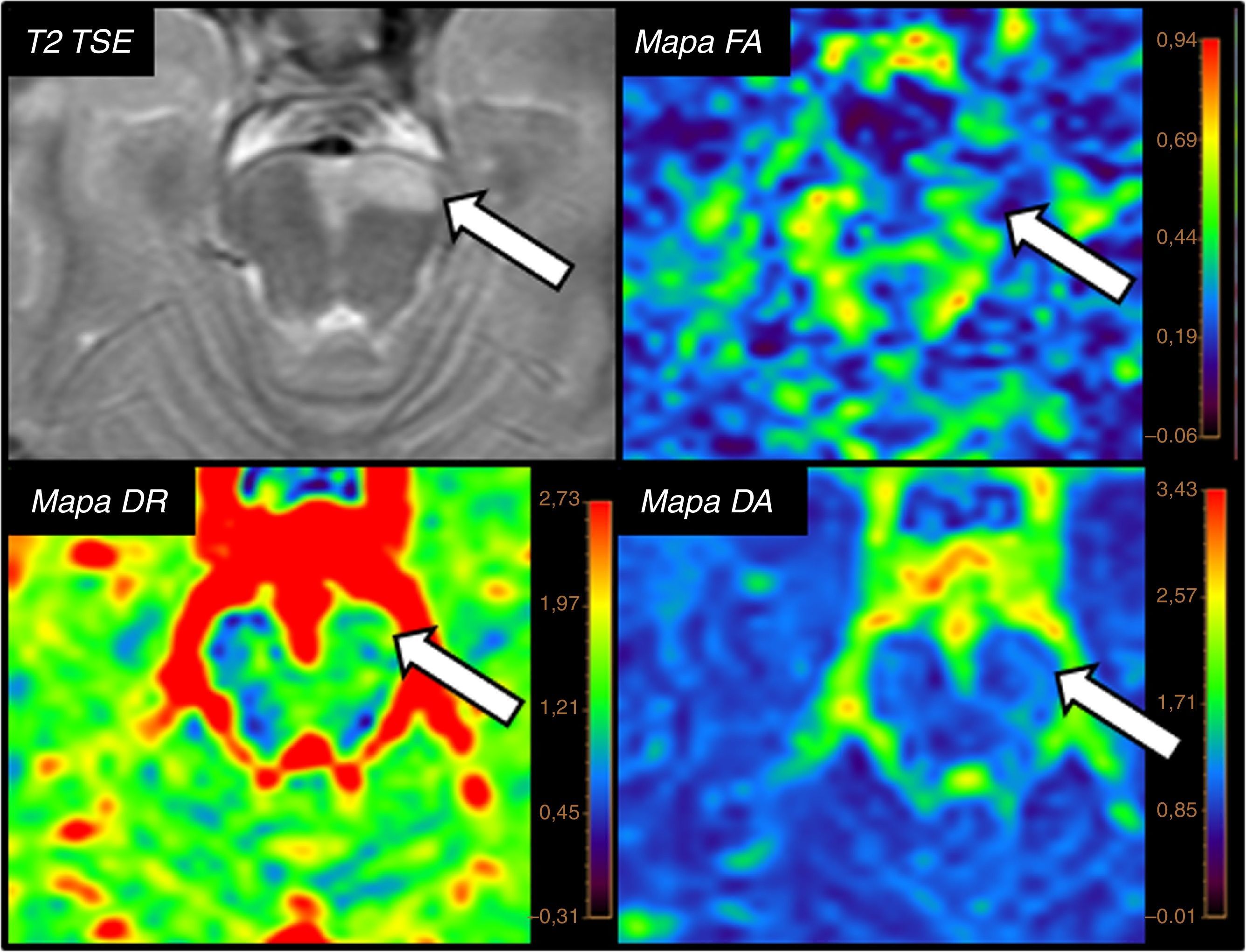
Paciente de 26 años con diagnóstico de esclerosis múltiple, que muestra lesión en pedúnculo cerebral izquierdo con descenso en los valores de fracción de anisotropía (FA) (0,3) con respecto a pedúnculo contralateral (0,8). Dicha lesión no muestra variaciones significativas en los valores de difusividad axial (DA), sin embargo, se identifica un incremento en los valores de difusividad radial (DR) (1,8×10−3 mm2/s) con respecto a pedúnculo contralateral (0,5×10−3 mm2/s), indicativo de daño selectivo de la vaina de mielina, acorde con su enfermedad de base.
Existen numerosas aplicaciones clínicas de los estudios basados en el DTI27. Entre ellas, la más destacada debido al salto cualitativo que ha supuesto es la valoración de la patología tumoral. FA y MD se han usado para caracterizar el área de alteración de la intensidad de señal peritumoral en secuencias potenciadas en T2 y FLAIR. En el caso de metástasis o meningiomas, dicho edema muestra valores de FA más bajos y valores de MD más elevados que en el caso de los gliomas de alto grado8,28. La explicación de este fenómeno parece basarse en la infiltración por células tumorales de la sustancia blanca adyacente a las lesiones gliales de alto grado, lo que permite su diagnóstico diferencial con metástasis únicas del SNC; sin embargo, estos datos no parecen ser extrapolables para la valoración del componente intratumoral29.
El uso de las reconstrucciones 3D basadas en DTI mediante la técnica de tractografía permite valorar la relación y dependencia de las lesiones del SNC con los principales haces de sustancia blanca, y puede estimar el grado de resecabilidad de las mismas en función de si existe desplazamiento, invasión o infiltración de dichos tractos5.
Otras aplicaciones clínicas del DTI incluyen la valoración de lesiones desmielinizantes, en las que se identificará como norma general el incremento en los valores de MD y descenso de FA debido al componente inflamatorio existente, siendo la DR es el parámetro más específico para la valoración del daño de la mielina30. Numerosos estudios han confirmado la mayor sensibilidad del DTI para la detección de alteraciones en la sustancia blanca aparentemente normal en pacientes con enfermedad desmielinizante31,32.
El DTI también se ha utilizado para el estudio de la epilepsia33 o incluso para enfermedades neurodegenerativas, y ha demostrado potencial utilidad en el diagnóstico diferencial de los distintos síndromes parkinsonianos34,35. Algunos autores han propuesto el uso de la FA como parámetro válido para monitorizar la respuesta al tratamiento en aquellos pacientes con hidrocefalia crónica del adulto tras la colocación de catéter de derivación36.
Parámetros derivados del modelo IVIMComo hemos referido anteriormente, el parámetro D nos permite obtener una medida más exacta y reproducible del verdadero coeficiente de difusión de los tejidos. Esto es de gran importancia en la valoración de la patología tumoral, ya que no es infrecuente que tumores de alto grado, en los que se espera encontrar valores bajos de ADC debido a su alta celularidad, presenten paradójicamente valores elevados de ADC como consecuencia de la existencia de fenómenos de necrosis asociada y de la influencia del componente vascular en la porción sólida del tumor. Dicho componente vascular en los tumores de alto grado se suele encontrar precisamente aumentado debido al proceso de neoangiogénesis inherente a este tipo de lesiones37.
D* y f son parámetros que hacen referencia al componente intravascular de un determinado vóxel de tejido. D* revela el movimiento del agua en el interior de la red vascular capilar, y f, derivada de dicha D*, refleja la densidad capilar activa, es decir, el porcentaje de capilares en cuyo interior se detecta movimiento del agua9.
Las aplicaciones clínicas del modelo IVIM se encuentran en la actualidad limitadas prácticamente al campo de la investigación38. De forma intuitiva podemos inferir que, en el caso de patología isquémica aguda, además de encontrar valores disminuidos de ADC (y por ende de D) tanto los valores de D* como de f se verán también reducidos debido al descenso del flujo en la red capilar distal39. Para la valoración de patología tumoral se ha demostrado una adecuada correlación entre los valores de D y ADC, siendo de utilidad para la estimación del grado tumoral y apreciándose igualmente correlación entre f y los parámetros derivados de los estudios de perfusión37,40 (fig. 9). También se ha postulado el uso del modelo IVIM para predecir la supervivencia en tumores de alto grado41 o incluso para estudios funcionales identificando un incremento en los valores de D* y f en aquellas áreas corticales con activación con los distintos paradigmas motores, visuales o cognitivos42.
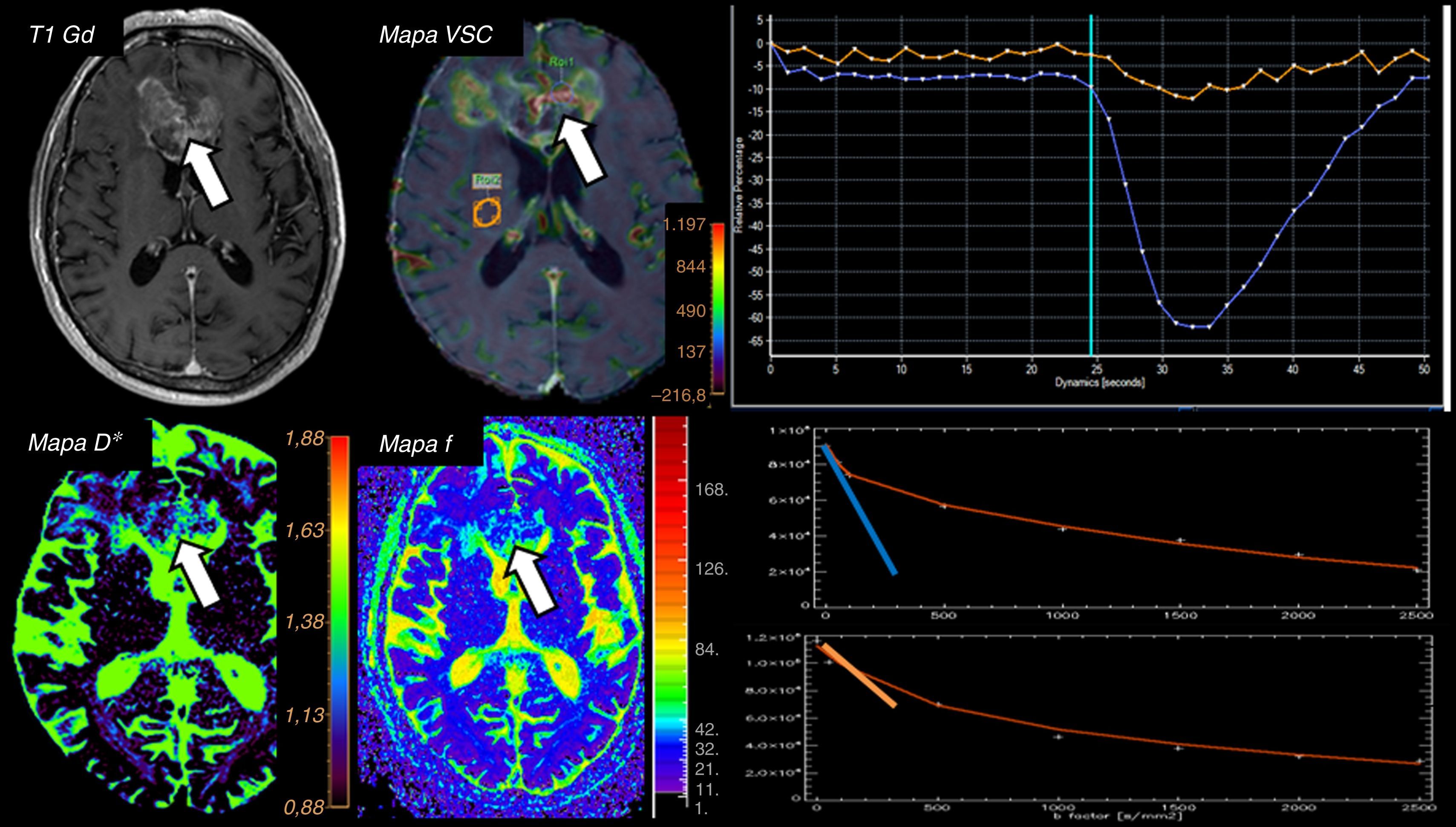
Paciente de 63 años con diagnóstico de glioblastoma. Se identifica una amplia lesión a nivel de ambos lóbulos frontales y rodilla de cuerpo calloso que muestra intenso realce tras la administración de contraste con incremento en sus valores de volumen sanguíneo cerebral (VSC). El análisis mediante el modelo IVIM muestra incremento de la pseudodifusión (D*) y de la fracción de perfusión (f) de hasta el 40% compatibles con zonas de neovascularización. La gráfica superior representa la intensidad de señal en el estudio de perfusión T2*, que muestra una caída más pronunciada (curva azul) en el componente solido tumoral en comparación con parénquima aparentemente sano (curva naranja), lo que sugiere neoangiogénesis. Las gráficas inferiores reflejan la caída de intensidad de señal de la secuencia de difusión siguiendo el modelo IVIM, objetivando una caída más pronunciada de la primera parte de la curva roja en el componente sólido tumoral (línea azul) en comparación con el parénquima aparentemente sano (línea naranja), lo que sugiere un predominio del componente vascular/capilar con rápido desfase de las moléculas de agua en su interior.
El principal parámetro derivado del análisis no gaussiano de la intensidad de señal de la secuencia de difusión es la Kurtosis (K) o Kurtosis media (MK). La K nos indica cuánto se aleja la distribución que estudiamos con respecto a la normal (gaussiana), teniendo en cuenta que si K = 0 estamos ante una distribución normal. La K puede ser matemáticamente tanto positiva como negativa, aunque en los tejidos biológicos, solo se considera la Kurtosis positiva43.
Valores elevados de K nos indicarán que el tejido a estudio es más complejo, más heterogéneo y se diferencia más de una distribución normal44. Dicha heterogeneidad se debe a la existencia de un mayor número de células, membranas, vasos y necrosis principalmente. Como ya hemos comentado, la K nos puede ayudar a añadir un mayor grado de especificidad a la caracterización de los tejidos con respecto a la difusión convencional. De esta manera, estudios experimentales han demostrado que existe un mayor grado de Kurtosis en tumores de alto grado con respecto a los de grado bajo, ya que la presencia de un mayor número de mitosis, membranas celulares, angiogénesis y necrosis esencialmente hace que dicho tejido sea más complejo que en los tumores de bajo grado en los que predomina el intersticio45.
Los estudios con el modelo de Kurtosis han demostrado también, con un mayor grado de significación estadística con respecto a la FA y MD, su utilidad para la valoración de la alteración de la intensidad de señal peritumoral. Aquellas áreas de edema con infiltración tumoral, debido a la existencia de células neoplásicas procedentes del tumor primario, mostrarán valores más elevados de K que en las zonas de edema vasogénico reactivo a lesiones metastásicas, en los que la K será menor46, lo que podría ayudar a distinguir con mayor precisión entre gliomas de alto grado y metástasis únicas del SNC (fig. 10).
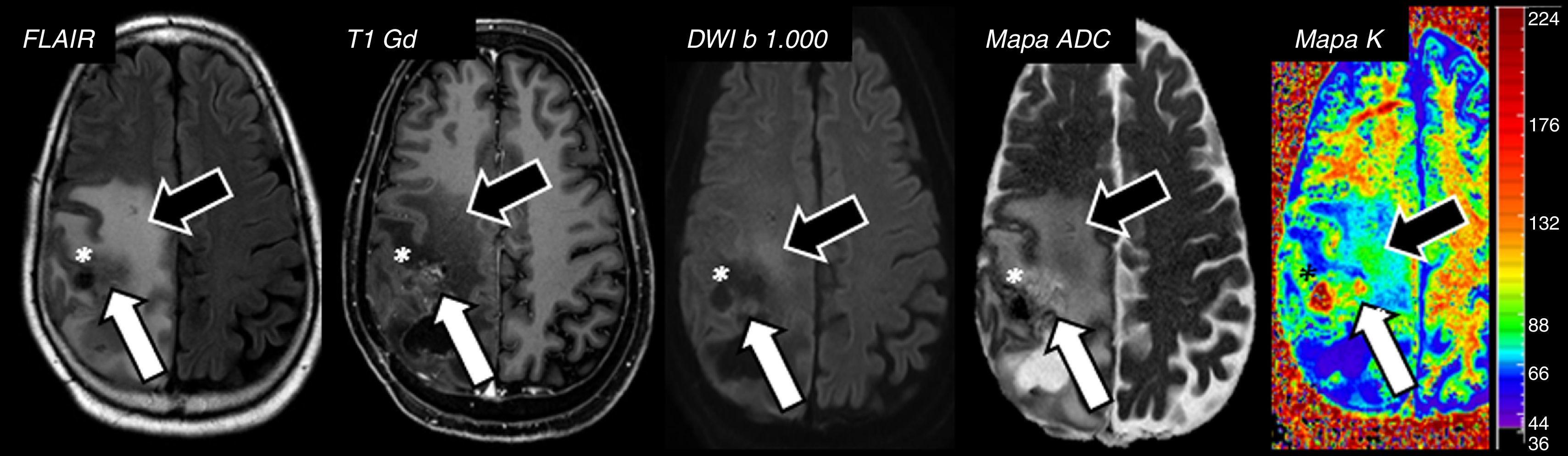
Paciente de 73 años con astrocitoma de grado III de la OMS tratado con cirugía, quimioterapia y radioterapia. A nivel de lóbulo parietal derecho se identifica una lesión compleja con componente sólido y quístico que asocia grave edema vasogénico. El análisis de Kurtosis muestra incremento de valores de K en el lecho quirúrgico, lo que representa áreas de incremento de heterogeneidad tumoral (flechas blancas). Nótese la presencia de áreas con aumento de valores de K en el espesor del edema vasogénico (flechas negras); dicha alteración, sugerente de infiltración tumoral, también parece identificarse en el estudio de DWI/ADC, pero de forma menos evidente. El asterisco indica un foco de probable falso positivo en el mapa de K debido a efecto black-out secundario a la presencia de restos hemorrágicos.
Otros estudios han demostrado un descenso en los valores de K en aquellas entidades que cursan con pérdida neuronal, como es el caso de la patología neurodegenerativa de tipo Alzheimer, lo que permite detectar cambios de una manera más precoz47.
Los estudios de DTI pueden experimentar una mala definición de la dirección dominante cuando existen varias direcciones en puntos de cruce de haces de sustancia blanca. Para intentar paliar esta limitación, se han desarrollado técnicas avanzadas de tractografía de alta resolución (HARDI, q-ball, difusión espectral) basándose en la aplicación de un elevado número de direcciones (>200) o valores b muy altos (>5000 s/mm2) a expensas de largos tiempos de adquisición. Los estudios de DTI basados en Kurtosis permiten obtener una mayor resolución espacial en los puntos de corte (debido a una mejor caracterización de la interacción del agua con las vainas de mielina) con un tiempo de adquisición más ajustado48.
ConclusionesLa aproximación clásica a los estudios de difusión junto con el desarrollo de nuevos modelos de análisis de la caída de intensidad de señal de la difusión, como son el IVIM o la Kurtosis, está permitiendo una mejor comprensión de los distintos procesos fisiopatológicos a nivel de SNC. Los distintos parámetros derivados de dichos modelos de análisis podrían ser considerados como biomarcadores y ayudarían a dar el paso de una interpretación de la difusión puramente cualitativa a un abordaje cuantitativo multiparamétrico, lo que aumentaría nuestra precisión para el diagnóstico, pronóstico y monitorización de tratamiento en múltiples escenarios clínicos.
Autoría- 1.
Responsable de la integridad del estudio: TMN y JPMB.
- 2.
Concepción del estudio: TMN.
- 3.
Diseño del estudio: TMN.
- 4.
Obtención de los datos: TMN y JPMB.
- 5.
Análisis e interpretación de los datos: TMN y JPMB.
- 6.
Tratamiento estadístico: No procede.
- 7.
Búsqueda bibliográfica: TMN y JPMB.
- 8.
Redacción del trabajo: TMN y JPMB.
- 9.
Revisión crítica del manuscrito con aportaciones intelectualmente relevantes: TMN y JPMB.
- 10.
Aprobación de la versión final: TMN y JPMB.
Los autores declaran que para esta investigación no se han realizado experimentos en seres humanos ni en animales.
Confidencialidad de los datosLos autores declaran que han seguido los protocolos de su centro de trabajo sobre la publicación de datos de pacientes.
Derecho a la privacidad y consentimiento informadoLos autores declaran que en este artículo no aparecen datos de pacientes.
Conflicto de interesesLos autores declaran no tener ningún conflicto de intereses