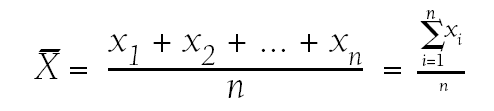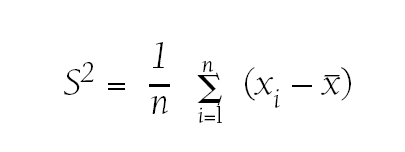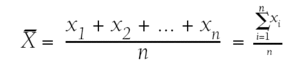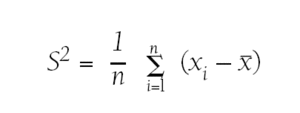INTRODUCCIÓN
La estadística se define como la ciencia matemática que se refiere a la recopilación, estudio e interpretación de los datos obtenidos en un estudio.
Se aplica a una amplia variedad de disciplinas, entre las que cabe destacar las ciencias de la salud; en particular, en el campo de la Atención Primaria es necesario conocer los fundamentos de la estadística ya que la medicina es cada vez más cuantitativa, los resultados se utilizarán para la toma de decisiones pues se obtienen conclusiones correctas de procedimientos diagnósticos y de diversas pruebas.
La bioestadística es la disciplina que trata del desarrollo y aplicación de la teoría y métodos estadísticos en aquellos fenómenos que surgen de las ciencias biomédicas1,2.
Como hemos estudiado en el capítulo "Selección de la muestra" de esta serie, para aplicar un análisis estadístico necesitamos recopilar información de cierta población que se define como el conjunto homogéneo de elementos que reúne unas características determinadas objeto de estudio. Por razones prácticas se estudia un subconjunto de la población denominado muestra, sobre el que realizamos las mediciones o el experimento para obtener conclusiones generalizables a la población. Los datos recogidos se analizan estadísticamente siguiendo dos propósitos: descripción e inferencia.
TIPOS DE DATOS
La naturaleza de las observaciones es importante a la hora de elegir el método estadístico más apropiado para el análisis. La característica observada de cada individuo de la muestra se denomina variable, por ejemplo: el peso, la edad, el nivel de colesterol en sangre, etc., y se pueden clasificar en dos grupos según el tipo de valores que toman3-5:
1) Variables cualitativas: son variables que representan una cualidad, no pueden medirse numéricamente pero pueden clasificarse en una o varias categorías. A su vez las variables cualitativas se dividen en ordinales y nominales, dependiendo de que esas categorías admitan cierto orden. Por ejemplo, el estado de un paciente (leve, moderado, grave) es una variable cualitativa ordinal y la variable sexo (hombre, mujer) es una variable cualitativa nominal.
2) Variables cuantitativas: son variables que toman valores numéricos y que se dividen a su vez en dos categorías: variables continuas, asociadas a procesos de medición como la edad, el peso, etc., y variables discretas, asociadas a procesos de conteo, por ejemplo, número de hijos, de casos de sida, etc.
Puede realizarse una transformación de una variable cuantitativa pasándola a una escala ordinal, este proceso se denomina categorización de una variable. Partiendo de una variable numérica creamos grupos de casos colapsándolos en k categorías. Por ejemplo, supongamos que hemos recogido la variable edad de los individuos que forman nuestra muestra, a partir de esta variable podemos crear una nueva variable (edad categorizada) de la forma siguiente: categoría 1 = joven (menores de 25 años), categoría 2 = mediana edad (individuos entre 26-59 años) y categoría 3 = mayor (individuos mayores de 60 años).
ESTADÍSTICA DESCRIPTIVA
La estadística descriptiva es la parte de la estadística que sintetiza y resume la información contenida en un conjunto de datos, por tanto, un análisis descriptivo consiste en clasificar, representar y resumir los datos2,3,6. La descripción se puede hacer utilizando dos tipos de procedimientos: mediante el cálculo de índices estadísticos que son números que resumen de modo sencillo la información contenida en los datos reales, o bien utilizando representaciones gráficas que son muy útiles, ya que pueden aportar mucha información en un solo golpe de vista5,7.
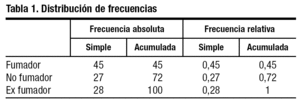
Si la variable a estudio es una variable cualitativa utilizaremos tablas de frecuencias, que consisten una representación estructurada de toda la información que se ha recogido sobre dicha variable. En estas tablas se detalla cada uno de los valores diferentes en el conjunto de datos con el número de veces que aparece, la frecuencia absoluta. Se puede completar añadiendo la frecuencia relativa que representa la frecuencia en porcentaje sobre el total de datos.
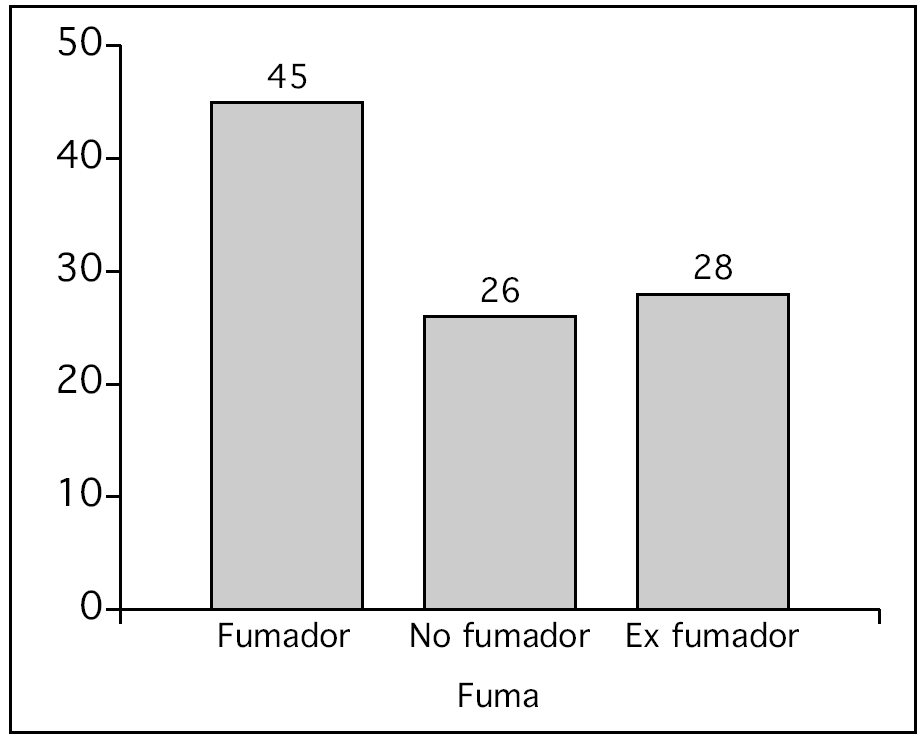
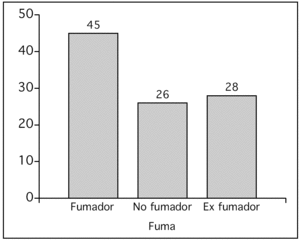
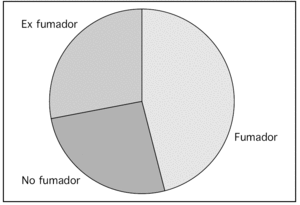
Si describimos una variable cualitativa gráficamente debemos utilizar un diagrama de barras en el que se representan tantas barras como categorías tiene la variable, de forma que la altura de cada uno de los rectángulos es proporcional a la frecuencia de casos en cada clase; o un diagrama de sectores, en el que se divide un círculo en tantas porciones como clases tiene la variable, de forma que a cada una de las clases le corresponde un arco de círculo proporcional a la frecuencia absoluta o relativa.
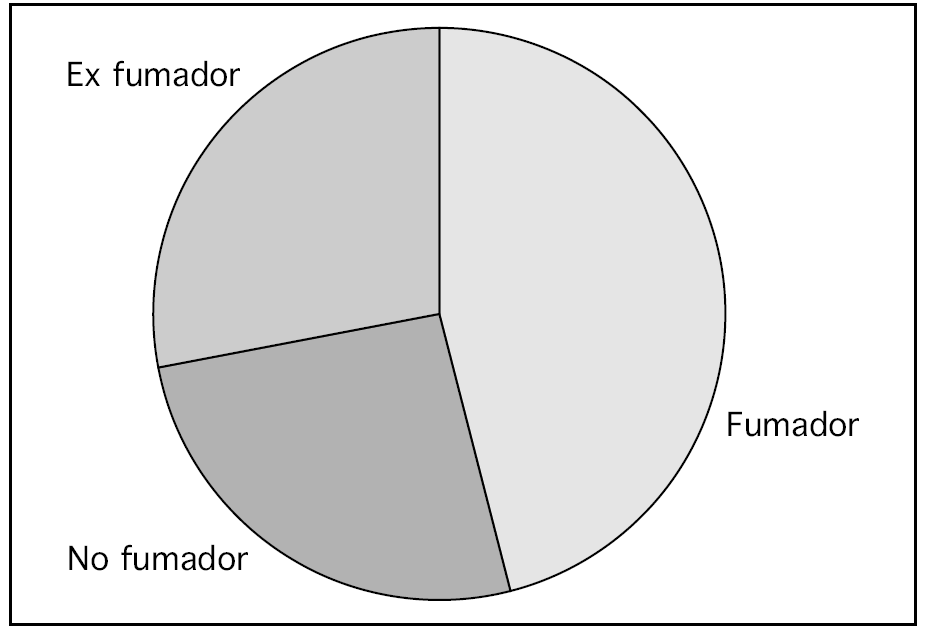
Supongamos que hemos recogido de una muestra de 100 individuos la variable "hábito tabáquico", dicha variable tiene tres categorías: "fumador, no fumador y ex fumador". La tabla de frecuencias se puede observar en la tabla 1 y las figuras 1 y 2.
Figura 1. Diagrama de barras.
Figura 2. Diagrama de sectores.
Las variables cuantitativas se describen mediante gráficos y medidas características.
Las medidas características se clasifican en cuatro grupos:
1) Medidas de tendencia central: nos indican el valor alrededor del cual se agrupan los datos, dentro de este tipo de medidas distinguimos:
Media: que se obtiene sumando los valores de la variable divididos por el número total de datos.
Mediana: es la observación que ocupa la posición central después de haber ordenado los datos, si el número de casos es impar será el dato que ocupa la posición (n + 1)/2, en el caso de que el número de observaciones sea par, la mediana se obtiene calculando la media de los datos que ocupan las posiciones n/2 y (n/2) + 1.
Moda: es el valor o valores más frecuentes de la distribución.
2) Medidas de dispersión: cuantifican la variabilidad de la distribución, es decir, nos dan una idea de la dispersión de los datos. Entre estas medidas distinguimos:
Varianza: mide la dispersión de los datos alrededor del valor medio. Cuanto mayor sea la varianza mayor es la variabilidad y cuanto menor sea más homogénea será la distribución.
Desviación típica: que se define como la raíz cuadrada de la varianza, informa sobre la dispersión de la distribución y se expresa en las mismas unidades que la variable.
Rango: es la diferencia entre el valor mayor y el valor menor de la distribución, por tanto, está muy influenciado por los outliers.
3) Medidas de posición: entre este tipo de medidas distinguimos:
Percentiles: el percentil de orden k es el valor de la variable que deja por debajo el k% de las observaciones.
Cuartiles: dividen el conjunto de datos en cuatro grupos de igual tamaño, el Q1 o 1.er cuartil deja por debajo el 25% de los datos, el Q2 o 2.o cuartil es la mediana y el Q3 o 3.er cuartil deja por debajo de sí el 75% de los datos.
4) Medidas de forma: describen dos aspectos de la distribución:
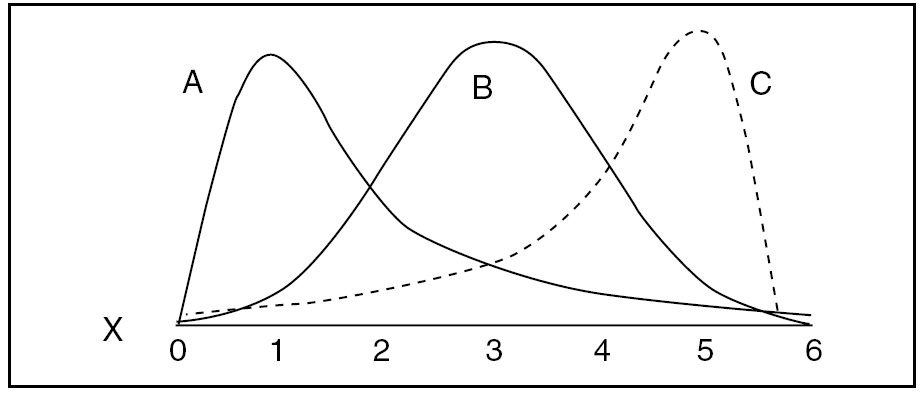
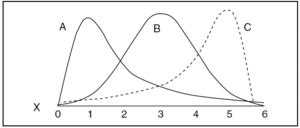
Asimetría: se define el coeficiente de asimetría como el grado en que los datos se reparten por encima y por debajo de la tendencia central (fig. 3).
Figura 3. Asimetría. A = asimétrica por la derecha; B = función simétrica; C = asimétrica por la izquierda.
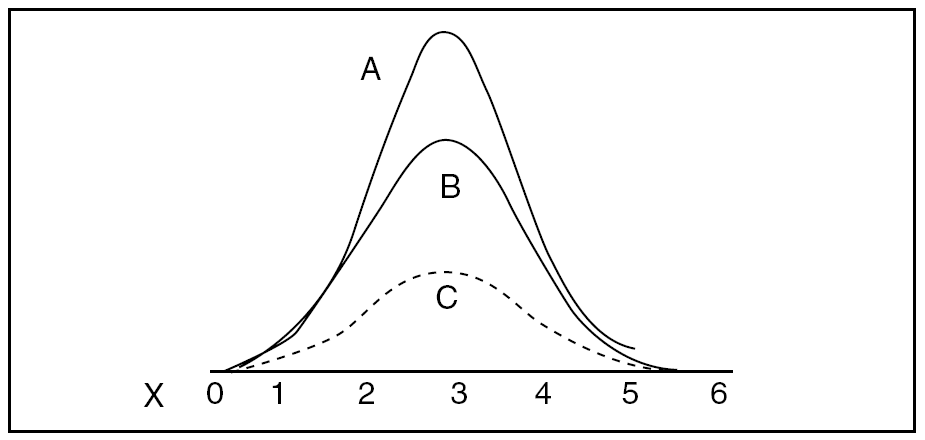
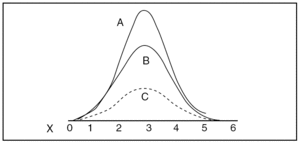
Curtosis: indica el grado de apuntamiento de la distribución en la zona central (fig. 4).
Figura 4. Curtosis. A = leptocúrtica; B = mesocúrtica; C = platocúrtica;
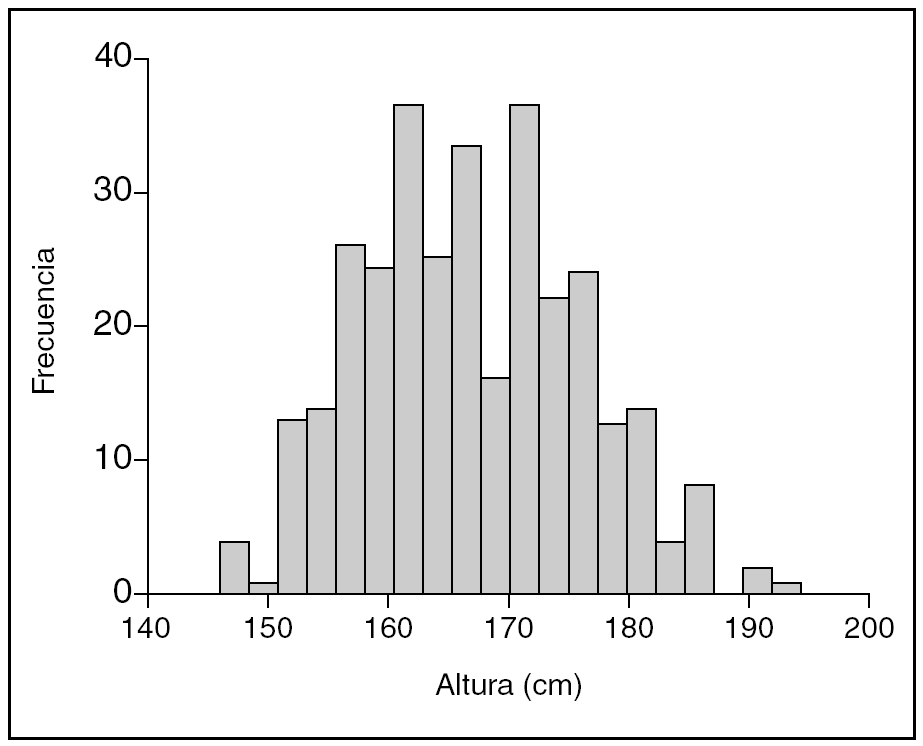
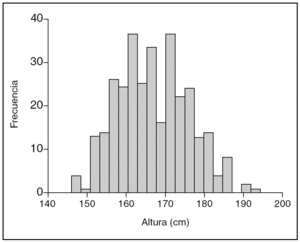
Para resumir una variable aleatoria numérica continua, como por ejemplo la edad, se puede utilizar el histograma, en el cual el rango de valores de la variable se divide en intervalos de igual amplitud, sobre cada intervalo se representa un rectángulo de forma que su altura mantiene la proporción entre las frecuencias (absolutas o relativas) y la longitud del intervalo (fig. 5).
Figura 5. Histograma, representa la variable aleatoria altura de una muestra de 316 individuos.
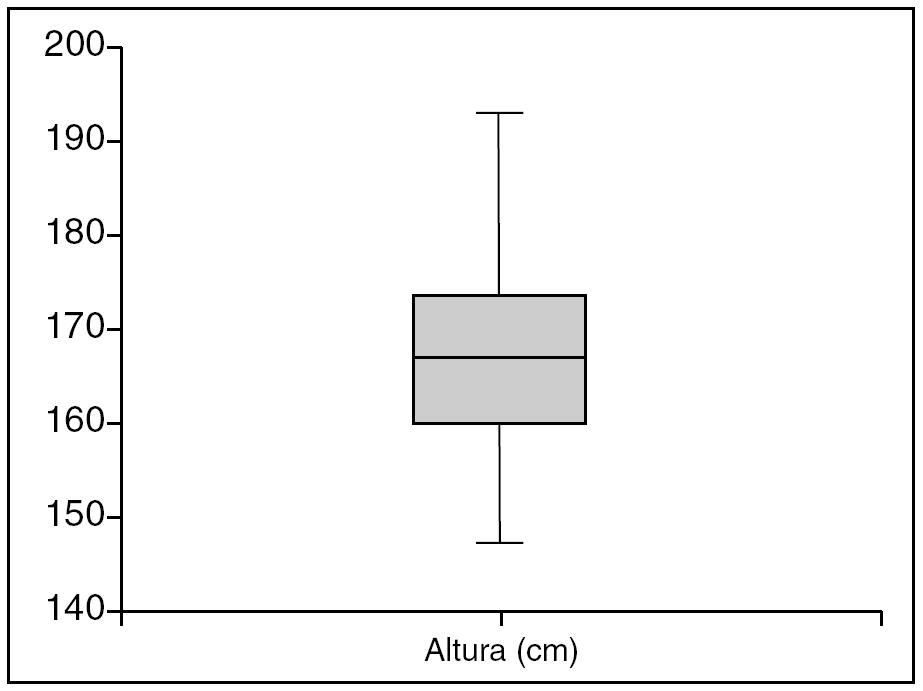
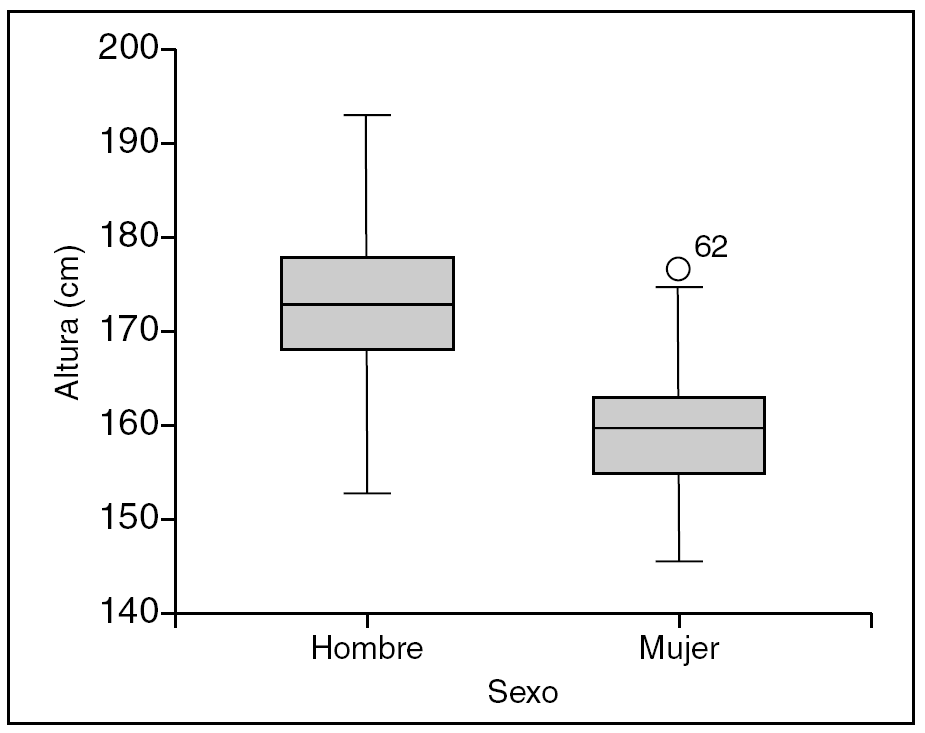
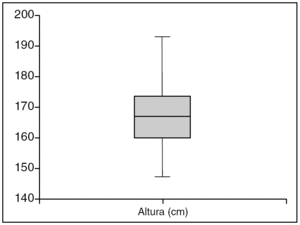
El diagrama de cajas es otra forma de describir gráficamente una variable de tipo numérico, este tipo de gráfico utiliza los percentiles, de forma que la caja central concentra el 50% de los datos (sus límites se corresponden con el 1.er y 3.er cuartil). La línea central representa la mediana. Los "bigotes" de los extremos de las cajas encierran el 95% de los datos centrales (pueden coincidir en algunos casos con los extremos de la distribución), se representan los valores extremos, denominados outliers, por puntos y por asteriscos. Una de las ventajas de este tipo de gráficos es que podemos de forma visual detectar posibles errores en los datos y además nos permite comparar grupos de sujetos (figs. 6 y 7).
Figura 6. Diagrama de cajas, representa la variable aleatoria altura de una muestra de 316 individuos.
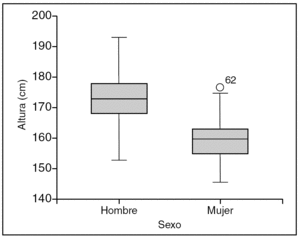
Figura 7. Diagrama de cajas, representa la variable aleatoria altura de una muestra de 316 individuos por sexo.
INFERENCIA ESTADÍSTICA
La inferencia se define como el conjunto de métodos estadísticos que permiten deducir cómo se distribuye la población e inferir las relaciones entre variables a partir de la información que proporciona la muestra recogida8. Por tanto, los objetivos fundamentales de la inferencia estadística son la estimación y el contraste de hipótesis.
Para que un método de inferencia estadística proporcione buenos resultados debe basarse en una técnica matemática (estadística) adecuada al problema planteado, además la muestra seleccionada debe ser representativa de la población y de tamaño suficiente (tabla 2).
La estimación estadística es el conjunto de técnicas que nos permitirán dar un valor aproximado de un parámetro poblacional a partir de la información obtenida de la muestra. Para realizar estimaciones utilizaremos ciertas fórmulas que dependen de los valores obtenidos en la muestra, se denominan estimadores. Un buen estimador debe ser insesgado, lo que significa que la estimación muestral debe coincidir con la poblacional; eficiente, es decir, de mínima varianza; y suficiente, debe utilizar toda la información contenida en la muestra.
La estimación de un parámetro poblacional utilizando un único valor se denomina estimación puntual; por ejemplo, para estimar la edad media poblacional utilizaremos la edad media muestral, pero este tipo de estimación tiene ciertos inconvenientes, ya que no podemos conocer cómo de precisa es esta medida.
La estimación por intervalos de confianza nos permite presentar una estimación acompañada de cierto margen de error (con un límite superior y un límite inferior), por tanto, un intervalo de confianza es simplemente un rango de valores que contiene el parámetro poblacional con cierta probabilidad.
Esta probabilidad se denomina nivel de confianza y se denota por (1-α), aunque habitualmente se expresa en tanto por ciento. Los niveles de confianza que se utilizan generalmente son del 95%, del 90% o del 99%, que se corresponden con un nivel de significación, que es la probabilidad de que la estimación falle, del 0,05, 0,1 y 0,01, respectivamente.
Para calcular intervalos de confianza se debe utilizar el error estándar, que es una medida de dispersión de la media muestral alrededor de la media poblacional. Se calcula como el cociente entre la desviación típica y la raíz cuadrada del número de observaciones (s/n).
PRUEBAS ESTADÍSTICAS
Las pruebas estadísticas8,9 forman parte de la teoría de decisión, a partir de la información que extraemos de la muestra estimamos características generales de la población de referencia. Existen tres tipos de pruebas estadísticas:
1) Pruebas de conformidad: en las que se comprueba si una estimación coincide con un valor teórico. Por ejemplo, queremos comprobar si la proporción de recurrencia de una úlcera duodenal al tomar cierto fármaco es inferior al 10%.
2) Pruebas de homogeneidad: comparan poblacionalmente dos o más grupos; supongamos que nos interesa comprobar si la proporción de recurrencia de la úlcera duodenal con un nuevo fármaco es igual a la proporción de recurrencia en pacientes tratados con otro fármaco.
3) Pruebas de relación: evalúan la relación entre variables.
Los contrastes de hipótesis o tests de hipótesis10 permiten comprobar si la información muestral concuerda con la hipótesis estadística formulada, nos permiten cuantificar hasta qué punto los resultados de un estudio particular dependen de la variabilidad de la muestra.
La hipótesis que se contrasta se denomina hipótesis nula y se denota por H0, se puede interpretar como la hipótesis que normalmente sería aceptada mientras los datos no indiquen lo contrario. Rechazar la hipótesis nula supone asumir una hipótesis complementaria, la hipótesis alternativa (H1), como correcta.
Para realizar un contraste de hipótesis debemos definir la hipótesis nula y la alternativa y definir una medida, el estadístico de contraste, que permite cuantificar la magnitud de la diferencia entre la información que proporciona la muestra y la hipótesis H0. Se pueden cometer dos tipos de errores11:
1) Error tipo I: rechazamos la hipótesis nula cuando es cierta.
2) Error tipo II: no rechazamos la hipótesis nula cuando es falsa.
En la práctica no es posible saber si estamos cometiendo un error tipo I o un error tipo II, pero existen ciertas recomendaciones para disminuir dichos errores. Por ejemplo, para disminuir el error tipo I deberíamos depurar la base de datos para evitar posibles outliers o valores extremos que puedan producir resultados significativos, utilizar un nivel de significación pequeño y disponer de una teoría que guíe las pruebas. Para reducir el error tipo II es aconsejable incrementar el tamaño muestral, estimar la potencia estadística o incrementar el tamaño del efecto a detectar.
Es necesario establecer a priori el nivel de significación (α) que se define como la probabilidad de cometer un error tipo I, normalmente se elige un valor pequeño, el 5% o el 1%. El valor del nivel de significación divide en dos regiones el conjunto de posibles valores del estadístico de contraste:
1) Zona de rechazo (con probabilidad α, bajo H0).
2) Zona de aceptación (con probabilidad 1-α, bajo H0).
Cuando analizamos la muestra obtendremos la significación del contraste, que se representa con la letra p, es un indicador de la discrepancia entre la hipótesis nula y los datos muestrales, de forma que cuanto más se acerque a cero tenemos mayor evidencia en contra de la hipótesis nula (si p es menor que el nivel de significación rechazaremos H0).
Debemos tener en cuenta que la significación estadística depende de la magnitud de la diferencia que queremos probar, cuanto mayor sea esta diferencia más sencillo será demostrar que es significativa. Al mismo tiempo depende también del tamaño muestral, cuanto más grande sea el número de observaciones más sencillo es detectar diferencias.
MODELOS DE REGRESIÓN
Los modelos de regresión estudian la relación cuantitativa12 entre una variable de interés, que se denomina variable respuesta o dependiente (Y), y un conjunto de variables explicativas (X1,X2,...,Xk). Puede ocurrir que exista una relación funcional, de forma que el conocimiento de las variables explicativas determina el valor de la variable dependiente, o, en cambio, que no exista ninguna relación, lo que significa que conocer el valor de las variables (X1,X2,...,Xk) no aporta ninguna información sobre la variable Y. Lo habitual es que exista cierta relación entre ellas de manera que el hecho de conocer el valor de las variables independientes nos permite predecir el valor de la variable respuesta. Existen tantos modelos como funciones matemáticas, los más utilizados son: el modelo de regresión lineal, polinómico, logístico, de Poisson, etc.
Los modelos de regresión se utilizan con dos objetivos:
1) Predicción: se pretende predecir la variable dependiente utilizando un conjunto de variables independientes.
2) Estimación: el interés se centra en apreciar la relación entre la variable respuesta y las variables explicativas.
Cuando utilizamos los modelos de regresión para la estimación debemos tener en cuenta dos conceptos importantes, la interacción y la confusión. Existe interacción cuando la asociación entre la variable respuesta y la variable independiente varía según los diferentes niveles de otra variable. Y existe confusión cuando la asociación entre la variable respuesta y la de exposición difiere significativamente si se considera, o no, una tercera variable, denominada variable de confusión.
El modelo de regresión más sencillo es el Modelo de Regresión Lineal13 que estudia la posible relación lineal entre la variable dependiente, que es una variable cuantitativa, y las variables independientes.
La metodología de la regresión lineal no se puede aplicar cuando la variable respuesta es dicotómica, por ejemplo, presencia/ausencia de una enfermedad. En estos casos el modelo de regresión que se debe utilizar es el Modelo Logístico14.
Correspondencia: J.L.R. Martín.
Área de Investigación Clínica.
Fundación para la Investigación Sanitaria en Castilla-La Mancha (FISCAM). Edificio Bulevar.
C/ Berna, n.o 2, local 0-2. 45003 Toledo.
Correo electrónico: jlrmartin@jccm.es
Recibido el 30-07-07; aceptado para su publicación el 30-07-07.