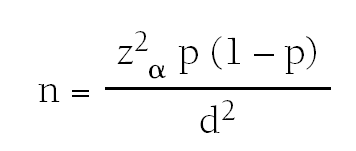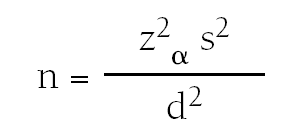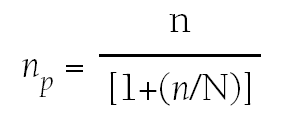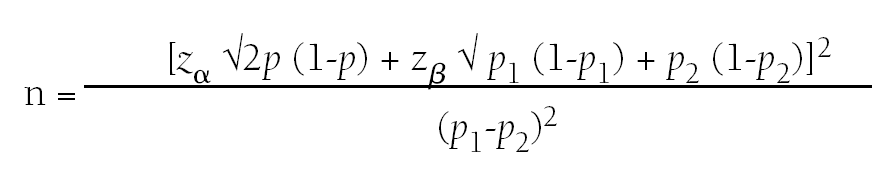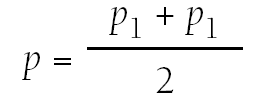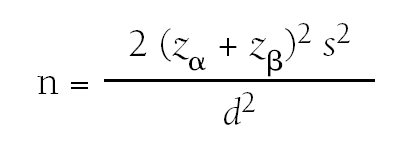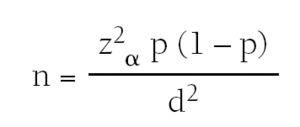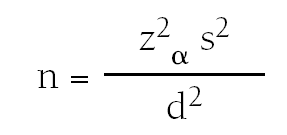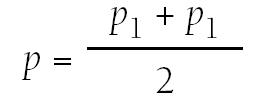En determinados casos, dentro de nuestro marco de trabajo y para responder a la pregunta de investigación, nos encontraremos con el problema de la incapacidad técnica (por la excesiva necesidad de recursos, de todo tipo, que conlleva) de manejar poblaciones completas a la hora de realizar nuestros estudios. Por ello, deberemos seleccionar un subconjunto de dicha población, que sea representativo, y cuyos resultados obtenidos sean extrapolables a la misma. A este subconjunto poblacional lo llamaremos muestra, y a las técnicas para la selección de una muestra a partir de una población lo denominaremos muestreo.
Este proceso nos permitirá ahorrar recursos y conseguiremos resultados similares a los obtenidos en el estudio poblacional completo.
La Teoría de Muestras está totalmente ligada a la Teoría de Estimación, es decir, a la Inferencia Estadística, que es la parte de la estadística que estudia los métodos para la obtención del modelo de probabilidad que sigue una variable aleatoria de una determinada población, a través de una muestra obtenida de la misma. Estimar el tamaño de la muestra significa calcular a priori el número de individuos necesarios para poder comprobar la hipótesis de estudio.
Para que los estudios tengan la validez y fiabilidad buscada es necesario que tal subconjunto de datos, o muestra, posea algunas características específicas que permitan, al final, generalizar los resultados hacia la población en total. Esas características tienen que ver principalmente con el tamaño de la muestra y con la manera de obtenerla.
Para definir mejor los objetivos y métodos que trata la Teoría de Muestras es necesario comenzar dando las siguientes definiciones:
POBLACIÓN
Población es el conjunto de entes del cual se quiere conocer cierto aspecto, al que hace referencia la pregunta de investigación. Es una entidad teórica definida como un grupo completo de individuos, cosas o hechos, que tienen algún rasgo en común. Por lo tanto, los elementos de una población no tienen que ser necesariamente seres humanos, como nos podría inducir a pensar la definición de la palabra, se puede considerar la población formada por las viviendas de una zona geográfica, las muestras de un laboratorio o los peces de una zona marítima.
MUESTRA
Al realizar un proyecto de investigación y gracias a las técnicas estadísticas derivadas de la Teoría de Muestras, no es necesario recoger los datos de todos los individuos que forman la población objeto de estudio. Es suficiente calcular el valor de alguna característica en un subconjunto de la población denominado muestra, definido como cualquier subconjunto formado por elementos de la población. Se puede estimar, a partir de este subconjunto, la frecuencia de una determinada condición o la magnitud de una asociación en dicha población.
Por ejemplo, supongamos que se desea conocer la altura media de los españoles, en este caso la población estaría formada por todos los individuos con nacionalidad española; para conocer la estatura media deberíamos medir uno por uno a todos los sujetos, sumar sus alturas y dividir por el número total de españoles. Este procedimiento, inviable, puede sustituirse por la medición de un número de individuos representativos de la población. Por supuesto, esta muestra nunca podría estar formada por los jugadores de distintos equipos de baloncesto, pues no sería un fiel reflejo de la realidad, la muestra debe comportarse como un espejo del conjunto población.
Las razones principales por las que se seleccionará una muestra en lugar de analizar toda la población son el tiempo y el dinero, es decir la eficiencia; incluir un número excesivo de individuos supondrá un incremento del coste y se expondrá a posibles factores de riesgo a un número innecesario de sujetos. Por lo tanto, su importancia está justificada por motivos científicos y éticos1.
Generalmente, el número de elementos que forman la muestra está determinado antes de efectuar el muestreo. Este número de elementos se denomina tamaño muestral.
MUESTREO
Es el conjunto de técnicas y procedimientos para seleccionar la muestra2,3.
Para que esta muestra sea representativa de la población debe cumplir dos condiciones:
1. Independencia en la selección de los individuos que forman la muestra.
2. Que todos los elementos de la población tengan la misma probabilidad de ser incluidos en la muestra.
Los métodos para seleccionar una muestra son numerosos, dependiendo del tiempo, del dinero y de la naturaleza de los elementos que conforman la población. Podemos clasificarlos de acuerdo a:
1. El número de muestras recogidas de una población.
2. La forma de seleccionar los elementos incluidos en la muestra.
Según el número de muestras recogidas de la población, los métodos se clasifican en tres tipos: muestreo simple, muestreo doble y muestreo múltiple.
En el muestreo simple se toma una única muestra, su tamaño debe ser suficiente para extraer conclusiones a nivel poblacional.
En el caso de realizar un muestreo doble, seleccionaremos una muestra inicial, si el resultado del estudio de dicha muestra no es concluyente se extraerá una segunda muestra, se combinan las dos muestras y se vuelven a analizar los resultados. En el caso de que obtengamos algún tipo de resultado con el primer subconjunto de elementos de la población, no sería necesario extraer la segunda muestra. Supongamos que nos interesa comprobar la calidad de un lote de productos de laboratorio, si la primera muestra tiene una calidad muy alta se acepta el lote, si la calidad es mala rechazaremos dicho lote, en cualquier otro caso recogeremos una segunda muestra.
El muestreo múltiple se realiza de forma similar al doble, en este caso el número de muestras que se recogerán sucesivamente es superior a dos.
Dependiendo de la forma de seleccionar los elementos incluidos en la muestra nos encontramos con dos tipos de muestreo:
El muestreo probabilístico
En este tipo de muestreo la probabilidad de aparición de cualquier elemento de la población en la muestra es conocida. Se considera el único científicamente válido. Dentro de este tipo de muestreo distinguimos:
Muestreo aleatorio simple
Es aquel en que, a priori, todos los elementos de la muestra tienen la misma probabilidad de aparición. Partimos de un listado de las unidades de muestreo, las numeramos y seleccionamos un conjunto de números al azar. Este método puede ser reemplazado por una tabla de números aleatorios o por un programa que nos permita aleatorizar. Es un método sencillo que permite estimar parámetros y errores de muestreo, pero necesitamos disponer de un listado completo de la población.
Muestreo sistemático
En este caso seleccionamos los elementos de una manera ordenada, basándonos en una regla sistemática. La forma de seleccionar los individuos dependerá del número de elementos de la población y del tamaño de la muestra. Supongamos una lista de N elementos, si queremos una muestra de n sujetos, ordenamos los elementos de la población y obtenemos el coeficiente de elevación k = N/n. Después se elige al azar un elemento, denominado origen, comprendido entre 1 y k que nos indica el punto de arranque de la selección. Luego de manera sistemática tomamos el que esté k lugares después del primero y así sucesivamente. Como el primer elemento de la muestra es seleccionado al azar, una muestra sistemática nos permite obtener estimaciones y errores de muestreo. El muestreo sistemático es fácil de aplicar y no siempre es necesario disponer de un listado de los elementos poblacionales. Cuando la población está ordenada según cierta tendencia conocida, cubrimos todos los tipos de unidades. Pero si la constante de muestreo está asociada con el fenómeno de interés, las estimaciones pueden estar sesgadas.
Muestreo estratificado
Puede ocurrir que se conozca previamente el comportamiento de la característica que se está analizando en la población de referencia, es decir, la población se reparte en subconjuntos tales que la característica considerada en los elementos de cada subconjunto se comporta de forma homogénea. En este caso se puede establecer un tipo de muestreo que utilice este conocimiento. Se estudiará una serie de subpoblaciones o estratos de la población, por lo tanto en la muestra debe haber una representación de todos y cada uno de los estratos considerados. En este tipo de muestreo debemos dividir la población en grupos, en función de esa característica relevante; estos grupos serán más homogéneos que la población como un todo. Entonces, los elementos de la muestra son seleccionados al azar o por un método sistemático dentro de cada estrato.
Muestreo por conglomerados
En este caso se consideran "conglomerados de elementos" en lugar de seleccionar elementos de la población, es decir, se toman al azar grupos de elementos y la muestra estará formada por todos los sujetos o por n individuos (seleccionados por muestreo aleatorio o sistemático) de los conglomerados seleccionados. En este método, aunque no todos los grupos son muestreados, cada grupo tiene la misma probabilidad de ser elegido, por lo tanto la muestra es aleatoria. Es útil cuando la población es muy grande y dispersa, pero las estimaciones son menos precisas, pueden tener mayor error muestral. Supongamos que muestreamos por áreas de residencia, seguramente los individuos que vivan en la misma área se parezcan, por ejemplo si consideramos el nivel económico, entonces la variabilidad entre los elementos obtenidos de las áreas seleccionadas es mayor que la variabilidad obtenida si hacemos un muestreo aleatorio de toda la población. Por lo tanto, utilizando una muestra de conglomerados obtendremos la misma precisión en la estimación que si utilizamos una muestra aleatoria simple siempre que la variabilidad de los elementos dentro de cada conglomerado sea semejante a la variabilidad poblacional.
El muestreo no probabilístico
En este caso la selección de los elementos de la muestra no es por azar, lo realiza el investigador. Estas muestras son menos representativas de la población que las obtenidas por muestreo probabilístico, pero se consiguen rápidamente y el coste es inferior. La principal desventaja es el riesgo de obtener demasiado sesgo, que puede hacer imposible generalizar los resultados. Dentro de esta clase de muestreo existen dos tipos:
Muestreo de casos consecutivos
El investigador elegirá a los sujetos que cumplan los criterios de selección en un intervalo temporal o hasta que se alcance un número de muestra suficiente.
Muestreo de conveniencia
Consiste en seleccionar los elementos más fácilmente accesibles, por ser fáciles de recoger o económico, por ejemplo incluir voluntarios.
MÉTODOS DE SELECCIÓN DE LA MUESTRA. TAMAÑO MUESTRAL
En la fase de diseño de todo proyecto de investigación debemos determinar el tamaño muestral necesario para ejecutar dicho trabajo3-5. Si no se realiza este cálculo y el número de elementos muestrales es insuficiente, la estimación de los parámetros no es precisa y posiblemente no encontramos diferencias significativas entre grupos cuando sí existen. Por otra parte, la inclusión de un número excesivo de sujetos encarece el estudio y requiere más tiempo y esfuerzo, además de ser poco ético pues estamos sometiendo a exploraciones o intervenciones a un número innecesario de pacientes.
Como ya se ha comentado, el cálculo del tamaño muestral y las técnicas de muestreo están relacionadas con la estimación. Debemos considerar entonces dos situaciones, los dos problemas fundamentales que estudia la Inferencia Estadística que nos permitirá extraer conclusiones válidas de la población a partir de los resultados muestrales: estimación de parámetros (por ejemplo estimar el nivel de colesterol promedio) y el contraste de hipótesis (por ejemplo estudiar si el nivel de colesterol promedio es igual en hombres que en mujeres).
Estimación de parámetros
Es el cálculo aproximado del valor poblacional de cierto parámetro de interés a partir de los valores observados en la muestra.
Si por ejemplo queremos estimar el nivel de colesterol medio en pacientes que presentan problemas cardiacos, tomando como base el resultado de una muestra particular de tamaño n, una estimación puntual sería el valor del promedio muestral del nivel de colesterol.
Supongamos que recogemos el nivel de colesterol de 100 individuos que padecen alguna afección cardiaca, obtenemos que el nivel de colesterol medio para esta muestra es de 220 mg/100 ml, con una desviación estándar de 13 mg/100 ml. Es sencillo imaginar que si utilizamos otra muestra de pacientes obtendríamos otros valores. Por lo tanto, la estimación puntual de un parámetro depende de la muestra particular y además no podemos cuantificar la proximidad (o lejanía) de este valor puntual a la media teórica, para ello debemos calcular el intervalo de confianza (IC), que nos da una idea de la precisión de la estimación, nos permite conocer entre qué límites es más probable que se encuentre el verdadero valor poblacional.
Para calcular el tamaño de muestra necesario para estimar la media o proporción poblacional debemos conocer la variabilidad del parámetro; si no se conoce podemos obtener una aproximación en los datos aportados por la literatura científica o por un estudio piloto. Utilizaremos como medida de la variabilidad la desviación típica poblacional si trabajamos con una variable cuantitativa y en el caso de que sea una variable cualitativa utilizaremos el producto p(1-p), siendo p = probabilidad de éxito.
Debemos fijar también el error de estimación, que es una medida de la precisión y se corresponde con la amplitud del IC (si queremos mayor precisión, es decir, un error de estimación menor, el IC deberá ser más estrecho, aumentaríamos entonces el tamaño muestral), y el nivel de confianza, que se define como la probabilidad de que el verdadero valor del parámetro poblacional estimado pertenezca al intervalo de confianza obtenido.
Tamaño muestral para la estimación de una proporción
Si deseamos estimar una proporción debemos conocer:
1. El valor aproximado de la proporción que queremos estimar. Lo obtendremos revisando la literatura; si no disponemos de esa información utilizaremos el 50% que maximiza el tamaño muestral (p = 0,5).
2. La precisión con la que queremos realizar la estimación.
3. El nivel de confianza, normalmente al 95%, que da lugar a un coeficiente zα = 1,96.
Aplicaremos la fórmula siguiente:
donde n = número de sujetos necesarios.
zα = valor del coeficiente z correspondiente al nivel deconfianza fijado.
p = valor poblacional esperado.
d = precisión.
Por ejemplo, supongamos que queremos estimar la proporción de asmáticos en una determinada zona geográfica, a partir de los datos previos sabemos que esta proporción es de aproximadamente el 6% (p = 0,06), si queremos realizar la estimación con una confianza del 95% (zα = 1,96) y con una precisión del ± 3% (d = 0,03), necesitaríamos 241 sujetos.
Tamaño muestral para la estimación de una media
Cuando queremos estimar una media, el cálculo es similar al anterior. En este caso debemos conocer también el nivel de confianza y la precisión de la estimación, además debemos tener una idea de la desviación típica s (o de la varianza s2) de la distribución de la variable cuantitativa en la población de referencia.
En este caso la fórmula para calcular el valor de n es:
donde:
n = número de sujetos necesarios.
zα = valor del coeficiente z correspondiente al nivel deconfianza fijado.
s2= varianza de la distribución de la variable en la población.
d = precisión.
Si, por ejemplo, nos interesa conocer el nivel de colesterol medio en pacientes que padecen alguna enfermedad cardiaca, con una precisión de 5 mg/dl, un nivel de confianza del 95% y tenemos información por un estudio piloto que la desviación típica es de 50 mg/100 ml, aplicaríamos la fórmula y determinaríamos que el número necesario de pacientes que necesitamos es 385.
Nos podemos encontrar situaciones en las que la población de referencia es finita, en este caso, si necesitamos extraer una muestra, aplicaríamos la siguiente corrección para poblaciones finitas:
donde:
np = número de sujetos necesarios que extraemos de la población finita.
n = número de sujetos necesarios calculado para poblaciones infinitas.
N = tamaño de la población.
Volvemos al ejemplo anterior, donde calculábamos el número necesario de pacientes con algún tipo de afección cardiaca necesarios para estimar el nivel de colesterol medio poblacional; el resultado que obteníamos es 385 sujetos. Si la población de referencia es de 2.000 enfermos cardiacos, entonces aplicando la fórmula anterior determinamos que el tamaño de la muestra debe ser 323.
Contraste de hipótesis, comparación de grupos
Como en la estimación de parámetros, nuestro interés cuando comparamos grupos es obtener alguna conclusión sobre un parámetro poblacional, por ejemplo queremos conocer si el nivel medio de colesterol en sangre es igual en hombres que en mujeres, o si un fármaco nuevo es más eficaz que el que se utiliza para el tratamiento de una enfermedad.
Para llevar a cabo dicha prueba debemos plantear dos hipótesis, la hipótesis nula H0, que recoge las opciones: no existe diferencia o asociación, o cualquier diferencia observada se debe al azar, y la hipótesis alternativa H1, existe diferencia o asociación, la diferencia observada no se debe al azar. El investigador debe realizar el test utilizando muestras de las poblaciones que queremos comparar y a partir de los resultados obtenidos, utilizando pruebas de significación, evaluará si existen diferencias significativas.
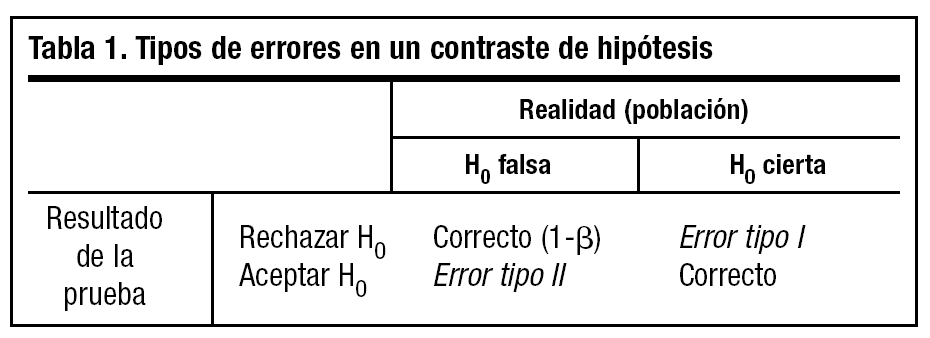
Cuando realizamos una prueba de hipótesis podemos cometer dos tipos de errores: el error tipo I o error α, que se produce cuando rechazamos la hipótesis nula cuando es cierta en la población, y el error tipo II o error β, que se comete cuando se acepta H0 siendo falsa en la población. Se denomina potencia estadística al valor 1-β, que representa la probabilidad de observar en la muestra una diferencia o asociación que existe en la población (tabla 1).
Para calcular el tamaño muestral en este tipo de análisis necesitamos:
1. Determinar la magnitud de la diferencia clínicamente relevante que queremos detectar comparando dos proporciones o dos medias. Si la diferencia es muy amplia se puede detectar con más facilidad y entonces necesitaremos menos sujetos.
2. Definir si el contraste es unilateral o bilateral. En el caso de un contraste unilateral se quiere probar si uno de los parámetros es mayor (o menor) que el otro, por ejemplo cuando contrastamos si un fármaco es más eficaz que otro. En un contraste bilateral se prueba la igualdad, por ejemplo contrastar si los fármacos difieren en su eficacia.
3. Determinar el riesgo de cometer el error tipo I; habitualmente se acepta un riego a del 5%.
4. Establecer el riesgo de cometer un error tipo II; normalmente se sitúa entre un 5% y un 20%. En muchos casos en lugar de determinar este error β se fija la potencia estadística del contraste (1-β), es decir la capacidad de la prueba para detectar la diferencia, habitualmente entre un 80-90%.
5. Debemos conocer la variabilidad poblacional de la variable en estudio.
Veamos como podemos calcular el tamaño muestral en los distintos contrastes de hipótesis.
Comparación de dos proporciones
El contraste de proporciones es una de las pruebas estadísticas más utilizadas en la investigación clínica; se comparan dos grupos utilizando una variable aleatoria cualitativa. Para calcular el tamaño muestral necesario aplicaremos la fórmula siguiente:
donde:
n = número de sujetos necesarios en cada una de las muestras.
zα = valor de z correspondiente al riesgo a fijado.
zβ = valor de z correspondiente al riesgo b fijado.
p1 = valor de la proporción en el grupo de referencia, placebo, control o tratamiento habitual.
p2 = valor de la proporción en el grupo del nuevo tratamiento, intervención o técnica.
p = valor medio de las dos proporciones p1 y p2 →
Por ejemplo, supongamos que nos interesa evaluar si un fármaco A es mejor que otro tratamiento B para controlar el nivel de colesterol; para este estudio diseñamos un ensayo clínico. La eficacia del tratamiento A está alrededor del 60% y se considera clínicamente relevante si el fármaco B mejora los niveles de colesterol en sangre en un 80%. Fijamos el riesgo a en un 5% y queremos una potencia estadística de un 80%. Calculamos entonces el número necesario de pacientes que debemos incluir en nuestro estudio.
p1 = 0,6 y p2 = 0,8, entonces p = 0,7, aplicamos la fórmula y obtenemos n = 40 pacientes para cada grupo.
Comparación de dos medias
Cuando queremos calcular el tamaño muestral necesario para comparar dos medias debemos aplicar la fórmula siguiente:
donde:
n = número de sujetos necesarios en cada una de las muestras.
zα = valor de z correspondiente al riesgo α fijado.
zβ = valor de z correspondiente al riesgo β fijado.
s2 = varianza de la variable cuantitativa que tiene el grupo de referencia.
d = valor mínimo de la diferencia que se desea detectar.
Planteamos un ejemplo. Queremos comparar si el nivel de colesterol en sangre es igual en sujetos que padecen algún tipo de enfermedad cardiaca y en sujetos completamente sanos, tenemos por lo tanto un contraste bilateral. Sabemos que en la población de interés el nivel de colesterol tiene una desviación típica de 50 mg/dl y se establece que la diferencia mínima entre ambos grupos que se considera de relevancia clínica es de 30 mg/dl. El riesgo de error α que estamos dispuestos a asumir es de 0,05. Nos interesa poder detectar la diferencia con una capacidad del 80%. Aplicando la fórmula anterior nos da como resultado 44 pacientes en cada grupo, en total deberíamos incluir en el estudio un mínimo de 88 sujetos.
Correspondencia: J.L.R. Martín.
Jefe del Área de Investigación Clínica.
Fundación para la Investigación Sanitaria en Castilla la Mancha (FISCAM).
Edificio Bulevar.
C/ Berna, n.o 2, local 0-2.
45003 Toledo.
Correo electrónico: jlrmartin@jccm.es
Recibido el 11-06-07; aceptado para su publicación el 11-06-07.