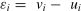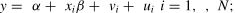Over the years, technological advancements and digital transformation have brought significant changes to the Italian education sector. University performance measurement, particularly in terms of efficiency, has been widely debated, given universities’ critical role in driving innovation and discovery. This study aims to compare nonparametric and parametric approaches to estimate the efficiency of Italian universities, with a focus on research, collaboration, and innovation. Specifically, data envelopment analysis and stochastic frontier analysis were applied using three different input-output combinations to evaluate the efficiency of 62 Italian public universities in 2021. The findings are valuable from both theoretical and practical perspectives. By identifying best practices and offering targeted insights into areas for performance improvement, this study contributes to the ongoing development of Italian universities and their global competitiveness in research, cooperation, and innovation.
In recent years, Italian universities have undergone a major transformation, aiming to strengthen connections between academia and external actors within the innovation ecosystem (Compagnucci & Spigarelli, 2024). Through the dissemination of knowledge, universities increasingly contribute to societal and economic development while also playing a critical role in workforce training (Maral & Çetin, 2024). In this context, the concept of efficiency is essential (Dipierro & De Witte, 2024; Kallio et al., 2020) because it concerns how inputs are converted into outputs. This capability is especially important in the university setting, where institutions often operate under resource constraints (Agasisti & Johnes, 2015).
Renowned for its rich history and diverse academic traditions, the Italian higher education sector warrants the attention of practitioners who can support policymakers in guiding ongoing university transformations. Recent challenges demand proactive measures from Italian universities to remain aligned with advancements in knowledge, promote collaboration with industry and institutions, and support innovation (Frondizi et al., 2019). However, to the best of the authors’ knowledge, empirical research on the efficiency of Italian universities—specifically in the context of research, collaboration, and innovation—remains limited.
According to the systematic literature review by Rella and Vitolla (2024), there has been limited effort to jointly apply the two most widely used techniques for measuring university efficiency: data envelopment analysis (DEA) and stochastic frontier analysis (SFA). To address this gap, we aim to undertake a comparative evaluation of the efficiency of Italian universities, focusing on key dimensions such as research, cooperation, and innovation (Abramo et al., 2020). Specifically, we apply the most commonly used nonparametric and parametric approaches—DEA and SFA (Agasisti & Dal Bianco, 2006; Tavares et al., 2021)—to highlight their respective theoretical and methodological advantages and limitations. Each method provides distinct benefits and addresses specific shortcomings, making them complementary tools for assessing the efficiency of complex systems such as universities. These tools are essential for evaluating university performance, especially from a managerial perspective committed to fostering knowledge development. Through a comparative lens, this study employs DEA and SFA to offer a comprehensive assessment of Italian university efficiency in relation to research, cooperation, and innovation activities. DEA and SFA are applied to a data set comprising 62 Italian public universities using three different input-output combinations. This allows us to assess efficiency across multiple activity domains. The data set includes information on research publications, academic collaborations, patent applications, and financial resources, providing a multidimensional and detailed view of university efficiency. By adopting this integrated approach, we aim to answer the following empirical research question (RQ):
RQ: To what extent are Italian universities efficient when assessed using DEA and SFA approaches?
By identifying best practices and offering specific insights into areas where universities can improve performance, this study aims to support the ongoing development of Italian universities and strengthen their global competitiveness in research, cooperation, and innovation. Universities today operate in an increasingly challenging environment, often facing significant budget constraints that necessitate a focus on competitiveness. By optimizing resource management and enhancing efficiency, universities can increase both their attractiveness and competitive positioning (Dipierro & De Witte, 2024). Effective resource management also improves the ability of universities to meet the needs of internal and external stakeholders (Ashmarina et al., 2015).
In pursuing these objectives, this study contributes to the academic field by recommending actionable strategies that can enhance the impact of universities on innovation and knowledge production in Italy, thereby supporting broader socio-economic development. The proposed perspective is also adaptable to other European contexts. Specifically, the findings offer policy-relevant insights for resource allocation and institutional reforms within the higher education sector.
This article is structured as follows: Section 2 outlines the literature review, Section 3 details the methodology, Section 4 describes the materials, Section 5 presents the results, and Section 6 provides the discussion and conclusions.
Literature reviewThe concept of efficiencyDefining efficiency is a complex task due to the wide range of interpretations proposed by scholars and practitioners over time. In this study, we adopt the definition provided by Charnes et al. (1978), which considers efficiency as the ability to convert inputs into outputs. There are various ways to calculate efficiency scores, but the most widely used approach involves estimating a frontier that identifies optimal values, followed by comparing the efficiency scores derived from input-output combinations (Førsund et al., 1980; Lovell, 1993; Worthington & Dollery, 2000).
Following this overview of the efficiency concept, it is essential to examine how it is measured empirically. As noted earlier, methodological approaches are typically classified into two main categories: parametric and nonparametric. While both aim to quantify efficiency, they differ substantially in terms of structure and underlying assumptions.
Neither method is inherently superior because each offers distinct strengths and limitations (Salerno, 2003). In this context, the present study focuses on two widely adopted approaches: DEA, a nonparametric, non-statistical, and deterministic method, and SFA, a parametric, statistical, and stochastic method. These techniques are extensively discussed in the literature and were recently reviewed in a systematic analysis by Rella and Vitolla (2024), to which readers are referred for additional insights. Their review highlights a significant gap in prior studies, particularly the underutilization of combined DEA and SFA approaches and the limited attention given to the research, collaboration, and innovation goals of universities. The following sections present the theoretical foundations and empirical considerations necessary to understand and apply DEA and SFA in the context of higher education.
A panoramic view of data envelopment analysisDEA has become a central analytical tool in operational research (OR), significantly contributing to the evolution of performance measurement methodologies (Mergoni et al., 2024). DEA is a decision-making technique grounded in linear programming (Charnes et al., 1978). Specifically, it evaluates production frontiers and measures the relative efficiency of a set of decision-making units (DMUs) that utilize similar inputs to produce similar outputs (Nguyen & Pham, 2020). Graphically, DMUs located on the frontier are considered efficient, while those below the frontier are deemed inefficient. The relative efficiency of each DMU is calculated based on its distance from this frontier, as measured by the DEA model.
Building on Farrell’s (1957) foundational definition of efficiency, DEA evolved into two primary models. Charnes et al. (1978) developed a model based on constant returns to scale (CRS) and an input-oriented perspective. Subsequently, Banker et al. (1984) introduced the variable returns to scale (VRS) model, which is more widely supported in recent literature due to its ability to account for non-proportional relationships between inputs and outputs.
In empirical applications, Johnes (2004, 2006) and Førsund et al. (2018) explored various dimensions of DEA in the higher education context. Their contributions discuss the methodological foundations, technical background, strengths and weaknesses, and the multiple perspectives through which DEA can be applied. In line with this, Avkiran (2001) assessed the efficiency of 36 Australian universities, focusing on service delivery, fee-paying enrollments, and overall performance. Similarly, Glass et al. (2006) calculated the efficiency scores of 98 non-specialist UK universities in 1996, with emphasis on teaching and research quality. Continuing in this direction, Nazarko and Šaparauskas (2014) examined the efficiency of 19 Polish universities with respect to educational and research quality, whereas Contreras and Lozano (2022) assessed the overall efficiency of 47 Spanish universities. Guironnet and Peypoch (2018) evaluated the performance of 7735 American colleges and universities in the period 2012 to 2013, focusing on teaching and research outcomes. A similar approach was adopted by Tavares et al. (2021) in their analysis of 45 Brazilian federal universities.
Despite the considerable scholarly attention, an important empirical gap remains. To the best of the authors’ knowledge, no existing study has independently evaluated the efficiency of universities in terms of research, collaboration, and innovation objectives.
A panoramic view of stochastic frontier analysisDeveloped independently by Aigner et al. (1977), Battese and Corra (1977), and Meeusen and van den Broeck (1977), SFA is a parametric approach that incorporates both inefficiency and random error in the estimation process. This methodology estimates and decomposes the composite error term in a single step. Thus, it accounts for the presence of stochastic error when constructing the efficiency frontier rather than attributing all deviations from the frontier solely to inefficiency (Nguyen & Pham, 2020). The academic literature identifies two key estimators for SFA: the JLMS estimator (Jondrow et al., 1982), which calculates technical inefficiency, and the BC estimator (Battese & Coelli, 1988), which focuses on estimating technical efficiency (Sena, 2003). In contrast to DEA, which is deterministic, SFA adopts a stochastic approach that considers data noise when calculating the distance from the efficiency frontier, offering a more flexible evaluation of performance (Letti et al., 2022).
Empirical applications of SFA in the context of higher education remain relatively limited. Agasisti and Gralka (2019) applied SFA to measure the overall efficiency of 55 Italian and 70 German public universities over the period 2001 to 2011. Similarly, Letti et al. (2022) examined a sample of 56 Brazilian federal universities from 2010 to 2016, whereas Naderi (2022) investigated the efficiency of a comprehensive university in Iran.
Despite these contributions, existing studies primarily focus on overall institutional efficiency. To date, no study has applied SFA to evaluate university efficiency with a specific focus on research, collaboration, and innovation activities.
A comparison of data envelopment analysis and stochastic frontier analysisThe number of studies comparing nonparametric and parametric approaches, specifically DEA and SFA, remains limited and somewhat inconsistent. In the higher education context, McMillan and Chan (2006) showed that efficiency measures obtained through DEA and SFA yield different university rankings. Similar patterns have also been observed in other sectors, including banking (Nguyen & Pham, 2020; Weill, 2004), healthcare (Hollingsworth, 2008; Jacobs, 2001), and energy (Bauer et al. (1998); Hossin et al., 2023) argued that no universally superior method exists for estimating efficiency. However, with the support of robust statistical tests, distributional analysis, efficiency rankings, and correlation assessments, comparisons between nonparametric and parametric methods can generate valuable insights and highlight notable differences in outcomes.
In empirical applications, Miranda et al. (2012) reported minimal differences between DEA and SFA, noting that both approaches identified the same top and bottom 20 higher education institutions (HEIs) in terms of efficiency. In contrast, Gralka et al. (2019) found divergent outcomes. Their DEA-based results produced consistent efficiency levels, while SFA estimates showed minor variations over time and weaker correlations. Similarly, Letti et al. (2022) emphasized the differing conclusions of the two methods: DEA suggested that specialized HEIs are more efficient, whereas SFA indicated that generalist HEIs demonstrate greater efficiency.
Based on the literature reviewed, there is a compelling need for further empirical evidence on the efficiency measurement of under-explored dimensions of university activity, such as research, cooperation, and innovation. This need is particularly evident in the Italian context. The extent to which Italian universities operate efficiently—especially in terms of research output, collaborative networks, and innovation—has not been thoroughly investigated in the academic literature. Moreover, additional inquiry is required to determine whether a single methodological framework can effectively estimate and evaluate the efficiency of HEIs. In response to these gaps, this study investigates the performance of Italian universities across research, cooperation, and innovation by applying both DEA and SFA and systematically comparing the results. This involves examining the theoretical foundations, practical applications, advantages, and limitations of each approach. Guided by the methodology presented in the following section, the study focuses on Italian public universities—an under-examined setting that deserves closer attention due to ongoing structural transformations, dependence on public funding, and persistent regional disparities.
MethodologyThis study applies both nonparametric and parametric methodologies: DEA and SFA, respectively. The two approaches are then compared to evaluate the efficiency levels of Italian public universities with respect to research, cooperation, and innovation.
Data envelopment analysisThis study employs DEA, a nonparametric technique initially introduced by Farrell (1957), later extended by Charnes, Cooper, and Rhodes (1978), and further refined by Färe et al. (1994). DEA measures efficiency by assessing how inputs are transformed into outputs. In this context, the units of analysis—referred to as DMUs—are Italian public universities. Efficiency is represented by a frontier, and the distance of each DMU from this frontier reflects its level of inefficiency.
The analysis investigates the input–output transformation process through three separate DEA models, each corresponding to a distinct dimension of university performance: research, cooperation, and innovation. All three models use the same input—current expenditures—while the outputs vary to reflect the different performance dimensions being assessed.
All analyses follow an output-oriented approach, where outputs are maximized while inputs are held constant. This orientation was chosen due to the nature of the higher education sector, where inputs are typically exogenously determined and beyond the direct control of institutions (Agasisti & Johnes, 2015). The analysis is conducted under the assumption of VRS, which is preferred over the CRS assumption when assessing university efficiency. VRS better accommodates non-proportional relationships between inputs and outputs (Dipierro & De Witte, 2024), a critical consideration in a sector affected by technological advances, imperfect competition, regulatory changes, budget constraints, and entry-related conditions. VRS is especially relevant in capturing the complexity and heterogeneity of educational institutions (Dipierro and De Witte, 2024).
The results of the DEA models are expressed as efficiency scores ranging from 0 to 1. A score of 1 indicates that a university is efficient. A score below 1 signifies relative inefficiency. A score of 0 denotes complete inefficiency.
The DEA analysis was conducted using R software via the DeaR package. The methodological foundation is based on the linear programming model developed by Charnes et al. (1978).
where j=1,…,n,vi,ur≥0,and where v and u represent the weight of input and output variables, respectively.Stochastic frontier analysisThe second methodological approach employed in this study is SFA, a parametric technique introduced by Aigner et al. (1977). Its primary advantage lies in the ability to measure efficiency while simultaneously accounting for statistical noise.
Parametric models assume that the efficiency frontier can be identified using a functional form that closely fits the observed data set. This is expressed as:
where y represents the output, x is the vector of inputs, β is the vector of parameters, and ε is the composite error term.A key feature of SFA is its decomposition of the error term (ε) into two components: a symmetric term representing random noise (v) and a one-sided term capturing inefficiency (u). These two components are assumed to be statistically independent. The decomposition is expressed as:
where vᵢ denotes the random noise, and uᵢ represents the inefficiency component.In this study, the stochastic frontier is modeled using a Cobb–Douglas functional form combined with a half-normal distribution for the inefficiency term. The model is specified as a cost frontier and follows this formulation:
whereFrom this perspective, selecting an inefficiency distribution is a critical assumption that must be made at the outset of the analysis. It is not a choice based on model characteristics, and no statistical tests are available to validate the distributional assumptions.
To calculate technical inefficiency, this study adopts the BC approach developed by Battese and Coelli (1988), which estimates technical efficiency as the expected value of exp(−u)|e,E(exp(−u)|e).
Three SFA models are estimated. All models use the same input—current expenditures—while the outputs vary depending on the dimension being assessed. The first model evaluates research efficiency using the number of publications as output. The second focuses on cooperation, with the number of affiliations as output. The third assesses innovation, using the number of patents as the output variable.
The efficiency scores generated from these models range from 0 to 1. A score of 1 indicates that a university is efficient. A score below 1 signifies relative inefficiency. A score of 0 reflects complete inefficiency. This part of the analysis was conducted using the frontier package in R.
Data envelopment analysis versus stochastic frontier analysisPrevious research highlights a substantial body of literature on DEA, whereas considerably fewer studies have applied SFA or employed a combined approach (Rella and Vitolla, 2024). In light of this imbalance, the present study aims to compare the two methodologies to explore their respective advantages and limitations. The key characteristics, strengths, and drawbacks of DEA and SFA are summarized in Table 1.
Advantages and limitations of DEA and SFA.
The Italian university system comprises 97 universities, including 67 state universities, 19 legally recognized non-state universities, and 11 online universities. This study focuses exclusively on state universities, selected based on multiple criteria to ensure data set robustness and comparability. State universities were chosen due to their adherence to transparency and accountability standards, which support accurate efficiency assessments. A total of 62 state universities were included in the analysis. Institutions issuing equivalent qualifications to university degrees and those that did not disclose financial information for the reference year were excluded. This selection ensures that the universities included offer consistent and comprehensive input-output data, as sourced and described in the following section. The use of publicly available secondary data enhances the reliability and comparability of the analysis while minimizing bias and strengthening transparency and validity. The selection process also ensures the sample is representative of the Italian public higher education system. The analysis was conducted for the year 2021 to compare two methodological approaches—nonparametric and parametric—for evaluating the performance of Italian universities in terms of research, cooperation, and innovation.
VariablesThe variables used in this study are divided into inputs and outputs and are applied consistently across both DEA and SFA. The selection of variables is grounded in the relevant literature. To evaluate the three core dimensions—research, collaboration, and innovation—different input-output combinations are computed. Notably, the input remains the same across all three configurations, while the outputs vary depending on the activity being assessed.
The selected input is current expenditures, defined as the total of several operating costs expressed in euros (€). This choice is supported by the literature, particularly for its importance in evaluating university efficiency (Rella et al., 2024). According to Thanassoulis et al. (2011), current expenditures are especially relevant for public managers and policymakers and are preferable to more granular categories of spending due to their comprehensive nature and parsimony in variable use, an important consideration when applying DEA and SFA methodologies. Current expenditures encompass costs related to all three evaluated activities and are thus compatible with the outputs described in the following section. This variable was extracted from the income statements of each university, as published on the websites of the 62 institutions included in the analysis. Specifically, within each balance sheet, current expenditures are reported under Section B, Item IX, and are expressed in euros. The breakdown of cost components comprising current expenditures is detailed in Table 2.
Components of current expenditures.
The output variables used in this analysis serve as proxies for the research, cooperation, and innovation missions of universities. Specifically, the number of publications is used to represent research activity, the number of affiliations reflects cooperation, and the number of patents serves as an indicator of innovation. These data refer to the year 2021 and were retrieved from the Scopus database. Each university was individually queried to obtain the number of publications, affiliations, and patents specific to the year under analysis.
Descriptive statisticsThe input and output variables are described using the minimum (Min), first quartile (Q1), mean (Mean), median (Median), third quartile (Q3), maximum (Max), and standard deviation (SD). Table 3 presents the descriptive statistics for the Italian universities included in the 2021 analysis. The input variable, current expenditures, displays substantial variation across universities. The maximum value is considerably higher than the minimum, indicating the presence of small institutions with limited financial resources. Specifically, the minimum value is 3.5 million euros and refers to Istituto Universitario di Studi Superiori di Pavia, while the maximum value is 234 million euros and captures Alma Mater Studiorum - Università’ di Bologna. The distribution of current expenditures is highly asymmetric, as reflected by the difference between the mean and quartile values. A large proportion of values lie on the right side of the distribution, suggesting considerable disparities in financial resource allocation. Focusing on output variables (i.e., publications, affiliations, and patents), reveals the great discrepancy between minimum and maximum values, as well as among the quartile values. From this perspective, the minimum number of publications is 41 and refers to Università’ degli Studi di Napoli – L’ Orientale, whereas the maximum number of publications is 11,363 and refers to Università’ degli Studi di Roma - La Sapienza. The mean value is 2758.6. These results demonstrate a very low number of publications produced by Italian universities compared to the global average, and it reflects the low investments in research and development in Italy. Regarding affiliations, the maximum value is 844 and refers to Alma Mater Studiorum - Università’ di Bologna, whereas the minimum value is 0, corresponding to 28 of the 62 sampled universities or almost half of the sample. Finally, for patents, the maximum is 953 and refers to Università degli Studi di Parma, whereas the minimum value is 0 and corresponds to only 10 of the sampled Italian universities.
Descriptive statistics of input and outputs.
In this study, three DEA models were applied to measure the efficiency of Italian public universities in the areas of research, cooperation, and innovation. Table 4 presents descriptive statistics for the efficiency scores, including the minimum (Min), first quartile (Q1), median, mean, third quartile (Q3), maximum (Max), SD, skewness, and kurtosis. The first DEA model evaluates research efficiency, using one input—current expenditures—and one output—the number of publications. The average efficiency score for this model is relatively high (0.7618), although there is room for improvement. The minimum score, 0.0592, was recorded by Università degli Studi “G. d'Annunzio,” whereas the maximum score of 1.000 was achieved by 11 of the 62 sampled universities. The second DEA model assesses cooperation efficiency, again using current expenditures as the input and the number of affiliations as the output. The mean efficiency score is 0.8006, which is also relatively high. The minimum value, 0.0592, corresponds to Università degli Studi di Napoli “L’Orientale,” whereas the maximum score of 1.000 was achieved by 14 universities in the sample. The third DEA model investigates innovation efficiency, using current expenditures as the input and the number of patents as the output. The mean efficiency score for this model is 0.3086, indicating relatively low performance in innovation. Eleven universities scored the minimum value of 0.000, whereas seven universities achieved the maximum efficiency score of 1.000.
Descriptive statistics of the efficiency scores obtained from DEA and SFA.
The three DEA models reveal notable differences in efficiency outcomes. The most evident discrepancy lies in the mean efficiency scores. The first two models—focused on research and cooperation—demonstrate relatively high mean scores, with cooperation appearing to be slightly more efficient than research. In contrast, innovation efficiency displays a significantly lower mean score. This result can be interpreted from both negative and positive perspectives. From a negative standpoint, the number of patents produced by Italian universities is small. Digital platforms, innovative tools, and smart technologies remain underdeveloped and underutilized. This reflects a lack of technical expertise and the persistent challenge of translating scientific findings and intellectual property into practical innovation within the Italian university system. On a more positive note, the low innovation score may serve as a stimulus for improvement. As Italy’s education sector continues to grow, progress in innovation will require dedication, long-term planning, and consistent support. Encouragingly, the recent allocation of public funding suggests a commitment to fostering more innovative practices.
The additional statistical measures reported in Table 4 further support these discrepancies across the three dimensions of efficiency assessed in Italian public universities.
Efficiency according to stochastic frontier analysisTo measure efficiency within Italian public universities in terms of research, cooperation, and innovation, three SFA models were also produced. Table 4 provides descriptive statistics of the efficiency scores for the SFA, including the minimum (Min), first quartile (Q1), median, mean, third quartile (Q3), maximum (Max), SD, skewness, and kurtosis.
The first SFA model aims to analyze the research efficiency level and considers one input (current expenditures) and one output (number of publications). The mean efficiency score is moderately high (0.6950), although there is significant room for improvement. The minimum value is 0.0813, recorded by Università degli Studi di Napoli – “L’Orientale,” whereas the maximum value is 0.9444, which refers to Università degli Studi del Molise.
The second SFA model investigates the cooperation efficiency level and considers one input (current expenditures) and one output (number of affiliations). The mean score for this model is 0.7022, which is also moderately high. The minimum value is 0.5008 and refers to Politecnico di Milano, whereas the maximum value is 0.8373 and refers to Istituto Universitario di Studi Superiori di Pavia.
The third SFA model aims to explore the innovation efficiency level and considers one input (current expenditures) and one output (number of patents). The mean score of this model is 0.5929, which represents a medium value. The minimum value is 0.1623 and refers to IMT Alti Studi di Lucca, whereas the maximum value is 0.8316 and refers to Università degli Studi della Campania - 'Luigi Vanvitelli' and Università degli Studi di Macerata.
The three SFA models also provide results that underline some discrepancies between the different dimensions of efficiency within Italian universities. However, these differences are not as noticeable as in the DEA models, even though they follow the same trend. The average values of these three models demonstrate a moderately low score related to innovation efficiency. Moreover, the efficiency values from the SFA models are slightly more balanced than those from the DEA models. A possible explanation is that nonparametric scores entirely attribute deviation from the frontier to inefficiency, whereas the parametric SFA allows for a random error term (Cummins and Weiss, 2000; Suarez-Fernandez et al., 2021). In this case, the other statistical measures in Table 4 highlight the same pattern of discrepancy across the three aspects of Italian universities’ efficiency.
Comparing efficiency according to data envelopment analysis and stochastic frontier analysisTo compare the DEA and the SFA models, several aspects can be further explored. Specifically, descriptive statistics and correlation analyses are carried out to identify clear signals of difference between the results provided by the two methodological approaches.
Starting with the descriptive statistics, it is important to highlight the subtle but meaningful discrepancies among the models. The fact that nonparametric scores entirely attribute deviation from the frontier to inefficiency, whereas the parametric SFA allows for a random error term, suggests that before drawing final conclusions, it is essential to consider whether randomness (i.e., DEA or SFA) has been taken into account when estimating efficiency. Moreover, skewness and kurtosis are also examined. The skewness values are negative for all models except the third DEA model. These values indicate that the density functions of the efficiency scores have longer tails on the left side and that the mass of the distribution is concentrated on the right. In contrast, the kurtosis values are positive and high for all DEA and SFA models, suggesting that the data are predominantly clustered around the average value.
Additional observations from the descriptive statistics involve the quartile values. These results are clearly visible in the boxplot (see Fig. 1), which offers strong support for a visual comparison of the range and distribution of the efficiency scores.
Four of the six models present a median between 0.6 and 0.8 (Research_DEA, Research_SFA, Cooperation_SFA, and Innovation_SFA), whereas the remaining two models (Cooperation_DEA and Innovation_DEA) show median values of 0.9 and 0.3, respectively. Furthermore, in the first two DEA models, both the median and the first quartile are higher than in the other models, and in the Cooperation_DEA model, the third quartile is positioned higher than the others. Moreover, some outliers are visible, particularly affecting two of the DEA models (Research_DEA and Cooperation_DEA) and one of the SFA models (Research_SFA).
Fig. 2 presents the scatterplots, which demonstrate the relationship between the different nonparametric and parametric models. In this case, the authors analyzed the phenomenon by pairing the efficiency levels of the same dimension of Italian public universities obtained using different methodological approaches.
The distributions appear different, which is also due to the distinct sets of assumptions underlying the two methodological approaches. From this perspective, the first scatterplot, which investigates the research aspect (Research_DEA and Research_SFA), does not show a substantial discrepancy between the two methods. Similarly, the second scatterplot, which explores the cooperation aspect (Cooperation_DEA and Cooperation_SFA), presents more or less the same trend in the efficiency scores. In contrast, the last scatterplot, which considers the innovation aspect (Innovation_DEA and Innovation_SFA), demonstrates a considerable difference between the two methodological approaches. Despite these discrepancies, the choice of methodology should not determine the results. The findings from both are considered valid and relevant, including for policymakers and public managers to apply political and managerial policies in the estimation of the efficiency of Italian public universities.
Furthermore, we reinforce what has already been observed by providing rankings of the efficient Italian public universities, according to the different combinations of methodologies and dimensions of efficiency. Table 5 provides a top 5 ranking of efficient Italian public universities to give a snapshot of the findings.
Top 5 ranking of efficient Italian public universities.
In a sample of 62 universities, 21 institutions appear within the top five positions of the efficiency rankings. This result suggests that, depending on the different efficiency dimensions and methodological approaches, universities occupy varying positions in the efficiency measurement rankings. However, a noteworthy pattern concerns the Istituto Universitario degli Studi Superiori di Pavia, which ranks in the top position four times—specifically in Research_DEA, Cooperation_DEA, Innovation_DEA, and Cooperation_SFA—and once in the fifth position. Moreover, Università degli Studi del Molise appears three times, including two first-place rankings and one second-place ranking. IMT Alti Studi di Lucca, Università degli Studi di Genova, and Università degli Studi di Milano – Bicocca each appear twice among the top 5 most efficient universities. In other cases, a high variance is observed in the efficiency rankings of the universities.
Following the efficiency rankings, a correlation analysis is now presented to compare the Pearson and Spearman indexes. Additionally, Fig. 3 and Table 6 graphically and numerically present the most commonly used method to compare DEA and SFA model results (Agasisti & Dal Bianco, 2006), namely correlation analysis.
Pearson and Spearman correlation of DEA and SFA models.
Note: *** Significant at the 1% level; ** Significant at the 5% level; * Significant at the 10% level.
In PANEL A of Table 6, the Pearson correlation shows a positive correlation between Innovation_DEA and Research_DEA (0.336) at the 1% significance level and a strong positive correlation between Research_SFA and Cooperation_DEA (0.827) at the 1% significance level. In contrast, there is a negative correlation between Innovation_SFA and Innovation_DEA (-0.325) at the 5% significance level, and between Innovation_SFA and Cooperation_SFA (-0.352) at the 1% significance level. In PANEL B of Table 6, the Spearman correlation provides similar results as the Pearson correlation, though at different significance levels. In this case, there is a positive correlation between Innovation_DEA and Research_DEA (0.315) at the 5% significance level and a positive correlation between Research_SFA and Cooperation_DEA (0.652) at the 1% significance level. A negative correlation is observed between Innovation_SFA and Innovation_DEA (-0.342) at the 1% significance level and between Innovation_SFA and Cooperation_SFA (-0.313) at the 5% significance level. The findings obtained from these two correlation coefficients are very similar, highlighting the importance of considering more than one methodological approach when estimating efficiency.
Discussion and conclusionsIn the evolving landscape of universities, their greater scope of activity places universities at the forefront of societal advancement (Godonoga & Sporn, 2023). This study applied nonparametric and parametric efficiency approaches—DEA and SFA, respectively—to estimate the efficiency levels of Italian public universities in terms of research, cooperation, and innovation. The novelty of this study lies in investigating the different dimensions of efficiency within Italian public universities, focusing on the transformation process currently impacting the education sector.
Specifically, the study analyzed 62 Italian public universities for the year 2021, with particular attention to applying different methodologies to compute and estimate efficiency levels using relevant outputs such as publications, affiliations, and patents. The methodological approaches used were DEA and SFA. More specifically, both were applied to estimate the three efficiency dimensions of Italian public universities: research, cooperation, and innovation. DEA models were employed using a VRS model and an output-oriented configuration, following the existing scientific literature. SFA models were computed using the Cobb-Douglas functional form and half-normal distribution.
Due to their methodological features, DEA and SFA are widely used by scholars to estimate efficiency within the education sector. However, no empirical study to date has explored the efficiency of research, cooperation, and innovation using both approaches in the context of Italian public universities. In light of this, the present study offers two main contributions: the application, implementation, and comparison of two different efficiency approaches—nonparametric and parametric—and the exploration of the efficiency levels of Italian public universities in terms of research, cooperation and innovation.
The findings reveal the feasibility and accuracy of both methods in estimating the efficiency levels of Italian public universities. Certainly, each method includes specific characteristics, with strengths and weaknesses, as recognized in the scientific literature. Nevertheless, the differences in assumptions and methodological features provide meaningful insights for the estimation and comparison of efficiency results. The comparison between DEA and SFA revealed notable discrepancies, confirming that no single methodology is universally superior. Rather, the different approaches are capable of capturing diverse aspects in the estimation and evaluation of efficiency, depending on their underlying background, foundations, advantages, and limitations. These results support the perspectives of Bauer et al. (1998), McMillan and Chan (2006), and Miranda et al. (2012).
From the efficiency scores of the six computed models, it was possible to extract valuable information in terms of differing results and perspectives. Overall, there is substantial room for improvement, particularly within the innovation dimension. Subsequently, the university rankings were developed based on the efficiency scores to examine whether the same universities remain efficient across the different methodologies and efficiency aspects. Finally, Pearson and Spearman correlations were calculated to implement the most widely used method for comparing DEA and SFA models, following the work of Agasisti and Dal Bianco (2006). This analysis suggests that no ideal methodology exists for measuring the efficiency levels of Italian public universities because it is essential to consider the assumptions of each approach. It is therefore difficult to prefer one model over another without first clarifying the goals of the research and the researcher's intentions because selecting a methodology often depends on whether the aim is to highlight specific favorable or unfavorable conditions of the observed units.
These points are relevant in terms of practical and policy implications. From a policy perspective, our results emphasize the importance of implementing both nonparametric and parametric tools for efficiency measurement in universities, taking into account the aspects discussed earlier. This is equally significant for university administrators because pursuing efficiency can support the timely achievement of institutional goals. One relevant example is the Sustainable Development Goal (SDG) related to education (SDG No. 4). By managing resources effectively, universities can enhance the quality of education and improve equitable access. Based on our analysis, we suggest that policymakers prioritize investment in research and development (R&D) because it can drive innovation, strengthen technological capabilities, and foster economic growth. Moreover, they should establish mechanisms to evaluate the impact of academic research on the economy, society, and innovation. Regular assessments of funded program outcomes are crucial, with policies adjusted accordingly based on collected data. Policymakers should also introduce regulations that support lifelong learning and continuous skills development. Promoting dialogue and collaboration among public officials, academic institutions, the private sector, and the broader community is essential to align policy objectives with stakeholder needs. Additionally, ethical standards in research—particularly in fields such as data science, artificial intelligence, and biotechnology—must be safeguarded through appropriate legal and regulatory frameworks. Financial systems should be developed to reward universities for efficiency in research output, global partnerships, and innovation. At the same time, institutions should be encouraged to streamline administrative processes and use resources more effectively.
Academics should aim to optimize resource use to enhance both the quantity and quality of research output. They should leverage international partnerships, exchange programs, and collaborations to promote diverse research perspectives and foster global networks of knowledge exchange. Furthermore, fostering inclusive academic environments, offering structured support, and encouraging diverse viewpoints are essential actions. To address complex societal challenges, universities should create systems that promote interdisciplinary and interdepartmental collaboration. Lastly, broader indicators of success (e.g., instructional efficiency, student outcomes, societal impact, and community engagement) should be considered. This comprehensive approach allows for a more holistic understanding of university efficiency.
The present work is not without limitations. The first limitation concerns the sample and the year of analysis. Specifically, the study investigates the efficiency levels of Italian state universities for the year 2021. Future research could expand the scope by including private and online universities to encompass the entire landscape of Italian higher education. Additional evidence is also needed by extending the time horizon to assess efficiency trends over multiple years. Moreover, future research may examine research, cooperation, and innovation efficiency in contexts beyond Italy. We acknowledge that the generalizability of our results may be limited. Therefore, this study encourages further applications to determine whether the findings hold in other educational systems. The second limitation relates to the use of only one output variable per model. Future studies could introduce additional variables and integrate qualitative methods to further explore research, collaboration, and innovation systems in universities. The third limitation involves the comparison between DEA and SFA models. This could be made more robust by incorporating external variables—often neglected in similar studies—to help explain discrepancies in technical efficiency between the two approaches.
Funding sourceThis research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors.
CRediT authorship contribution statementAngela Rella: Writing – review & editing, Writing – original draft, Visualization, Validation, Supervision, Software, Project administration, Methodology, Investigation, Formal analysis, Data curation, Conceptualization. Anna Rita Dipierro: Writing – review & editing, Writing – original draft, Visualization, Validation, Supervision, Software, Project administration, Methodology, Investigation, Formal analysis, Data curation, Conceptualization.
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Angela Rella and Anna Rita Dipierro conducted this research during their Ph.D. at LUM University. Currently, Anna Rita Dipierro is affiliated with the University of Calabria, where she receives support within the GRINS project– Growing Resilient, Inclusive and Sustainable from the European Union Next-Generation EU (GRINS PE00000018, CUP: H23C24000110006, Spoke 4 Sustainable Finance).