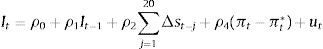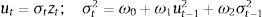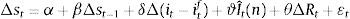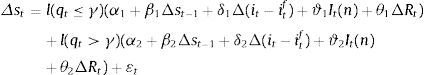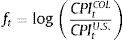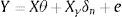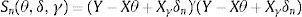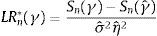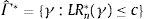This paper analyses the effectiveness of official interventions of the Colombian Central Bank in the foreign exchange market over the period of June 2008–December 2013. The estimation procedure suggested by Hansen (2000) is used to estimate a threshold model for the spot exchange rate that splits the data sample into two different regimes that depend on the extent of the misalignment of the exchange rate from a fundamental value. The estimation results provide empirical evidence of the existence of a coordination channel of intervention proposed by Sarno and Taylor (2001). According to the theory of the coordination channel, interventions by central banks work as signals that solve a coordination failure in the foreign exchange market when speculation moves the exchange rate from its fundamental value. The results suggest that foreign exchange interventions had a considerable and statistically significant effect in depreciating the domestic currency when the spot exchange rate was sufficiently below from its fundamental value.
Este artículo analiza la efectividad de las intervenciones del Banco de la República en el mercado cambiario colombiano durante el período junio 2008 - diciembre 2013. Para ello, se realiza la estimación de un modelo de umbrales para la tasa de cambio spot en el que la muestra es separada en dos regímenes que dependen en el grado de desviación de la tasa de cambio de un valor fundamental de acuerdo al procedimiento especificado por Hansen (2000). Los resultados de la estimación proporcionan evidencia sobre la existencia del canal coordinación de las intervenciones propuesto por Sarno and Taylor (2001). Según esta teoría, las intervenciones funcionan como señales que solucionan un problema de coordinación en el mercado cambiario cuando la tasa de cambio se desvía de su valor fundamental. Se concluye que las intervenciones cambiarias tuvieron un efecto considerable y estadísticamente significativo para depreciar la moneda local cuando la tasa de cambio estuvo suficientemente apreciada.
A considerable amount of literature has focused on several issues related to official interventions in foreign exchange markets during the last two decades. While there is no consensus about the effectiveness of these operations, its use remains attractive in developing countries where, as Hutchison (2003) refers, exchange rate movements are usually related to unstable market expectations, herding behaviour and contagion. Besides, the issue is not only whether interventions are effective or not but which is the channel of transmission. By knowing the channel through which interventions influence the exchange rate, authorities are able to improve the way in which they execute these operations in order to achieve better results.
This paper explores the effectiveness of official foreign exchange interventions in Colombia using daily data collected during the period of June 2008–December 2013. The empirical approach adopted is useful to investigate the existence of a ‘coordination channel’ proposed by Sarno and Taylor (2001) through which foreign interventions act as signals that correct a coordination failure in the foreign exchange market. The point of departure of the reasoning behind this theory is the movement of the spot exchange rate away from the equilibrium level generated by the existence of non-economic factors as speculative bubbles. In this context, it may be very difficult for individual market participants to reverse the trend of the exchange rate because agents may experience substantial losses by trading at a value consistent with the economic fundamentals (Taylor, 2005). Then, publicly announced interventions of central banks may be seen as coordinating signals that bring about a reversion of the exchange rate back to its fundamental value (Taylor, 2004).
An important implication of the coordinating channel is that interventions are more likely to be effective when the exchange rate sufficiently deviates from the level consistent with the underlying economic fundamentals. Therefore, in line with Jun (2008), I propose a threshold model in which the degree of misalignment of the exchange rate from the fundamental level is used to split the sample into two regimes. I have found that official interventions in Colombia are indeed significant in explaining the exchange rate return when the misalignment is below the estimated threshold, but that their effect is negligible otherwise. Consequently, results provide supportive evidence for the existence of a coordination channel of transmission in Colombia. Furthermore, results are useful to explain the mixed findings reported in the literature about the effectiveness of official foreign interventions conducted by the Colombian Central Bank.
The paper is organized as follows. Section 2 reviews the coordination channel proposed by Sarno and Taylor (2001). The econometric model is presented in Section 3. Section 4 describes the data. Estimation results are presented in Section 5. Finally, Section 6 provides some final remarks.
2The coordination channel of transmission of foreign exchange interventionResearch on foreign exchange interventions reports three channels by which official interventions influence the exchange rate: the portfolio balance channel, the signalling channel and the coordination channel.1 The theory of the portfolio balance channel asserts that when authorities intervene in the exchange markets, the relative supply of domestic currency bonds is modified and the exchange rate must change as investors try to rebalance their portfolios. For example, when authorities increase the supply of domestic bonds, demand of these kinds of assets must rise in order to restore the market equilibrium. Then, as Edison (1993) puts it: “The rise in demand can be achieved by a rise in domestic interest rates, by a depreciation of the domestic currency or by a fall in interest rates. […] If interest rates are determined in the money markets, then it is exchange rate that must change.” However, this effect only occurs when foreign and domestic bonds are imperfect substitutes so that investors are not indifferent to the relative holding of assets (Sarno & Taylor, 2001). Furthermore, note that if agents perceive the increase in the supply of domestic bonds as a rise in future taxation (i.e. Ricardian equivalence does hold), they will not increase their demand for these assets and the intervention will have no significant effect on the exchange rate (Dominguez & Frankel, 1993).
On the other hand, the signalling channel theory suggests that sterilized interventions modify the exchange rate because these operations reveal new information to the market and consequently shift agents’ expectations about the level of the exchange rate in the future. For instance, if authorities purchase domestic currency, agents may perceive this operation as a signal of concern about the weakness of that currency and anticipate a tighter future monetary policy. Since market participants expect an appreciation of the domestic currency in the future, their demand for this currency increases and, subsequently, the appreciation actually occurs (Kaminsky & Lewis, 1996; Mussa, 1981). Notwithstanding, in practice authorities pursue several macroeconomic goals and monetary instruments may be employed to stabilize the domestic prices rather than the exchange rate.
A third theory proposed by Sarno and Taylor (2001) upholds that interventions work as signals that solve a coordination failure in the foreign exchange market. To understand this theory, we may assume that foreign exchange markets are composed of two types of participants: ‘noise’ and ‘smart money’ traders. While noise traders use trend-following trading rules, smart money traders base their operations on economic fundamentals. Furthermore, non-economic factors, as the rules of noise traders, may prevail in the exchange rate market and cause speculative bubbles. In fact, a set of empirical literature provides evidence of this kind of behaviour (Taylor & Allen, 1992). Once this prevalence occurs, the exchange rate moves away from its fundamental value and smart money traders leave the market because at that point they will have lost confidence, credibility and/or liquidity (Reitz & Taylor, 2008). As a result, it may be very difficult for individual participants to reverse the trend and burst the speculative bubble.
By the time the exchange rate gets stuck into that trend, the market faces a coordination failure and, as stated by Reitz and Taylor (2008), “The central bank, perceiving this situation, then enters the market and announces its intervention, effectively acting as a coordinating signal to the fundamentalists [smart money traders], who follow it into the market, returning the exchange rate to a level consistent with the economic fundamentals” (p. 58). It is worth mentioning that this mechanism of the channel requires operations to be publicly announced to ensure the success of the coordinating signals.
On the whole, note that both the portfolio balance channel and the signalling channel are unlikely to work in practice for two reasons: (i) the increasing integration of international capital markets cause a high degree of substitution between financial assets (Sarno & Taylor, 2001) and (ii) many central banks have opted for domestic instead of external objectives (Schwartz, 2000), as is the case in Colombia.2 Conversely, the coordination channel seems more likely to explain the effectiveness of interventions and remains an interesting hypothesis that has attracted an important amount of empirical literature (Jun, 2008; Reitz & Taylor, 2008, 2012; Taylor, 2004, 2005).
3Modelling the effectiveness of interventionsThe coordination channel of transmission implies that foreign exchange interventions may not always be effective. According to the theory of the coordination channel (Reitz & Taylor, 2008; Sarno & Taylor, 2001), interventions may stabilize the exchange rate only when its value has moved sufficiently away from the fundamental level and the ability of smart money traders to reverse irrational speculative behaviour is damaged enough. Since there must be a positive relation between the degree of mean reversion and the degree of misalignment (Taylor, 2005), we would expect interventions to have a nonlinear effect of stabilization. Therefore, as suggested by Jun (2008), it is reasonable to adopt a criterion of ‘conditional effectiveness’: interventions should be effective only if the degree of misalignment is sufficiently large.
It must be noted (as discussed below) that during the whole sample period, the amount of U.S dollars sold by the Colombian Central Bank represented only 3% of total amount of intervention. Therefore, a different criterion of conditional effectiveness must be adopted for our data sample. Because authorities conducted purchases of foreign currency most of the time, a significant effect of interventions would be expected only when the exchange rate was sufficiently below (not beyond) its fundamental value.3 Therefore, our criterion of conditional effectiveness states that interventions would be effective if the Colombian peso is sufficiently appreciated.
The key question is the empirical meaning of the word ‘sufficiently’. Here, that word will be treated as an estimated threshold of the misalignment of the spot exchange rate from the level consistent with the economic fundamentals. If interventions are effective through the coordination channel, one would expect its effect on the exchange rate to be significant if the operation is conducted when the spot exchange rate is below the estimated threshold and negligible otherwise.
The empirical strategy involves a two-stage model formed by two equations: the first one describes the behaviour of the official foreign interventions and the second explains the exchange rate percentage changes. This specification allows us to control for any kind of endogeneity problem since foreign interventions react to the movements of the exchange rate as long as they may influence its behaviour.4 For the first equation, following Echavarría, Melo, Téllez, and Villamizar (2013a), a simple reaction function for official interventions of the Central Bank can be described by
where It corresponds to the amount of the intervention in day t, ρ0 is a constant, ∑j=120Δst−j is the accumulated daily variation of the exchange rate during the last 20 market days, (πt−πt∗) is the difference between the observed inflation and its target, and ut is an error term. The delayed amount of interventions (It−1) is expected to explain the dynamic of daily interventions since these kind of operations were very clustered in Colombia during the period in question (Rincón & Toro, 2011). In addition, the exchange rate variation of the last 20 days was an important criterion utilized by the Central Bank of Colombia for certain types of interventions and the degree of adjustment of monthly inflation to its target is useful to characterize the macroeconomic conditions at the moment of intervention.5 Given the daily frequency of It in (1), the error term may be described as the following GARCH process:where zt is independently and identically distributed with mean zero and unit variance. As a result, (1) is a AR(1)-GARCH(1,1) regression model.For the second equation of the model, let st be the logarithm of the spot exchange rate Peso/USD at time t, then a simple linear econometric model for the percentage change of the exchange rate (or its return) may be expressed as
where α is a constant, Δ(it−itf) represents the first difference of the interest rate differential (it,itf denote the interest rates of domestic and foreign deposits), Iˆt(n) is the instrumented variable of interventions obtained from the estimation of model (1), ΔRt is the first difference of a measure of risk and εt is an error term. An average amount of operations is used in order to capture possible delayed effects of intervention. The delayed change of the exchange rate (Δst−1) captures a potential trend-following or persistent behaviour that has been well documented in the literature (Reitz & Taylor, 2012; Taylor & Allen, 1992). The interest rate differential Δ(it−itf) is expected to influence the exchange rate percent changes through capital flow movements and the measure of risk (ΔRt) captures the exchange rate response to financial shocks or financial market's volatility.According to the linear model in (3), interventions are effective if the parameter that measures the effect of operations ϑ is positive and significantly different from zero so purchases of U.S. dollars increase the exchange rate. Nevertheless, this model implies that interventions must have a linear effect on the exchange rate without explicitly considering the degree of misalignment. To properly test whether interventions are conditionally effective under the coordination channel, Eq. (3) will be modelled as a threshold model. In short, we will allow exchange rates to switch between different regimes. Each regime depends on the deviation of the exchange rate from its fundamental value (i.e. the degree of misalignment). The model can be then written as
where l(⋅) is a function that takes the value of 1 if the expression inside the parenthesis is true and 0 otherwise; qt is called the ‘threshold’ variable which is measured here as the deviation of the spot exchange rate from its fundamental value (ft), and εt is an error term. The model in (4) is useful to test the conditional effectiveness of foreign exchange intervention since the sample is split into two groups or regimes. In the first regime the misalignment of the exchange rate is below the threshold (qt≤γ); irrational behaviour of uninformed traders prevails in the market and fundamentalists are not able to shift the level back with individual actions. Therefore, under this regime foreign exchange interventions are required and the coordination channel theory predicts successful operations. As a result, ϑ1 should be positive and significantly different from zero. Alternatively, in the second regime where the misalignment is above the threshold (qt>γ), interventions are ineffective because they do not work as coordinating signals and ϑ2 should be either negative or zero.Threshold models are especially useful to estimate regressions where subsamples depend on continuous variables. Similarly to Jun (2008), we applied the theory and procedure proposed by Hansen (2000) to estimate the parameters and the threshold value γ in (4). Following Hansen (2000), concentration is the computationally easiest method to obtain the conditional ordinary least squares (OLS) estimators in (3). To estimate the model (4), we also need to assume that qt and all explanatory variables are stationary. In addition, since we use daily observations, heteroskedasticity is suspected and a White-correction procedure is necessary.
To verify the existence of the threshold effect, the heteroskedasticity-consistent Lagrange multiplier test for a threshold suggested by Hansen (1996) is employed. As long as the threshold γ is not defined under the null hypothesis, the p-values are calculated by fixing the regressors obtained in (4) and generating a bootstrap of Δst using a distribution based on the estimated residuals of the threshold model6 (Hansen, 2000).
4DataThe data set contains daily observations of exchange rate percentage return (Δst), observed levels of inflation and its corresponding targets (πt,πt∗), domestic and foreign interest rates (it,itf), official interventions by the Colombian Central Bank (It) and the risk measure (Rt). The exchange rate returns are calculated as 100[log(St)−log(St−1)] with the spot Peso/US$ exchange rate. i and if are the interest rates of Colombian and U.S. one-day deposits, respectively. Official foreign exchange interventions are measured in US$ 100 million and an average of the last n days is calculated. The value of n is determined by estimating different models with a range of n=[1,…,5] and choosing the value that minimizes the sum of squared residuals (Jun, 2008). Rt is measured as the five-year credit default swaps for Colombia (CDS).
Furthermore, we assume that the fundamental value ft of the exchange rate corresponds to the purchasing power parity (PPP) level as is conventional in the literature of official interventions (Neely, 2005; Reitz & Taylor, 2008, 2012). Thus, ft may be written as follows
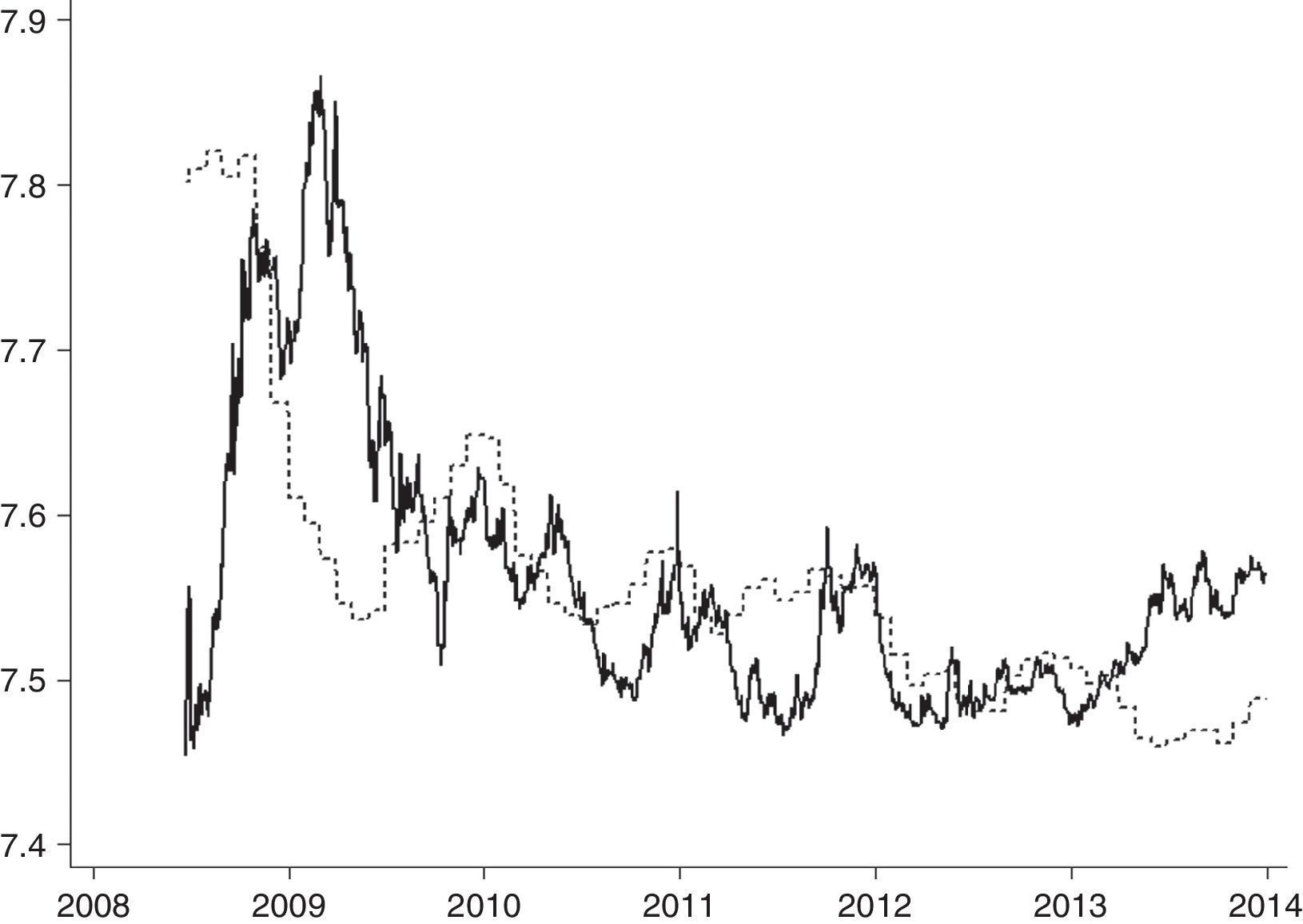
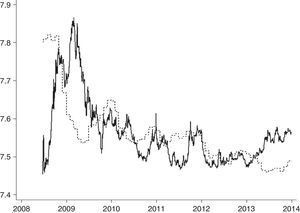
where CPItU.S and CPItCOL are the consumer price indices for the U.S. and Colombia, respectively. The PPP fundamental measure was normalized to the spot exchange rate in order to obtain comparable data. Accordingly, the threshold variable qt in (4) is measured as the deviation of the exchange rate from its fundamental value (qt=100[log(St)−log(ft)]). Daily levels of the spot exchange rate in logarithms and the fundamental value are depicted in Fig. 1.Spot exchange rates Peso/USD and PPP fundamental levels in logarithms. Notes: The figure depicts time series of the spot exchange rate Colombian Peso/USD (continuous line) and the level consistent with the PPP fundamental (dashed line) in the sample period June 25, 2008 to December 30, 2013.
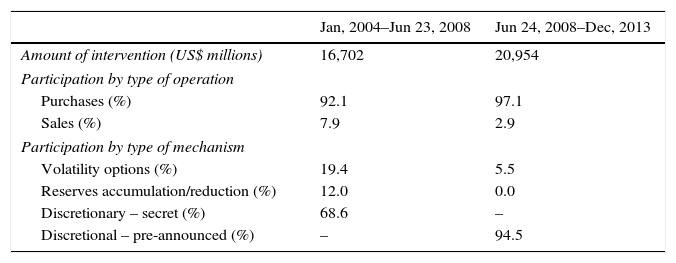
The sample period is June 25, 2008 to December 30, 2013. While trustful data is available before the middle of 2008, the sample begins at this date for a theoretical reason. Recall that the coordination channel requires operations to be publicly announced. Until 2008, the Colombian Central Bank had three intervention mechanisms: (i) option-transactions to control volatility, (ii) option-transactions to reduce or accumulate foreign reserves and (iii) direct discretionary operations. While option-based foreign exchange intervention mechanisms (i) and (ii) were publicly available, discretionary operations were secret and the amount of interventions was announced only after the following month (Rincón & Toro, 2011). Following a period of strong speculative attacks, the authorities opted for a new mechanism of pre-announced direct interventions by the end of June 2008. It should be noted that after the end of the implementation process of the inflation target monetary regime in 2004 and before June 2008, publicly available interventions of types i and ii only accounted for 31% of the total amount of intervention (Table 1). Thus, from 2004 to June 2008 secret interventions prevailed and the implicit assumption of the coordination channel did not hold for most of that period. Conversely, during our sample period all interventions were publicly available and pre-announced operations represented 95% of total amount of intervention. As a result, our sample period is convenient to test the existence of a coordination channel of intervention effectiveness.7
Colombian Central Bank foreign exchange interventions.
| Jan, 2004–Jun 23, 2008 | Jun 24, 2008–Dec, 2013 | |
|---|---|---|
| Amount of intervention (US$ millions) | 16,702 | 20,954 |
| Participation by type of operation | ||
| Purchases (%) | 92.1 | 97.1 |
| Sales (%) | 7.9 | 2.9 |
| Participation by type of mechanism | ||
| Volatility options (%) | 19.4 | 5.5 |
| Reserves accumulation/reduction (%) | 12.0 | 0.0 |
| Discretionary – secret (%) | 68.6 | – |
| Discretional – pre-announced (%) | – | 94.5 |
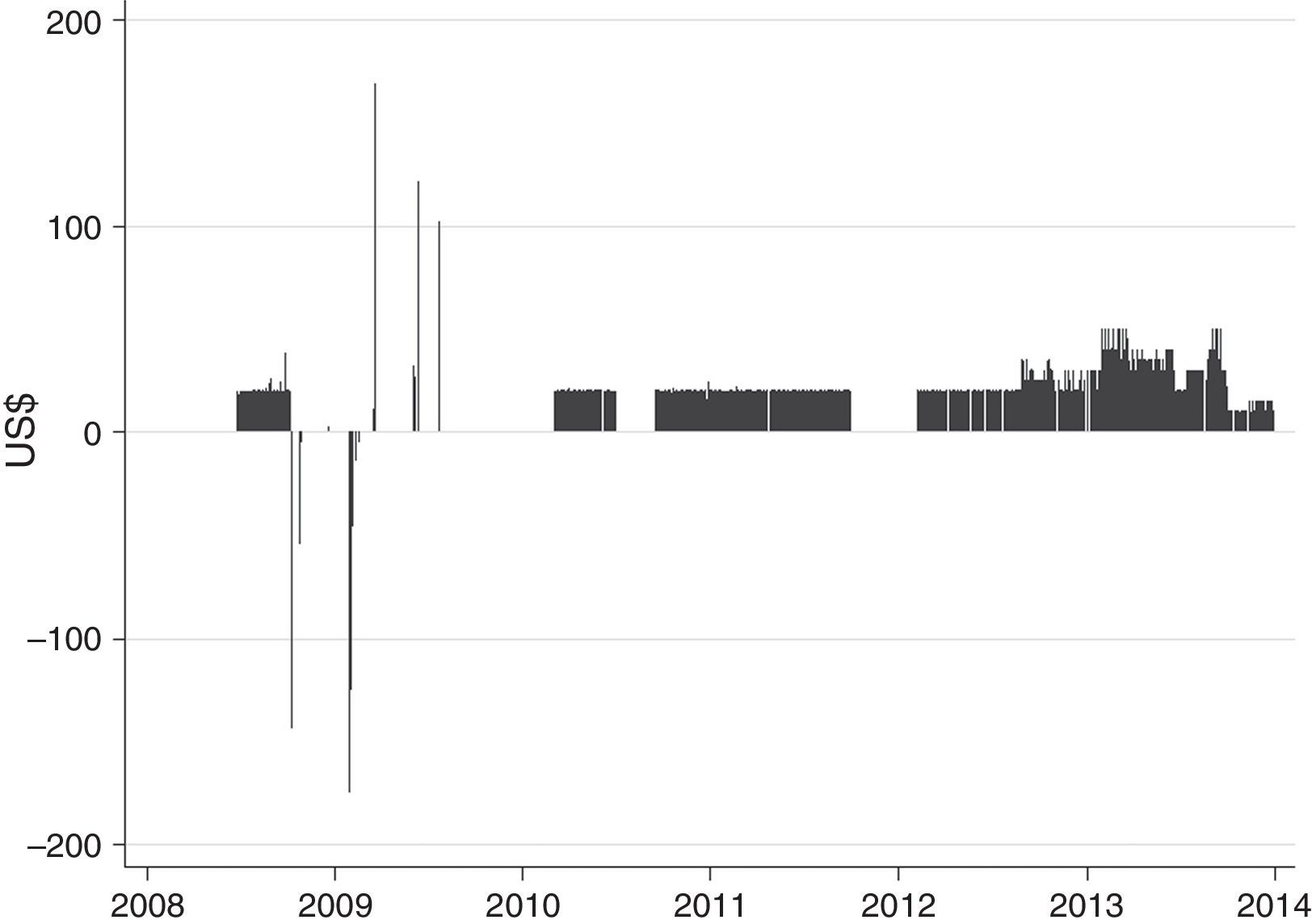
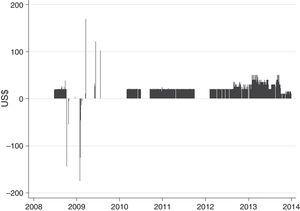
As can be seen in Fig. 2, interventions conducted by the Colombian Central Bank during the sample period were very clustered and frequent. After its introduction in June 2008, pre-announced interventions were conducted daily with amounts of US$ 20 million per day but were interrupted by October of that year with the onset of the international crisis (Rincón & Toro, 2011). Following a period of sporadic option-based interventions in 2009, the same daily pattern of pre-announced operations were carried out until the end of the sample period with temporary interruptions by mid-2010 and the end of 2011.
Colombian Central Bank Interventions. Notes: The figure displays daily foreign exchange interventions conducted by the Central Bank of Colombia. Purchases of foreign currency are depicted as positive values while sales are depicted as negative values. Operations are measured in million U.S dollars.
The estimation procedure was performed as suggested by Hansen (2000). In first place, the reaction function for official interventions (1) was estimated and the instrumented variable of official exchange interventions was employed to estimate the threshold model (4) using the OLS method.8 After estimating different models, n=1 was chosen as the right number of days to measure the amount of intervention. Accordingly, the variable I(n) at time t will be measured as the amount of sales or purchases conducted by the Central Bank at t−1 (It−1). Secondly, the model was tested against the linear effect model (3) to verify the existence of a threshold effect. Using 5000 bootstrap replications, the p-value for the threshold model was significant at 0.027 and, accordingly, the null hypothesis of linearity was rejected. Thus, a nonlinear multi-regime model that splits the sample based on the degree of misalignment qt seems to perform better than a linear model.
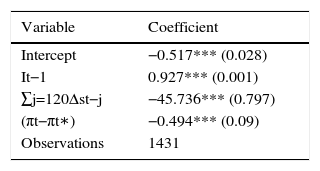
Table 2 contains the estimation results of the reaction function of the Central Bank of Colombia for official interventions. Results reveal that all variables are significant at 1% level to explain the behaviour of interventions during the period in question. Furthermore, each coefficient has the expected sign: authorities increase the purchases of foreign currency if they executed operations the day before and decrease those interventions in the presence of positive cumulative variation of the exchange rate during the last 20 days and inflationary pressures.
Estimations results, reaction function for official interventions.
| Variable | Coefficient |
|---|---|
| Intercept | −0.517*** (0.028) |
| It−1 | 0.927*** (0.001) |
| ∑j=120Δst−j | −45.736*** (0.797) |
| (πt−πt∗) | −0.494*** (0.09) |
| Observations | 1431 |
Notes: The table presents the estimation results of model (1). The sample period is June 25, 2008 to December 30, 2013. Parameters were estimated using a AR(1)-GARCH(1,1) regression. Standard errors are presented in parentheses. *** denote significance at 1% level. There is no evidence of autocorrelation or remaining ARCH effects in the residuals.
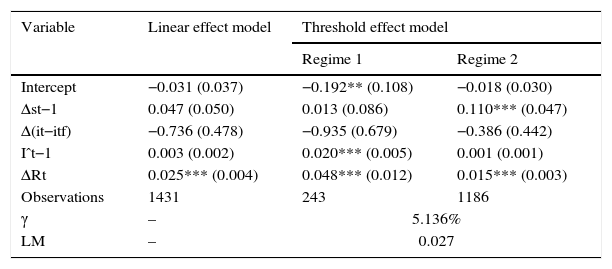
Table 3 present the estimation results of the threshold model for the percentage variations of the exchange rate.9 In the linear effect model the coefficient of the average amount of intervention is positive but it is not significant. The average purchases of US$ 100 million of the last day increase the exchange rate by approximately 0.003%. After this model, foreign exchange interventions were ineffective during the sample period as a whole. All the remaining variables, except the risk measure, are also insignificant to explain the exchange rate return but have the expected signs. Interestingly, when the sample is split with a threshold γ=−5.1% of deviation from the spot exchange rate from its fundamental PPP value, the parameter of the average amount of intervention is very significant under the regime 1 and remains not significantly different from zero under the regime 2. All the remaining variables are appropriately signed and coefficients are significantly different from zero, except for the lagged percentage change of the exchange return in regime 1 and the interest rate differential in both regimes. Furthermore, the p-value for a Wald test on the null hypothesis of ϑ1=0 was insignificant at 0.0 and the p-value for null hypothesis of ϑ2=0 was significant at 0.5.
Estimations results, threshold model.
| Variable | Linear effect model | Threshold effect model | |
|---|---|---|---|
| Regime 1 | Regime 2 | ||
| Intercept | −0.031 (0.037) | −0.192** (0.108) | −0.018 (0.030) |
| Δst−1 | 0.047 (0.050) | 0.013 (0.086) | 0.110*** (0.047) |
| Δ(it−itf) | −0.736 (0.478) | −0.935 (0.679) | −0.386 (0.442) |
| Iˆt−1 | 0.003 (0.002) | 0.020*** (0.005) | 0.001 (0.001) |
| ΔRt | 0.025*** (0.004) | 0.048*** (0.012) | 0.015*** (0.003) |
| Observations | 1431 | 243 | 1186 |
| γ | – | 5.136% | |
| LM | – | 0.027 | |
Notes: The table presents the estimation results of models (3) and (4). The sample period for both models is June 25, 2008 to December 30, 2013. Parameters were estimated using the OLS method. Standard errors in parentheses are robust to heteroskedasticity. LM denotes the p-value for the heteroskedasticity-consistency Lagrange Multiplier test for a threshold suggested by Hansen (1996). **, *** denotes significance at 5% and 1% levels, respectively.
The estimation results of the threshold model suggest that official foreign exchange interventions were effective when the spot exchange rate was sufficiently below its fundamental value γ≤5,1%. Under these circumstances, purchases of US$ 100 million raised the exchange rate by approximately 0.02%. While the magnitude of the effect is not extremely high, it is still considerable in contrast to other studies that find negligible effects on the level of the exchange rate return (Rincón & Toro, 2011; Villamizar, 2014). Likewise, the conditional effectiveness criterion allows us to assert that foreign exchange interventions had a significant impact on the exchange rate return in approximately 17% of the sample period.
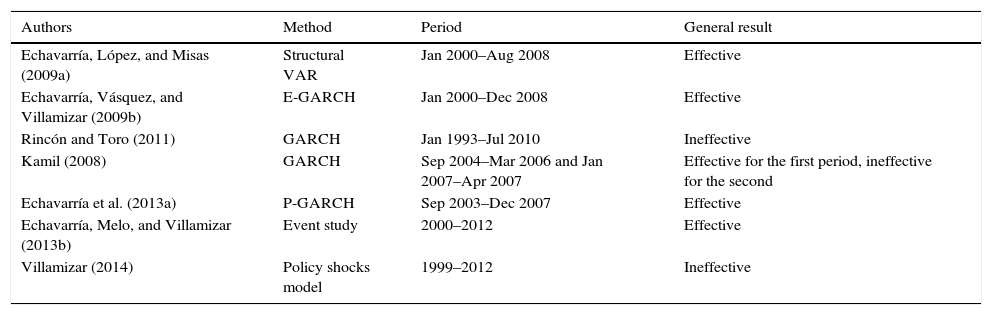
Finally, it is worth to mention the advantages and caveats of our approach and results. First, as pointed by Jun (2008), this multi-regime model is useful to explain the presence of mixed results in the empirical literature on intervention effectiveness (some general results recorded by this literature in the Colombian case are briefly summarized in Table 4). This is a relevant advantage of adopting a conditional effective criterion since an empirical model may find no significant effects of interventions if “the majority of the intervention operations in a given sample period fail to satisfy the conditions under which intervention becomes effective” (Jun, 2008). Second, this econometric framework allows us to analyze nonlinearities in the exchange rate movements that are reported in recent research (Kilian & Taylor, 2003; Peel & Taylor, 2000). Third, results suggest an interesting implication of economic policy. Namely, authorities may increase the efficacy-cost ratio of interventions by waiting to the proper moment to execute the operations.10 Nevertheless, the estimation results depend on the measure of the fundamental value. Trustful information about the rules utilized by traders to determine the fundamental value of the exchange rate in Colombia is not yet available. Surveys about these rules may be very beneficial to future research about the effectiveness of foreign exchange interventions in Colombia.
General results reported by the empirical literature on the effectiveness of foreign exchange interventions in Colombia.
| Authors | Method | Period | General result |
|---|---|---|---|
| Echavarría, López, and Misas (2009a) | Structural VAR | Jan 2000–Aug 2008 | Effective |
| Echavarría, Vásquez, and Villamizar (2009b) | E-GARCH | Jan 2000–Dec 2008 | Effective |
| Rincón and Toro (2011) | GARCH | Jan 1993–Jul 2010 | Ineffective |
| Kamil (2008) | GARCH | Sep 2004–Mar 2006 and Jan 2007–Apr 2007 | Effective for the first period, ineffective for the second |
| Echavarría et al. (2013a) | P-GARCH | Sep 2003–Dec 2007 | Effective |
| Echavarría, Melo, and Villamizar (2013b) | Event study | 2000–2012 | Effective |
| Villamizar (2014) | Policy shocks model | 1999–2012 | Ineffective |
In this paper time series data was analyzed in order to determine the degree of effectiveness of official interventions of the Colombian Central Bank in the foreign exchange market over the period June 2008–December 2013. In particular, the estimation procedure suggested by Hansen (2000) was utilized to estimate a threshold model for the spot exchange rate in which the data sample is split in two different regimes that depend on the extend of misalignment of the exchange rate from a fundamental value approximated by the purchasing power parity.
The estimation results provide empirical evidence of the existence of a coordination channel of intervention proposed by Sarno and Taylor (2001). According to the theory of the coordination channel, interventions of central banks work as signals that solve a coordination failure in the foreign exchange market when speculation moves the exchange rate away from its fundamental value. In line with the results of Jun (2008), I find that foreign exchange interventions carried out by the Central Bank of Colombia had a considerable and statistically significant effect to depreciate the domestic currency when the spot exchange rate was sufficiently below its fundamental value.
Furthermore, results are also useful to explain the mixed findings reported in the literature in the case of Colombia and may be helpful to design new strategies to intervene the foreign exchange market in the future. Indeed, authorities may increase the efficacy-cost ratio of interventions by waiting to the proper moment to execute the operations with a thorough analysis of market's believes about the degree of misalignment.
Conflict of interestThe author declares no conflict of interest.
See Table A.1.
Tests for unit roots.
| Variable | Augmented Dickey–Fuller unit root test | Phillips–Perron unit root test |
|---|---|---|
| Δst−1 | −35.882*** | −35.864*** |
| Δit−itf | −7.953*** | −38.473*** |
| Iˆt−1 | −3.087*** | −18.507*** |
| ΔRt | −20.610*** | −26.829*** |
| qt | −3.414*** | −3.418*** |
Notes: The table presents the t-statistics of the Augmented Dickey–Fuller and Phillips–Perron unit root tests for all the explanatory variables (Δst−1,Δ(it−itf),Iˆt−1,ΔRt) and the threshold variable (qt). *** denote insignificance at 1% level according to the MacKinnon p-values.
This section summarizes the method developed by Hansen (2000) to construct confidence intervals for least squares estimations of threshold parameters. Following a matrix notation, a threshold model can be expressed as
where Y,e are the n×1 vectors of the endogenous variable and the error term, and X,Xγ are the n×m matrices of the exogenous and the threshold variables, respectively. θ,γ and δn are parameters. These parameters are estimated as least-square estimators that minimize the sum of squared error function:Conditional on γ, Sn(θ,δ,γ) may be expressed as a concentrated function Sn(γ) and the estimated threshold γˆ is then the value that minimizes Sn(γ). To estimate γˆ, confidence regions are constructed based on the likelihood ratio statistic LRn(γ). In presence of heteroskedasticity the statistic can be written as follows:
where ηˆ2 is a nuisance parameter and σˆ2 is the estimated conditional variance of the threshold variable.1111For a detailed description on the estimation of the nuisance parameter see Hansen (2000).
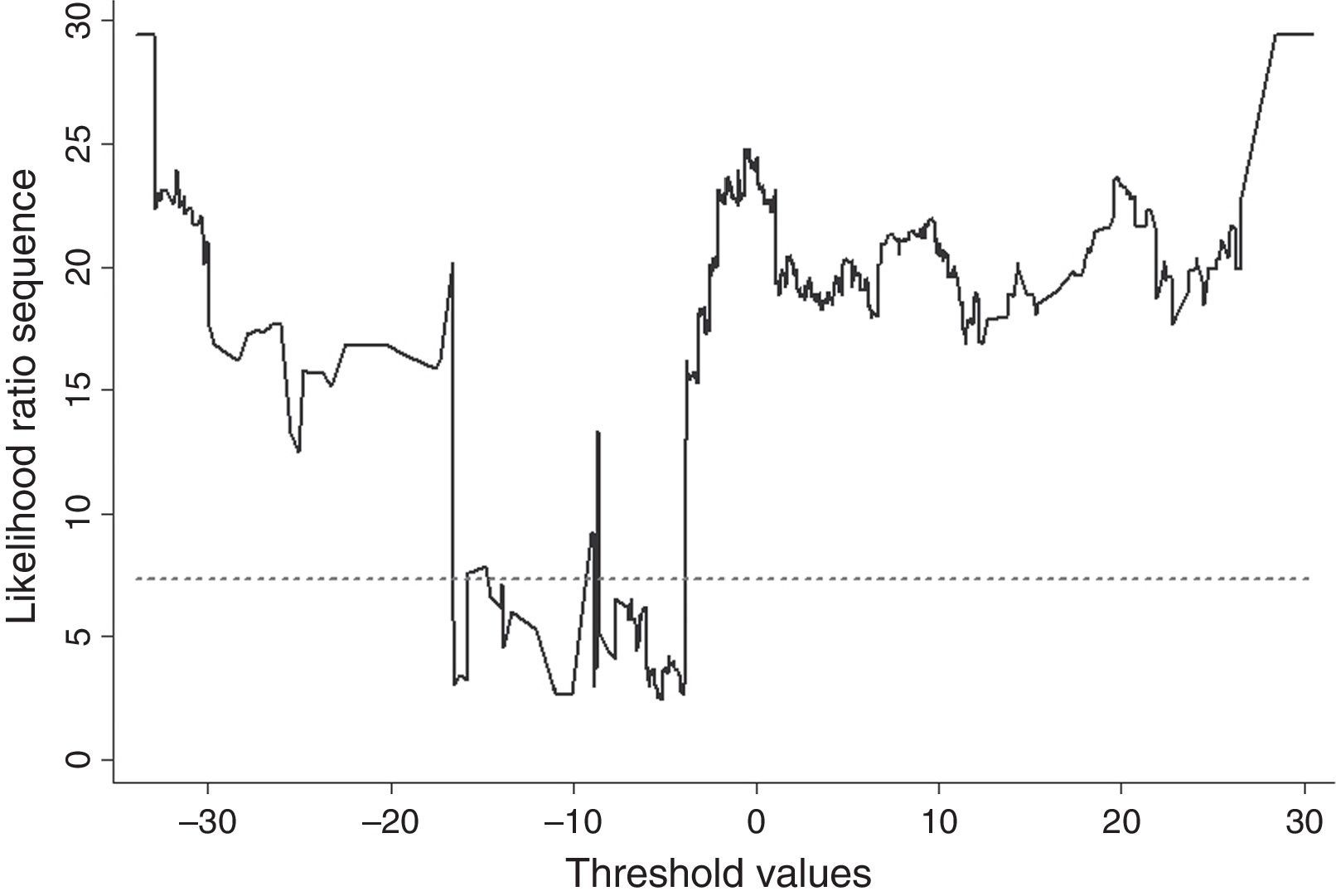
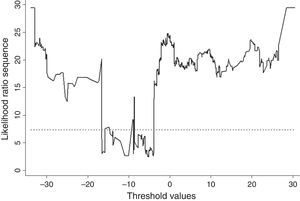
Therefore, the confidence region for a desired asymptotic level C can be defined as:where c is the C-level asymptotic critical value constructed by Hansen (2000). Fig. A.2 plots the likelihood ratio sequence LRn∗(γ) as a function of different values of our threshold variable qt for the particular case of model (4). The estimated threshold is the value that minimizes the sequence which in this case occurs at γˆ=−5,136.Confidence interval construction for the threshold. Notes: The figure depicts the likelihood ratio LRn∗(γ) sequence for the construction of a confidence interval for the threshold variable of model (4) (continuous line). Additionally, the Hansen (2000) 95% critical value is plotted (dashed line).
A detailed review of concepts and literature about foreign exchange interventions may be found in Neely (2001) and Sarno and Taylor (2001).
Since 1991, the main objective of the Central Bank of Colombia is to stabilize domestic prices: while the Central Bank defended a specific level of the exchange rate with monetary instruments until September of 1999 through fixed bands, the adoption of a free floating regime emphasized the importance of the domestic objectives over the external ones: “The long-term essential objective of the Colombian monetary policy is to maintain the purchasing power of money […]” (Banco de la República, 2000). This prevalence has also been emphasized in official statements of the authorities about the consistency between monetary policy and foreign exchange policy: “The Bank has repeatedly affirmed that currency intervention is conducted without jeopardizing the inflation target” (Banco de la República, 2007).
A model in which the misalignment of the exchange rate from its fundamental value is measured in absolute terms would be an interesting alternative. Nevertheless, since the main objective of the Central Bank during our period was depreciating the domestic currency, this alternative would not be appropriate. For instance, if the spot exchange rate is sufficiently above the fundamental value, an intervention in which the Central Bank purchases foreign currency would not be perceived as a coordinating signal by private agents. This version of the model or an extension with more regimes would be convenient in a context in which purchases and sales were executed with more symmetry by the economic authorities.
I am grateful to an anonymous reviewer for making this point clear.
The consistency between monetary policy and foreign interventions is an important issue addressed by the Board of Directors of the Colombian Central Bank: “When an intervention is made, the public may think the central bank has an inflation objective and also an exchange-rate objective. Should a contradiction be perceived in achieving the two objectives at the same time, the credibility of both will come into question, and the effectiveness of intervention in the currency market may be reduced” (Banco de la República, 2007).
Since Δst has daily observations, the introduction of a GARCH(1,1) process is recommended to capture the conditional standard variance of the error term. However, the introduction of the GARCH process is difficult to implement since the test for threshold effects suggested by Hansen (2000) involves thousands of bootstrap replications. For this reason, in this paper I do not model the conditional variance of exchange returns explicitly using a GARCH process. The successful introduction of this type of process in a nonlinear multi-regime model lead to more complex frameworks as smooth transition regression (STR)-GARCH models (see Reitz & Taylor, 2008).
It may be that, even when authorities conduct the interventions anonymously, agents spread the information about these operations quickly in the market through unofficial sources, traders’ relationships, monitoring of the level of central banks’ international reserves, among others (Dominguez, 2003; King, 2003). As Reitz and Taylor (2008) point out, “to what extent central banks allowed operations to be publicly available information is an empirical issue” (p. 71). Since there is not such empirical analysis for the case of Colombia, secret interventions conducted before June 2008 cannot be treated as useful data for our purposes.
The p-value of the Augmented Dickey-Fuller and the Phillips-Perron unit root tests for all the explanatory variables (Δst−1,Δ(it−itf),Iˆt−1,ΔRt) and the threshold variable (qt) were insignificant at the 1% level (see Appendix 1).
See Appendix 2 for further details on the estimation of the threshold model.
Official announcements of the authorities to clarify the motives of intervention in the presence of a significant degree of misalignment may also improve the effectiveness of interventions as long as the signal could be even more clear. The advantages and setbacks of this kind of transparency policy are not yet clear and may be appropriate to investigate its connection with the coordination channel of transmission in future studies.