Principales métodos de análisis en los estudios de cohortes de sujetos diagnosticados de infección por el virus de la inmunodeficiencia humana (VIH)

Resumen

En este trabajo se describen los principales métodos estadísticos utilizados en el análisis de los datos procedentes de estudios de cohortes y se presenta una descripción detallada de la aplicación de estos métodos a la investigación del virus de la inmunodeficiencia humana (VIH) y del sida. En primer lugar, se describen los métodos para el análisis de episodios en personas-tiempo. En segundo lugar, se presentan los métodos de supervivencia para el estudio de variables que miden el tiempo transcurrido hasta la ocurrencia del episodio de interés. En este contexto, se presenta la aplicación de estos métodos para describir el período de incubación del sida y la supervivencia desde la seroconversión a VIH, determinar los factores y los marcadores biológicos asociados a la progresión de la infección por VIH y evaluar la efectividad de los tratamientos. Finalmente, se presentan los métodos analíticos para el estudio de marcadores medidos repetidamente en el tiempo.

Abstract

This paper provides an overview of the main statistical methods used in the analysis of data from cohort studies and presents a detailed description of the way these methods are applied in HIV/AIDS research. First, we describe methods for analyzing events in person-time data. Second, we present survival methods for the analysis of time-to-event data. In this context, we illustrate the application of these methods to describe the AIDS incubation period and survival from HIV seroconversion, to determine the factors and biological markers associated with disease progression, and to evaluate effectiveness of therapy. The review ends by illustrating the statistical methods used for the analysis of markers measured repeatedly over time.

Introducción

El principal objetivo del análisis de datos de cualquier estudio epidemiológico es describir y comparar el episodio resultado de interés (en inglés outcome) en diferentes grupos de individuos. La validez de las inferencias epidemiológicas se sustenta sobre la base de que los grupos son comparables respecto a cualquier otro factor diferente a la variable de exposición principal que pueda explicar la heterogeneidad en el comportamiento de la variable de interés. En los estudios de cohortes, debido a la falta de aleatorización en la asignación de los individuos a los diferentes grupos de comparación, es necesario el uso de métodos de regresión en la fase de análisis que aseguren la comparabilidad de los grupos.

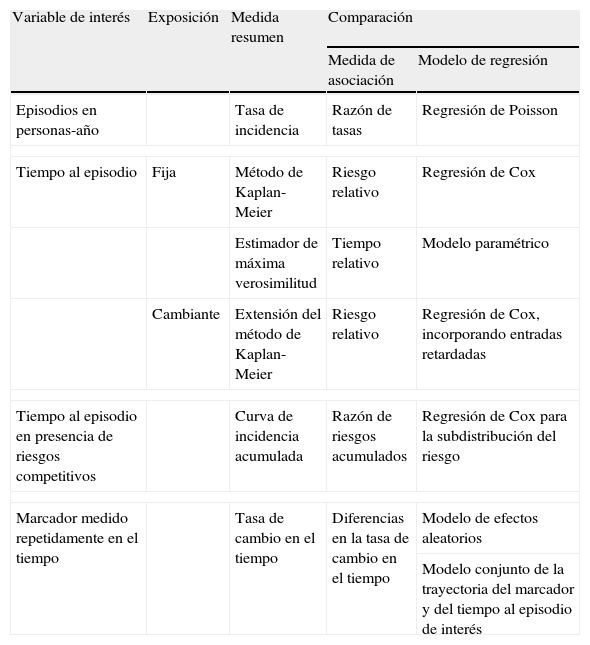
La tabla 1 resume las medidas de frecuencia, las medidas de asociación y los métodos de regresión utilizados en el análisis de las variables resultado de interés más estudiadas en los estudios de cohortes: episodios en personas-tiempo, tiempo al episodio y cambio en un marcador medido repetidamente en el tiempo. En las siguientes secciones, se presenta una descripción detallada de la aplicación de estos métodos a la investigación del virus de la inmunodeficiencia humana (VIH) y del sida.

Tabla 1.

Resumen de los principales métodos para el análisis de datos procedentes de estudios de cohortes

Variable de interés	Exposición	Medida resumen	Comparación
			Medida de asociación	Modelo de regresión
Episodios en personas-año		Tasa de incidencia	Razón de tasas	Regresión de Poisson
Tiempo al episodio	Fija	Método de Kaplan-Meier	Riesgo relativo	Regresión de Cox
		Estimador de máxima verosimilitud	Tiempo relativo	Modelo paramétrico
	Cambiante	Extensión del método de Kaplan-Meier	Riesgo relativo	Regresión de Cox, incorporando entradas retardadas
Tiempo al episodio en presencia de riesgos competitivos		Curva de incidencia acumulada	Razón de riesgos acumulados	Regresión de Cox para la subdistribución del riesgo
Marcador medido repetidamente en el tiempo		Tasa de cambio en el tiempo	Diferencias en la tasa de cambio en el tiempo	Modelo de efectos aleatorios
				Modelo conjunto de la trayectoria del marcador y del tiempo al episodio de interés

Episodios en personas-tiempo

Los métodos para el análisis de episodios en personas-tiempo permiten describir la tasa de incidencia del episodio de interés y determinar los factores asociados. La estimación de la tasa de incidencia se obtiene dividiendo el número de episodios ocurridos durante el período de observación por el total de personas-tiempo a riesgo. El tiempo que permanece a riesgo un individuo es el transcurrido desde el inicio del período de observación hasta la ocurrencia del episodio de interés o el fin de su período de observación.

El efecto de un cofactor en la tasa de incidencia del episodio de interés puede investigarse mediante el cálculo de la tasa de incidencia en cada valor del cofactor y obteniendo razones de tasas (RT) comparando la tasa de incidencia de cada valor con la del valor de referencia. En el caso de cofactores continuos, o si se requiere del ajuste simultáneo por otras variables, es necesario utilizar modelos de regresión de Poisson para derivar las RT¹.

En el caso de episodios recurrentes que pueden presentarse más de una vez en cada individuo durante el período de observación (p. ej: varias enfermedades definitorias de sida en el tiempo), son necesarios métodos analíticos de mayor complejidad^2,3.

Análisis de datos que miden el tiempo al episodio

Introducción

El principal problema en el análisis de datos que miden el tiempo al episodio es la existencia de tiempos al episodio de interés no observados exactamente y que, además, no presentan una distribución normal; éstas son las principales razones para el uso de los métodos conocidos como métodos de supervivencia. En las siguientes secciones se presenta la aplicación de los métodos de supervivencia para describir el período de incubación del sida y la supervivencia desde la seroconversión al VIH, determinar los factores y los marcadores biológicos asociados a la progresión y evaluar la efectividad de los tratamientos.

Período de incubación del sida y supervivencia desde la seroconversión al virus de la inmunodeficiencia humana

Las cohortes de seroconvertores, cohortes de individuos con una fecha de seroconversión al VIH conocida o estimada con fiabilidad, proporcionan los datos más apropiados para el estudio del período de incubación del sida y de la supervivencia desde la seroconversión al VIH⁴. El procedimiento más utilizado es el método no paramétrico de Kaplan-Meier⁵, que permite estimar la curva de supervivencia o, equivalentemente, la función de incidencia acumulada del episodio de interés. Los modelos paramétricos^6,7 también se han utilizado en la descripción del período de incubación del sida y la supervivencia desde la seroconversión a VIH, aunque no hay consenso sobre cuál es la mejor parametrización. En un artículo publicado recientemente, Cox et al⁸ presentaron la aplicación de la distribución paramétrica conocida como gamma generalizada en el contexto de la infección por VIH. Esta distribución es una familia de distribuciones que contiene las distribuciones más utilizadas (exponencial, Weibull, lognormal y gamma) y que incluye los 4 tipos de función de riesgo más comunes (monotónicamente creciente, monotónicamente decreciente, con forma de bañera y con forma de arco), lo que permite mayor flexibilidad en la modelización.

Aunque las cohortes de seroconvertores proporcionan los datos más apropiados para estudiar el período de incubación del sida y la supervivencia desde la seroconversión al VIH, la baja incidencia de infección por VIH y la poca frecuencia de individuos que cumplen el criterio de seroconvertor, requieren no sólo el seguimiento de un elevado número de individuos no infectados para conseguir una cohorte de tamaño razonable sino también su seguimiento prolongado para disponer de un número de episodios suficiente que permita obtener estimaciones precisas.

Las cohortes de seroprevalentes, cohortes formadas por individuos que estaban infectados por VIH antes de su entrada en la cohorte y su fecha de seroconversión se desconoce, superan estas dificultades, ya que en el momento de la entrada en la cohorte ha transcurrido parte de la historia natural de la infección y es necesario menos tiempo de seguimiento para observar el episodio de interés en un número considerable de individuos. La principal limitación en el uso de estas cohortes es la ausencia de información desde la seroconversión hasta la entrada en la cohorte⁹. Se han propuesto 2 alternativas, conocidas como el método de los datos externos y el método de la elongación, para determinar la duración de la infección en el momento de la entrada en la cohorte. La primera combina la información sobre la fecha de ocurrencia del episodio de interés de los individuos de la cohorte seroprevalente con información de fuentes externas, generalmente de cohortes de seroconvertores o datos de vigilancia, sobre la fecha de seroconversión¹⁰. La segunda utiliza datos individuales para determinar el tiempo que cada seroprevalente lleva infectado en el momento de su entrada en la cohorte y se añade ese tiempo al total del seguimiento observado.

Algunos autores proponen como fecha probable de seroconversión la fecha de inicio de comportamientos de alto riesgo, probables de resultar en infección (fecha de inicio de contactos sexuales con personas infectadas por VIH)¹¹. Otros proponen modelos basados en la comparación de los valores de marcadores inmunológicos y hematológicos de los seroprevalentes con una subcohorte de seroconvertores y se asume que las trayectorias de los marcadores son similares en ambas cohortes¹². Una vez imputada la fecha de seroconversión en los individuos seroprevalentes, el estudio del período de incubación del sida y de la supervivencia desde la seroconversión se realiza mediante la extensión del método de Kaplan-Meier, que incorpora el truncamiento a la izquierda para ajustar por la no observación de los progresores rápidos. No considerar el truncamiento a la izquierda resultaría en una sobrestimación de la mediana del período de incubación del sida y de la supervivencia desde la seroconversión al VIH.

Una aproximación alternativa para yuxtaponer subcohortes de seroprevalentes y de seroconvertores consiste en imputar el tiempo residual libre del episodio a los seroconvertores, basado en marcadores de los individuos seroprevalentes¹³.

Estimación del efecto de los cofactores en el riesgo de desarrollar sida o muerte

El efecto de un cofactor en el episodio de interés puede investigarse fácilmente mediante la representación gráfica de las curvas de supervivencia de Kaplan-Meier en los diferentes niveles del cofactor, utilizando el test del log-rango para su comparación. La cuantificación de la magnitud de la asociación entre el cofactor a estudio y el episodio de interés se obtiene mediante el cálculo de los riesgos relativos (RR) derivado de un modelo proporcional de Cox^14,15. Los modelos proporcionales de Cox modelizan el efecto que las covariables tienen en el riesgo, es decir, en el riesgo instantáneo de desarrollar el episodio de interés. La relación directa entre la función de riesgo y la función de supervivencia permite que los resultados del modelo de Cox sean directamente interpretables en términos acumulados, esto es, como el efecto que las covariables tienen en la supervivencia o, equivalentemente, en el riesgo acumulado de desarrollar el episodio de interés.

El modelo de Cox se basa en la asunción de proporcionalidad de riesgos, es decir, asume que la razón de los riesgos entre los diferentes niveles del cofactor es constante en el tiempo. Una solución analítica para manejar variables que no cumplen la proporcionalidad de riesgos consiste en estratificar por esa variable en el modelo de regresión de Cox. Esta aproximación permite controlar por la variable sin necesidad de asumir la proporcionalidad de riesgos, pero no permite resumir su efecto de forma sencilla. El análisis de cofactores que varía en el tiempo se realiza mediante modelos proporcionales de Cox para variables cambiantes en el tiempo.

Los modelos paramétricos también permiten estudiar el efecto de los cofactores en la variable de interés mediante el cálculo de cuantiles relativos (tiempos relativos: la razón de los tiempos que un porcentaje dado de individuos con diferentes exposiciones tarda en desarrollar el episodio de interés) y, en el caso de las distribuciones Weibull y exponencial, también mediante el cálculo de RR⁸.

Marcadores como factores pronóstico

El método más utilizado para determinar el impacto que un marcador medido en un momento puntual tiene en la progresión de la enfermedad consiste en obtener las curvas de Kaplan-Meier en cada nivel del marcador y los RR derivados de un modelo de Cox. Mellors et al¹⁶, utilizando este procedimiento, mostraron que la carga viral, seguida de los linfocitos CD4, era el marcador que mejor predecía la progresión de la infección. Rodríguez et al¹⁷ cuestionaron el valor pronóstico de la carga viral como principal determinante de la inmunodeficiencia y argumentaron que explica menos del 10% de la variabilidad de la pendiente de las células CD4 en pacientes con infección por VIH no tratados. Como respuesta, Mellors et al¹⁸ evaluaron nuevamente el valor pronóstico de la carga viral, de los linfocitos CD4 y de la pendiente de los linfocitos CD4 en la progresión a sida y a muerte en pacientes con VIH no tratados de la cohorte del estudio MACS (Multicenter AIDS Cohort Study ‘Estudio de Cohorte Multicéntrico sobre el Sida’) y mostraron que la carga vírica es el predictor más importante del tiempo al sida y a muerte, lo que explica alrededor del 50% de la variabilidad de ambos episodios. La carga viral basal únicamente explica el 3% de la variabilidad en la pendiente de los linfocitos CD4. Se argumenta como principal razón de este resultado la gran variabilidad de la pendiente de los linfocitos CD4, razón que también explica el bajo valor pronóstico de la pendiente de los linfocitos CD4 para el tiempo al sida y a muerte.

Los árboles de regresión son un método alternativo que permite incorporar la interacción entre marcadores. Estos métodos gráficos permiten dividir a la población en grupos con riesgos de progresión significativamente diferentes, sin necesidad de realizar las asunciones de los modelos lineales generalizados¹⁹. Mellors et al¹⁶ utilizaron árboles de regresión para mostrar gráficamente el efecto conjunto de la carga viral y de los linfocitos CD4 en la progresión a sida, y estos resultados proporcionaron las bases de las guías clínicas para el tratamiento de los individuos infectados por VIH en Estados Unidos.

Si los marcadores se miden repetidamente en el tiempo, es necesario utilizar modelos proporcionales de Cox para variables cambiantes en el tiempo.

Evaluación de la respuesta a los tratamientos

Los estudios de cohortes permiten evaluar el impacto que los diferentes tratamientos tienen en la progresión del VIH y del sida fuera del contexto del ensayo clínico mediante el cálculo de 2 medidas para las que Muñoz et al proponen la terminología de efectividad individual y efectividad poblacional^20,21. La efectividad individual utiliza las pautas de tratamiento individual e intenta reproducir los resultados sobre la eficacia de los tratamientos de los ensayos clínicos con datos de estudios observacionales al comparar la respuesta de los individuos que reciben tratamiento con la de aquéllos que no lo hacen. La efectividad poblacional compara la incidencia de la enfermedad observada en una población o en un período calendario en la que algunos individuos, frecuentemente los más enfermos, reciben tratamiento con la incidencia en una población en la que prácticamente ningún individuo recibe tratamiento.

Efectividad individual

Los modelos proporcionales de Cox se han utilizado frecuentemente para evaluar la efectividad individual de los tratamientos en la progresión de la infección por VIH, modelizando las pautas de tratamiento que reciben los pacientes como variables cambiantes en el tiempo. Sin embargo, la aplicación de los métodos de supervivencia estándar para evaluar la efectividad individual de los tratamientos a partir de estudios de cohortes está sujeta a sesgos derivados de la falta de aleatorización en la asignación de los tratamientos. Los individuos que reciben tratamiento son aquellos que han sobrevivido un tiempo suficiente para tener ocasión de recibirlo y, a la vez, son aquellos que lo necesitan, dado que sus condiciones los sitúan a un mayor riesgo de desarrollo de la enfermedad (sesgo por indicación). Dado que el inicio del tratamiento se basa a menudo en niveles bajos de linfocitos CD4 y en niveles altos de carga viral, la evolución de estos marcadores debe considerarse en el control del sesgo por indicación. Sin embargo, diferentes autores han mostrado que el ajuste por la historia pasada de los marcadores en un modelo de Cox produce estimaciones sesgadas del efecto cuando la evolución de estos marcadores está afectada por la historia pasada de tratamientos, siendo necesario la utilización de los modelos estructurales²².

Los modelos estructurales son una nueva clase de modelos que superan las limitaciones de los métodos de supervivencia estándar y permiten estimar el efecto causal que un tratamiento tiene en el episodio de interés, minimizando el sesgo de indicación por tratamiento, presente en los estudios de cohortes debido a la ausencia de aleatorización en la asignación de los tratamientos. Los parámetros de los modelos estructurales pueden estimarse mediante estimación G, lo que da lugar a lo que se conoce como modelos estructurales anidados, o mediante la asignación de pesos obtenidos como el inverso de la probabilidad de recibir el tratamiento que recibe cada individuo, que da lugar a los denominados modelos marginales estructurales²².

Hernán et al²³ con la aplicación de modelos marginales estructurales mostraron un claro efecto protector de tratamiento antirretroviral de gran actividad (TARGA) en la progresión a sida y a muerte. En España, Pérez-Hoyos et al²⁴ aplicaron estos modelos en la cohorte de seroconvertores del Grupo Español Multicéntrico para el Estudio de Seroconvertores (GEMES). En ambos trabajos se comparan los resultados de un modelo de Cox estándar con los resultados proporcionados por los modelos marginales estructurales, lo que muestra que los modelos estándar no permiten detectar el efecto protector del tratamiento porque no ajustan apropiadamente por la carga vírica y los linfocitos CD4, variables cambiantes en el tiempo que son simultáneamente variables confusoras y variables intermedias.

Efectividad poblacional

El impacto que un tratamiento tiene en la progresión de la enfermedad en una población y fuera de las condiciones de un ensayo clínico puede aproximarse mediante el cálculo de la efectividad poblacional. Esta medida compara la incidencia de la enfermedad observada en una población en la que algunos individuos, frecuentemente los más enfermos, reciben tratamiento con la incidencia en una población en la que prácticamente ningún individuo recibe tratamiento. Dado que la introducción y la disponibilidad de un tratamiento en una población están relacionadas con el período calendario (p. ej: TARGA empieza a estar disponible a partir de 1996), la estimación de la efectividad poblacional se realiza mediante la comparación de la incidencia de la enfermedad en diferentes períodos calendarios en los que diferentes tratamientos están disponibles y son administrados a la población, asumiendo que los sujetos que lo necesitan lo reciben. En los últimos períodos calendario suele haber no sólo individuos en los últimos estadios de la enfermedad (niveles bajos de linfocitos CD4) sino también un alto porcentaje de individuos libres de la enfermedad en duraciones de infección prolongadas. Estos factores operan en direcciones opuestas: los individuos en los últimos estadios de la enfermedad estarán sujetos a un mayor riesgo de sida y de muerte que las personas en estadios más tempranos de la infección, mientras que las personas libres de la enfermedad en mayores duraciones de infección (indicador de algún grado de inmunidad) tendrán un menor riesgo de sida y de muerte. Por tanto, el análisis de la efectividad poblacional del tratamiento del VIH debe ajustar por la duración de la infección o el estadio de la enfermedad para controlar este sesgo, conocido como sesgo de supervivencia. De esta forma, la comparación del riesgo de sida o de muerte en diferentes períodos calendario se realiza entre individuos comparables respecto al riesgo básico para desarrollar el episodio de interés.

En el análisis, el período calendario se trata como una variable externa cambiante en el tiempo. Así, un individuo contribuye al análisis con tantos registros como períodos calendario se hayan observado de estar a riesgo para el episodio de interés. De este modo, cada contribución está caracterizada por la duración de la infección que el individuo tiene a la entrada de un período, la duración de la infección que el individuo tiene a la salida de un período y el estatus respecto al episodio de interés a la salida del período. Esta modelización permite la comparación del riesgo del episodio de interés en diferentes períodos calendario entre individuos con la misma duración de la infección.

Las medidas de efectividad a escala poblacional son susceptibles de falacia ecológica, es decir, efectividad causada por cambios en exposiciones diferentes a los tratamientos que se pretende evaluar. Para poder estimar de forma precisa la efectividad poblacional de un determinado tratamiento resulta necesario disponer de datos relativos a cambios importantes producidos en la población relacionados con el acceso y la utilización de los servicios sanitarios, el uso de profilaxis y la adherencia a los tratamientos.

Detels et al²⁵ fueron los primeros en publicar la efectividad poblacional del TARGA en la cohorte MACS. Posteriormente, tanto cohortes de ámbito nacional²⁶ como de ámbito internacional²⁷ han mostrado la marcada disminución de la incidencia de sida y de muerte desde la introducción y la disponibilidad de TARGA.

Aproximaciones analíticas en presencia de riesgos competitivos

Los métodos de supervivencia estándar descritos previamente se han utilizado desde el inicio de la epidemia para describir el período de incubación del sida, determinar los cofactores y los marcadores asociados y evaluar el impacto que los diferentes tratamientos tienen en la progresión de la enfermedad. Sin embargo, en el estudio del tiempo al sida, la mortalidad previa al sida actúa como un episodio competitivo que previene la ocurrencia del episodio de interés, lo que viola la asunción de independencia entre el tiempo al episodio y el tiempo a la censura sobre la que se sustentan los métodos de supervivencia descritos previamente. El aumento considerable de la mortalidad no sida en la era del tratamiento antirretroviral ha motivado el interés por los métodos para el análisis de datos en presencia de riesgos competitivos. Los riesgos competitivos se refieren a la situación en la que un individuo puede experimentar más de un tipo de episodios resultado, de forma que los diferentes episodios compiten por ser el primero que experimentará el individuo.

El método más utilizado para estimar la probabilidad de desarrollo del episodio de interés en presencia de riesgos competitivos es el método no paramétrico de Kaplan-Meier, que considera a los individuos que desarrollan primero un episodio competitivo, diferente al episodio de interés, como observaciones censuradas. Sin embargo, las estimaciones obtenidas a partir de este método no son interpretables. La razón de esto es que no se cumple la asunción básica del método de Kaplan-Meier: independencia entre la distribución del tiempo al episodio y la distribución del tiempo a la censura (distribución del tiempo a los episodios competitivos). Únicamente bajo el supuesto de que ambas distribuciones son independientes el estimador de Kaplan-Meier se interpretaría como la probabilidad de desarrollo del episodio de interés en una situación hipotética en la que los episodios competitivos pudieran eliminarse. Sin embargo, a partir de los datos observados la asunción de independencia no puede testarse.

En esta situación, son necesarios métodos alternativos que permitan estimar directamente, y no como uno menos la probabilidad de supervivencia derivada del estimador de Kaplan-Meier, las curvas de incidencia acumulada para cada tipo de episodio. Putter et al³ proporcionan una descripción detallada de la fórmula para estimar la curva de incidencia acumulada.

El efecto de una covariable en el episodio de interés puede investigarse mediante la representación gráfica de las curvas de incidencia acumulada en cada nivel de la covariable a estudio. La comparación de las curvas de incidencia acumulada puede realizarse mediante un test que desarrolló Gray²⁸, similar al test del log-rango.

Si la covariable a estudio es continua o se requiere del ajuste por otras variables, son necesarios modelos de regresión. El análisis estándar de los datos en presencia de riesgos competitivos ha consistido en la modelización de la función de riesgo de causa específica mediante modelos proporcionales de Cox. Estimar el riesgo de causa específica se reduce a un modelo de Cox estándar respecto a la censura (los individuos que desarrollan primero un episodio competitivo, diferente al episodio de interés, se censuran en la fecha de ocurrencia del episodio competitivo) pero la interpretación es diferente. El hecho de que en presencia de riesgos competitivos no haya una relación directa entre la función de riesgo y la función de supervivencia no permite la interpretación de los parámetros de este modelo en términos de incidencia acumulada. Los resultados de este modelo deben interpretarse como el efecto que las covariables tienen en el riesgo, es decir, en el riesgo instantáneo de desarrollar el episodio de interés como primer episodio, condicionado a estar vivo y libre del episodio hasta ese momento. Únicamente bajo la asunción de que los diferentes episodios son independientes, los riesgos de causa específica serían equivalentes a los riesgos marginales modelizados en un análisis de supervivencia estándar.

Para estimar el efecto de las covariables en la incidencia acumulada del episodio de interés en presencia de riesgos competitivos, Fine y Gray²⁹ han propuesto un modelo de riesgos proporcionales para la subdistribución del episodio de interés, que reestablece la relación directa entre la subdistribución del riesgo y la función de incidencia acumulada. Los resultados de este modelo son directamente interpretables en términos acumulados, es decir, como el efecto que las covariables tienen en el riesgo acumulado de desarrollar el episodio de interés.

La diferencia principal entre modelizar el efecto de las covariables en la función de riesgo de causa específica o en la función de incidencia acumulada de causa específica está en la población considerada a riesgo. Mientras que en el riesgo de causa específica la población a riesgo decrece cada vez que se produce un episodio competitivo, en la función de incidencia acumulada los individuos que desarrollan un episodio competitivo permanecen a riesgo después de la ocurrencia del episodio competitivo. En una situación ideal de no censura, la subdistribución del riesgo (y, por tanto, la función de incidencia acumulada) puede calcularse censurando a los individuos que desarrollan primero un episodio diferente al episodio de interés en infinito. Bajo censura administrativa, únicamente la subdistribución del riesgo puede aproximarse censurando a los individuos que desarrollan un episodio competitivo diferente al episodio de interés, en su fecha de censura potencial. Sin embargo, bajo una situación de censura a la derecha general, resulta necesario estimar una distribución del tiempo a la censura a partir de los datos para estimar la subdistribución del riesgo.

La aproximación de la subdistribución del riesgo en presencia de variables cambiantes en el tiempo (p. ej: período calendario) no es un tema suficientemente cubierto en la literatura médica y sobre el que haya consenso. En investigación en VIH se han propuesto 2 fechas potenciales de censura para aproximar la subdistribución del riesgo: fecha de fin del seguimiento^30,31 y fecha de fin del período calendario^31,32. En la primera, los individuos que desarrollan primero un episodio competitivo se censuran al final de su seguimiento. En la segunda, los individuos que desarrollan primero un episodio competitivo se censuran al final del período calendario en el que desarrollaron el episodio competitivo. En la actualidad, el profesor Geskus está trabajando en el desarrollo de nuevos métodos, basados en la asignación de pesos, que permiten estimar la subdistribución del riesgo incorporando el truncamiento a la izquierda³³.

En este apartado se han presentado las aproximaciones más utilizadas para el análisis de datos en presencia de riesgos competitivos. Sin embargo, otros autores han propuesto abordajes diferentes basados en seudoobservaciones³⁴.

Análisis de un marcador medido repetidamente en el tiempo

En el estudio de la trayectoria de los marcadores nos enfrentamos fundamentalmente a 2 problemas metodológicos: la variabilidad interindividual e intraindividual en las mediciones de los marcadores (el error en las mediciones de laboratorio y la variación diurna en los niveles del marcador) y la presencia de datos faltantes.

Un procedimiento que se ha utilizado frecuentemente en el estudio de la trayectoria de los marcadores consiste en obtener la tasa de cambio del marcador para cada individuo mediante modelos de regresión convencionales y, posteriormente, utilizar procedimientos estándar para investigar diferencias entre grupos de individuos. Este procedimiento, aunque simple y fácilmente interpretable, pierde validez si el número de observaciones no es el mismo y en los mismos instantes de tiempo para todos los individuos y carece de flexibilidad para modelizar tendencias no lineales.

Los modelos mixtos o modelos de efectos aleatorios son una aproximación alternativa para el estudio de la trayectoria de los marcadores, que permite incorporar la correlación entre mediciones repetidas del marcador en un mismo individuo³⁵. En estos modelos, la tasa de cambio en el marcador de la población (o de un grupo específico de población) se obtiene como una media ponderada de la estimación sujeto-específica con pesos proporcionales a su precisión. Margolick et al³⁶ mediante el modelo de efectos aleatorios más simple (modelo de interceptos aleatorios) mostraron que la concentración de linfocitos CD4 permanece relativamente estable durante todo el curso de la infección por VIH hasta, aproximadamente, entre uno y 5 años antes de la aparición del sida, momento a partir del que comienzan a bajar de forma muy marcada. El modelo de interceptos y pendientes aleatorias es un modelo ligeramente más complejo que el anterior, que permite que cada individuo tenga su propio intercepto y su propia pendiente. Mellors et al¹⁶ con este modelo mostraron la estrecha relación entre la carga viral en un momento determinado y la consiguiente bajada de las células CD4, resultados que se usaron para definir las guías para el uso del tratamiento antirretroviral frente al VIH.

Los modelos de efectos aleatorios proporcionan resultados no sesgados si la ausencia de datos de marcadores es no informativa. Aunque en muchas ocasiones la ausencia de datos de los marcadores no sigue un patrón, en ocasiones la ausencia de datos del marcador se debe a que los individuos que progresan rápidamente no han regresado al hospital porque han muerto y no hemos sido informados. También es posible que sean los que progresan más rápido los que con más frecuencia acuden al hospital y de los que se tiene³⁷ mayor número de medidas del marcador.

En la literatura médica reciente, se han discutido en detalle los sesgos derivados de la censura informativa en el análisis de la trayectoria de los marcadores y se han propuesto métodos de análisis alternativos³⁷. La mayoría de estos métodos propone modelizar conjuntamente la trayectoria del marcador y del tiempo al episodio de interés, bajo el supuesto de que la probabilidad de muerte o de progresión de la enfermedad de un individuo está relacionada con la trayectoria de sus marcadores. Estos métodos combinan un modelo lineal de efectos aleatorios para la trayectoria del marcador con un modelo de supervivencia para el proceso de censura informativa causado por la muerte o la progresión de la enfermedad.

Conclusión

En resumen, en este trabajo se han descrito los principales métodos estadísticos utilizados en el análisis de los datos procedentes de estudios de cohortes y se ha presentado la aplicación de estos métodos a la investigación en VIH y sida. Aunque son numerosos los avances metodológicos que se han producido en las últimas décadas, también son numerosos los retos metodológicos que habrá que afrontar en un futuro en el contexto de la infección por VIH.

Agradecimientos

Este artículo se ha financiado con ayuda de la Red de Investigación en Sida (RIS) (ISCIII RD06/0006). También ha recibido fondos del CIBERESP y del FIPSE (beca 36.491 [A/05]).