Method Effects and Gender Invariance of the Rosenberg Self-esteem Scale: A Study on Adolescents

Abstract

Rosenberg's self-esteem scale has been extensively used in all areas of psychology to assess global self-esteem (Rosenberg, 1965, 1979). Its construct validity, and specifically its factor structure, has almost from the beginning been under debate. More than four decades after its creation the cumulated evidence points that the scale measures a single trait (self-esteem) but confounded by a method factor associated to negatively worded items. The aim of the study is to examine the measurement invariance of the RSES by gender and test potential gender differences at the latent (trait and method) variable level, while controlling for method effects, in a sample of Spanish students. A series of completely a priori structural models were specified, with a standard invariance routine implemented for male and female samples. The results lead to several conclusions. Conclusions: a) the scale seem gender invariant for both trait and method factors; b) there were small but significant differences between males and females in self-esteem, differences that favored male respondents; and c) there were statistically non-significant differences between men and women in the method factor's latent means.

Resumen

La Escala de Autoestima de Rosenberg (EAR) ha sido utilizada extensamente en todas las áreas de la Psicología para evaluar la autoestima (Rosenberg, 1965, 1979). Su validez de constructo, y particularmente su estructura factorial, ha estado en debate casi desde que fue construida. Más de cuatro décadas después de su creación, la evidencia acumulada señala que la escala evalúa un solo rasgo (autoestima), aunque se confunde con un método factorial asociado de manera negative con reactivos verbales. El objetivo de este estudio fue evaluar la estabilidad de la medición de la EAR entre sexos y poner a prueba potenciales diferencias entre los mismos en un nivel latente de la variable (rasgo y estado), controlando efectos de método, en una muestra de estudiantes españoles. Se especificaron una serie de modelos estructurales a priori, con rutinas implementadas de invarianza estándar para muestras de hombres y mujeres. Los resultados llevan a diferentes conclusiones: a) La escala parece ser invariable ante el sexo tanto para factores de rasgo como de estado; b) existieron diferencias pequeñas, pero significativas, entre hombres y mujeres en autoestima, favoreciendo ligeramente a los hombres; y, c) no existieron diferencias estadísticamente significativas entre hombres y mujeres en las medias de la variable latente del factor.

The different studies conducted on self-esteem during last years have highlighted the presence of gender differences, both in global and domain-specific instruments (e. g., Gentile, et al., 2009; Kling, Hyde, Showers, & Buswell, 1999), even though these differences had not been pointed out in major previous reviews (Maccoby & Jacklin, 1974; Wylie, 1979). From the evidence accumulated through studies, the strongest one is the meta-analytical evidence. In a recent meta-analysis dealing with gender differences in domain specific self-esteem, which included 428 effect sizes from 115 scientific papers, men rated significantly higher than women in physical appearance self-esteem (d = 0.35), athletic self-esteem (d = 0.41), personal self-esteem (d = 0.28) and self-satisfaction self-esteem (d = 0.33), whereas women rated higher than men in behavior self-esteem (d = -0.17) and moral-ethical self-esteem (d = -0.38), and no statistically significant gender differences were found for academic, social, familiar, and affective self-esteems (Gentile et al., 2009).

As regards gender differences in global self-esteem instruments, Rosenberg Self-Esteem Scale (RSES; Rosenberg, 1965) is the most widely used scale in this topic (e. g., Kling et al., 1999; Owens & Kling, 2001). In a meta-analysis developed by Kling et al. (1999) about gender differences on global self-esteem measurement, 62% of the effect sizes examined (135 of 218) were based on the RSES. This study showed a small but statistically significant difference between men and women in self-esteem, favoring men (d = 0.22). Nevertheless, the accuracy of the gender differences found in self-esteem, as recently noted by DiStefano and Motl (2009a), heavily rely on the assumption of gender invariance of the measurement instruments, or in this particular case, on the psychometric invariance of the RSES.

Several studies have analyzed the RSES factorial structure, and also its gender invariance (Byrne & Shavelson, 1987; Hoelter, 1983). These authors have assessed to which extent the scale measures the same construct for both sexes, finding the same factorial structure and the same factor loadings in both cases. However, the study of the gender factorial invariance has not considered the method effects associated to negatively worded items, which had systematically been found in the RSES latent structure (e. g., Carmines & Zeller, 1979; Corwyn, 2000; DiStefano & Motl, 2006,2009a; Horan, DiStefano, & Motl, 2003; Marsh, 1996; Marsh, Scalas, & Nagesgast, 2010; Motl & DiStefano, 2002; Quilty, Oakman, & Risko, 2006; Supple, Su, Plunkett, Peterson & Bush, 2013; Tomás & Oliver, 1999; Wang, Siegal, Falck, & Carlson, 2001).

As affirmed by DiStefano and Motl (2009b), the consistent existence of these method effects associated to negatively worded items may have important implications in the study and of factorial invariance of the RSES. For example, a recent study by Supple, Su, Plunkett, Peterson & Bush (2013) evaluated factor structure and method effects associated to negatively worded items of the RSES with samples of European American, Latino, Armenian, and Iranian adolescents. Their findings suggested that method effects in the RSES were more pronounced among ethnic minority adolescents, and they pointed out that accounting for method effects is necessary to avoid biased conclusions regarding cultural differences in self-esteem. In particular, with respect to gender invariance, the chance exists that method effects could well be a cause of mean differences between sexes, if one gender is more likely to present these method effects than the other. To our knowledge DiStefano and Motl (2009b) have been the only authors that have studied gender invariance of the RSES while simultaneously considering method effects in a confirmatory factor analysis framework. Particularly, they studied method effects associated to negatively worded items and the RSES invariance across gender, using a standard invariance routine as recommended in the literature (Cheung & Rensvold, 2002; Finney & Davis, 2003; Vandenberg & Lance, 2000). They found small but significant differences favoring males in self-esteem latent means (d = -.10), but non-significant differences between sexes in the latent method factor means (d = -.10). Vasconcelos-Raposo, Fernandes, Teixeira, and Berlleti (2012) tested the gender invariance of the RSES in Portuguese adolescents, and they found evidence for partial equivalence. However, they only tested equal factor loadings: metric but not scalar invariance.

There is also evidence about the effects of gender on method effects associated to negatively worded items in the RSES that comes from a different framework, Multiple Indicators Multiple Causes (MIMIC) models. For example, DiStefano and Motl (2009a) examined whether responses to negative item phrasing were related to the personality traits and if such relationships differed by sex. They discovered a single personality trait related to negatively item worded for both males and females, the tendency toward risk taking behaviors: the stronger an individual's tendency toward risk taking behavior, the less likely that individual is to endorse a negatively keyed item. They also reported that more personality traits had a significant effect on the method factor in the female sample, such as fear of negative evaluation and private self-consciousness than in the male sample. That is, gender acted as a moderator. In a recent study Tomás, Oliver, Galiana, Sancho and Lila (2013) found, also with MIMIC models, that gender significantly explained method effects associated to negatively worded items in both state and trait self-esteem scales, including the RSES. However, MIMIC models assume rather than test gender invariance, and therefore these results could not hold if gender invariance is not tenable (Thompson & Green, 2006).

The assessment of factors influencing the occurrence of method effects associated to negatively worded items or others, is not trivial, as it is showed by the fact that several researches have showed socio-demographics impact on other type of method bias. For instance, a relation between educative level and the tendency to give extreme responses has repeatedly been reported (Greenleaf, 1992; Marín, Gama, & Marín, 1992; Mirowsky & Ross, 1991), or a relation between gender and acquiescence (Piquero, Macintosh, & Hickman, 2002). Nevertheless, and despite existing data on the socio-demographics impact in some method bias, studies including evidence on the relation between gender and self-esteem, together with evidence on a method factor in self-esteem instruments, specifically in Rosenberg’ self-esteem scale, are very scarce. In this sense, and as it has been done by DiStefano and Motl (2009b), it seems necessary the study of the RSES gender factorial invariance taking into account method effects across populations and languages.

Consequently, the research objective is to study gender factorial invariance in self-esteem and the expected method effect associated to negatively worded items, in Rosenberg’ self-esteem scale in a sample of Spanish adolescents.

Method

Sample

The research design is a survey design of 390 high school and first year university students, all of them from Valencia (Spain). Participants are a convenience sample. Their mean age was 17.8 (SD = 3.69). 43.3% were men (n = 167) and 56.7% women (n = 219). 68.7% were high school students, while the remaining 31.3% were students at the University of Valencia. They university students were freshmen either at the Psychology or Physiotherapy degrees, 50.82 and 49.18%, respectively.

Instruments

The survey included several scales, but for the purpose of this study the only scale used is the Spanish version of the RSES (Rosenberg, 1965, 1979). RSES is a 10-item self-report questionnaire assessing global self-esteem (Rosenberg, 1965). Items scored from 1 to 4 (1= strongly agree, 2= agree, 3= disagree, 4= strongly disagree), and it is thought to represent a single trait factor of global self-esteem (Carmines & Zeller, 1979; Marsh, 1996; Tomás & Oliver, 1999). Five items were negatively worded (numbers 3, 5, 8, 9, and 10).

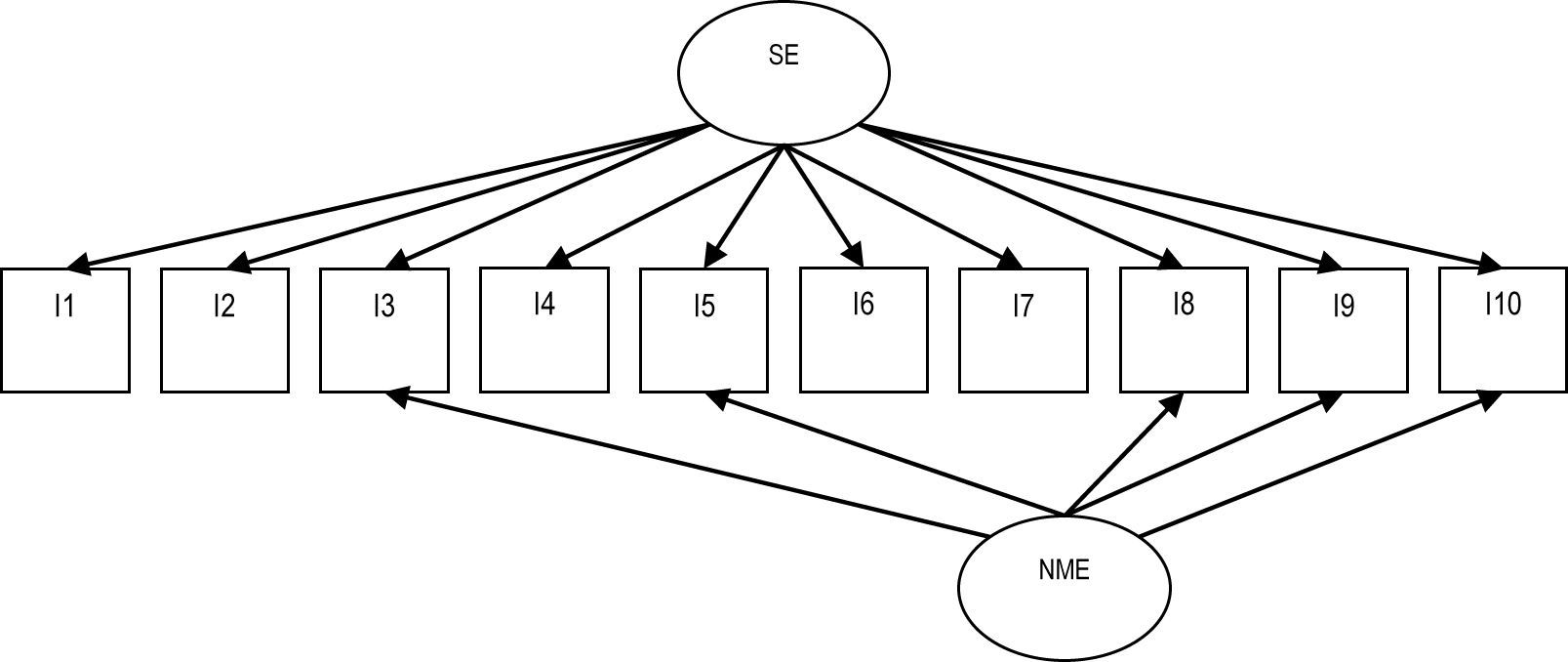
Statistical analyses

A completely a priori confirmatory factor model based on previous research on method effects for the RSES was specified (Tomás & Oliver, 1999; Tomás et al., 2013). The model is presented in Figure 1, and it was tested in a multi-sample invariance routine for women and men. All models were estimated with EQS 6.1 software and the Maximum Likelihood estimator as the fit function, with Satorra- Bentler corrections for the standard errors (Bentler, 1995), given the ordinal nature of the items and the non-normality of the distributions.

Figure 1.

Correlated trait, correlated methods model. Self-esteem and negatively worded items method factors underlying the ten items in the RSES. Note: SE = self-esteem; NME = negative method effects

The equivalence or invariance routine is the standard procedure (Byrne, 2006; Thompson & Green, 2006). This routine comprised a hierarchical set of steps. First, the model in Figure 1 was separately tested in both groups. After the determination of good fit for each group, a configural model was tested simultaneously for both groups and established as the baseline model. This model tests the so called weak factorial invariance. Then, an equality constraint was specified for trait factor loading scores across groups, and this model tested for metric invariance at the trait level. Then, an equality constraint was specified for all (trait and method) factor loadings across groups, this model tested for metric invariance for both trait and method factors. Finally a model with constrained item means tested for scalar invariance or strong factorial invariance.

The plausibility of the models was assessed using several fit criteria (Hu & Bentler, 1999; Tanaka, 1993): (a) chi-square statistic (Kline, 1998; Ullman, 1996); (b) the comparative fit index (CFI; Bentler, 1990) of more than .90 (and, ideally, greater than .95; Hu, & Bentler, 1999); (c) the root mean squared error of approximation (RMSEA) of .08 or less (and, ideally less, than .06) (Hu, & Bentler, 1999); (d) GFI as a measure of proportion of variance-covariance explained for the model, with values of more than .90 as indicative of reasonable fit (Hoyle & Panter, 1995); and (e) the standardized root mean squared residuals (SRMR) of .08 or less (and, ideally less than .05) (Hu & Bentler, 1999). Based on the recommendations of Hu and Bentler (1999), the size of our model and using maximum likelihood estimation, suggests that a CFI of at least .90, a RMSEA less than .06, and a SRMR less than .08, together, would indicate a very good fit between the hypothesized model and the data. The models in the invariance routine are nested. When nested models are compared there are two rationales (Little, 1997), the statistical and the modeling ones. The statistical approach employs χ² differences (Aχ²) to compare constrained to unconstrained models, with non-significant values suggesting multi-group equivalence or invariance. However, this statistical approach has been criticized (Cheung & Rensvold, 2002; Little, 1997) and a modeling approach that uses practical fit indices to determine the overall adequacy of a fitted model has been recommended. From this point of view, if a parsimonious model (such as the ones that posit invariance) evinces adequate levels of practical fit, then the sets of equivalences are considered a reasonable approximation of the data. Usually, this last approach translates into the CFI differences (ACFI), to evaluate measurement invariance. CFI differences lower than .01 (Cheung & Rensvold, 2002) or 0.05 (Little, 1997) are usually employed as cut-off criteria

Results

As a previous step in the equivalence routine, the confirmatory model in figure 1 was separately tested in both samples. The model adequately fitted the data in the female sample: χ² = 54.26, p= .004; CFI = .941; RMSEA = .065 [.036 - .092]; GFI = .925; SrMr = .055. In the same way, the model also fitted well the male sample: χ² = 46.70, p= .026; CFI = .922; RMSEA = .063 [.022 - .096]; GFI = .914; SRMR = .063.

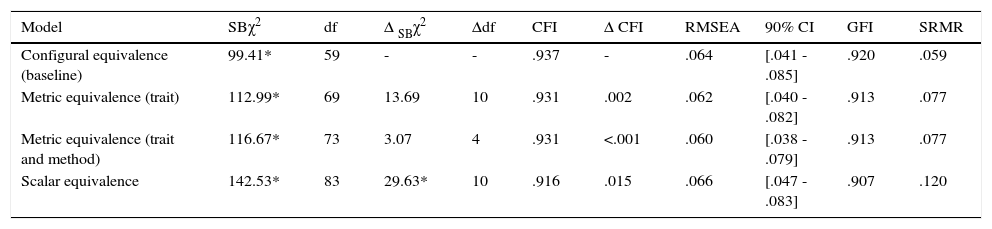
Given that the model fitted well in both samples, the invariance routine already explained was implemented. The fit indices for this hierarchy of models are presented in Table 1. Although all individual chi-square statistics were significant (p< .05), the practical fit indices showed very good model fit in every case. Therefore, a test of factorial invariance by gender seems adequate. With respect to the invariance routine, the comparison of models yielded quite clear results. Metric invariance for trait factor loadings was clear, as both statistical and practical approaches to model comparison agree that there were no statistically significant differences between baseline and metric (trait) invariance models, and therefore the more parsimonious (invariant) model could be retained. Exactly the same result was found when metric invariance of method factor loadings was added to the second model, the chi-square difference was not statistically significant (p > .05) and practical fit indices remained extremely similar or even slightly improved (i.e. the RMSEA). Therefore, according to the results, the RSES could be considered metrically invariant by gender. When intercepts were included in the model and made invariant by gender the chi-square difference was statistically significant (p = .001), but differences in practical fit were minimum and the most parsimonious model (scalar invariance) showed adequate levels of practical fit, and consequently the sets of equivalences are considered tenable.

Table 1.

Tests of equivalence between males and females.

Model	SBχ^2	df	Δ SBχ^2	Δdf	CFI	Δ CFI	RMSEA	90% CI	GFI	SRMR
Configural equivalence (baseline)	99.41*	59	-	-	.937	-	.064	[.041 - .085]	.920	.059
Metric equivalence (trait)	112.99*	69	13.69	10	.931	.002	.062	[.040 - .082]	.913	.077
Metric equivalence (trait and method)	116.67*	73	3.07	4	.931	<.001	.060	[.038 - .079]	.913	.077
Scalar equivalence	142.53*	83	29.63*	10	.916	.015	.066	[.047 - .083]	.907	.120

Notes: * = p< .05; _Sbχ2 = Satorra-Bentler chi-square; df = degrees of freedom; □□= differences.

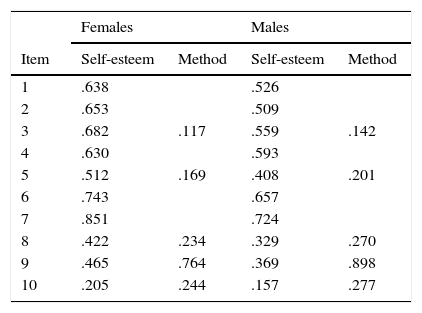
The standardized factor loadings in the retained model are presented in Table 2. Once the strong invariance was established the latent means differences could be investigated. The latent mean values were fixed to zero in the female group and freely estimated in the male group. Estimated latent mean values showed that males had higher self-esteem than females (Mean difference = 3.975, z = 2.28, p < .05, d = .28). However, latent mean differences in method effects were not statistically significant (Mean difference = -.027, z = .084, p > .05, d = .21).

Table 2.

Standardized factor loadings from the retained invariance model between females and males for self-esteem and negative method factors of the Rosenberg Self- Esteem Scale.

Item	Females		Males
	Self-esteem	Method	Self-esteem	Method
1	.638		.526
2	.653		.509
3	.682	.117	.559	.142
4	.630		.593
5	.512	.169	.408	.201
6	.743		.657
7	.851		.724
8	.422	.234	.329	.270
9	.465	.764	.369	.898
10	.205	.244	.157	.277

Discussion and conclusions

The aim was to study gender factorial invariance in self-esteem and the expected method effect associated to negatively worded items, in Rosenberg’ self - esteem scale in a sample of Spanish adolescents. The results were quite clear and similar to those found in other versions of the scale. With respect to the presence of method effects, once again method effects associated to negatively worded items were found and they explain a relevant part of the variance in the self-esteem items. This is a very well established result across languages and populations (Corwyn, 2000; DiStefano & Motl, 2006, 2009a, 2009b; Greenberger, Chen, Dmitrieva & Farrugia, 2003;Horan, et al., 2003; Marsh, 1996; Motl & DiStefano, 2002; Quilty, Oakman & Risko 2006; Tomás & Oliver, 1999; Tomás et al., 2013; Supple et al., 2013; Vasconcelos-Raposo et al., 2012; Wang et al., 2001).

With respect to the equivalence of the RSES by gender, the results showed evidence of strong factorial invariance. Both metric and scalar invariance could be maintained, and for both self-esteem and method factors. To our knowledge, the study by DiStefano and Motl (2009b) is the only one that has tested gender invariance of the method effect associated to negatively worded items, and they had a similar result: gender had not an effect on the method factor. However, their data showed evidence of partial invariance for the trait (self-esteem) factor. The absence of gender effect on method factors found in these two studies of gender invariance are not completely general. At least two other studies found some effect of sex on method effects associated to negatively worded items, either a direct (Tomás et al., 2013) or a moderator effect (DiStefano & Motl, 2009a). However, these last two studies used MIMIC models and not a measurement invariance routine.

There were statistically significant latent mean differences in self-esteem. These differences are very much alike to the ones found by DiStefano and Motl (2009b), d= .28 in the current study vs. d= .207, favoring males. However, the effect size may be considered low, especially considering the latent nature of the comparison. These effects sizes are also in line with existing meta-analytical results based mostly on studies using the RSES (Kling et al., 1999).

Nevertheless, further research on gender invariance of self-esteem for different populations and languages is needed, as most of the studies on gender invariance of self-esteem have not considered the presence of method effects associated to negatively worded items.