Inventory of Interpersonal Problems–Personality Disorders: adaptation to Brazil and test of a bifactor model

Abstract

Objective

The Inventory of Interpersonal Problems–Personality Disorders (IIP-PD-47) has a controversial factor structure, as some studies have provided support for 5 correlated factors, and others have suggested the existence of a general second-order dimension. One approach of data modelling that reconciles multidimensionality and the existence of a general factor is the bifactor analysis. We used unrestricted exploratory-confirmatory bifactor modelling to validate the Brazilian version of the IIP-PD-47.

Methods

The sample consisted of 1,091 subjects aged 18-64 years who answered the IIP-PD-47 and a collateral measure of pathological traits, the Dimensional Clinical Personality Inventory 2 (IDCP-2).

Results

After testing many candidate models, our data were best represented by a bifactor model with one general factor and five specific uncorrelated factors. Nevertheless, a closer inspection of the discriminant validity of each IIP-PD-47 factor revealed strong support for the general factor and a factor capturing aggressive behaviours, but less support for the additional four specific factors.

Conclusions

The theoretical and practical implications of these findings are discussed, and some recommendations are offered about the need for controlling response styles when assessing PD traits via self-report inventories. Our findings indicate that the Brazilian version of IIP-PD has promising psychometric properties.

Resumen

Objetivo

El Inventario de Problemas Interpersonales-Trastornos de la Personalidad (IIP-PD-47) tiene una estructura factorial controvertida, ya que algunos estudios han apoyado 5 factores correlacionados y otros han señalado la existencia de una dimensión general de segundo orden. Un enfoque del modelado de datos que concilia la multidimensionalidad y la existencia de un factor general es el análisis de bifactores. Para validar la versión brasileña del IIP-PD-47, se utilizó un modelo bifactorial confirmatorio exploratorio sin restricciones.

Métodos

La muestra incluyó a 1.091 sujetos de 18 a 64 años que respondieron al IIP-PD-47 y una medida colateral de rasgos patológicos, el Inventario de Personalidad Clínica Dimensional 2 (IDCP-2).

Resultados

Después de probar muchos modelos candidatos, nuestros datos se representaron mejor mediante un modelo bifactorial con 1 factor general y 5 factores específicos no correlacionados. Sin embargo, una inspección más cercana de la validez discriminante de cada factor IIP-PD-47 reveló un fuerte respaldo del factor general y un factor que capta comportamientos agresivos, pero menos respaldo a los 4 factores específicos adicionales.

Conclusiones

Se discuten las implicaciones teóricas y prácticas de estos hallazgos y se ofrecen algunas recomendaciones sobre la necesidad de controlar los estilos de respuesta al evaluar los rasgos de la EP a través de inventarios de autoaplicados. Nuestros hallazgos indican que la versión brasileña de IIP-PD tiene propiedades psicométricas prometedoras.

Introduction

Personality disorders (PDs) are characterized by persistent and maladaptive patterns of feelings, thoughts, and behaviors that deviate significantly from the expected societal norms.^1,2 These disorders have a prevalence rate of 10% in Western countries,^3–5 although the estimates are much higher (10-20%) among individuals in treatment in primary healthcare or who have any diagnosed psychiatric disorders.^6–10 Assessment of PDs is essential because these conditions might hinder compliance with treatment, then rendering a worse prognosis and higher mortality.^11–16

Self-report measures represent the best screening approach for the assessment of PDs.^17,18 These instruments afford a reduction in costs and a faster assessment of patients, the reason why they are appropriate for use in diverse scenarios, especially in public services.^17,19 PDs are commonly underdiagnosed, especially because mental health professionals are less familiar with these conditions.^3,16,20 Therefore, the availability of validated screening tools for clinicians and practitioners is of tantamount utility for the correct identification of patients with PDs.

One of the widely used inventories for the screening of PDs is the Inventory of Interpersonal Problems-Personality Disorder scales (IIP-PD-47).²¹ The IIP-PD-47 was developed in the United States, based on the longer Inventory of Interpersonal Problems with 127 items.²² The IIP-PD-47 contains 28 items found to be discriminative of having any PDs versus not having PDs, plus 19 additional items that are sensitive in the screening of individuals with Cluster C PDs. Pilkonis²¹ reported the results of a factor analysis that indicated a five correlated factors structure for the total 47 items measure: interpersonal sensitivity, interpersonal ambivalence, aggression, need for social approval, and lack of social skills. Kim et al.²³ also found evidence supporting the unidimensionality of each of the five subscales of the instrument.

Later et al.²⁴ tested other candidate factor models using confirmatory factor analysis, and they found support for a hierarchical model with one second-order factor accounting for the correlations between the original five factors. The same hierarchical model was replicated in a study using nonclinical data.²⁵ The existence of an overarching factor lends support for the use of a cutoff performed on a total score calculated by summing all item responses of a given subject. This total score proved both specific and sensitive in detecting individuals who do exceed established DSM thresholds.^23,25,26

Bifactor models

One approach of data modeling that reconciles multidimensionality and the existence of a general factor is the bifactor analysis. In bifactor models, each item is free to simultaneously load on a general (and orthogonal) factor and one or more specific factors.²⁷ As reported elsewhere (e.g., Sharp et al.²⁸), personality pathology can be adequately represented in a bifactor structure containing a general factor called “g,” and content factors called “s.” Although previous studies have already identified the existence of a general factor in the IIP-PD-47, the strategy employed was rather a hierarchical structure where the first-order factors were allowed to load on a broad, second-order trait (e.g., Kim et al.²⁴, and Stern et al.²⁵). Contrasting with a hierarchical factor model, a bifactor analysis provides researchers with the direct loading estimates of each item on the general factor. This information is useful because it affords the identification of the most discriminative items for this broad PD component, which can guide, for example, further studies of item selection to compose an even abbreviated version of the instrument. Hence, testing the plausibility of a bifactor model for the IIP-PD would represent a potential contribution to the field.

Restricted versus unrestricted factor models

Standard confirmatory factor models (CFA) often have their items connected to only one trait factor, and the cross-loadings on the remaining factors constrained to zero.²⁹ This specification is consistent with the ideal “simple structure,” a concept delineated by Thurstone (1940) in the context of exploratory factor analysis to characterize a solution where each item loads maximally on one factor, and the closest possible to zero on the remaining factors. Albeit restricted CFA models are optimal ways of operationalizing Thurstone's simple structure concept, they might not be reasonable to real data. As evidence suggests, restricted CFA models of personality traits will tend to produce a rather poor fit to the data.^30,31 This happens because, even if small and close to zero, existing cross-loadings that are treated as non-different from zero will lastly degrade model fit.³² As all the previous studies compared the IIP-PD-47 CFA models under the standard restricted specification, a further contribution would be testing restricted versus unrestricted versions of each competing model reported. This could be achieved by using Exploratory Structural Equation Modeling (ESEM),³³ a strategy we implement in the current investigation.

Adapting instruments to other cultures

Adapting instruments into other cultures is essential for many reasons. The lack of psychometrically sound screening measures of PDs poses a challenge to the field of personality assessment in developing countries, such as Brazil.¹⁹ Once introduced in a new culture, adapted instruments can inspire further studies on a given subject and afford cross-cultural comparisons. The IIP-PD has been adapted to other cultures, including Italy,³⁴ Korea,³⁵ and Spain.³⁶ In these studies, the IIP-PD factor structure was best represented by 5 factors plus a general, second-order factor of personality pathology. However, so far, no adapted versions of the instrument were found for Latin American countries, which represents a significant gap in the field. Data from non-rich countries are necessary because a large variability in many psychological traits is found when results obtained from different cultures are compared.³⁷ Having the IIP-PD adapted into Brazilian Portuguese would afford the collection of prevalence estimates in the general population in Brazil and maybe other countries and, thereafter, more precise cross-cultural comparisons.

The current study

The primary purpose of this study was to investigate the factor structure of a Brazilian version of the IIP-PD-47, testing the relative fit of a series of candidate factor models —restricted and unrestricted— including a bifactor structure. Besides, we also tested the relationships of the newly adapted instrument with a collateral measure of pathological personality traits, namely, the Dimensional Clinical Personality Inventory 2 (IDCP-2).^38,39 We hypothesized that:

H1: A bifactor model would provide the best representation for the structure of the IIP-PD-47, with items explained by a general factor plus the five content factors reported by Pilkonis.²¹

H2: Unrestricted models that allow the existence of item cross-loadings would yield a better fit to the data when compared to their restricted counterparts.

H3: Each IIP-PD-47 factor would prove uniquely associated with the pathological dimensions measured by the IDCP-2: distrust in relationships, self-devaluation, fear of abandonment, vulnerability, individualism, irritable mistrust, antagonism, violence, impulsivity, masochism, submissiveness, social isolation, and general avoidance.

In regard to this last hypothesis, we expected the discriminant validity of each IIP-PD-47 factor to be represented by partial associations with the IDCP-2 factors even when the influence of the remaining IIP-PD-47 is taken into account.

Methods

Participants

Using a cross-sectional design, we recruited a convenience sample from the community sample. The total number of participants was 1091 adults, mostly white (69.5%), female (71.1%), single (61.9%), and graduate students (42.7%; undergraduate students comprised 41.7% of the sample). Participants’ age ranged from 18 to 64 years old (27.39 ± 9.08), with 38.3% reported having participated in psychotherapy, and 14.5% reported having received psychiatric treatment.

Instruments

Inventory of Interpersonal Problems Personality Disorders -47 (IIP-PD-47; Pilkonis²¹)

The IIP-PD-47 is a self-report measure comprised of 47 items on a 5-point Likert scale where 0 is “Not at All” and 4 is “Extremely”. The items are organized into 5 scales: Interpersonal Sensitivity (PD1), Interpersonal Ambivalence (PD2), Aggression (PD3), Need for Social Approval (C1), and Lack of Sociability (C2). Previous studies suggest this tool has sound psychometric properties as a screening measure of PDs.^23,26

Dimensional Clinical Personality Inventory 2 (IDCP-2; Carvalho et al.³⁹)

The IDCP-2 is a self-report measure that assesses pathological traits. It is composed of 206 items answered on a 5-point Likert scale where 0 is “I do not relate at all,” and 4 is “I relate to this a lot.” The IDCP-2 encompasses 12 dimensions that are divided into 47 factors. Many studies support the psychometric properties of this measure.^41–44

Procedure

A Brazilian Research Ethics Committee approved this study. The procedures of translation and cultural adaptation followed guidelines that are specific to mental health assessment tools.⁴⁵ The items and instructions of the IIP-PD were translated and back-translated by the authors of this study, and the author approved the back-translation of the original version of the instrument (P. Pilkonis). Data collection was done online via Google Forms. The link inviting individuals to participate in the study was shared on the social media website Facebook, as well as by e-mail, using the snowball strategy to reach a larger number of participants.

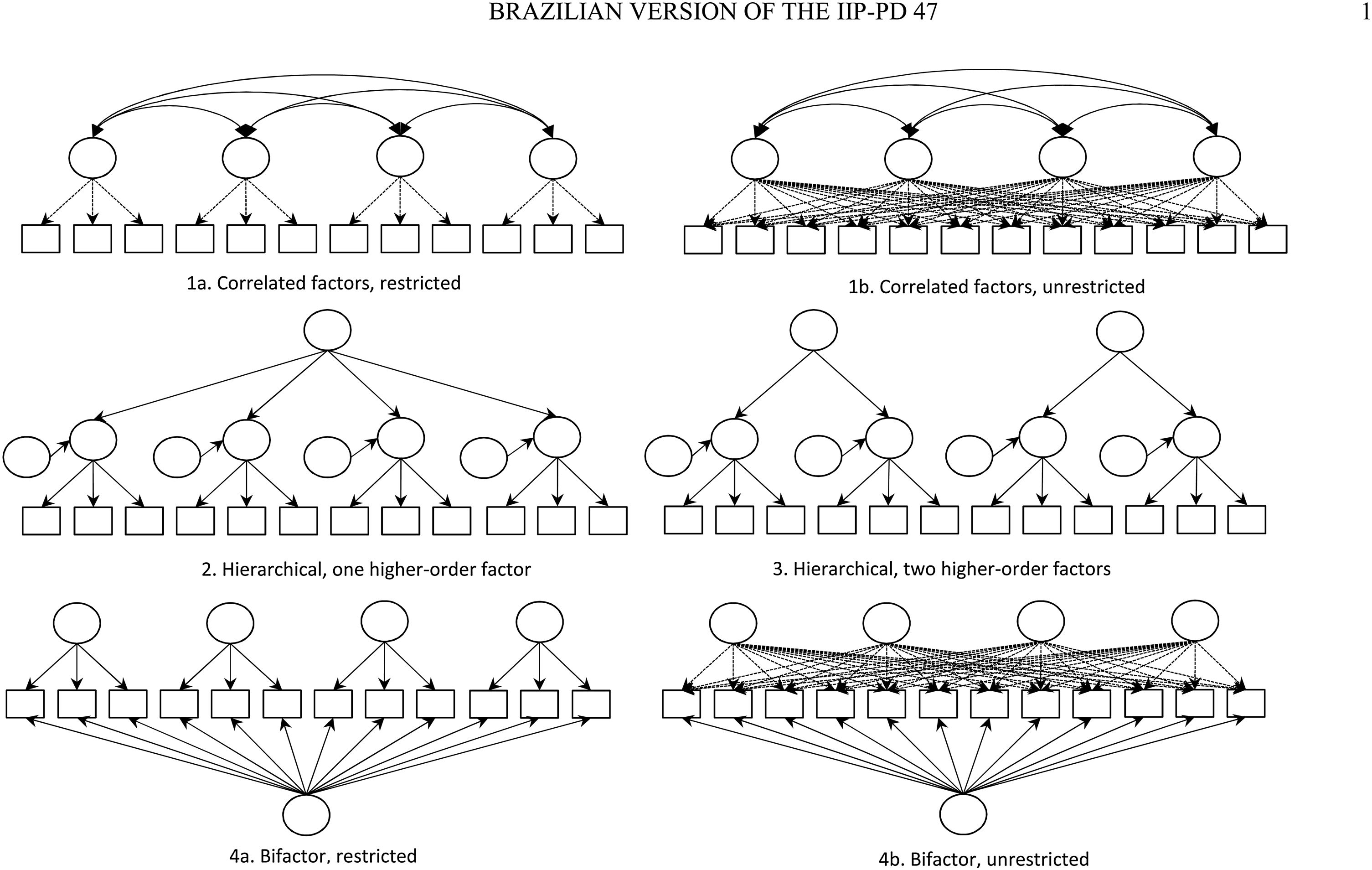
Data analysis

We conducted data analysis using Mplus version 7.11 and the Statistical Package for the Social Sciences (SPSS) version 20. We tested the fit of 4 distinct model possibilities: a) 5 correlated factors (restricted and unrestricted); b) 5 factors plus one second-order factor (hierarchical); c) 5 factors plus 2 second-order factors (hierarchical), namely, internalization (connected to need for social approval, and lack of social skills), and externalization (connected to interpersonal sensitivity, interpersonal ambivalence, aggression), and d) one general factor plus 5 specific factors (bifactor), all of them uncorrelated (restricted and unrestricted). Figure 1 presents a simplified diagram of each of these models (for the sake of simplicity, model diagrams contain only 4 factors and 3 items per factor). As illustrated, models 1 and 4 were tested under 2 modeling perspectives: restricted CFA with no cross-loadings allowed, and unrestricted ESEM, with items allowed to cross-load on the distinct factors in the model. We compared the plausibility of the competing models using the following fit indices: χ²/df ratio (< 2), Confirmatory Fit Index (CFI) > .90, Tucker-Lewis Index (TLI) >.90, and Root Mean Square Error of Approximation (RMSEA) < .05).⁴⁶

Figure 1.

Simplified diagram representations of the concurrent models.

To aid in the interpretation of the factors obtained via ESEM, a factor congruence analysis was carried out using the psych package.⁴⁷ To do so, we constructed a binary target matrix (items in rows, factors in columns), where every item had a “1” score on its expected factor and “0” on the remaining factors. The congruence of the obtained factor loadings from the ESE Models with this target matrix was then estimated. Values closer to 1 indicate the empirical factor loadings match the expected loadings defined theoretically. Reliability analysis of the resulting scales was conducted using the omega coefficient, which measures the amount of variance attributable to general and specific factor components from a bifactor solution. Finally, the partial associations between the IIP-PD and the IDCP-2 factors were tested using Structural Equation Modeling.

Results

In the first step, we tested the relative fit of our candidate models, with results described in Table 1. As expected, unrestricted factor models yielded a better fit to the data when contrasted to their standard restricted CFA correspondents. Both the unrestricted 5-factor model and the unrestricted bifactor models achieved a reasonable fit. Factor correlations for model 1b were all positive and moderate in size (from r = .32 to r = .42), while factors from the bifactor model were all orthogonal to each other. As these models are not nested, they cannot be directly compared in their fit indices or by using a DIFF test, the reason why we decided to inspect the theoretical coherence of the resulting factor loadings produced by each model. The factor loadings yielded by the two best-fitting models can be found in Table 2, where the first column contains the theoretical allocation of items according to the original structure described by Pilkonis et al.²¹

Table 1.

Model fit information.

Model	χ^2	df	χ^2/df	RMSEA	CFI	TLI
Model 1a. Five correlated factors, restricted	4696.77	1024	4.59	.079	.849	.841
Model 1b. Five correlated factors, unrestricted	1826.41	856	2.13	.044	.960	.950
Model 2. One second-order factor, restricted	4956.14	1029	4.82	.081	.839	.830
Model 3. Two second-order factors, restricted	4954.90	1028	4.82	.081	.839	.830
Model 4a. Bifactor, restricted	3921.95	984	3.99	.072	.879	.867
Model 4b. Bifactor, unrestricted	1612.13	814	1.98	.041	.967	.956

Table 2.

Estimates from the best fitting models.

Item	Original factor	Model 1b					Model 4b
		F1	F2	F3	F4	F5	FG	F1	F2	F3	F4	F5
i1*	IS	.38	.25	.14	−.14	.07	.35	.33	.26	.03	.10	.07
i2	NSA	.08	.10	−.22	.44	.16	.37	.05	−.07	−.23	−.30	.02
i3	LS	.82	−.02	.03	−.04	.08	.43	.69	.04	.03	−.01	.03
i4	LS	.80	.01	.00	−.04	.13	.43	.70	.08	−.09	−.02	.00
i5	NSA	.54	.17	−.05	.15	.07	.53	.43	.09	.02	−.11	.09
i6*	IA	.17	.54	.09	−.04	.00	.48	.11	.41	.13	.04	.05
i7*	IA	.02	.84	.00	.03	−.01	.60	.00	.63	.04	−.02	−.10
i8	NSA	.38	.25	−.09	.27	−.04	.56	.24	.09	.12	−.16	.02
i9	LS	.94	−.09	.08	.02	.02	.54	.76	−.04	.11	.02	.01
i10	LS	.90	−.08	−.01	.08	−.14	.52	.70	−.06	.24	−.03	−.06
i11	LS	.57	.11	−.11	.09	.07	.41	.49	.10	−.08	−.12	−.02
i12*	IA	.72	.10	.00	−.02	−.48	.42	.48	.07	.61	.03	−.02
i13*	IA	.66	.16	.08	−.14	−.48	.37	.44	.16	.64	.11	.01
i14*	IA	−.02	.40	.04	.02	.18	.31	−.01	.29	−.10	−.03	.15
i15	LS	.30	.21	−.05	.39	−.05	.61	.18	.02	.10	−.15	.04
i16*	IA	−.09	.92	.02	−.05	.03	.53	−.09	.69	.05	−.01	−.03
i17*	IS	.06	.32	−.05	.39	.24	.57	.01	.08	−.16	−.20	.19
i18*	IS	−.03	.30	.05	.31	.13	.50	−.08	.09	−.04	−.09	.14
i19*	IA	.14	.45	.10	.01	−.07	.45	.04	.31	.27	.02	.14
i20*	IA	.15	.67	.06	.10	−.19	.64	.02	.44	.34	.00	−.04
i21*	IA	.70	.07	.05	.09	−.40	.52	.45	.00	.56	.02	−.01
i22*	IS	.09	.20	.07	.21	.22	.43	.00	.01	.03	−.10	.31
i23	LS	.65	−.04	−.05	.25	−.08	.53	.50	−.09	.10	−.09	−.05
i24	NSA	.14	.18	−.07	.25	.27	.39	.08	.00	−.11	−.21	.28
i25	LS	.59	−.04	−.02	.34	.08	.60	.45	−.13	−.03	−.12	.07
i26*	AG	.04	.00	.85	.01	.13	.59	−.02	−.02	.10	.59	.23
i27*	IS	−.04	.03	.26	.58	.40	.70	−.13	−.24	−.18	−.05	.32
i28*	AG	.09	.06	.74	.01	.39	.60	.02	−.01	−.02	.42	.44
i29*	IS	−.03	.05	.36	.57	.35	.77	−.12	−.22	−.16	.05	.27
i30*	AG	.05	−.05	.88	−.04	−.02	.52	.04	.01	.07	.69	.07
i31	NSA	.01	−.03	−.01	.72	−.01	.62	−.11	−.30	.01	−.17	−.03
i32*	IS	.07	.14	.32	.39	−.04	.68	.03	.02	−.08	.19	−.14
i33*	AG	−.09	.13	.62	.18	−.04	.59	−.10	.06	.03	.44	−.02
i34	NSA	−.01	.01	.29	.56	.02	.69	−.05	−.15	−.18	.13	−.14
i35	LS	.24	.00	.23	.44	−.04	.67	.16	−.11	−.07	.11	−.15
i36	NSA	.05	−.02	.12	.76	.07	.77	−.06	−.30	−.08	−.00	−.01
i37	NSA	.10	−.07	.11	.68	−.04	.68	.00	−.28	−.05	−.05	−.11
i38	NSA	.03	−.05	.00	.71	.09	.62	−.07	−.32	−.07	−.18	.04
i39*	AG	.06	.02	.83	−.11	.32	.50	.02	.02	−.00	.54	.38
i40*	IS	−.17	.00	.26	.46	−.04	.49	−.23	−.18	.06	.11	−.02
i41*	IS	−.02	.25	.44	.26	−.05	.67	−.04	.14	−.02	.31	−.11
i42*	AG	−.04	−.05	.88	.05	−.07	.54	−.03	.01	.01	.71	−.05
i43*	IS	.03	−.09	.64	.25	.02	.59	−.01	−.13	−.02	.44	.01
i44*	IA	−.04	.11	.52	.25	−.13	.59	−.07	.04	.03	.40	−.18
i45	LS	.27	−.07	.19	.32	.19	.53	.23	−.13	−.26	.06	−.01
i46*	IS	.02	.14	.20	.45	−.05	.63	−.04	−.03	−.02	.08	−.13
i47*	AG	.09	.10	.50	.13	−.15	.54	.03	.06	.15	.39	−.10

AG: aggression; IA: interpersonal ambivalence; IS: interpersonal sensitivity; LS: lack of sociability; NSA: need for social approval.

*

Items included in a briefer version of the IIP PD.

Despite the goodness of fit, both models yielded factor loading patterns somewhat different than reported in the Pilkonis’ studies. Except for the general factor from the bifactor structure (one whith all items loaded consistently as expected for a scale that admits a general sum score), factors F1 to F5 from both models were only moderately consistent with the factor structure proposed by Pilkonis et al.²¹ To aid in this interpretation, we also conducted a congruence analysis of each factor solution with the 5 original IIP-PD-47 five factors. The results can be found in Table 3. Three aspects seem to confirm our qualitative evaluation of the obtained loadings described in Table 2. Namely, in each solution: a) no empirical factors matched the theoretical IS factor; b) occurrences existed in which distinct empirical factors were congruent with the same theoretical factor (in the 5-factor model, F2 and F5 had their highest coefficients for IA; in the bifactor model, F2 and F3 were both congruent with IA, and F4 and F5 were more consistent with AG); and c) no congruence coefficient achieved the minimum threshold of .90.

Table 3.

Factor congruence for the five-factor and the bifactor models.

	Five correlated factors					Bifactor
	F1	F2	F3	F4	F5	FG	F1	F2	F3	F4	F5
IS	.04	.26	.34	.49	.29	.50	−.04	−.04	−.13	.14	.26
IA	.29	.67	.12	.04	−.40	.39	.21	.59	.62	.10	−.03
AG	.03	.04	.83	.04	.17	.38	−.01	.03	.10	.82	.35
NSA	.17	.10	.01	.66	.15	.46	.08	−.28	−.15	−.22	.05

AG: aggression; IA: interpersonal ambivalence; IS: interpersonal sensitivity; NSA: need for social approval.

Taken together, the findings from the factor analysis support the existence of a general factor, but not the replicability of the originally proposed 5 correlated factors structure. On the one hand, the hierarchical omega coefficient, which measures the amount of common variance attributable to the general factor, was .66. This supports the existence of an overarching factor in the IIP-PD. On the other hand, omega total, which considers the variance from both the general factor and the (5) specific factors from the IIP-PD, was .96. Hence, the specific IIP-PD factors apparently add information to the item scores beyond the general factor. Accordingly, in the next step, we compared the external validity of the general factor against the five specific factors in structural equation modeling. We investigated the magnitude of the association of the general factor with the personality pathology factors from the IDCP. Moreover, we investigated the incremental validity of the IIP-PD specific factors over the general factor by looking at the magnitude and the statistical significance of their unique associations with the external personality pathology factors. Following one reviewer's recommendations, we also conducted regression analyses using the original IIP-PD-47 5-factor structure to predict the IDCP pathological traits. In all these alternative regression analyses, the obtained R² was smaller than reported here on Table 4, what also adds support to our bifactor model as a better representation of the IIP-PD-47 factor structure. The table containing these additional analyses is available as supplementary material.

Table 4.

Explained variance and standardized coefficients for the IIP-PD-47 predicting the IDCP-2 scores using the bifactor structure of the IIP-PD.

IDCP-2 factors	R^2	IIP-PD
		GF	F1	F2	F3	F4	F5
Distrust in relationships	.46	.59*	.18*	.13*	−.05	.20*	.13*
Self-devaluation	.61	.65*	.20	−.11	−.18*	.16*	−.27*
Fear of abandonment	.44	.63*	−.10	−.14	.05	−.03	−.10*
Vulnerability	.63	.63*	.00	.12	−.19	.41*	−.09
Individualism	.45	.56*	.09	.29*	−.10	.17*	−.11
Irritable mistrust	.51	.47*	.06	.08	−.03	.52*	.06
Antagonism	.60	.42*	.04	.11	.03	.62*	−.14
Violence	.60	.58*	−.03	.02	−.12*	.49*	.03
Impulsivity	.40	.50*	−.05	.11	.16*	.27*	−.20*
Masochism	.46	.64*	−.04	−.20	−.03	−.03	−.04
Submissiveness	.30	.47*	−.08	−.22	.16	−.06	−.03
Social isolation	.28	.32*	.29*	.20*	−.06	.18*	−.09
General avoidance	.69	.71*	.34*	−.02	−.19	−.10	−.16

GF: general factor.

The IIP-PD-47 factors were able to explain 28% up to 69% of the variance in the IDCP-2 factors, which confirms that these 2 instruments assess similar constructs. However, as seen in Table 4, in most cases, the amount of explained variance is largely due to the IIP-PD-47 general factor, with very few significant standardized coefficients yielded for the specific factors. Despite some isolated contributions, the only specific IIP-PD-47 factor that was consistently and uniquely associated with the IDCP-2 factors was F4. This factor, which captured the common variance mainly among aggression items (Table 2), was moderate to highly associated with the IDCP-2 measures of vulnerability, irritable mistrust, antagonism, and violence.

Discussion

The focus of this study was on IIP-PD-47, one of the most widely used inventories for the screening of PDs. Our 3 hypotheses were partially corroborated. First, as expected, a bifactor model with a general factor and 5 specific orthogonal factors provided the best fit to the data. This not only confirms the multi-causality and complexity of PD traits but also lends further support for the existence of a general PD factor, as found elsewhere.²⁸ As seen in Table 2, all items loaded consistently on a general PD factor, something that is necessary to support the use of the scale as a total sum score.^24,26 Factor loadings on this general factor ranged from small (.31) to large (.77). This means that, even if each item was written to capture a specific trait content, they also contain information about this general PD factor, which represents the common variance across items. Additionally, shared variance across items might not only capture a general PD factor, but can also explain the comorbidity frequently observed in PD.^1,5,7,10 The usefulness of the loadings reported in Table 2 transcends the purpose of the current study, as they can guide the selection of an abbreviated IPP-PD version. One could, for instance, test the sensitivity and the specificity of a short version composed of the items with the highest factor loadings on the general factor, while also keeping a balanced number of behavioral representations of each theoretical dimension.

Nevertheless, we should also stress that the interpretability of this bifactor structure was only partially consistent with the originally proposed five correlated factors reported by Pilkonis et al.²¹ For instance, both the specific factors F1 and F3 proved congruent with the original interpersonal ambivalence factor, and both F4 and F5 were congruent with the original aggression factor. However, previous factor structure evidence is also controversial. So far, four studies tested the IIP-PD-47 structure, two of them conducted in North American samples,^24,25 one in Europe (Italy),³⁴ and another in Asia (Korea).³⁵ Although the 4 studies replicated the original 5-factor structure²¹, a general second-order factor was required to achieve a good fit to the data in those studies performed with non-US populations. These findings seem to suggest structural instabilities in the IIP-PD-47, an issue that would require cross-cultural comparisons to inspect the possibility of differential item functioning in at least some items.

The second main finding was that, as anticipated, including cross-loadings in the IIP-PD-47 factor structure increased model fit. Even though the IIP-PD-47 apparently consists of largely unidimensional indicators of PD traits, cross-loadings were non-zero in both the 5 correlated factors and the bifactor model. As reported in the study of van Prooijen et al.,³² cross-loadings as small as .20 can deprecate fit if they are not properly modeled. This exemplifies how ESEM models are best suited for personality traits, as they do not impose implausible constraints on the data, then avoiding treating the items as “pure” unidimensional indicators. Based on our findings, we recommend exploratory-confirmatory factor models as the best modeling approach to the study of the structure of pathological traits.

The third main result in our study concerns the discriminant validity of the factors we found. Our findings are mixed in a sense they largely provide evidence that the IIP-PD-47 is predominantly unidimensional, but also indicates that at least one specific factor provides incremental information over the general factor. More specifically, F4 in our bifactor model, which accounted mostly for the items capturing aggressive behaviors, was uniquely associated with the IDCP-2 factors even after controlling for the general IIP-PD-47 factor. Accordingly, this indicates that an aggression factor should be taken into consideration for clinical purposes, as it offers psychometric information not contained in the general factor (i.e., the total sum score). The correlates of this F4 factor (vulnerability, irritability, antagonism, and violence) suggest it can be especially useful for screening Cluster B PDs (antisocial, borderline, narcissistic, and histrionic). Hence, correlational studies using the IIP-PD-47 should also consider the benefits of bifactor models, which are capable of decomposing general and specific trait components that are relevant for the assessment of PDs. Nevertheless, in what concerns the remaining 4 specific factors, we did not find any consistent patterns of external associations that would merit computing additional subscale scores. In brief, the current study supports the use of the IIP-PD-47 as a unidimensional scale, with some evidence also for computing the score for an aggression subscale.

Of course, our conclusions must be weighted by some limitations. It is not rare that self-report data of personality traits, particularly comprising items with undesirable content, will also capture response styles. As repeatedly demonstrated, an instrument composed of items with negative valence and pejorative statements will tend to elicit social desirability, which might appear in the form of a general factor.^48-50 We are not suggesting that the general IIP-PD-47 factor we found is entirely social desirability, but we cannot discard the possibility that it captures both a trait and a social desirability component. This issue should receive a closer inspection from further studies. Moreover, acquiescence or the tendency to agree more than disagree⁵¹ is another systematic variance component that merits attention. Acquiescence adds systematic nuisance variance to the data, which might distort factor structure, internal consistency, and external associations of a self-report instrument.⁵² Further studies should consider using multidimensional models for the control of response styles, then partialling out trait and artifact variance for a better understanding of the structure of PD dimensions.⁵³

Despite these limitations, the current study suggests that the Brazilian version of the IIP-PD-47 is psychometrically sound and that it can be useful in many research and applied settings of personality assessment and screening.

Conflict of interests

We declare that there are no conflicts of interests.