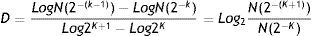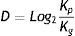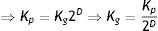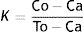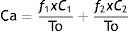To confirm the applicability of an exponential mathematical law based on dynamic systems in the evaluation of cardiac dynamics, reducing the time of evaluation from 21 to 16h, as has been achieved in the area of cardiology by developing innovative diagnostic methodologies that allow us to establish differences between normal and pathological cardiac dynamics.
Material and methodsStarting from 180 ambulatory and continuous electrocardiographic records between normal and pathological patients, a heart rate sequence was simulated for 16 and 21h with values of heart rate and beats per hour of each record, to construct the attractor of each dynamic. Later, the fractal dimension of each attractor and its occupation in the generalized space of Box-Counting was calculated. Finally, the mathematical diagnosis was determined at 16 and 21h and sensitivity, specificity and Kappa coefficient were calculated respectively to the conventional diagnostic taken as the gold standard.
ResultsIt was possible to establish that the values between 206 and 349 for the Kp grid were associated with normal diagnoses, while values between 36 and 194 were related to disease in 16h. Sensitivity and specificity were 100%, and the Kappa coefficient was 1.
ConclusionThe application of the exponential mathematical law to electrocardiographic registers in 16h allowed us to establish correct diagnoses of clinical applicability.
The dynamic systems theory studies the initial state and evolutionary tendency of systems1 through the variables of its behavior over time.2 The evolution of systems can be evidenced graphically in a geometric space called the phase space, where the representation of dynamic variables gives place to what we know as an attractor.3 There are different kinds of attractors, punctual and cyclic attractors are predictable,4 while chaotic attractors are not, and represent highly irregular trajectories. Therefore they are quantified by fractal geometry5 and the Box-Counting method.6
Today, nearly 30% of the total of worldwide deaths are due to cardiovascular diseases (CVD). Thus they are of great interest in medical science. One of the most utilized methods to analyze cardiac dynamics is ambulatory cardiac monitoring, which is performed by Holter devices, in charge of registering cardiac dynamics in times of 24 and 48h, and are able to observe transitional and sudden changes in heart rate, ST segment, QT and RR intervals, etc.7
It has been shown that, in cardiology fields, there is a need to conduct oriented researches to comprehend the behavior of cardiac dynamics globally, taking as a base heart rate variability, using RR changes in time.8–10 However, until recently, such cases have only been analyzed by homeostatic model assessments, under which regularity is associated with normality and disease is associated with the loss of ability to maintain a regular heart rate when at rest, in the presence of pathology or in old age.
On the other hand, new emergent perspectives have improved cardiac system comprehension.11 Proper interpretation of electrical signals of the heart and the establishment of differences in heart rate variability have been researched in aspects of physical activity12,13 and autonomic variability.14 It has been shown that there are different difficulties at the time of analyzing cardiac dynamics from the usual methods, as there is information that we are not yet able to comprehend in a series of physiological times. Therefore, nonlinear dynamic perspectives have emerged, among others.15
RR interval changes in time enable heart rate variability studies, but they do not have diagnostic responses for each particular case. However, the theory of dynamic systems, chaos theory, and fractal analysis have been incorporated in search of new responses.16–20
Cardiac dynamic systems have been shown to display chaotic behavior,21 wherewith a new health and disease concept is given,22 different from those stated in the homeostasis framework, where the disease is related to highly regular or chaotic models, and normality is a state between these two ends. Different methodologies oriented toward the analysis of cardiac dynamics have been created in light of new understandings.23–27 However, their clinical applicability is still being debated.28
There are increasingly more physical and mathematical theories being embedded in the comprehension of cardiac dynamics, in the interest of making better prescriptions and diagnostic approaches in its behavior.17–22
One of these methodologies is the exponential mathematical law developed by Rodriguez29 with the objective of analyzing cardiac dynamics within 21h. By means of a geometric behavior observation of cardiac dynamics, those studies have shown that occupation spaces of the attractors tend to decrease as the cardiac system reaches acute disease.29,30
The above was proven on cardiac dynamics with patients with clinically diagnosed arrhythmia31,32 through the aforementioned mathematical law. Thus its diagnostic capability over this pathology was corroborated in studies with 40 and 70 electrocardiographic records, which allowed them to differentiate between varying grades of numerical forms of aggravation, also detecting sub diagnosed pathologies that were considered the evolution toward the disease by mathematical law.31,32
The purpose of this work is to prove that it is possible to make a reliable and clinically useful diagnosis by mathematical law through a cardiac dynamics evaluation within 16h, developed in dynamic systems and with a basis in fractal geometry, proving that this methodology has the predictive and diagnostic capability even with the decreased time of evaluation of the records.
MethodsDefinitionsDelay map: The delay map is the geometric space of dimension n>1, in which ordinated pairs of the same consecutive dynamic variable are charted, which generates a geometric object called an attractor.
Box-Counting method: The Box-Counting method is a mathematical calculation in which the fractal dimension of an object is found, which is established by the following equation:
The fractal dimension is denominated by D, N being the number of squares occupied by the object, and k corresponding to the degree of partition of the grid.
Simplified Box-Counting equation: By simplifying Eq. (1), leaving it only regarding Kg and Kp (grids of large squares and small squares, respectively) you get:
Mathematical exponential law: This is the law that is obtained by algebraically removing Eq. (2), and that is used to evaluate chaotic cardiac attractors.
D is the fractal dimension.
SamplingA total of 180 continuous electrocardiographic and Holter records were taken from patients over 21 years old, 60 within the boundaries of normality and 120 with some type of pathology, as established by a cardiology expert according to conventional clinical parameters. These records came from the databases of the Insight group.
ProcedureThe clinical diagnoses of the 180 patients were concealed. Then, minimum and maximum heart rate values were measured, as well as the total heart beats each hour for 16 and 21h; with these values, a semi-random sequence of frequencies was generated by an equiprobable algorithm through previously developed software.29
Next, to this, an attractor was built for each dynamic, and its spatial occupation was determined on the delay map by superimposing two grids, Kp of 5beats/min and Kg of 10beats/min. Finally, the fractal dimensions were calculated with Eq. (1).
In the end, to determine the mathematical diagnosis, Eq. (3) was used, applying the previously established limits for normality and disease in the dynamics evaluated at 21h, according to which the occupation spaces of the attractors of the acute pathological dynamics were below 73 in the Kp grid. The dynamics with values greater than 200 were categorized as normal, and those that were between 73 and 200 were those that were evolving toward aggravation.29
Later, the agreement between mathematical and physical diagnoses was evaluated at 21 and 16h.
Statistical analysisTo carry out the statistical analysis, the clinical diagnoses were revealed, to establish the agreement between the physical–mathematical diagnosis at 16h and the conventional medical diagnosis, taking as a base the normal cases and with acute illness and as the gold standard the diagnoses proffered by the expert.
Sensitivity and specificity were determined from a contingency table that considered the true positives, false positives, false negatives and true negatives.
Cohen's Kappa coefficient was calculated by the following equation:
where Co is the number of agreements observed in patients with the same diagnosis from the mathematical methodology and the gold standard; To is the total number of cases; Ca is the number of attributable agreements calculated randomly through the following formula:In which f1 is the number of cases with normal mathematical values; C1 is the number of cases diagnosed conventionally as normal; f2 is the number of cases diagnosed conventionally as diseased; C2 represents the number of cases diagnosed conventionally with some kind of pathology, and To is the total number of cases.
Ethical aspectsThis study was declared a research with minimum risk according to parameters established by the Colombian Ministry of Health in resolution 8430 from 1993, since mathematical and physical calculation have been made over noninvasive tests, which have been previously prescribed by conventional protocols, protecting the integrity and anonymity of participating subjects. Finally, it complies with ethical principles established in the Helsinki Declaration of the World Medical Association.
ResultsDiagnoses of some of the electrocardiographic records belonging to the study are shown in Table 1. Results show that fractal dimensional of attractors of normal dynamics were between 1.992 and 1.082, while the fractal dimensional for abnormal cases was between 1.992 and 0.856. In the registers obtained during a period of 16h, results show that the fractal dimensions of attractors of normal dynamics were between 1.898 and 1.043, and abnormal between 1.921 and 0.900, confirming that the fractal dimension is not a variable that allows us to differentiate normality from disease (see Table 2).
Information selected from the data of the initial clinical diagnosis of some of the continuous electrocardiographic and Holters records chosen for the study.
| No. | Clinical diagnosis |
|---|---|
| 1 | Stroke. Atrial tachycardia, atrial fibrillation |
| 2 | ACV, carotid artery |
| 3 | Arrhythmia. Ectopia earphone infrequent. Sinus tachycardia episode up to 156bpm without discarding |
| 4 | Blocking second degree ventricular auricle. Rhythm of atrial fibrillation with uncontrolled ventricular response, dimorphic ventricular ectopias with frequent duplets, 7 episodes of ventricular tachycardia |
| 5 | AV block, first degree |
| 6 | Premature ventricular contractions |
| 7 | Arrhythmia control. Slight decrease in the variability of HR |
| 8 | Atrial fibrillation control |
| 9 | Ischemic dilated cardiomyopathy |
| 10 | Normal |
| 11 | Normal |
| 12 | Normal |
| 13 | Normal |
| 14 | Normal |
| 15 | Normal |
| 16 | Normal |
| 17 | Normal |
| 18 | Normal |
| 19 | Normal |
| 20 | Normal |
| 21 | Normal |
| 22 | Tachyarrhythmia |
| 23 | Tachycardia |
| 24 | Paroxysmal supraventricular tachycardia, WPW |
| 25 | Ventricular tachycardia |
| 26 | Tachycardia, frequent supraventricular extrasystole, atrial tachycardia, monomorphic frequent ventricular extrasystole without repetitive phenomena |
| 27 | WPW |
| 28 | WPW, dyspnea, and headache which correlate with sinus tachycardia. WPW syndrome |
| 29 | Normal |
| 30 | AMI, ejection fraction 45% |
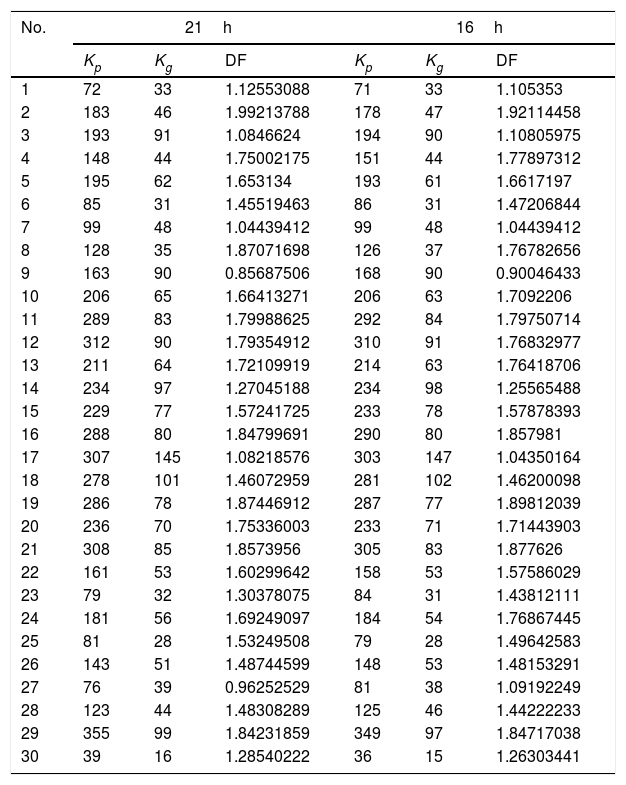
Values of the spaces occupied by the chaotic heart attractors evaluated at 16 and 21h corresponding to the continuous electrocardiographic and Holters records of Table 1.
| No. | 21h | 16h | ||||
|---|---|---|---|---|---|---|
| Kp | Kg | DF | Kp | Kg | DF | |
| 1 | 72 | 33 | 1.12553088 | 71 | 33 | 1.105353 |
| 2 | 183 | 46 | 1.99213788 | 178 | 47 | 1.92114458 |
| 3 | 193 | 91 | 1.0846624 | 194 | 90 | 1.10805975 |
| 4 | 148 | 44 | 1.75002175 | 151 | 44 | 1.77897312 |
| 5 | 195 | 62 | 1.653134 | 193 | 61 | 1.6617197 |
| 6 | 85 | 31 | 1.45519463 | 86 | 31 | 1.47206844 |
| 7 | 99 | 48 | 1.04439412 | 99 | 48 | 1.04439412 |
| 8 | 128 | 35 | 1.87071698 | 126 | 37 | 1.76782656 |
| 9 | 163 | 90 | 0.85687506 | 168 | 90 | 0.90046433 |
| 10 | 206 | 65 | 1.66413271 | 206 | 63 | 1.7092206 |
| 11 | 289 | 83 | 1.79988625 | 292 | 84 | 1.79750714 |
| 12 | 312 | 90 | 1.79354912 | 310 | 91 | 1.76832977 |
| 13 | 211 | 64 | 1.72109919 | 214 | 63 | 1.76418706 |
| 14 | 234 | 97 | 1.27045188 | 234 | 98 | 1.25565488 |
| 15 | 229 | 77 | 1.57241725 | 233 | 78 | 1.57878393 |
| 16 | 288 | 80 | 1.84799691 | 290 | 80 | 1.857981 |
| 17 | 307 | 145 | 1.08218576 | 303 | 147 | 1.04350164 |
| 18 | 278 | 101 | 1.46072959 | 281 | 102 | 1.46200098 |
| 19 | 286 | 78 | 1.87446912 | 287 | 77 | 1.89812039 |
| 20 | 236 | 70 | 1.75336003 | 233 | 71 | 1.71443903 |
| 21 | 308 | 85 | 1.8573956 | 305 | 83 | 1.877626 |
| 22 | 161 | 53 | 1.60299642 | 158 | 53 | 1.57586029 |
| 23 | 79 | 32 | 1.30378075 | 84 | 31 | 1.43812111 |
| 24 | 181 | 56 | 1.69249097 | 184 | 54 | 1.76867445 |
| 25 | 81 | 28 | 1.53249508 | 79 | 28 | 1.49642583 |
| 26 | 143 | 51 | 1.48744599 | 148 | 53 | 1.48153291 |
| 27 | 76 | 39 | 0.96252529 | 81 | 38 | 1.09192249 |
| 28 | 123 | 44 | 1.48308289 | 125 | 46 | 1.44222233 |
| 29 | 355 | 99 | 1.84231859 | 349 | 97 | 1.84717038 |
| 30 | 39 | 16 | 1.28540222 | 36 | 15 | 1.26303441 |
Occupational spaces of the attractors in the Kp and Kg grids at 21h, were found to be between 206, 355, 64 and 145 respectively for normal dynamics, and between 39, 195, 16 and 91 respectively for abnormal dynamics. At 16h, the occupation spaces for the grids Kp and Kg in normal dynamics were found to be between 206, 349, 63 and 147, respectively, and for pathological dynamics were found to be between 36, 194, 15 and 90, respectively (see Table 2). There was found to be a coincidence between mathematical diagnoses at 16 and 21h in 100% of cases.
The results were corroborated by statistical analysis regarding conventional diagnoses, where sensitivity and specificity was 100%, and the coefficient of kappa was 1, which, according to the criteria of Landis and Koch demonstrates an almost perfect correlation with respect to the gold standard.
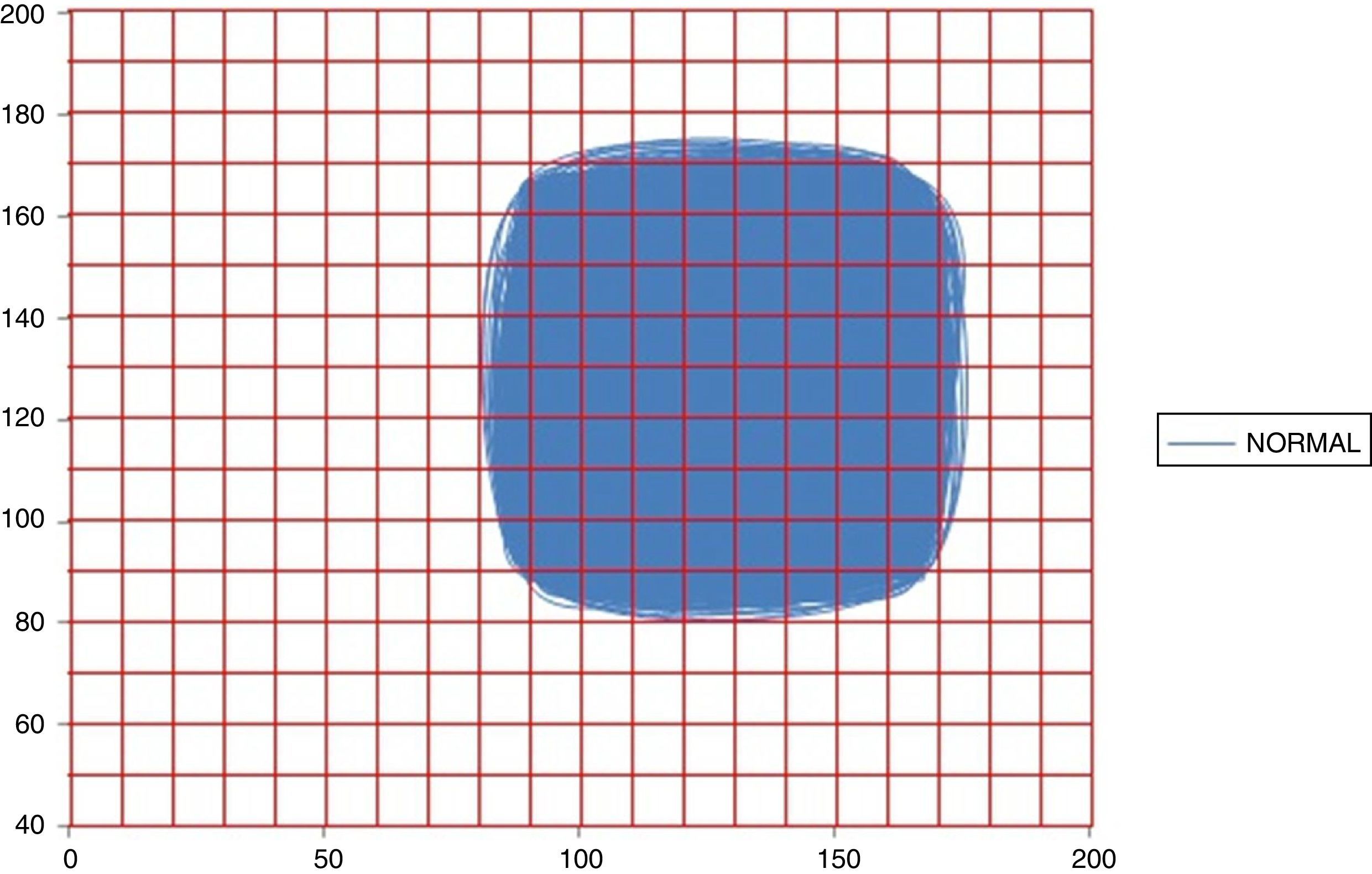
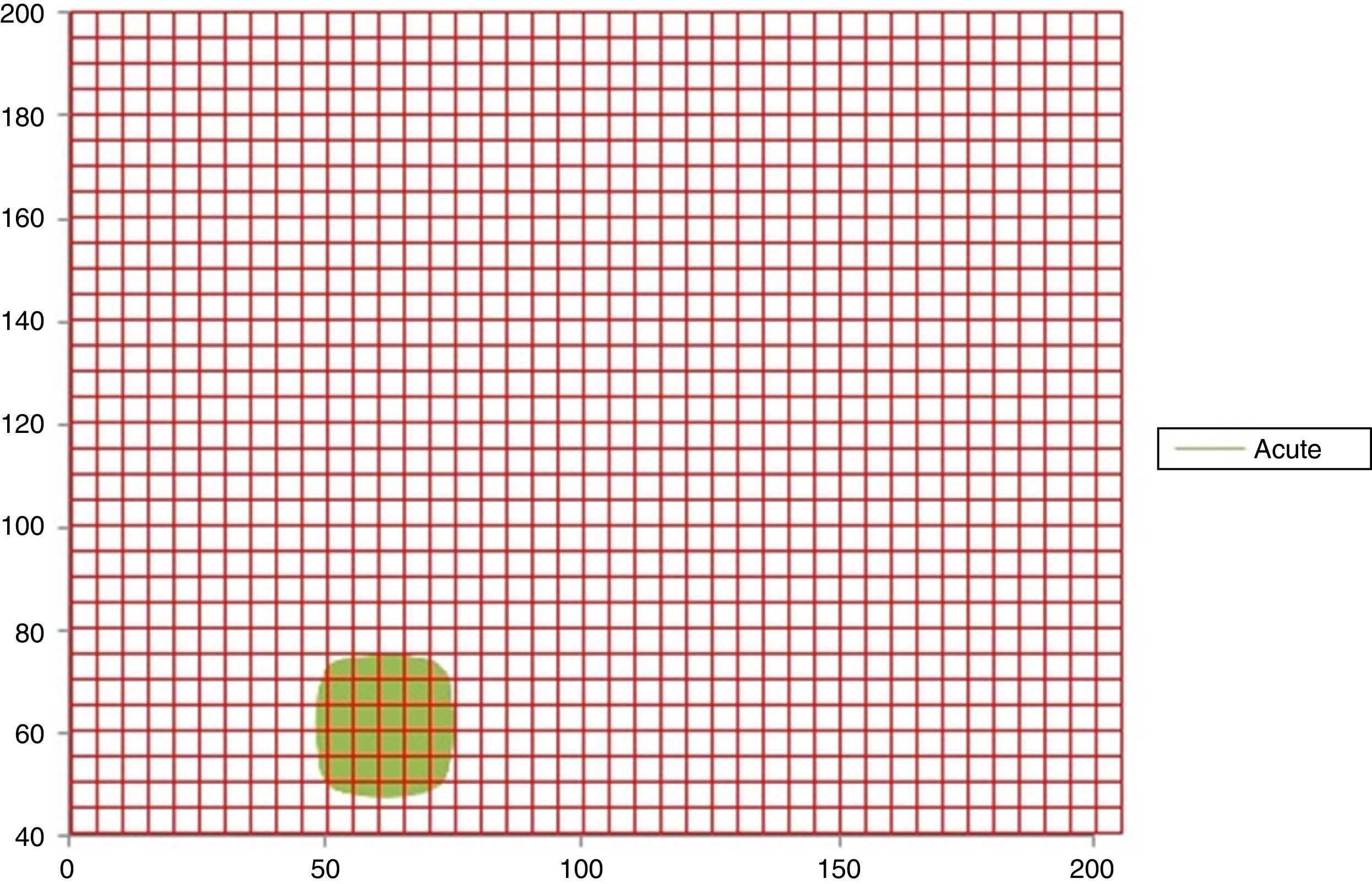
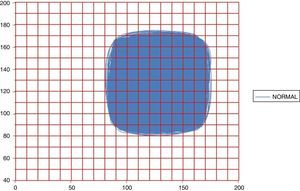
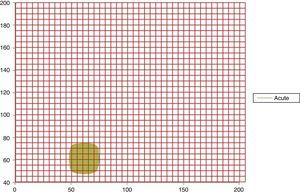
In Figs. 1 and 2 it can be observed the attractors for a normal and acute dynamic, respectively. Evidence that the occupation space of the normal attractor is much bigger than the acute dynamic attractor corroborating the obtained results.
Attractor of a normal dynamic in 16h with the Kg grid superimposed, with spaces of occupation of Kp=349 and Kg=97 (No. 29 of Table 1).
Attractor of a sharp dynamic at 16h with the Kp grid superimposed, with spaces of occupation of Kp=36 and Kg=15 (No. 30 of Table 1).
This is the first work in which, starting from the quantification of the occupation spaces of chaotic cardiac attractors analyzed in the context of a mathematical law, the evaluation time of cardiac dynamics was reduced from 21 to 16h with 180 continuous electrocardiographic ambulatory records. Also, evidencing diagnostic utility independent from the system of recording heart rate values and being able to differentiate between normal, pathological and transitional dynamics between both states in electrocardiographic and continuous registers of 16h, with which this mathematical methodology is configured as a tool for clinical application. It allows for a timely diagnosis of the clinical condition of each patient regardless of population, statistical or causal factors, appealing to the mathematical order that underlies the phenomena of the cardiac system, finding agreement between the methodology and conventional clinical diagnosis through values of sensitivity and specificity of 100% and a Kappa coefficient of 1.
Likewise, the mathematical quantification of the cardiac dynamics allows us to make numerical distinctions between disease and normality independent of the circadian cycle, the clinical state of the patient or other considerations. Regarding the diagnostic test performed, the methodology showed its objectivity and reproducibility, as evidenced in previous studies.30–32
In the framework of the theory of dynamic systems, different methodologies have been developed to characterize and differentiate cardiac dynamics with high precision.33–35 Recently, dynamic systems have allowed for characterization of the patient's cardiac dynamics in the Intensive Care Unit, taking a register of 16h and succeeding in evaluating in a successful manner and in less time the cardiac dynamics independent of the clinical state of the study and the scenario in which they where.35
Although work has been carried out using fractal geometry applied to medicine36–40 in order to differentiate between normality and disease, the vast majority of them use isolated fractal measures and look for ranges that characterize normality and disease. However, they have not been definitive in establishing clear differences between normality and disease, for which mathematical methodologies have been developed that allow this distinction to be made.41,42 Just as the present case, where normality of pathological states is distinguished by a mathematical law that establishes the order, underlying the occupation of the attractors in the fractal space of box-counting.
Modern theoretical physics bases its procedure on the realization of abstractions and the inductive thinking of observable phenomena, by means of which it is possible to establish theoretical relations under physical–mathematical laws, allowing for the establishment of generalizations and subsequent applications to each particular case.
This thought was adopted not only in the achievement of the presented methodology, but perspective diagnoses of the cardiac dynamics of the adult have been obtained from this, among which one is based on the probability and the proportions of the entropy.33,43,44 The advent of a methodology based on the empirical law of Zipf/Mandelbrot45 with applicability in the intensive care unit and a method based on the theory of probability was also made possible, with which, through numerical ranges, it was possible to differentiate normality from disease in patients with a pacemaker implant46 and with some type of arrhythmia.47
This physical–mathematical perspective has contributed extensively in different areas of medicine. For example, from the theory of sets and dynamic systems, it was possible to establish predictions of mortality in the ICU.35 Also, it was possible to evaluate neonatal cardiac dynamics in patients undergoing sepsis,48 in other fields, predictions of clinical application have been evidenced, in arterial41 and cellular morphometry,49 in hematology,50 in infectious disease,51 in the prediction of epidemics,52,53 and in immunology, specifically in the prediction of peptide binding of Plasmodium falciparum to HLA class II.54
FundingThis paper is product of the project PIC-2014-19, which was funded by “Universidad el Bosque”.
Conflict of interestThere are no conflicts of interests.
We want to thank “Universidad el Bosque,” specifically its Research divisions, for the support given to us for the project PIC-2014-19, this article is a product of said project.
We extend our acknowledgment to the Research Center of Country Clinic, especially to the physicians at the Research Center, the epidemiologist Adriana Lizbeth Ortiz, and chief nurse Silvia Ortiz, nurse Sandra Rodriguez, Dr. Tito Tulio Roa Director of Medical Education, Dr. Jorge Alberto Ospina Medical Director, and Dr. Alfonso Correa Director of the Research Center. Thank you all for the constant support to our research group.