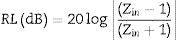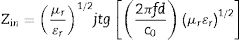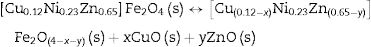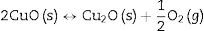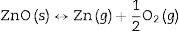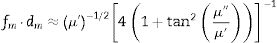The shielding properties of a Cu-doped Ni–Zn polycrystalline ferrite in the frequency range 1MHz to 1GHz were explored. Samples of composition (Cu0.12Ni0.23Zn0.65)Fe2O4 were prepared by the traditional ceramic route. The complex relative permittivity (εr=ε′−jε″) and permeability (μr=μ′−jμ″) of the absorber ceramics were measured, and the minimum reflection-loss RL, matching frequency fm, matching thickness dm and bandwidth for RL≤−20 dB were calculated using the theory of the absorbing wall. Effect of the main process parameters (pressing pressure P, sintering temperature T, and sintering time t) on the electromagnetic properties and microwave-absorbing characteristics was deeply investigated. The rise of the three selected process parameters was observed to improve the sintered microstructure of the final specimens (monitored by the relative density ϕ and the average grain size G), provided that abnormal grain growth does not occurred. The increase in sintered relative density and average grain growth modifies complex permeability and permittivity in the explored frequency range, enhancing the shielding properties of the material.
Se han analizado las propiedades de blindaje de una ferrita policristalina de Ni–Zn dopada con Cu en el rango de frecuencia de 1MHz-1GHz. Las muestras de composición (Cu0.12Ni0.23Zn0.65)Fe2O4 se prepararon por la ruta tradicional cerámica, midiendo la permitividad (εr=ε′−jε″) y la permeabilidad (μr=μ′−jμ″) relativas complejas de las cerámicas absorbentes y se calcularon, utilizando la teoría de la pared absorbente, la pérdida por reflexión mínima RL, la frecuencia a la que se produce esta RL mínima fm, el espesor óptimo de pieza dm y el ancho de banda para RL≤−20dB. Se ha llevado a cabo una investigación rigurosa del efecto de los principales parámetros del proceso (presión de prensado P, temperatura de sinterización T y tiempo de sinterización t) sobre las propiedades electromagnéticas y los parámetros característicos de estos absorbedores, observándose que el aumento de los tres parámetros de proceso seleccionados mejoran la microestructura final de las muestras sinterizadas (monitorizadas por la densidad relativa ϕ y el tamaño medio de grano G siempre que no se produzca un crecimiento anormal del grano. El aumento de la densidad relativa y el tamaño medio de grano de las piezas sinterizadas modifican la permeabilidad y la permitividad complejas en el rango de frecuencia explorado, mejorando las propiedades de blindaje del material.
The current high technological level of our society has made the electromagnetic interference (EMI) between electronic devices a serious problem [1–5]. This kind of pollution can lead not only to serious disturbance or damage to electronic equipment but also to human health aspects [6]. One of the most extended uses of ferrites is as a shielding material for electromagnetic interference (EMI) suppression, absorbing the unwanted electromagnetic signals that perturbs the normal operation of electronic devices [7]. The ferrites used in EMI applications are classified into two generic types: NiZn and MnZn-ferrites. Among these, NiZn-ferrites (most of them Cu-doped) are the most broadly used since the frequencies for many EMI suppression applications are in the higher MHz band [7,8].
In order to obtain bulk bodies, particulate ferrites must be processed. As found in literature, there are mainly two types of bulk bodies: ferrite composite materials (in which ferrite particles are embedded in a binder matrix) [9] and sintered ferrites (in which ferrite particle are processed as any other ceramic material, including forming and sintering stages at relatively high temperature) [8]. In both cases, magnetic properties depend on chemical composition (stoichiometry) and on microstructure (mainly grain size and relative density). Indeed, final properties can be disrupted due to impurity content and/or heterogeneous final microstructure.
To consider a soft Ni–Zn ferrite a shielding material the reflection-loss absolute value RL should be above 35dB. Different studies have been undertaken to explore the shielding properties of Ni–Zn ferrites in RF range. Some has been focused on the effect of chemical composition on the attenuation properties, as Ruiz et al. [10] who analyzed the effect of Cu content in a CuxNi0.4−xZn0.6Fe2O4 ferrite observing an optimum attenuation for x=0.2, or Leal et al. [11] who found that the best performance of electromagnetic absorption in the X-band was presented by the sintered NiZnCu ferrite with 0.3mol of Cu, with 99.8% attenuation in the 11.5GHz frequency, thus confirming its efficiency and great potential to be applied as a narrowband electromagnetic radiation absorber material. In the same way, Ma and coworkers [12] studied the influence of different metal ions on the absorption properties of nano Ni–Zn ferrites concluding that the increasing of Co2+ dopant rise the bandwidth of the absorber and improve the performance of the materials in the GHz low frequency. Same conclusion was achieved with 0.15 Cu2+ dopant addition, but, on the contrary, Mn2+ additions were found to decrease the absorbance performance.
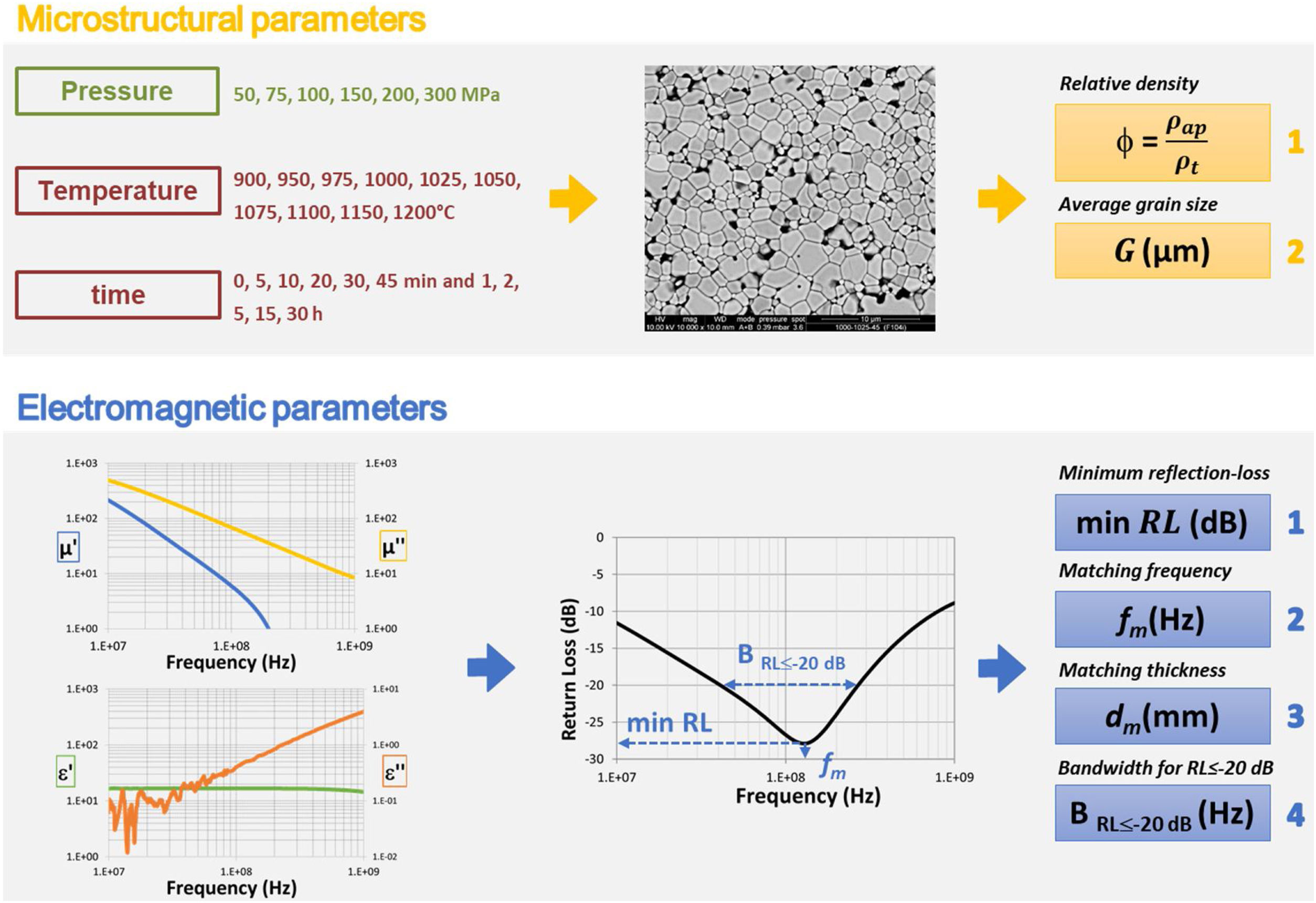
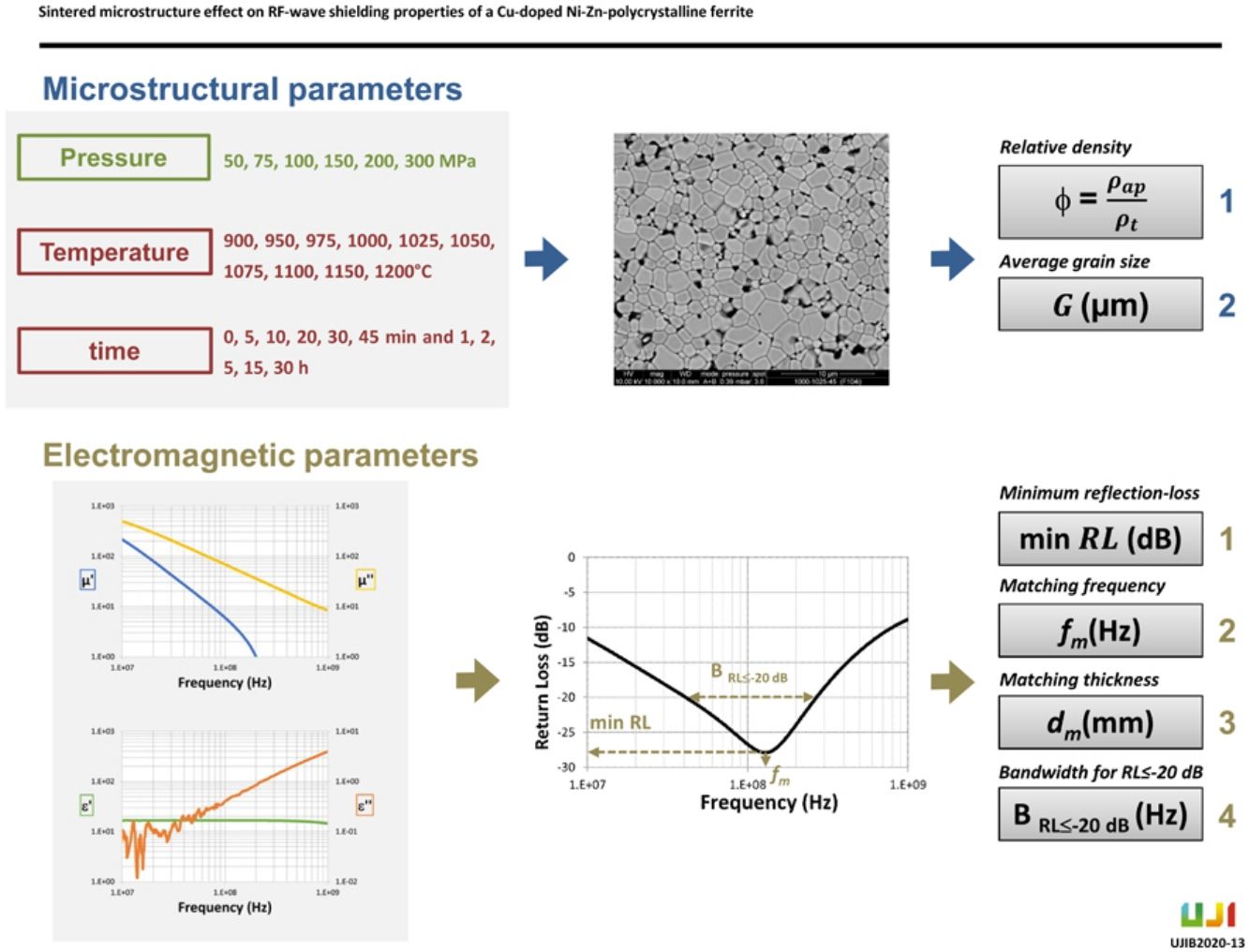
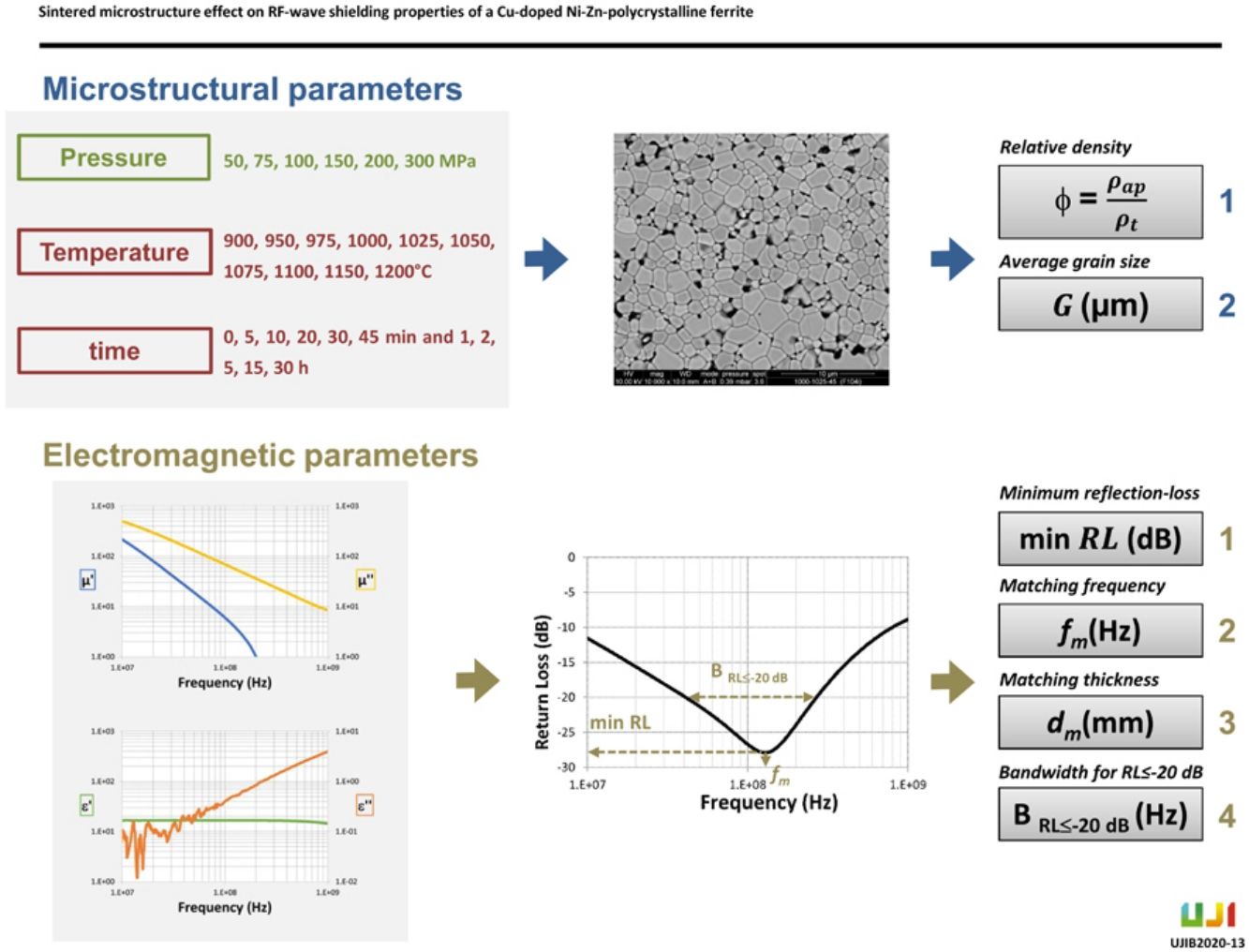
Most of the literature about shielding NiZn ferrite materials are focused on ferrite-polymer composites [13–15] studying, either the effect of the particle size [16,17] and the dopant used on the ferrite [14,17], or the influence of the ferrite ratio in the formulated composite on the electromagnetic properties and microwave-absorbing characteristics [9]. However, the effect of sintered microstructure of the ferrite on the shielding properties of the Ni–Zn ferrites remains elusive and in-depth analyses cannot be found in the literature. Thus, the aim of this paper is to conduct a systematic research to study the possible relationships among the main microstructural parameters (i.e., relative density ϕ and average grain size (G)) and the electromagnetic and absorption properties of polycrystalline Cu-doped Ni–Zn ferrites, obtained by the traditional ceramic route, in the 1MHz to 1GHz frequency range, as outlined in the abstract summary of the experimental procedure shown in Fig. 1.
Experimental procedurePreparation of ferriteAs in previous publications [18,19], a polycrystalline spray-dried ferrite granules of chemical composition (Cu0.12Ni0.23Zn0.65)Fe2O4 (supplied by Fair-Rite Products Corp.) was used as raw material. The ferrite granules had an average size of 175μm, made up of ferrite particles with an average size of 1–2μm and a narrow particle-size distribution (around 4μm). True density of the ferrite powder was experimentally determined on a helium pycnometer to be 5380kg/m3. The granules were used to form cylindrical and toroidal test specimens (3mm thick and 19mm in external diameter for both specimens and 6mm internal diameter for the toroidal ones), by uniaxial pressing at 50, 75, 100, 150, 200 and 300MPa. The specimens were sintered in air in an electric laboratory kiln at ten peak sintering temperatures (900°, 950°, 975°, 1000°, 1025°, 1050°, 1075°, 1100°, 1150° and 1200°C) and different dwell times (up to 30h), using the following thermal cycle: (i) Preheating stage (burnout of organic additives used in the compaction stage): 2h dwell at a peak temperature of 500°C. (ii) Densification and grain-growth stage: heating at a rate of 12°C/min to peak sintering temperature (hereafter sintering temperature), and dwell at this temperature for a given time (hereafter sintering time). (iii) Cooling stage: cooling was performed, from sintering to room temperature, at a rate of 20°C/min. The initial point (0.0h) corresponds to the non-isothermal heating time required to reach each tested sintering temperature from room temperature.
Summing up, six compaction pressures (P), ten sintering temperatures (T) and eleven sintering times (t) were tested (see Supplementary Tables 1–10), leading into 660 different final microstructures of the studied ferrite, which have allowed to obtain a wide range of characteristic microstructure parameters: relative density ϕ and average grain size G (see Fig. 1).
Physical characterization of ferriteBulk density was determined by the Archimedes method and relative density (ϕ) of each specimen was calculated as the quotient of bulk density to theoretical density (5380kg/m3). Average grain size (G) was obtained from the grain size distribution, which was determined by image analysis of the cross-sectional area of the rectangular thermal etched surface of each cylindrical test specimen, observed by scanning electron microscopy (SEM) (see Fig. 2 and Supplementary Figs. 1 and 2). Image processing was performed with the image analyser software ImageJ. For the characterization of each sample more than 1000 grains were measured. The grain's irregular area was determined by the “Analyze particles function”, and the diameter was calculated assuming that all grains were spherical. Grain size distributions were obtained by representing the accumulated frequency vs diameter, where G is the grain diameter at which 50% of the grains in area are smaller.
Measurement of microwave-absorbing behavior of ferriteThe measurement of ε′, ε″, μ′ and μ″ versus frequency were determined on an Agilent E4991A RF impedance/material analyser, in a frequency range of 1MHz to 1GHz, using an Agilent 16454A magnetic and 16453A dielectric material test fixture fixtures.
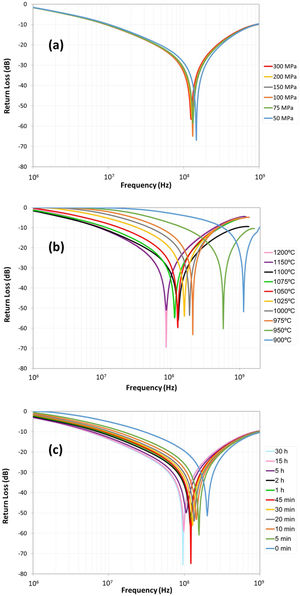
The absorbing characteristics can be represented as the reflection-loss RL[17,20]:
where Zin is the normalized input impedance relating to the impedance free space Z0=μ0/ε0=120πΩ, εr=ε′−jε″ is the complex relative permittivity of the material, μr=μ′−jμ″ is the complex relative permeability of the material, d is the thickness of the ceramic absorber, c0 the velocity of light in free space (≈3×108m/s) and f the frequency.The impedance-matching condition representing the perfectly absorbing properties is given by Zin=1. This condition is satisfied at a particular matching thickness dm and a matching frequency fm, where minimum reflection-loss RL occurs. The impedance matching conditions is determined by the combinations of six parameters ε′, ε″, μ′, μ″, fm and dm Also knowing the εr and μr, the RL value versus frequency can be evaluated at a specified thickness.
Results and discussionSintered microstructural parameters, that is relative density ϕ and average grain size G, of the 660 sintered Cu-doped Ni–Zn-polycrystalline ferrite specimens are shown in Supplementary Tables 1–10. The scanning electron micrographs of the polished and etched cross-section areas of the sintered specimens at the six uniaxial pressures tested are shown in Fig. 2. The effect of sintering temperature and sintering time on the final microstructure of the sintered specimens are shown in Supplementary Figs. 1 and 2, respectively.
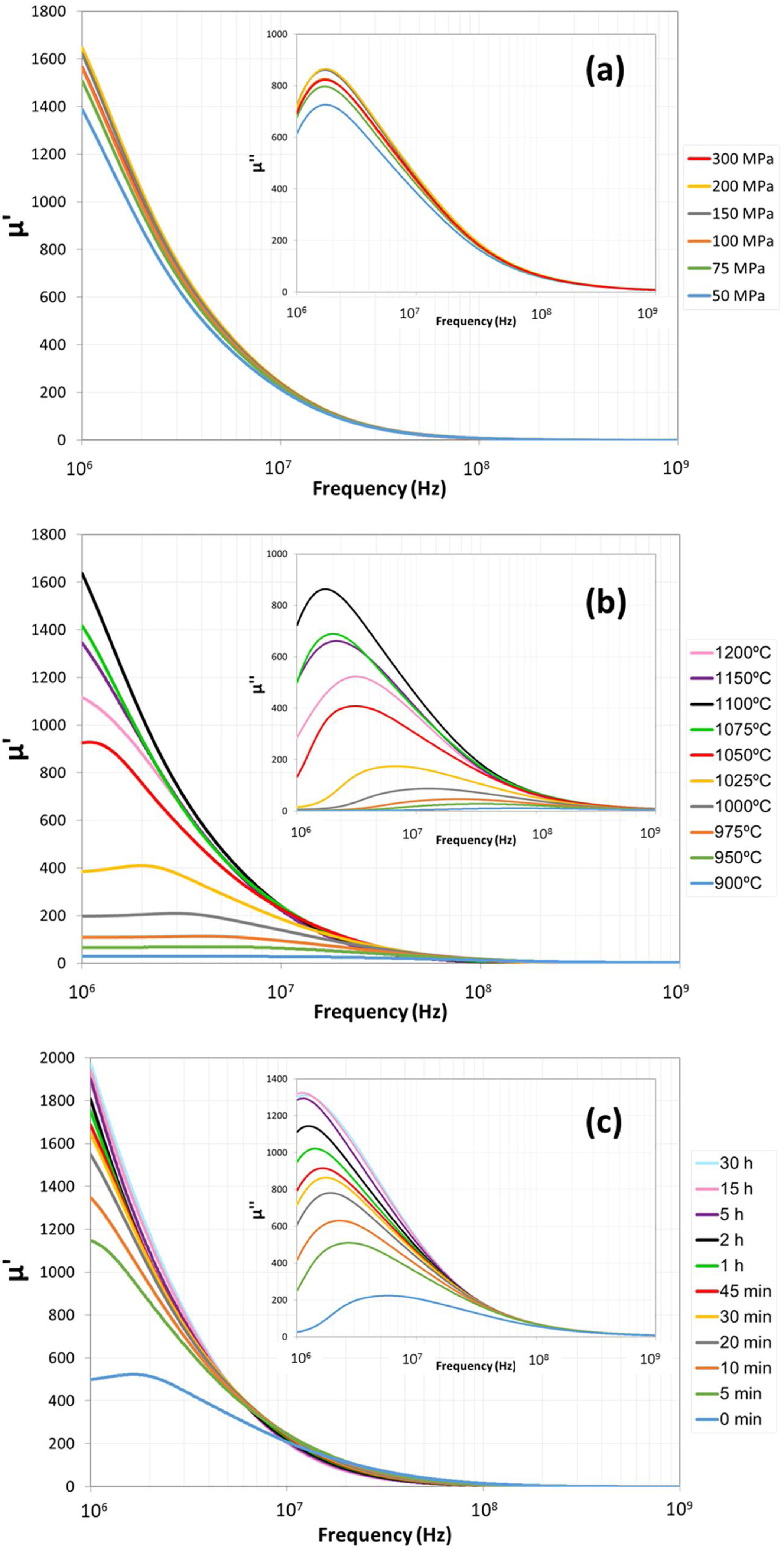
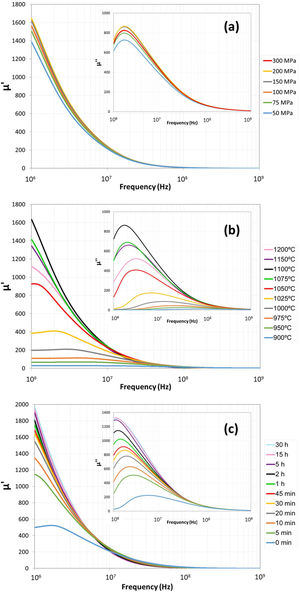
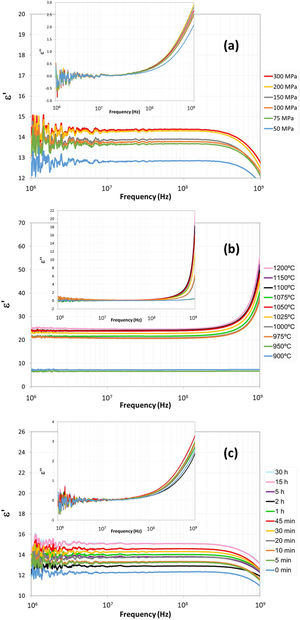
The frequency dependences of complex relative permeability μr=μ′−jμ″, complex relative permittivity εr=ε′−jε″ and reflection-loss RL for the Cu doped-NiZn polycrystalline ferrite are presented in Figs. 3–5. Effects of pressing pressure P, sintering temperature T and sintering time t are shown in each figure in panels (a), (b) and (c), respectively.
The real part μ′ of complex permeability decreases with increasing frequency in all cases. The pressing pressure P effect is shown in Fig. 3(a). Data indicate that the μ′ values rapidly decreased from 106 to 108Hz, tending to zero from this frequency value. The six tested pressing pressures are quite similar but the μ′ values slightly increase with increasing P in the low frequency range (below 107Hz). When analyzing the sintering temperature T effect (Fig. 3(b)), it is shown that increasing T shorten the frequency range in which μ′ values are maintained constant and increase the μ′ values in the low frequency range below 107 Hz, up to 1100°C. Higher temperatures conduct to lower μ′ values. Finally, Fig. 3(c) shows the sintering time t effect and it indicates that, excluding the lowest time which presents a frequency range in which μ′ values are maintained constant, all the tested times present a similar μ′ curve in which μ′ values decreased up to 108Hz, tending to zero for higher frequencies. In this case, the μ′ values significantly increase with increasing sintering time t in the low frequency range below 107Hz.
The resonance frequency, at which μ′ has its maximum value, remains constant with pressing pressure P (Fig. 3(a) inset), decreases with the rise in sintering temperature T (Fig. 3(b) inset) and in sintering time t (Fig. 3(b) inset).
At it is widely accepted, permeability in ferrites proceeds via two mechanisms, domain wall motion and domain rotation [21,22]. Lower permeability μ′ values are normally due to smaller grains, and higher μ′ are commonly obtained because, among other considerations, domain wall oscillations can contribute to permeability as the grains are larger. At low frequencies the domain wall motion is dominating to the initial permeability. The existence of a large amount of grain boundaries in ferrites with small grain sizes prevents the domain wall motion and thereby weakens the μ′[23]. Also, a higher μ′ value is related to higher densities because there is a decrease in the intergranular porosity and hence a reduction in the demagnetizing field due to pores. In polycrystalline ferrites, unavoidable pores and other imperfections generate a demagnetizing field. Anisotropy field consists of magnetic anisotropy field and demagnetizing field. As the pores volume decreases and the grains became bigger, the saturation magnetization increases while demagnetizing field decreases [24]. It is well known that porosity is a limiting factor for initial permeability, either intergranular (on the grain boundaries) or intragranular (inside the grains). At the first stages of sintering, initial permeability is influenced only by grain boundary porosity (grain size is low and no intragranular porosity us formed). As sintering proceeds grain size and densification increase, the effect of intergranular porosity reduces and, simultaneously, the influence of intragranular porosity increases. Sintering at high temperatures increases lattice parameter and grain growth, enhancing the intragranular porosity and reducing initial permeability [25,26]. Both the pores in the matrix and grain boundaries act as domain wall pinning factors [27] but, compared to intragranular porosity, intergranular porosity has negligible effect on initial permeability [25]. Intergranular pores produce demagnetizing field, which decreases the temperature dependence of initial permeability. Intragranular pores pin and restrict the movement of the domain wall and lower the volume swept by wall bulging, resulting in a decrease in the contribution of the domain wall motion to permeability [28]. Thus, maximum initial magnetic permeability is achieved when pore-to-pore distance of entrapped pores does not change significantly with the change in microstructure from inter- to intragranular porosity [29].
This is why permeability broadly increases with pressing pressure, sintering time and sintering temperature, provided that not exaggerated and/or abnormal grain growth is occurred, since larger grains usually include pores within grains (see Supplementary Figs. 1 and 2) which hinder the magnetization process [30]. Another reason for the decrease of the permeability values is the present of defects in the grain boundaries, as polycrystalline ferrites grain boundaries normally act as a sink of impurities. Defects such as impurities, non-magnetic second phases, grain boundaries and chemical inhomogeneity impede the rotation of spins and the motion of the domain walls, worsening this electromagnetic property of the final specimen [18,19].
As it was previously stated by the authors [31,32], sintering temperature T and sintering time t (as well as green relative density and cooling speed) have a marked influence on the partial decomposition of the CuNiZn ferrite and ZnO and CuO crystal precipitation. As T and t rise, pore size distribution gets finer and narrower, and the network formed between the particles become more tortuous, making it difficult for oxygen to enter, so that the oxygen concentration inside the sample decreases. At low oxygen partial pressure and high temperatures (as for 1150° and 1200°C), part of the iron III of the ferrite reduces, causing the partial decomposition of the CuNiZn ferrite and the formation of ZnO and CuO (Eq. (3)). The CuO obtained is unstable at high temperatures, as reported in the traditional chemistry literature [33,34], taking place its decomposition (Eq. (4)). In the same way, ZnO easily decompose at low oxygen partial pressure and high temperatures into Zn and O2 (Eq. (5)), and Zn volatilization occurred because of its low boiling point of 907°C [35].
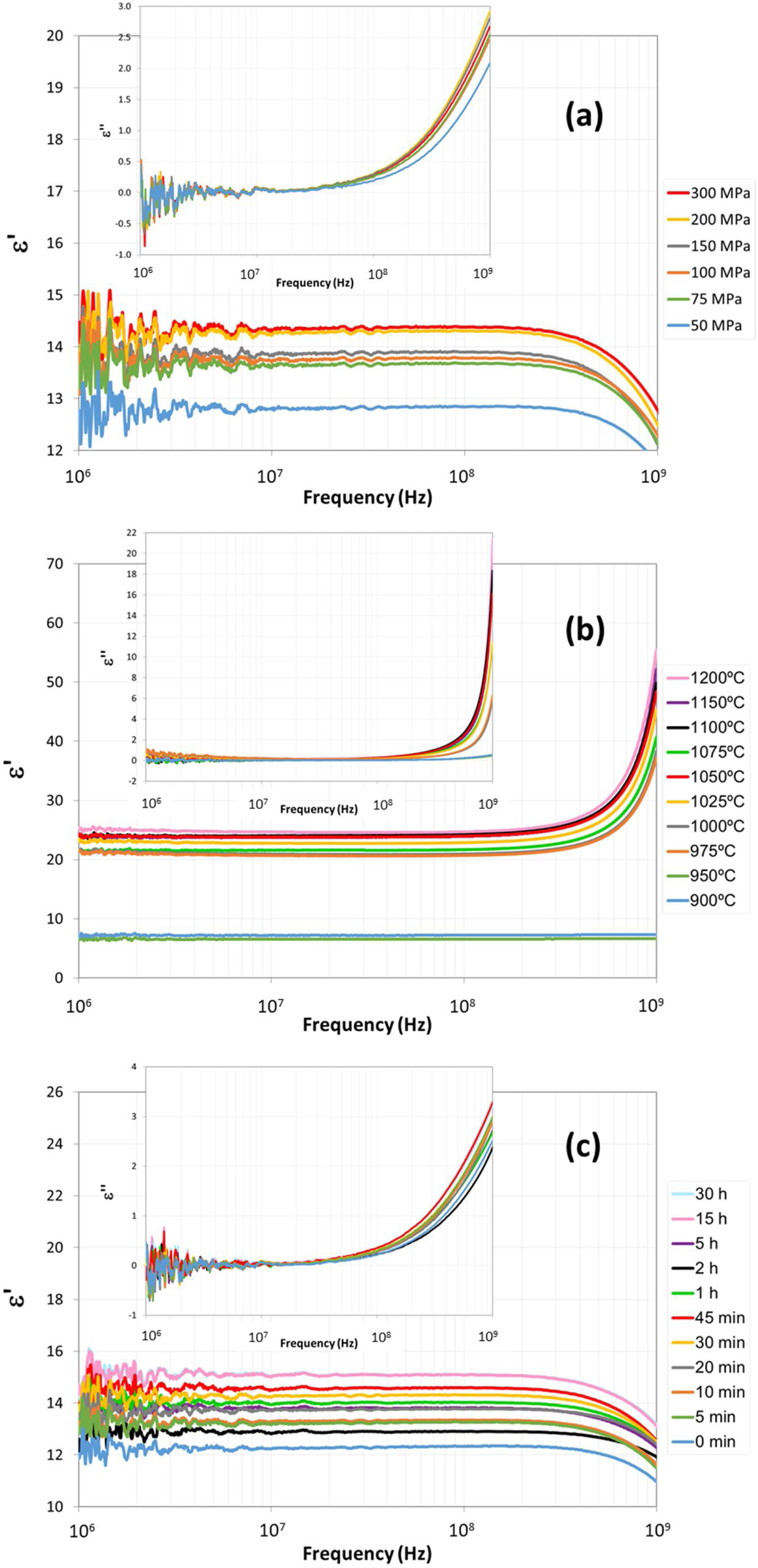
The O2 and Zn vapor produced, according to Eqs. (3)–(5), increases and/or expands the pores in the sample, which resulted in the lower relative density (higher porosity) of the specimens sintered at the highest conditions of temperature/time (see Supplementary Tables 1–10).Permittivity increases with the three studied process parameters: pressing pressure P (Fig. 4(a)), sintering temperature T (Fig. 4(b)) and sintering time t (Fig. 4(c)), with a more marked rise in the case of temperature. The real part of the relative dielectric permittivity ε′ remains nearly constant with low values (ε′<25−15) and the relative imaginary part ε″ (ε″≪1) is negligible for all cases practically throughout the studied frequency range. Only those frequencies close to 109Hz conducted to appreciable changes in the permittivity values.
The dielectric permittivity ε′ is a result of the contribution of four types of polarizations, namely, interfacial, dipolar, electronic an ionic. The obtained ε′ values are nearly constant, possibly because the interfacial and dipolar polarizations play a dominant role at lower frequencies, decreasing their contributions with frequency [10]. The dispersion in dielectric permittivity is more pronounced at lower frequencies than a higher ones [36].
Among other factors, polarization is related to the sample density and homogeneity. Some authors reported that Cu addition in NiZn ferrites may introduce some inhomogeneity that favors polarization, causing an increase in ε′[37]. However, in our case, the increase in ε′ must be mainly related to the increase in density as no chemical composition changes have been conducted in the studied specimens. During a normal grain growth densification process, the relative density increases with pressing pressure P, sintering temperature T and sintering time t[38], as can be observed in Supplementary Fig. 3, which justifies the observed increase in values with these studied process parameters.
Complex electrical permittivity of polycrystalline solids depends on the microstructure of the sintered bodies (porosity) and the constituent permittivities (grain and gas phase, ferrite and air in our case) [39], and varies with the angular frequency, changing the involved polarization mechanism at high values. Dielectric loss tangent (tan δε=ε″/ε′) increases with porosity (although it has also been found to increase when grain size decreases [40]) and it also increases with angular frequency, up to a maximum, beyond which polarization falls.
Measured values of real μ′ and imaginary μ″ parts of complex relative permeability μr=μ′−jμ″, as depicted in Fig. 3, and measured values of real ε′ and imaginary ε″ parts of complex relative permeability εr=ε′−jε″, as depicted in Fig. 4, were used to the calculation of reflection-loss RL in the sintered Cu doped-NiZn polycrystalline ferrites. These calculations were performed using the model of a single-layered EM-wave absorber proposed by Naito and Suetake [41]. In this model, the input wave impedance Zin at the air/absorber interface is given by Eq. (1).
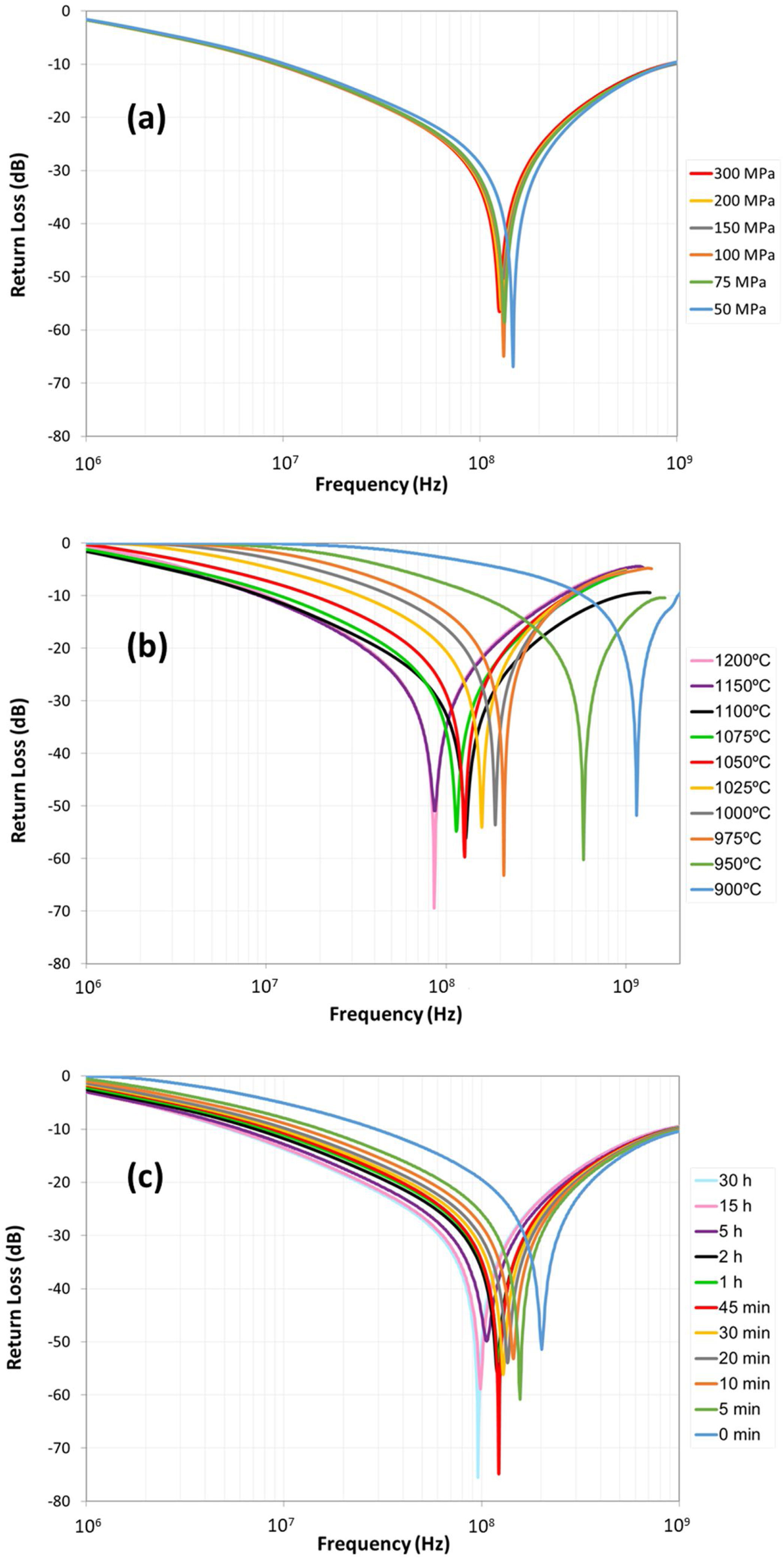
The frequency dependence of reflection-loss RL for the sintered polycrystalline ferrites can be found in Fig. 5, where the effects of pressing pressure P, sintering temperature T and sintering time t are shown in panels (a)–(c), respectively. The pressing pressure P effect is depicted in Fig. 5(a). Data indicate that the frequency-reflection-loss curves are quite similar for all the tested pressing pressures, observing a slightly shift of the curves to lower frequency values. When analyzing the sintering temperature T effect (Fig. 5(b)), it is shown that the frequency-reflection-loss curves are substantially modified with the rise in this process parameter, observing a large shift to a lower frequency range. Finally, Fig. 5(c) depicts the sintering time t effect, showing the same shift to lower frequencies of the frequency–reflection–loss curve, albeit more moderately. In conclusion, the increase of all the three studied process parameters (P, T and t) shifts the maximum RL to lower frequencies. A value of RL greater than 20dB means that the material absorbs 99% of the input power [10]; therefore, as all the RL values are above 50dB, they can all be considered as appropriate shielding materials. Overall, the samples exhibit a relatively wide attenuation bandwidth in the frequency region from 2E7Hz to 2E8Hz.
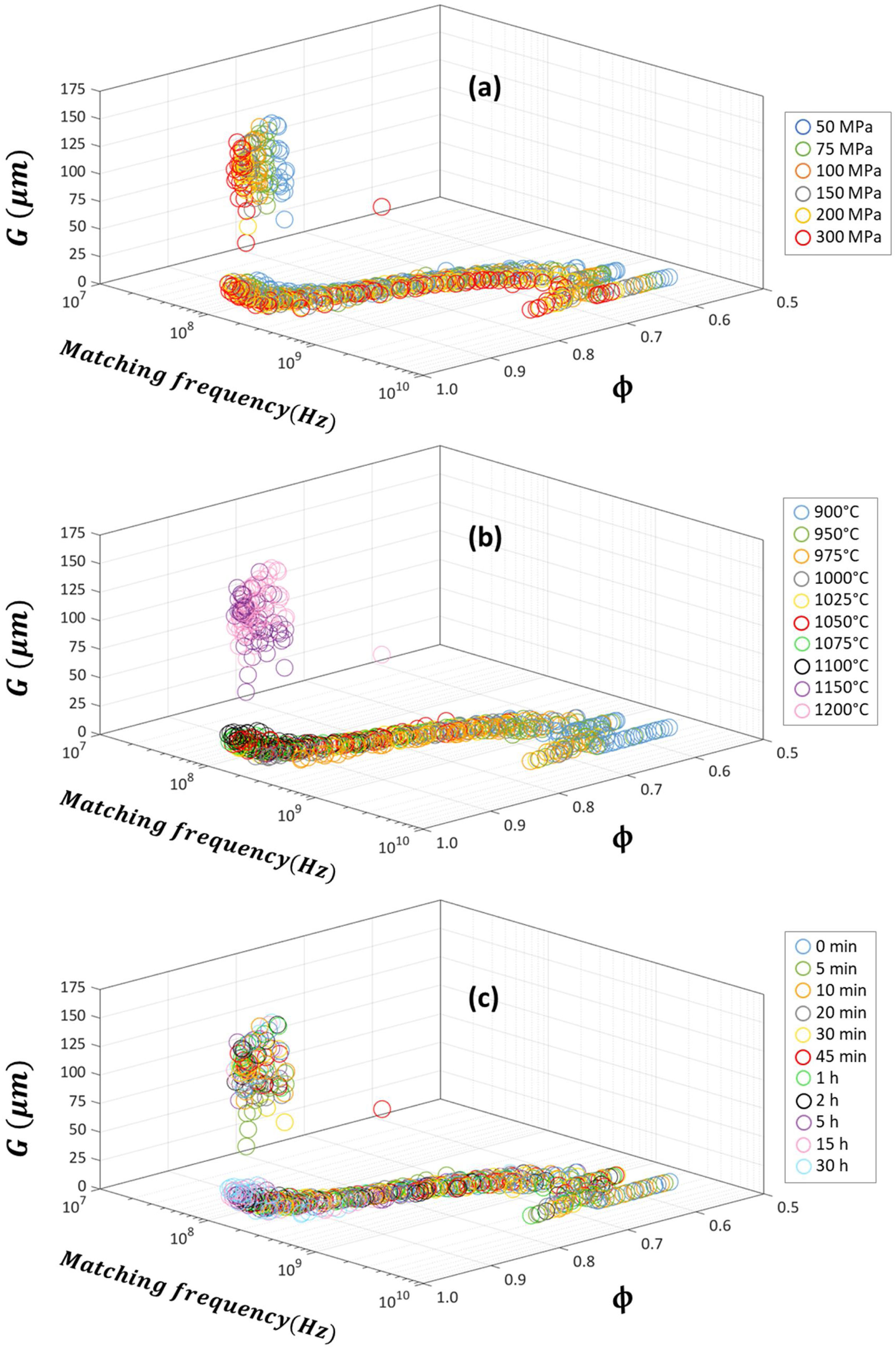
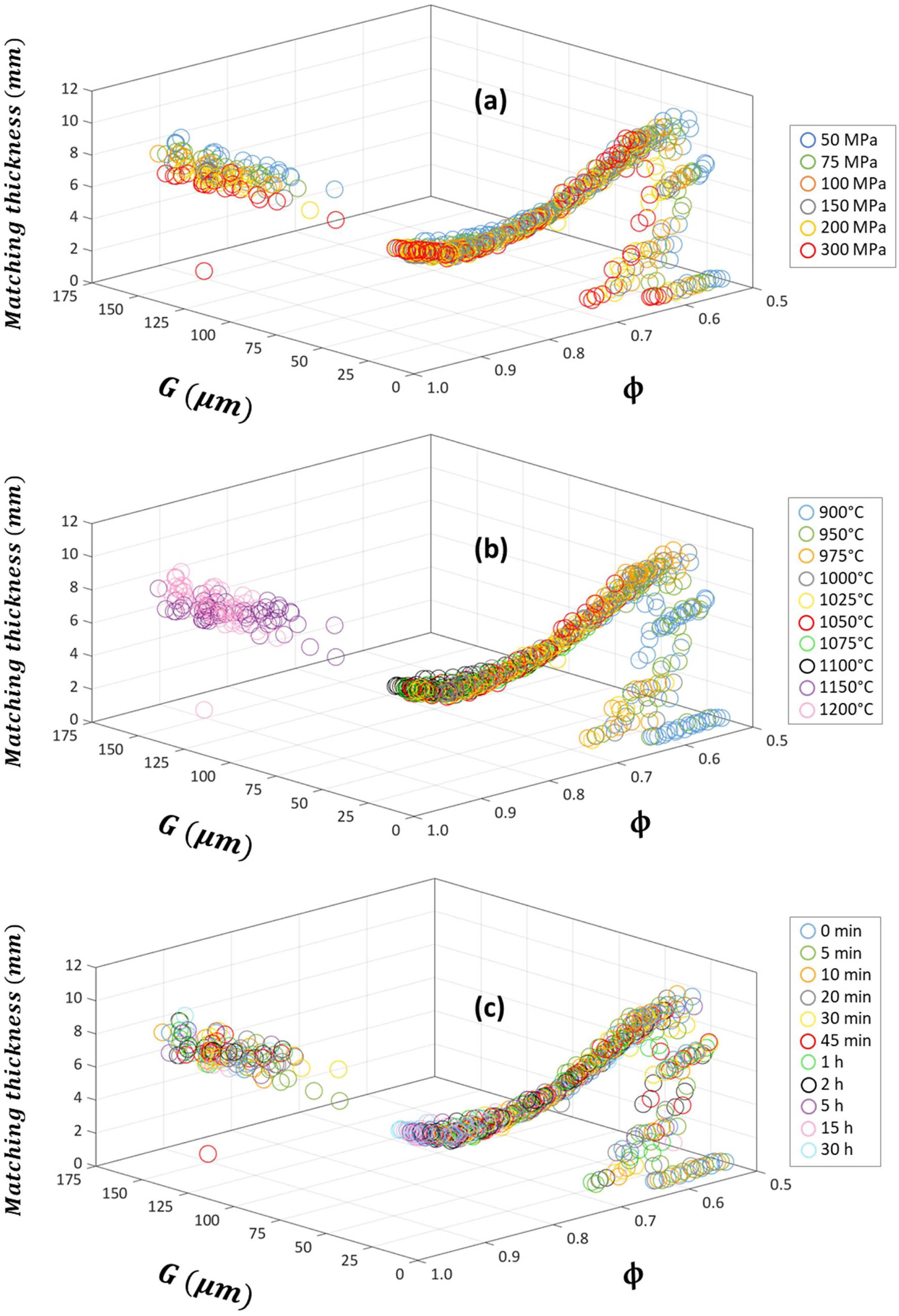
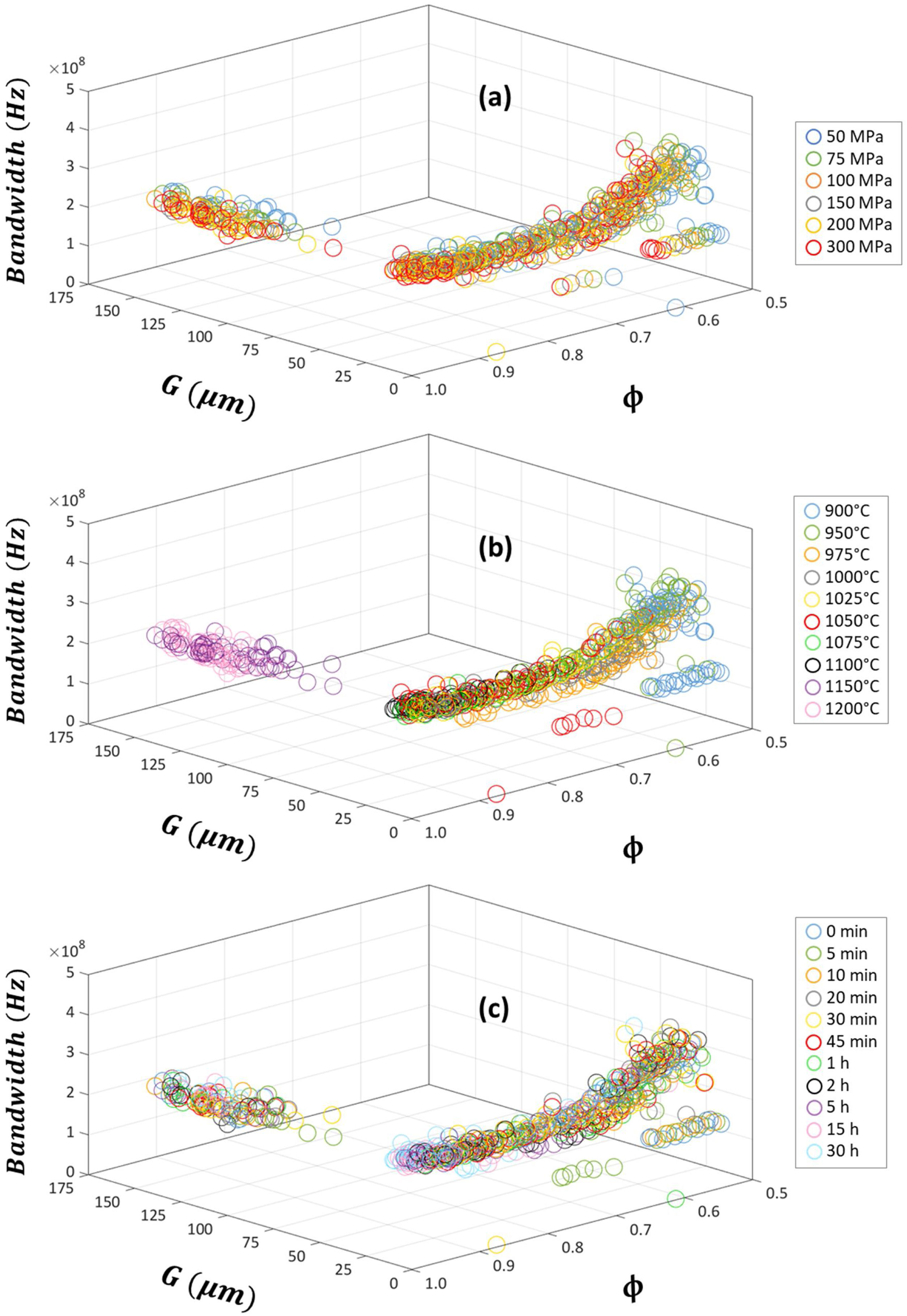
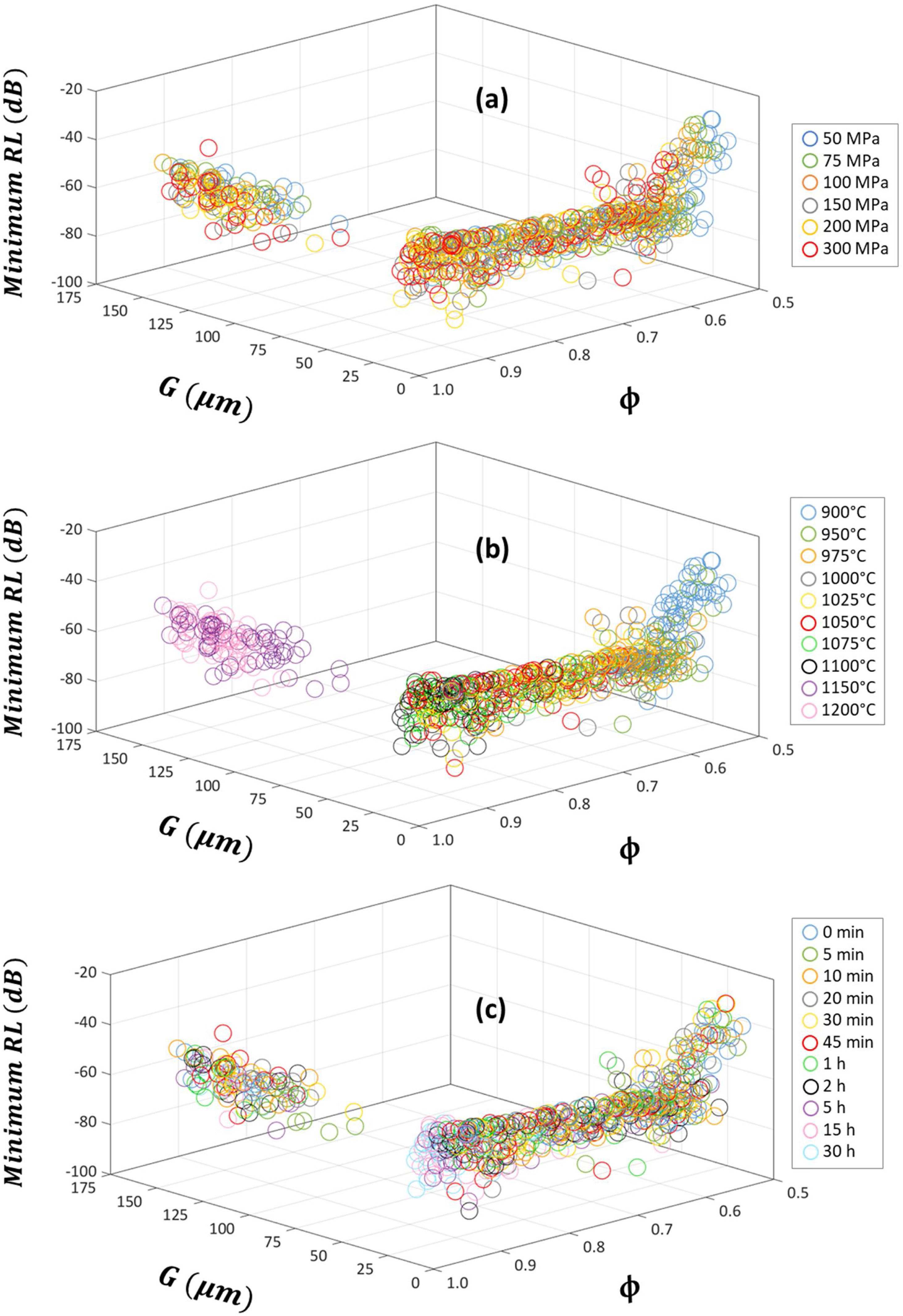
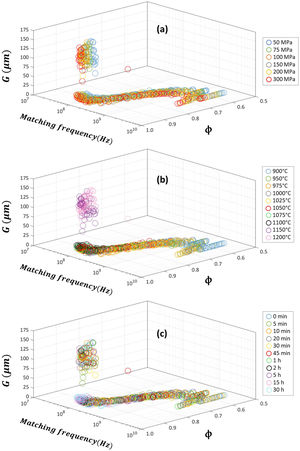
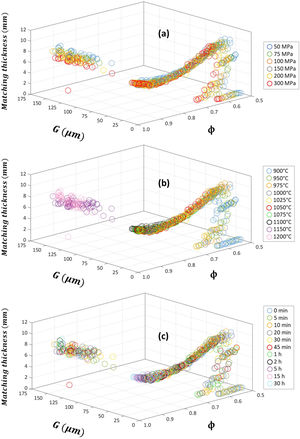
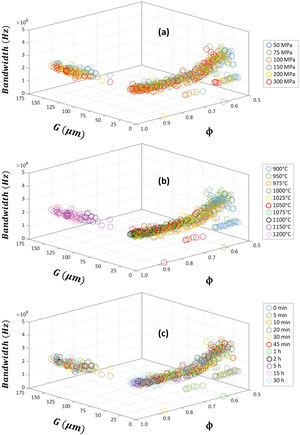
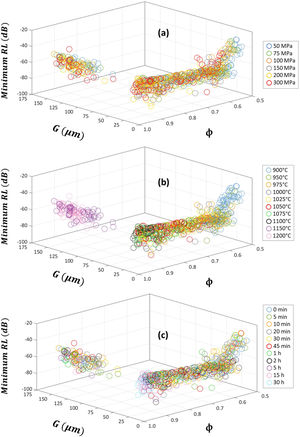
The calculated absorption parameters, i.e. the matching frequency fm, matching thickness dm, bandwidth for RL≤−20 dB and minimum of reflection-loss RL, are listed in the Supplementary Tables 1–10 and depicted in Figs. 6–9, where the effects of pressing pressure P, sintering temperature T and sintering time t are shown in panels (a), (b) and (c), respectively. Larger average grain size G scale graphs of these figures are shown in Supplementary Figs. 4–7, respectively.
The sintered microstructure (relative density ϕ and average grain size G) dependence of matching frequency fm of the sintered Cu-doped Ni–Zn-polycrystalline ferrite can be found in Fig. 6. The pressing pressure P, sintering temperature T and sintering time t effects are depicted in panels (a), (b) and (c), respectively. Larger average grain size G scale graphs are shown in Supplementary Fig. 4, with the same panel distribution for the three studied process parameters. In general, it is observed that the matching frequency fm is influenced by both the relative density ϕ and the average grain size G, decreasing with the rise of both microstructural parameters as long as abnormal grain growth is not occurred, which in our case is perfectly identified in the samples sintered at 1150° and 1200°C (Fig. 6(b)). All three process parameters (P, T and t) enhanced the sintered microstructure of the final specimen, decreasing the calculated matching frequency fm.
The sintered microstructure (relative density ϕ and average grain size G) dependence of matching thickness dm of the sintered Cu-doped Ni–Zn-polycrystalline ferrite can be found in Fig. 7. The pressing pressure P, sintering temperature T and sintering time t effects are depicted in panels (a), (b) and (c), respectively. Larger average grain size G scale graphs are shown in Supplementary Fig. 5, with the same panel distribution for the three studied process parameters. In general, it is observed that the matching thickness dm decreases with the rise of the relative density ϕ and increases rapidly at low average grain size G values and subsequently peaks. The maximum value of the matching thickness dm is observed around 1μm, tending to a constant value of 6mm for higher average grain sizes, and worsening when abnormal grain growth is observed. As aforementioned, all three process parameters enhanced the sintered microstructure of the final specimen, generally decreasing the calculated matching thickness dm, provided that normal grain growth occurs.
The reason for matching frequency fm (and also matching thickness dm) variation in polycrystalline ferrites according to the main microstructure parameters (relative density ϕ and average grain size G) may be found in the basic principles for designing EM-wave absorbers. The following relationship between fm and dm can be written [42]:
This relation states that fm·dm value is affected mainly by μ′ values. From Supplementary Fig. 1 it follows that increasing P, T and t causes the increase of μ′, which results in the decrease of fm·dm value. Also fm value decreases with increasing relative density ϕ and average grain size G (see Fig. 6).
The sintered microstructure (relative density ϕ and average grain size G) dependence of bandwidth for RL≤−20dB of the sintered Cu-doped Ni–Zn-polycrystalline ferrite can be found in Fig. 8. The pressing pressure P, sintering temperature T and sintering time t effects are depicted in panels (a), (b) and (c), respectively, and larger average grain size G scale graphs are shown in Supplementary Fig. 6. As the relative density ϕ increases, the bandwidth slightly decreases, tending to a constant value of 2E8Hz. Similarly, the bandwidth also decreases with the rise of average grain size G, but this reduction is not constant but more pronounced at low G and lighter at higher values of the parameter, tending to the same constant value of the bandwidth. Unlike the previous absorption parameters, abnormal grain growth (mainly occurred at 1150° and 1200°C) does not significantly worsen the bandwidth, reaching similar values for G>25 μm.
The sintered microstructure (relative density ϕ and average grain size G) dependence of minimum reflection-loss RL of the sintered Cu-doped Ni–Zn-polycrystalline ferrite can be found in Fig. 9. The pressing pressure P, sintering temperature T and sintering time t effects are depicted in panels (a), (b) and (c), respectively. Larger average grain size G scale graphs are shown in Supplementary Fig. 7, with the same panel distribution for the three studied process parameters. Data indicates that the minimum reflection-loss RL quickly increases at short relative density ϕ and average grain size G values, tending to a constant value of −60dB, and worsening when abnormal grain growth is occurred. As in the previous absorption parameters, the rise of the three studied process parameters (P, T and t) generally improve the final microstructure, enhancing the absorbing capacity of the ferrite. It is well known that multidomain have a greater capacity to absorb electromagnetic radiation due to their greater contribution to domain wall motion, which promotes a higher resonance effect, dissipating energy as heat, and hence, rising the reflective property of the material [23,43]. Larger grain size values suggest the formation of multidomain structures that promote greater domain wall motion, hereby improving magnetic characteristics and, therefore, a better electromagnetic radiation absorption capacity of the final specimen. But, as set before, when a minority of grains begin to grow at the expense of the surrounding grains, some pores get trapped inside those grains (see Fig. 2 and Supplementary Figs. 1 and 2), increasing the number of pinning sites and hindering the domain wall motion, and thereby, reducing magnetic properties. Also, bigger grains are usually related with unwanted phenomena of secondary phase precipitation, as can be observed in the SEM micrographs in Supplementary Figs. 1 and 2. These precipitated crystals were observed to occur first at triple joint points, then on grain boundaries and, finally, when the triple joint points and grain boundaries are saturated, inside the ferrite grains [31,32], hindering the magnetization process through the inhibition of spin rotation and domain wall motion and worsening therefore the electromagnetic performance of the ferrite as shown in Figs. 6–9 and Supplementary Figs. 4–7.
ConclusionsAn in-depth analysis of the effect of sintered microstructure, mainly characterize by the relative density ϕ and the average grain size G, of a Cu-doped Ni–Zn polycrystalline ferrite on their shielding properties has been conducted in the 1MHz to 1GHz frequency range. Three have been the process parameters in the traditional ceramic route selected to modify the final sintered microstructure: the pressing pressure P, the sintering temperature T and the sintering time t of the thermal cycle used in the sintering stage. In addition, four absorption parameters were calculated to characterize the shielding properties of the material: the matching frequency fm, the matching thickness dm, the bandwidth for RL≤−20dB and the minimum of the reflection-loss RL.
The variation of the pressing pressure (50≤P≤300 MPa), sintering temperature (900°≤T≤1200 °C) and sintering time (0≤t≤30h) has allowed obtaining a widely-dispersed range of sintered microstructures (660 specimens) with both kinds of grain growth processes: normal and abnormal.
It has been found that the four studied absorption parameters depend on the sintered microstructure and can be modified by changing the process parameters, indicating that electromagnetic absorption characteristics on the current ferrite composition can be tailored by changing the processing conditions of the shielding material. Generally, the rise in pressing pressure P, sintering temperature T and sintering time t, conduct to a better sintered microstructure, therefore improving the shielding properties of the final specimens, provided that abnormal grain growth and/or second precipitated phases are not conducted, which has been mainly observed for the sintering temperatures of 1150° and 1200°C.
This knowledge could be used to design a better ferrite shielding material, which will be that with the greatest reflection-loss absolute value |RL|, the widest bandwidth, the smallest matching thickness, and the lowest matching frequency.
The best performance of electromagnetic absorption in the 1MHz to 1GHz band was presented by the (Cu0.12Ni0.23Zn0.65)Fe2O4 ferrite uniaxially pressed at 200MPa and thermally treated at 1050°C with a dwell time of 2h, reaching a maximum |RL| of 82.55dB at a frequency of 1.31×108Hz, with an attenuation bandwidth of 2.39×108Hz and a matching thickness of 6.4mm.
This study has been supported by Ministerio de Economía y Competitividad (Spain) through grant number (MAT2016-76320-R) and by Universitat Jaume I (Spain), grant numbers (UJIB2017-48 and UJIB2020-13). Complex relative permeability and permittivity determination were carried out at the central facilities (Servei Central d’Instrumentació Científica) of the Universitat Jaume I.