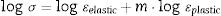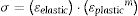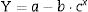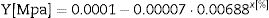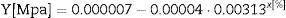Modeling the mechanical behavior of a kaolin ceramic paste owing to the variation in the particle size

Abstract

The mechanical behavior of mineral pastes is controlled by minerals of clay origin since their laminar type morphology allows a special configuration of the particles, which allows them to dissipate mechanical forces applied by means of high plastic deformations. In this research, a clay used in the ceramics industry was evaluated and two granulometries called MG 270 (53 μm) and MG 325 (43 μm) were studied. Simple compression tests were performed to evaluate the mechanical performance of each of these materials. The simple compression data allowed to determine the radial flow of the particles within the control volume (specimens evaluated), the random organization of the clayey material demonstrates a rapid energy dissipation, translated into rapid advances from elastic state to plastic states of deformation. Later, the finite element method (FEM) was used to simulate the possible states of stress and deformation that are produced in ceramic pastes constituted by this type of clay. This allowed to obtain a graphic idea of the distribution of stresses and deformations, areas of stress concentration are evidenced, where it is possible that the start of microcracks occurs, which are generally the cause of generalized fracture and sudden faults of the ceramic paste.

Resumen

El comportamiento mecánico de las pastas minerales es controlado por los minerales de origen arcilloso, ya que su morfología tipo laminar admite una configuración especial de las partículas que les permite disipar esfuerzos mecánicos aplicados mediante altas deformaciones plásticas. En esta investigación se evaluó una arcilla empleada en la industria cerámica, y se estudiaron dos granulometrías denominadas MG 270 (53 μm) y MG 325 (43 μm). Se ejecutaron ensayos de compresión simple para evaluar el desempeño mecánico de cada uno de estos materiales. Los datos de compresión simple permitieron determinar el flujo radial de las partículas dentro del volumen de control (especímenes evaluados), la organización al azar del material arcilloso evidencia una rápida disipación energética, traducida en rápidos avances de estado elástico a estados plásticos de deformación. Posteriormente se empleó el método de elementos finitos (finit element method [FEM) para la simulación de los posibles estados de esfuerzo y deformación que son producidos en pastas cerámicas constituidas por este tipo de arcilla. Esto permitió obtener una idea gráfica de la distribución de esfuerzos y deformaciones, se evidencia zonas de concentración de esfuerzos, donde es posible que ocurra el inicio de microgrietas, que generalmente son las causantes de la fractura generalizada y las fallas súbitas de la pasta cerámica.

Introduction

The plasticity of the pastes is defined as the capacity of anelastic deformation without cracking [1–3], which is the result of a complex mechanical behavior of highly concentrated dispersions of particles in an aqueous medium that has dissolved and complexed ions in solution. Plasticity is a property of clays, which is determined mainly by the size of the particles in the form of plates, therefore, the smaller the planar particles of the clay, the more plasticity it can achieve [1,4,5]. This is associated with a physicochemical behavior of the surface of clays, so that the superficial electric potential also affects plasticity in principle [1,6–8].

This implies that the study of plasticity is a specific theme of the rheology of clays and the interaction of these with the other minerals present in the paste, acting as lubricants in the interstices of the particle packs that make up the paste [9–13] and in whose scenario the adsorption on the clay material of the ionic groups of water (H+ and OH−) and other ions in solution surrounding the particles also appear [9,14,15].

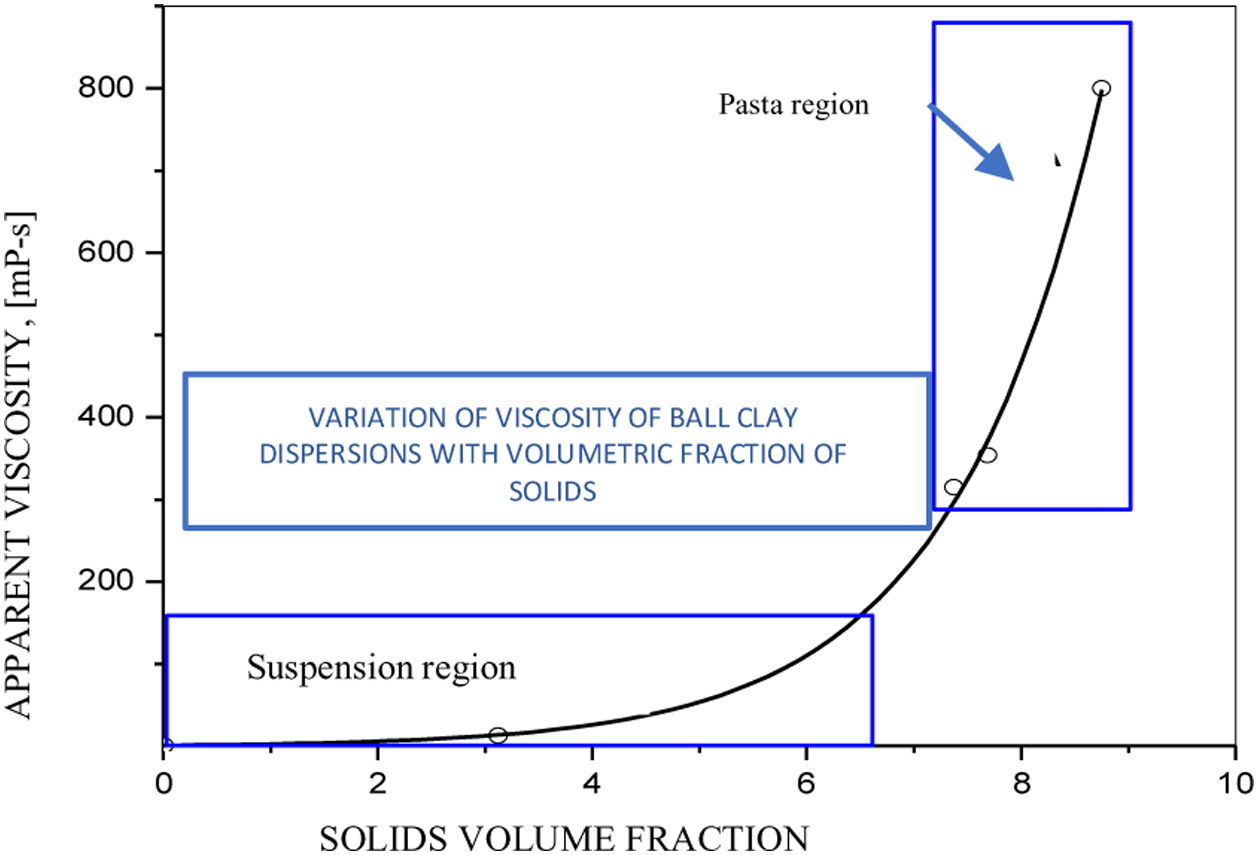
It is widely known that the addition of solid materials drastically influence the rheological behavior of suspensions and pastes, specifically those that are formed by a Newtonian fluid phase and a particulate system composed of a single mineral (see Fig. 1), being studied by several investigators [7,15–22], and there is a good level of understanding of the effects generated by the particle size distribution, the volumetric fraction of solids in the suspension, as well as some electro-viscous effects generated by hydrogen potentials (pH) and the presence of potential determining ions that exert a strong control of the Z potential at the surface of the solids.

Fig. 1.

Variation of the viscosity of a “Ball clay” dispersion, and suspension and paste regions [22].

On the other hand, there is a consensus about the dynamic effects of the suspension composed of a single mineral, when subjected to “creep” tests, allowing to determine the relaxation times t_R, as a measure of the memory of the suspensions [20].

It has been established that the water content, particle size and particle size distribution, and particle–particle interactions, are the most important factors that influence plasticity. The increase in water content improves the plasticity of the ceramic systems, but has the drawback of increasing the shrinkage in the drying process [23]. With a substantial increase in contraction, there is a greater chance of originating microcracks. The modification of particles and the interactions of particles is done by the addition of dispersants or coagulants. The size of the particles and their size distribution are limited by the different physical and chemical properties of each material, being inherent and specific to each material.

Some authors [7] suggest that the addition of clay materials of organic and inorganic origin improve and drastically control the viscosity and mechanical behavior of ceramic suspensions, reflected in the optimization of deformation processes and conformation of ceramic bodies. It has been established that water content, particle size and particle size distribution, and particle-particle interactions are the most important factors that influence plasticity [16,24,25]. The increase in water content improves the plasticity of the ceramic systems, but has the drawback of increasing the contraction in the drying process. With a substantial increase in contraction, there is a greater chance of originating microcracks.

The colloid chemistry plays a fundamental role in the explanation of these phenomena, as it is seen at present it is to relate the chemical theory with the rheological concepts to explain these complex behaviors, Other studies are based on performing a procedure that involves chemical properties of the materials in the constitutive models and how these affect the rheology of the suspension, focusing their work on explaining the thixotropic behavior that occurred in caolithic ceramic pastes with the addition of colloidal carbon particles. They found that the high addition of carbon particles avoids thixotropic behavior, with predominant dominance of the solid component; the edge-face contact of the particles is not the one that governs the thixotropic behavior, being the random contact of the particles the one that determines and controls the rheology of the paste.

The interface physics chemistry is skillful in describing the interparticle interactions, but the relationships that arise integrating mineralogical and chemical components of the dispersants do not yield good results. At present, these types of relationships are still being considered to explain complex phenomena by making changes and new advances in modeling, and it is essential to identify the variables that really affect and control the process.

The modeling of behaviors still unknown in the light of classical rheology, may have some complexity, but it is necessary to determine theoretically and adequately explain the effects of materials that are used daily in the ceramic industry; literally continues to develop new products in the darkness of neglected theoretical knowledge, by the desire to produce more every day, whatever the cost, without the minimum theoretical support that is essential for the optimal development of the processes of conformation. In the same way it is necessary to clarify that the bibliography review is not absolute, in the rheological research every day new developments and advances arise, this information not being divulged by the industry, since it is part of the fast race toward commercial success and technological.

The simple compression test is carried out for soft materials such as clays, it allows to identify the mechanical behavior of clay materials subjected to uniaxial stresses; From these tests, characteristic data of the mechanisms of deformation, identification of linear regions of elastic behavior and non-linear regions of plastic behavior were obtained; these deformation regions were evidenced with the stress–deformation graph [3,26,27], where the beginning of the anelastic deformations can be glimpsed that indicate the capacity of each clayey material to dissipate the mechanical energy applied in plastic deformation [26,28–30].

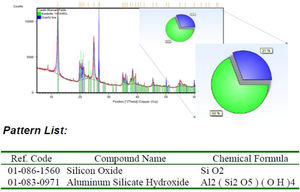
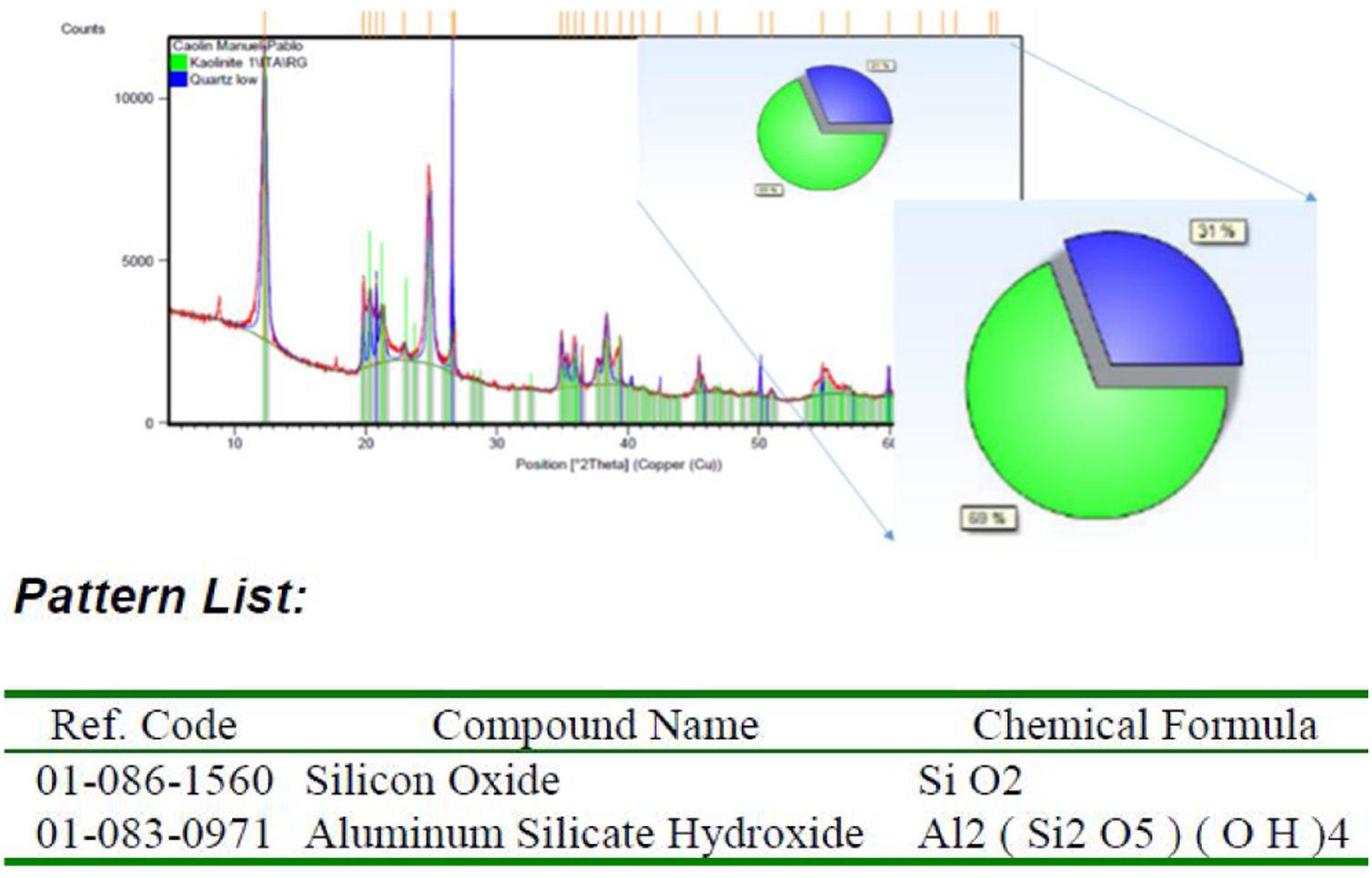
Materials and method

Clay samples

The clay used was kaolin belonging to an active mine located in the Municipality of La Unión, Antioquia, Colombia. In order to characterize the kaolin sample, the technique used to quantify the crystalline phases was X-ray diffraction (XRD) (Siemens, D5000). To quantify the initial amount of iron in the kaolinitic mineral and subsequent characterization of the aqueous discharge solutions, the atomic absorption spectrophotometer (Thermoscientific, Ice 3000®) equipped with a hollow cathode iron lamp was used. For the characterization of the particle size distribution of the kaolin, a MasterSize 2000E® particle size distribution meter was used.

The results of the X-ray diffraction (see Fig. 2) show in the ore 69% of Kaolinite Al₂Si₂O₅-(OH)₄ and 31% of quartz (SiO₂). The sample does not report the contaminants of the kaolin that generate the change of the coloration as the Hematite and the Goethite, this is due to the low concentration that it has in the kaolin, that is why an atomic absorption spectrophotometry was performed, determining a percentage initial iron of 0.19% by weight.

Fig. 2.

DRX of Kaolin.

Preparation of the sample

The mineral was named MG and was properly sieved and separated in meshes number 270–325. These granulometries were selected based on industrial criteria, since these are generally the sizes used to prepare the ceramic suspensions. The clays were sieved in the wet way; suspensions were prepared with 15 kg of material and 45 L of water. The dispersion and homogenization of clay materials was carried out in approximately 1 h. After completing this step, the suspension was sieved. The resulting suspension was filtered on a PHENETON 34-PH5 filter press, with a capacity of 30 L. Of the 30 L processed, approximately 7 kg of pulp was obtained with humidity of around 40% w/w.

After this, the paste was homogenized in a McCALLISTER 10 R type mixer. The processing capacity of this equipment is of minimum 10 kg, therefore, it was necessary to carry out several stages of pressed filter to obtain the necessary amount of pulp. The rotation speed of the homogenizer mechanism recommended for this procedure is 5 rpm; To obtain a paste with suitable characteristics, it is recommended to carry out three stages of homogenization. It is important to highlight the importance of this stage, since the homogenizing equipment has the ability to rebuff the processed ceramic paste, that is, it has a vacuum chamber that is capable of greatly releasing the air present in the paste, thus eliminating possible regions of origin of failure, since the air acts as a concentrator of stress, causing a decrease in the deformation capacity of the studied system.

Due to the requirements of the equipment used to evaluate the specimens, these were prepared with dimensions of 100 mm × 50 mm; from this final stage about 25 specimens were obtained for each cut, that is, a total of 150 specimens were prepared, which were mechanically evaluated by simple compression and triaxial compression.

Geomechanically tests

The main objective of this research is to evaluate the behavior and mechanical performance of clay materials used in the manufacture of ceramic elements; Two widely used and certified tests by the ASME were proposed, that is, standardized tests that allow having coherent and standardized data that give reason for the mechanisms of deformation and material failure. In this particular case, the soil mechanics test, identified as Simple Compression Test, was used; This test is carried out for soft materials such as clays under study, it allows to identify the mechanical behavior of clay materials subjected to uniaxial stresses; From these tests, characteristic data of the deformation mechanisms were obtained, linear regions of elastic behavior and non-linear regions of plastic behavior were identified; These deformation regions were evidenced with the typical stress–deformation graph, where the beginning of the anelastic deformations can be glimpsed that indicate the capacity of each clayey material to dissipate the mechanical energy applied in plastic deformation.

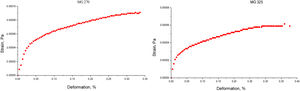
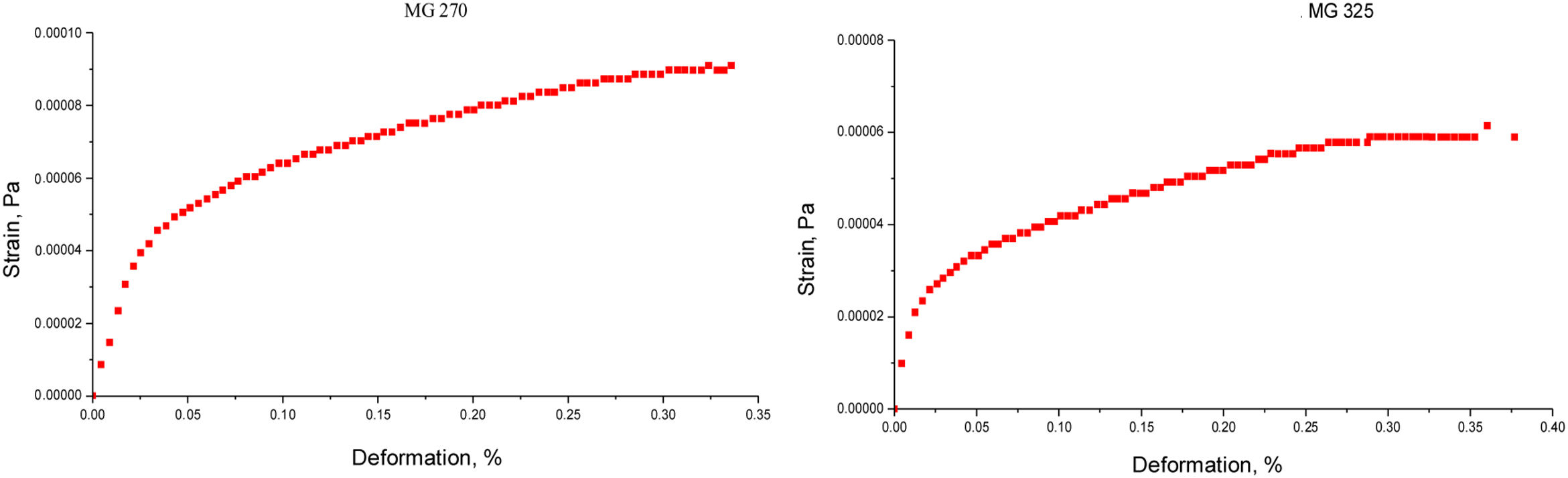
Results and discussion

Deformation tests

The study of the mechanical behavior of ceramic pastes, only focused from the structural point of view, related to the distribution of particle size and the specific surface area, that is, the chemical and mineralogical properties of the clays were not taken into account, since it only seeks to understand the dissipation of mechanical energy from the theory of the mechanics of the continuous medium (Fig. 3).

Fig. 3.

Stress–deformation of the mineral sample.

The stress–deformation graph for clay MG 270 shows the total deformation capacity of this material in terms of percentage. It was evidenced that the ceramic system has a short region of linear deformation, which indicates that the dissipative process of plastic order has early start. The maximum percentage reached by the system is around 35%; this means that the ceramic paste specimen constituted only by MG 270 clay was able to deform only 35% of its total dimension before reaching the final fracture.

The total deformation capacity of the MG 325 ceramic paste in relation to the particle size distribution does not vary greatly, the anelastic region is similar to that achieved by MG 270, the elastic jump toward the plastic deformation regions is performed with greater speed. The anelastic region is identical, reaching total values of 35% in deformation, these values are obtained with smaller magnitudes of stress, which seems to indicate a better packing of the particles due to distributions of smaller sizes to 45 μm. The packing of the particles promotes the lower values of interparticle cohesion, the construction of landslide or deformation planes, are used as paths where the applied stress is dissipated. The dissipation of mechanical energy depends on the capacity of interparticle cohesion, this related directly with the ease of construction of the deformation planes mentioned. If the clay material has high values of interparticle cohesion, the total deformation will be low, therefore, the characteristic value of this property is an indirect indicator of the total capacity of deformation or energy dissipation of the evaluated material.

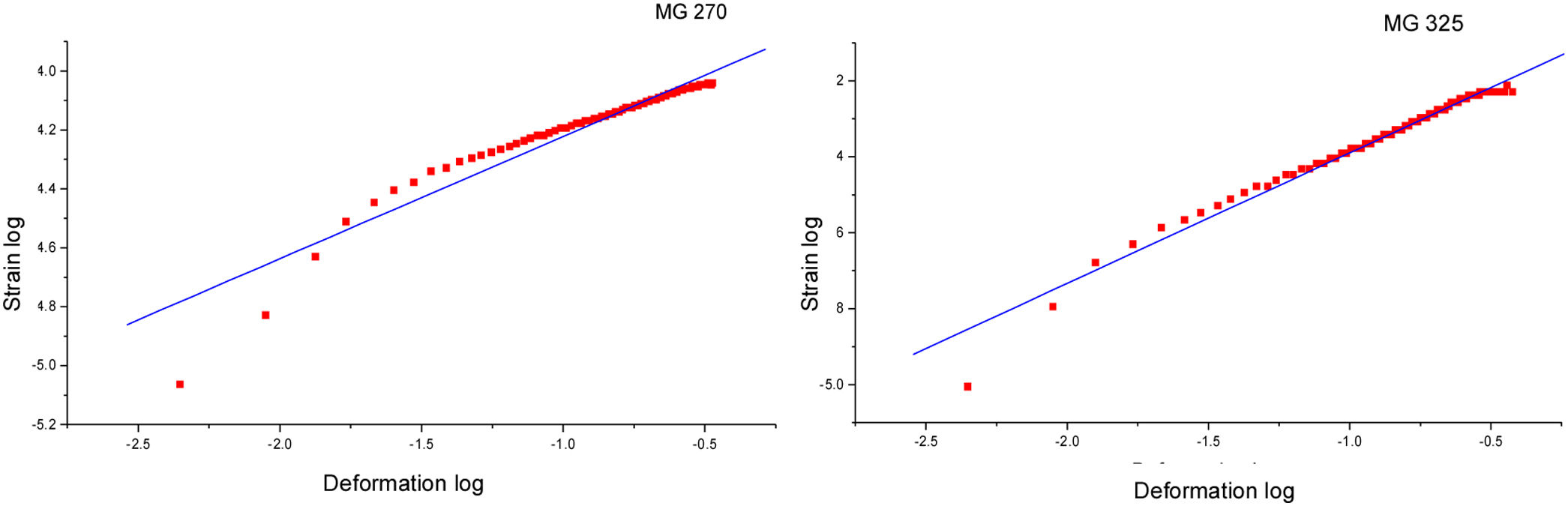
Mathematical model

From the obtained graphs, a behavior was found mostly adjusted to linearity, therefore, it was decided to raise the models from the logarithmic point of view. This offers the advantages of finding linear models that are easy to use and apply, away from the various complications offered by different numerical models of a higher order, which must be solved by advanced numerical methods.

In this case the numerical model describing this behavior is as follows:

where m is the slope of Fig. 4. The values obtained from R = 0.9595; SD = 0.04853, in other hand MG 270 and R = 0.9801; SD = 0.02152. In the case of MG 270 and MG 325, high correlation between the experimental and simulated data is evident in the region of high deformation but in the region of low deformation a low correlation of the data is evident. Applying laws of logarithms and equating to zero we have:

Fig. 4.

Linearization of the simple compression graphs of the tests of the ceramic samples.

This expression is valid for modeling the total mechanical deformation behavior. Now we proceed to propose a numerical expression for the anelastic behavior of MG 270 and MG 325.

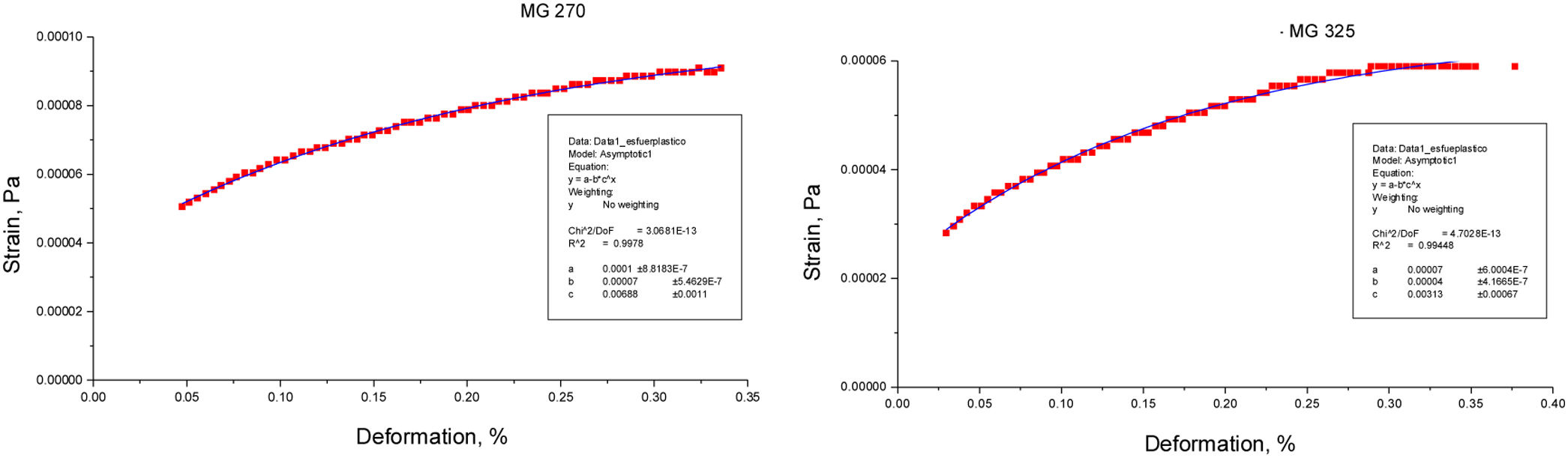
The curve that follows the plastic deformation region is not totally linear, therefore, an expression of asymptotic structure of values with high numerical correlation is considered (Fig. 5). The expression that describes this behavior is:

where Y is the stress of creep, a, b and c are constant and x(εplastic) is the plastic deformation that can be obtained from (2). For MG 270 the following expression is obtained:

Fig. 5.

Anelastic behavior of ceramic samples.

and for MG 325 the following expression is obtained:

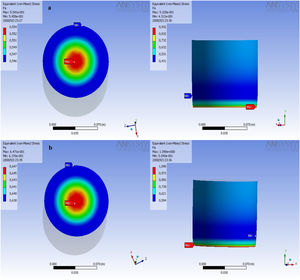
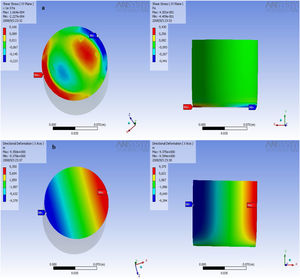
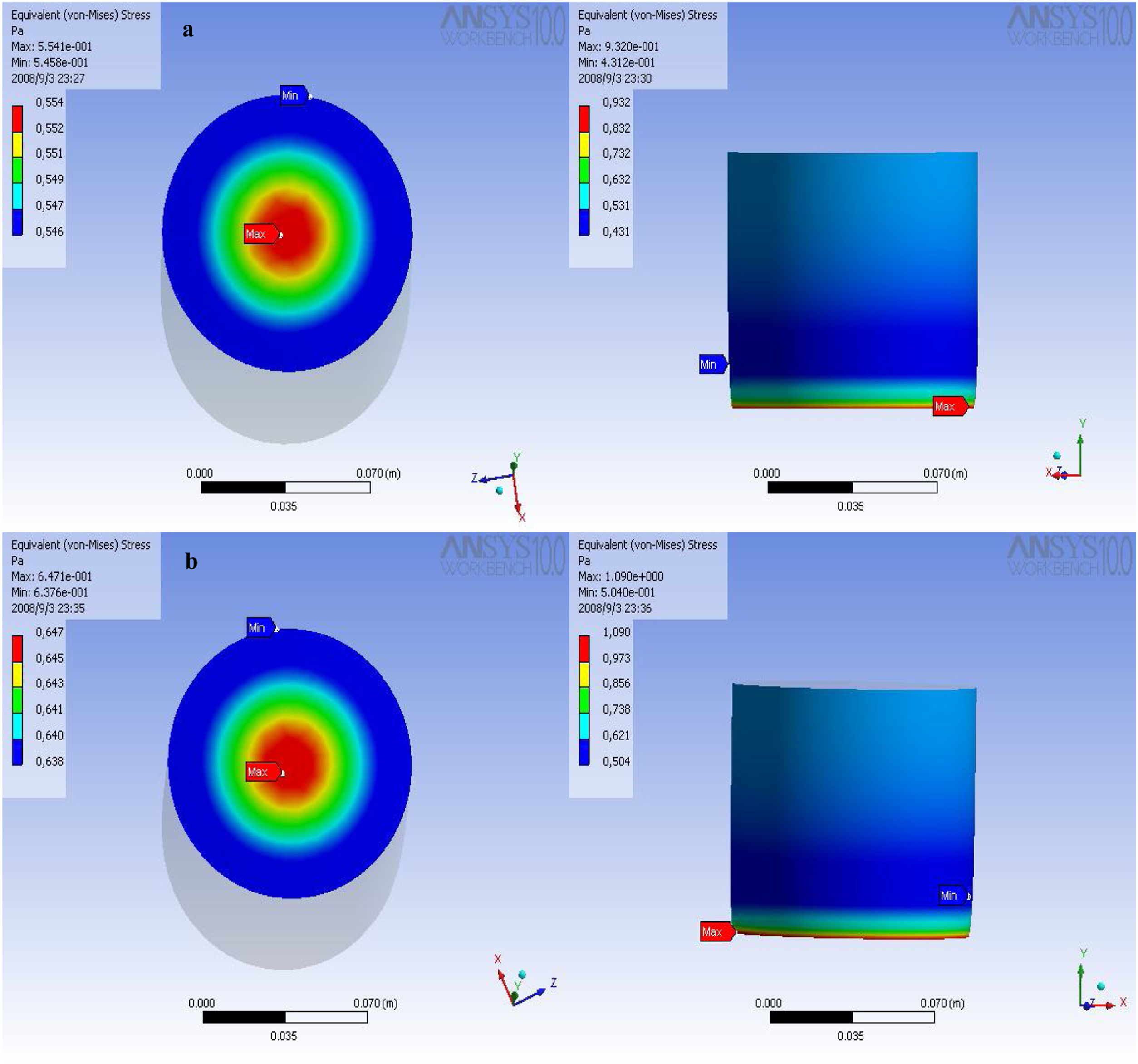
Finite element simulation

The theoretical analysis criteria used to perform the simulations are based on the theoretical framework, in this case the Von Mises criterion was used, the fundamental basis of high-order analyzes, that is, considerably high magnitudes of deformation. In this case, the stress distribution achieved by MG 270 and MG325 (Fig. 6a and b, respectively) are presented on the upper face, where the mechanical stress or load is applied. The application of the load was tried to perform most possibly close to those applied in the conventional process of deformation (manufacture in plant). The region of red color, is where the greatest stress occurs, the distribution of the load is performed radially, indicating the synchronized movement of the particles; the effort is dissipated toward the edges or periphery of the specimens. This radial behavior is influenced by the geometry of the particles, as will be observed in the following simulations, the behavior is maintained, regardless of the particle size distribution. The planes of deformation constructed by the particles move in such a way that it is possible to find constant deformations in the periphery. The mobility of the particles is only obstructed in the lower face of the specimen, it is there in that specific region where the particles are unable to continue with their trip, until the final failure of the ceramic system occurs.

Fig. 6.

Distribution of efforts achieved in the upper face, where the effort or mechanical load is applied by (a) MG 270, (b) MG 325.

The stress distribution on the perimeter of the MG 270 and MG 325 specimens (Fig. 7a and b, respectively), showing a progressive decrease of resistance, stress descend from the center of application of the load until again a maximum point in the lower region. The progressive decrease of the resistance is attributed to a progressive accumulation of the particles, these lose mobility, since the planes of deformation undergo blockages and it is not possible for them to continue moving within the control volume.

Fig. 7.

Distribution of shear stress in the samples (a) MG 270, (b) MG 325.

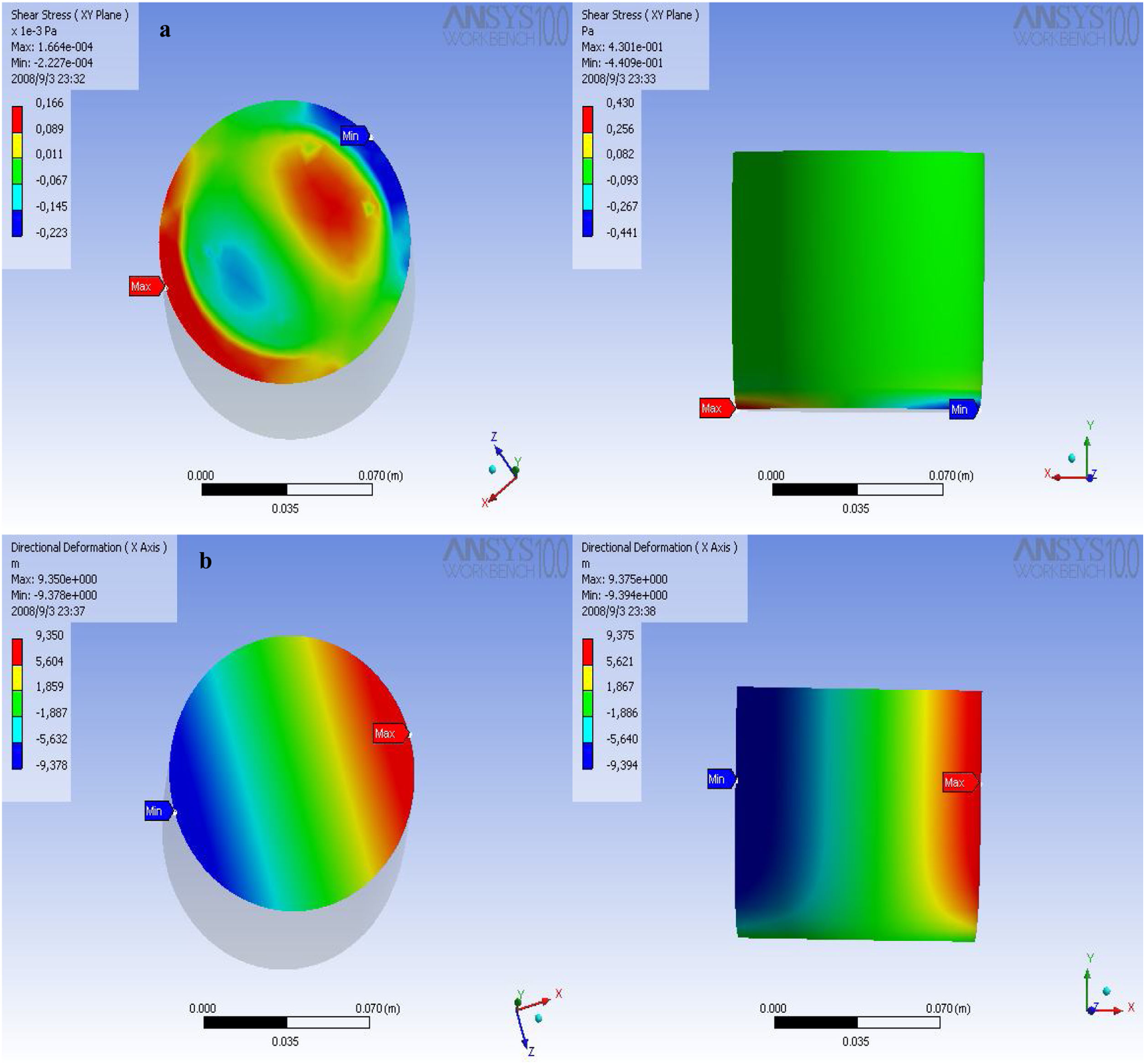
Fig. 7a shows the distribution of shear stress in the specimens, the magnitude of the shear stress is lower compared to those obtained in the Von Mises criterion. The particles are forced to move asynchronously, but keeping the radial distribution shown above, on this side you can see intermediate regions of concentration of stress, at the edges of the specimen, there are two distributions of opposite magnitudes, high values in an edge and low values on the opposite edge. The intermediate region shows blockage of the deformation planes, because the green and blue areas have values that indicate tension and the red regions have values related to compression, which indicates blocking of the deformation states. In these regions mobility is drastically reduced by this behavior, causing strong concentrations of stress responsible for the final failure. In these regions the microcracks are born, which travel throughout the ceramic system, until reaching peripheral regions as shown in the distribution of shear stress, where the negative magnitudes indicate tension, and it is known that these clay materials, offer excellent resistance to compression, but not tension, therefore in these regions the failure eventually occurs; in the specimens evaluated, the angle of failure is at 45° indicating that the fracture occurs by shear stress. In this case the von Mises criterion is broadly generous, since its logical structure, states that the failure or distortion of the bodies occurs by shear stress, the values obtained with this criterion are higher compared with those achieved in the theory of shear stress.

For the distribution of size 325 mesh, a similar behavior is evidenced. Von Mises stress distribution is performed radially, which proves what is found in mathematical models where the logical structure is maintained for all materials. Stresses are concentrated in the middle region of the upper face, the load distribution is slightly higher, and coincides with the graphical data of stress–deformation. The displacement of the particles is executed in a descending manner, finding the lowest values in the peripheral region of the specimens. The magnitudes of stress in the peripheral middle region are smaller, therefore, it is expected that in this area the greatest deformations will be found.

The directional deformation shows slight displacement toward an edge, in the middle region there is progressive blockage of the planes of deformation, since stresses indicate tension state, directional deformation show systematic decay. In the middle region of the periphery, it is possible to observe a logarithmic distribution of the deformation, the clay particles lose mobility in this zone, due to the change of orientation of the stresses. In the distribution of loads can be found shear stresses and normal stresses, these two types of loads are supported by the particles, are forced to move in different directions, finding regions like the central where several planes of deformation converge with different directions, causing the loss of mobility and the concentration of particles. It is to be expected that the stress travels through the particles, the charges are observed as applied energy that moves through the control volume, and the way to dissipate this is the deformation of the ceramic system.

The shear stress is distributed with some radial symmetry, again the middle regions, concentration of stresses, and systematic blockages of the deformation planes are found. It is interesting to find regions of high stress limiting regions of low stress (tension stress), the planes of deformation travel in a radial direction, when they reach the periphery, change the orientation of the stresses, dissipating in the peripheral region. Although in this region almost all stress is strained, there is no concentration of stress, the final failure is reached quickly.

Conclusions

It was proposed in this investigation to perform the analyzes based on two fundamental properties, particle size distribution and specific surface area. It was found that the capacity of mechanical deformation of the ceramic pastes constituted by these materials does not depend on these properties, the characteristic values of total deformation have no direct correlation with this, the variation that was expected (due to theoretical connotations), were not evident, the values of deformation did not suffer great changes with this measurement.

In this research always cited the expression “Dissipation of mechanical energy”, this is not more than the energy term of the total deformation, the ability of these materials to dissipate mechanical energy in deformation depending on how it was raised in this work of the properties physical, since the ceramic paste is a solid with some amount of water retained, therefore, the mechanisms of deformation must have close relationship initially with the physical variables. From this premise, the idea arises to think that the mineralogical properties do not have strong weight on the dynamics of deformation, theoretically it is stated that the crystalline structure of clay materials plays a fundamental role in this, since if the material is capable of retaining higher water content, it is possible that present greater mechanical behavior, taking into account that the maximum values of water retained that these materials can have does not amount to more than 50% in total weight. A percentage of around 40% was found in the evaluated materials, reasonably close to the reference value, showing that the mechanical behavior did not change with this value, the deformation magnitudes compared from this scenario did not have relevance, since all the evaluated materials they have the same humidity value.

The strong tendency toward the morphology of the particles, changes the concepts that had previously, where it was posited that all the deformation capacity revolved around the chemistry of the suspensions, the wide use of rheology modifying materials, does not assure that the deformation mechanisms are improved, since we must bear in mind that physical variables have a fundamental weight in this.

The proposed mathematical models follow a logarithmic structure, the linearity achieved with this proposal is evident in the graphs, distorting the need to think that all behavior of plastic deformation must be a non-linear phenomenon. The relationship found between the models and the distribution of stress and deformation are evident in the way that the particles are organized in certain regions of the volumes evaluated. The experimental data offer a high correlation with the computational regressions performed, which greatly facilitated the numerical analysis of the phenomenon.

The simulations carried out using the finite element method were used to describe the mechanisms of particle failure and flow, the possibility of having graphical data of the regions under stress states is essential since it offers an extended evaluation scenario that allows to some extent, to have an idea of the possible regions of the pulp where failures or stress concentrations may occur. On the other hand, a similar behavior was evidenced for all the pastes, the mechanisms of deformation and stress distribution did not vary from material to material, this is argued in the fact that the materials have a similar mineralogical origin, and the morphology between one and other.

Acknowledgements

The Corona Group is thanked for the information provided in this investigation.