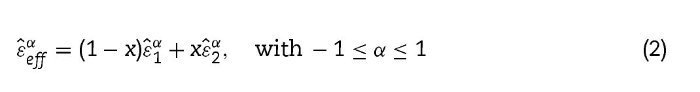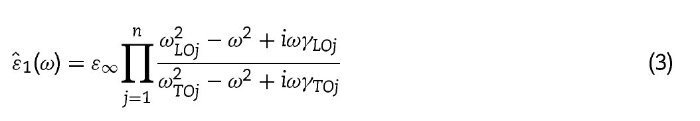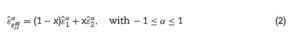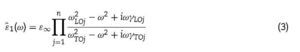PbZr0.38Ti0.62O3 and PbZr0.36Ti0.64O3 thick films deposited by screen printing on (0 0 0 1) single crystal sapphire substrates and prepared at two different sintering temperatures, were studied by Fourier-transform infrared reflectivity, time-domain THz transmission spectroscopy and micro-Raman spectroscopy. The dielectric response is discussed using the Lichtenecker model to account for the porosity of the films and to obtain the dense bulk dielectric functions. Results are compared with bulk tetragonal PZT 42/58 ceramics. The dynamic response in the films is dominated by an overdamped lead-based vibration in the THz range, as known in PZT, but its evaluated dielectric contribution is affected by the porosity and roughness of the surface.
Varias películas gruesas de PbZr0,38Ti0,62O3 (PZT 38/62) y PbZr0,36Ti0,64O3 (PZT 36/64) han sido depositadas mediante serigrafía en sustratos de zafiro y estudiadas mediante espectroscopía de reflectividad en el infrarrojo por transformada de Fourier, espectroscopía de transmisión de terahercios y microespectroscopía Raman. Su respuesta dieléctrica es discutida mediante el modelo de Lichtenecker, que tiene en cuenta la porosidad y es capaz de obtener las funciones dieléctricas efectivas de las películas porosas y también las de las cerámicas densas teóricas. Los resultados son comparados con los obtenidos en cerámicas densas de PZT 42/58. La respuesta dinámica de las películas está dominada por una vibración sobreamortiguada de los átomos de plomo en el rango de terahercios, como es conocido en el material PZT, pero su contribución dieléctrica está afectada por la porosidad y por la rugosidad de la superficie de las películas.
Introduction
Probably, the best and most used piezoelectric material nowadays is the ceramic solid solution Pb(Zr1−xTix)O3 (PZT 100(1 − x)/100x) [1,2], in its pure form, but also partially substituted with other atoms as La, Nb, Fe, Sn, etc. to improve targeted properties [2–4]. The tetragonal form of PZT ceramics has been much less studied than the famous morphotropic phase boundary (MPB) [5], where piezoelectric coefficients are enormously enhanced, or even less than the rhombohedral phase [6]. This is because, first, it was thought that the behaviour of this side of the phase diagram was simple, like in the end member PbTiO3, but, second, due to the technological problems of growing dense quality ceramics with high tetragonality. Therefore, most of the experiments on tetragonal PZT ceramics have been performed in samples much closer to the MPB. However, for a full understanding of the PZT system at the complicated MPB, it is necessary to understand also the behaviour of the tetragonal ceramics far away from it. As it turned out, the simplest part of the PZT diagram is not so simple at all [7–10].
Pure and dense highly tetragonal ceramics of PZT are quite difficult to prepare, which is inconvenient for the study of the PZT system. One of the problems of processing tetragonal PZT ceramics is the internal mechanical stress created by the strain generated in dense materials by the cubic–tetragonal transition. When the amount of Ti in the material is higher than about 70%, the great anisotropy in strain between the polar axis and the plane perpendicular to it creates high stresses within domains and grains, and these ceramics tend to break apart. To avoid this problem a small amount of dopants is usually added during the processing of ceramics, but this adds extra atoms into the lattice, which can affect the dielectric behaviour of PZT samples. A possible way to overcome the doping is growing pure PZT films on suitable substrates allowing the stress to relax.
In this paper, thick films deposited by screen printing on sapphire substrates have been studied at room temperature by Fourier transform infrared (FTIR) spectroscopy, time-domain terahertz transmission spectroscopy (TDTTS), and Raman scattering to analyze their homogeneity and dielectric properties. Raman maps were taken at room temperature and compared with the spectra of dense ceramics of similar composition. The measured flatness and porosity, together with the overall phonon response of the films, were then tested by far-infrared (FIR) reflectivity and the dielectric response below the polar phonons was measured using TDTTS. The results obtained on these films were compared with the dielectric data measured on bulk tetragonal PZT 42/58 ceramics. The effect of porosity on the reflectivity was evaluated using the Bruggeman and the Lichtenecker models of the effective medium [12,13].
Experimental
Thick PbZrxTi1−xO3 (PZT 100x/100[1 − x]) films were deposited by screen printing technique from corresponding solid-state synthesized powders on sapphire substrates (c-cut) for two compositions (36/64 and 38/62). The films were sintered at two different temperatures (950 ¿C and 1000 ¿C) for 2 h. The resulting films had thicknesses between 23 and 30 μm and were partially porous, with a grain size in the micrometre range (see Fig. 1). The porosity in two films was estimated by weighting (using the theoretical density of PZT amounting to 8.0 g/cm3) and show values about 40–45 %. These were subsequently used during the fitting of the effective dielectric function. The films were sufficiently transparent in the THz range but opaque in the IR range so that the measured FTIR reflectance could be taken as the effective IR reflectivity of the porous films.
Fig. 1 – Optical micrograph of the PZT 38/62 film sintered at 1000 ¿C.
Room temperature FIR reflectivity measurements were performed under quasi-normal incidence (∼10¿) using a FTIR spectrometer BRUKER IFS 113 v. Spectra were taken in the range 30–3000 cm−1 with a resolution of 2 cm−1 and a DTGS pyroelectric detector. Time-domain transmission THz spectroscopy (TDTTS) measurements were carried out in the 5–50 cm−1 range using a custom-made spectrometer based on fs sapphire-Ti lasers [14].
Raman spectra were taken using the 514.5 nm line of an Ar laser at a power of 25 mW (∼4 mW on the sample) and recorded in back-scattering geometry using a RM-1000 RENISHAW Raman Microscope, equipped with a grating filter enabling good stray-light rejection, in the 10–900 cm−1
range. The diameter of the laser spot on the sample surface amounted to 2–3 μm. Spectra were recorded using the natural polarization of the laser without any analyzer.
Results and evaluation
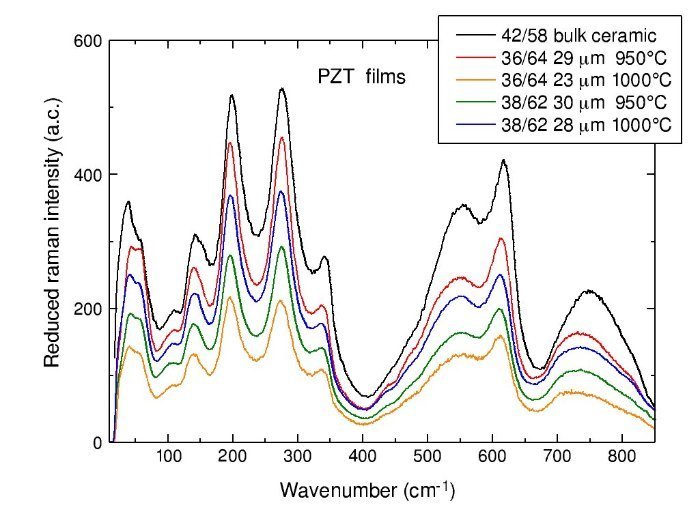
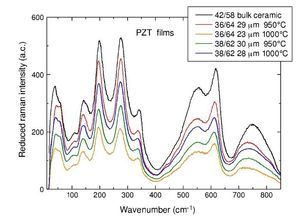
We checked the quality of the samples by Raman scattering in several spots and mapping lines across the films. Samples display the typical spectra of tetragonal PZT in bulk ceramics. In Fig. 2 experimental Raman spectra of the films, taken at room temperature and normalized for the Bose–Einstein population factor, are presented and compared to the one of tetragonal bulk ceramics of composition 42/58 [9].
Fig. 2 – Raman spectra of the screen-printed tetragonal PZT films of compositions 38/62 and 36/64 compared with the spectra of bulk PZT 42/58 ceramics.
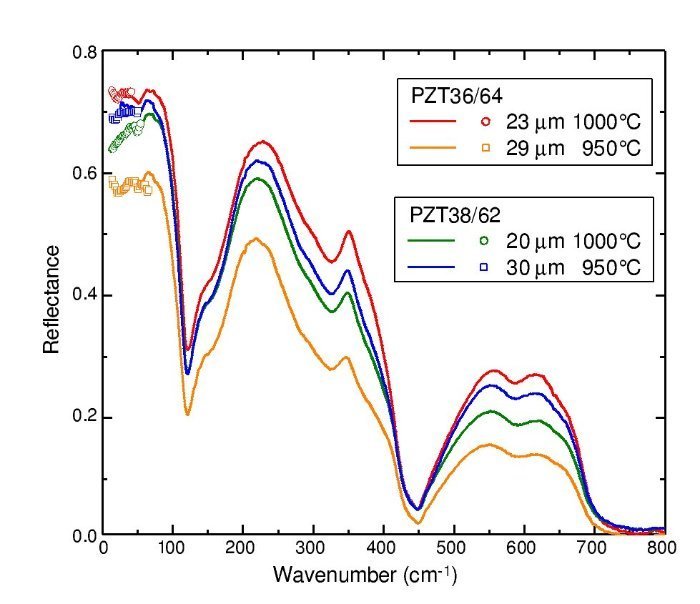
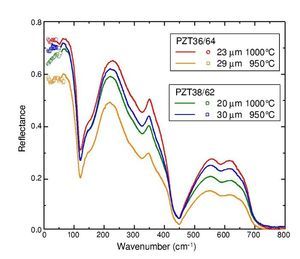
Room temperature FIR reflectivity spectra of the thick film samples are shown in Fig. 3. On the low-frequency end, the data calculated from the TDTTS experiment are also plotted.
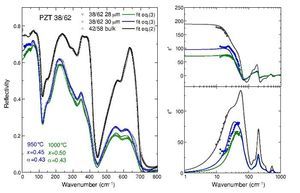
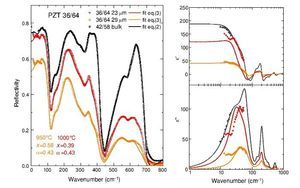
Fig. 3 – Reflectivity spectra of the tetragonal PZT films of compositions 38/62 and 36/64 at two different sintering temperatures.
Reflectivity spectra were adjusted to the THz data, since the photometric accuracy of the TDTTS experiment is higher than that of the FTIR. The evaluation of the TDTTS data for the case of films can be found in Ref. [15].
In order to combine both data we performed a joint fit of the IR reflectivity and the permittivity in the THz range. In the model used, the normal reflectivity R(ω) of the sample is related to the effective complex dielectric permittivity ¿eff (ω) of the film by
The actual reflectivity and the complex permittivity of a porous sample can be quite well approximated by the Lichtenecker model [12], when the porosity is high, and with the assumption that the pores are much smaller than the wavelength of the radiation, as recently shown for a set of porous Pb(Mg1/3Nb2/3)O3 ceramics [13]. In this case, the effective permittivity of the porous film can be calculated by
Here ¿1 and ¿2 are the dielectric functions of the components involved, x is the volume fraction of one of the components, and α is a fitting exponent related to the shape and topology of both components [16].
In our case, we took ¿1 as the dielectric function of the tetragonal PZT films, using the corresponding reflectivity of the dense bulk PZT 42/58 already published, and ¿2 as the permittivity of air. Therefore, ¿2 = 1, x corresponds to porosity and ¿1 is calculated by fitting, using the well-known generalized oscillator model, suitable for broad and asymmetric reflectivity bands,
where ε∞ is the permittivity at frequencies much higher than all polar phonon frequencies; ωTOj and ωLOj are the transverse
and longitudinal frequencies of the jth phonon mode; γTOj and γLOj the respective damping constants; and Δεj refers to its dielectric strength (contribution to the permittivity ε′ ).
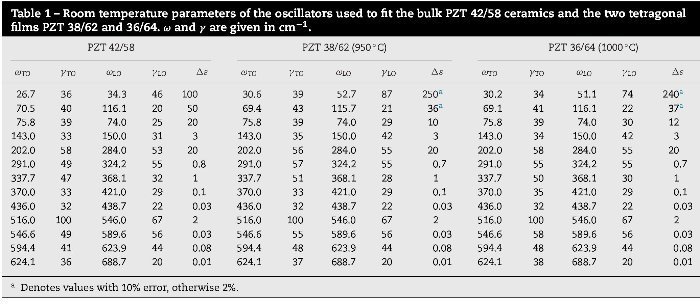
The parameters corresponding to the fit of the bulk PZT 42/58 ceramics (Table 1) were taken from [9], and slightly modified to fit the 38/62 and the 36/64 compositions. The porosity was fixed according to the measured one in these two films and all the frequencies were kept constant, except for the first two oscillators. Then, modifying α and slightly some damping constants, it was possible to obtain a rather reasonable fit. The actual parameters used to fit the bulk and the films are presented in Table 1. The first row corresponds to a mode in the THz range, with a frequency of about 30–40 cm−1.
This mode contributes the most to the permittivity, and it is known to be enhanced when composition approaches the MPB [7]. Its eigenvector is related to anharmonic Pb vibrations [9,11]. It is highly damped in all the compositions (with γTO1 > ωTO1)—in agreement with the anharmonic character of the Pb atom dynamics—, and it had to be substantially modified when fitting the reflectivity of the films. The second fitted mode is also related to Pb vibrations, and it is known to be the soft mode of the ferroelectric phase transition. It shows an underdamped character ( γTO2 < ωTO2) and its dielectric strength is the highest of all the phonon modes ( Δε2 ∼ 50). In general, the contribution of the phonons is quite constant and not depending on the composition, except for the anharmonic vibration in the THz range. This is affected by the topology and porosity of the films and, because of this, the Lichtenecker model including high porosity attributed higher values to its contribution to the permittivity Δε1. It is also possible that in the bulk ceramic, calculated without taking into account any porosity, its dielectric strength was slightly underestimated.
Discussion
The fitted reflectivity and complex permittivity of the PZT films are shown in Figs. 4 and 5, compared to results on bulk PZT 42/58. From the shape of the reflectivity spectra, much lower than in the bulk, it is possible to see that the porosity of the films is much higher than in bulk ceramics. The Raman mapping showed that microscopically the films are homogeneous and well crystallized, however reflectivity is very sensitive to porosity and roughness of the surface. These spectra show also that the shape of the reflectivity bands is deformed with respect to the bulk, especially for the modes with A1 symmetry (near 350 and 600 cm−1), whose eigenvectors are along the polarization [9]. This proves that the reflectivity at high frequencies is more sensitive to this kind of defects. The right panels in Figs. 4 and 5 show the real and imaginary part of the dielectric function obtained from the fits, together with the experimental points measured by TDTTS.
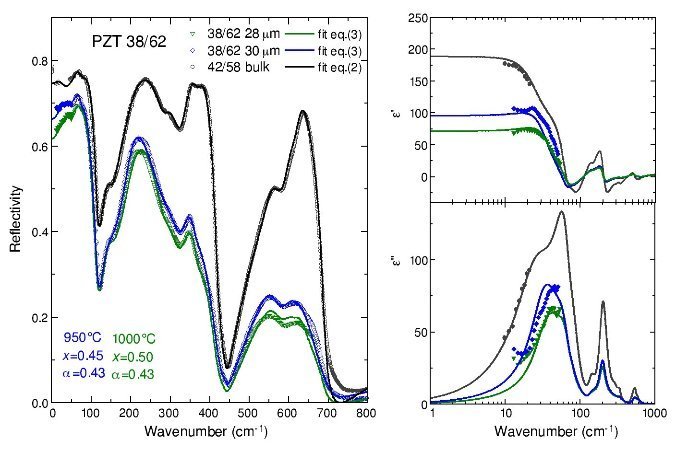
Fig. 4 – Fits of the reflectivity spectra (left panel), and permittivity and losses (right panels) obtained by the Lichtenecker model of Eq. (3) for the PZT 38/62 films at two different sintering temperatures. Black symbols correspond to the bulk ceramics PZT 42/58.
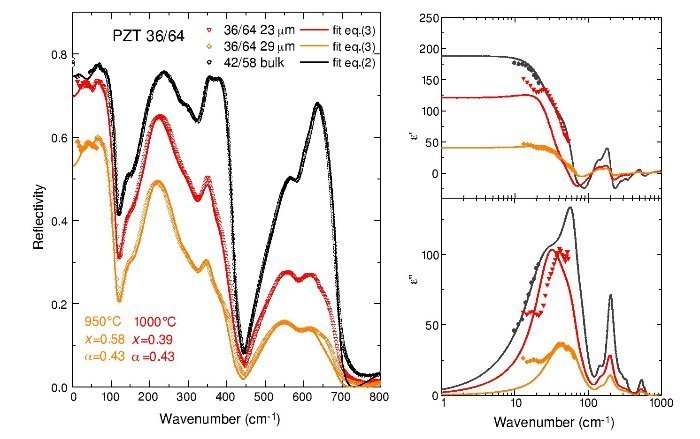
Fig. 5 – Fits of the reflectivity spectra (left panel), and permittivity and losses (right panels) obtained by the Lichtenecker model of Eq. (3) for the PZT 36/64 films at two different sintering temperatures. Black symbols correspond to the bulk ceramics PZT 42/58.
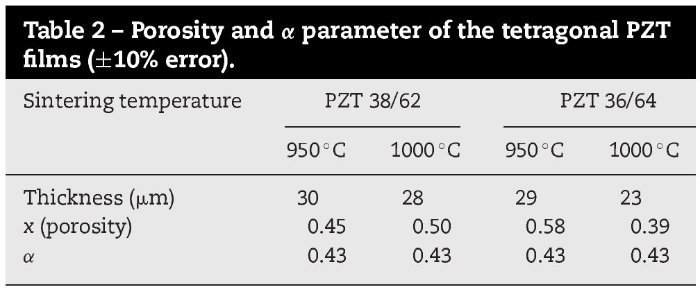
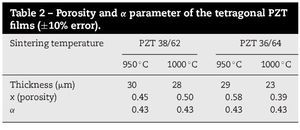
The films of composition 38/62 are depicted in Fig. 4. Black points refer to the measurements in the bulk PZT 42/58 ceramics, and the fit was done only with Eq. (2), because the density of the ceramics was higher that 95%, so the porosity was not taken into account. Films sintered at 950 ¿C and 1000 ¿C, were fitted with Eqs. (2) and (3), and the Lichtenecker model gave us an estimation of its porosity and topology. Results of the Lichtenecker parameters for all the PZT films are shown in Table 2. Porosity of these films is about 50 %, and α ∼ 0.43; this means that also the pores are partially percolated (full percolation for both components would corresponds to α = 1 [16]). The error in the estimated values is about 10%. Both films had a similar thickness (28 and 30 μm), and a similar dielectric response. By comparison of ε′ in the THz range one can see that films had lower values compared to the bulk, and that higher porosity results in lower permittivity and losses.
It is known that the dielectric behaviour in this frequency range is dominated by an overdamped excitation related to anharmonic Pb atoms vibration, and its dielectric strengthΔε1 is much higher at the MPB than away from it, decreasing almost monotonically in the tetragonal side when Ti content is increased [7]. The dielectric strength of the lowest frequency mode is Δε1 ∼ 100 in tetragonal bulk PZT 42/58 (see Table 1), however the value extrapolated from the fits of the films—for an ideal dense sample with zero porosity—gives an estimationΔε1 ∼ 250. On the other hand, its effective contribution to ε′ in porous films (as seen in Fig. 4b) must be less than 100. This implies that porosity and topology affect also its contributionΔε1, and this might be because there is an extra relaxation near below the THz range.
The PZT films of composition 36/64 are depicted in Fig. 5. Again, the black points refer to the measurements in the bulk PZT 42/58 ceramics. The films, sintered at 950 ¿C and 1000 ¿C, are quite different. The sintering at 1000 ¿C resulted in a thinner film (23 μm) but more dense. The sintering at 950 ¿C resulted in a thicker film (29 μm), but the overall reflectivity is much lower, and the permittivity and losses in the THz range are consequently reduced. Comparing to the previous film, we see that the less porous film, PZT 36/64 sintered at 1000 ¿C has, below 100 cm−1, a response more similar to the bulk. The film sintered at 950 ¿C showed much higher porosity (x = 0.58), but it was well fitted with almost the same oscillator parameters. Just Δε1, corresponding to the mode in the THz range, had to be reduced. The reflectivity and complex permittivity of both films indicates that actually below 30 cm−1 another relaxation could be present, as suggested from the lowest-frequency points in the TDTTS experiment. This is the reason why the lowest mode cannot be completely well evaluated.
In both compositions, PZT 38/62 and 36/64, this extra excitation affects the distribution of the dielectric strength in the three lowest-frequency modes related to Pb vibrations. The contribution to ε of the first THz mode is overestimated, and the contributions from the second and third modes, with ωTO ∼ 70 and 75 cm−1, respectively, are underestimated, in comparison to the bulk PZT 42/58. A fit taking into account permittivity values at GHz frequencies would help to find better estimations.
Conclusions
Tetragonal PZT films deposited by screen printing technique were characterized by Raman, FIR and TDTTS. Results obtained on films were compared with dielectric data measured on bulk tetragonal PZT 42/58 ceramics. The effect of the porosity on the reflectivity was taken into account using the Bruggeman and the Lichtenecker effective medium models.
PZT films showed a high porosity and they were not completely flat, therefore reflectivity decreases monotonically with the frequency. The Lichtenecker model provided a reasonable estimation of the dielectric properties, even for quite porous films; however, it could not account perfectly well for the lowest-frequency mode, which corresponds to a central mode related to anharmonic Pb vibrations in the THz range. The dielectric contribution of this mode was affected by the porosity and the topology of the films and to obtain a better estimation, it is necessary to measure the dielectric response at frequencies lower that the THz range.
Acknowledgments
Authors wish to thank J. Petzelt for the reading of the manuscript.
This work was supported by the Czech Grant Agency (project No. 14-25639S) and the Slovenian Research Agency (P2-0105).
Article history:
Received 7 October 2015
Accepted 5 November 2015
Available online 17 November 2015
∗ Corresponding author.
E-mail address: buixader@fzu.cz (E. Buixaderas).
http://dx.doi.org/10.1016/j.bsecv.2015.11.003