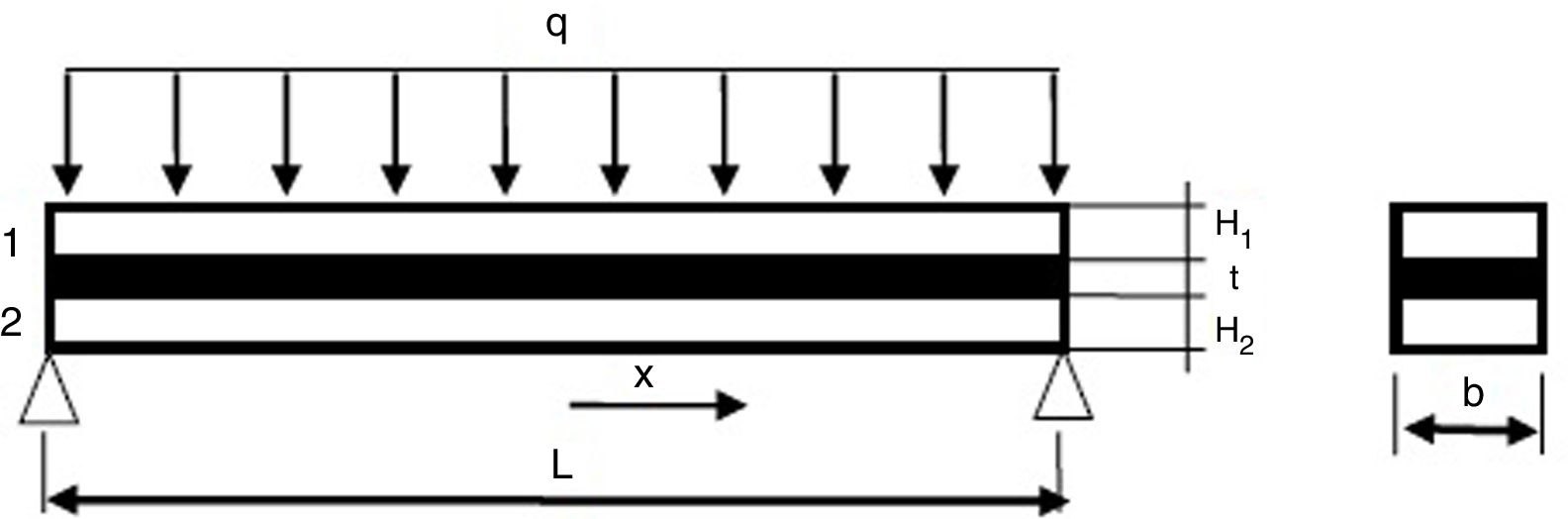
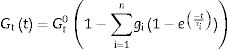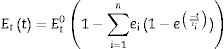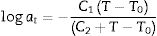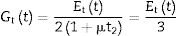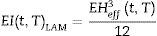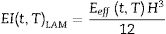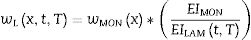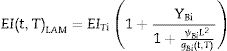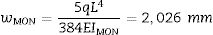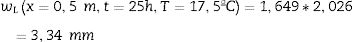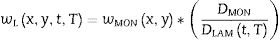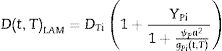En el cálculo de vigas y placas de vidrio laminado el vidrio se suele considerar como un material con propiedades elástico-lineales, mientras que los materiales poliméricos que conforman el laminado presentan un comportamiento viscoelástico. Como consecuencia, el comportamiento mecánico del vidrio laminado depende del tiempo y de la temperatura. Por otro lado, las mallas de elementos finitos utilizadas para la modelización numérica de estos elementos suelen ser muy densas debido a que los espesores de las capas de vidrio —y sobre todo los de las capas poliméricas— son mucho más pequeños que las otras dimensiones del elemento (ancho y largo). Por esta razón, el cálculo numérico de estos elementos suele ser un alto coste computacional. En los últimos años se ha propuesto el concepto de rigidez efectiva (alternativamente espesor efectivo y módulo de elasticidad efectivo) para el cálculo simplificado de vigas y placas de vidrio laminado. En este trabajo se propone una metodología para calcular la deformada de vigas y placas de vidrio laminado sometidas a cargas estáticas, utilizando un modelo monolítico elástico-lineal (que puede ser analítico o numérico) junto con las ecuaciones de la rigidez efectiva del elemento laminado. Las ecuaciones presentadas en este trabajo se validan mediante ensayos en vigas simplemente apoyadas y placas apoyadas en las cuatro esquinas, siendo el error máximo obtenido del 10%.
In the calculation of laminated glass elements, glass layers are commonly considered as linear-elastic whereas the polymeric interlayers present viscoelastic behavior. Consequently, the mechanical behavior of laminated glass elements depends on time and temperature. Many finite elements are needed to calculate these elements because the thickness of the glass layers (and above all that of polymeric interlayers) are much smaller than the other two dimensions of the element (with and length). For this reason, the calculation of these elements is very high time consuming. Recently, several authors have proposed the effective stiffness concept (alternatively effective thickness or effective Young's modulus) for the simplified calculation of laminated glass elements. In this work, a methodology is proposed to predict the deflection of laminated beams and plates under static loadings using a linear elastic monolithic model (analytical or numerical) and the equations of the effective stiffness for the laminated glass. The equations proposed in this work have been validated by experimental tests carried out in simply-supported beams and in a plate supported at the four corners, the maximum error being less than 10%.
Largo de la placa
Ancho de la viga o placa
Rigidez a flexión en placas
Distancia del plano medio de la capa al plano medio de la viga completa
Módulo de elasticidad del vidrio
Módulo de elasticidad efectivo
Coeficiente de módulo de la serie de Prony
Módulo de relajación de la capa viscoelástica
Módulo de elasticidad inicial de la capa viscoelástica
Función de forma en vigas (modelo de Galuppi y Royer-Carfagni)
Función de forma en placas (modelo de Galuppi y Royer-Carfagni)
Módulo de relajación a cortante de la capa viscoelástica
Módulo de cortadura inicial de la capa viscoelástica
Espesor de la capa 1 de vidrio
Espesor de la capa 2 de vidrio
Espesor de la capa 3 de vidrio
Momento de inercia
Longitud de la viga
Coeficiente de Poisson del vidrio
En vigas, coeficiente que depende de la longitud, del tipo de carga y las condiciones de apoyo
En placas, coeficiente que depende de la geometría, del tipo de carga y las condiciones de apoyo
Tiempo
Espesor de la capa polimérica
Temperatura
Coeficiente de tiempo en la serie de Prony
Temperatura de referencia
Desplazamiento
Desplazamiento del modelo laminado
Desplazamiento del modelo equivalente monolítico
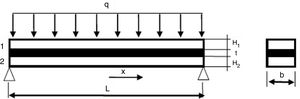
El vidrio laminado es un material compuesto o estructura de tipo sándwich formado por la adhesión de, al menos, dos capas de vidrio y un material polimérico [1–5]. En general, las capas de vidrio forman las capas exteriores y el material polimérico se sitúa en las capas intermedias. La configuración más simple que se presenta en el vidrio laminado consiste en tres capas: dos de vidrio y una intermedia polimérica (fig. 1). No obstante, existen multitud de combinaciones posibles, de tal forma que cuando existe más de una capa polimérica, al conjunto se le denomina vidrio laminado multicapa.
El vidrio laminado (viga, placa, etc.) combina las propiedades del material cerámico con las ventajas de un material polimérico, es decir, el comportamiento del laminado es una combinación de ambos [6,7]. Cada capa de vidrio que forma el elemento laminado puede ser recocida, templada o termoendurecida. Cuando la sección transversal está compuesta por diferentes tipos de vidrio (por ejemplo, una capa de vidrio recocido y otra de vidrio templado), se denomina elemento híbrido [6,7].
Por lo que respecta a las capas poliméricas, estas presentan un comportamiento viscoelástico [8–12], es decir, las propiedades mecánicas varían tanto con la temperatura (a la que se somete el material polimérico) como con el tiempo de aplicación de las cargas. Por esta razón, el material polimérico es el que condiciona ciertas propiedades del laminado (velocidad de deformación y de cambio de la rigidez con la temperatura), y consecuentemente estas propiedades serán diferentes en función del material que se elija para las capas intermedias. El butiral de polivinilo (PVB) es el material más común para las capas intermedias, aunque el uso de polímeros como el etilvinilacetato (EVA) o SentryGlas permite mejorar ciertas propiedades, como son reducir la higroscopicidad o proporcionar una mayor rigidez.
La respuesta estática del vidrio laminado depende tanto del tiempo de aplicación de las cargas como de la temperatura a la que está sometido el laminado. En el cálculo de estos elementos se suele considerar el vidrio como un material elástico-lineal, mientras que el comportamiento mecánico del material polimérico se suele considerar como viscoelástico, por lo que el cálculo tiene que ser de tipo cuasi estático. Por otro lado, el espesor de las capas de vidrio —y sobre todo el de las capas poliméricas— es mucho más pequeño que las otras dimensiones del elemento, por lo que las mallas de elementos finitos utilizadas para la modelización numérica suelen ser muy densas (muchos elementos 3D). Estos dos factores hacen que el cálculo estático de estos elementos sea de un gran coste computacional.
La respuesta del vidrio laminado está acotada por dos límites [13]: 1)el correspondiente al caso en el que la respuesta de dicho elemento consiste en dos capas de vidrio superpuestas y sin conexión entre sí, en adelante denominado «2 láminas», y 2)el denominado límite monolítico, en el que se cumplen las hipótesis de Euler-Bernoulli (las secciones planas permanecen planas) para la sección entera del elemento, por lo que la respuesta del elemento compuesto se puede calcular con un modelo monolítico con idéntica sección transversal.
De forma general, suele distinguirse entre viga y placa laminada, en función de si se trata de un elemento unidimensional o bidimensional, respectivamente.
Con el objeto de simplificar los cálculos, en los últimos años se ha propuesto el concepto de rigidez efectiva para el cálculo de elementos de vidrio laminado, que consiste en utilizar un modelo monolítico cuya rigidez es igual a la del laminado, con la condición de que los desplazamientos en ambos casos sean iguales. Debido al comportamiento viscoelástico del material polimérico, la rigidez efectiva depende del tiempo y de la temperatura, por lo que su implementación en modelos numéricos no es una técnica sencilla.
Además, se utiliza el concepto de rigidez secante [3,4] (también denominada solución cuasi-elástica), que consiste en considerar el material polimérico como elástico lineal, pero considerando en cada instante de tiempo ti los módulos de elasticidad Eti y de cortadura Gti. Esta simplificación es equivalente a considerar la rigidez del material polimérico igual a la que tendría si la deformación fuese constante durante todo el proceso de carga. Con estas simplificaciones se pueden utilizar las fórmulas del cálculo elástico lineal, pero utilizando una rigidez efectiva que depende del tiempo y de la temperatura. Se ha demostrado [3,4] que esta solución proporciona resultados conservadores en vigas de vidrio laminado con PVB como material intercalar.
En este trabajo se propone una metodología para el cálculo simplificado de flechas en vigas y placas de vidrio laminado sometidas a cargas estáticas, utilizando modelos monolíticos y el concepto de rigidez secante. Para el cálculo solamente se necesita el desplazamiento de una viga o placa monolítica con las mismas dimensiones, las mismas condiciones de contorno y la misma carga que la laminada objeto de estudio, junto con las rigideces de las vigas monolítica y laminada. De esta forma se evita utilizar modelos de elementos finitos con elementos sándwich tipo placa o elementos 3D. Las ecuaciones propuestas en este trabajo están basadas en los modelos desarrollados por Galuppi y Royer-Carfagni [4] y los resultados obtenidos han sido validados experimentalmente y mediante modelos numéricos.
Hipótesis de cálculoLos modelos propuestos por distintos autores [13–16] para describir el comportamiento mecánico de elementos de vidrio laminado están generalmente basados en las siguientes hipótesis:
- •
Las capas de vidrio presentan un comportamiento elástico lineal hasta la rotura. Por otra parte, la contribución del cortante en la deformación se desprecia. [6,7,17–20].
- •
Aunque el comportamiento del vidrio se considera elástico lineal, el comportamiento de la sección completa no satisface las hipótesis de Euler-Bernoulli y las tensiones normales presentan una distribución lineal en forma de zigzag a lo largo del espesor.
- •
No existe desplazamiento relativo entre las capas elásticas y las viscoelásticas, es decir, las capas intermedias se suponen con adhesión perfecta entre sí [7,25].
- •
La capa polimérica transmite tensiones cortantes, pero se desprecian las tensiones normales longitudinales, es decir, no es necesario conocer Ett. En consecuencia, el comportamiento de la capa intermedia se caracteriza mediante el módulo de cortadura Gtt[6,7,17,18,20,21].
- •
La capa polimérica presenta un comportamiento viscoelástico-lineal caracterizado por el módulo de elasticidad transversal Gtt,T, lo que implica que todas las variables consideradas en el modelo (rigidez, flexión, tensiones, espesor efectivo, etc.) son dependientes tanto del tiempo como de la temperatura [9–12].
- •
La tensión normal σz en la dirección perpendicular al plano del propio elemento laminado se puede despreciar en las capas de vidrio y en la capa intermedia. Esta hipótesis implica que todas las capas tienen el mismo desplazamiento transversal wx,t.
- •
El material polimérico tiene capacidad de deformación suficiente, de tal manera que no se produce el fallo del vidrio antes de la rotura del material polimérico.
- •
Las deformaciones del elemento laminado se consideran pequeñas, es decir, los efectos de la no linealidad geométrica se desprecian [20].
El butiral de polivinilo (PVB) se puede considerar como un material viscoelástico-lineal cuyas propiedades mecánicas dependen tanto de la temperatura como del tiempo [9,10]. Este comportamiento viscoelástico se puede entender considerando que dicho material posee propiedades comunes a un material elástico lineal y a un fluido viscoso newtoniano, interpretados generalmente como muelles y émbolos, respectivamente [9–11].
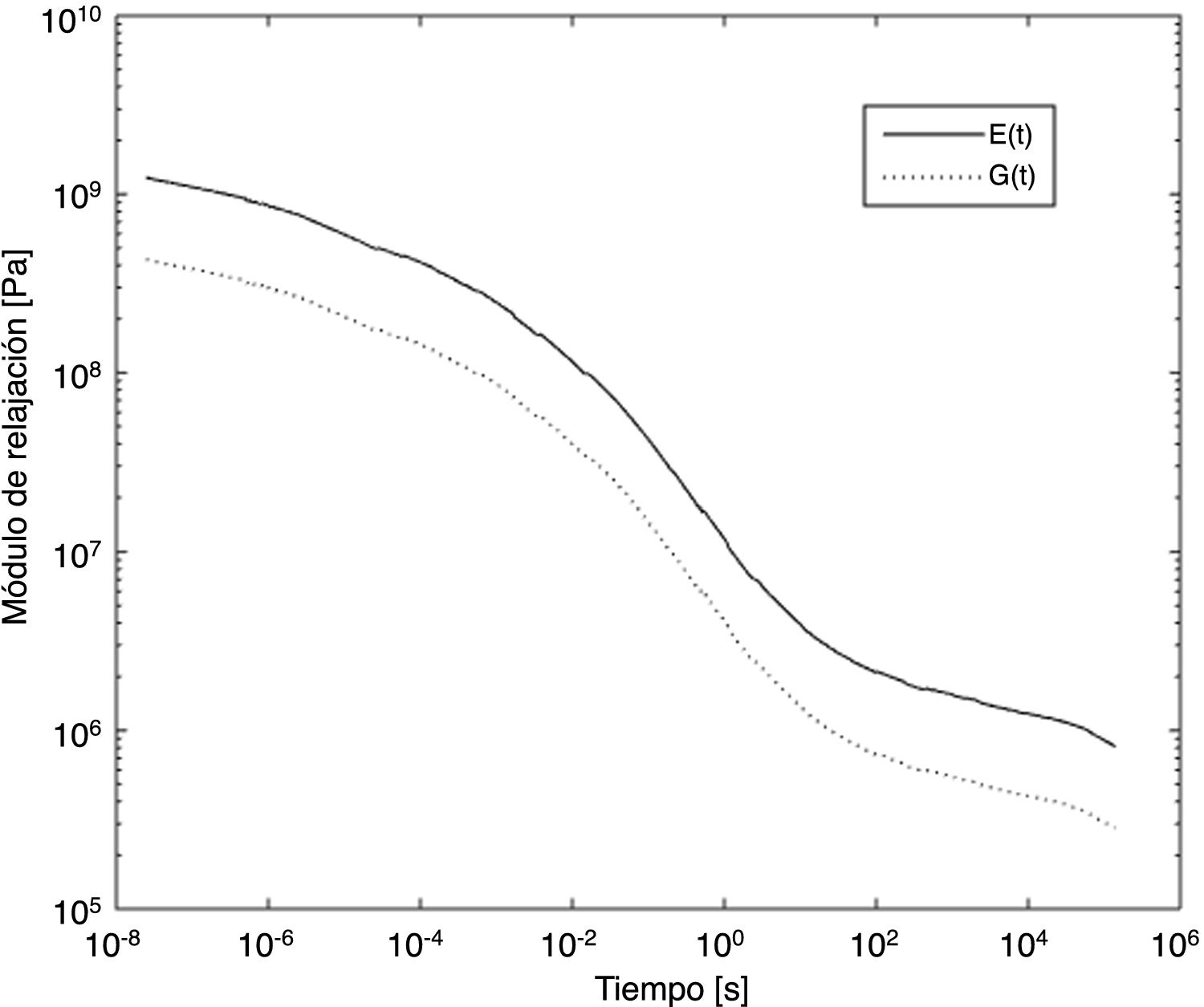
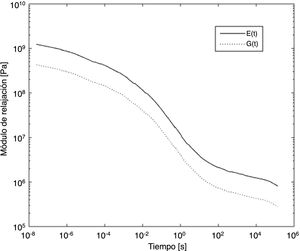
En la mayor parte de los materiales viscoelásticos, como es el caso del PVB, el comportamiento del material viscoelástico se define mediante series de Prony [22], de modo que el módulo de cortadura, Gtt, viene dado por:
donde gi y τi son los coeficientes de Prony estimados del material viscoelástico. El módulo de relajación Et(t) puede expresarse también mediante:Para tener en cuenta el efecto de la temperatura en las propiedades de la capa viscoelástica, se considera que el material presenta un comportamiento reológicamente simple [9]. Este hecho permite determinar una relación entre el tiempo y la temperatura para estos materiales usando el principio de superposición tiempo-temperatura (TTS, por sus siglas en inglés), como, por ejemplo, el modelo propuesto por Williams-Landel-Ferry (WLF) [9,22,23]. La expresión del factor de desplazamiento propuesto en este modelo para una temperatura T se muestra en la ecuación (3), donde T0 es la temperatura de referencia y C1 y C2 son las constantes características del material. Una vez que el modelo TTS se ajusta para una temperatura de referencia, T0, se pueden obtener las propiedades del material para una temperatura diferente, T. Para ello se calcula la constante at con la ecuación (3) y se determina una nueva escala de tiempos con tT=tT0at, donde tT0 y tT corresponden a las temperaturas T0 y T, respectivamente. Finalmente se calcula el módulo EttT con la ecuación (1) considerando t=tT.
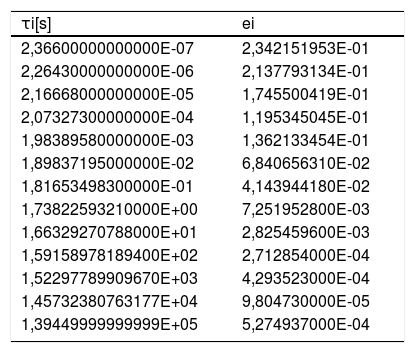
La caracterización experimental del PVB se realizó en un trabajo anterior [24] con un equipo DMA RSA3 (T.A. Instruments, Texas, EE.UU.) sometiendo probetas de PVB con un espesor de t=0,38mm a ensayos de relajación a tracción durante 10min para obtener el módulo Ett. El PVB se ensayó a diferentes temperaturas, desde −15°C hasta 50°C, con el objetivo de aplicar el principio de TTS para la construcción de la curva maestra. Los coeficientes de la ecuación del modelo de WLF [25], C1=12,60 y C2=74,46 para la temperatura de referencia T0=20°C, se obtuvieron ajustando las curvas experimentales a las diferentes temperaturas. Ajustando los datos a la ecuación (2) en la que se han utilizado 13 términos, se obtienen los coeficientes ei y ti indicados en la tabla 1. En este trabajo el módulo de cortadura Gtt se ha obtenido a partir de Ett, considerando μ=0,5 mediante:
Coeficientes para el PVB
| τi[s] | ei |
| 2,36600000000000E-07 | 2,342151953E-01 |
| 2,26430000000000E-06 | 2,137793134E-01 |
| 2,16668000000000E-05 | 1,745500419E-01 |
| 2,07327300000000E-04 | 1,195345045E-01 |
| 1,98389580000000E-03 | 1,362133454E-01 |
| 1,89837195000000E-02 | 6,840656310E-02 |
| 1,81653498300000E-01 | 4,143944180E-02 |
| 1,73822593210000E+00 | 7,251952800E-03 |
| 1,66329270788000E+01 | 2,825459600E-03 |
| 1,59158978189400E+02 | 2,712854000E-04 |
| 1,52297789909670E+03 | 4,293523000E-04 |
| 1,45732380763177E+04 | 9,804730000E-05 |
| 1,39449999999999E+05 | 5,274937000E-04 |
Los resultados obtenidos correspondientes al módulo de relajación, Et (t, T0), así como al módulo tangencial de relajación, Gtt,T0, se representan en la figura 2.
Ajustando los datos experimentales a la ecuación se obtienen los coeficientes indicados en la tabla 1.
Espesor efectivoVarios autores [1–4] han propuesto el concepto de espesor efectivo para el cálculo de desplazamientos en elementos de vidrio laminado. El espesor efectivo se puede definir como el espesor necesario en un elemento de vidrio monolítico para reproducir el mismo desplazamiento que el del elemento laminado, ambos sometidos a la misma carga y condiciones de contorno y con la misma longitud y anchura.
Como la rigidez del elemento de vidrio laminado EIt,TLAM es dependiente de la temperatura y del tiempo, el espesor efectivo también depende de estas variables, por lo que para cada instante de tiempo y para cada temperatura se tiene un espesor Hefft,T diferente:
De forma análoga, se puede definir un módulo de elasticidad efectivo, en el que se mantiene un espesor constante para todas las situaciones de trabajo y se tiene un módulo de elasticidad efectivo Eefft,T dependiente del tiempo y de la temperatura:
No obstante, las ecuaciones del módulo de elasticidad efectivo y las del espesor efectivo se obtienen a partir de la rigidez EIt,TLAM. Por esta razón, cuando se calcula el desplazamiento de una viga o placa mediante dichas ecuaciones analíticas, ambos métodos proporcionarán el mismo resultado [26]. El concepto de espesor efectivo fue propuesto inicialmente por Bennison [2] y más tarde utilizado por Galuppi y Royer-Carfagni [3–5]. Aunque en ecuaciones analíticas no tiene ninguna trascendencia utilizar la rigidez efectiva EIt,TLAM, el espesor efectivo Hefft,T o el módulo de elasticidad efectivo Eefft,T, el método más sencillo para su implementación en un modelo de elementos finitos es el módulo de elasticidad efectivo, pues se trata de un modelo en el que se define un espesor constante, mientras que el módulo de elasticidad depende del tiempo y de la temperatura.
Cálculo de elementos de vidrio laminado tipo vigaEn este apartado se propone un método para calcular la deformada de una viga laminada utilizando un modelo monolítico. Es decir, se pueden utilizar las fórmulas de cálculo estático de vigas o, en su defecto, un modelo numérico monolítico. Por tanto, no es necesario un modelo numérico con elementos 3D o con elementos tipo sándwich.
Las ecuaciones que se presentan se deducen de considerar que la forma de las deformadas de las vigas laminada y monolítica son iguales (aunque con magnitudes distintas) siempre que estén sometidas a la misma carga y con la misma longitud y las mismas condiciones de contorno, hipótesis que se ha demostrado que proporcionan resultados bastante precisos [3–5]. Bajo estos supuestos, si se conoce la deformada wMONx de una viga monolítica de la misma longitud, las mismas condiciones de contorno, la misma carga y de espesor igual al total de la viga laminada objeto de estudio, la deformada de la viga laminada se puede obtener mediante la expresión:
Donde EIt,TMON es la rigidez de la viga monolítica EI=EbH312 e EIt,TLAM es la rigidez de la viga laminada que viene dada por [4,5]:
Donde E es el módulo de elasticidad del vidrio, ITi es la suma de los momentos de inercia de las capas de vidrio respecto a su centro de gravedad, el subíndice «i» representa el número de capas de vidrio, YBi es un parámetro geométrico adimensional, ψBi es un coeficiente que depende del tipo de carga que actúa sobre la viga y de las condiciones de contorno (los valores más comunes están tabulados en [5], aunque para cálculos aproximados puede utilizarse la expresión ψB=π(βL)2, donde β es el coeficiente a pandeo de la viga) y gBi es un parámetro que depende de Gtt,TydeE. En la tabla 2 se muestran las ecuaciones para calcular estos parámetros en los casos de 2 y 3 capas de vidrio.
Ecuaciones para el cálculo de vigas formadas por 2 y 3 capas de vidrio
| VIGAS | ||
|---|---|---|
| Número de capas (i) | 2 capas de vidrio | 3 capas de vidrio |
| YBi | YB2=bH122H1H2IT2H1+H2 | YB3=A1d12+A2d22+A3d32IT3 |
| d1 | d1=H2H12H1+H2 | d1=H2H12+H3H12+H23H1+H2+H3 |
| d2 | d2=−H1H12H1+H2 | d2=d1−H12 |
| d3 | − | d3=d1−H12+H23 |
| H12 | H12=t1+H1+H22=d1−d2 | H12=t1+H1+H22=d1−d2 |
| H23 | − | H23=t2+H2+H32=d2−d3 |
| ITi | IT2=I1+I2=bH13+H2312 | IT3=I1+I2+I3=bH13+H23+H3312 |
| gBi | gB2(t,T) = Gt(t,T)EH122tbL2IT2YB2 | gB3(t,T) = Gt(t,T)bH122t1+H232t2 L2E IT3YB3 |
Las ecuaciones anteriores se utilizan para estimar el desplazamiento en el punto medio de una viga de vidrio laminado de longitud L=1m, ancho b=0,1m y espesores H1=2,84mm,t=0,37 mm,H2=2,80 mm simplemente apoyada y sometida a una carga uniformemente distribuida q=19,7 N/m[24].
Para determinar la validez de la ecuación se realiza un ensayo experimental. La carga distribuida se reproduce mediante la colocación sobre la viga de siete cargas concentradas equiespaciadas. La viga se ensayó durante 24h a una temperatura media de T=17,5oC, midiéndose el desplazamiento del punto central (punto de mayor desplazamiento).
El primer paso consiste en calcular la flecha en el punto en el que se desea conocer el desplazamiento para una viga monolítica simplemente apoyada de longitud L=1 m, espesor H=H1+t+H2=6,01 mm y con carga distribuida q=19,7Nm. La flecha de una viga monolítica simplemente apoyada puede calcularse mediante la expresión:
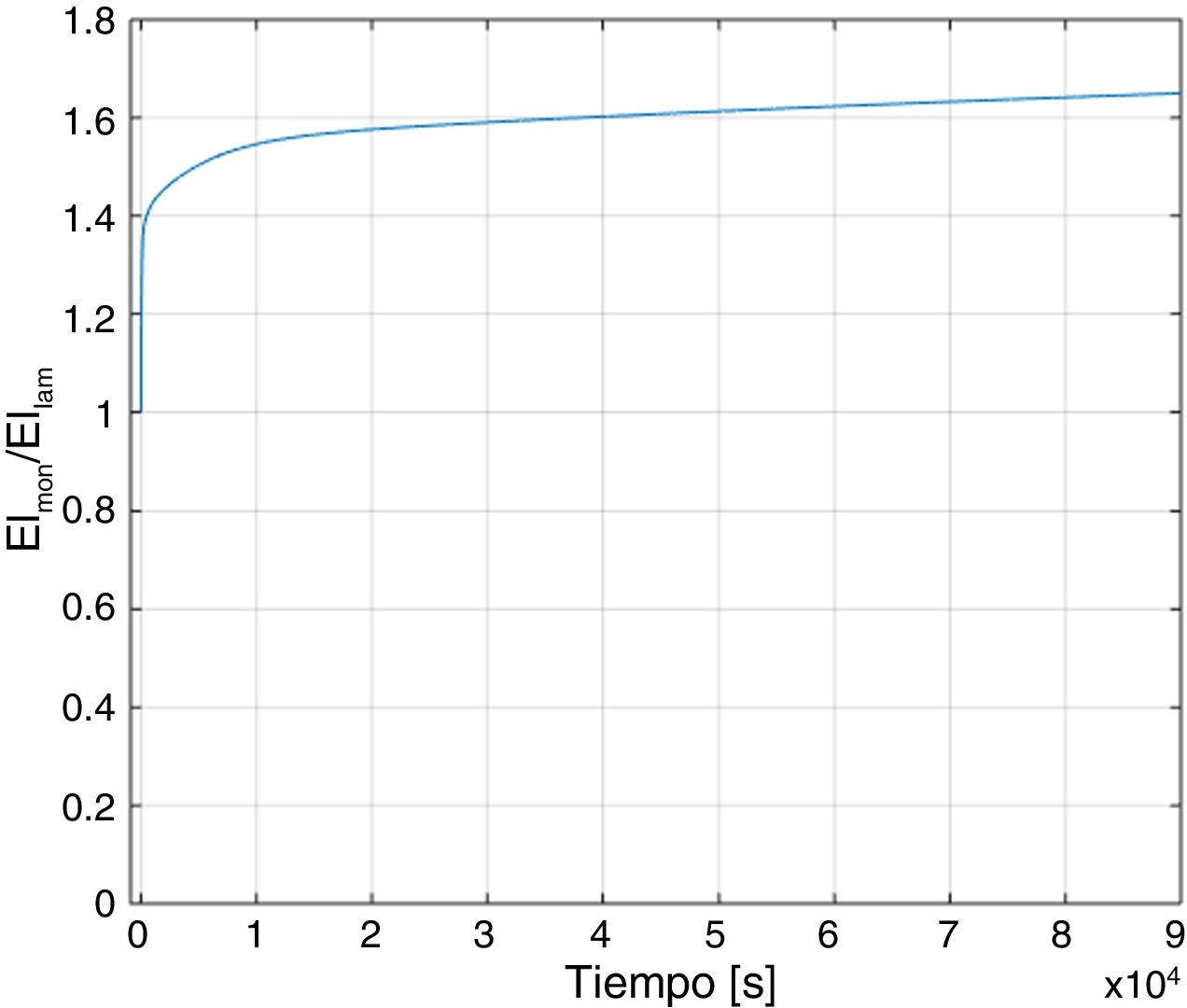
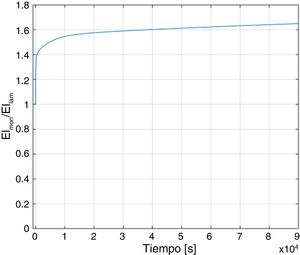
Por otro lado, la relación entre la rigidez de la viga equivalente monolítica y la viga laminada se muestra en la figura 3, en la que ψB=16817l2[5]. Esta relación es constante para una viga con una geometría y temperatura determinadas, pero depende del tiempo de aplicación de la carga: al inicio (t=0s) la relación es 1 y aumenta con el tiempo a medida que en el material polimérico se relaja, llegando a ser 1,649 para t=25h.
Para calcular el desplazamiento de la laminada en el punto de máximo desplazamiento para t=25h, se aplica la ecuación (7).
De forma general, se puede obtener el valor del desplazamiento en cualquier otro punto a partir del desplazamiento de la viga monolítica equivalente:
Las predicciones analíticas se validaron experimentalmente ensayando la viga durante 25h (90.000s) a una temperatura media de T=17,5°C. La carga distribuida se reproduce colocando 7 cargas concentradas equiespaciadas.
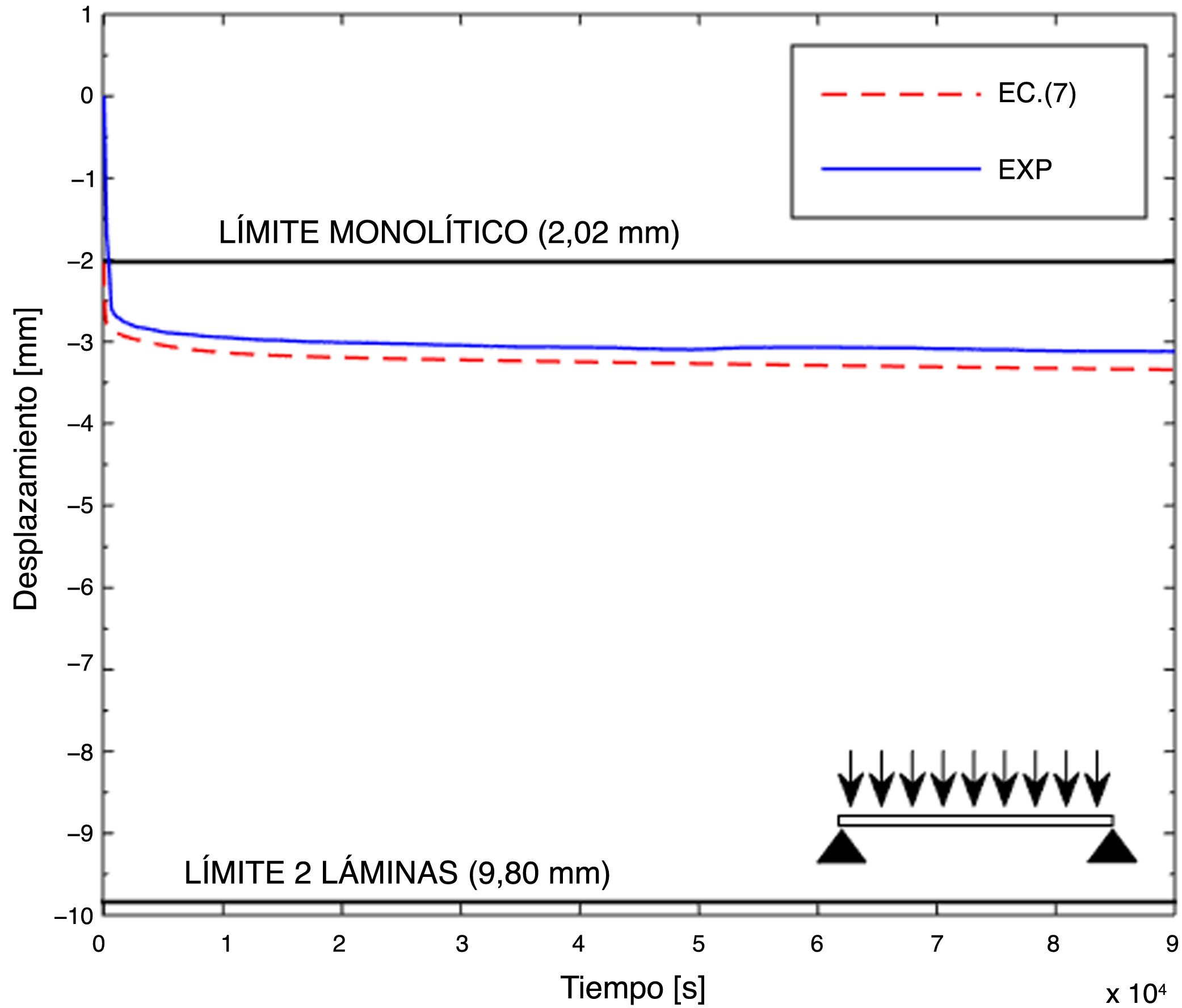
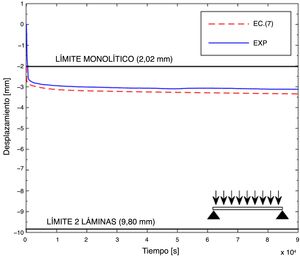
En la figura 4 se representa el desplazamiento predicho con la ecuación (7) junto con el medido experimentalmente (EXP). Se puede observar que la flecha predicha analíticamente en el centro de la viga es mayor que la obtenida experimentalmente, siendo el error menor al 10%
El límite «2 láminas» corresponde al caso límite en el que el módulo de cortadura del polímero Gtt=0.
En el caso del PVB, el valor mínimo de Gtt=Gt∞=0,37Mpa, lo que significa que el límite «2 láminas» no se alcanza nunca. No obstante, se puede estar cerca de ese límite con vigas cortas y condiciones de contorno asociadas a valores altos de ψB.
Aplicación a viga no simétrica de vidrio laminadoCon el objeto de comprobar estas ecuaciones en vigas no simétricas, se realizó un ensayo estático en una viga de vidrio laminado con espesores de H1=3,85mm, t=0,76mm y H2=7,8mm con carga de q=38,25Nm, temperatura T=18,3°C, longitud L=1m y un tiempo de aplicación de la carga de 24h.
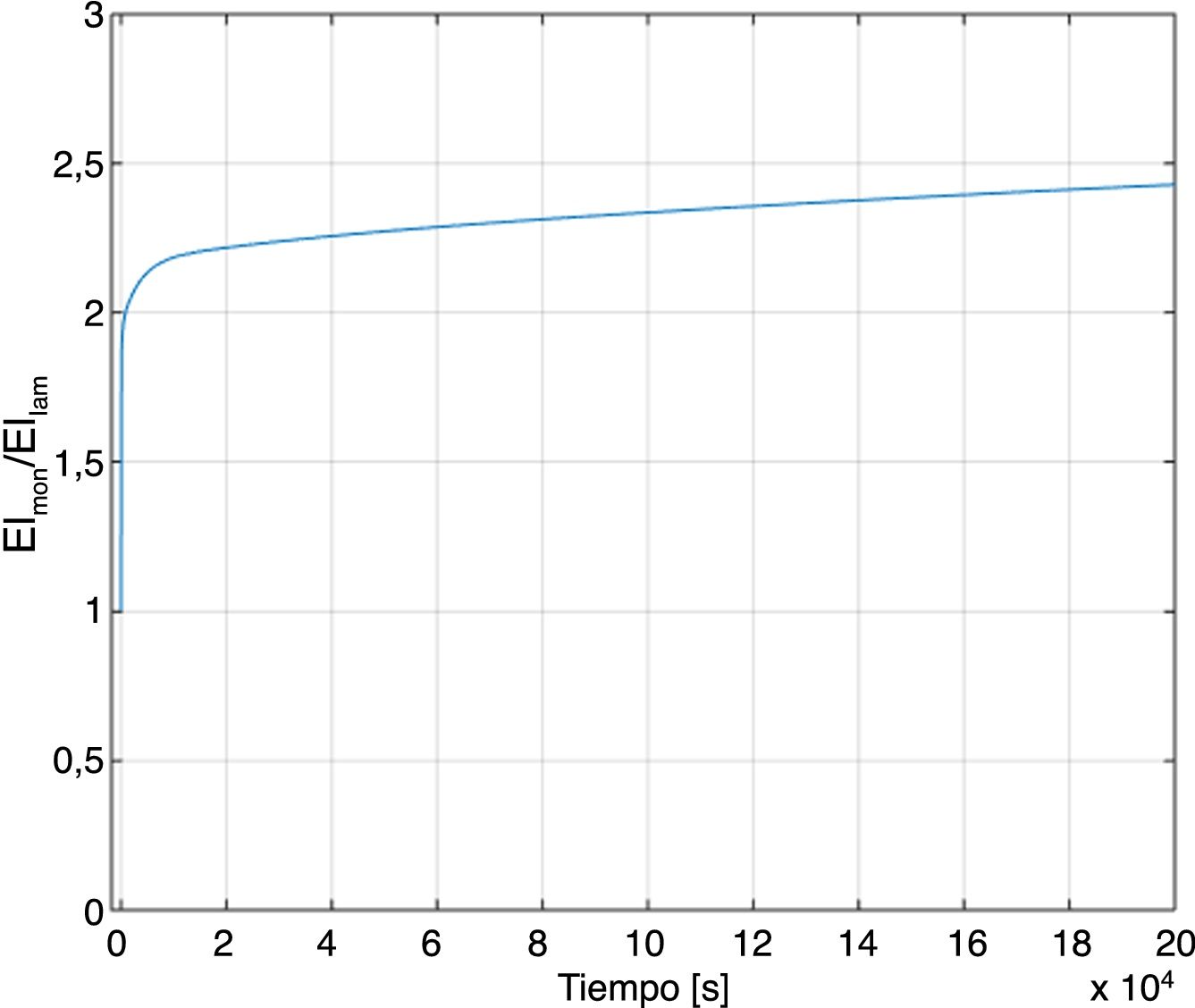
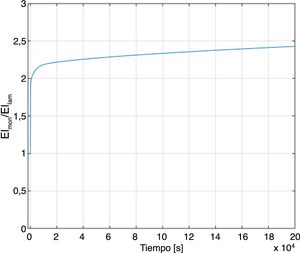
La relación EIMON/EILAM se muestra en la figura 5. De los resultados mostrados se observa que la flecha de la viga laminada puede llegar a ser hasta casi 2,5 veces la monolítica.
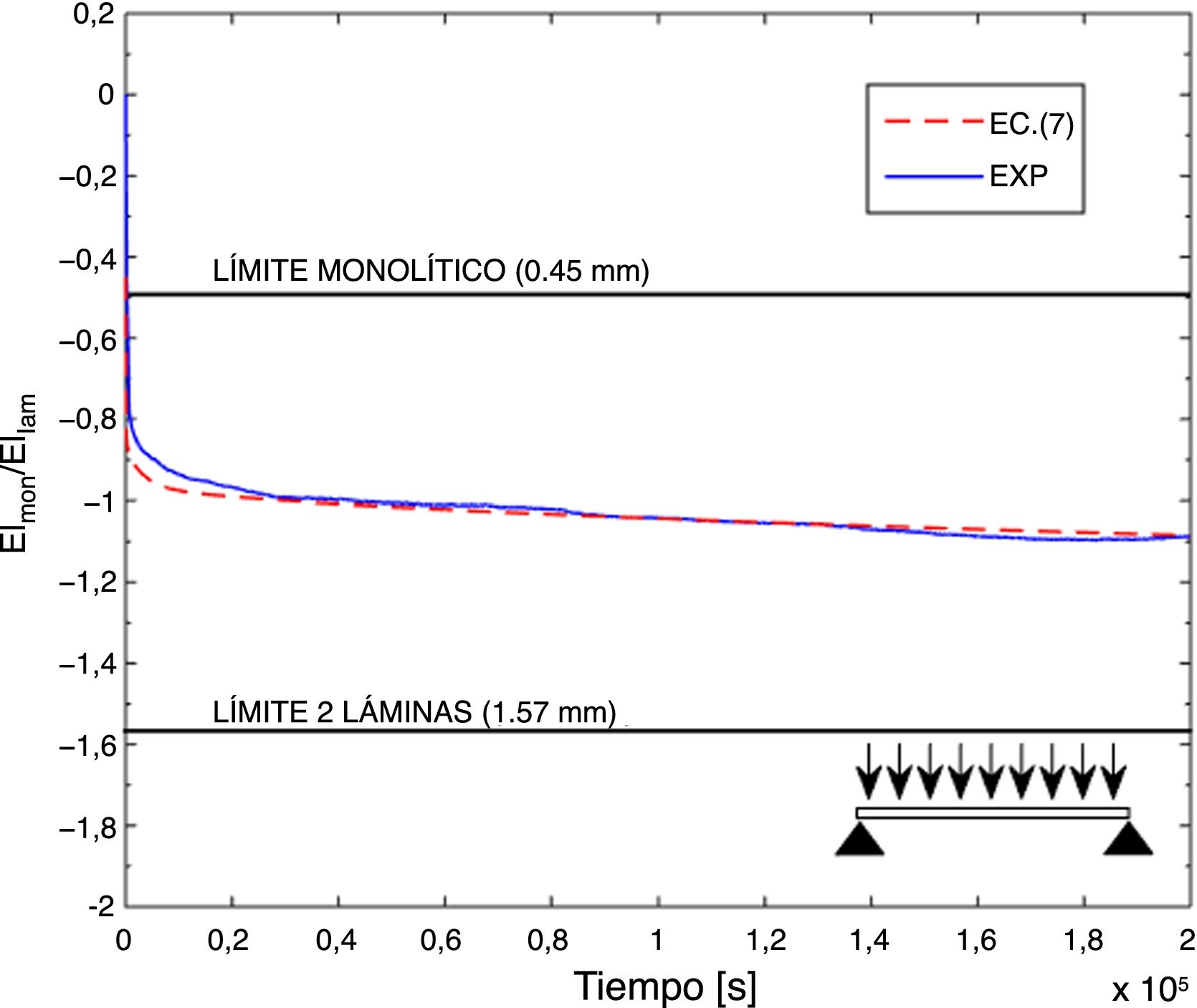
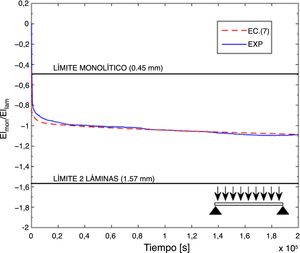
En la figura 6 se representa el desplazamiento predicho para el punto central con la ecuación (7) junto con el obtenido experimentalmente. Se puede observar que el modelo analítico predice el desplazamiento en el centro de la viga para cualquier instante de tiempo con un error menor del 10%, siendo la flecha predicha analíticamente mayor a la experimental. Esta viga presenta un mayor espesor que la anterior, por lo que el desplazamiento máximo está más cercano al límite «2 láminas».
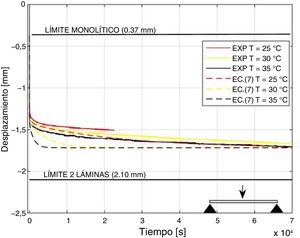
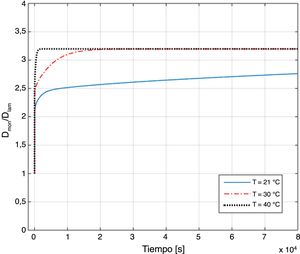
Aplicación a viga de vidrio laminado sometida a diferentes temperaturasPara considerar el efecto de la temperatura, la ecuación (7) se aplica a una viga de vidrio laminado con espesores H1=3,05mm, t=0,77mm y H2=3,12mm, L=0,5m y b=30mm. La viga se ensayó dentro de una cámara climática a diferentes temperaturas: T=25 °C, 30 °C y 35 °C.
La viga se apoyó en sus dos extremos, aplicándose una carga puntual de 10N en el centro del vano. Descontando las dimensiones de los apoyos, la luz o distancia libre entre apoyos se redujo a L=0, 470m. La disposición de la viga dentro de la cámara climática con la carga aplicada puede verse en la figura 7.
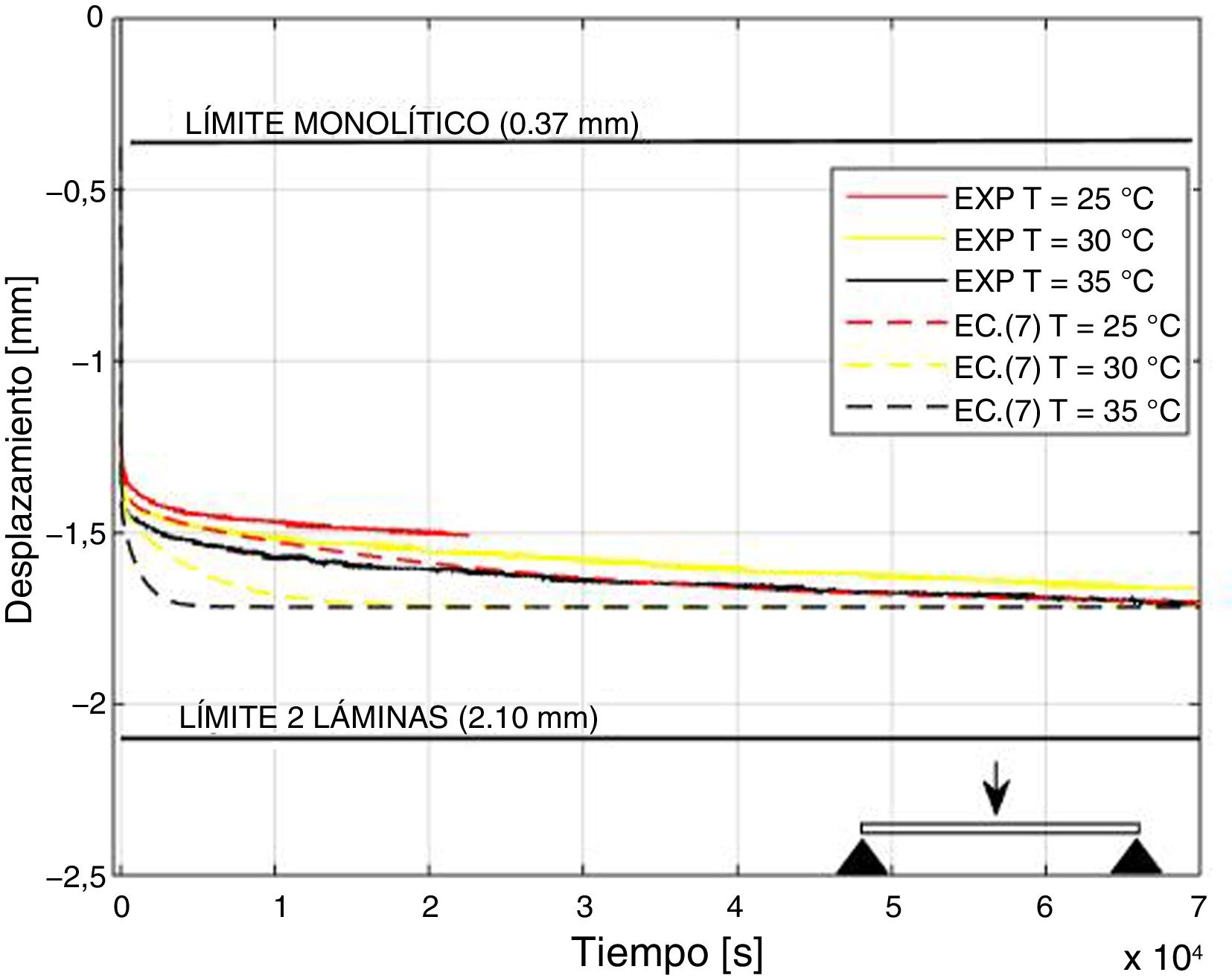
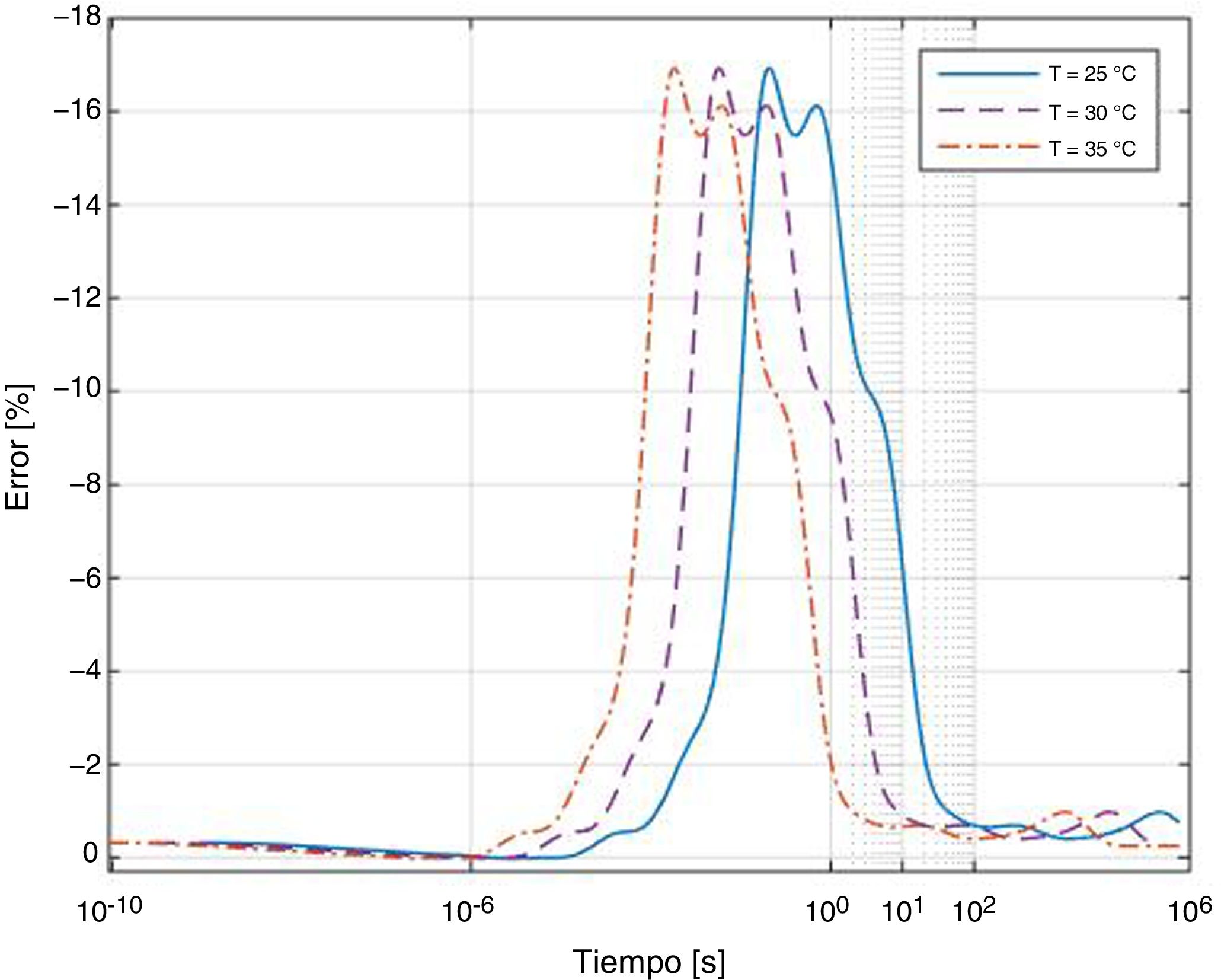
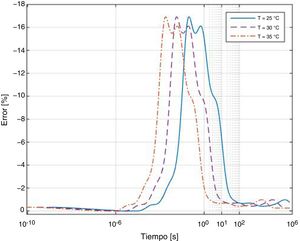
Las predicciones obtenidas con la ecuación (7), correspondientes al punto central, junto con los valores medidos experimentalmente con un sensor láser de desplazamiento, se muestran en la figura 8. Se puede observar que el modelo analítico reproduce el efecto que provoca la temperatura en el desplazamiento de la viga: a mayor temperatura, menos tiempo se tarda en alcanzar un determinado valor de desplazamiento. Estos resultados están de acuerdo con los obtenidos en investigaciones previas [26]. Por otro lado, se puede ver que la ecuación reproduce el desplazamiento con un error menor al 10% para todos los casos, exceptuando el caso de T=35°C, en el que para tiempos menores a 5h el error aumenta hasta el 17%, aproximadamente.
Por otro lado, se realizó un modelo numérico del tipo viscoelástico utilizando el programa de simulación por elementos finitos ABAQUS. Se utilizaron elementos Shell Continuum de 8nodos con integración reducida SC8R para las capas de vidrio, mientras que las capas de PVB fueron modelizadas con elementos 3D y 8nodos (C3D8). El comportamiento del PVB se definió como viscoelástico utilizando los coeficientes de Prony mostrados en la tabla 1 y el comportamiento del vidrio se consideró elástico-lineal con un módulo de elasticidad de 70GPa y un coeficiente de Poisson de 0,22.
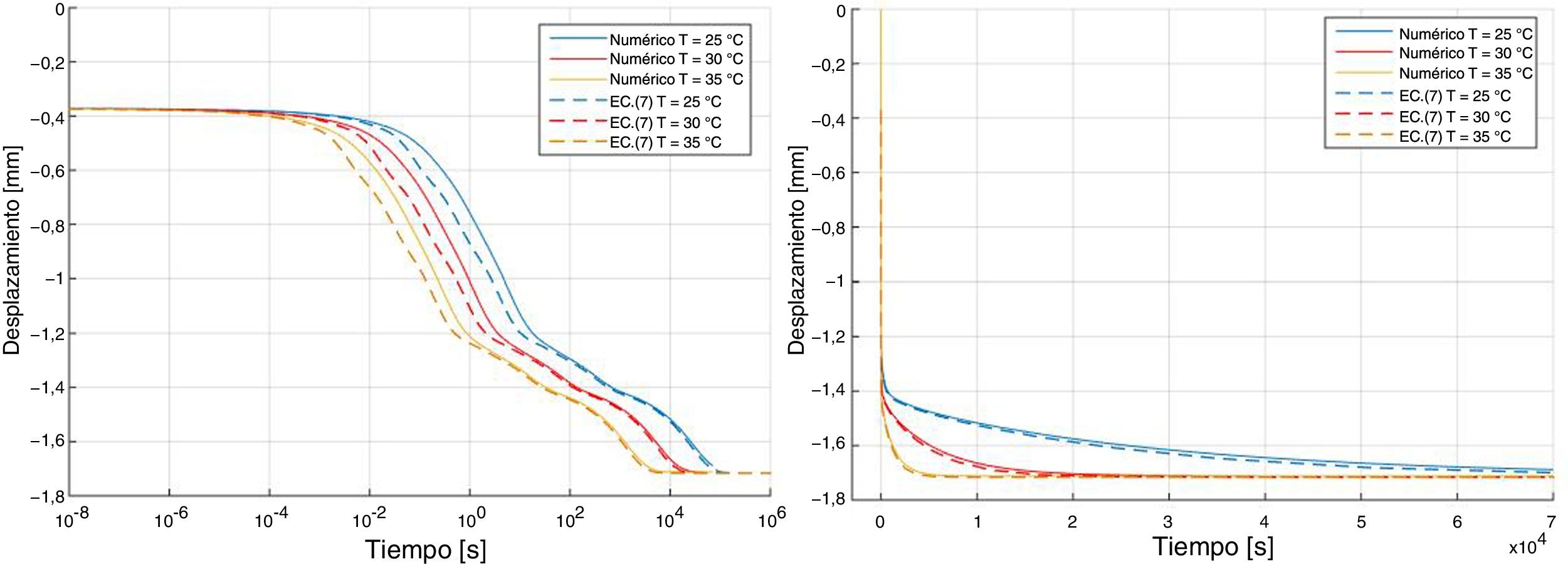
Los resultados de desplazamientos obtenidos en la simulación numérica, junto con los obtenidos mediante la ecuación (7), pueden verse en la figura 9. Para cada instante de tiempo las predicciones analíticas son mayores que las obtenidas numéricamente, es decir, la predicción analítica es conservadora. No obstante, a largo plazo los desplazamientos máximos obtenidos son muy similares. Los errores entre los diferentes métodos, calculados mediante la ecuación (7), pueden verse en la figura 10. Se puede apreciar como los errores obtenidos con ambos métodos son menores del 17% para tiempos inferiores a 20s, punto a partir del cual las diferencias se reducen a menos del 2%. Los desplazamientos predichos analíticamente son mayores a los obtenidos experimentalmente.
Para el cálculo de desplazamientos en una placa rectangular de vidrio laminado de dimensiones a×b se propone una ecuación similar a la de vigas:
Donde wMONx,y es la forma que adopta la deformada de una placa monolítica de sección constante, con las mismas dimensiones que la laminada, de espesor la suma de todas las capas y sometida a las mismas condiciones de carga y apoyo que la placa laminada en estudio. DMON es la rigidez de la placa monolítica y la rigidez de la placa laminada Dt,TLAM se obtiene mediante la expresión:
Donde las expresiones de los parámetros DTi,YPi,gPi se indican en la tabla 3.
Ecuaciones para el cálculo de placas rectangulares formadas por 2 y 3 capas de vidrio
| PLACAS | ||
|---|---|---|
| Número de capas (i) | 2 capas de vidrio | 3 capas de vidrio |
| H12 | H12=t1+H1+H22 | H12=t1+H1+H22 |
| H23 | − | H23=t2+H2+H32=d2−d3 |
| Di | Di=EHi3121−μ2 | Di=EHi3121−μ2 |
| DTi | DT2=D1+D2=EH13121−μ2+EH23121−μ2 | DT3=D1+D2+D3=E121−μ2H13+H23+H33 |
| d1 | d1=H2H12H1+H2 | d1=H2H12+H3H12+H23H1+H2+H3 |
| d2 | d2=−H1H12H1+H2 | d2=d1−H12 |
| d3 | - | d3=d1−H12+H23 |
| YPi | YP2=12H122H1H2H13+H23H1+H2 | YP3=∑3i=112Didi2Hi2DT3 |
| gPi | gP2t,T=Gtt,TE/1−μ2H1+H2a2H1H2t | gP3t,T=Gtt,T1−μ2H122t1+H232t2a2EH1d12+H2d22+H3d32=Gtt,TH122t1+H232t2a2Yp3DT3 |
El coeficiente ψP depende de la geometría de la placa y de sus condiciones de apoyo. Los valores más comunes del coeficiente ψP están tabulados en [5].
Al igual que en el caso de vigas, la ecuación (13) se deduce considerando que la forma de las deformadas de las vigas laminada y monolítica son iguales [3–5].
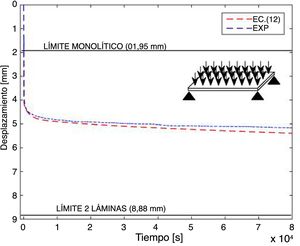
Aplicación a placa de vidrio laminadoLas ecuaciones anteriores se aplicaron para predecir la flecha de una placa de dimensiones a=1,4 m, b=1 m, espesores de H1=7,87 mm, t=0,71 mm y H2=7,80 mm y apoyada en las cuatro esquinas. Los cálculos se realizaron a una temperatura de T=21,5°C y aplicando a la placa una carga uniformemente repartida de valor q=914,2N/m2.
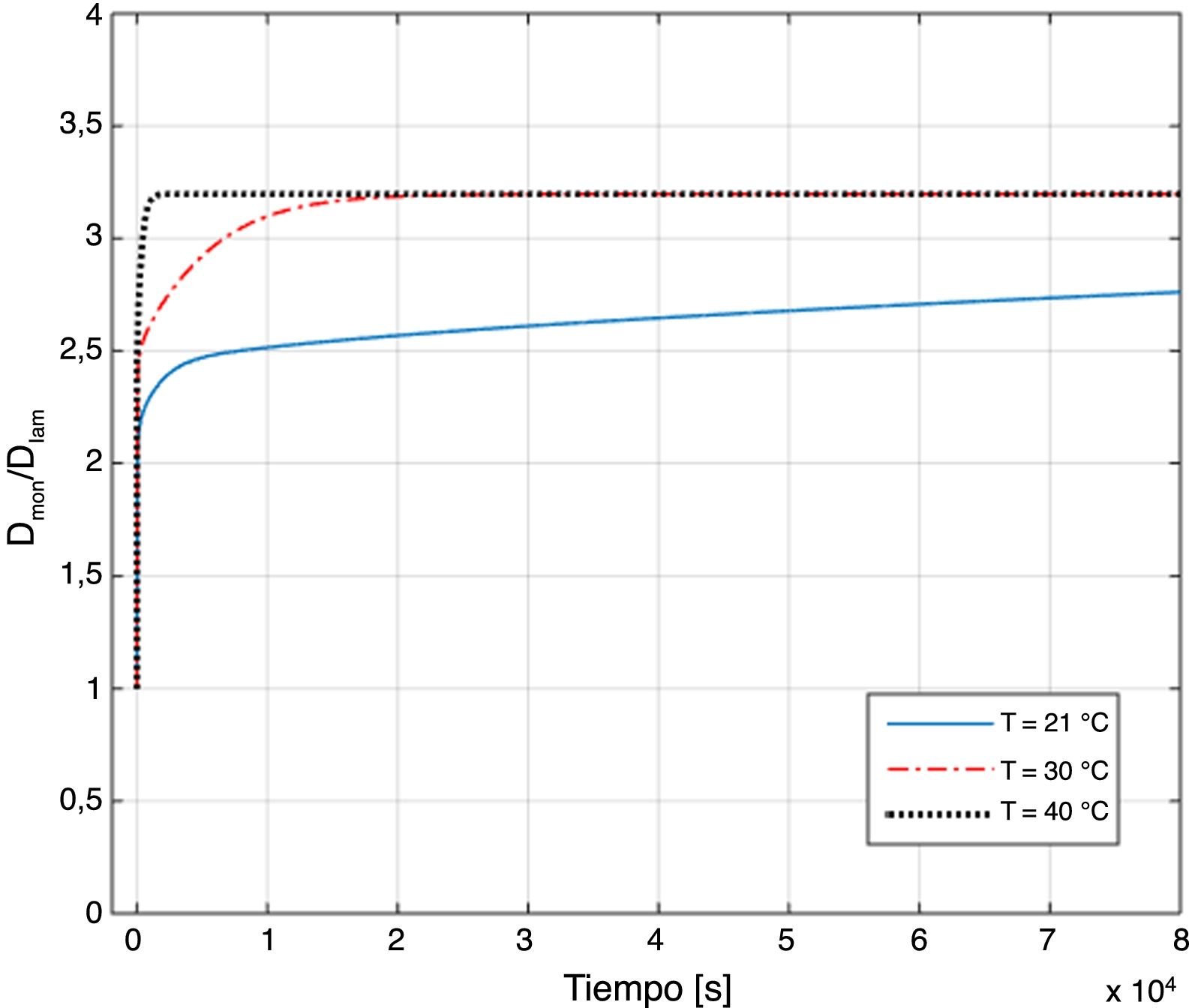
La relación de rigideces DMONDLAMt,T para la placa estudiada se muestra en la figura 11 junto a los resultados que se obtendrían para otras temperaturas. De las predicciones se observa que el efecto de la temperatura no modifica el valor máximo alcanzado, sino el tiempo que tarda en alcanzarse este.
Las predicciones analíticas se validaron experimentalmente mediante un ensayo estático [26] realizado apoyando la placa sobre cuatro bolas de madera de 5cm de diámetro y cargando la placa con una carga de q=914,2N/m2. La temperatura se mantuvo aproximadamente constante durante el transcurso del ensayo con un valor de T=21,5°C.
Los desplazamientos en el centro de la placa se midieron mediante un sensor láser de desplazamiento conectado a un sistema de adquisición de datos NI CompactDAQ y controlado mediante el software labVIEW.
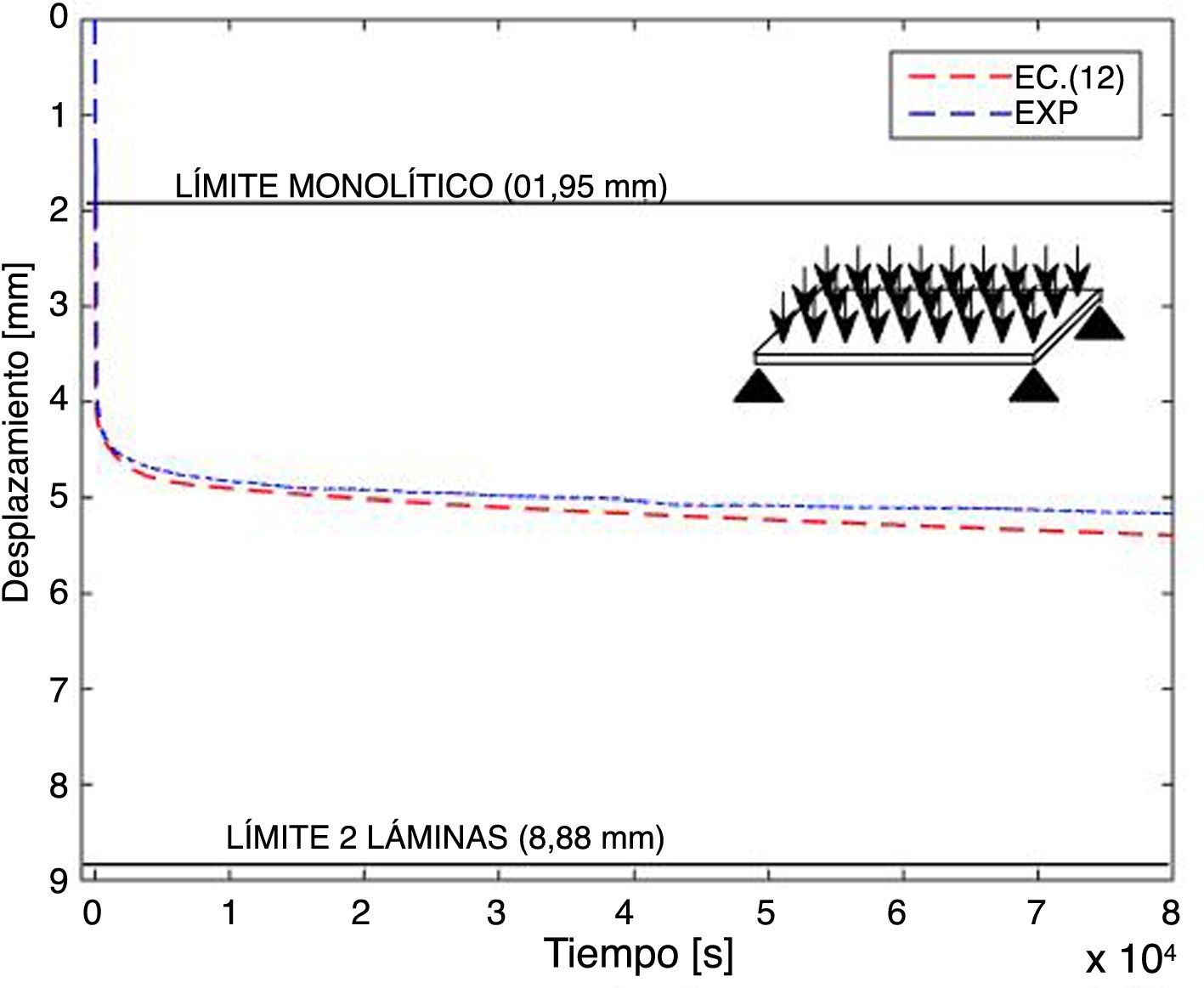
El desplazamiento predicho en el punto medio de la placa junto con el obtenido experimentalmente se muestra en la figura 12. Se puede observar que en este caso la ecuación (12) predice el desplazamiento con un error menor al 5%. Nuevamente, la flecha predicha analíticamente es mayor a la obtenida experimentalmente.
ConclusionesEn el cálculo numérico en elementos de vidrio laminado se necesitan mallas muy densas porque el espesor de las capas de vidrio y sobre todo el de las capas poliméricas, es mucho más pequeño que las otras dimensiones del elemento. Por otro lado, el comportamiento de los materiales poliméricos es viscoelástico y el cálculo debe ser cuasi-estático. Por estas razones, el cálculo de estos elementos es de un gran coste computacional.
En este trabajo se propone una metodología rápida y sencilla para el cálculo de desplazamientos en vigas y placas rectangulares de vidrio laminado, basada en el concepto de la rigidez secante [3,4], que puede ser muy útil en la fase de pre-dimensionamiento. El método necesita como datos de partida la rigidez efectiva del elemento laminado, que puede calcularse con las expresiones incluidas en este artículo, y los desplazamientos de un modelo monolítico elástico-lineal (analítico o numérico), que tiene que tener las mismas dimensiones, las mismas condiciones de contorno y estar sometido a la misma carga que el laminado. En las tablas 2 y 3 se muestran las expresiones de todos los parámetros que se necesitan para el cálculo de desplazamientos y vigas y placas de vidrio laminado con 2 o 3capas de vidrio, utilizando las ecuaciones (7) y (12). Además, con el objeto de ilustrar la aplicación de la técnica, se muestran ejemplos de cálculo de vigas y placas.
La metodología que se propone se ha validado mediante ensayos estáticos realizados en dos vigas simplemente apoyadas y en una placa de vidrio laminado apoyada en las cuatro esquinas, sometidas a una carga uniformemente distribuida. Además, para tener en cuenta el efecto de la temperatura se ensayó una viga con una carga puntual en el centro a diferentes temperaturas. Los resultados obtenidos indican que las ecuaciones (7) y (12) predicen los desplazamientos en vigas y placas de vidrio laminado con un error aceptable para cálculos prácticos de ingeniería.
FinanciaciónLos autores agradecen la financiación económica recibida del Ministerio de Economía y Competitividad a través del proyecto de investigación BIA2014-53774-R.