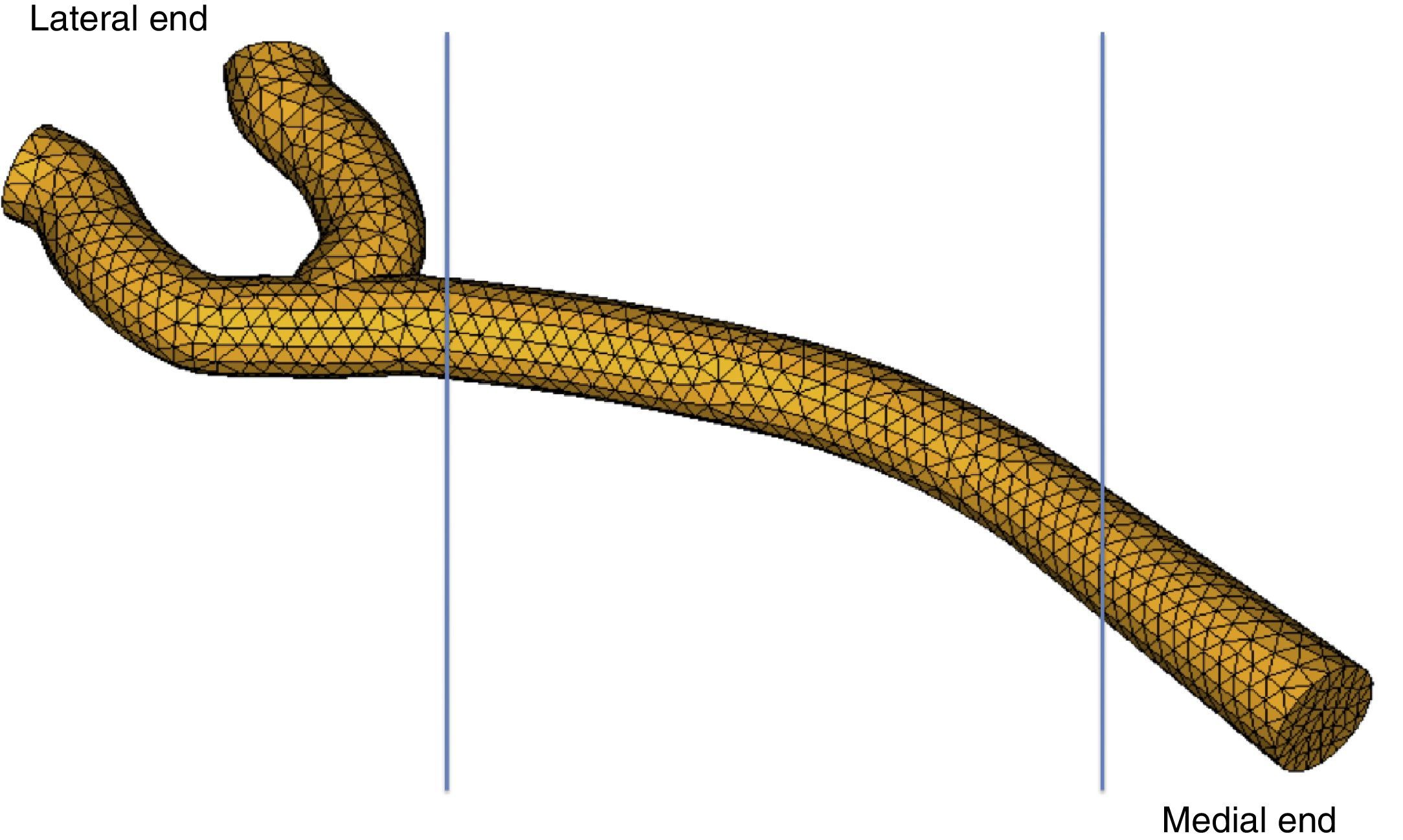
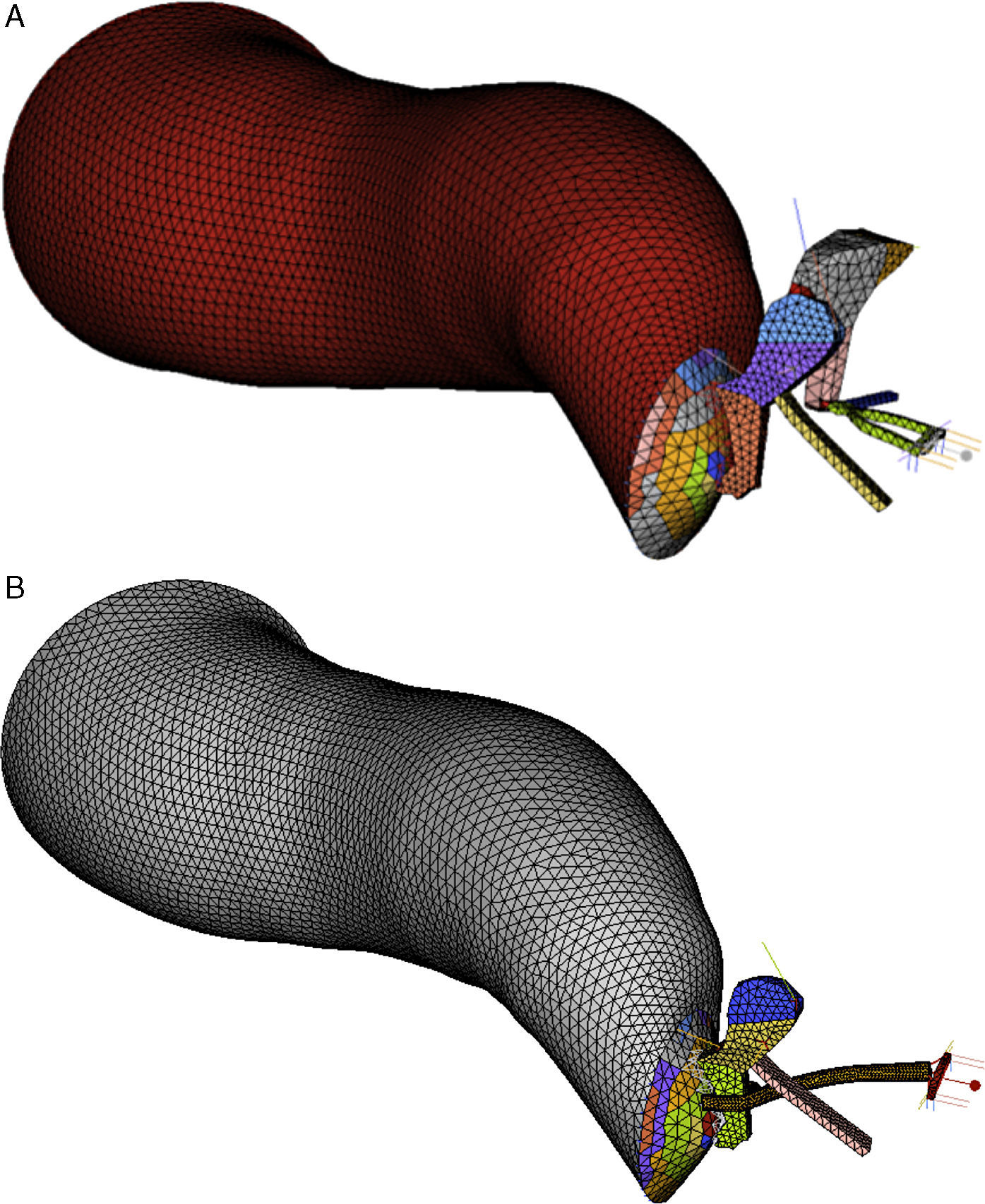
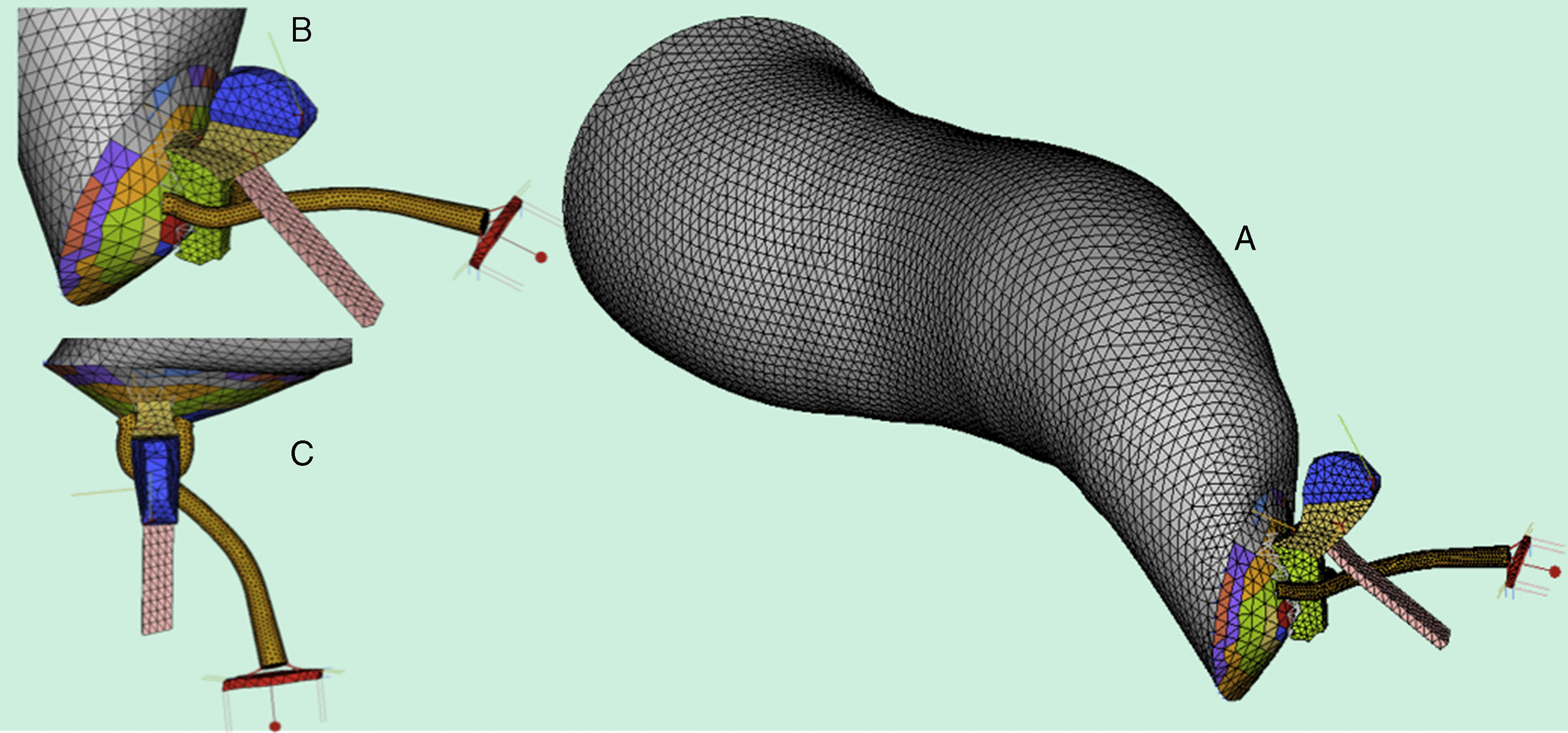
Many designs of prostheses are available for middle ear surgery. In this study, we propose a design for a new prosthesis, which optimises mechanical performance in the human middle ear and improves some deficiencies in the prostheses currently available.
Our objective was to design and assess the theoretical acoustic–mechanical behaviour of this new total ossicular replacement prosthesis.
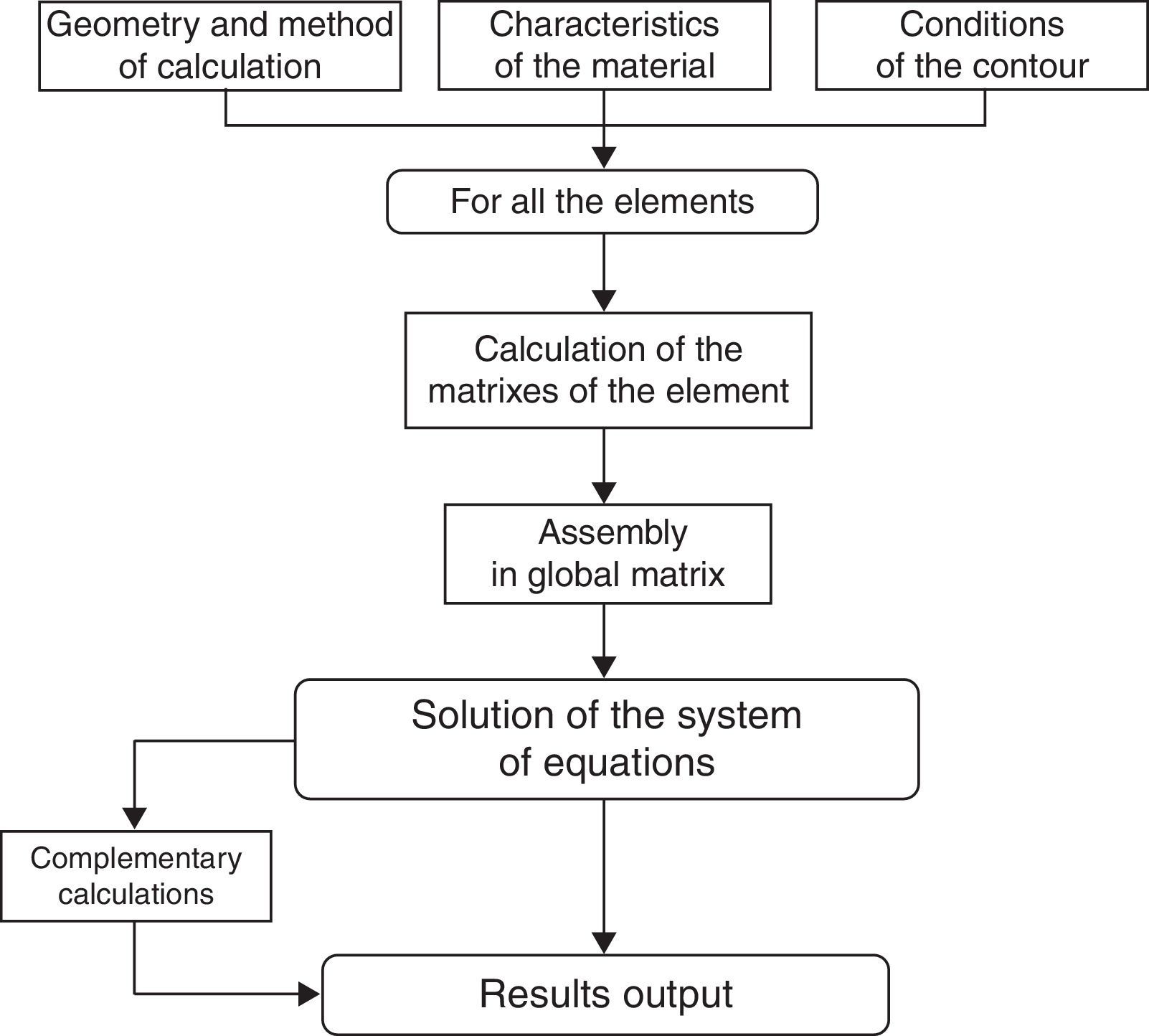
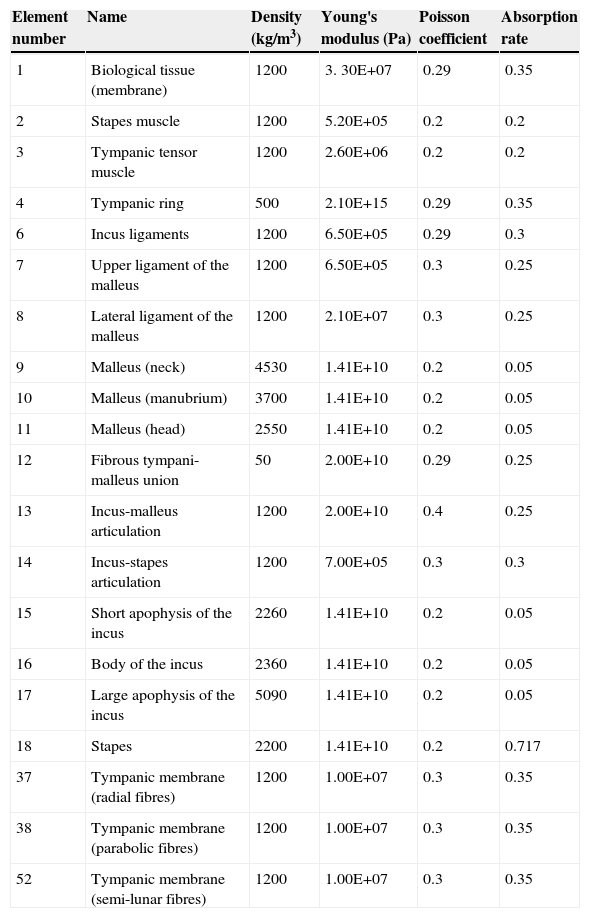
MethodsThe design of this new prosthesis was based on an animal model (an iguana). For the modelling and mechanical analysis of the new prosthesis, we used a dynamic 3D computer model of the human middle ear, based on the finite elements method (FEM).
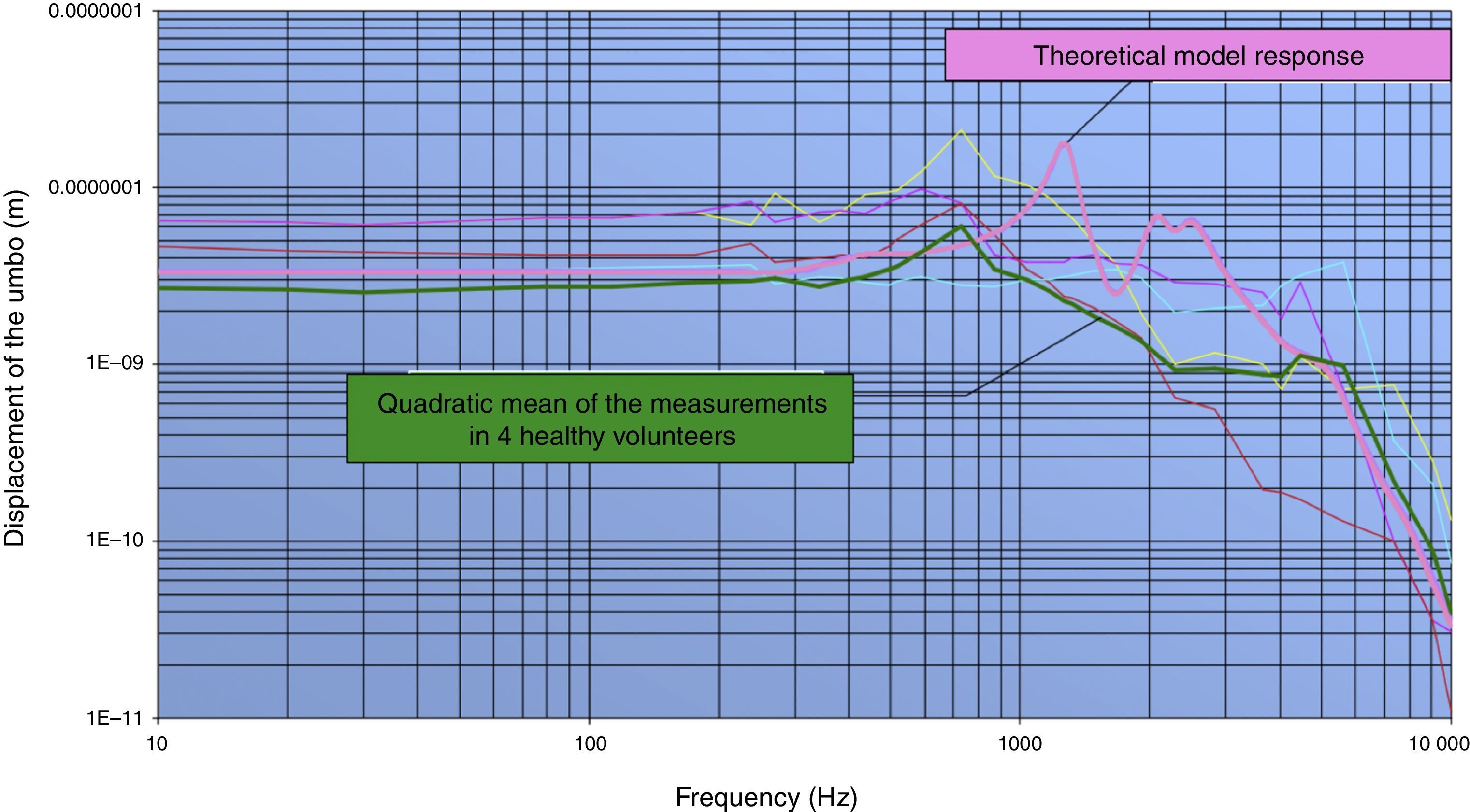
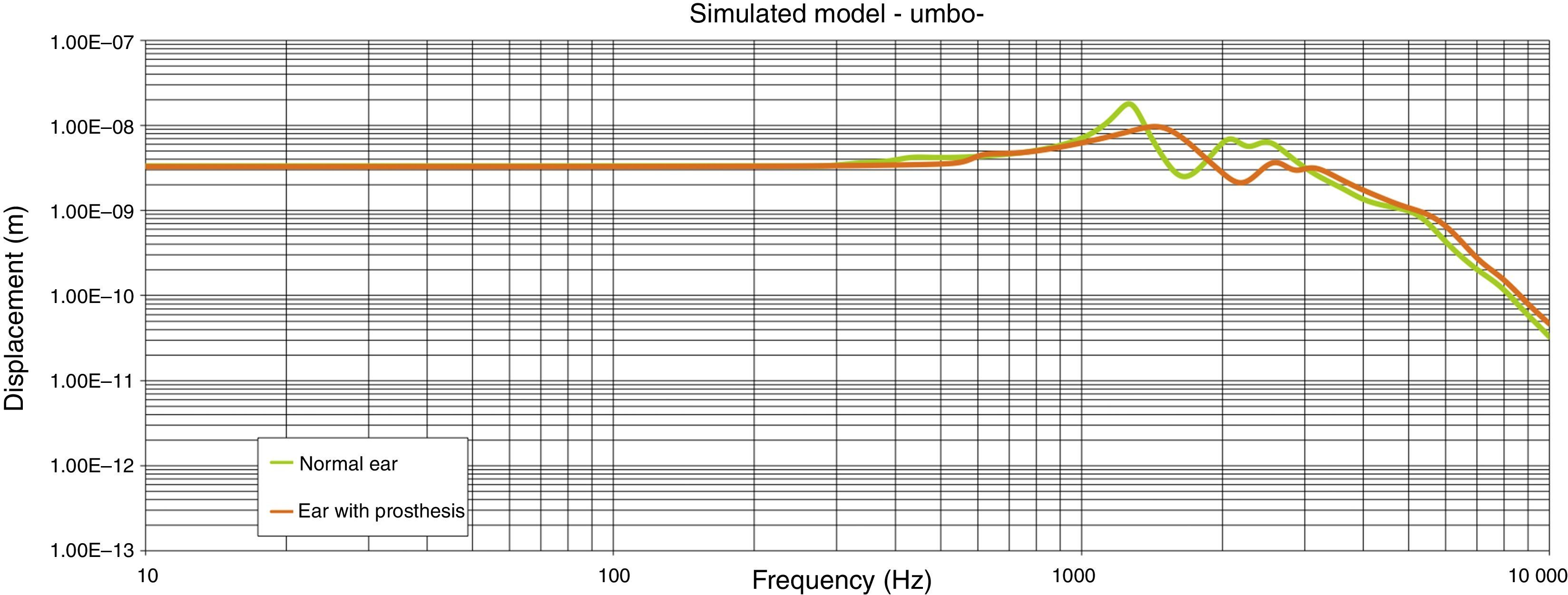
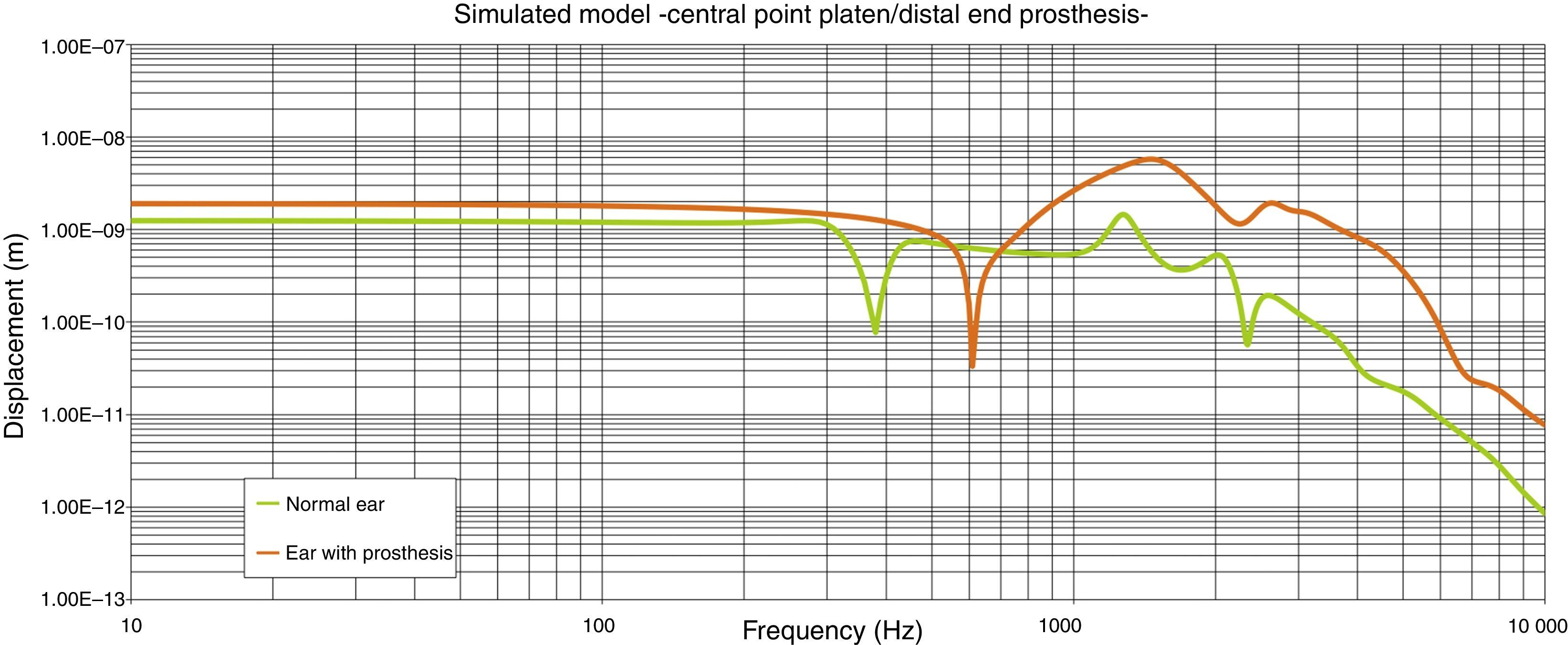
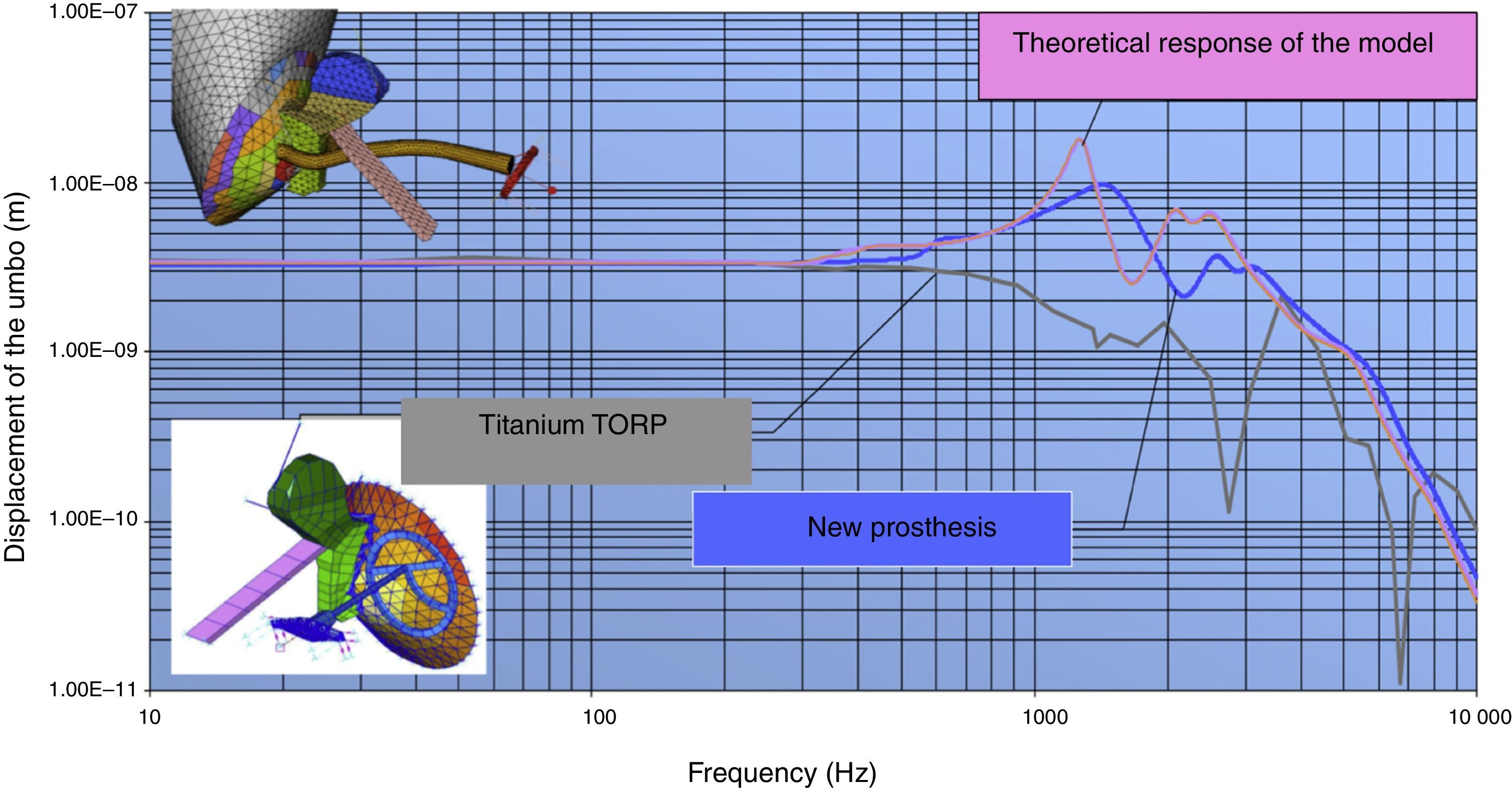
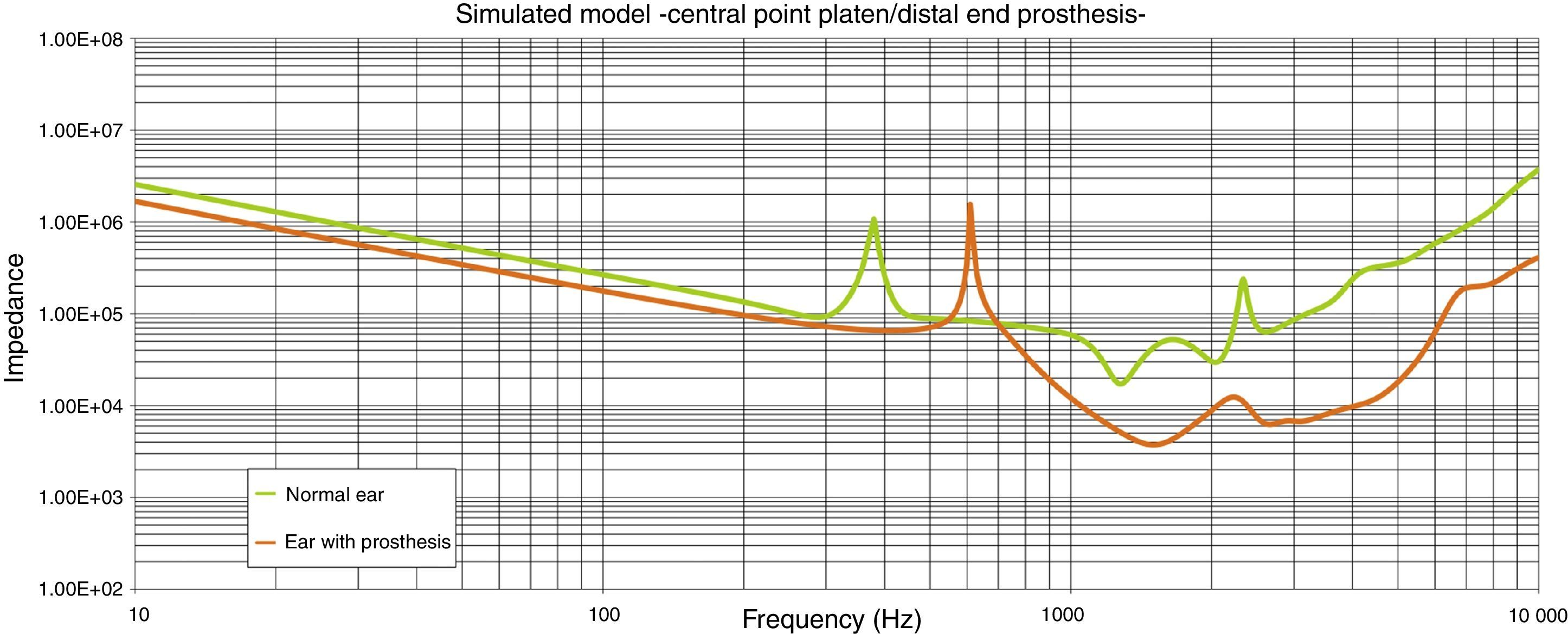
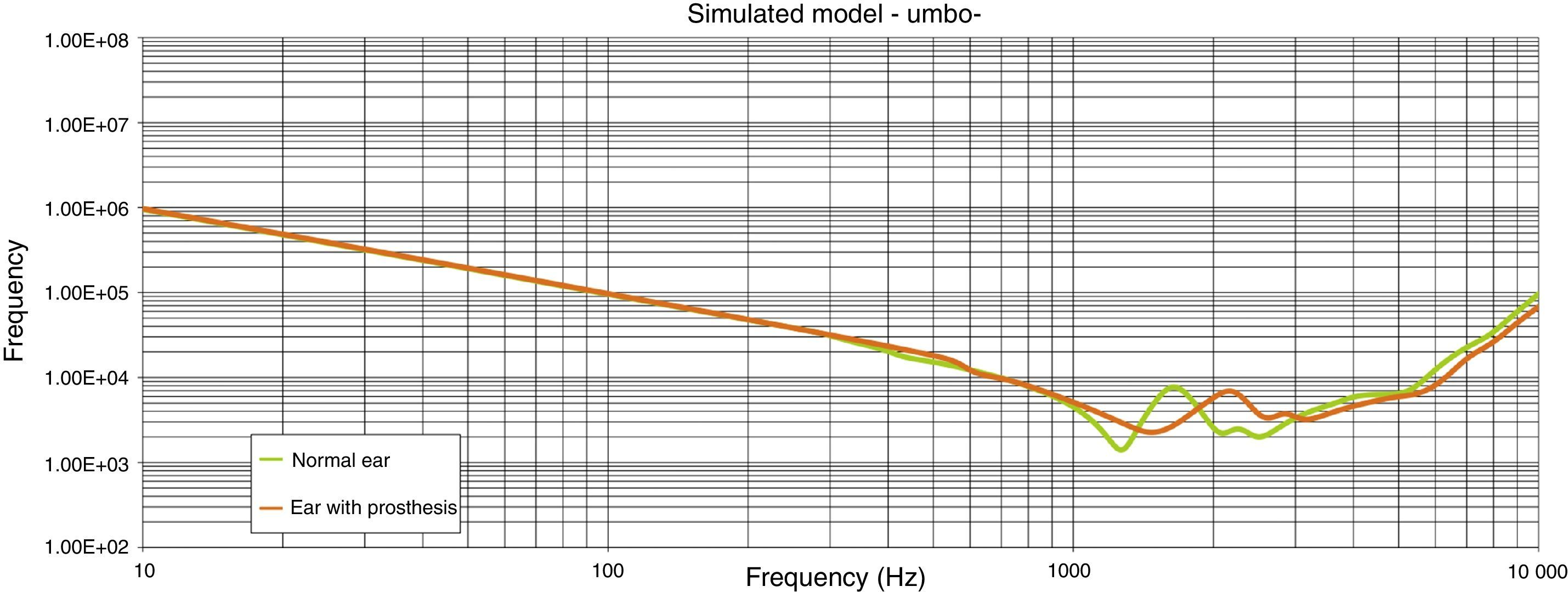
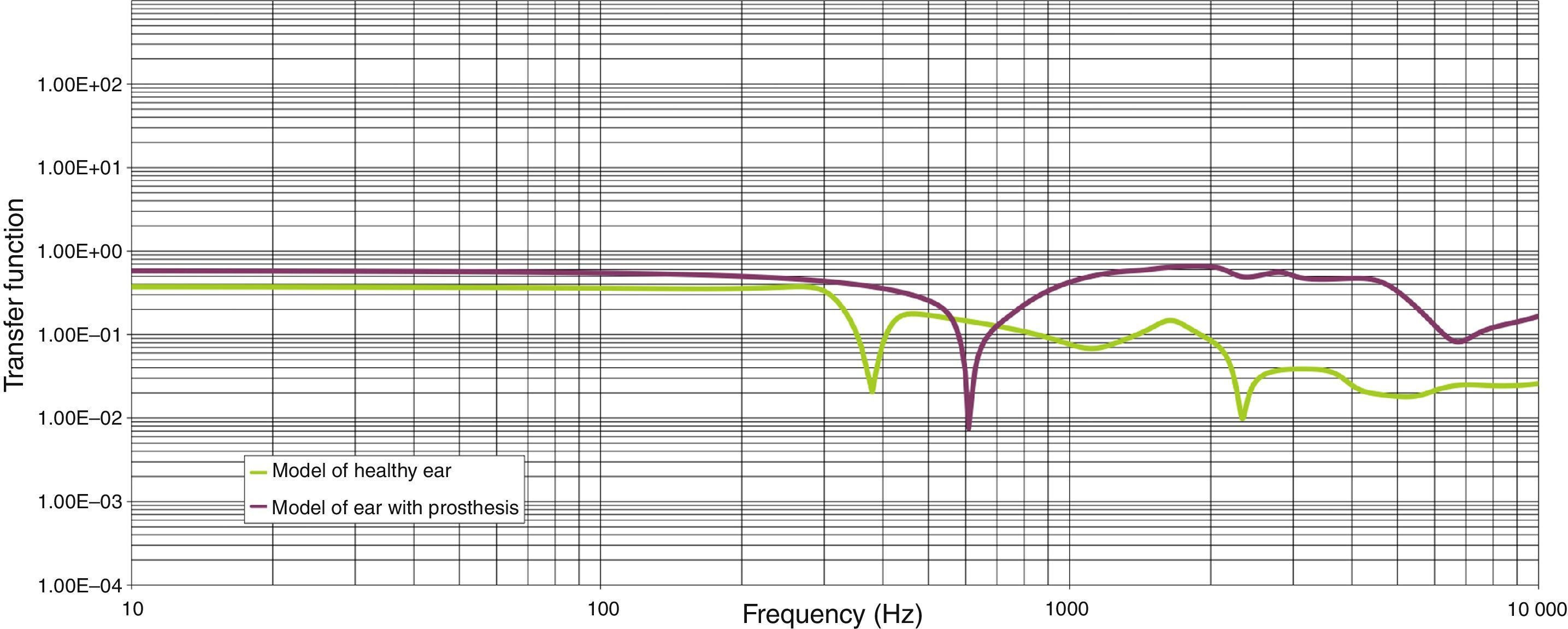
ResultsThe new malleovestibulopexy prosthesis design demonstrates an acoustical–mechanical performance similar to that of the healthy human middle ear. This new design also has additional advantages, such as ease of implantation and stability in the middle ear.
ConclusionsThis study shows that computer simulation can be used to design and optimise the vibroacoustic characteristics of middle ear implants and demonstrates the effectiveness of a new malleovestibulopexy prosthesis in reconstructing the ossicular chain.
Existen numerosas prótesis diseñadas con el fin de sustituir elementos osiculares en el oído medio. En este trabajo presentamos el diseño de una nueva prótesis de sustitución osicular total anclada en el mango del martillo y analizamos su comportamiento mecanoacústico teórico.
MétodosPara el diseño de la prótesis hemos utilizado el método de los elementos finitos (FEM) basándonos en un modelo computarizado 3D dinámico del oído medio humano, analizando su comportamiento mecánico.
ResultadosLa prótesis resultante presenta un comportamiento mecanoacústico teórico superponible al del oído humano sano. Posee, además, otras ventajas biológicas como son estabilidad y la facilidad de implantación.
ConclusionesLa simulación computarizada puede ser utilizada para diseñar y optimizar las características vibroacústicas de prótesis implantables en el oído medio. Mostramos la eficiencia mecanoacústica de un nuevo diseño de prótesis de maleovestibulopexia útil en la reconstrucción de la cadena osicular.