Este trabajo está enfocado a la obtención de resultados numéricos que permitan la detección y caracterización de grietas sub-superficiales en sólidos mediante la incidencia de ondas elásticas de Rayleigh. Los resultados se obtienen a partir de ecuaciones integrales de frontera, que pertenecen al campo de la elastodinámica. Una vez que se aplican las condiciones de frontera se obtiene un sistema de ecuaciones integrales del tipo Fredholm de segunda especie y orden cero, el cual es resuelto mediante eliminación gaussiana. El método que se emplea para la discretización de dichas ecuaciones es conocido como «método indirecto de elementos frontera», el cual puede ser visto como una derivación del teorema clásico de Somigliana. A partir de los análisis realizados en el dominio de la frecuencia emergen picos de resonancia que permiten inferir la presencia de grietas mediante los cocientes espectrales. Se analizaron varios modelos de medios agrietados donde se pretende evidenciar la gran utilidad que presenta el uso de los cocientes espectrales para identificar grietas. Se estudiaron los efectos de la orientación y la localización de las grietas. Los resultados obtenidos presentan buena concordancia con los publicados previamente.
This work is focused on the finding of numerical results for detection and characterization of sub-surface cracks in solids under the incidence of Rayleigh's elastic waves. The results are obtained from boundary integral equations, which belong to the field of dynamics of elasticity. Once applied the boundary conditions, a system of Fredholm's integral equations of second kind and zero order is obtained, which is solved using Gaussian elimination. The method that is used for the solution of such integral equations is known as the Indirect Boundary Element Method, which can be seen as a derivation of the Somigliana's classic theorem. On the basis of the analysis made in the frequency domain, resonance peaks emerge and allow us to infer the presence of cracks through the spectral ratios. Several models of cracked media were analyzed, where analyses reveal the great utility that displays the use of spectral ratios to identify cracks. We studied the effects of orientation and location of cracks. The results show good agreement with the previously published.
Es bien sabido que la presencia de grietas en componentes estructurales conduce a problemas de estabilidad e integridad estructural. Las grietas en materiales y componentes usados en la ingeniería mecánica y civil causan la reducción de la capacidad estructural y pueden conducir a inestabilidad o colapso.
El desarrollo de estudios para la identificación y caracterización de las grietas tiene su origen en una gran variedad de áreas, citando, por ejemplo, a Griffith [1]. El progreso tecnológico centrado en ensayos no destructivos (NDT) de los materiales ha conducido al desarrollo de dispositivos tales como generadores de pulsos (ondas mecánicas) y receptores que pueden llegar a frecuencias tan altas como 200MHz. Por otro lado, los avances teóricos y en los modelos numéricos [2,3] han demostrado ser útiles para una interpretación conjunta con los desarrollos en el campo de NDT [4,5]. Un panorama general de resultados teóricos en relación a la interacción de las ondas elásticas con grietas puede verse en Zhang y Gross [6]. La identificación y caracterización de grietas de superficie y sub-superficiales que utilizan las ondas de Rayleigh son de mucho interés en la industria; véanse, por ejemplo, las referencias [7–12]. Principalmente y desde el punto de vista teórico, Achenbach et al. han desarrollado formulaciones que han contribuido enormemente a la comprensión encaminada a la caracterización de grietas mediante el uso de ondas elásticas, citando por ejemplo [13–16].
Adicionalmente, se han desarrollado diversas investigaciones en el campo de las ecuaciones integrales de frontera aplicadas a la identificación y caracterización de cavidades y grietas [17–19]. Una contribución sumamente importante fue la desarrollada en [20], la cual está encaminada al estudio de las ecuaciones integrales hipersingulares con fines de identificación de grietas, remarcando su valioso y auxiliar uso en análisis de NDT. Por otro lado, para fines de identificación de grietas se ha demostrado que las ondas irradiadas dependen de una integral del tensor de Green de tracciones ponderada con la apertura de la cara de la grieta y las cuales son relativamente insensibles a concentraciones de esfuerzos [21]. Las ecuaciones integrales de frontera de desplazamientos se utilizaron para la localización de grietas aplicando vibraciones o ultrasonido en Rus y Gallego [22], y su principal objetivo fue el de evaluar la capacidad de solucionar problemas pertenecientes al campo de NDT.
Este trabajo considera el estudio de las ecuaciones integrales de frontera, las cuales pueden ser derivadas del teorema clásico de Somigliana, para abordar la detección y caracterización de discontinuidades sub-superficiales mediante ondas de Rayleigh. Particularmente, este método puede ser visto como uno perteneciente a los métodos de elemento frontera (MEF), y adquiere el carácter de indirecto (MIEF) debido a que las incógnitas, conocidas como densidades de fuerza, se obtienen en un paso intermedio. El sistema de ecuaciones integrales, de tipo Fredholm de segunda especie y orden cero, se obtiene a partir de la aplicación de las condiciones de frontera en los puntos de colocación. Estos puntos de colocación se establecen en los puntos medios de cada elemento frontera (elementos constantes). Para la solución del sistema de ecuaciones integrales obtenido se ha empleado el método de eliminación gaussiana, debido a que este representa un método simple que permite la obtención de soluciones exactas a las ecuaciones lineales. Se ha tenido especial cuidado de evitar problemas de mal condicionamiento del sistema de ecuaciones, y por lo tanto fue posible obtener soluciones precisas para los modelos aquí planteados. Es importante mencionar que a partir del análisis en el dominio de la frecuencia se observan picos de resonancia que pueden estar relacionados con la presencia de grietas sub-superficiales y que aparecen claramente empleando los cocientes espectrales.
2Ecuaciones integrales de fronteraSi se considera un dominio sólido elástico V delimitado por su frontera S, los campos difractados de desplazamientos y tracciones, bajo una excitación armónica, pueden ser expresados, despreciando las fuerzas de cuerpo, por medio de las ecuaciones integrales de frontera:
ydonde uidx=i-ésima componente de desplazamiento en un punto x, Gijx;ξ=función de Green, que representan el desplazamiento en dirección i en x debido a la aplicación de una fuerza unitaria en dirección j en el punto ξ, ϕjξ es la densidad de fuerza en dirección j en el punto ξ. El producto ϕjξ dSξ es la distribución de la fuerza en la superficie S (los subíndices i, j se limitan a ser 1 o 3). El subíndice de la diferencial muestra la variable sobre la cual se va a realizar la integración. Esta ecuación integral puede obtenerse a partir de la representación integral de Somigliana [23]. Además, se ha demostrado que si ϕjξ es continua a lo largo de S, en ese caso el campo de desplazamientos es continuo a través de S [24]. tidx=i-ésima componente de tracciones, c=0, 5 si x tiende a la frontera S «desde dentro» de la región, c=−0, 5 si x tiende a S «desde fuera» de la región, o c=0 si x no está en S. Tijx;ξ=función de tracciones de Green, o sea, la tracción en la dirección i en el punto x, vinculado al vector unitario ni(x), debido a la aplicación de una fuerza unitaria en dirección j en ξ sobre S. Las funciones de Green para desplazamientos y tracciones para un espacio infinito pueden ser consultadas en Sánchez-Sesma y Campillo [23].
3Planteamiento del problemaEn términos generales, en la propagación de ondas en medios agrietados, los campos de desplazamientos y tracciones pueden ser representados por la suma de un campo libre (superíndice «o») y de un campo difractado (superíndice «d»), esto es: ui(x)=uio(x)+uid(x) y ti(x)=tio(x)+tid(x), respectivamente. El campo libre se expresa, por ejemplo, por la incidencia de las ondas P, SV o de Rayleigh. Las condiciones en la superficie libre se conocen como de tracciones libres y se representan como ti(x)=0.
Las ecuaciones integrales establecidas en las ecuaciones (1) y (2) permiten la inclusión de grietas o discontinuidades debido al uso del concepto de multi-región. El dominio de estudio puede ser discretizado en regiones, y la unión entre ellas debe satisfacer a las condiciones de frontera que representan la continuidad (uiR(x)=uiE(x) y tiR(x)=tiE(x)) para una región R y una región E, por ejemplo. Para incluir una grieta entre las 2 regiones se deben establecer las condiciones de frontera de tracciones libres en las caras de las grietas y se escriben como tiR(x)=0 y tiE(x)=0.
Cada superficie se divide en elementos frontera cuya longitud es igual o menor a 1/6 de la longitud de ondas SV obtenida a cada frecuencia. Por ejemplo, para una superficie libre, la unión entre las regiones R y E y la discontinuidad o grieta se requieren los elementos frontera N, M y K, respectivamente. Entonces, las ecuaciones (1) y (2) pueden ser escritas, considerando los campos libres y difractados y las condiciones de frontera descritas anteriormente, como:
yLa región R está formada por la frontera ∂R=∂1R∪∂2R∪∂3R, mientras que la región E lo está por la frontera ∂E=∂1E∪∂2E. ∂1R y ∂1E representan los segmentos continuos entre la región R y E, ∂2R es la correspondiente a la discontinuidad o grieta perteneciente a la región R, ∂2E es la discontinuidad o grieta en el lado de la región E, y ∂3R es la superficie libre que pertenece a la región R.
Para el proceso de discretización de las fronteras, incluyendo las caras de las grietas, se emplean elementos frontera constantes. Este tipo de elementos han sido usados en la solución de diversos problemas relacionados con la difracción de ondas elásticas y han mostrado ser eficientes para obtener respuestas precisas [25]. A partir de la discretización de las ecuaciones (3) a la (7) se forma un sistema de ecuaciones del tipo Fredholm de segunda especie y orden cero. Su solución se realiza empleando el método de eliminación gaussiana. Una vez que se obtienen los valores de la incógnitas (ϕ’s) es posible determinar el campo difractado de desplazamientos y de tracciones. El sistema de ecuaciones integrales resultante es el que se muestra a continuación. G y T se refieren a la función de Green de desplazamientos y de tracciones, respectivamente. El superíndice representa a la región de integración (R o E) y los subíndices se asocian a los grados de libertad considerados (x, z), asociados a 1 y 3, respectivamente.
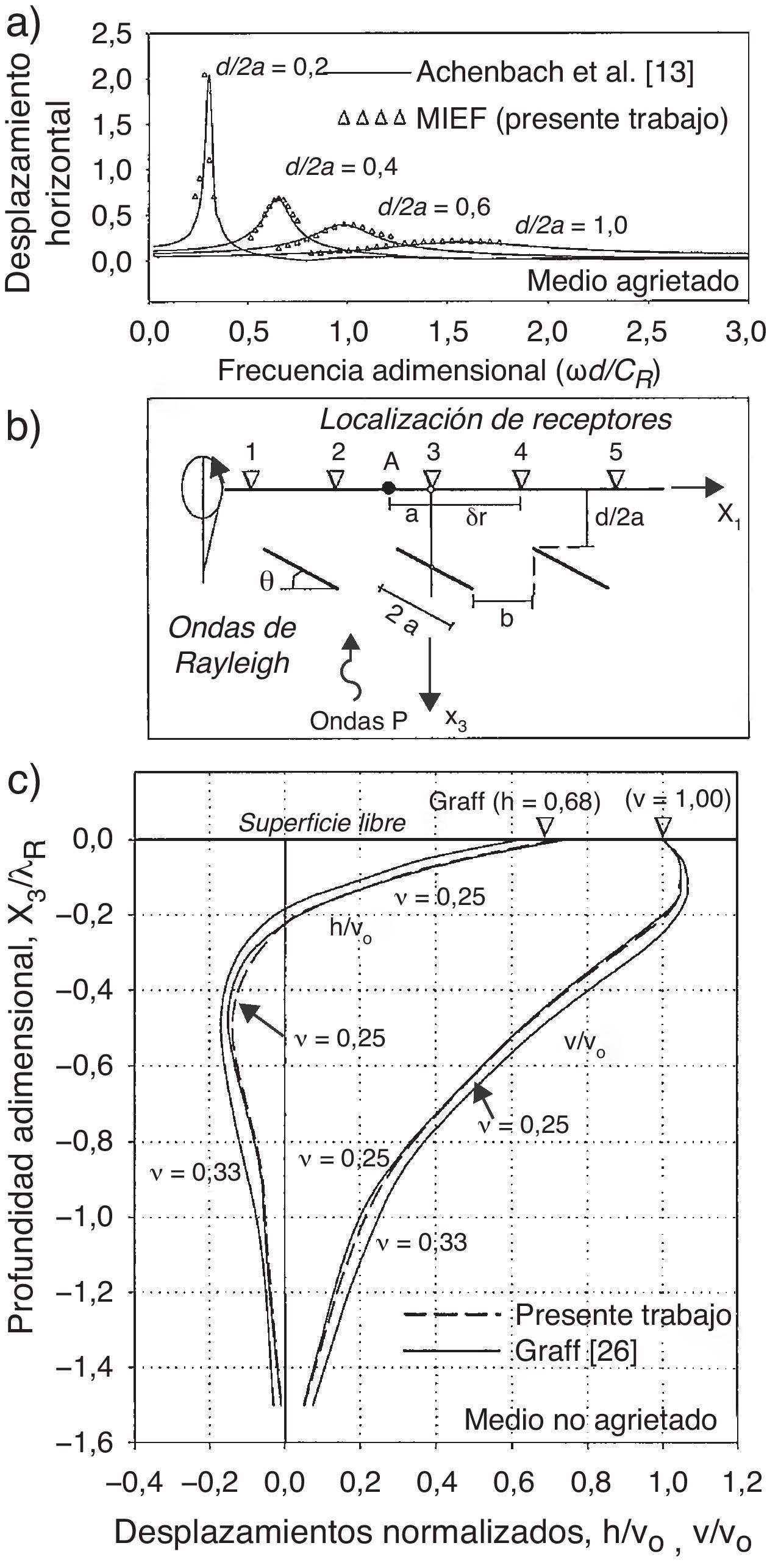
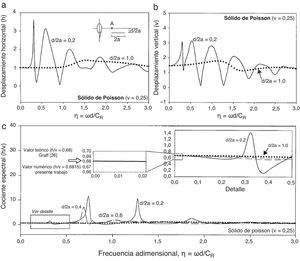
4Validación y ejemplos numéricosComo se mencionó anteriormente, el campo incidente puede ser representado por cualquier tipo de onda que se propaga en el plano, es decir, onda P, SV o de Rayleigh. La formulación integral aquí presentada es validada empleando 4 relaciones de profundidad de grieta, dadas por d2a= 0,2, 0,4, 0,6 y 1,0, donde d es la profundidad de la grieta y 2a es su longitud. Para este fin de validación se utiliza la incidencia de ondas P. El rango de frecuencias analizado es de 0≤η≤3, 0, donde η=ωdCR, ω es la frecuencia angular y CR representa la velocidad de las ondas de Rayleigh; el sólido considerado satisface la relación de Poisson de ν=0, 25. Achenbach et al. [13] estudiaron estas mismas relaciones de profundidad para una grieta horizontal y calcularon los desplazamientos horizontales obtenidos en la superficie (punto A, fig. 1b) del sólido agrietado y encontró que las grietas provocan, en un análisis en frecuencia, picos de resonancia que pueden ser de utilidad para identificar y caracterizar grietas. Los resultados obtenidos por Achenbach et al. [13] y los obtenidos mediante la presente formulación integral se presentan en la figura 1a. La congruencia entre ambos resultados es satisfactoria. Resulta claro que las grietas superficiales tienden a describir picos de resonancia agudos. A medida que las grietas tienden a ser más profundas (p.ej., d2a=1,0), los picos de resonancia se vuelven menos evidentes. Para detalles adicionales referentes al proceso de validación de resultados, referimos al lector a consultar la referencia [25].
a) Comparación de los resultados obtenidos por Achenbach et al. [13] y el presente trabajo para un medio sujeto a la incidencia de ondas elásticas P. b) Modelos de medios agrietados estudiados en el presente trabajo. c) Desplazamientos, debidos a ondas de Rayleigh, normalizados en función de la profundidad, donde vo es el valor para el desplazamiento vertical en la superficie; resultados de Graff [26] y del presente trabajo.
Adicionalmente, en la figura 1c se grafican los resultados obtenidos por Graff [26] correspondientes a una onda de Rayleigh que se propaga en medios con características definidas por su relación de Poisson (ν=0, 25 y ν=0, 33). Él muestra los desplazamientos normalizados con respecto a la profundidad, para las 2 relaciones de Poisson consideradas. Menciona, además, que la energía se encuentra localizada cerca de la superficie libre y desaparece en casi una longitud de onda de Rayleigh (λR), como es claramente observado. Por lo tanto, el uso eficaz de las ondas Rayleigh para detección de grietas podría limitarse a las grietas superficiales. Graff [26] grafica los desplazamientos horizontales (h) y verticales (v) y obtiene los valores de h=0,68 y v=1,00 en la superficie libre, para una relación de Poisson de ν=0, 25. Por lo tanto, la relación espectral para este caso es h/v=0,68. La figura 1c incluye curvas obtenidas en el presente trabajo para ν=0, 25 (línea discontinua). Se observa una buena concordancia entre los resultados obtenidos mediante el MIEF y Graff [26]. Los modelos agrietados estudiados en el presente trabajo y a los cuales se les calcula su cociente espectral se ilustran en la figura 1b.
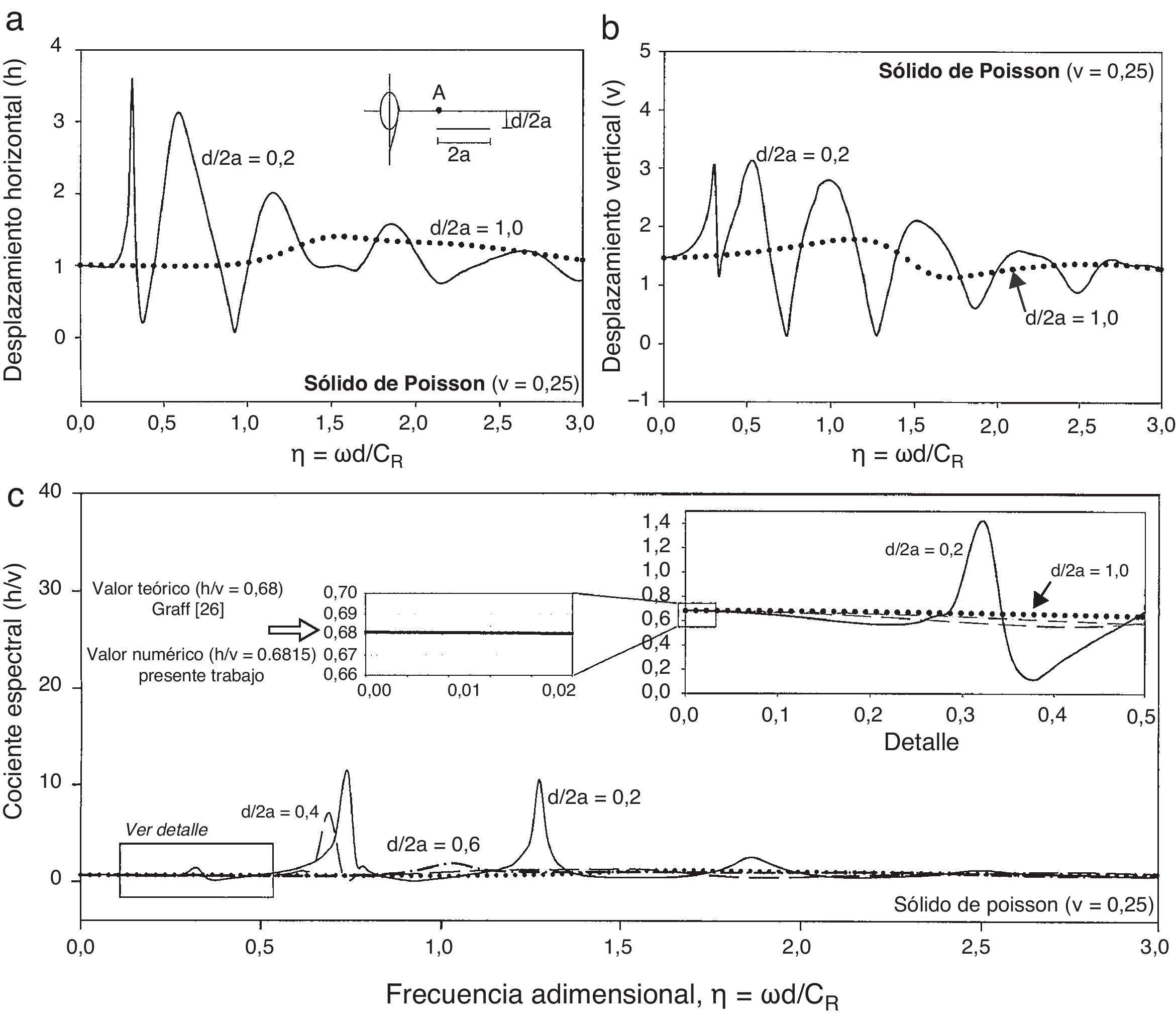
Para estudiar la influencia de las grietas ante la incidencia de las ondas de Rayleigh se consideraron 4 relaciones de profundidad d2a= 0,2, 0,4, 0,6 y 1,0. El análisis en frecuencia se llevó a cabo para el rango de 0≤η≤3, 0. Se seleccionó un sólido de Poisson, es decir, ν=0, 25. Los desplazamientos horizontales y verticales medidos en el punto A (ver detalle en la fig. 2a) se muestran en las figura 2a y 2b, respectivamente, para la grieta más superficial (d2a=0,2) y la grieta más profunda (d2a=1,0). Se espera que una grieta superficial cause alteraciones importantes en las ondas Rayleigh, mientras que una grieta profunda presente un efecto casi insignificante para ambas componentes de desplazamientos. Esto es claramente observable en estas figuras.
Grietas sometidas a la incidencia de las ondas Rayleigh. a) Desplazamientos horizontales para las profundidades de grieta d2a=0,2 y d2a=1,0. b) Desplazamientos verticales para las profundidades de grieta d2a=0,2 y d2a=1,0. c) Relación espectral h/v para profundidades de grieta d2a= 0,2, 0,4, 0,6 y 1,0.
La figura 2c muestra un cociente espectral h/v casi constante para todas las relaciones de profundidad, excepto para las grietas de profundidad d2a=0,2 y d2a=0,4. En el detalle amplificado de la figura 2c se puede observar el primer pico causado por la profundidad de grieta d2a=0,2, así como el comportamiento constante mostrado para una grieta con una profundidad d2a=1,0. Adicionalmente, se puede observar que a bajas frecuencias la relación espectral h/v tiende a 0,6815 para cualquier profundidad de la grieta, y este valor incluso se mantiene para el caso de cuando no existe grieta, lo cual concuerda con lo obtenido por Graff [26], quien obtuvo valores de h=0,68 y v=1,00 en la superficie (fig. 1c). Por lo tanto, el cociente espectral h/v=0,68, obtenido por Graff [26], concuerda satisfactoriamente con el obtenido en el presente trabajo (fig. 2c).
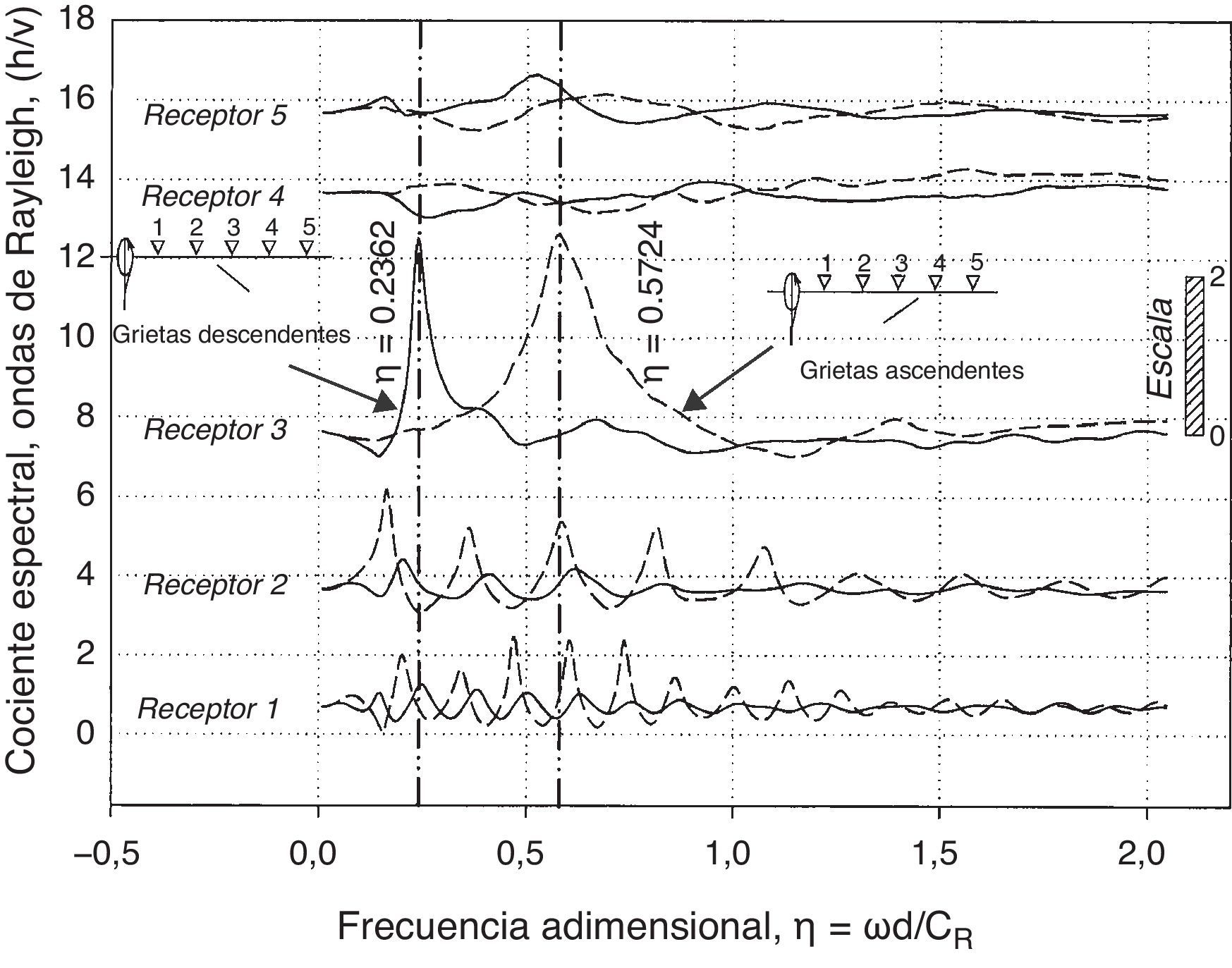
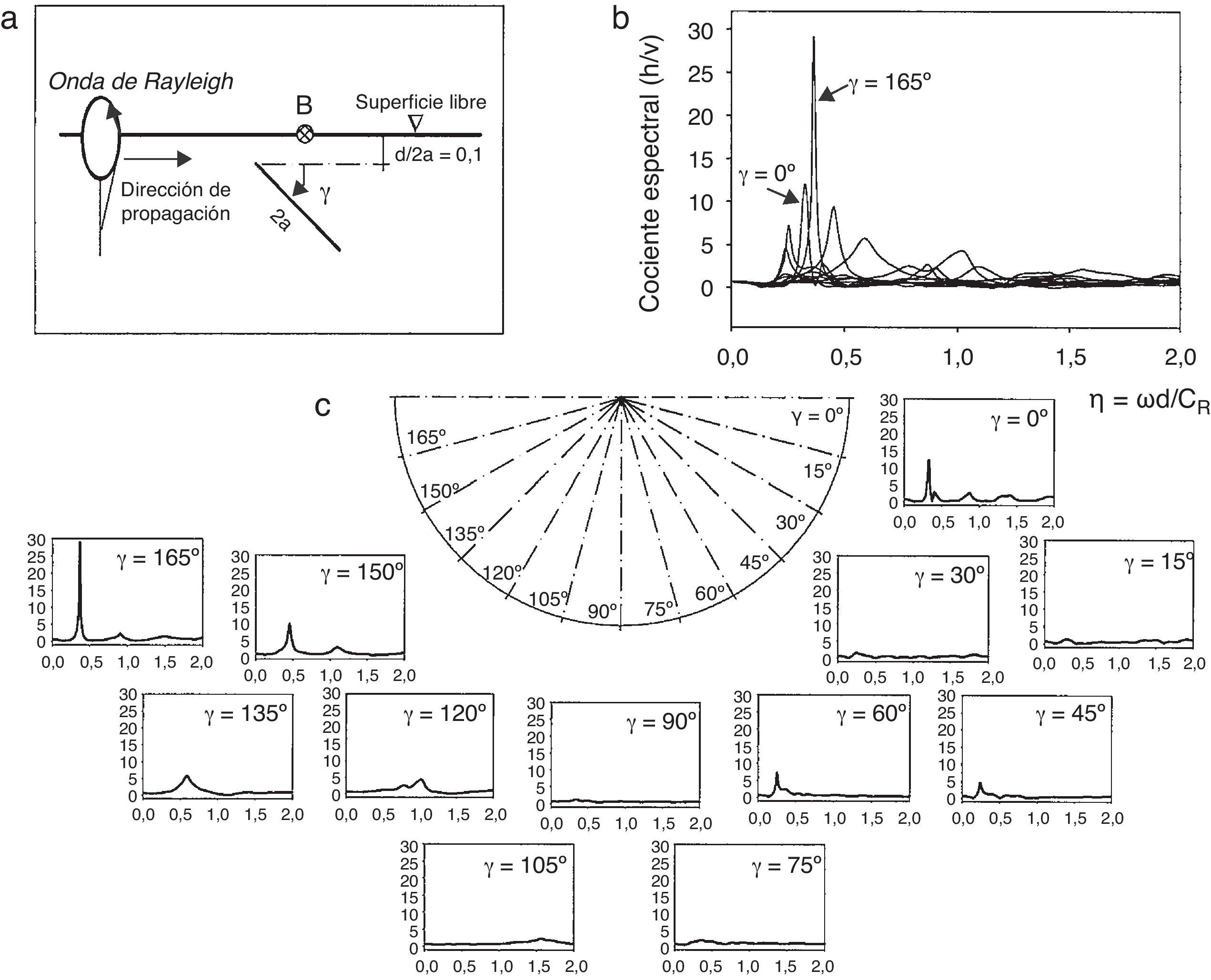
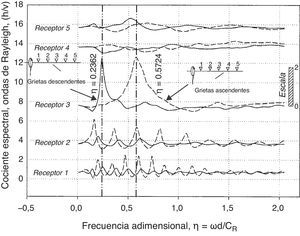
Con el propósito de observar el comportamiento de los cocientes espectrales en función de la orientación de la grieta, en la figura 3 se presentan estos para un ángulo θ=45∘ (grieta descendente) y θ=135∘ (grieta ascendente). La relación de profundidad considerada es de d2a=0,1, en ambos casos. Se determinaron los cocientes espectrales para los 5 receptores mostrados en la figura 1b, el incremento de distancia entre ellos es de δr=2/a. Los comentarios más importantes que surgen de estos 2 casos estudiados se mencionan a continuación. La grieta descendente (línea continua) provoca la difracción de energía al interior del medio. Por esta razón, los receptores 4 y 5 no registran fuertes amplificaciones y no se presentan interacciones de onda de Rayleigh entre la cara superior de la grieta y la superficie libre. Estas interacciones se observan claramente en los receptores 1 y 2. Un comportamiento similar se observa para la grieta ascendente (línea discontinua), excepto que las reflexiones de las ondas son muy evidentes para los receptores 1 y 2. Para el receptor 3, se presentan picos de resonancia muy importantes. Para el caso de grietas descendentes se tiene una amplificación sumamente relevante en η=0, 2362, mientras que para grietas ascendentes este pico se observa en η=0, 5724. Este hecho implica que los picos de resonancia que se presentan en los cocientes h/v dependen de la dirección en la que viajan las ondas de Rayleigh, y también de la orientación de las mismas grietas. Es decir, una misma grieta responderá de diferente manera, mostrando picos de resonancia dependiendo la dirección de incidencia de las ondas de Rayleigh, lo cual puede tener implicaciones prácticas.
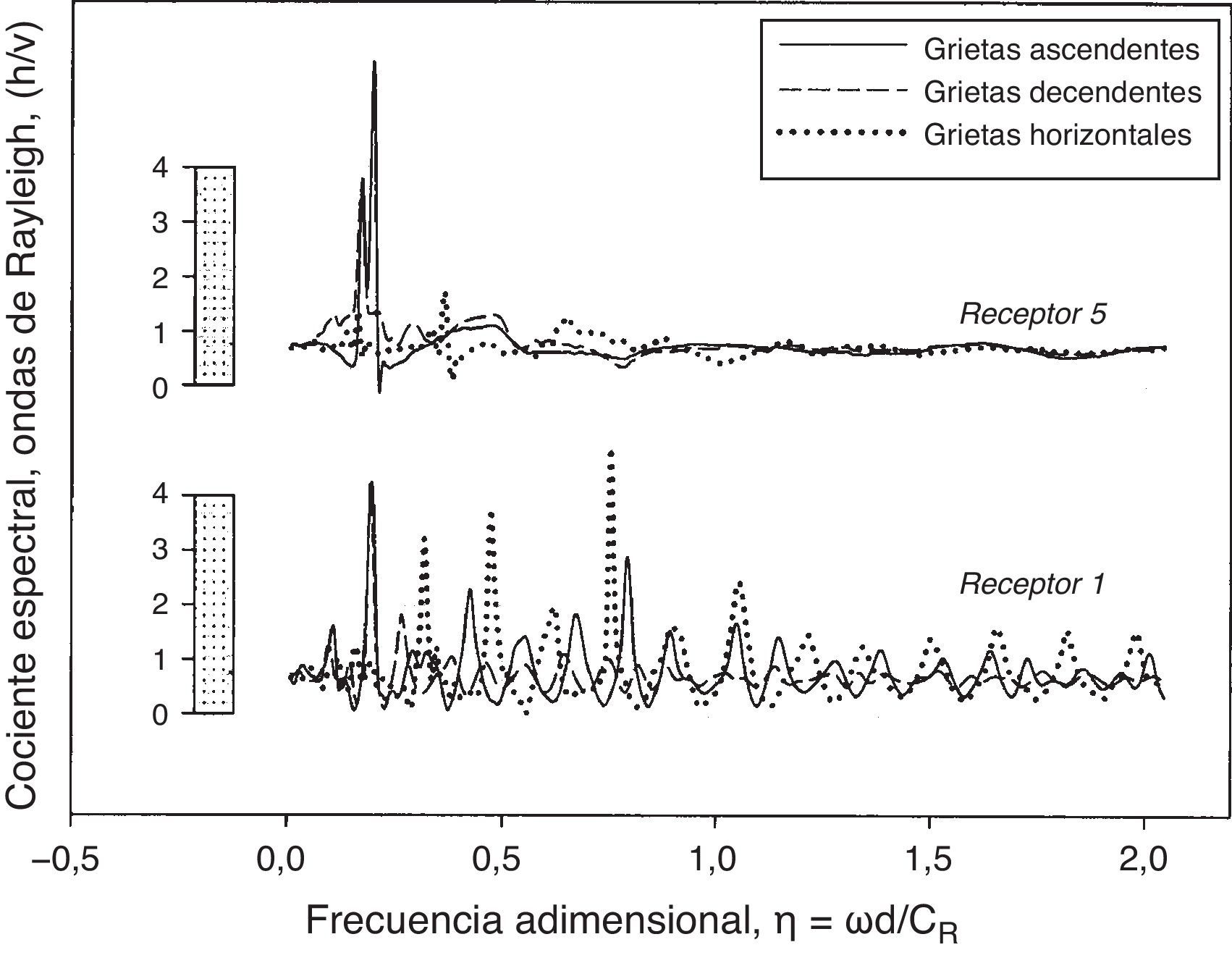
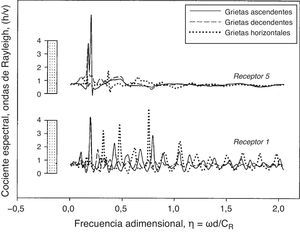
Para observar los cocientes espectrales h/v debido al agrietamiento múltiple, se modelaron sistemas de 3 grietas. Se consideraron primeramente grietas: ascendentes consecutivas (θ=135∘), descendentes (θ=45∘) y horizontales (θ=0∘), y se determinaron los cocientes espectrales en los receptores 1 y 5. La distancia desde el receptor 1 a 5 es de 32/2a, d2a=0,1, b/2a=0,7171 (fig. 1b) para las grietas no horizontales y para grietas horizontales b/2a=1,0. En la figura 4, las grietas descendentes (línea discontinua) muestran pocas interacciones de las ondas para ambos receptores, como era de esperar, debido a la difracción de energía hacia el interior del medio. Sin embargo, las grietas ascendentes (línea continua) y horizontales (línea punteada) presentan más interacciones de ondas entre la cara superior de la grieta y la superficie libre. Este efecto es más evidente en el receptor 1. En todos los casos, el receptor 5 muestra una respuesta atenuada a altas frecuencias.
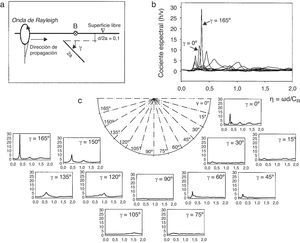
Como se mencionó anteriormente, los picos de resonancia causados por la incidencia de las ondas de Rayleigh son más fuertes para algunas direcciones de propagación u orientación de la grieta. Esta característica puede originar problemas al momento de identificar o caracterizar grietas. Por lo tanto, una grieta podría presentar picos de resonancia evidentes cuando esta se somete a una dirección dada de las ondas Rayleigh, mientras que la misma grieta puede no presentar picos importantes de resonancia para otra incidencia u orientación. En la figura 5 se grafican los cocientes espectrales calculados en el punto B para 12 orientaciones de la grieta de acuerdo con la figura 5a. Los cocientes espectrales se grafican en la figura 5b, mientras que la respuesta detallada para cada ángulo de incidencia se ilustra en la figura 5c. Es notable que para las grietas horizontales o casi horizontales se observen picos de resonancia agudos. El valor máximo de h/v es cercano a 30 y corresponde a una grieta con de ángulo γ=165∘. La grieta vertical muestra un valor h/v casi constante para todo el rango de frecuencias estudiado.
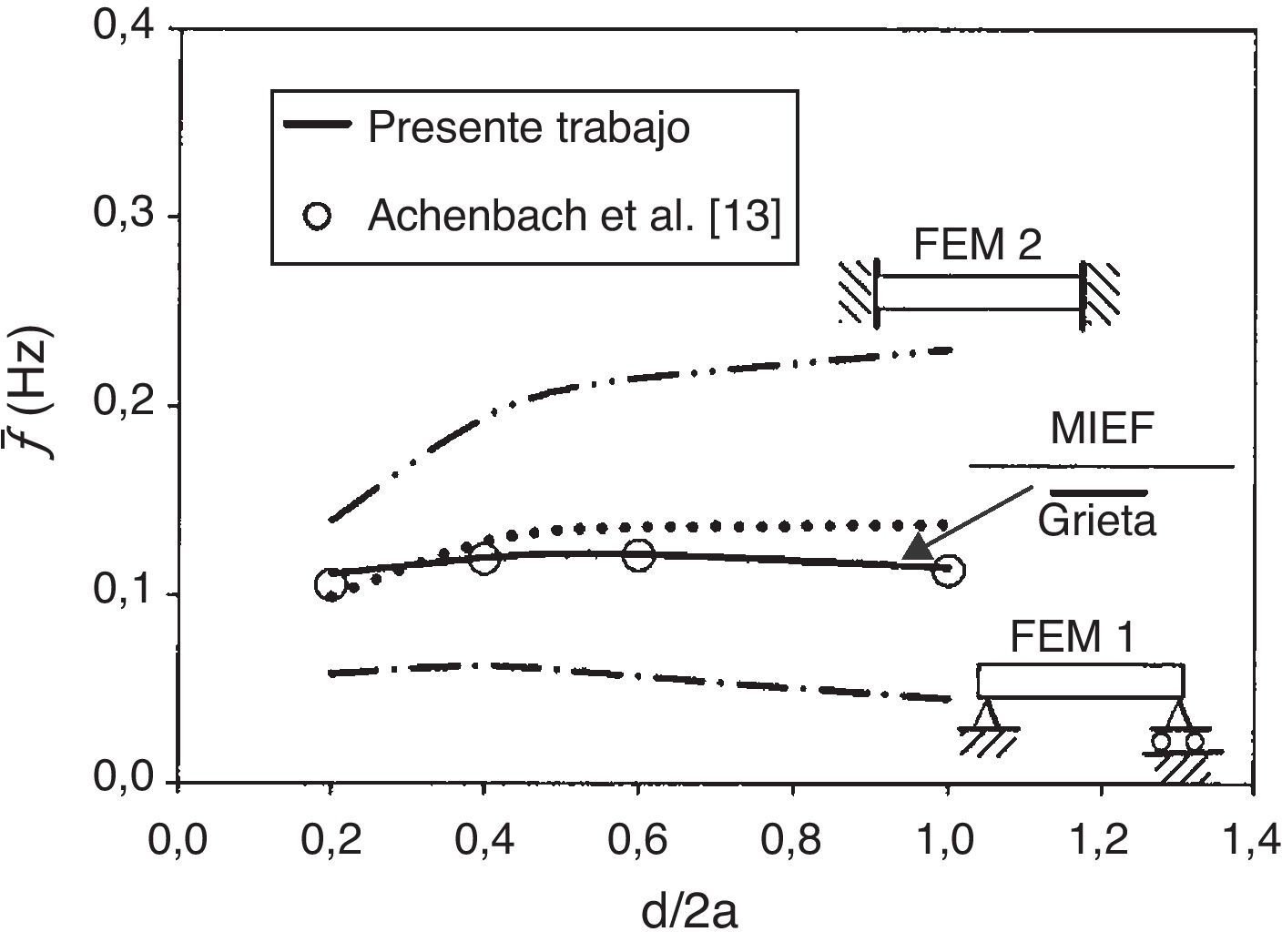
Finalmente, en la figura 6 se relacionan las frecuencias de resonancia f¯ (obtenidas a partir de los picos mostrados en la figura 1a) con los tamaños de las grietas horizontales. Adicionalmente, y con el propósito de dar una explicación a dichas frecuencias de resonancia, se consideró que el espacio entre la cara superior de la grieta y la superficie libre se podría idealizar como una viga sujeta a flexión. Se estimó que el comportamiento real en frecuencia para una grieta horizontal tendría que estar contenido entre las 2 condiciones de frontera extremas para las vigas. Para esto, se consideró primeramente una viga simplemente apoyada en sus extremos (FEM 1) y después una viga con los extremos fijos (FEM 2). La longitud de las vigas es de 2a, y las alturas de ellas satisfacen la relación d/2a=0,2, 0,4, 0,6 y 1,0. La relación de Poisson empleada fue de ν=0, 25. Los modelos numéricos de estas vigas fueron realizados utilizando el programa comercial conocido ANSYS versión 9.0. Las vigas se modelaron en condiciones de deformación plana y se emplearon elementos finitos del tipo Plane82. Las frecuencias de resonancia, tanto del presente trabajo como de los resultados obtenidos por Achenbach et al. [13], se grafican en la figura 6. Así también, se grafican las frecuencias de resonancias obtenidas a partir de los análisis FEM 1 y FEM 2. La línea punteada representa el promedio de los análisis realizados mediante el método de elementos finitos (FEM 1 y FEM 2). Se observa que los resultados obtenidos mediante el presente trabajo y los de Achenbach et al. [13] muestran buena concordancia, y además, que la idealización mediante vigas es una buena herramienta para estimar de manera aproximada dichas frecuencias.
Frecuencia de resonancia (f¯) vs. relación d/2a. Los resultados obtenidos en el presente trabajo se grafican con línea continua, mientras que los obtenidos por Achenbach et al. [16] se grafican con círculos. Se observa buena concordancia entre ambos resultados. Las curvas raya punto y raya punto punto representan los resultados obtenidos mediante el método de elementos finitos modelando una viga con 2 condiciones de frontera. La línea punteada representa el promedio de los análisis FEM.
El presente trabajo se deriva de las ecuaciones integrales del tipo Fredholm de segunda especie y orden cero. Después de la aplicación de las condiciones de frontera y el uso del concepto de multi-región, fue posible determinar un sistema de ecuaciones integrales en el que las incógnitas, conocidas como densidades de fuerza, se obtuvieron para cada una de las frecuencias analizadas. Este método de elementos frontera puede ser visto como una conceptualización de teorema clásico de Somigliana. La excitación del sistema se llevó a cabo por la incidencia de las ondas P y de Rayleigh. Para este último tipo de ondas se determinaron cocientes espectrales, los cuales pueden ser útiles para la identificación y la caracterización de grietas contenidas en sólidos.
Los resultados obtenidos en el presente trabajo fueron validados con los resultados publicados por Achenbach et al. [13] y Graff [26]. La presencia de grietas o discontinuidades provoca picos de resonancia que pueden ser identificados mediante un análisis de frecuencia. Los picos de resonancia son más agudos cuando las discontinuidades son someras. Además, se observó que una grieta podría presentar picos de resonancia evidentes cuando se somete a una dirección de excitación, mientras que la misma grieta puede no presentar picos importantes de resonancia para otra incidencia de ondas de Rayleigh. Finalmente, se emplearon modelos de elementos finitos para explicar las frecuencias de resonancias que emergen en los análisis de frecuencia en medias agrietados, y los resultados fueron satisfactorios.



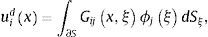
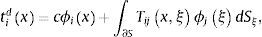
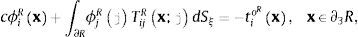
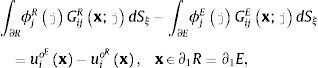
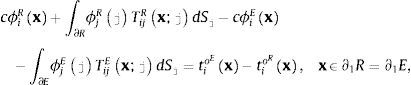
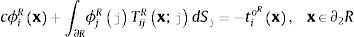
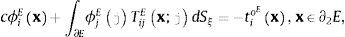

![a) Comparación de los resultados obtenidos por Achenbach et al. [13] y el presente trabajo para un medio sujeto a la incidencia de ondas elásticas P. b) Modelos de medios agrietados estudiados en el presente trabajo. c) Desplazamientos, debidos a ondas de Rayleigh, normalizados en función de la profundidad, donde vo es el valor para el desplazamiento vertical en la superficie; resultados de Graff [26] y del presente trabajo. a) Comparación de los resultados obtenidos por Achenbach et al. [13] y el presente trabajo para un medio sujeto a la incidencia de ondas elásticas P. b) Modelos de medios agrietados estudiados en el presente trabajo. c) Desplazamientos, debidos a ondas de Rayleigh, normalizados en función de la profundidad, donde vo es el valor para el desplazamiento vertical en la superficie; resultados de Graff [26] y del presente trabajo.](https://static.elsevier.es/multimedia/02131315/0000003000000001/v1_201312240906/S021313151200065X/v1_201312240906/es/main.assets/thumbnail/gr1.jpeg?xkr=ue/ImdikoIMrsJoerZ+w96p5LBcBpyJTqfwgorxm+Ow=)
![Frecuencia de resonancia (f¯) vs. relación d/2a. Los resultados obtenidos en el presente trabajo se grafican con línea continua, mientras que los obtenidos por Achenbach et al. [16] se grafican con círculos. Se observa buena concordancia entre ambos resultados. Las curvas raya punto y raya punto punto representan los resultados obtenidos mediante el método de elementos finitos modelando una viga con 2 condiciones de frontera. La línea punteada representa el promedio de los análisis FEM. Frecuencia de resonancia (f¯) vs. relación d/2a. Los resultados obtenidos en el presente trabajo se grafican con línea continua, mientras que los obtenidos por Achenbach et al. [16] se grafican con círculos. Se observa buena concordancia entre ambos resultados. Las curvas raya punto y raya punto punto representan los resultados obtenidos mediante el método de elementos finitos modelando una viga con 2 condiciones de frontera. La línea punteada representa el promedio de los análisis FEM.](https://static.elsevier.es/multimedia/02131315/0000003000000001/v1_201312240906/S021313151200065X/v1_201312240906/es/main.assets/thumbnail/gr6.jpeg?xkr=ue/ImdikoIMrsJoerZ+w96p5LBcBpyJTqfwgorxm+Ow=)
