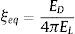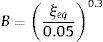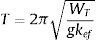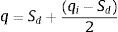Existen varios modelos que definen el comportamiento no lineal de los aisladores de triple péndulo de fricción; uno de ellos es el de cinco fases, propuesto por un grupo investigador de la Universidad de Buffalo, cuyo cálculo se presenta en este artículo. Al existir cierto grado de dificultad al realizar un análisis sísmico con este modelo, en el artículo se propone una alternativa de cálculo simplificado. Concretamente, se propone un método simplificado de análisis sísmico que consiste en encontrar la rigidez efectiva para el sismo de diseño, utilizando los puntos del diagrama de histéresis que definen el comportamiento del modelo ante sismos. Como aplicación ilustrativa se realiza el análisis sísmico del Bloque Estructural 2 del nuevo centro de Investigaciones Científicas y de Post Grado de la Universidad de Fuerzas Armadas ESPE.
There are several models that define the nonlinear behavior of the triple friction pendulum isolator; one of them is the five regimes of operation proposed by the University of Buffalo, which is described in this article. This approach has some degree of difficulty in order to implement a seismic analysis through this model; therefore, a simplified method of seismic analysis is proposed in this article. The proposal is based specifically on finding the effective stiffness to the design earthquake (DE) using the hysteresis curve points that defines the behavior of the model under seismic forces. As a practical application, the seismic analysis of Block 2 of the new Research Department and Graduate studies of the Universidad de Fuerzas Armadas ESPE is considered.
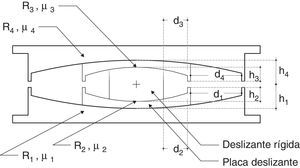
Básicamente se conocen tres tipos de aisladores de péndulo de fricción: primera generación, en la cual una superficie es cóncava y la otra es recta; segunda generación tanto la placa inferior como la superior son cóncavas; y la tercera generación, corresponde al aislador indicado en la figura 1, en que se tiene un aislador dentro de otro aislador. Para los aisladores de tercera generación se ha logrado reducir dimensiones en los mismos y permitir mayores desplazamientos, además de conseguir un desempeño relacionado con la demanda [11–15].
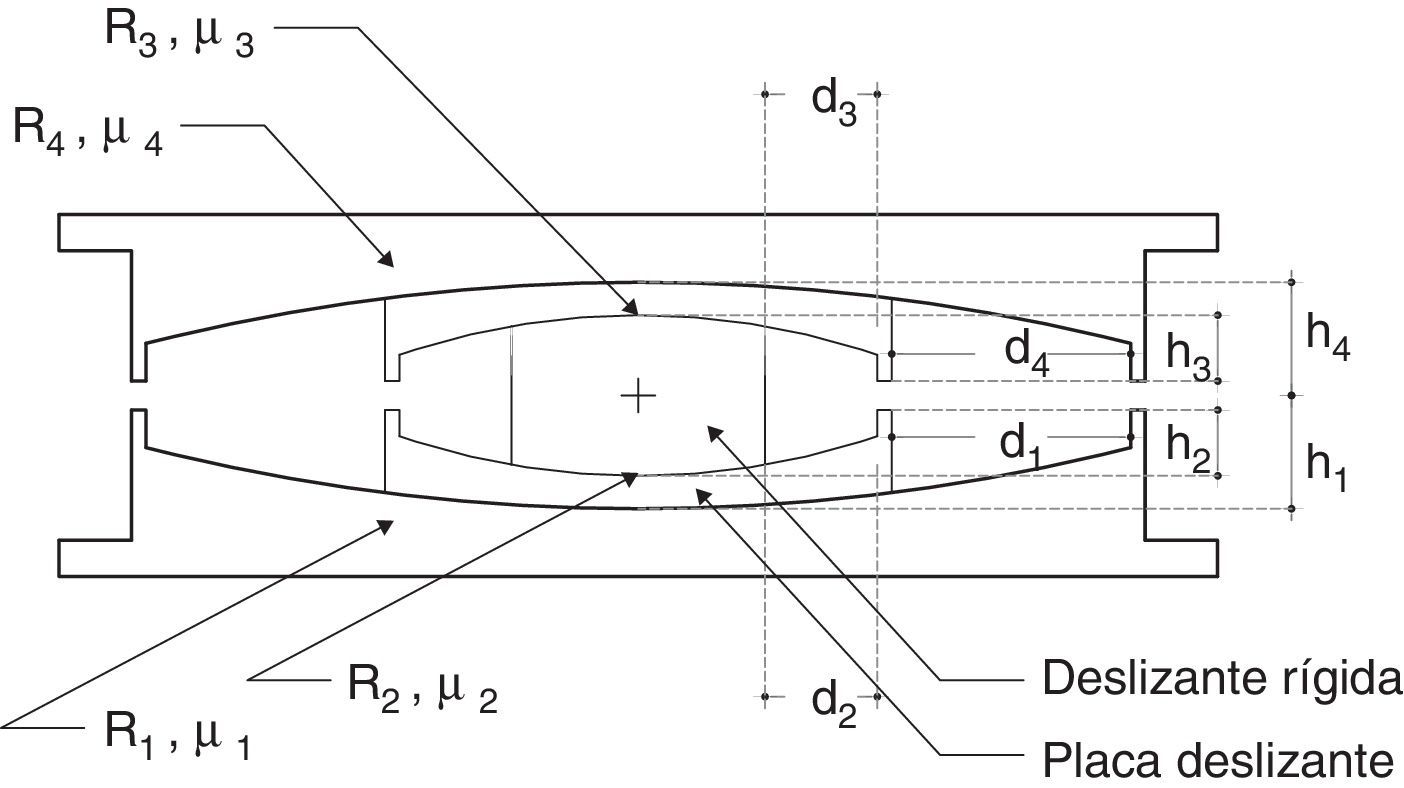
En este artículo se presenta, en primer lugar, las 5 fases en que trabaja un aislador friccional triple péndulo de acuerdo al modelo de Fenz y Constantinou [9], luego el método simplificado propuesto por Fadi y Constantinou [8] y, posteriormente, se propone una variante a este método. Para ello es necesario describir primero las variables de la geometría del disipador que se indica en la figura 1: R1, R4, radios de curvatura de las placas 1 y 4; R2, R3; radios de curvatura de las placas interiores 3 y 4; μ1, μ4; coeficientes de roce (fricción) en las superficies 1 y 4; μ2, μ3; coeficientes de roce en las superficies 2 y 3; d1, d4; capacidad de desplazamiento en las superficies 1 y 4; d2, d3; capacidad de desplazamiento en las superficies 2 y 3; h1, h2, h3, h4 alturas al borde inferior y superior de las placas 2 y 3.
Todas estas dimensiones y coeficientes de roce son proporcionados por el proyectista estructural a la empresa que fabrica los aisladores quien tiene la obligación de ensayarlos y entregar la curva de histéresis para que el proyectista verifique que corresponde al modelo con el cual realizó el cálculo estructural [8,9].
Valores comunes de las dimensiones del aislador indicado en la figura 1 son: R1=R4≫R2=R3; d1=d4, y d2=d3; h1=h4, y h2=h3. En cuanto a los coeficientes de rozamiento μ2=μ3<μ1=μ4. Para describir las fases en que trabaja el aislador se utilizan las siguientes ecuaciones:
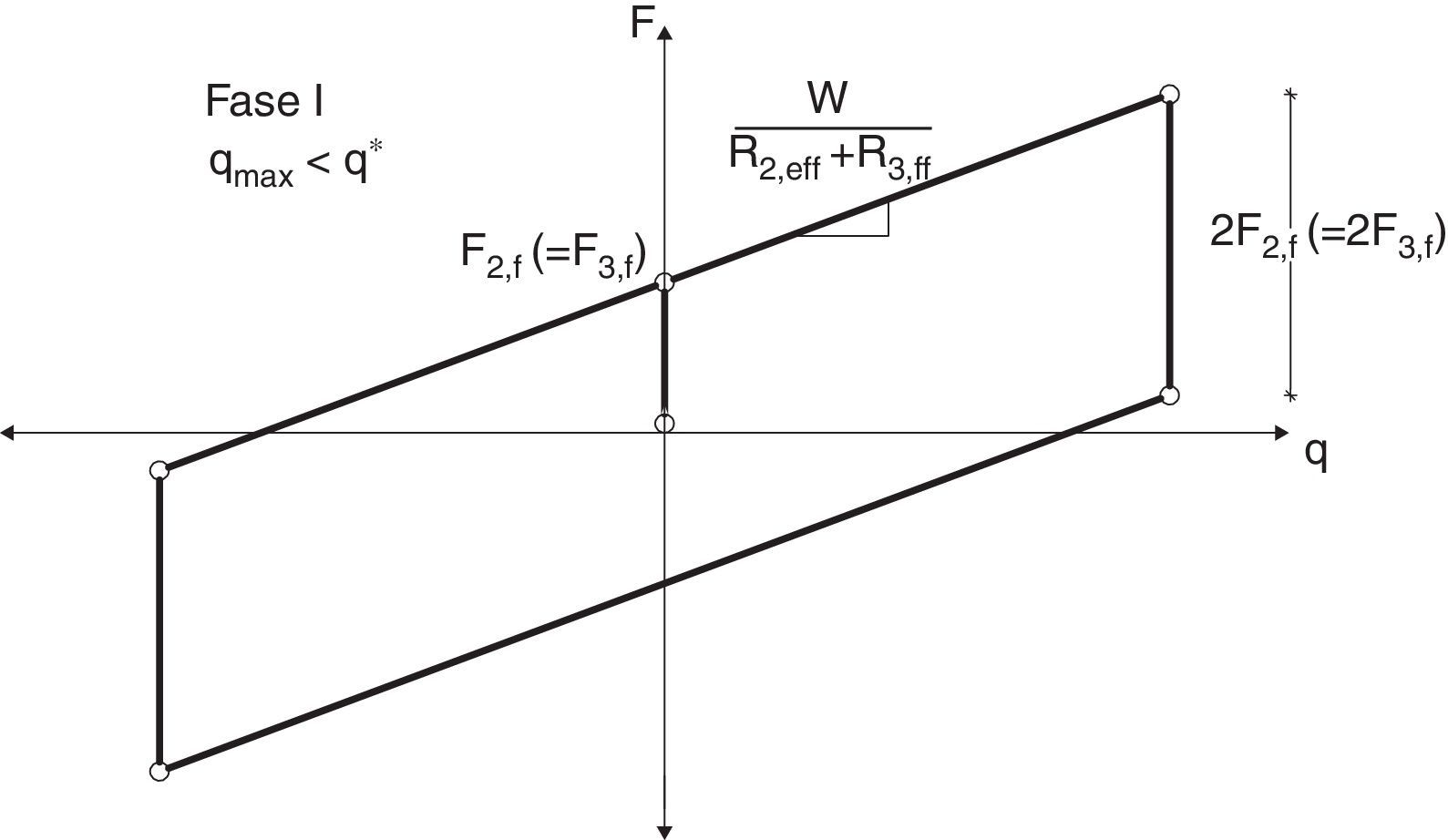
donde el subíndice i varía de 1 a 4; Ri,eff es el radio efectivo; di* es el desplazamiento lateral efectivo de la placa i; Fi,f es la resistencia característica.Antes de presentar el método simplificado propuesto por Fadi y Constantinou [8] se debe indicar que el aislador triple péndulo trabaja en 5 fases de acuerdo al grado de demanda sísmica. En la primera fase el aislador se desliza en las superficies 2 y 3 (véase la fig. 1); en esta fase, la fuerza lateral F y el desplazamiento lateral q, en esta fase vienen definidos por las siguientes ecuaciones [8]:
donde W es el peso que gravita sobre el aislador; las restantes variables han sido definidas anteriormente. En la figura 2 se indica la curva de histéresis correspondiente a la primera fase [9]. El diagrama de histéresis de la figura 2 corresponde a un FPS de la primera generación, desarrollado con todos los detalles en la referencia [4].Diagrama de histéresis en Fase I[9].
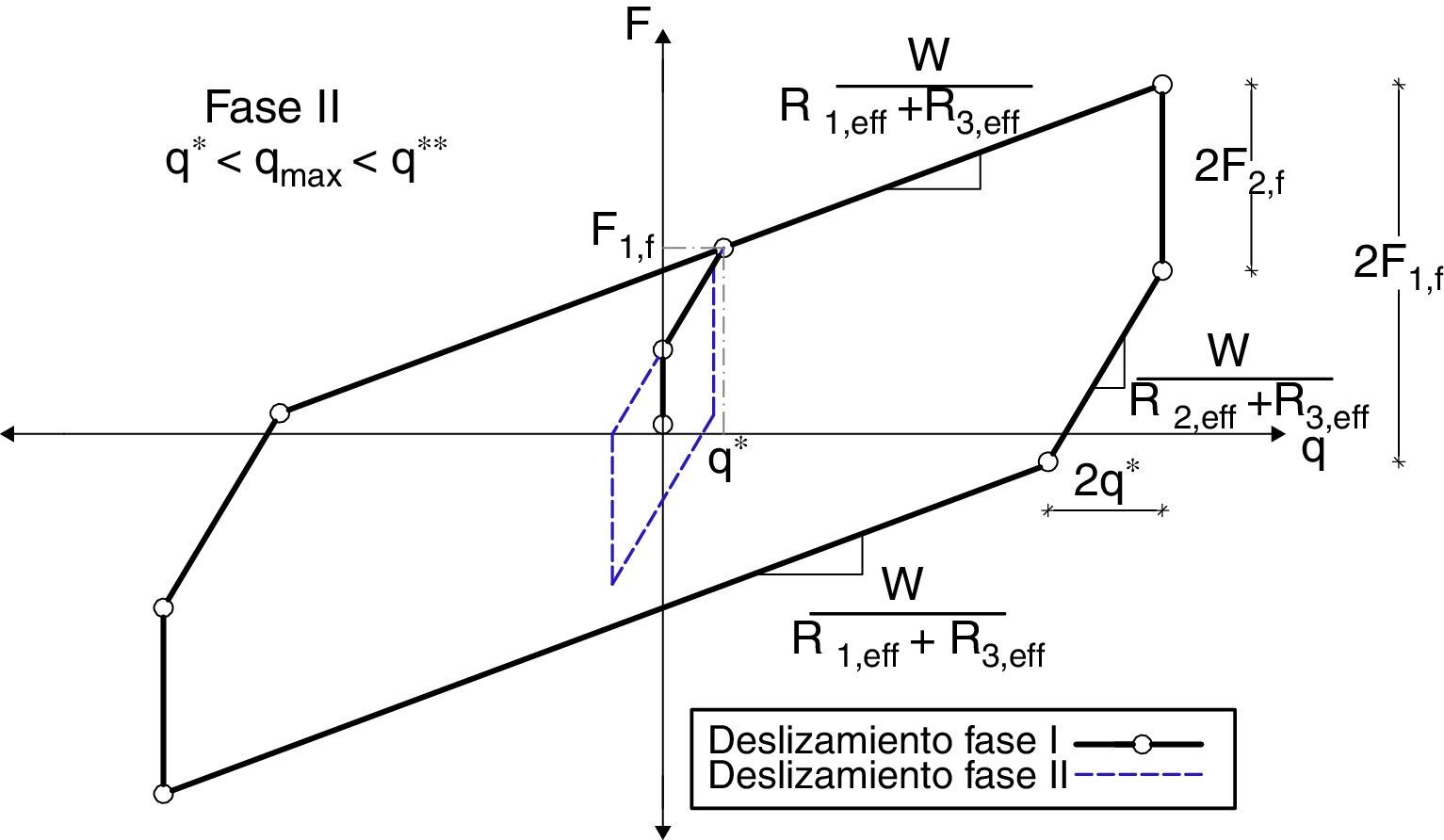
En la segunda fase, el deslizamiento del aislador interno se produce en las superficies 1, 2 y 3, como en un aislador de la segunda generación en el que el cojinete es el aislador interno [2]. La fuerza lateral F y desplazamiento lateral q, propuestas por Fenz y Constantinou [9] son:
donde todas las variables han sido ya definidas. En la figura 3 se muestran las curvas de histéresis correspondientes a las fases I y II.Diagrama de histéresis en Fase II[9].
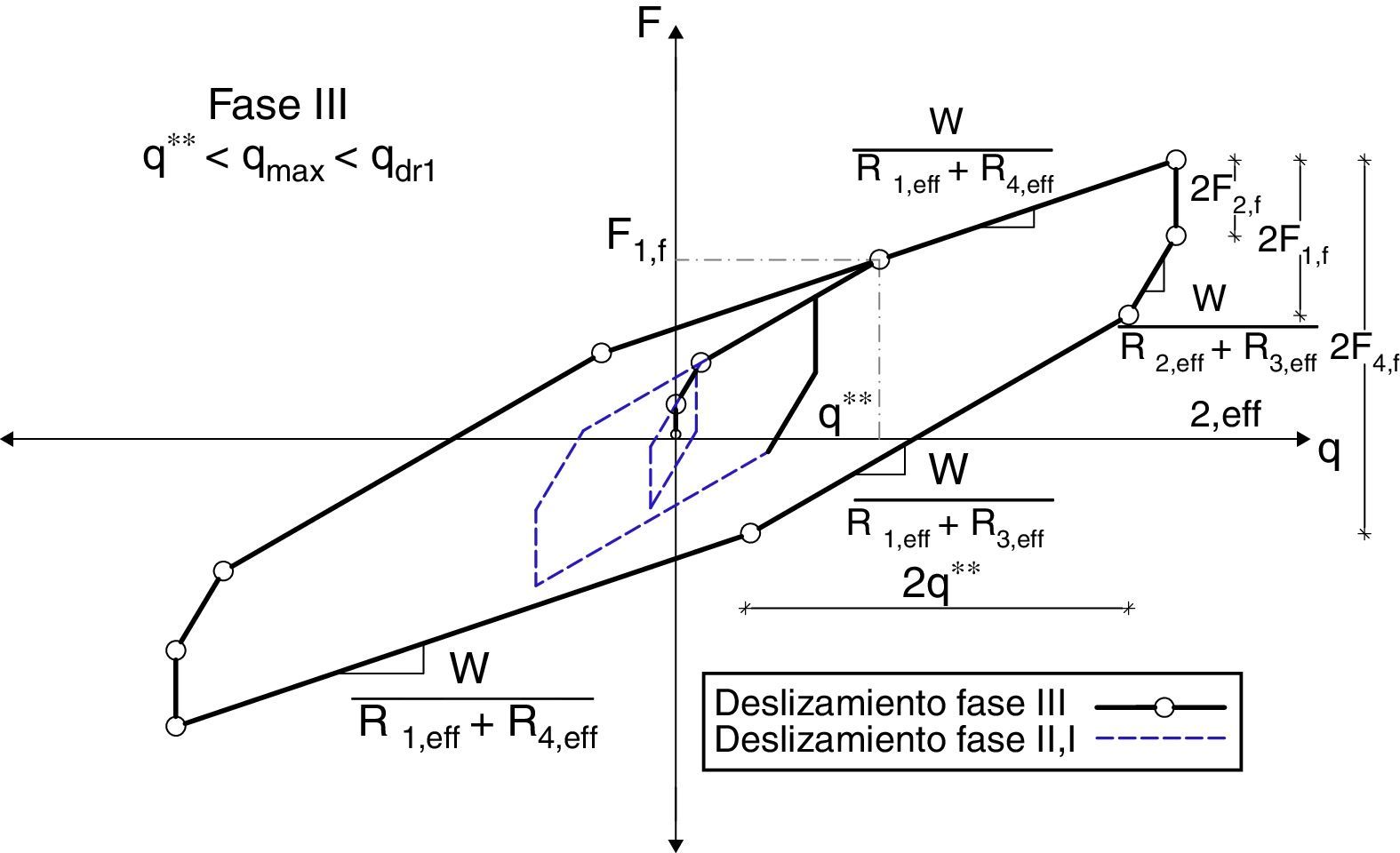
La tercera fase se inicia en F4f, cuando el desplazamiento lateral supera q**. En este régimen se están deslizando las cuatro superficies. En la figura 4 se indica el diagrama de histéresis de la fase III y las ecuaciones que definen la fuerza y desplazamientos, que son:
Diagrama de histéresis en Fase III[9].
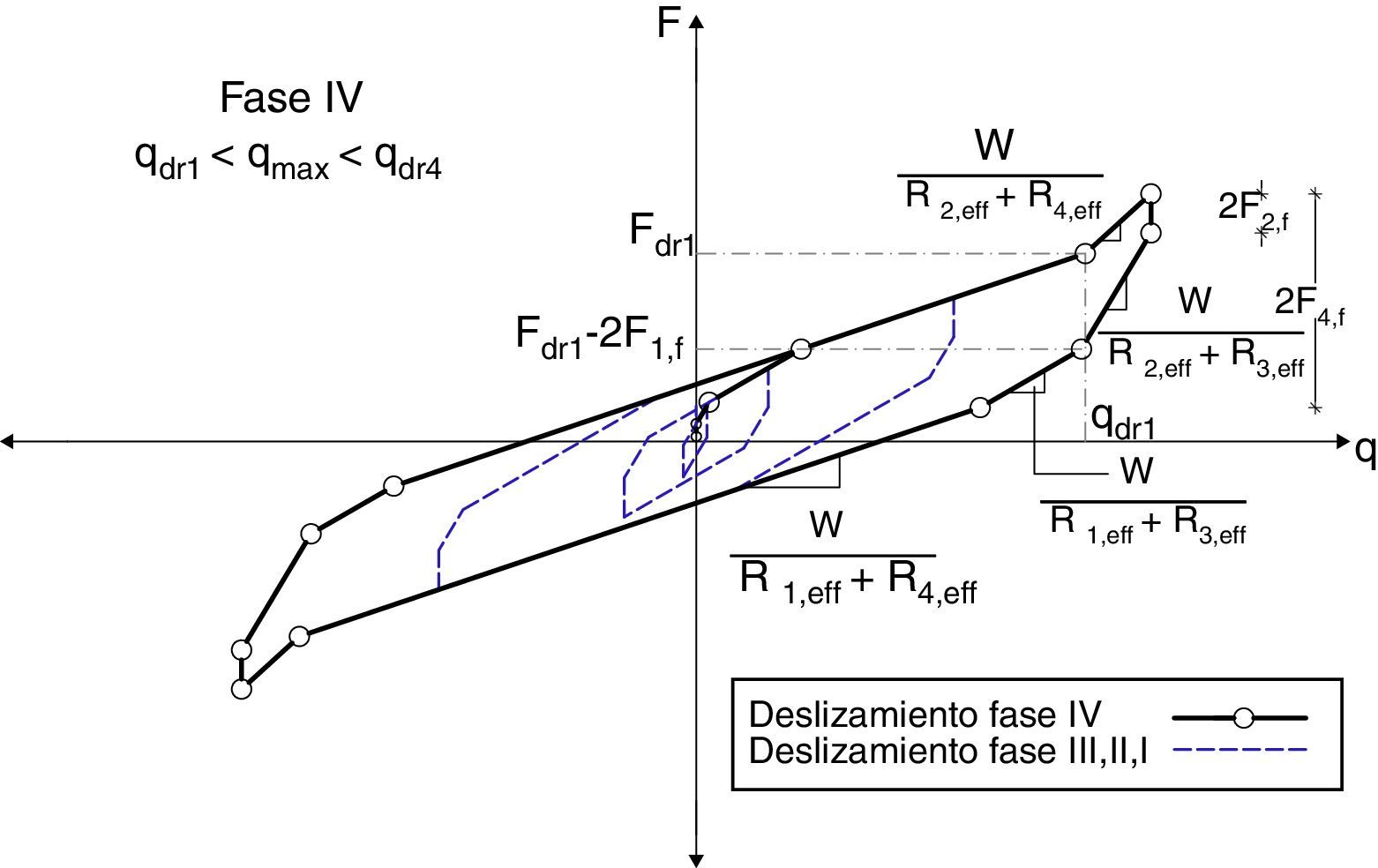
En la fase IV el aislador interior topa con uno de los bordes y se inicia con una fuerza Fdr1=WR1,effd1+F1,f; asociada a un desplazamiento qdr1. La fuerza y desplazamiento lateral vienen dadas por las siguientes ecuaciones:
En la figura 5 se muestra la curva de histéresis correspondiente a la fase IV y las anteriores; hasta ésta fase se puede considerar que el aislador está operable.
Diagrama de histéresis en Fase IV[9].
Existe una fase V, que está relacionada con el impacto del aislador interior con los topes, y que se dibuja con líneas entrecortadas para indicar su existencia; sin embargo, esta fase no se debe considerar en un diseño estructural.
2Método simplificado de Fadi y ConstantinouEl método simplificado de Fadi y Constantinou no solo es aplicable a aisladores FPS de la tercera generación, sino también de la segunda, de la primera, así como a los aisladores elastoméricos. Lo que difiere entre estos aisladores es el modelo de la curva de histéresis [6,8].
El método supone que el sistema de aislación puede modelarse como un sistema de un grado de libertad (aproximación que da muy buenos resultados). Se debe determinar la carga total WT que llega al sistema de aisladores; el número total de aisladores N, y utilizar un procedimiento de cálculo numérico para definir la curva de histéresis del aislador que se desea y seleccionar el espectro de análisis, que puede ser de desplazamientos o de aceleraciones.
El cálculo se realiza en forma iterativa, imponiéndose un desplazamiento inicial q, con el cual se construye el diagrama de histéresis hasta la fase que le contiene para el caso de los aisladores FPS de tercera generación. De acuerdo al desplazamiento impuesto se determina la fuerza lateral F, utilizando una de las ecuaciones que se han indicado en el apartado anterior, dependiendo de la fase en que se encuentre de acuerdo al desplazamiento. Luego se halla la rigidez efectiva kef dividiendo la fuerza F para el desplazamiento q.
Se determina también el factor de amortiguamiento equivalente ξeq dividiendo la energía disipada ED en un ciclo de histéresis (área en el lazo) para 4πEL, siendo EL la energía elástica. Se sobre entiende que el diagrama de histéresis se construyó teniendo presente los N aisladores. Se halla el factor B con el que se encuentra el espectro para cualquier amortiguamiento dividiendo por B el espectro correspondiente a 5% de amortiguamiento
Se determina el período del sistema de aislación T y con este valor se ingresa al espectro de desplazamientos reducido por el factor B y se obtiene el desplazamiento espectral Sd
siendo g la aceleración de la gravedad. Se comprueba si la diferencia entre el desplazamiento inicial q y el desplazamiento encontrado Sd es menor que una tolerancia prefijada. Si es menor, finaliza el proceso del cálculo; caso contrario, se repite el análisis con un nuevo valor de q, para que la convergencia sea rápida se utiliza el método de la biseccióndonde qi es el valor inicial y q es el nuevo desplazamiento. Una vez que se tiene la diferencia menor que la tolerancia, se determina la rigidez efectiva en cada aislador, dividiendo la rigidez efectiva para el número de aisladores.3Alternativa propuesta al método simplificadoFadi y Constantinou [8] recomiendan que en lugar de calcular el diagrama de histéresis en forma analítica, mediante las ecuaciones presentadas en el apartado 1 para el caso del aislador triple péndulo, se trabaje en base a la curva de histéresis hallada en laboratorio por el fabricante de los aisladores. A partir de esta curva se proceda en forma similar a la indicada en el apartado anterior para determinar la rigidez efectiva de un aislador kef, el período T del sistema de aislación y el factor de amortiguamiento considerando los N aisladores [8].
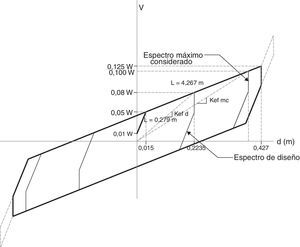
La alternativa que se propone en este artículo es calcular la rigidez efectiva y el factor de amortiguamiento equivalente directamente de la curva de histéresis encontrada en el laboratorio para el sismo de diseño “DE”, que tiene un período de retorno de 475 años, y para el sismo máximo considerado “MCE”, que tiene un período de retorno de 2475 años; para ello se utilizan los puntos finales de la fase II, (análisis con el sismo “DE”) y el punto final de la fase “III” (análisis con el sismo “MCE”), sin necesidad de realizar el cálculo iterativo.
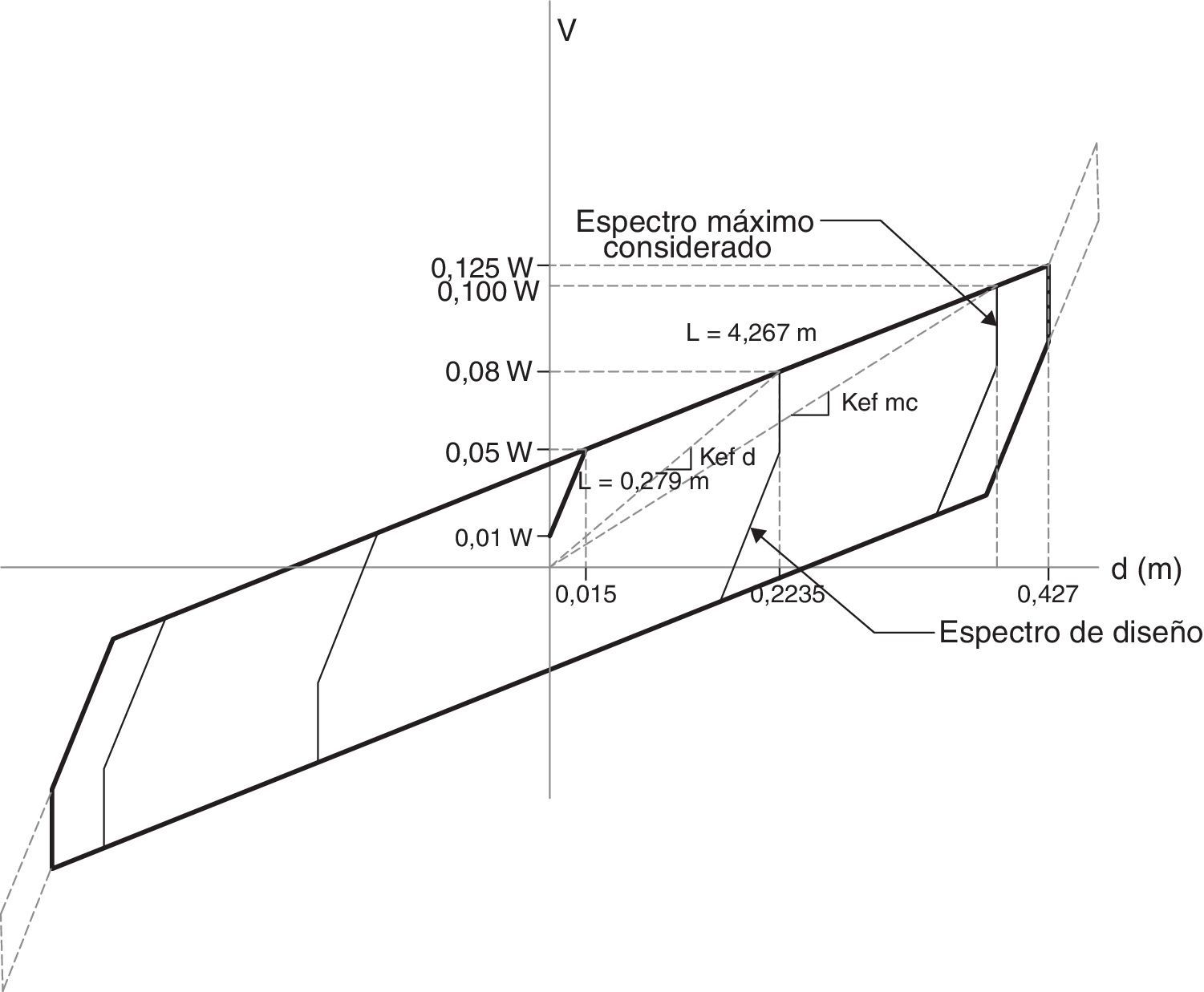
En la figura 6 se muestra el diagrama de histéresis que relaciona el desplazamiento lateral con el cortante, para un aislador FPS de 75/75cm, que tiene una altura de 30cm. y que soporta una carga vertical de 270.000 Kg y que tiene con una capacidad máxima de desplazamiento de 44cm [7].
En la figura 6 se indican las 5 fases descritas en el apartado 1, destacando que la fase V se encuentra en los extremos con línea entrecortada. En la variante propuesta se determina directamente de este gráfico la rigidez efectiva kefd que se utilizará para el análisis sísmico ante el sismo de diseño y la rigidez efectiva kefmc para el análisis con el sismo máximo considerado. El factor de amortiguamiento se obtiene de esta gráfica empleando métodos numéricos. Para hallar la energía disipada correspondiente al sismo “DE”, se encuentra el área de la fase II y para el sismo “MCE” el área encerrada en la fase III. De manera similar se calcula la energía elástica, con lo que se determina el factor de amortiguamiento equivalente para los dos sismos.
El sismo de diseño empleado en el análisis sísmico está definido por el espectro prescrito en la Norma Ecuatoriana de la Construcción NEC-15, evaluado en Sangolquí, en un perfil de suelo tipo C, que tiene un período de retorno de 475 años. Para el sismo máximo considerado las aceleraciones del espectro “DE” se multiplica por 1,5 [10].
Por otra parte, a partir de la curva de histéresis indicada en la figura 6 se obtiene la rigidez efectiva, el factor de amortiguamiento equivalente, el período de vibración y el desplazamiento esperado, siguiendo la metodología descrita en el apartado 2, tanto para el sismo “DE” como para el sismo “MCE”. Este procedimiento de cálculo constituye el Método Simplificado.
En la Variante Propuesta del método simplificado, se determina la rigidez efectiva y el factor de amortiguamiento equivalente directamente de la figura 6. Luego, se realiza el análisis sísmico, en coordenadas de piso, de una estructura de 5 pisos, colocando aisladores sísmicos FPS de la tercera generación de 75/75/30 sobre las columnas del primer piso, tema que se explica a continuación.
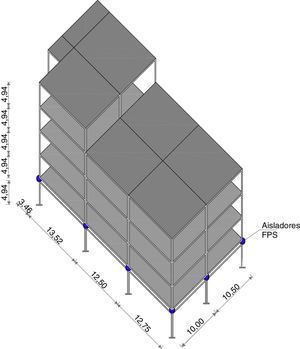
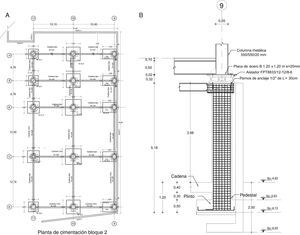
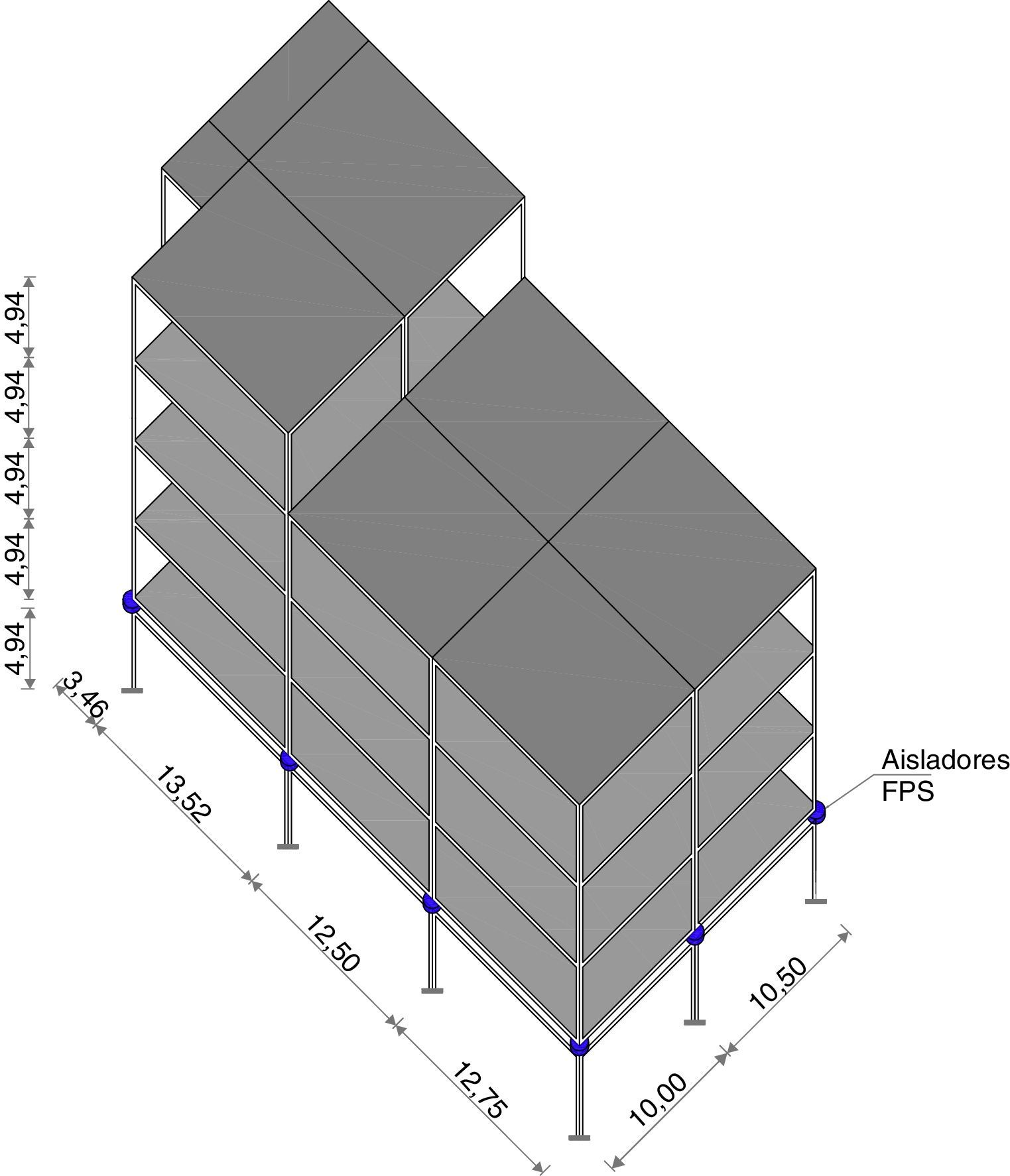
4Estructura analizadaSe analiza el Bloque Estructural 2 del nuevo Centro de Investigaciones Científicas y de Post Grado de la Universidad de Fuerzas Armadas ESPE, que tiene un subsuelo y 4 pisos y 15 aisladores FPS de la tercera generación sobre las columnas del primer piso. En consecuencia se tiene una subestructura de 1 piso y una superestructura de 4 pisos. La estructura es irregular en planta y elevación como se observa en la figura 7.
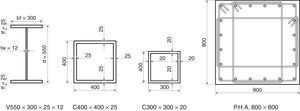
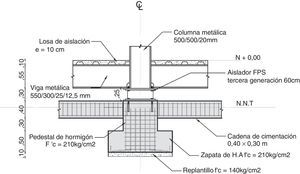
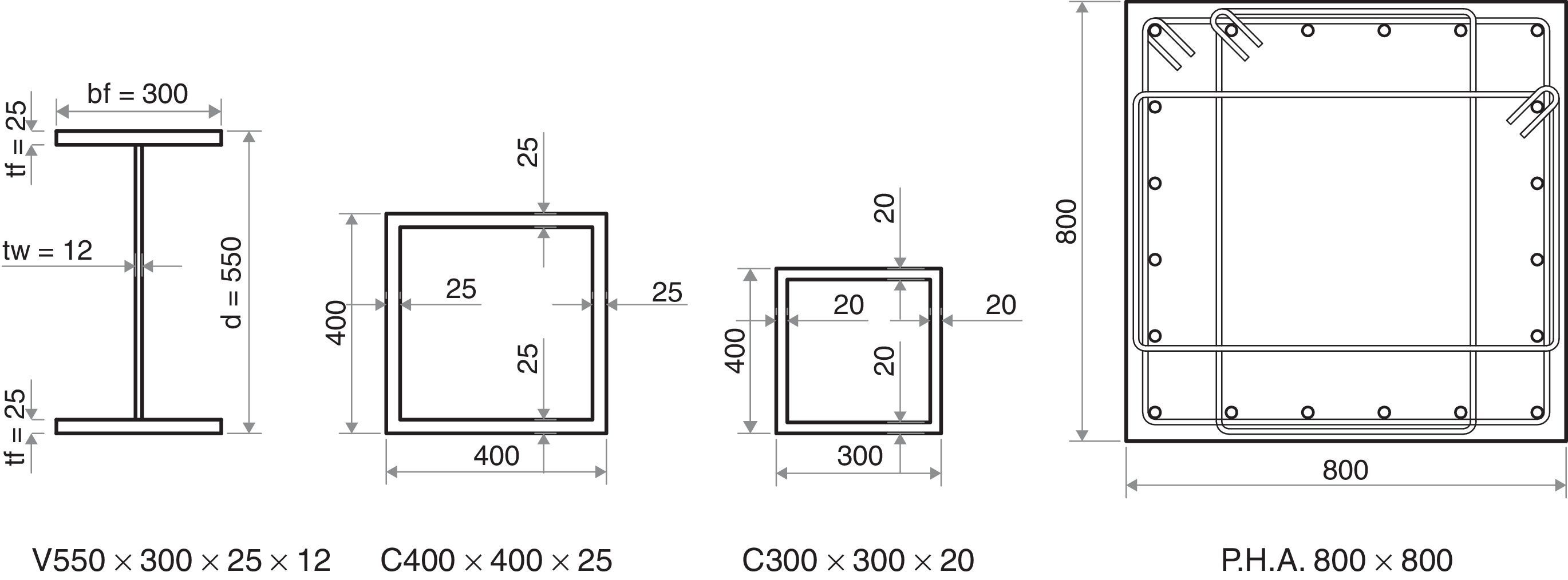
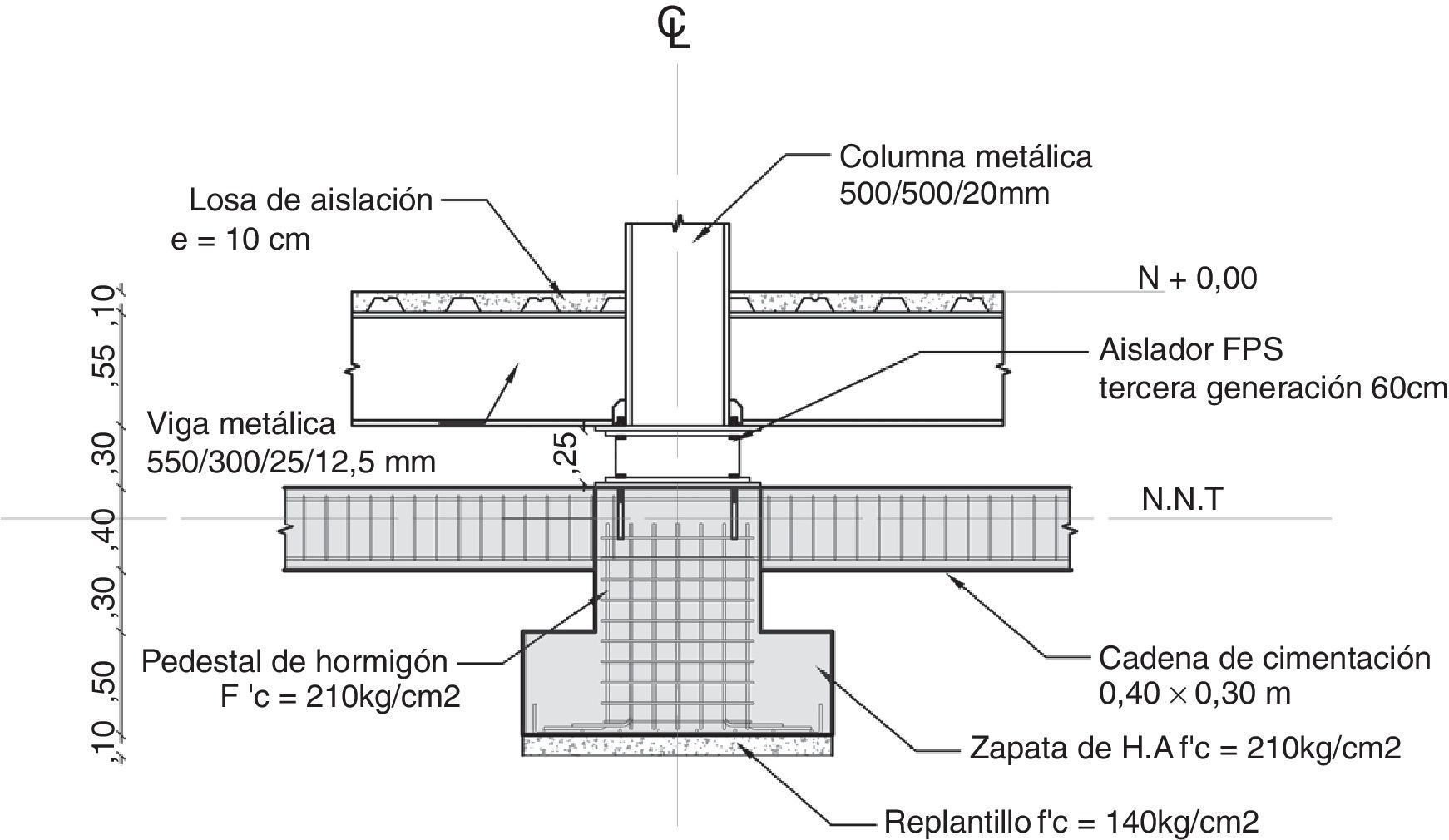
Las columnas de la subestructura (subsuelo) son de hormigón armado de 80/80cm, y de la superestructura son de acero, perfiles tubulares cuadrados de 400/400/25mm. Las vigas son de acero en forma de “I” de 550/300/25/12mm., como se muestra en la figura 8, y sostienen a la placa colaborante colocada sobre un perfil deck, que tiene una altura promedio de 7.5cm, de espesor. Bajo el aislador existe otra viga de acero tipo “I” de 300/300/20/12mm.
La carga media que llega al sistema de aislación se encuentra alrededor de las 250.000kg. por lo que, en la realidad, se colocan 12 aisladores FPS de la tercera generación de 70/70 y con una altura de 25cm, y 3 aisladores de las mismas características de 60/60/25cm.
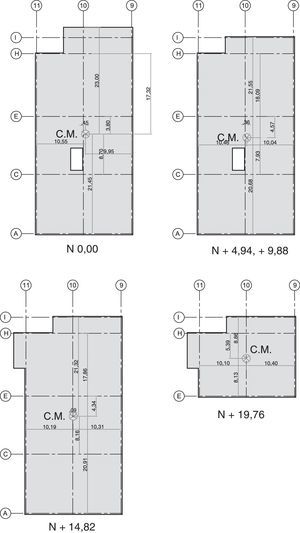
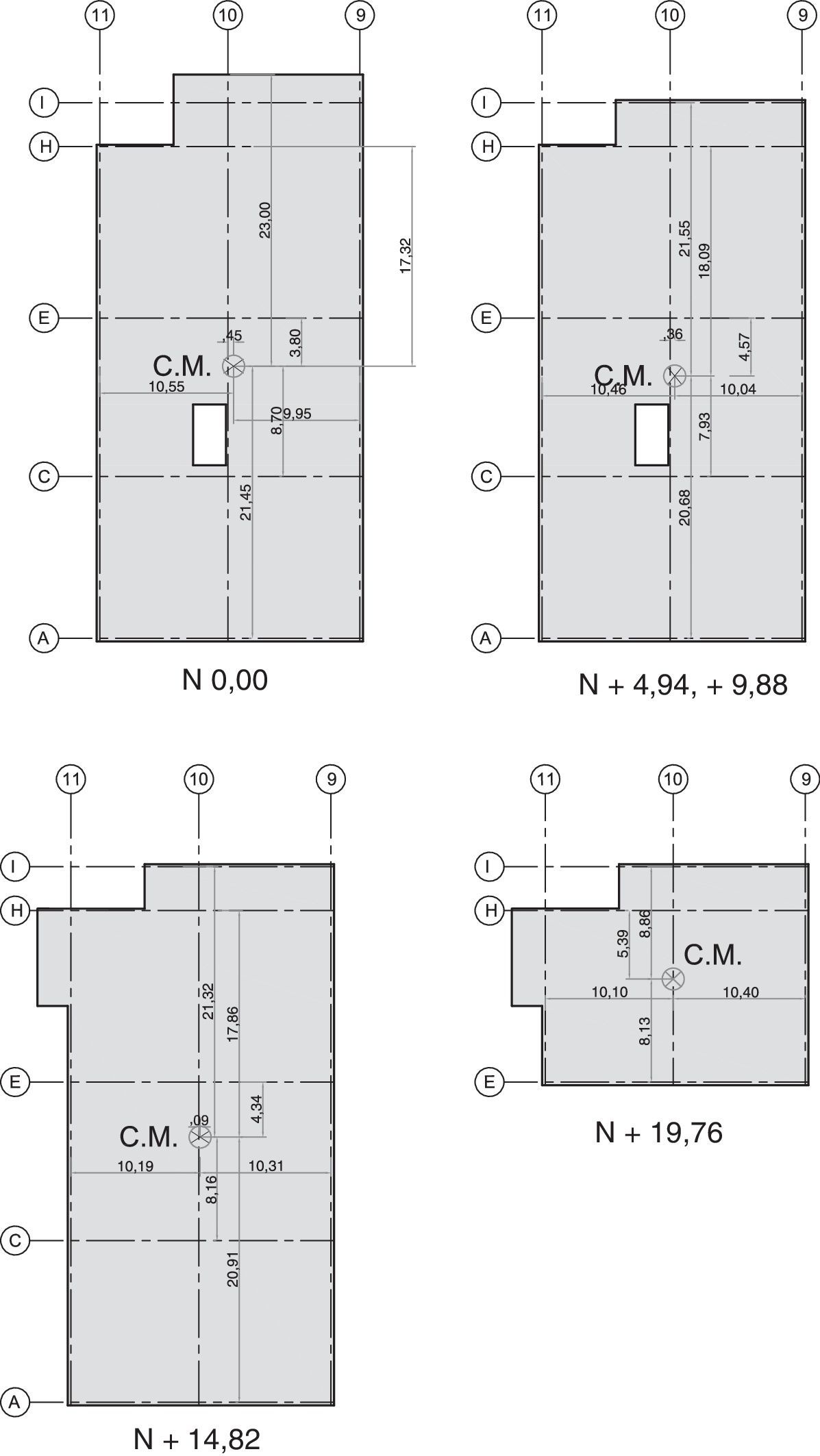
Por disponer la curva de histéresis de un aislador de 75/75/30cm, para una carga vertical de 270.000kg. (muy similar a las cargas que van a gravitar en el Bloque Estructural 2) se considera este aislador para el análisis sísmico. El mismo que se realizó en un modelo de losa rígida, considerando tres grados de libertad por planta, los mismos que se hallan ubicados en el centro de masas de cada piso que se indican en la figura 9.
La carga permanente más el 25% de la carga viva con la que se realizó el análisis sísmico es de 850kg/m2 para los tres pisos de la superestructura y de 650kg/m2, a nivel de las cubiertas.
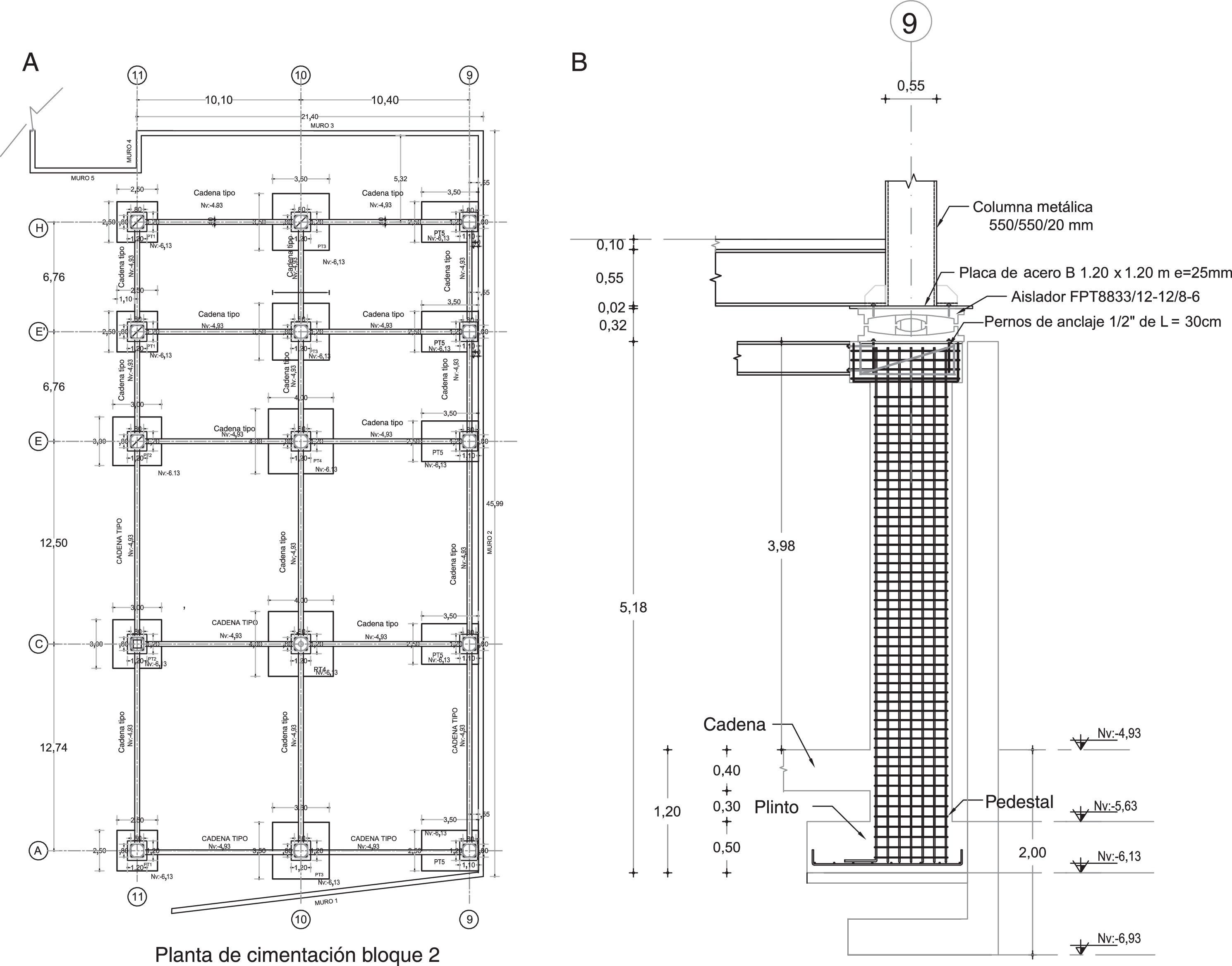
En la figura 10a se presenta la planta de los plintos cuadrados, de diferentes secciones, las cadenas de amarre de las columnas y los muros perimetrales; a la derecha se observa las columnas de hormigón armado del subsuelo de 80/80cm., el aislador, la viga de acero de la losa de aislación. A la derecha del Eje 9 se tiene el Bloque Estructural 1, que se encuentra en un nivel 4.94 m, más arriba del Bloque 2, y también tiene aisladores sísmicos pero por la diferencia del terreno van directamente sobre su cimentación, lo cierto es que los aisladores del Bloque 1 y del Bloque 2 se encuentran a la misma altura y existe una junta de construcción de 1.20 m, entre sus dos fachadas, para evitar cualquier choque por un posible movimiento fuera de fase.
En la figura 11 se aprecia, que el aislador FPS se encuentra anclado a la columna inferior de hormigón de 80cm, de lado y la columna superior de acero tubular de 40cm, de lado, mediante placas de acero de 3cm, de espesor. Se indica además las vigas de acero superior e inferior. Como ya se había indicado, el aislador fue modelado como un elemento corto de longitud L, como se aprecia en la gráfica cuya rigidez horizontal es la rigidez efectiva que se calculó en la forma descrita en el apartado anterior. Las distancias Li, Lj sirven para encontrar la matriz de transfrencia al sistema de coordenadas globales del elemento aislador [1,3].
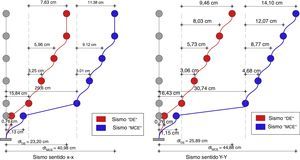
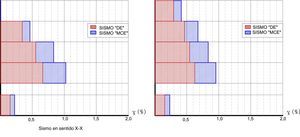
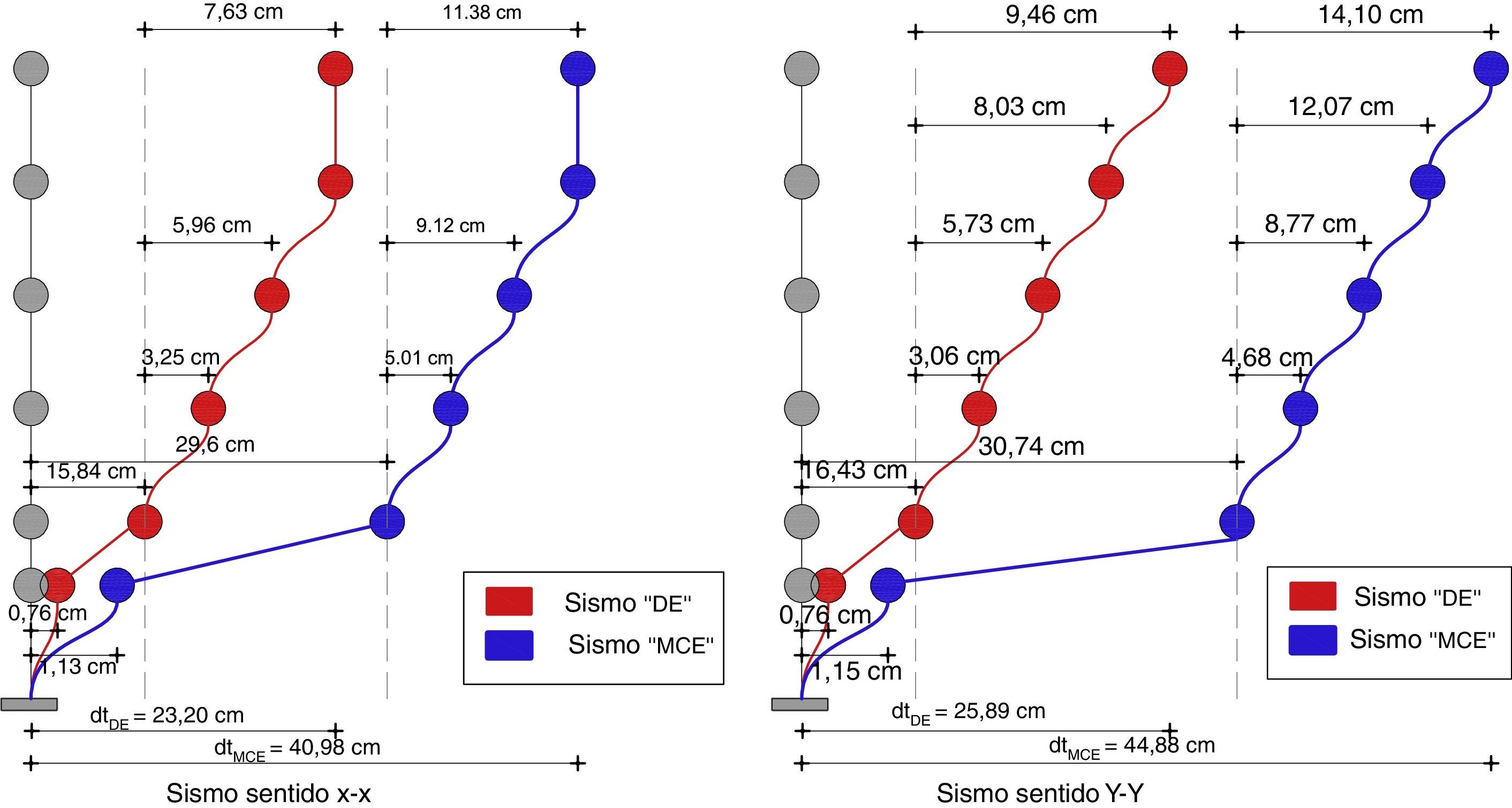
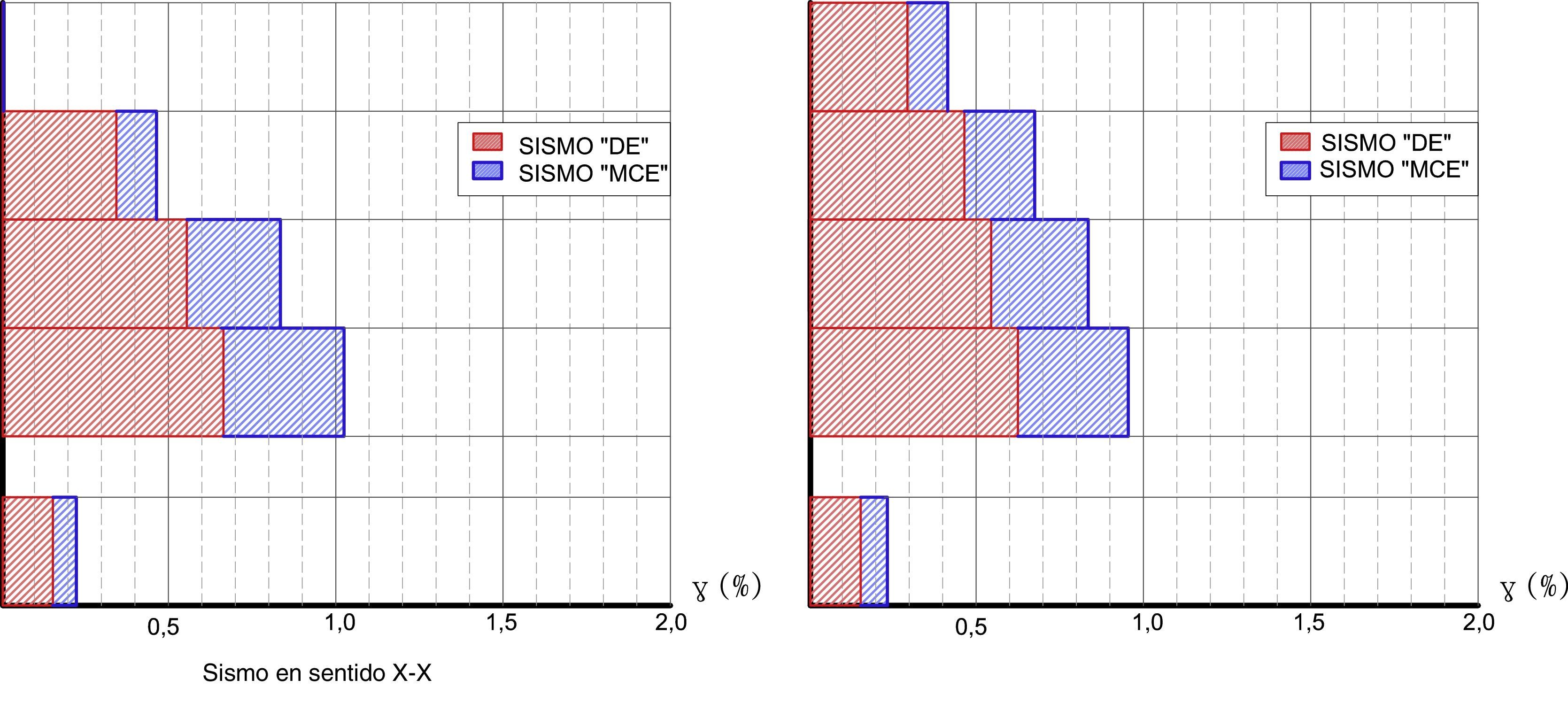
En la figura 12 se presenta las respuestas máximas probables en desplazamiento, en el centro de masas para sismo en Sentido X y en sentido Y, para los sismos DE y MCE, se trabaja con el criterio de combinación modal de la combinación cuadrática completa [5]. En la figura 13 se indican las derivas de piso encontradas en la subestructura y en la superestructura, para los dos sismos de análisis.
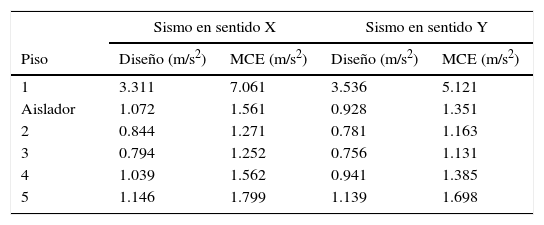
En el análisis sísmico se considera al aislador como un elemento corto, lo que conlleva a tener un piso más. Con esta acotación en la tabla 1 se presenta las aceleraciones de piso en el Bloque Estructural 2. Esta información sirve para cuantificar las pérdidas esperadas en los componentes (equipos) que no es materia de este artículo pero si era importante presentarlo.
Aceleraciones de piso en el Centro de Masas
| Sismo en sentido X | Sismo en sentido Y | |||
|---|---|---|---|---|
| Piso | Diseño (m/s2) | MCE (m/s2) | Diseño (m/s2) | MCE (m/s2) |
| 1 | 3.311 | 7.061 | 3.536 | 5.121 |
| Aislador | 1.072 | 1.561 | 0.928 | 1.351 |
| 2 | 0.844 | 1.271 | 0.781 | 1.163 |
| 3 | 0.794 | 1.252 | 0.756 | 1.131 |
| 4 | 1.039 | 1.562 | 0.941 | 1.385 |
| 5 | 1.146 | 1.799 | 1.139 | 1.698 |
En la tabla 1, se aprecia que la aceleración que ingresa a los aisladores es relativamente alta y la que se transmite a la estructura es baja de tal manera que los aisladores trabajan como un filtro, en el sentido que reducen las aceleraciones que ingresan a la estructura.
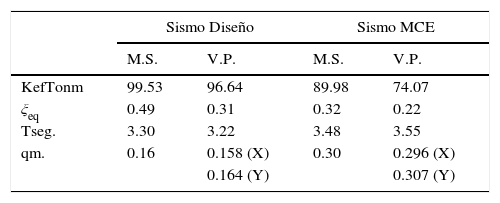
6Comparación de resultadosAntes de comparar los resultados encontrados mediante el método simplificado M.S. con la variante propuesta V.P., en este artículo se debe manifestar que en los dos métodos solo se halla la respuesta en el sistema de aislación modelado como un sistema de un grado de libertad con lo que se determina básicamente la rigidez efectiva horizontal del aislador y el factor de amortiguamiento equivalente. Después, para encontrar las repuestas de toda la estructura a nivel de desplazamientos o fuerzas se debe proceder en la forma indicada en el apartado anterior o utilizando cualquier otro método de análisis sísmico espacial de estructuras. En la tabla 2 se compara: la rigidez efectiva kef en un aislador; el factor de amortiguamiento equivalente ξeq de un aislador; el período fundamental de la estructura aislada T; y el desplazamiento esperado q en el sistema de aislación tanto para el sismo de diseño como para el sismo máximo considerado [8].
Existen diferencias pequeñas a nivel de rigidez efectiva y un poco mayor a nivel de factor de amortiguamiento equivalente, sin embargo, los períodos de vibración y desplazamientos máximos probables del sistema de aislación son muy parecidos tanto para la dirección X como para la dirección Y.
7ConclusionesSe ha presentado un modelo de cinco fases para estudiar el comportamiento no lineal de un aislador de triple péndulo de fricción. Al tratarse de un modelo con cierto grado de complejidad en la determinación de la rigidez efectiva de acuerdo al nivel de desplazamientos del aislador, se ha propuesto un método simplificado de análisis sísmico. Dicho método consiste en obtener directamente la rigidez efectiva a partir de los puntos que definen la tercera fase del comportamiento del aislador y utilizar los puntos que determinan la cuarta fase del modelo ante el sismo máximo considerado. Del estudio realizado se desprende las siguientes conclusiones:
Es más exacto determinar la rigidez efectiva y el factor de amortiguamiento, en la forma indicada en el párrafo anterior, a partir del prototipo que entrega el fabricante de los aisladores. Claro está que en el diseño de la geometría del aislador se habrá comprobado que la capacidad de desplazamiento es mayor que la demanda y que en lo posible no va a ingresar a la quinta fase ante el sismo máximo considerado.
En la tabla 2 se ve una muy buena aproximación entre los valores obtenidos al aplicar el modelo simplificado (MS) que trabaja en forma iterativa para calcular los parámetros indicados en la tabla y la variante propuesta (VP).
Con la variante propuesta el Proyectista tiene más control del cálculo estructural e interviene algo fundamental que está realizando en base al prototipo entregado por el fabricante de los aisladores.



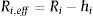
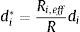
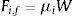
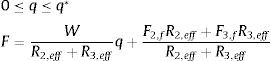
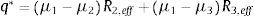
![Diagrama de histéresis en Fase I[9]. Diagrama de histéresis en Fase I[9].](https://static.elsevier.es/multimedia/02131315/0000003300000012/v1_201703160028/S0213131516300050/v1_201703160028/es/main.assets/thumbnail/gr2.jpeg?xkr=ue/ImdikoIMrsJoerZ+w96p5LBcBpyJTqfwgorxm+Ow=)
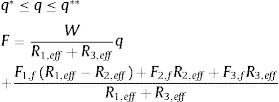
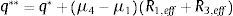
![Diagrama de histéresis en Fase II[9]. Diagrama de histéresis en Fase II[9].](https://static.elsevier.es/multimedia/02131315/0000003300000012/v1_201703160028/S0213131516300050/v1_201703160028/es/main.assets/thumbnail/gr3.jpeg?xkr=ue/ImdikoIMrsJoerZ+w96p5LBcBpyJTqfwgorxm+Ow=)
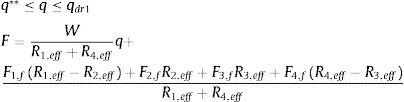
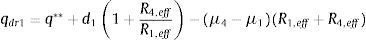
![Diagrama de histéresis en Fase III[9]. Diagrama de histéresis en Fase III[9].](https://static.elsevier.es/multimedia/02131315/0000003300000012/v1_201703160028/S0213131516300050/v1_201703160028/es/main.assets/thumbnail/gr4.jpeg?xkr=ue/ImdikoIMrsJoerZ+w96p5LBcBpyJTqfwgorxm+Ow=)
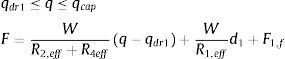
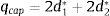
![Diagrama de histéresis en Fase IV[9]. Diagrama de histéresis en Fase IV[9].](https://static.elsevier.es/multimedia/02131315/0000003300000012/v1_201703160028/S0213131516300050/v1_201703160028/es/main.assets/thumbnail/gr5.jpeg?xkr=ue/ImdikoIMrsJoerZ+w96p5LBcBpyJTqfwgorxm+Ow=)