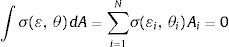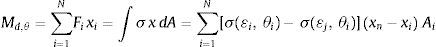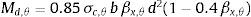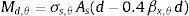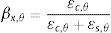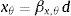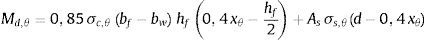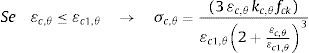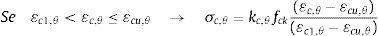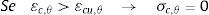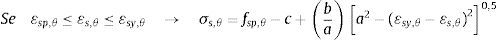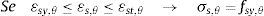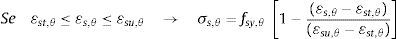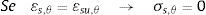Estudo do desempenho de vigas em situação de incêndio a partir do modelo de fibras

Resumo

Neste trabalho apresenta‐se a análise numérica de vigas de concreto armado de seção retangular e T e de vigas mistas de aço e concreto submetidas a altas temperaturas. Para a obtenção dos resultados numéricos, os quais se referem às relações momento x curvatura para diferentes temperaturas, bem como os valores máximos atingidos para os momentos fletores, utilizou‐se o método ou modelo de fibras, sendo as relações constitutivas dos materiais (concreto e aço) definidas a partir das considerações do EUROCODE 2 parte 1.2 e da ABNT NBR 15200. A partir dos resultados obtidos, os quais são comparados com as respostas de expressões analíticas definidas pela ABNT NBR 6118 e pela ABNT NBR 8800, é possível se identificar a resistência residual da estrutura à medida que o tempo de exposição ao fogo aumenta e também demonstrar a redução efetiva de sua rigidez.

Abstract

This paper presents the numerical analysis of reinforced concrete beams with rectangular and T sections and of steel–concrete composite beams subjected to high temperatures. To obtain the numerical results, which refer to the moment x curvature relations for different temperatures, as well as the maximum values achieved for the bending moments, it was used the fibers method or fibers model, with the constitutive relations of materials (concrete and steel) defined by the considerations of the EUROCODE 2 part 1.2 and by the ABNT NBR 15200. From the results obtained, which are compared with the responses of analytical expressions defined by ABNT NBR 6118 and by ABNT NBR 8800, it is possible to identify the residual strength of the structure as the fire exposure time increases and also demonstrate the effective reduction of its rigidity.

1

Introdução

O concreto é um material formado pela junção de cimento, aglomerantes (água e areia) e agregados, como por exemplo, a brita. Este material apresenta baixa condutividade térmica e quando associado às armaduras forma as peças de concreto armado. O concreto simples que reveste as barras de aço acaba protegendo as mesmas das ações de intempéries, corrosão ou de um incêndio e, além disso, origina um considerável aumento na rigidez da peça e consequentemente na sua resistência.

No caso de um incêndio em uma edificação, o concreto é capaz de proteger o aço do calor excessivo, garantindo um tempo de fuga maior de pessoas, caso haja um sinistro de grandes proporções. Porém, em função do tempo de exposição ao fogo e da taxa de aquecimento, os constituintes do concreto podem reagir quimicamente, dando início a processos mecânicos como expansões, fragmentações, fissurações e perda de resistência. A fissuração e a fragmentação superficial explosiva, ou «spalling», que leva a uma grande degradação do material podendo afetar de modo significativo a sua capacidade estrutural, dependem diretamente de como a temperatura gera tensões na matriz sólida e da pressão exercida pelas fases fluidas presentes nos poros [1].

No presente trabalho apresentam‐se os resultados numéricos correspondentes à avaliação do desempenho de vigas de concreto armado e vigas mistas de aço e concreto em situação de incêndio a partir do modelo ou método de fibras. Classifica‐se como viga mista a estrutura que permite o trabalho conjunto entre a viga metálica e uma faixa da laje de concreto; para que aconteça essa interação, deve haver ligação mecânica entre a viga de aço e a laje de concreto, proporcionada por elementos denominados de conectores de cisalhamento.

O modelo de fibras é um método clássico utilizado para a análise de elementos mistos de aço e concreto e também de seções de concreto armado ou metálicas, em que é possível modelar vigas, pilares, etc. No modelo de fibras a seção transversal é subdividida em pequenas regiões, não necessariamente de áreas iguais, sendo que cada região apresenta uma fibra de material distribuída ao longo da seção. Cada fibra pode assumir diferentes relações tensão x deformação, representando diferentes materiais. Em geral usam‐se relações constitutivas uniaxiais. Sendo assim, considerando‐se que as seções planas permanecem planas após a deformação e utilizando‐se as relações constitutivas para cada material, pode‐se calcular a tensão em cada fibra em função de sua deformação, e fazendo‐se o somatório das forças e momentos determinam‐se os esforços resistentes da seção [2].

Franssen [3] desenvolveu o programa SAFIR [4] para servir como plataforma para a implementação de vários elementos finitos e modelos constitutivos. O programa é utilizado em inúmeras pesquisas sobre o comportamento de estruturas de aço, concreto e mistas de aço e concreto à temperatura ambiente e em situação de incêndio e também na calibração de procedimentos de projeto [5–8]. Neste programa a seção transversal do elemento estrutural é discretizada em fibras triangulares ou retangulares e em qualquer ponto longitudinal de integração todas as variáveis (temperatura, tensões e deformações) são constantes em cada fibra, caracterizando um modelo de fibras. Hajjar et al.[9] apresentaram uma formulação, também baseada no modelo de fibras, em que se considerou o deslizamento relativo entre o concreto e o aço.

Sfakianakis [10] propôs um método de fibras alternativo em que o mecanismo de falha da seção transversal foi determinado através de algoritmos envolvendo computação gráfica, sendo válido para seções transversais com geometria qualquer e eliminando problemas de convergência relacionados com processos iterativos.

Embora a maior desvantagem do método de fibras seja a necessidade de grande quantidade de memória e um alto custo computacional para a realização das modelagens numéricas, é um dos mais flexíveis e poderosos disponíveis, sendo a sua grande vantagem a possibilidade de aplicação em análises de estruturas com seções transversais com geometria qualquer.

Portanto, neste trabalho desenvolveu‐se um programa computacional denominado MDCOMP (2014), baseado no modelo de fibras e implementado em linguagem FORTRAN, destinado à determinação da resistência última de vigas em situação de incêndio. Com a finalidade de mostrar a eficiência do método proposto realizaram‐se comparações com as respostas obtidas a partir de expressões analíticas definidas pela ABNT NBR 6118 [11] e pela ABNT NBR 8800 [12] para vigas de concreto armado de seção retangular e T e de vigas mistas de aço e concreto.

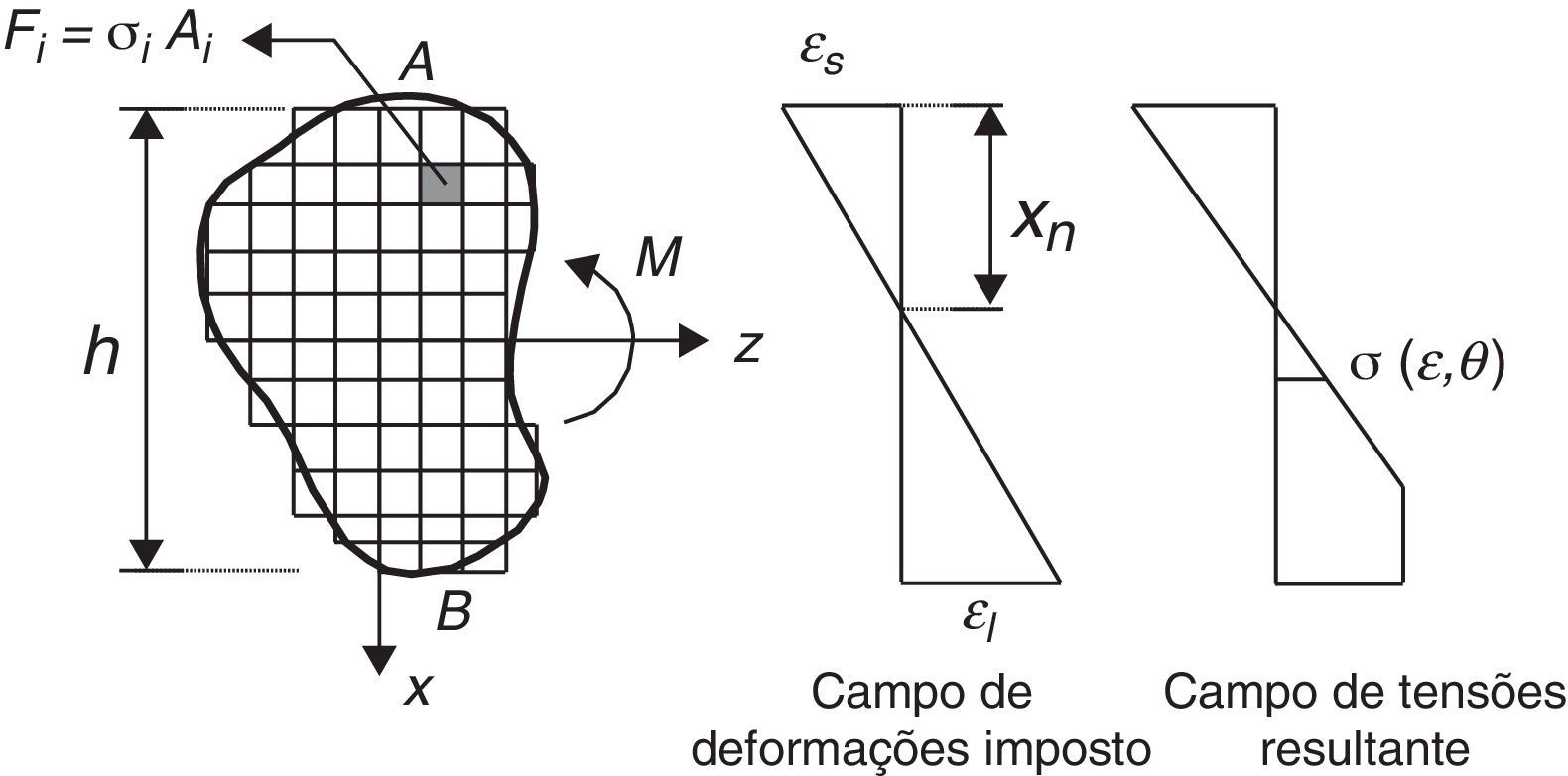
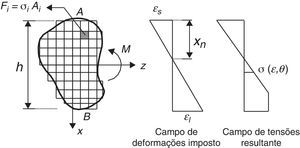
2

Momento fletor resistente de uma viga pelo modelo de fibras

O modelo de análise adotado baseia‐se na integração das funções não‐lineares de tensão geradas durante a flexão. Sendo assim, a seção transversal é discretizada em N elementos submetidos apenas a solicitações axiais de tração ou de compressão e a flexão da viga é obtida a partir da consideração do comportamento de todas as fibras (elementos), como mostra a figura 1.

Figura 1.

Discretização da seção transversal aplicada à flexão inelástica reta.

Sendo A_i a área do i‐ésimo elemento e σεi,θi sua respectiva tensão, calculada a partir da temperatura θ_i e da deformação ε_i, o equilíbrio das tensões normais na seção transversal submetida à flexão pura é obtido pelo modelo de fibras a partir de:

O campo de deformações obedece à hipótese de Bernoulli, que estabelece que as seções permanecem planas durante a flexão, sendo, portanto, descrito por uma função linear. Seu cálculo é feito definindo‐se 2 pontos A e B com deformações ε_s e ε_I, respectivamente. Atribuindo‐se uma deformação ao ponto A, calcula‐se a deformação no ponto B, de modo a satisfazer o equilíbrio das forças axiais descrito na equação (1). Uma vez definido o campo de deformações, o momento fletor resistente da seção é calculado da seguinte forma:

em que F_i é a resultante de forças em cada elemento, x_i é o braço de alavanca e x_n a posição da linha neutra, medida a partir da coordenada do ponto de deformação ε_S.

3

Momento fletor resistente de uma viga de seção retangular

As expressões analíticas definidas pela ABNT NBR 6118 [11] para o cálculo do momento fletor resistente na região comprimida e tracionada da seção, desprezando‐se a contribuição do concreto na região tracionada em situação de incêndio, são, respectivamente:

Nestas equações σ_c,θ é a tensão de compressão do concreto em incêndio, b é a largura da seção transversal da viga e d é a altura útil da viga. O parâmetro β_x,θ que relaciona as deformações no concreto εc,θ e no aço εs,θ a altas temperaturas, e x_θ, que define a posição da linha neutra da seção, são avaliados a partir das expressões:

As deformações dos materiais são definidas com base nas prescrições do EUROCODE 2 parte 1.2 [13] e são incrementadas a cada passo de tempo.

4

Momento fletor resistente de uma viga de seção T

Realizando‐se o equilíbrio de momentos em relação a um ponto localizado na linha neutra da seção da viga chega‐se à seguinte expressão para o cálculo do momento fletor resistente:

Nesta equação b_f é a largura efetiva da viga ou a largura da mesa definida com base na distribuição não uniforme de tensões em vigas (efeito de «shear lag»), h_f é a espessura da laje ou a largura da mesa, bw é a largura da alma ou da nervura da seção T, A_s é a área de aço na região tracionada da seção e σ_s,θ é a tensão normal da armadura a altas temperaturas.

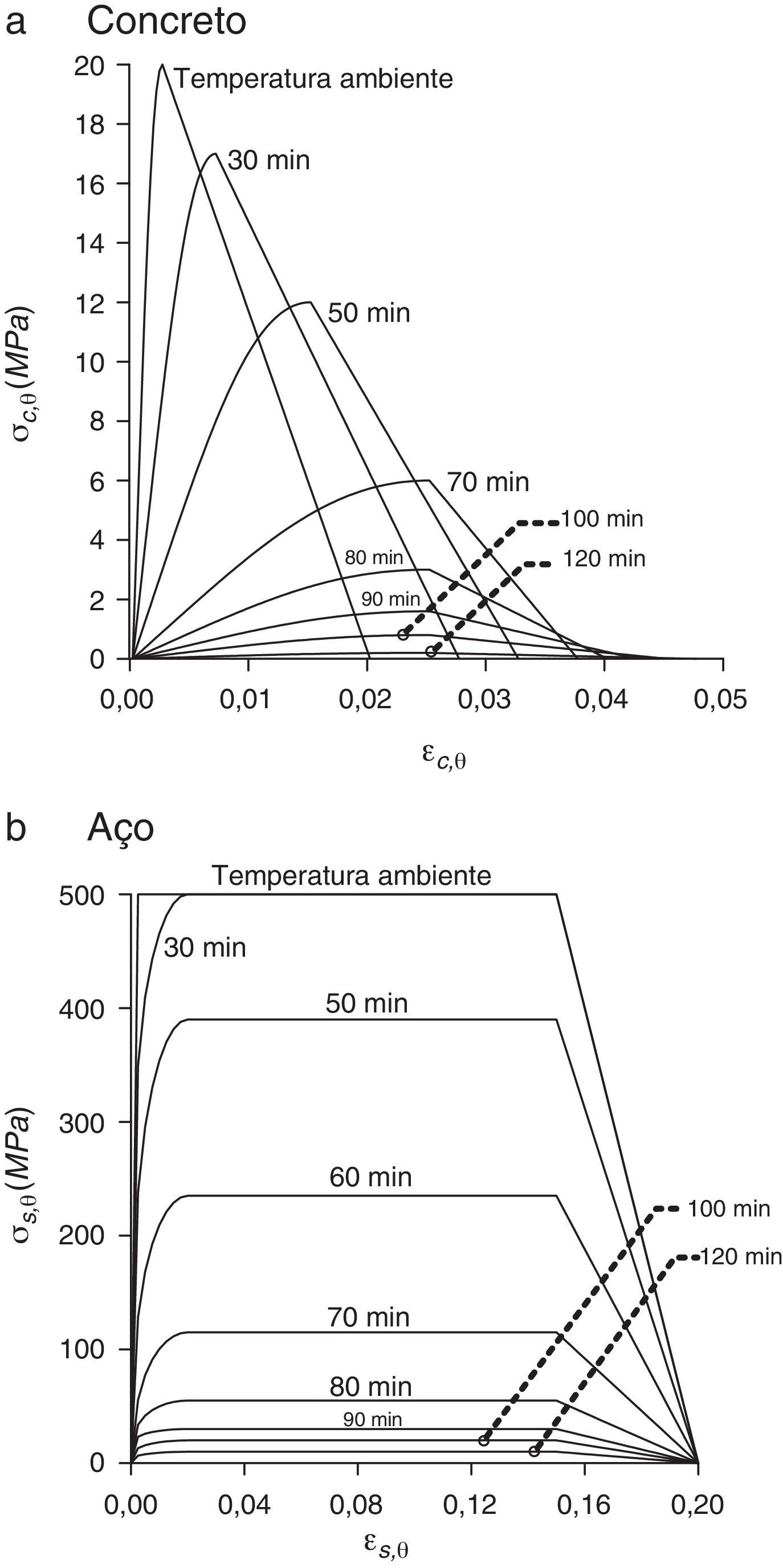
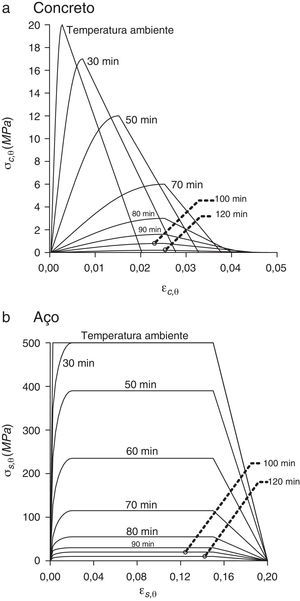
5

Relação tensão x deformação segundo o EUROCODE 2

Neste item apresentam‐se as relações constitutivas dos materiais definidas pelo EUROCODE 2 parte 1.2 [13] e que foram utilizadas para a determinação dos esforços em cada fibra das seções analisadas neste trabalho.

As relações tensão x deformação do concreto segundo o EUROCODE 2 parte 1.2 [13] são:

Nestas equações σ_c,θ e ε_c,θ são, respectivamente, a tensão normal e a deformação do concreto a altas temperaturas, k_c,θ é o fator de redução da resistência do concreto e f_ck é a resistência característica do concreto aos 28 dias. Os valores limites de deformação ε_c1,θ e ε_cu,θ para diferentes valores de temperatura são apresentados no EUROCODE 2 parte 1.2 [13].

Por sua vez, as relações tensão x deformação do aço definidas segundo o EUROCODE 2 parte 1.2 [13] são dadas por

Nestas equações σ_s,θ e ε_s,θ são, respectivamente, a tensão normal e a deformação do aço a altas temperaturas, E_s,θ é o módulo de elasticidade do aço em situação de incêndio, f_sy,θ, ε_sy,θ são, respectivamente, a tensão e a deformação de escoamento do aço.

As expressões para o cálculo dos valores de deformação ε_sp,θ, ε_st,θ e ε_su,θ relacionados com os limites de aplicação de cada uma das equações tensão x deformação, bem como dos parâmetros a, b e c podem ser encontradas no EUROCODE 2 parte 1.2 [13].

Na figura 2 apresentam‐se as curvas tensão x deformação do concreto e do aço para diferentes tempos de exposição ao fogo obtidas a partir do programa computacional MDCOMP (2014) e com base nas equações (6) e (7).

Figura 2.

Relação tensão x deformação em situação de incêndio.

6

Exemplos

Nesta seção apresentam‐se os resultados da análise numérica, a partir do modelo de fibras, do desempenho de 2 vigas de concreto armado e de uma viga mista de aço e concreto em situação de incêndio, considerando‐se que todas as faces da seção transversal das vigas estão expostas ao fogo, isto é, a temperatura é prescrita (condição de contorno de Dirichlet) e igual em todas as faces das seções e, além disso, não existem faces isoladas termicamente ou adiabáticas (com fluxo de calor nulo). Sendo assim, o campo de temperaturas para cada passo de tempo mostra valores constantes em cada fibra que compõe as seções. Comparações são feitas com as respostas analíticas obtidas a partir das considerações da ABNT NBR 6118 [11] e da ABNT NBR 8800 [12].

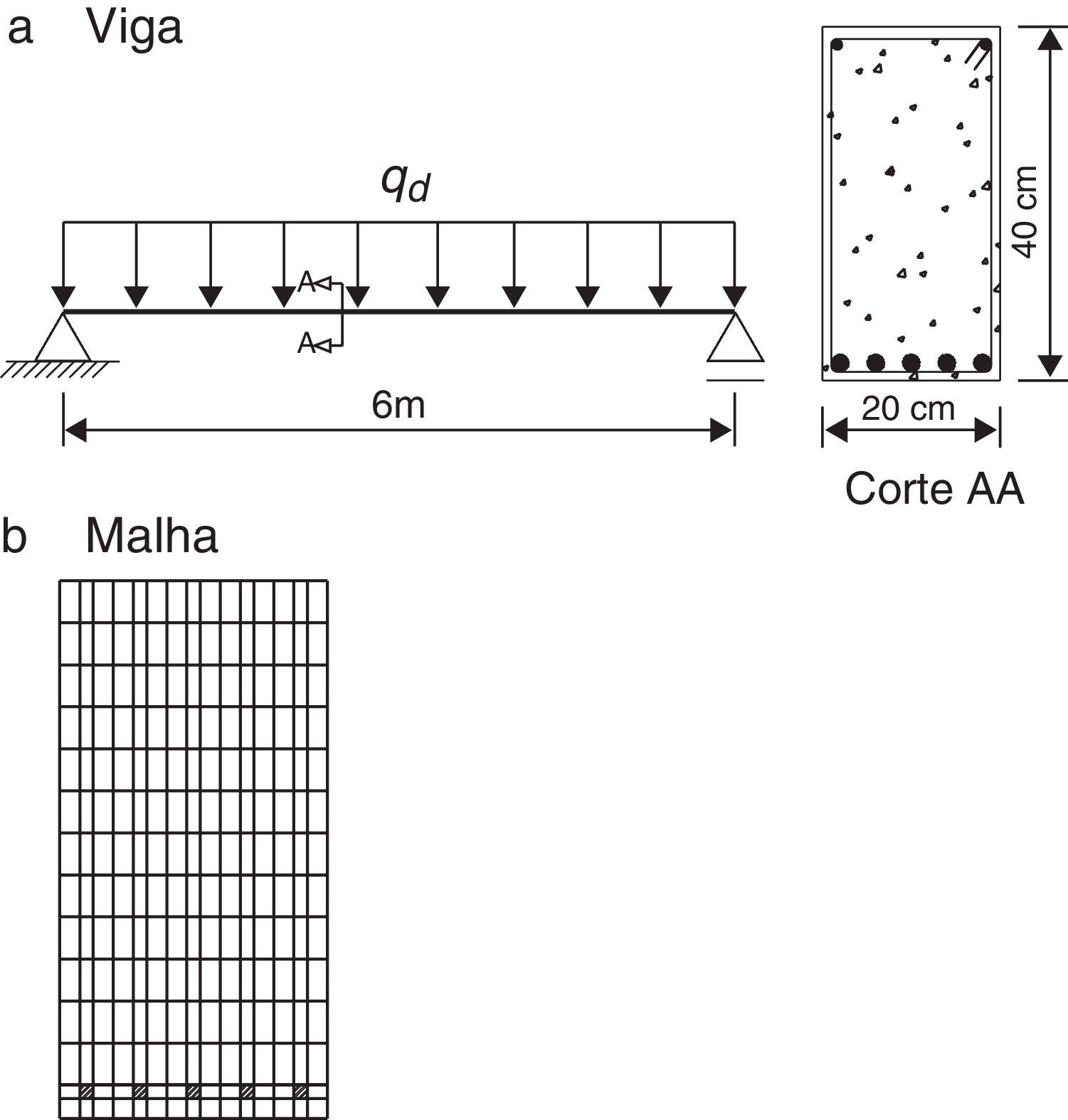
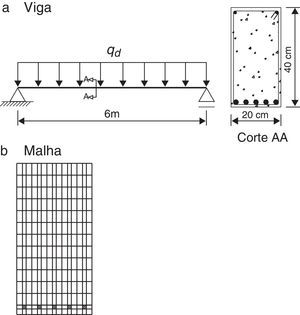
6.1

Viga de concreto armado de seção retangular

Neste exemplo tem‐se a análise de uma viga de concreto armado com f_ck = 20MPa, 6 m de comprimento e seção transversal retangular com b = 20cm e h = 40cm, como mostra a figura 3. A viga apresenta uma camada de armadura na região tracionada, com barras de diâmetro ϕ = 10mm, 2 armaduras de montagem com ϕ = 6, 3mm e cobrimento c = 20 mm nas 2 direções.

Figura 3.

Viga de concreto armado de seção retangular.

O tempo de exposição da viga ao fogo foi de 120 min, ou seja, até se atingir a temperatura de 1.200 °C e para a análise numérica a seção transversal da viga foi discretizada com um total de 210 fibras (ver fig. 3b).

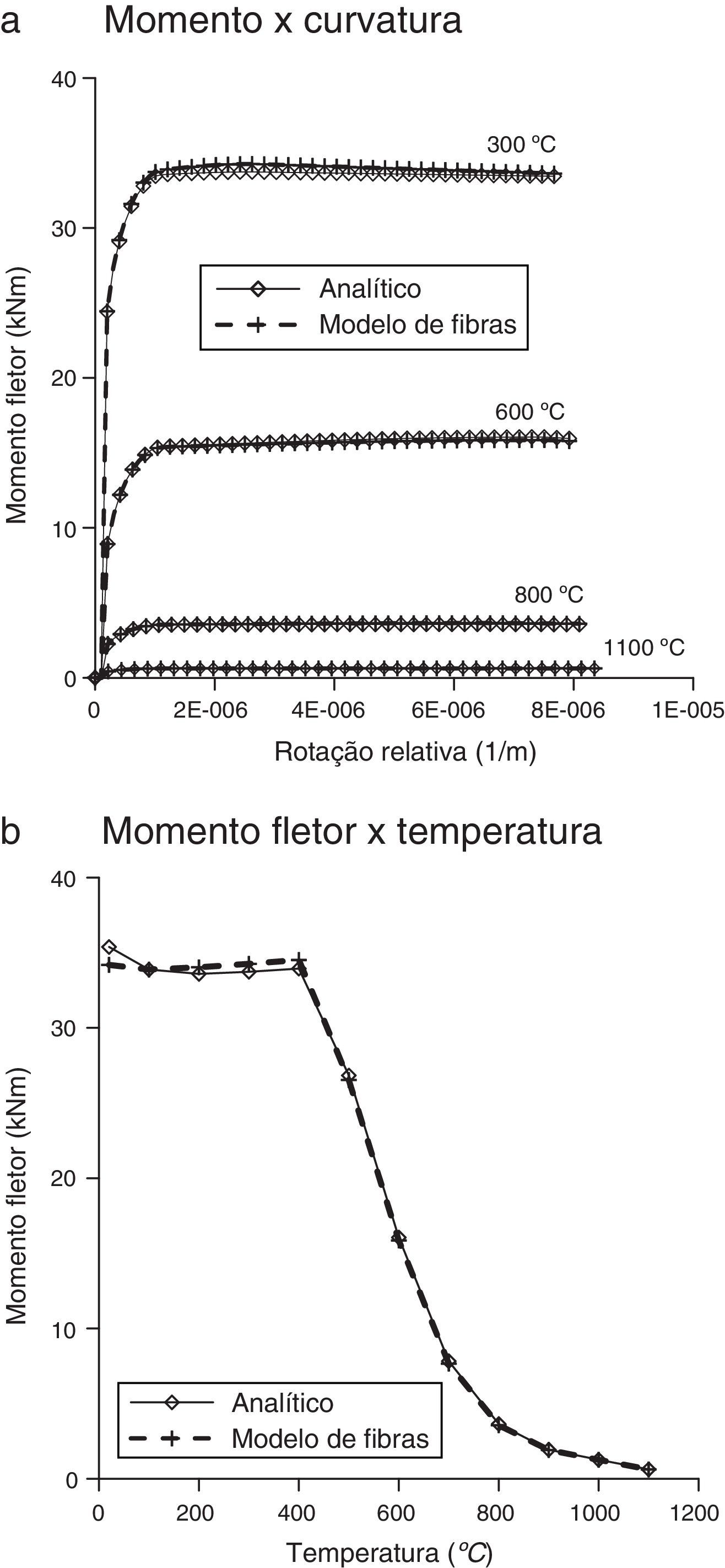
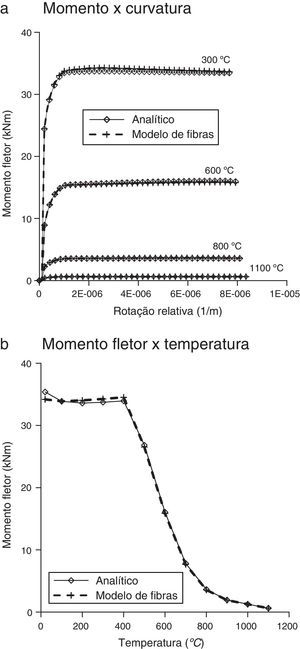
Na figura 4a apresentam‐se as relações momento x curvatura para as temperaturas de 300 °C, 600 °C, 800 °C e 1.100 °C determinadas com o programa MDCOMP (2014), sendo as mesmas comparadas com os resultados analíticos obtidos a partir das considerações da ABNT NBR 6118 [11]; na figura 4b mostra‐se a degradação do momento fletor máximo da viga com a elevação da temperatura.

Figura 4.

Momento x curvatura para a viga de seção retangular.

Nas tabelas 1 e 2 apresentam‐se os valores da rigidez da viga, bem como da posição da linha neutra para diferentes valores de temperatura. Por fim, na tabela 3 apresentam‐se os resultados numéricos correspondentes ao momento fletor máximo e as comparações com as respostas analíticas baseadas na ABNT NBR 6118 [11].

Tabela 1.

Relação rigidez x temperatura para a viga de seção retangular

θ (°C)	20	100	200	500	900
Rigidez analítica 108 kNm2	1,717	1,694	1,456	0,819	0,746
Rigidez modelo de fibras 108 kNm2	1,710	1,694	1,456	0,819	0,746

Tabela 2.

Variação da posição da linha neutra em função da temperatura xθ

θ (°C)	20	100	200	300	400	500	600	700	800	900	1.000	1.100
xθ (cm)	3,41	3,79	4,17	4,54	4,89	5,24	5,59	5,93	6,25	6,58	6,89	7,21

Tabela 3.

Momento máximo em situação de incêndio para a viga de seção retangular

θ (°C)	20	100	200	300	400	500	600	700	800	900	1.000	1.100
Analítico (kNm)	35,37	33,88	33,59	33,73	33,94	26,83	16,05	7,82	3,64	1,93	1,26	0,62
Modelo de fibras (kNm)	34,18	33,88	34,03	34,26	34,52	26,53	15,85	7,66	3,56	1,91	1,26	0,62
Modelo de FibrasAnalítico	1,03	1,00	0,99	0,98	0,98	1,01	1,01	1,02	1,02	1,01	1,00	1,00

6.2

Viga de concreto armado de seção T

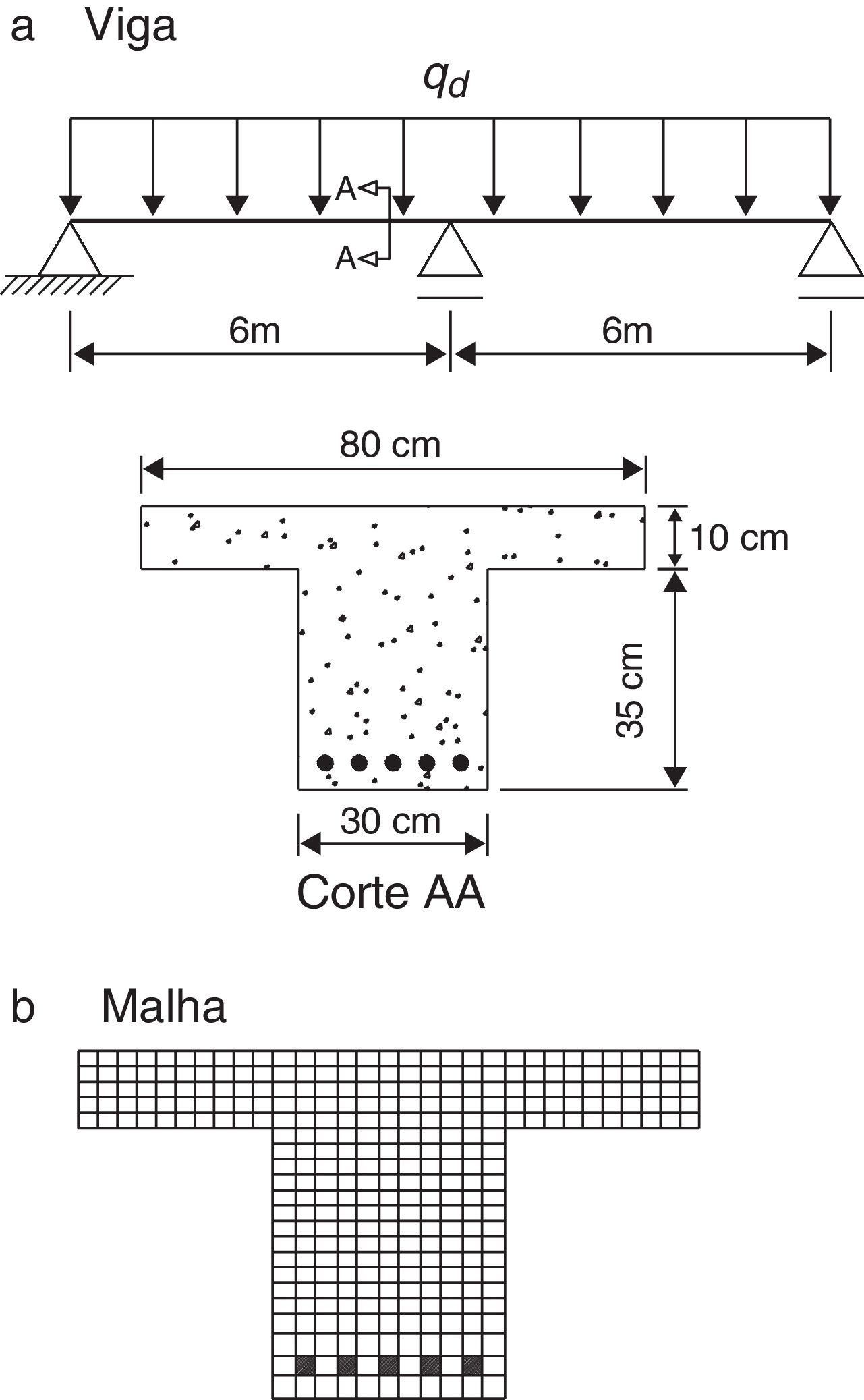
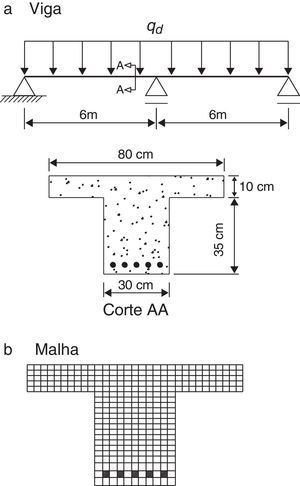
Neste exemplo analisou‐se uma viga contínua de concreto armado com f_ck = 20MPa, com 2 vãos de 6 m e seção transversal T com b_f = 80 cm (largura da mesa), h_f = 10 cm (espessura da mesa), hw=35 cm (altura da alma ou nervura) e bw=30 cm (largura da alma ou largura da nervura), como mostra a figura 5. A armadura longitudinal da viga é composta por barras de diâmetro ϕ = 25 mm, com cobrimento c = 30 mm nas 2 direções.

Figura 5.

Viga de concreto armado com seção T.

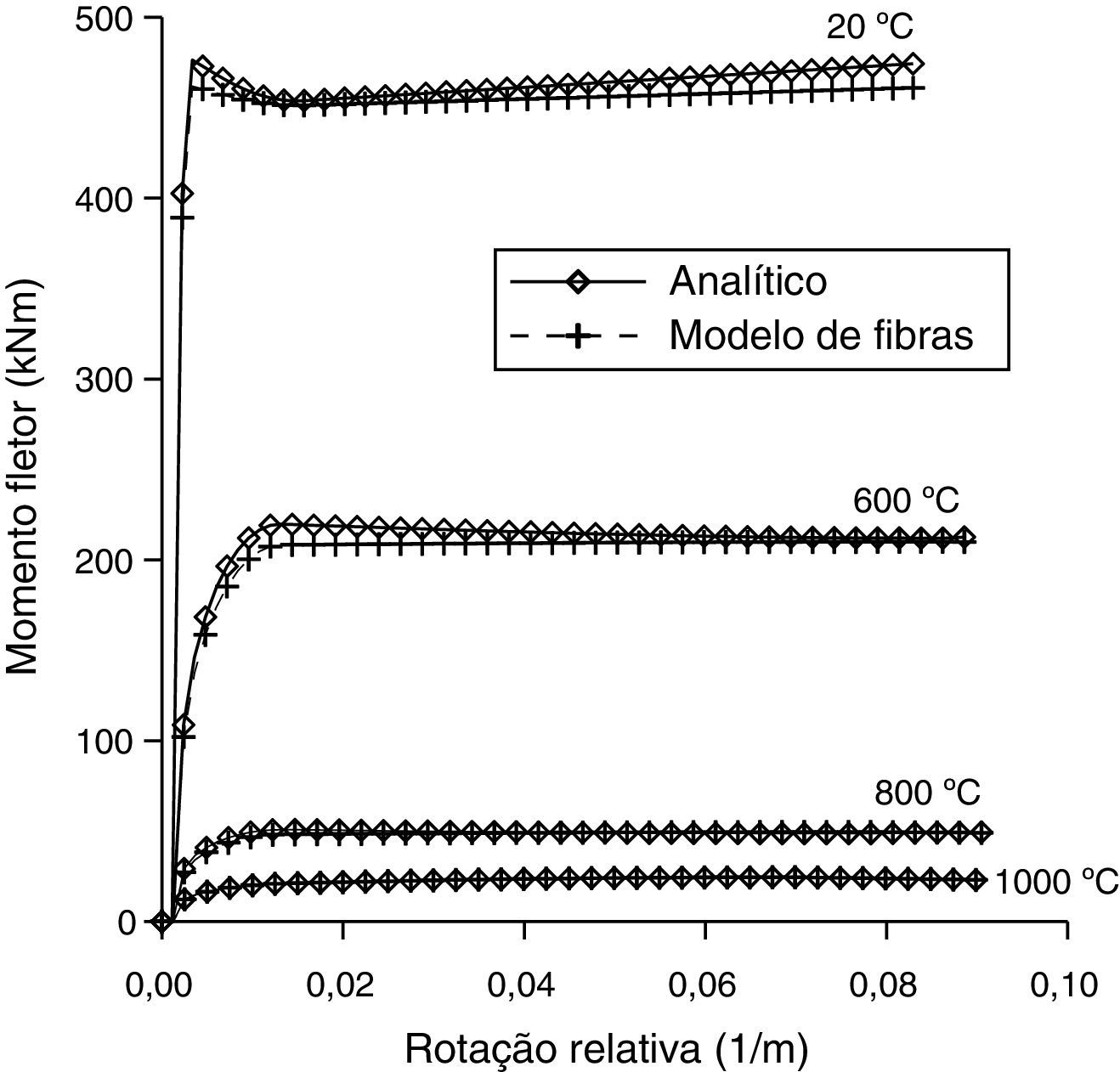
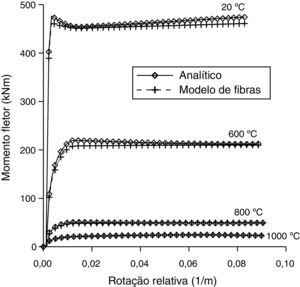
Para a análise numérica, a seção transversal foi discretizada com um total de 331 fibras (ver fig. 5b). Na figura 6 mostram‐se as curvas momento x rotação relativa para as temperatura de 20 °C, 600 °C, 800 °C e 1.000 °C, sendo os resultados numéricos comparados com os analíticos.

Figura 6.

Momento x curvatura para a viga de seção T.

Na tabela 4 apresentam‐se os valores dos momentos no estado limite último determinados com as considerações normativas vigentes no Brasil e com auxílio do modelo de fibras para diferentes temperaturas.

Tabela 4.

Momento máximo em situação de incêndio para a viga de seção T

θ (°C)	20	100	200	300	400	500	600	700	800	900	1,000	1,100
Analítico (kNm)	476,4	476,4	471,3	470,2	468,8	365,1	219,7	106,7	50,8	27,6	18,4	9,2
Modelo de fibras (kNm)	461,9	459,4	454,9	452,0	449,1	348,0	208,2	101,4	48,2	26,2	17,3	8,5
Modelo de FibrasAnalítico	0,97	0,96	0,96	0,95	0,95	0,95	0,94	0,94	0,94	0,94	0,94	0,93

6.3

Viga mista de aço e concreto

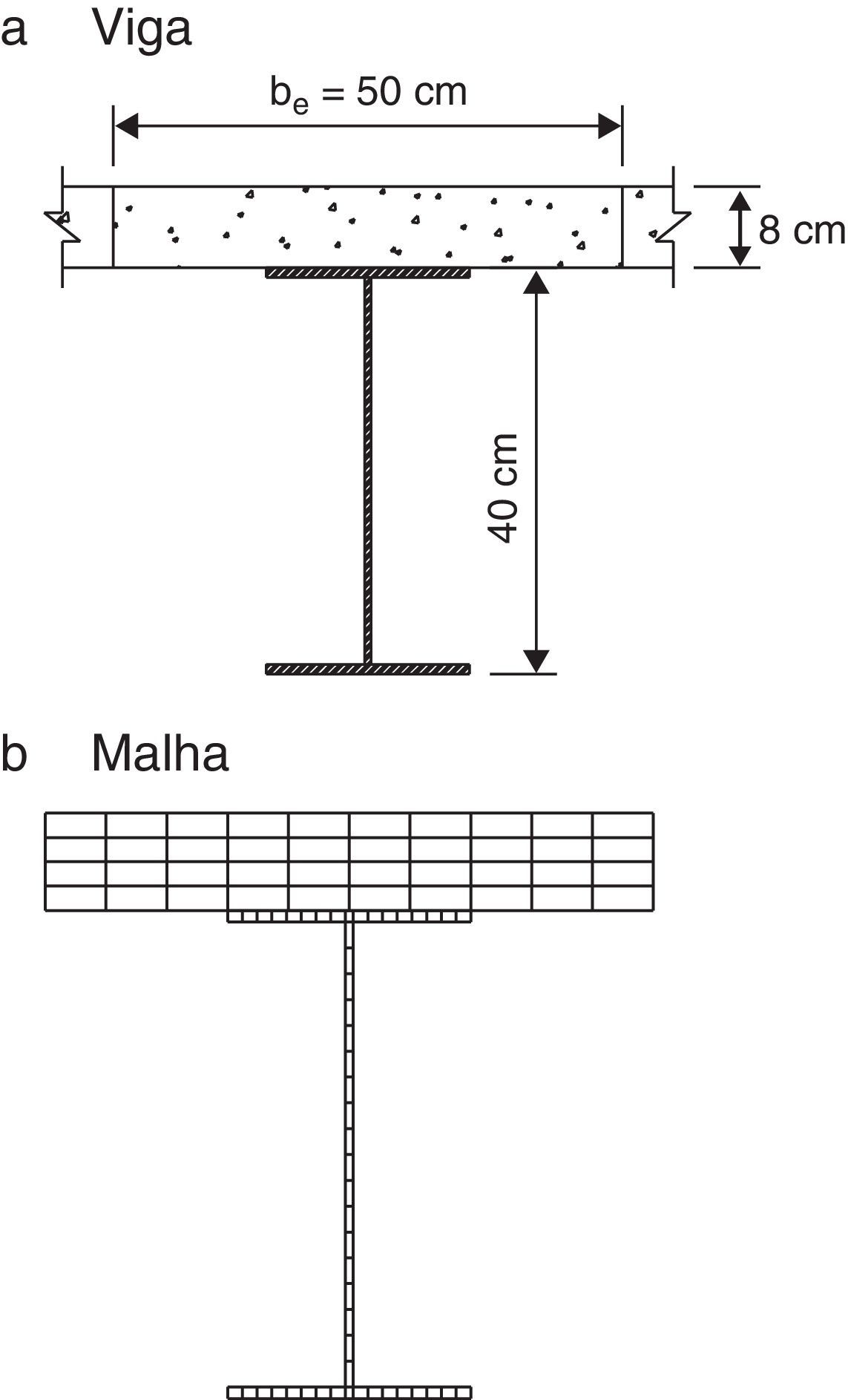
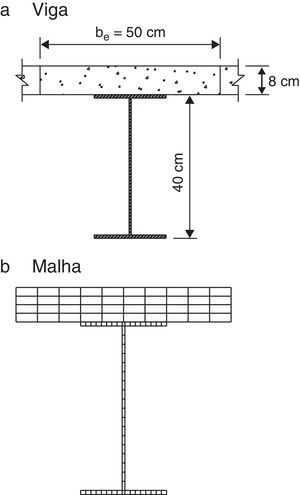
Neste exemplo tem‐se a análise de uma viga mista de aço e concreto com 4 metros de comprimento considerando‐se que há interação completa entre o aço e o concreto. A seção de aço é constituída por um perfil soldado VS 400 x 49 kg/m em aço MR250 fy=250MPa e a laje maciça tem 8 cm de espessura em concreto de f_ck = 20MPa, como mostra a figura 7. Para a análise numérica, a laje de concreto e o perfil metálico foram discretizados com 40 e 52 fibras, respectivamente (ver fig. 7b).

Figura 7.

Viga mista de aço e concreto.

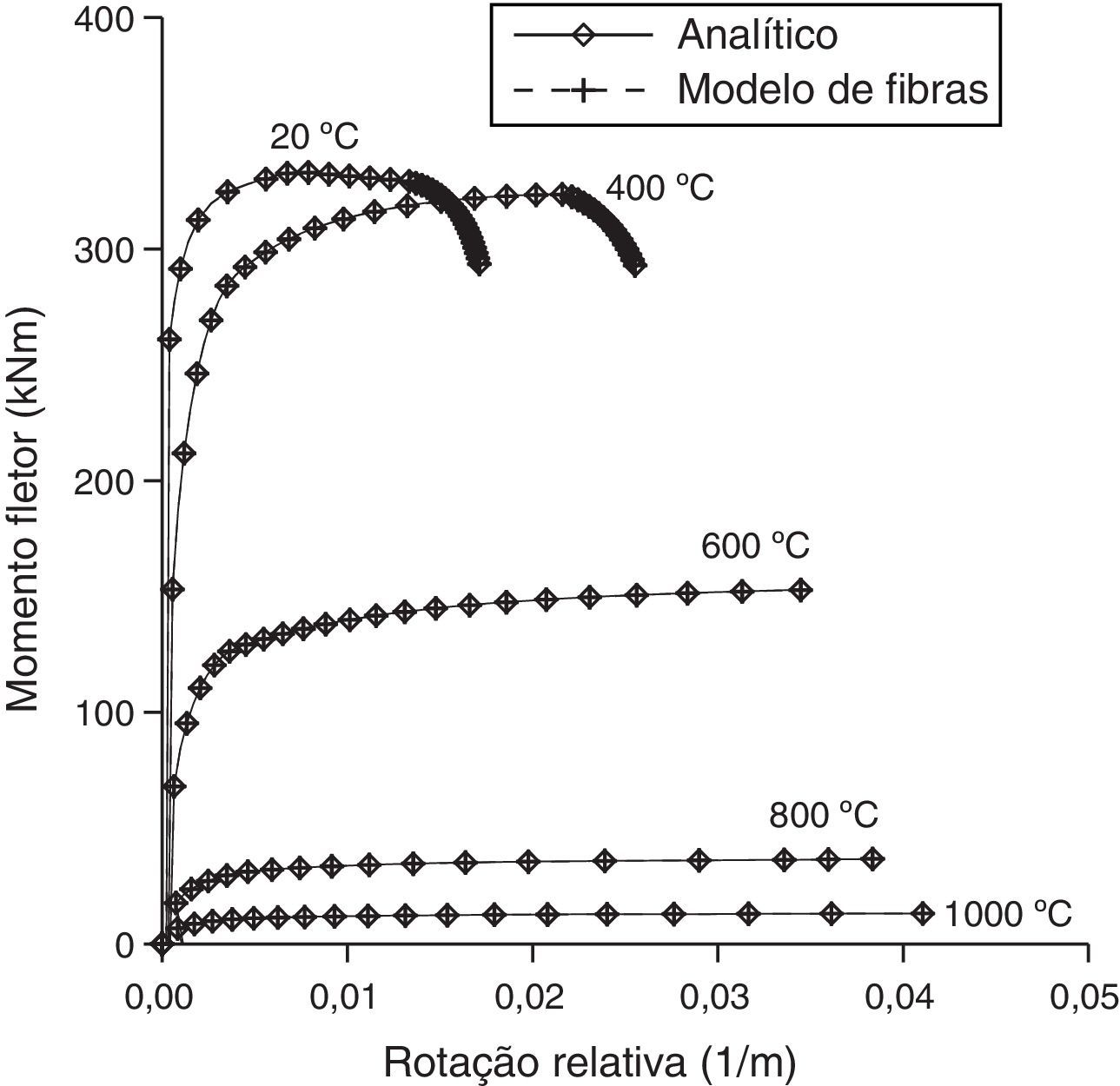
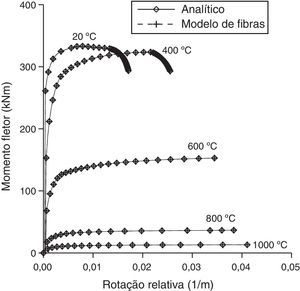
Na figura 8, apresentam‐se as curvas momento x rotação para as temperatura de 20 °C, 400 °C, 600 °C, 800 °C e 1.000 °C, sendo os resultados numéricos comparados com os analíticos.

Figura 8.

Momento x rotação para a viga mista de aço e concreto.

Por fim, na tabela 5 mostram‐se os resultados numéricos correspondentes ao momento fletor máximo para a análise a altas temperaturas e as comparações com as respostas analíticas baseadas na ABNT NBR 8800 [12].

Tabela 5.

Momento máximo em situação de incêndio para a viga mista de aço e concreto

θ (°C)	20	100	200	300	400	500	600	700	800	900	1,000	1,100
Analítico (kNm)	333,3	333,3	331,7	328,3	323,7	253,3	156,0	78,9	37,9	20,6	13,3	6,1
Modelo de fibras (kNm)	333,1	333,1	331,5	328,1	323,5	253,2	155,9	78,8	37,8	20,6	13,3	6,1
Modelo de FibrasAnalítico	0,99	0,99	0,99	0,99	0,99	0,99	0,99	0,99	0,99	1,00	1,00	1,00

7

Conclusões

O modelo numérico de fibras foi utilizado neste trabalho para o desenvolvimento de um programa computacional para avaliação do desempenho de vigas de concreto armado e vigas mistas de aço e concreto em situação de incêndio. Para isso, utilizaram‐se as prescrições definidas pela parte 1.2 do EUROCODE 2 [13] e das normas brasileiras ABNT NBR 15200 [14], ABNT NBR 6118 [11] e ABNT NBR 8800 [12].

A partir dos resultados obtidos que se referem às relações momento x rotação relativa e momento x temperatura pode‐se afirmar que a estratégia proposta fornece resultados confiáveis para o desempenho de vigas a altas temperaturas, uma vez que as respostas determinadas a partir da discretização da seção são praticamente coincidentes com as respostas analíticas (ver figs. 4, 6 e 8 e tabelas 3, 4 e 5.

Na figura 4b e na tabela 1 observa‐se a considerável redução da rigidez da viga de concreto armado de seção retangular à medida que as temperaturas se elevam, o que contribui para uma significativa diminuição da resistência da estrutura.

Para o exemplo da viga mista de aço e concreto devido à presença do perfil metálico e de sua maior condutividade térmica em relação ao concreto, verifica‐se maior aumento de temperatura no perfil metálico e, consequentemente, uma redução mais significativa de resistência à flexão do que as vigas de concreto armado. A viga mista de aço e concreto após uma hora e 50 minutos de exposição ao fogo apresentou uma resistência igual a 1,78% de sua resistência à temperatura ambiente (20 °C). Dentre os diversos efeitos que ocorrem nas vigas mistas de aço e concreto em caso de um incêndio de grandes proporções afirma‐se que, em determinado momento, devido à elevação da temperatura, a viga deixa de suportar o peso da laje, ocorrendo o que se chama de efeito de membrana. Este fenômeno se deve ao aumento da rotação da viga decorrente da redução de sua rigidez e resistência e, portanto, a laje passa a sustentar a viga metálica. Fazendo‐se um comparativo entre os efeitos ocorridos na viga de concreto armado de seção T e na viga mista de aço e concreto observa‐se que a viga mista apresenta maior redução da rigidez e maior aumento de curvatura (rotação relativa) à medida que a temperatura aumenta (ver figs. 6 e 8).

Por fim, conclui‐se que a estratégia proposta neste trabalho permitiu de forma bastante satisfatória a avaliação do desempenho de vigas de concreto armado e de vigas mistas de aço e concreto em situação de incêndio.