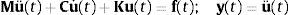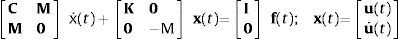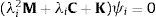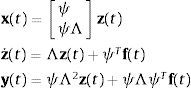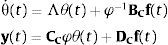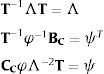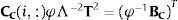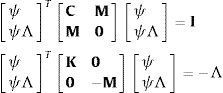Estimación de las masas modales de una estructura en servicio mediante transformación en el espacio de estados

Resumen

Este trabajo se centra en presentar una metodología práctica para estimar los parámetros modales de estructuras en uso y se aplica a la pasarela peatonal del Museo de Ciencia de la ciudad de Valladolid, España. El trabajo consiste no sólo en calcular frecuencias propias y factores de amortiguamiento asociados a cada uno de los modos estimados, como proporcionan muchos programas comerciales a partir de los registros de aceleraciones de ensayos OMA (Operational Modal Analysis) y/o EMA (Experimental Modal Analysis), sino también calcular las masas generalizadas correspondientes a cada uno de los modos estimados de la estructura. Para ello, en primer lugar se obtiene una representación del sistema dinámico en el espacio de estados mediante la técnica SSI (Stochastic Subspace Identification) y en segundo lugar, mediante la adecuada matriz de transformación se llega a la representación que permite identificar los parámetros físicos del sistema (matrices de masa, amortiguamiento y rigidez), lo que permite obtener masas modales y/o modos normalizados respecto de la matriz de masa, principal novedad de la metodología propuesta.

Abstract

This paper focuses on estimating the modal parameters of in-service infrastructures, applied to the pedestrian footbridge of the Science Museum of the city of Valladolid (Spain). The work consists not only on determining natural frequencies and damping factors associated to each of the estimated modes, as many commercial software provide from acceleration measurements through OMA (Operational Modal Analysis) and/or EMA (Experimental modal Analysis), but also to calculate the generalized masses corresponding to each of the estimated modes of the structure. For this purpose, firstly a dynamic representation of the system is obtained in the state space by SSI technique (Stochastic Subspace Identification) and secondly, by the appropriate transformation matrix, it leads to the representation that identifies the physical parameters of the system (matrices of mass, damping and stiffness), which allows to obtain modal masses and/or normalized mode shapes with respect to the mass matrix, which is the main contribution of the practical methodology presented in this paper.

1

Introducción

En la actualidad, el diseño y construcción de un gran número de obras de ingeniería industrial y civil, tales como chimeneas industriales, torres, edificios altos, puentes, pasarelas o viaductos, ya no está apenas limitada por los materiales -cada vez más resistentes- y los sistemas constructivos -cada vez con mayor componente tecnológico-, lo que ha provocado que sean cada vez más esbeltas, ambiciosas y complejas.

Este hecho, junto con las actuales demandas sociales relativas a la percepción y confort, en algunos casos recogidas en las normativas y guías, suscitan la necesidad de integrar el cálculo dinámico de manera más sistemática en el análisis y diseño asistido por ordenador de estructuras esbeltas que son las más susceptibles de sufrir movimientos o vibraciones significativas.

Un caso particularmente relevante es el de las pasarelas peatonales, ya que generalmente son propensas a ser excitadas por las personas que las ocupan, apareciendo movimientos apreciables que incluso pueden llegar a ser molestos o, en algunos casos inadecuados o peligrosos desde el punto de vista de la resistencia estructural [4].

Para facilitar la integración del análisis dinámico es imprescindible disponer del mayor número posible de metodologías de cálculo que permitan la identificación de los parámetros más relevantes que definen el comportamiento de la estructura [11,12].

Respecto a la metodología de cálculo dinámico, la técnica de análisis modal de estructuras es una de las más importantes, estando estructurada en tres fases principales: recolección de datos, identificación del sistema y por último estimación de los parámetros modales [8].

Es la segunda etapa, la de identificación del sistema, la que juega un papel crucial en el número y tipo de parámetros modales que se puedan estimar [10], basándose los métodos de identificación clásicos en aplicar una excitación al sistema y a continuación registrar y procesar la correspondiente respuesta (Experimental Modal Analysis/EMA) [5].

Las propiedades modales de una estructura obtenidas por simulación (problema de valores propios) pueden ser diferentes de los valores experimentales debido principalmente a la suposición asociada con el modelado analítico. Las propiedades dinámicas pueden medirse por los experimentos después de que haya concluido la construcción de la estructura. La masa de una estructura se puede estimar con bastante precisión mediante un simple cálculo, sin embargo la masa modal es una propiedad dinámica relacionada no sólo con la distribución de la masa, sino también con las formas de la vibración. En este estudio la técnica de identificación del sistema se amplía para obtener la masa modal de una estructura.

El método de identificación más utilizado en la actualidad se denomina SSI (Stochastic Subspace Identification). Este método se ha aplicado en muchas situaciones para extraer los parámetros modales de las estructuras existentes (por ejemplo puentes y edificios) solicitadas por la vibración ambiental. Sin embargo, la información modal que se obtiene de estos métodos de identificación, es incompleta ya que proporciona estimaciones de frecuencias, factores de amortiguamiento y modos de vibración asociados, pero dichos modos no están normalizados respecto de la matriz de masa o, dicho de otra forma, esos métodos no calculan las masas generalizadas correspondientes a cada uno de los modos estimados [1]. Es por lo tanto muy interesante disponer de técnicas adicionales que a partir de toda la información obtenida al aplicar el método SSI nos permitan estimar todos los parámetros modales, incluidos las masas modales de cada modo de vibración [2].

En las formulaciones de elementos finitos, la identificación de los parámetros físicos generalmente se refiere al ajuste de las matrices de masa, amortiguamiento y rigidez en el sistema de ecuaciones diferenciales de segundo orden del problema dinámico. Aunque el método más empleado consiste en el ajuste de los parámetros modales del sistema para calibrar un modelo de elementos finitos (FEM Updating) [7], un posible enfoque es identificar estos parámetros directamente a partir de los datos experimentales. La identificación de los parámetros en una formulación diferencial de primer orden también ha recibido considerable atención pero, como es bien sabido, si se parte de un espacio de estados modelo y se trata de identificar los parámetros del modelo de segundo orden, cuestiones como la no unicidad de la solución complican la resolución del problema inverso. Sin embargo, los parámetros físicos del modelo de segundo orden se pueden obtener mediante la resolución de un problema simétrico de valores propios [3,6,9]. El requisito mínimo es que en todos los grados de libertad se debe ubicar o bien un sensor o un actuador, con al menos una localización de ubicación conjunta con par sensor-actuador. De esta forma se consigue una solución para el problema inverso.

Indicar que el trabajo se ha organizado de la manera siguiente: en primer lugar, tras esta introducción, se presenta la metodología empleada. A continuación se diserta sobre los resultados obtenidos y en el último apartado se presentan las principales conclusiones.

2

Metodología

Los parámetros físicos del problema modal y dinámico (modelos de segundo orden) se pueden estimar mediante la resolución de un problema simétrico de valores propios complejos. El requisito mínimo para esta metodología es que todos los grados de libertad contengan o bien un sensor o bien un actuador con al menos un par sensor-actuador conjunto. De esta manera, aunque son posibles otras configuraciones, el enfoque que se propone en este trabajo proporciona una solución sencilla y práctica al problema inverso.

2.1

Formulación en el espacio de estados

Una de las formulaciones bien conocidas para los sistemas dinámicos es la expresión matricial de la segunda ley de Newton, que una vez discretizada en el dominio espacial resulta:

donde u(t) indica el vector de desplazamientos nodales, con (˙) y (¨) representando la primera y segunda derivada respecto al tiempo respectivamente, el vector f(t) contiene las excitaciones externas que solicitan el sistema, las magnitudes M, C y K son las matrices simétricas definidas positivas de masa, amortiguamiento y rigidez, respectivamente, para un sistema de N grados de libertad, y y(t) el vector respuesta del sistema, en nuestro caso de interés, las aceleraciones.

Otra formulación consiste en la definición del vector de estado x(t), de manera que las ecuaciones del movimiento pueden escribirse mediante un sistema de ecuaciones diferenciales de primer orden de una forma más conveniente como:

La ventaja de escribir las ecuaciones del movimiento de esta forma es que el problema de valores propios asociado es simétrico y puede plantearse en forma matricial como:

donde ψ = [ψ₁ψ₂ . . . ψ_2N] es la matriz que contiene los autovectores del problema complejo de valores propios siguiente:

y Λ es la matriz diagonal de valores propios complejos λ_i = ς_i ± jω_i (siendo j=−1, ω_i la frecuencia en rd/s y ς_i se puede relacionar fácilmente con el factor de amortiguamiento).

Una vez que el problema de valores propios ha sido resuelto podemos reescribir la ecuación (2) mediante la siguiente transformación. Resultando finalmente:

Denominaremos el sistema anterior (5) como modelo modal simétrico.

2.2

Identificación del sistema dinámico

La técnica de identificación consta de dos fases bien definidas: en primer lugar la determinación del modelo de primer orden del sistema y en segundo lugar la transformación del modelo identificado al correspondiente modelo de segundo orden. A partir de los datos de aceleración registrados en los sensores y de la fuerza aplicada mediante el actuador, es posible identificar (mediante el método SSI) una representación en el espacio de estados en una base arbitraria, que se puede expresar como:

donde A_C, B_C, C_C y D_C son las matrices del sistema en tiempo continuo. Ahora, si se considera la transformación x = φθ el sistema en tiempo continuo puede escribirse en forma modal como se indica:

donde Λ es la matriz que contiene los valores propios del modelo de espacio de estados identificado y φ es la correspondiente matriz de vectores propios. Denominaremos a este sistema (7) como modelo modal no simétrico.

Si el sistema de primer orden (6) se identificó utilizando datos que realmente corresponden a un sistema que responde a la ecuación de segundo orden (1), los modelos representados por las ecuaciones (5) y (7) son dos representaciones diferentes del mismo sistema dinámico. Por lo tanto, podemos buscar una matriz de transformación (T) que relacione ambas expresiones, es decir:

Supongamos que el grado de libertad i-ésimo contiene un sensor y un actuador. El requisito de co-localización junto con el hecho de que la matriz T es diagonal permite determinar dicha matriz de manera unívoca mediante la siguiente expresión:

Dependiendo de la configuración de sensores y actuadores la información relativa a un cierto grado de libertad está embebida ya sea en la matriz de entrada o en el matriz de salida. En este caso, la matriz de salida contiene información de los N grados de libertad, con lo cual, los autovectores ψ se calculan con la última de las expresiones indicadas en (8). Y una vez calculados dichos autovectores, las matrices de masa, amortiguamiento y rigidez se pueden obtener haciendo uso de las condiciones de ortogonalidad, éstas son:

Lo que implica que tras las correspondientes operaciones algebraicas podemos estimar los parámetros físicos del sistema dinámico según:

Y por último, como es sabido, conocida la matriz de masa, la determinación de las masas generalizadas/modales o de los modos de vibración normalizados es algo inmediato.

3

Resultados numéricos

Una vez expuesta la metodología, procedemos a la validación de la misma presentando un primer problema numérico pero suficientemente general (validación), para después aplicar dicha metodología al análisis de un caso general más complejo (ejemplo) y de una estructura real actualmente en uso.

3.1

Validación

El problema que vamos a plantear es el de una viga biapoyada de longitud L = 10.4 m, módulo de Young E = 2.1 · 10¹¹ Pa, densidad ρ = 7850.0 kg/m³, inercia Iz = 604 · 10⁻⁸ m⁴ y sección transversal de área A = 53.8 · 10⁻⁴ m². También se supone un factor de amortiguamiento de 5% para cada uno de los modos de vibración de dicha viga. Se simula mediante herramienta matemática de manera que se obtienen las aceleraciones en las posiciones (1/4, 1/2, 3/4) · L (sensores 1, 2 y 3, respectivamente) cuando se aplica una fuerza externa conocida (f(t) = 10² · sin(2πt)) en la misma sección donde se ubica el sensor 1 (para el grado de libertad 1, corresponde el par sensor-actuador).

A continuación, se sigue la metodología de este trabajo. Primero se identifica el sistema en base a un modelo de espacio de estados a partir de los datos de respuesta. En segundo lugar se determinan los factores de escala dados por la matriz diagonal T y los vectores propios ψ. Después se estiman las matrices de masa, amortiguamiento y rigidez del modelo de segundo orden (M, C y K, respectivamente). Por último se calculan todos los parámetros modales.

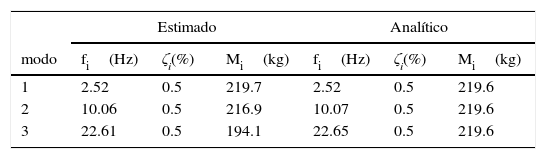
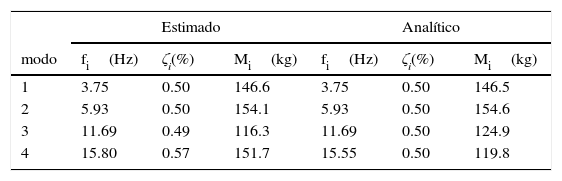
En la tabla 1 se recogen los resultados estimados de los parámetros modales: frecuencias propias (f_i), factores de amortiguamiento (ζ_i) y masas generalizadas (M_i) asociados a los tres primeros modos de vibración de la viga, asimismo, se indica la solución analítica correspondiente.

Tabla 1.

Viga biapoyada. Parámetros modales

	Estimado			Analítico
modo	fi (Hz)	ζi(%)	Mi (kg)	fi (Hz)	ζi(%)	Mi (kg)
1	2.52	0.5	219.7	2.52	0.5	219.6
2	10.06	0.5	216.9	10.07	0.5	219.6
3	22.61	0.5	194.1	22.65	0.5	219.6

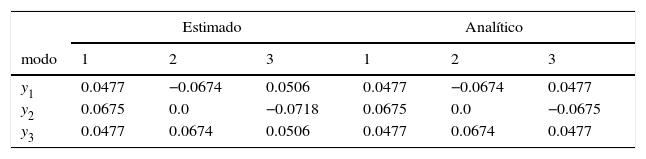
La tabla 2 muestra los modos normalizados respecto de la matriz de masa correspondientes a los tres primeros modos de vibración. Se observa, al igual que en la tabla 1, que los resultados para el tercer modo de vibración son poco precisos, esto se debe a que el tipo de carga aplicada en el ejemplo no es capaz de excitar el tercer modo. Hubiera sido más conveniente haber excitado con un fuerza con contenido variado en frecuencias.

Tabla 2.

Viga biapoyada. Modos de vibración normalizados

	Estimado			Analítico
modo	1	2	3	1	2	3
y1	0.0477	−0.0674	0.0506	0.0477	−0.0674	0.0477
y2	0.0675	0.0	−0.0718	0.0675	0.0	−0.0675
y3	0.0477	0.0674	0.0506	0.0477	0.0674	0.0477

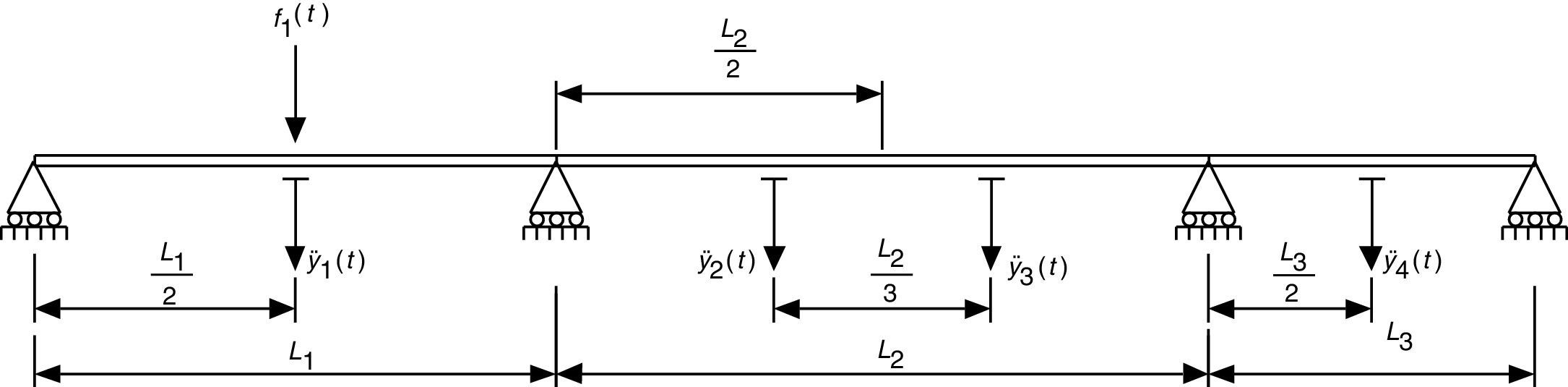
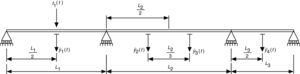
3.2

Ejemplo

A continuación se va a mostrar la metodología de este trabajo para identificar el modelo modal de la viga continua de tres vanos, indicada en la figura 1. La longitud de cada uno de los vanos es: L₁ = 8 m, L₂ = 10 m y L₃ = 5 m. Las propiedades del material y de la sección son respectivamente: módulo de Young E = 2.1 · 10¹¹ Pa, densidad ρ = 7850 kg/m³, área de la sección transversal A = 53.8 · 10⁻⁴ m² y momento de inercia I_z = 604.0 · 10⁻⁸ m⁴.

Figura 1.

Viga continua.

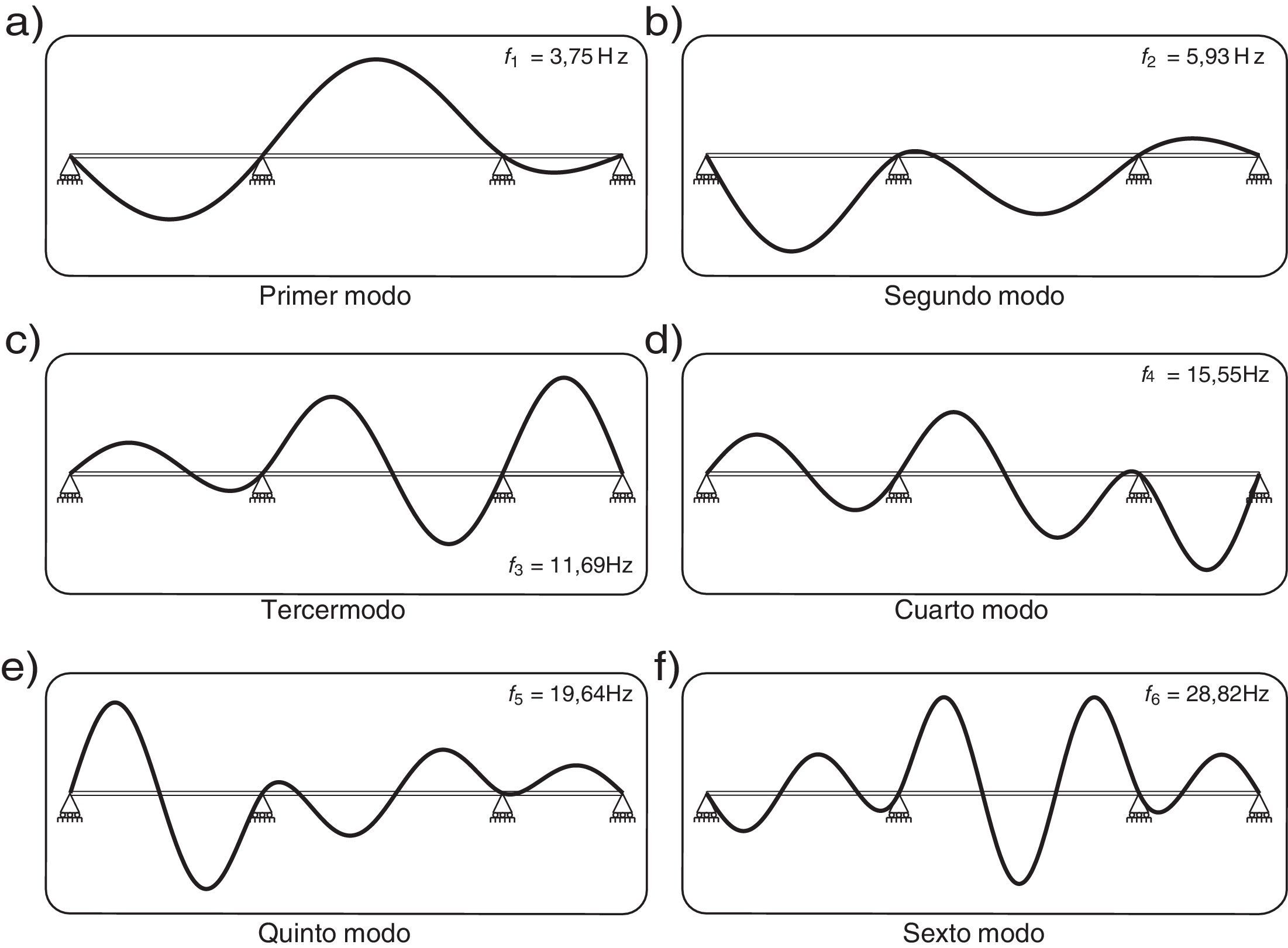
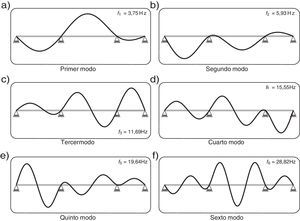
De la resolución analítica del problema de análisis modal de dicha viga se obtienen los modos de vibración y frecuencias propias que se muestran en la figura 2. A continuación, se aplica una fuerza de tipo armónico (f₁(t) = 10² · sin(2πt)) en la sección que indica la figura 1. Asimismo, se asume de nuevo un factor de amortiguamiento ζ_i = 0.5% para cada uno de los modos de vibración y se calcula la respuesta dinámica de la estructura mediante el método de superposición modal (se consideran los seis primeros modos calculados anteriormente) con el objeto de generar los registros de aceleraciones en los puntos de la estructura indicados en la figura 1 de un minuto de duración con un tiempo de muestreo T_s = 0.005 s, para posteriormente emplear dichos registros, junto con el de la fuerza aplicada, como punto de partida en la aplicación de la metodología objeto de este trabajo.

Figura 2.

Viga continua. Modos de vibración.

Es decir, la idea es suponer que solamente contamos con la información recogida en los registros de aceleraciones y el registro de fuerza aplicada, según el esquema de la figura 1. Se identifica el sistema y con el modelo obtenido en el espacio de estados se aplica la metodología expuesta y se obtienen las estimaciones que se resumen a continuación.

En la tabla 3 se recogen los resultados estimados de las frecuencias propias y los factores de amortiguamiento asociados a los cuatro primeros modos de vibración de la estructura y también los resultados analíticos correspondientes.

Tabla 3.

Ejemplo. Viga continua. Parámetros modales

	Estimado			Analítico
modo	fi (Hz)	ζi(%)	Mi (kg)	fi (Hz)	ζi(%)	Mi (kg)
1	3.75	0.50	146.6	3.75	0.50	146.5
2	5.93	0.50	154.1	5.93	0.50	154.6
3	11.69	0.49	116.3	11.69	0.50	124.9
4	15.80	0.57	151.7	15.55	0.50	119.8

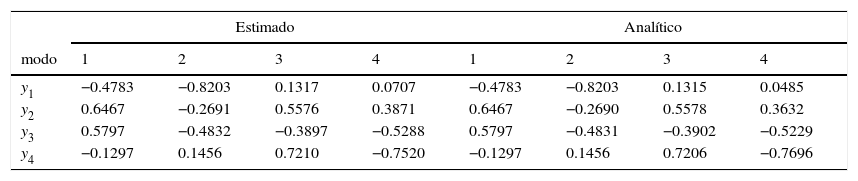
La tabla 4 muestra los cuatro primeros modos de vibración de la viga continua, estimados y teóricos. Se observa que los resultados para el tercer y cuarto modo de vibración difieren ligeramente de los analíticos. Esto puede deberse a que su participación en la respuesta dinámica bajo la fuerza armónica propuesta es pequeña y por lo tanto la incertidumbre grande.

Tabla 4.

Ejemplo. Viga continua. Modos de vibración

	Estimado				Analítico
modo	1	2	3	4	1	2	3	4
y1	−0.4783	−0.8203	0.1317	0.0707	−0.4783	−0.8203	0.1315	0.0485
y2	0.6467	−0.2691	0.5576	0.3871	0.6467	−0.2690	0.5578	0.3632
y3	0.5797	−0.4832	−0.3897	−0.5288	0.5797	−0.4831	−0.3902	−0.5229
y4	−0.1297	0.1456	0.7210	−0.7520	−0.1297	0.1456	0.7206	−0.7696

3.3

Aplicación a un caso real

En esta sección se describe la identificación de los parámetros modales de la pasarela peatonal del Museo de la Ciencia de la ciudad de Valladolid. Esta identificación consistió en un análisis modal experimental del vano de la estructura más sensible a las vibraciones inducidas por el tránsito de peatones.

3.3.1

Descripción de la estructura

La estructura estudiada es una pasarela peatonal sobre el río Pisuerga que une el Museo de la Ciencia con el centro de la ciudad. Construida en el año 2004, es una estructura de 234 metros compuesta de cuatro vanos: tres formados por barras metálicas tubulares y uno de hormigón. El vano principal (vano 3 en la fig. 3) tiene 111 metros y cuenta con un sistema de tendones externos postensados. El segundo vano (vano 2) tiene 51 metros y los otros dos vanos son más cortos y rígidos. El sistema de tendones externo del vano 3 hace que sea suficientemente rígido. Sin embargo, el vano 2 (fig. 4), es más sensible a excitaciones dinámicas producidas por humanos. En dicho vano se alcanzan niveles de vibración que, según la opinión de los usuarios, a veces son molestos, particularmente cuando un corredor cruza el puente.

Figura 3.

Vista general de la estructura en estudio.

Figura 4.

Vista del Vano 2.

3.3.2

Análisis modal experimental

La identificación de los parámetros modales de la estructura mediante OMA tiene el inconveniente de no identificar la masa modal, parámetro necesario para obtener el modelo modal completo y para realizar las estimaciones de la respuesta utilizando las guías y normativas. Por ello es necesario utilizar otros métodos para estimar este parámetro, siendo lo más inmediato hacer un EMA en el que la fuerza de excitación es conocida.

La fuerza de excitación empleada para este caso se generó con un excitador electrodinámico de APS Dynamics modelo 400 en modo inercial colocado en el centro del vano. La fuerza inducida por el excitador se calculó midiendo la aceleración de la masa inercial y multiplicándola por su magnitud (30.4 kg). Se utilizó un barrido continuo en frecuencia entre 2.5 y 4.5 Hz. Para los registros de la respuesta se colocaron tres acelerómetros piezoeléctricos en la línea central del vano. Este método tiene la ventaja de conocer la excitación y el inconveniente de que se necesita un excitador capaz de hacer vibrar la estructura con suficiente intensidad como para ser percibida por los acelerómetros.

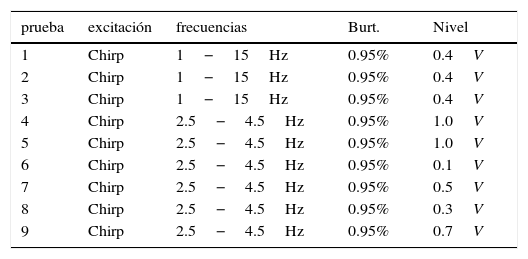
3.3.3

Resultados experimentales

Se llevaron a cabo un total de nueve pruebas (toma de datos). En la tabla 5 se indican los ajustes del excitador en cada uno de ellos.

Tabla 5.

Excitaciones inducidas en la pasarela

prueba	excitación	frecuencias	Burt.	Nivel
1	Chirp	1 − 15 Hz	0.95%	0.4 V
2	Chirp	1 − 15 Hz	0.95%	0.4 V
3	Chirp	1 − 15 Hz	0.95%	0.4 V
4	Chirp	2.5 − 4.5 Hz	0.95%	1.0 V
5	Chirp	2.5 − 4.5 Hz	0.95%	1.0 V
6	Chirp	2.5 − 4.5 Hz	0.95%	0.1 V
7	Chirp	2.5 − 4.5 Hz	0.95%	0.5 V
8	Chirp	2.5 − 4.5 Hz	0.95%	0.3 V
9	Chirp	2.5 − 4.5 Hz	0.95%	0.7 V

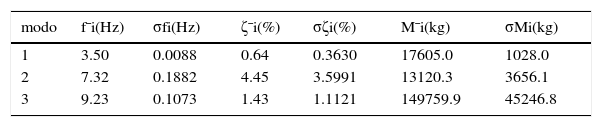
La tabla 6 recoge los valores medios estimados de las frecuencias propias (f¯i), los factores de amortiguamiento (ζ¯i) y las masas generalizadas (M¯i) correspondientes a los tres primeros modos, así como el valor correspondiente de la desviación típica de cada una de dichas magnitudes: frecuencias (σfi), factores de amortiguamiento (σζi) y masas generalizadas (σMi). Se comprueba que el método de identificación del sistema dinámico es preciso para estimar frecuencias de vibración, pero respecto a los resultados de amortiguamiento y masas generalizadas hay una variación importante.

Tabla 6.

Valores medios y desviación típica de los parámetros modales estimados

modo	f¯i(Hz)	σfi(Hz)	ζ¯i(%)	σζi(%)	M¯i(kg)	σMi(kg)
1	3.50	0.0088	0.64	0.3630	17605.0	1028.0
2	7.32	0.1882	4.45	3.5991	13120.3	3656.1
3	9.23	0.1073	1.43	1.1121	149759.9	45246.8

A continuación, en la tabla 7 se indican los tres primeros modos de vibración asociados a las masas generalizadas estimadas en la tabla anterior (tabla 6), mediante valor medio y desviación de cada una de las coordenadas. Precisamente a la vista de la desviación se puede concluir una mayor incertidumbre en la estimación de los modos 2 y 3.

Tabla 7.

Pasarela. Modos de vibración

modo	1	2	3	modo	1	2	3
y¯1	0.5146	1.0000	−0.9643	σy1	0.0067	0.0000	0.0801
y¯2	1.0000	0.3114	0.8966	σy2	0.0000	0.0636	0.1352
y¯3	0.7636	−0.7001	−0.5073	σy3	0.0067	0.1812	0.1376

Por último, se indica en la tabla 8 los modos de vibración normalizados respecto de la matriz de masa, en base a valores medios y desviación típica de las coordenadas medidas. Estos modos de vibración serían los que hay que utilizar para simular la respuesta dinámica de la pasarela mediante el método de superposición modal empleando simplemente los tres primeros modos de vibración de la estructura.

Tabla 8.

Pasarela. Modos de vibración normalizados

modo	1	2	3	modo	1	2	3
y¯1	0.0039	0.0090	−0.0026	σy1	0.0001	0.0013	0.0004
y¯2	0.0075	0.0028	0.0024	σy2	0.0002	0.0006	0.0004
y¯3	0.0058	−0.0062	−0.0013	σy3	0.0002	0.0014	0.0004

4

Conclusiones

Analizados los resultados experimentales obtenidos, la primera conclusión que merece la pena reseñar, por la relevancia que tiene sobre el resto de las interpretaciones de los datos resultantes, es que sólo se pueden obtener con precisión los parámetros modales que corresponden a los modos de vibración que seamos capaces de excitar. Aunque lógica, esta conclusión ha de estar siempre presente tanto en la planificación de las pruebas como en el postprocesado de los registros.

Relativo a la precisión en la estimación de los modos de vibración normalizados respecto a la matriz de masa, se considera que es suficiente, teniendo en cuenta además la dificultad que tiene su obtención a partir de los registros experimentales, ya que en los métodos de identificación de sistemas no se tiene en ningún momento una expresión explícita de la matriz de masa.

También se obtiene buena precisión en la determinación de las frecuencias propias, siendo menor en otras magnitudes como los factores de amortiguamiento, las masas generalizadas o los modos de vibración.

La obtención de los parámetros modales, incluidos los modos de vibración normalizados respecto a la matriz de masa, nos permiten la simulación de la respuesta de la pasarela peatonal y predecir su comportamiento dinámico frente a distintos tipos de solicitaciones (condiciones usuales o excepcionales de tráfico). Asimismo, tal y como comentamos en la introducción, nos permite el calibrado de dichos parámetros en las formulaciones de elementos finitos (FEM Updating) ya que son identificados directamente a partir de los datos experimentales.

La principal ventaja respecto a otros métodos de escalado de los modos [5,8,11] radica en que con una mínima información experimental respecto a la entrada (un solo canal coincidente con el correspondiente registro de salida) y sin necesidad de modelos computacionales complejos, con tan solo las transformaciones matemáticas indicadas, se consigue determinar las masas modales de los modos excitables.

Agradecimientos

Este trabajo ha sido realizado en parte con la financiación aportada al proyecto de investigación BIA2011-28493-C02 por el programa de apoyo a Proyectos de Investigación Fundamental No Orientada del Ministerio de Ciencia e Innovación. Asimismo, los autores agradecen al Ayuntamiento de Valladolid y al Museo de la Ciencia su apoyo en las pruebas de campo.