La falta de normalización en los resultados de los modos de vibración, ha sido la principal desventaja del análisis modal operacional, resuelto posteriormente mediante el método de modificación de masa, el cual supone un gran inconveniente para las obras civiles, ya que interrumpe el tráfico sobre las mismas, incrementando el tiempo del ensayo y notablemente su coste.
El objeto de este trabajo radica en efectuar un balance entre: el análisis modal tradicional (acompañado de simulaciones numéricas de la modificación de masa), frente al análisis modal operacional (conjuntamente con el método de modificación de masa); obteniendo unos resultados más óptimos y con un rango de error menor, incluso con la presencia de un alto nivel de ruido en la señal
De esta forma es posible, conocer de la forma más fiable, los parámetros modales de la estructura, y su alteración con la modificación de masa. Para ello se aplica la metodología expuesta a un puente metálico de gran luz, singular por su esbeltez, con una relación luz/canto de 56.6, la menor registrada en un puente, y que lo ha hecho figurar desde el año 2007 en el Libro Guinnes de los records.
The lack of standardization in vibration mode results has constituted the main shortcoming of operational modal analysis, subsequently resolved by means of the mass modification method. This is a major drawback for civil works, as it interrupts traffic on site, significantly increasing testing time and costs.
The purpose of this study is to achieve a balance between traditional modal analysis (accompanied by numerical simulations of mass modification) and operational modal analysis (in conjunction with the mass modification method), thereby obtaining more optimal results with a narrower range of error, even when the signal has a high level of noise.
It will thus be possible to reliably determine the modal parameters of the structure and their alteration due to mass modification. For this purpose, the proposed methodology is applied to a large span metal bridge, unique for its slenderness, with a span/depth ratio of 56.6, the lowest recorded on a bridge, as figured in the Guinness Book of Records since 2007.
La identificación de parámetros dinámicos se realiza, en general, a partir de registros de aceleración en determinados grados de libertad de la estructura, los cuales deben ser independientes y en número suficiente como para especificar los movimientos de la misma [1]. Las situaciones de excitación que se pueden contemplar se reducen a: excitación forzada o natural (ambiente).
Los registros obtenidos experimentalmente se tratan a continuación con diferentes técnicas, que básicamente se clasifican en dos grandes grupos:
- •
Análisis modal clásico: en donde hay un conocimiento, tanto de la respuesta de la estructura, como de la excitación aplicada, generada esta última por equipos electrohidráulicos normalmente [2]. Por lo que se puede determinar la relación entre ambos y obtener modos normalizados, así como estimar las masas modales a partir de ellos.
- •
Análisis modal operacional: no requiere una excitación artificial, ya que utiliza la del ambiente (tráfico, viento, peatones, etc.) solo emplea la respuesta de la estructura.
Este último se utiliza para obtener una descripción modal de la estructura bajo sus condiciones de operación. En lugar de cargar la estructura artificialmente y tratar la excitación ambiental como una fuente de ruido no deseado, la excitación natural se emplea como fuente de excitación [3,4].
Para ensayos con excitación ambiental se supone que las fuerzas desconocidas se aplican simultáneamente. Además, se supone que la fuerza de entrada es un ruido blanco, es decir, no depende de la frecuencia y tiene un espectro con un valor medio constante para cada frecuencia [5,6].
Como consecuencia de la alteración de la situación de carga en la estructura (puente vacío, en servicio, diferentes situaciones de carga como consecuencia de la utilización del método de modificación de masa), es conveniente identificar las frecuencias naturales en todos los casos para conocer el rango de frecuencias en el que pueden cambiar los modos de vibración, ante situaciones de carga diferentes.
La exactitud obtenida en la estimación de los factores de escala depende de la exactitud alcanzada en la identificación de los parámetros modales [7–9] y la estrategia de modificación de masa utilizada para alterar el comportamiento dinámico de la estructura [10–12]. La metodología para la modificación de masa está basada en la magnitud, la ubicación y el número de masas añadidas a la estructura.
Puede demostrarse que, para reducir la incertidumbre en la estimación de los factores de escala, se deben minimizar los errores en la estimación de los parámetros modales [13,14] durante la etapa experimental del análisis modal, así como la diferencia entre los modos de vibración modificados y no modificados [15–17].
No obstante, se requiere un cambio mínimo en la magnitud de la masa [16,17] al objeto de garantizar una desviación mínima de la frecuencia para evitar incertidumbres en la identificación del análisis modal [18,19]. Por otra parte, el cambio de masa no debería ser excesivamente alto con el fin de minimizar la diferencia entre los modos de vibración modificados y no modificados [20,21].
Un cambio de masa del orden de un 5% de la masa total, supone -en general- una modificación razonable en su magnitud [15,17].
Asimismo, en [22] se sugieren, basándose en sus propias experiencias experimentales, en particular en aplicaciones a puentes [23–25], que con seleccionar cambios de masa que alcancen desviaciones de la frecuencia del orden de un 1% ó 2%, ya se obtienen buenos resultados.
En general, el análisis modal operacional se basa en un programa experimental más amplio, consistente en dos etapas:
- •
Aplicación de un análisis modal operacional para obtener los parámetros modales.
- •
Realización de ensayos adicionales para calcular los factores de escala.
En [15,16] proponen que el factor de escala α que relaciona los modos de vibración normalizados y no normalizados, φ=α⋅ψ, sea determinado introduciendo un cambio de masa, definido mediante la matriz de cambio de masa Δm y aplicando la expresión
y ω0, ω1 son las frecuencias naturales del modo considerado, antes y después de la aplicación del cambio de masa.En pequeñas estructuras que se pueden ensayar en el laboratorio, o para grandes estructuras que pueden ser excitadas artificialmente sin problemas significativos, resulta preferible el análisis modal tradicional. La ventaja de emplear una excitación artificial es que hay más procedimientos para identificar los parámetros y características de los sistemas, con mayor precisión en la identificación de ciertas magnitudes, como en el caso de los coeficientes de amortiguamiento.
Sin embargo, las ventajas mencionadas previamente para el análisis modal operacional, se transforman en inconvenientes en su aplicación a través del método de cambio de masa, a ciertos tipos de estructuras civiles, como por ejemplo los puentes. Ya que para su realización es necesario interrumpir el tráfico rodado para las sucesivas operaciones de modificación de masa (generalmente mas de una) y posterior medición.
Además los valores del amortiguamiento que se obtienen con el análisis modal operacional, presentan una incertidumbre alta, ya que dependen de los parámetros de la identificación especialmente del nivel de excitación de la estructura. Por lo que los métodos del análisis modal clásico ofrecen unos resultados más fiables.
La principal aportación del presente estudio, es abrir una vía de trabajo que permita verificar como los parámetros modales obtenidos por:
- 1)
Un análisis modal tradicional, acompañados de simulaciones numéricas de la modificación de masa.
frente a:
- 2)
Los conseguidos del análisis modal operacional, conjuntamente con el método de modificación de masa.
permiten obtener unos resultados más óptimos y con un rango de error menor, incluso con la presencia de un alto nivel de ruido en la señal.
En este trabajo, se analiza esta cuestión desde un punto de vista práctico. Para ello se ha modelizado un puente -singular por su esbeltez- y sometido el mismo a una serie de simulaciones numéricas. El desarrollo de un diseño con un nuevo esquema estructural, complicadas geometrías y el empleo de nuevos materiales, como son los aceros de alto límite elástico, ha dado lugar a una estructura esbelta, ligera y poco amortiguada. En algunas ocasiones, durante el periodo de vida útil de este tipo de puentes experimentan elevados niveles de vibración, que suelen afectar al estado de servicio, y raramente comprometen la seguridad. El objeto de este análisis, es conocer de la forma más fiable posible, los parámetros modales de la estructura, y su alteración con la modificación de masa.
2Aplicación de técnicas de optimización para la determinación de parámetros modales por el método de identificaciónEn Villa [26–28], se abrió un nuevo camino para la resolución -a través de métodos de optimización y particularmente del programa GAMS- del problema inverso en análisis modal, que permite determinar el modelo modal a partir de la respuesta del sistema, mediante la aplicación de técnicas de optimización -a través de las FRF- para la determinación de parámetros modales por el método de identificación, que se ciñen exclusivamente a: sistemas con amortiguamiento histerético o estructural, niveles de amortiguamiento bajos, y métodos que trabajan en el dominio de la frecuencia.
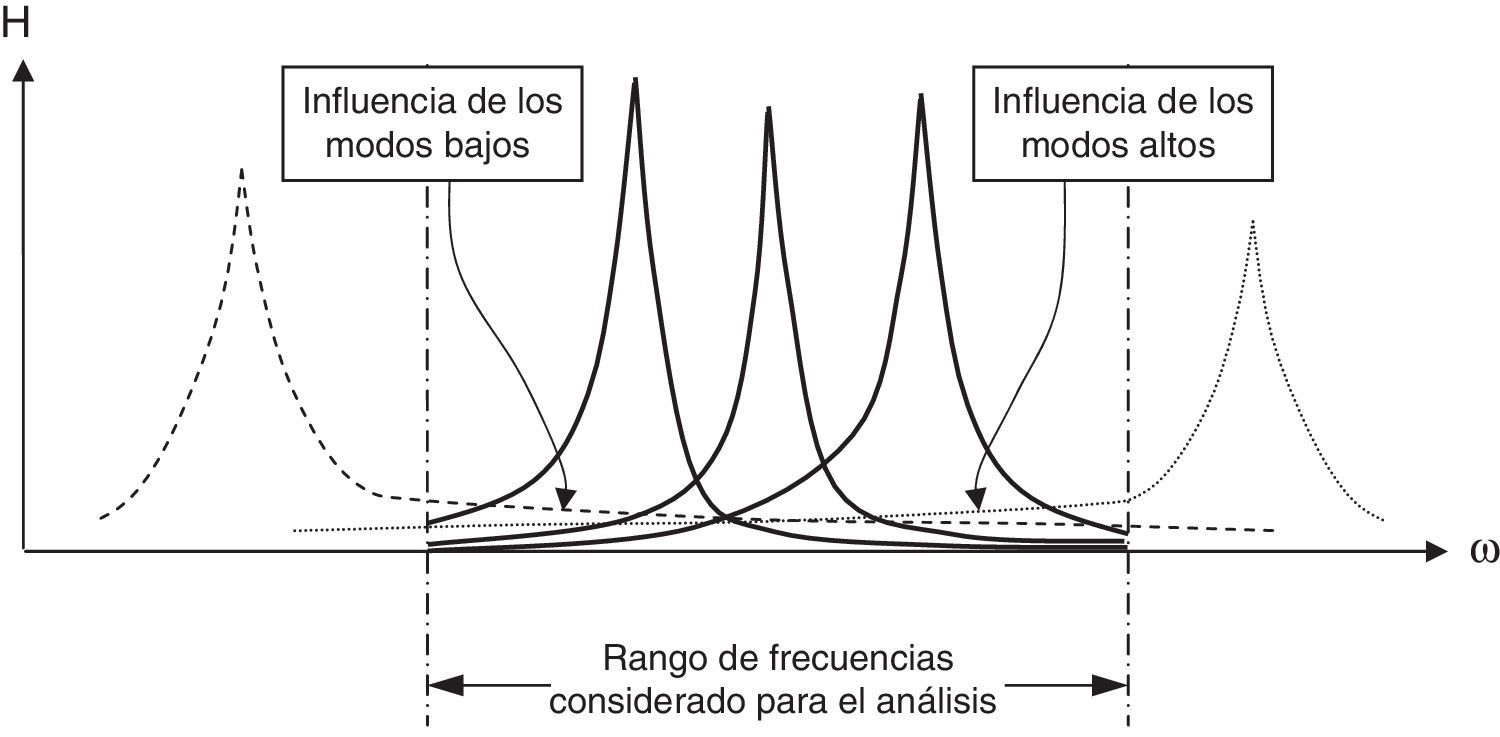
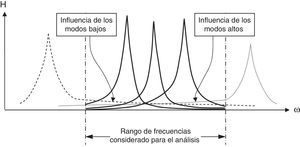
Asimismo en [26–28], se propusieron técnicas de descomposición para trabajar con magnitudes complejas, que permiten tratar separadamente la parte real e imaginaria. En modelos incompletos, se tiene en cuenta la influencia de los modos altos y bajos de forma rigurosa, a través del mismo algoritmo de optimización, que se encarga de ajustar la solución mediante complementos residuales móviles, tanto para los modos altos y bajos, como para la parte real y compleja de los modos por separado. Esto tiene un interés práctico, dado que el análisis se centra en un rango de frecuencias determinado (fig. 1), e incluso, en ocasiones dicho rango se encuentra condicionado por las limitaciones de los sensores de captación y/o del equipo analizador.
Con todo lo anterior, es posible modificar las propiedades inerciales del sistema [Δm], e incluir ruido en la señal para identificar los nuevos parámetros modales del sistema, y analizar los resultados obtenidos frente a un análisis modal operacional acompañado del método de cambio de masa.
3Modificación de la matriz FRF por la alteración de las propiedades inerciales del sistemaEn [29], se analiza el problema de la determinación de los nuevos parámetros modales de un sistema dinámico después de realizar modificaciones al mismo a través de dos vías: a partir del modelo modal, y del modelo de respuesta.
A partir del primero muestra cómo se pueden obtener las nuevas frecuencias naturales y modos de vibración de la estructura modificada siempre y cuando la matriz de modificación de masa [Δm], así como los parámetros modales originales: ω0, η0, Φ0 (frecuencias naturales, factores de amortiguamiento y matriz de modos de vibración complejos de la estructura sin modificar) son conocidos. Por lo que no es necesario el conocimiento de las matrices de masa, rigidez y amortiguamiento de la estructura original.
El orden del problema es igual al número de modos utilizados en el sistema original. Si coinciden, los nuevos parámetros modales son determinados exactamente. En cambio, si el número de modos usados en el problema modificado es menor, los nuevos parámetros modales son solo aproximados debido al efecto de truncamiento. Esta última es la situación más frecuente, ya que no es posible identificar el conjunto completo de parámetros modales de un sistema continuo, solo los incluidos en un determinado ancho de banda (en sistemas continuos el número de grados de libertad es infinito). Por tanto el truncamiento de modos es una fuente de error en la evaluación de los parámetros modales de la estructura modificada.
Mientras que, según el segundo, la relación entre fuerzas y desplazamientos en el dominio de la frecuencia viene dada por
en donde X0ω es la respuesta del sistema que se relaciona a través de la matriz FRF H0ω original del sistema, con la excitación externa Fω actuando en los g.d.l. considerados.Las modificaciones realizadas a la estructura se pueden describir mediante la matriz ΔBω de modificación de la rigidez dinámica [30]
Debe hacerse notar que si las modificaciones que se realizan a la estructura solo afectan a las propiedades inerciales (es decir no a la rigidez o amortiguamiento, solo a la masa) la expresión anterior es válida para los casos de amortiguamiento viscoso, y estructural o histerético [30].
En [29], se indica como predecir la respuesta del sistema Hω desde el conocimiento de la matriz FRF de la estructura sin modificar H0ω, y de las modificaciones inerciales ΔBω previstas en la misma
siendo I la matriz identidad.De esta forma, se puede predecir la respuesta del sistema desde el conocimiento de la matriz FRF de la estructura sin modificar y de las modificaciones inerciales previstas en la misma. Para datos obtenidos experimentalmente, las frecuencias representan un conjunto discreto de magnitudes. Esta operación debe ser repetida para todas las frecuencias de interés; lo cual representa una tercera dimensión de las matrices.
Esta última expresión con respecto a la establecida inicialmente en [29], presenta algunas características más favorables, como son:
- •
Solo es necesario realizar un única inversión de matriz.
- •
Es poco probable que dicha matriz esté mal condicionada, debido a su propia tipología, como suma de dos matrices: debido al comportamiento favorable de la matriz I con respecto a la operación de inversión, dado que el peso del segundo sumando es reducido, esto es, consta de la matriz FRF original por el producto de unas modificaciones pequeñas en comparación a la totalidad de la estructura [31].
Una alternativa para identificar posiciones favorables de el/los sensor/es de referencia -para cierto/s modo/s de interés- consiste en localizar filas de la matriz modal en las que los desplazamientos correspondientes a ese grado de libertad, en el/los modo/s que se pretenden identificar, sean lo mayores posibles. A este respecto, un análisis previo por elementos finitos de los modos de vibración de la estructura que se desea analizar experimentalmente, permite dar una primera idea de los modos de interés, de los grados de libertad para definir los mismos, así como de los conjuntos de datos necesarios y la ubicación y número de sensores de referencia, para que todas las direcciones medidas queden bien representadas en todos los conjuntos de datos.
Por otro lado, una vez determinados los parámetros modales experimentales reales de la estructura, y al objeto de realizar el/los ensayo/s posterior/es con la masa modificada, es conveniente determinar una estimación de la distribución de masa en la estructura, antes de efectuar los mismos. Su conocimiento, a la hora de efectuar la modificación de masa, permitiría que todos los grados de libertad afectados por ella, tuviesen un cambio de masa relativo muy similar, con el fin de reducir los errores introducidos por los cambios en los modos de vibración.
Ya más en concreto en lo que se refiere a puentes en viga cajón metálicos, la tipología de estos, consta de un sistema estructural de viga cajón continua asimétrica, totalmente metálica, cuyo canto, a su vez puede ser variable.
Los puentes pertenecientes a esta familia, transversalmente están formados por un cajón de forma trapecial cuya anchura superior comprende toda o parte de la del tablero, una altura de alma variable -si su canto no es constante- y un ancho constante del ala inferior. De este cajón trapecial, habitualmente se complementa mediante ménsulas, el ala superior, hasta alcanzar el ancho total del tablero. En resumen, se pueden definir como viga cajón de tablero ortótropo.
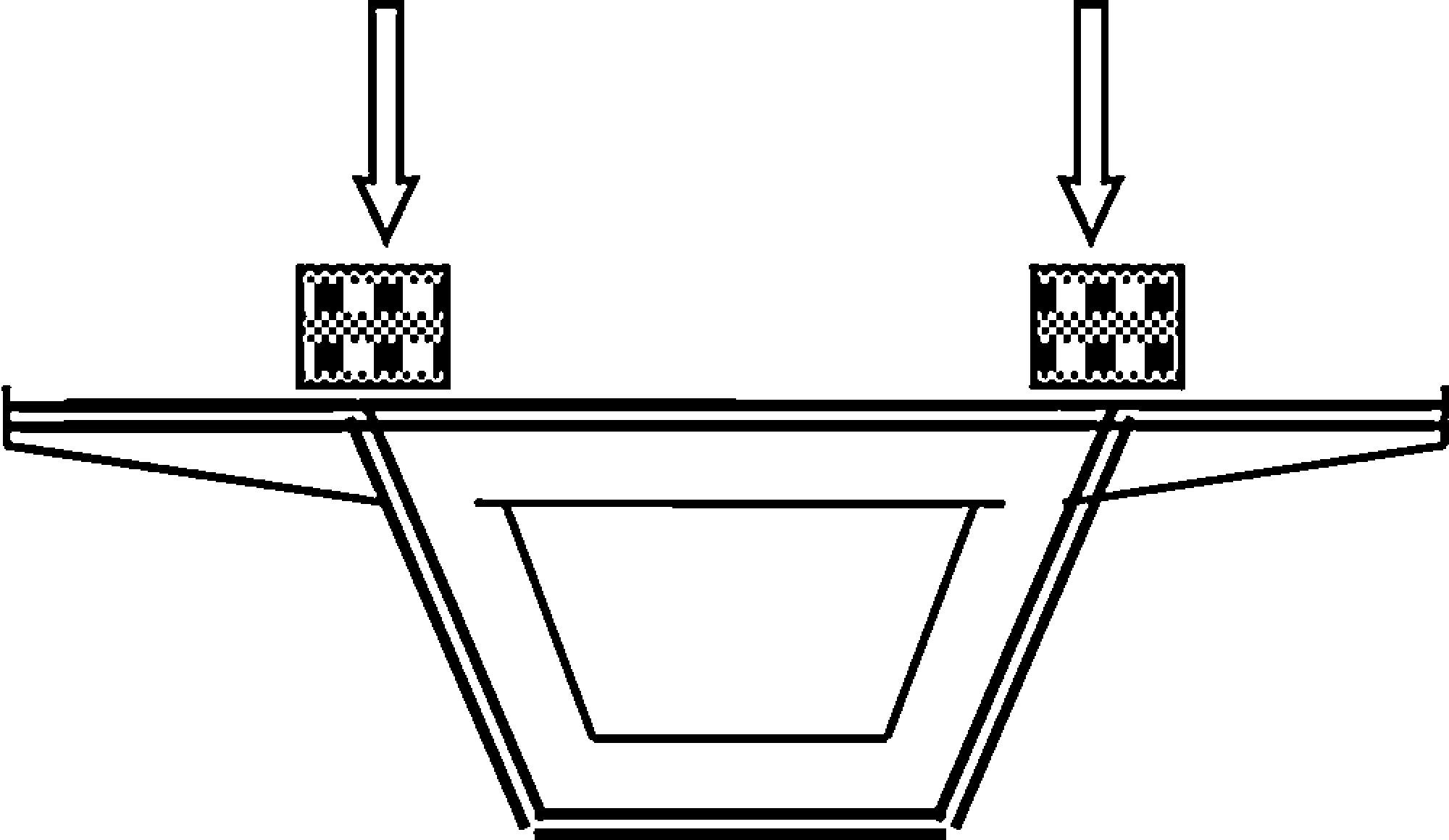
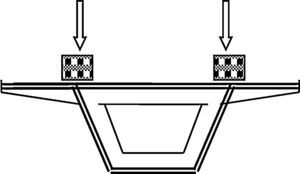
Así mismo, es conveniente situar los bloques (masas puntuales para la modificación de masa), en los puntos más rígidos de las secciones transversales, que, en general, se corresponden con los vértices superiores del trapecio, y especialmente en aquéllas en las que coincide un marco de rigidización transversal (fig. 2), con el fin de evitar la influencia de las oscilaciones locales de los elementos del tablero en la respuesta total.
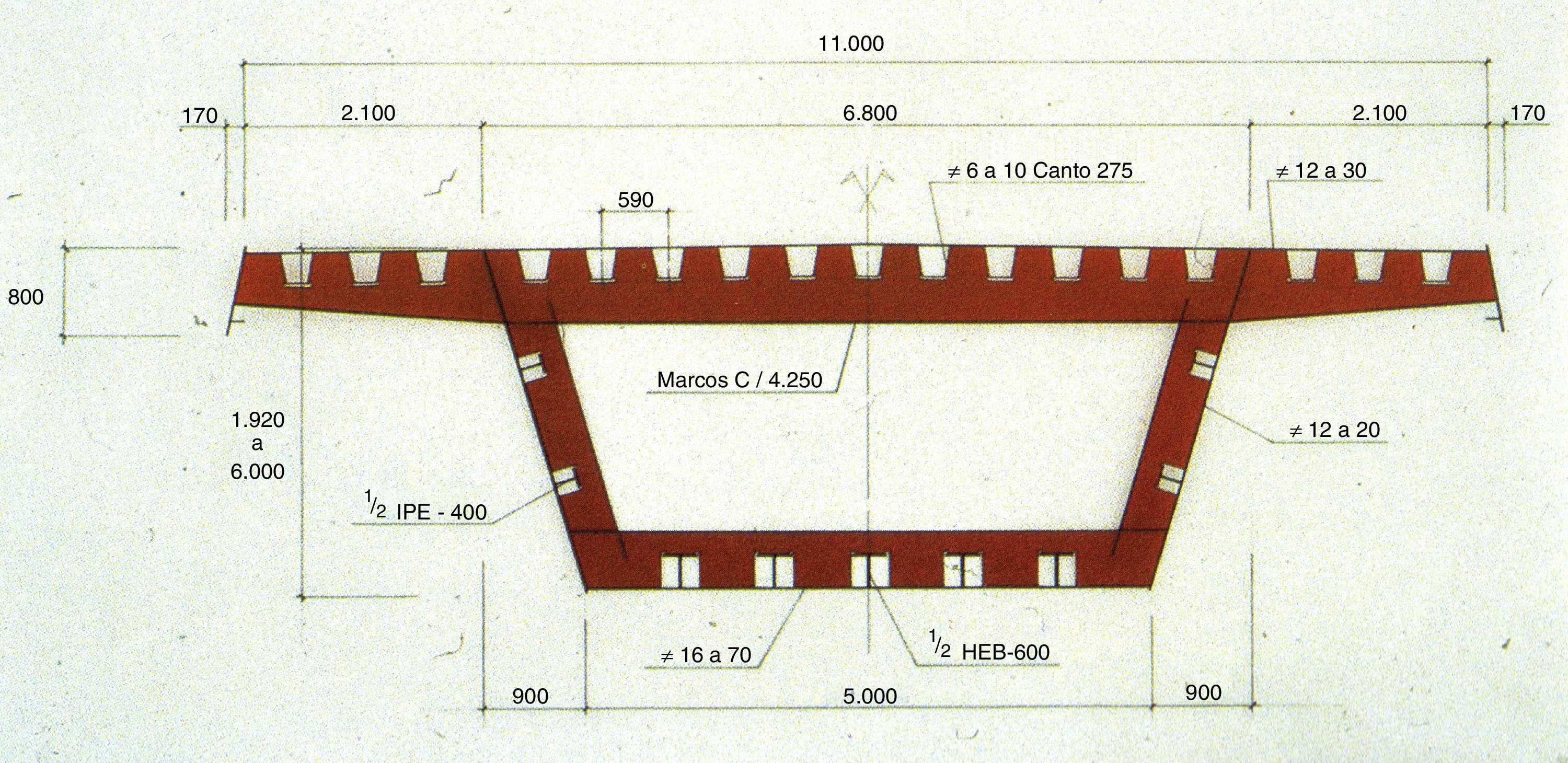
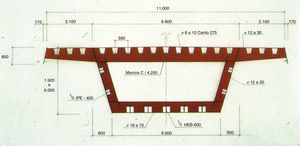
5Características del puente analizadoEl puente de La Cartuja, analizado en este trabajo, está ubicado en el Meandro de San Jerónimo, en Sevilla, sobre el río Guadalquivir [32,33], se trata de un puente de tipo viga cajón continua de sección variable, con tablero ortótropo, totalmente metálico, que respeta la visibilidad del entorno mediante una estructura discreta y elegante.
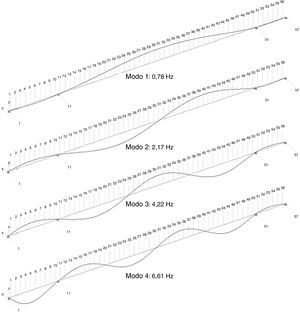
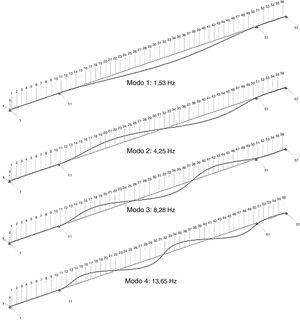
Consta de 3 vanos, con una longitud total de 238 m: 42.5 m en el vano lado Expo, 170 m en el vano central, y 25.5m en el vano lado Sevilla. La viga cajón o viga principal del puente, está rigidizada mediante marcos de rigidización transversal cada 4.25 m, los cuales dividen el puente en 56 módulos. El peso acabado del puente es de 1869 t, equivalente a 714 kp/m2 (figs. 3 y 4).
El ancho del tablero es de 11 m y el canto de la viga variable: desde los 1.92m del estribo lado Expo que aumenta progresivamente hasta llegar a los 6 m en la pila del mismo margen, para disminuir hasta alcanzar los 3 m manteniéndose prácticamente constante en buena parte del vano central y vano lateral lado Sevilla; lo cual representa una relación luz/canto de 56.6: este valor en su día fue el menor registrado en un puente, por lo que se convirtió en el puente más esbelto del mundo. Haciendo gala de una elegancia inédita hasta entonces. Figura desde el año 2007 en el Libro Guinnes de los records.
La continuidad de la viga del puente en los tres vanos, permite alcanzar esta esbeltez, gracias a los vanos laterales relativamente cortos y a las ménsulas ubicadas en el tablero y en los estribos, a través de los cuales se trasmiten reacciones negativas (fig. 3).
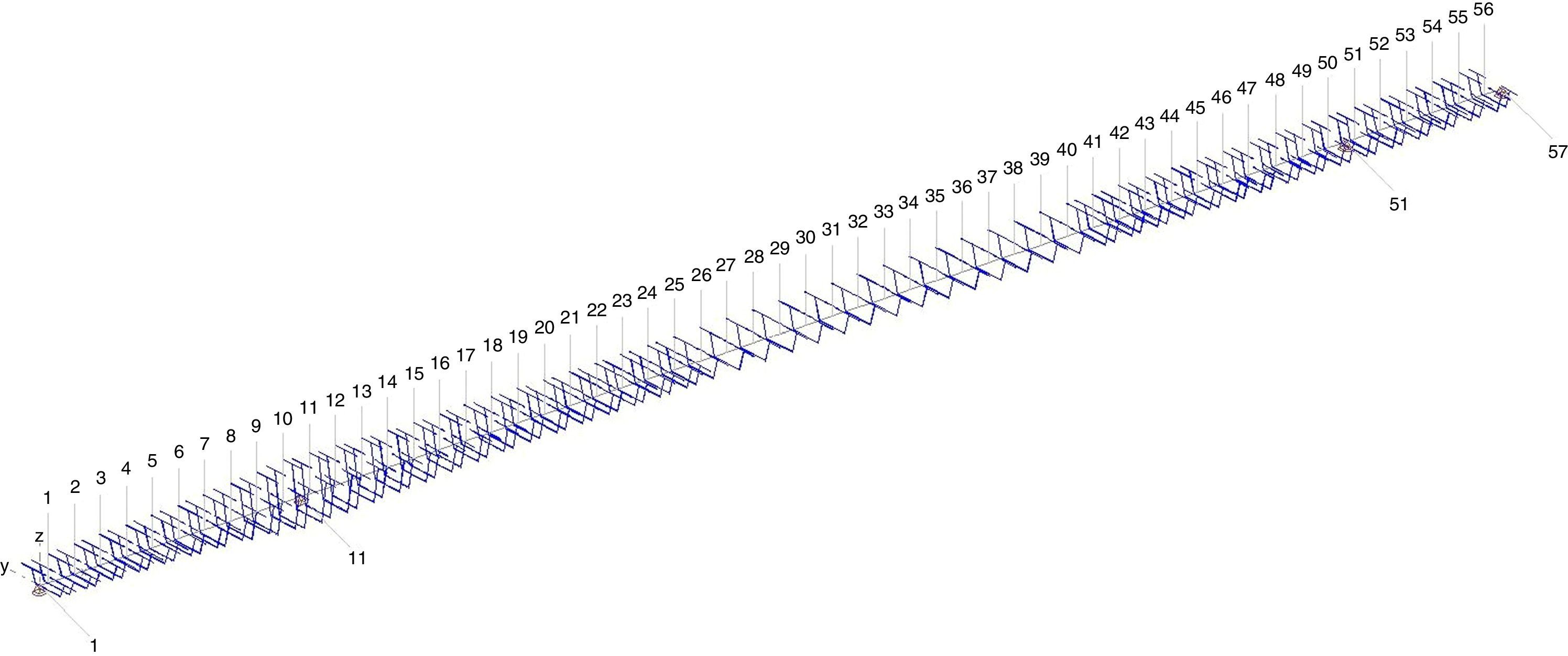
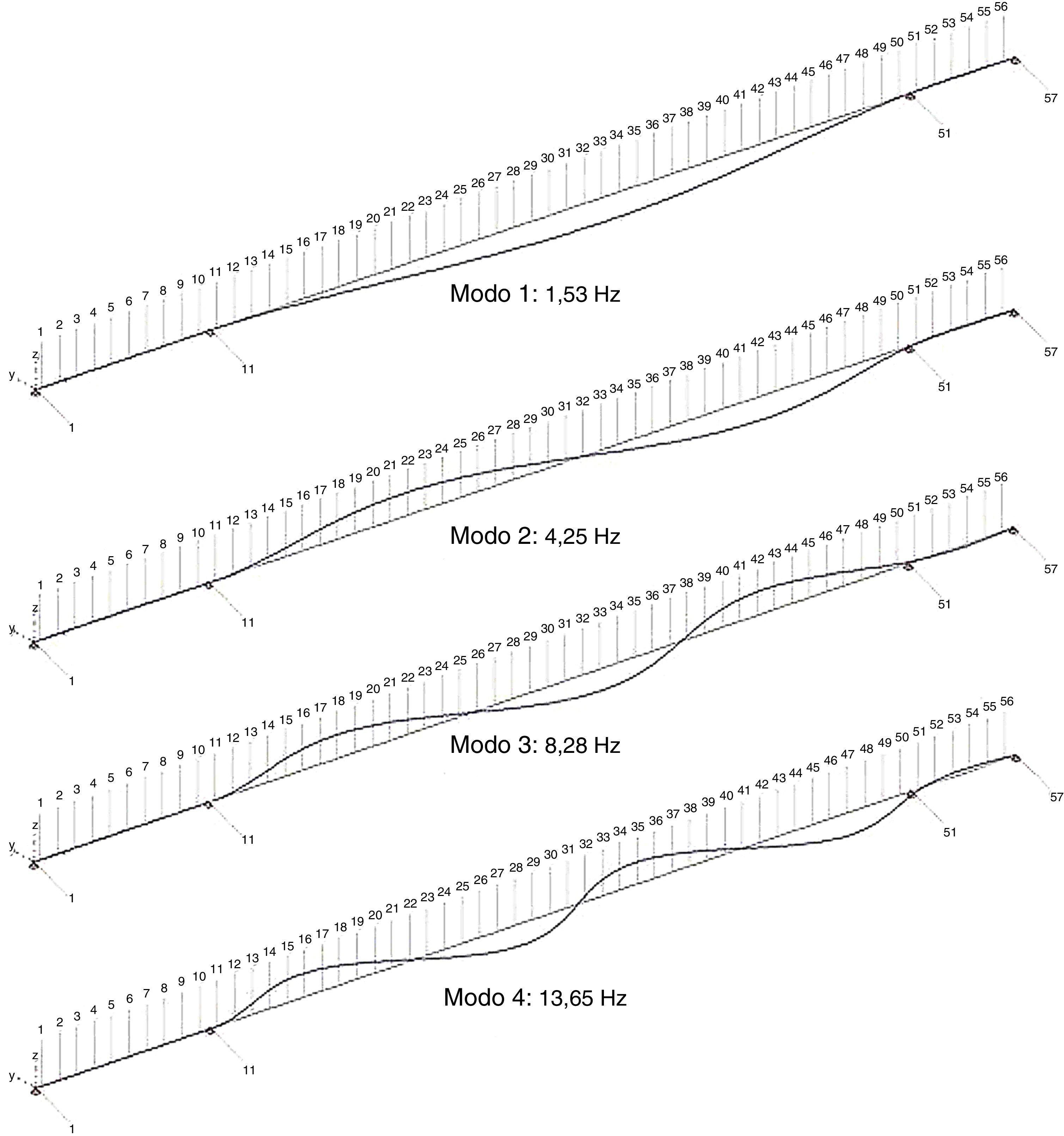
6Análisis de resultadosA continuación se muestran los resultados obtenidos para el Puente de la Cartuja, modelizado mediante 56 tramos de 4.25 m cada uno (fig. 5), utilizando la metodología de cálculo referenciada en el apartado 2.
Para simular ruido en el modelo de respuesta, que aquí se simula numéricamente, se añade un ruido blanco a la matriz de las FRF, de la siguiente manera [28]
donde H es la matriz que contiene los datos usados para la identificación, Ep es el nivel de ruido (del 3, 9 y 15%), y Nruido es una distribución normal estándar, con un valor medio de 0 y una desviación típica de 1, es decir N(0,1). Nótese que este ruido blanco afecta tanto a la parte real como a la imaginaria de los valores de la matriz FRF.La desviación de los factores de escala estimados αest, con respecto a los teóricos αteor, se calcula mediante la expresión
En la modelización del esqueleto resistente del Puente de la Cartuja, se ha tenido en cuenta el efecto del arrastre del esfuerzo cortante en las diferentes secciones transversales (fig. 5).
Se han realizado dos análisis dinámicos, en primer lugar, considerando la estructura descargada, y posteriormente con la estructura del puente sometido a un incremento de masa del 5%. Este incremento de masa se aplica mediante masas puntuales sobre la directriz del tablero. La modificación de masa es de un 5%, pero su valor en los diferentes tramos no es constante, ya que al ser la viga de canto variable, su masa varía de igual forma. Con dicha modificación inercial, se alcanza una desviación de frecuencia del 2.41% más que razonable.
Desde el modelo espacial, resolviendo el problema característico de autovalores y autovectores, se obtienen los datos de partida (ω0,η0,Φ0: modelo modal de la estructura sin modificar) para alimentar el algoritmo de optimización [26,27].
En la figura 6, a modo de ejemplo gráfico -y al objeto de evitar ocupar un espacio excesivo- se representa, en el dominio de la frecuencia, la FRF H3,3 (ω), es decir, la componente (3,3) de la matriz de funciones de respuesta en frecuencia [H(ω)].
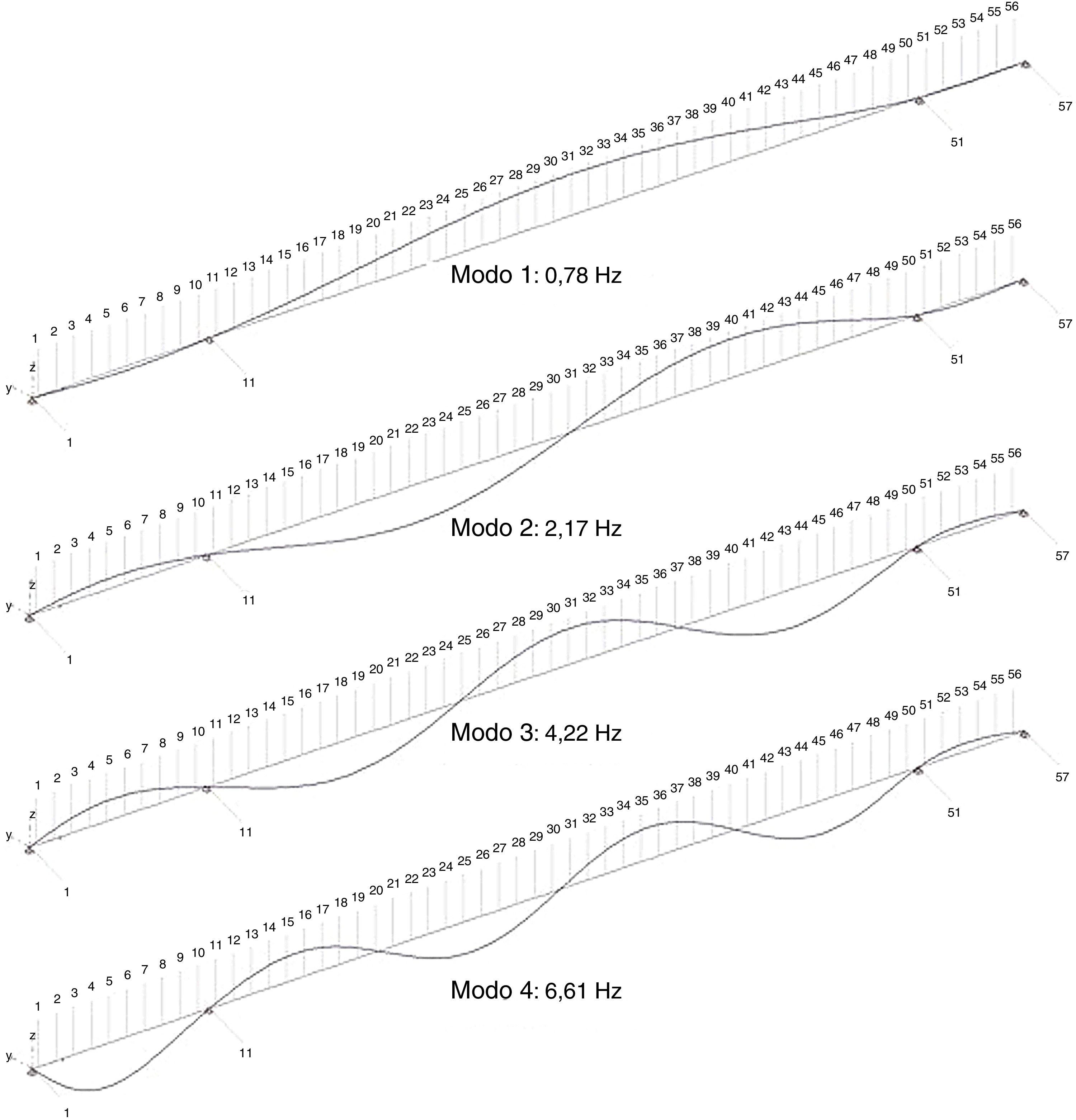
Se han identificado los 6 primeros modos en flexión vertical y los 4 primeros modos en flexión horizontal (figs. 7 y 8). La viga cajón del puente presenta un momento de inercia en el plano vertical mucho mayor, mientras que las cargas son menores; y por tanto su sensibilidad a oscilación horizontal es menor.
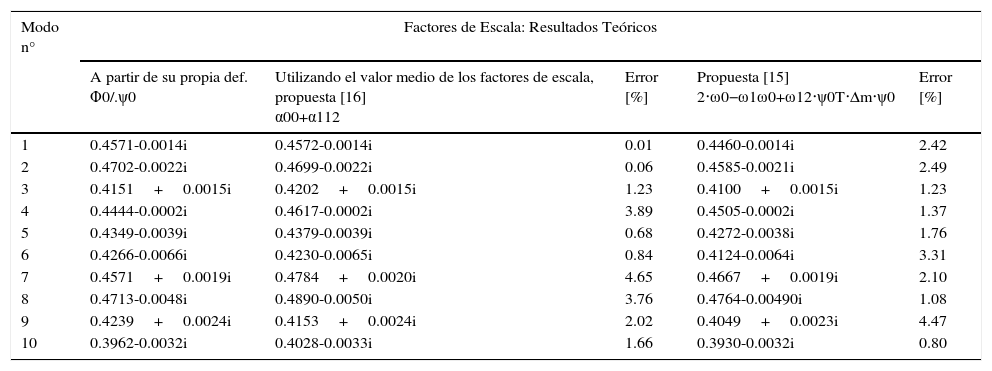
En la tabla 1 se muestran los resultados teóricos para los factores de escala, que se obtienen para los 10 primeros modos de oscilación (flexión vertical y horizontal) del sistema estructural, obtenidos a partir de su propia definición (como cociente -componente a componente- entre la matriz modal normalizada respecto de la masa y esta misma sin normalizar). Así como los alcanzados -con una modificación de masa del 5%-, a través de las expresiones propuestas en [16] (en este caso, se utiliza el valor medio de los modos no modificados y modificados, en la expresión para el cálculo de los factores de escala) y [15], junto con los errores cometidos en cada uno de ellos frente a los primeros.
Factores de escala, resultados teóricos para los 10 modos de vibración identificados
| Modo n° | Factores de Escala: Resultados Teóricos | ||||
|---|---|---|---|---|---|
| A partir de su propia def. Φ0/.ψ0 | Utilizando el valor medio de los factores de escala, propuesta [16] α00+α112 | Error [%] | Propuesta [15] 2⋅ω0−ω1ω0+ω12⋅ψ0T⋅Δm⋅ψ0 | Error [%] | |
| 1 | 0.4571-0.0014i | 0.4572-0.0014i | 0.01 | 0.4460-0.0014i | 2.42 |
| 2 | 0.4702-0.0022i | 0.4699-0.0022i | 0.06 | 0.4585-0.0021i | 2.49 |
| 3 | 0.4151+0.0015i | 0.4202+0.0015i | 1.23 | 0.4100+0.0015i | 1.23 |
| 4 | 0.4444-0.0002i | 0.4617-0.0002i | 3.89 | 0.4505-0.0002i | 1.37 |
| 5 | 0.4349-0.0039i | 0.4379-0.0039i | 0.68 | 0.4272-0.0038i | 1.76 |
| 6 | 0.4266-0.0066i | 0.4230-0.0065i | 0.84 | 0.4124-0.0064i | 3.31 |
| 7 | 0.4571+0.0019i | 0.4784+0.0020i | 4.65 | 0.4667+0.0019i | 2.10 |
| 8 | 0.4713-0.0048i | 0.4890-0.0050i | 3.76 | 0.4764-0.00490i | 1.08 |
| 9 | 0.4239+0.0024i | 0.4153+0.0024i | 2.02 | 0.4049+0.0023i | 4.47 |
| 10 | 0.3962-0.0032i | 0.4028-0.0033i | 1.66 | 0.3930-0.0032i | 0.80 |
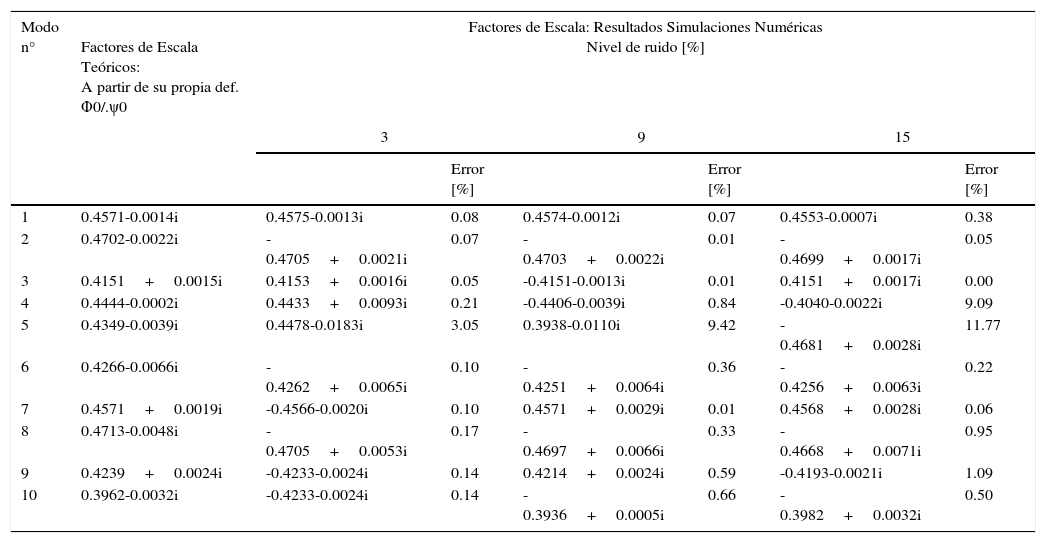
Para diferentes niveles de ruido en la señal, en la tabla 2 se exponen los resultados obtenidos para los factores de escala, desde el modelo de respuesta, aplicando el procedimiento de optimización descrito en [26–28]; así como el porcentaje de error cometido frente a los teóricos.
Resultados de las simulaciones numéricas con diferentes niveles de ruido
| Modo n° | Factores de Escala Teóricos: A partir de su propia def. Φ0/.ψ0 | Factores de Escala: Resultados Simulaciones Numéricas Nivel de ruido [%] | |||||
|---|---|---|---|---|---|---|---|
| 3 | 9 | 15 | |||||
| Error [%] | Error [%] | Error [%] | |||||
| 1 | 0.4571-0.0014i | 0.4575-0.0013i | 0.08 | 0.4574-0.0012i | 0.07 | 0.4553-0.0007i | 0.38 |
| 2 | 0.4702-0.0022i | -0.4705+0.0021i | 0.07 | -0.4703+0.0022i | 0.01 | -0.4699+0.0017i | 0.05 |
| 3 | 0.4151+0.0015i | 0.4153+0.0016i | 0.05 | -0.4151-0.0013i | 0.01 | 0.4151+0.0017i | 0.00 |
| 4 | 0.4444-0.0002i | 0.4433+0.0093i | 0.21 | -0.4406-0.0039i | 0.84 | -0.4040-0.0022i | 9.09 |
| 5 | 0.4349-0.0039i | 0.4478-0.0183i | 3.05 | 0.3938-0.0110i | 9.42 | -0.4681+0.0028i | 11.77 |
| 6 | 0.4266-0.0066i | -0.4262+0.0065i | 0.10 | -0.4251+0.0064i | 0.36 | -0.4256+0.0063i | 0.22 |
| 7 | 0.4571+0.0019i | -0.4566-0.0020i | 0.10 | 0.4571+0.0029i | 0.01 | 0.4568+0.0028i | 0.06 |
| 8 | 0.4713-0.0048i | -0.4705+0.0053i | 0.17 | -0.4697+0.0066i | 0.33 | -0.4668+0.0071i | 0.95 |
| 9 | 0.4239+0.0024i | -0.4233-0.0024i | 0.14 | 0.4214+0.0024i | 0.59 | -0.4193-0.0021i | 1.09 |
| 10 | 0.3962-0.0032i | -0.4233-0.0024i | 0.14 | -0.3936+0.0005i | 0.66 | -0.3982+0.0032i | 0.50 |
En el caso de los autovectores, al objeto de valorar la precisión, resulta interesante comparar el grupo de modos de vibración identificados, con los que se pueden alcanzar teóricamente; a este respecto, es más preferible una representación numérica -por ser más objetiva y más fácilmente contrastable- que su análoga gráfica.
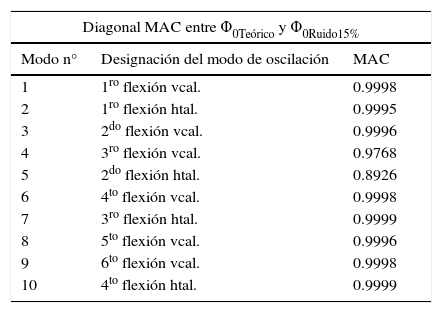
Finalmente, en la tabla 3, se indican los resultados de la diagonal de la matriz MAC (Modal Assurance Criterion) entre la matriz modal Φ0Teórico (del sistema no modificado), y la misma, obtenida a través de una simulación numérica con un nivel de ruido del 15%.
Diagonal MAC entre la matriz modal Φ0Teórico (del sistema no modificado), y la misma, obtenida a través de una simulación numérica con un nivel de ruido del 15%
| Diagonal MAC entre Φ0Teórico y Φ0Ruido15% | ||
|---|---|---|
| Modo n° | Designación del modo de oscilación | MAC |
| 1 | 1ro flexión vcal. | 0.9998 |
| 2 | 1ro flexión htal. | 0.9995 |
| 3 | 2do flexión vcal. | 0.9996 |
| 4 | 3ro flexión vcal. | 0.9768 |
| 5 | 2do flexión htal. | 0.8926 |
| 6 | 4to flexión vcal. | 0.9998 |
| 7 | 3ro flexión htal. | 0.9999 |
| 8 | 5to flexión vcal. | 0.9996 |
| 9 | 6to flexión vcal. | 0.9998 |
| 10 | 4to flexión htal. | 0.9999 |
Los valores de la tabla 3, permiten apreciar que ambos conjuntos de modos se corresponden perfectamente entre sí; este hecho se demuestra cuantitativamente por medio de las magnitudes de la matriz MAC, con valores de la diagonal principal que alcanzan el valor unidad, lo cual pone de manifiesto que el modelo está bien calibrado.
7ConclusionesDebido a los efectos de truncamiento, el análisis dinámico de la modificación de las propiedades inerciales de una estructura a través del modelo modal, presenta más limitaciones que el proceso de optimización de las funciones de respuesta en frecuencia.
A través de las simulaciones numéricas efectuadas, se hace notorio que la determinación de parámetros modales (modos de vibración normalizados según la masa), resulta más satisfactoria empleando análisis modal tradicional, en lugar de las novedosas técnicas que se derivan de utilizar modificación de masa acompañada del análisis modal operacional.
En cuanto al error cometido, la metodología propuesta es mucho más estable, frente a la presencia de un alto nivel de ruido en la señal.
Especialmente, en las grandes obras civiles como los puentes y viaductos (hasta cierto tamaño, siempre que el mismo permita que sean excitados artificialmente con un nivel adecuado); una de las ventajas del análisis modal operacional, radica en la posibilidad de no interrumpir el tráfico que se desplaza por los mismos. Sin embargo, cuando se realiza la modificación de masa, sí que es necesario interrumpir la circulación, con un tiempo y coste en general mayores que los correspondientes a un ensayo dinámico tradicional. Así como, con una exactitud en los resultados menor.
Por otra parte, si se pretende realizar una estimación de la masa modal, para ajustar un amortiguador de masa sintonizado, la mejor opción es el ajuste de funciones de respuesta en frecuencia obtenidas experimentalmente, mediante un análisis modal tradicional.




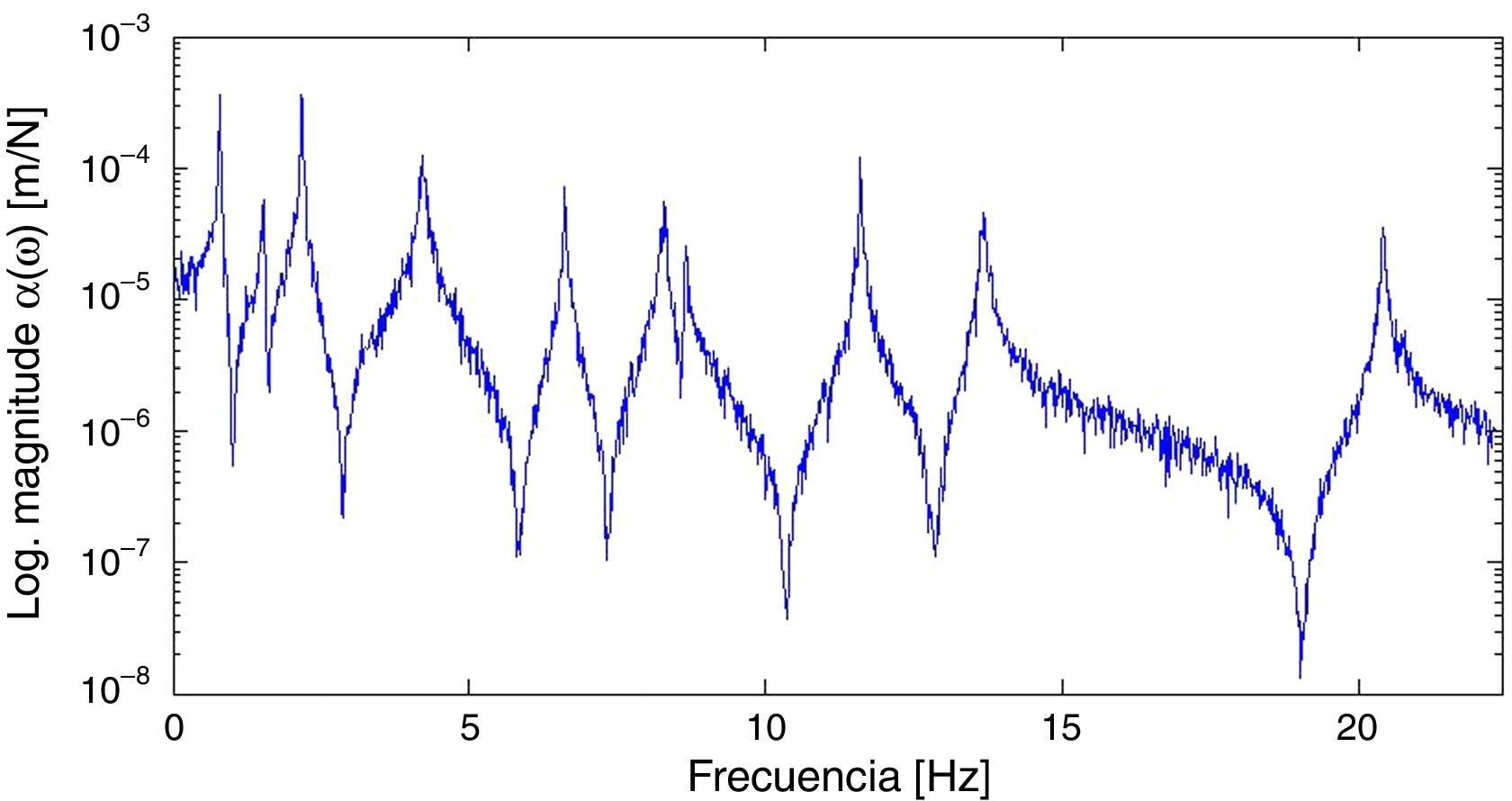
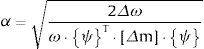
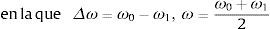
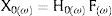

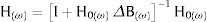


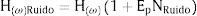
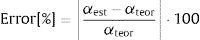
![Componente (3,3) de la matriz de funciones de respuesta en frecuencia [H(ω)]: H3,3(ω), con un nivel de ruido en la señal del 22%. Componente (3,3) de la matriz de funciones de respuesta en frecuencia [H(ω)]: H3,3(ω), con un nivel de ruido en la señal del 22%.](https://static.elsevier.es/multimedia/02131315/0000003300000034/v1_201705221028/S0213131516300086/v1_201705221028/es/main.assets/thumbnail/gr6.jpeg?xkr=ue/ImdikoIMrsJoerZ+w96p5LBcBpyJTqfwgorxm+Ow=)