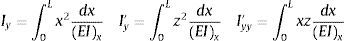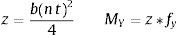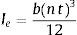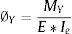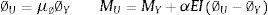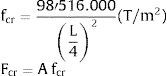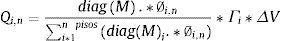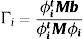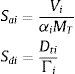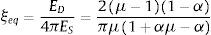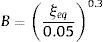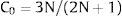Análisis de una estructura con disipadores sometidos a espectros de diseño y de control

Resumen

Las estructuras de Quito, Ecuador, son diseñadas para el espectro de la norma ecuatoriana de 2015, o para el hallado en la microzonificación de la ciudad de 2012. Estos espectros consideran en forma macro las fallas ciegas inversas sobre las que se halla la ciudad. En este artículo se destaca la importancia de verificar el diseño para los espectros de control que fueron desarrollados mediante métodos determinísticos para Quito en el 2015, los mismos que consideran la generación de sismos en las fallas ciegas.

En el artículo se presentan dos modelos de plasticidad extendida para los elementos estructurales y un modelo de plasticidad para los disipadores ADAS o TADAS. Luego se indica con cierto detalle la técnica del pushover multimodal y el método del espectro de capacidad con el cual se halla el punto de capacidad de una estructura que fue inicialmente calculada para los espectros de diseño. Dicha estructura ha sido reforzada con disipadores ADAS para que no colapse ante el espectro de control que tiene ordenadas más altas que el espectro de diseño.

Abstract

The structures of Quito, Ecuador, are designed for the spectrum of the Ecuadorian code of 2015, or using the study of microzoning of the city of 2012. These spectra consider in general the effect of the blind reverse faults belonging to the city area. In this article, it is pointed out the importance of checking the design for the deterministic control spectra developed for Quito in 2015 based on earthquakes simulated in the blinds faults.

In this paper we considered two models of extended plasticity for the structural elements and one model of plasticity for the ADAS and TADAS devices. Then, the technique of multimodal pushover is described, as well as the method of the capacity spectrum used to calculate the performance point of the structure. This structure was initially calculated by using design spectra and it had to be reinforced with ADAS devices in order to avoid its collapse for the control spectrum which has higher ordinates than the design one.

1

Introducción

Una buena parte de las estructuras de la ciudad de Quito, son diseñadas utilizando el espectro de la Norma Ecuatoriana de la Construcción de 2015 (NEC 2015) [1], cuyos factores de sitio, son muy generales, razón por la cual, otra parte de los proyectistas estructurales utilizan los espectros obtenidos en el estudio de la microzonificación sísmica de Quito, realizada por el grupo consultor ERN (Evaluación de Riesgos Naturales en América Latina) en el 2012. La fortaleza del trabajo realizado por ERN (2012) [2] radica en la determinación de factores de sitio para los suelos de la ciudad, basados en estudios estáticos y dinámicos, con profundidades que están entre 30 y 40 m. Los factores de sitio encontrados fueron normalizados de tal forma que puedan ser utilizados con las ecuaciones que definen las diferentes ramas del espectro la Norma del 2011 (NEC 2011) [3,4].

Por otra parte, los estudios de peligrosidad sísmica, para encontrar los espectros del NEC-11 y NEC-15, fueron realizados en forma probabilista considerando grandes volúmenes de litosfera como zonas fuentes. A estos espectros y a los hallados por ERN (2012) se les denomina, en este artículo, espectros de diseño.

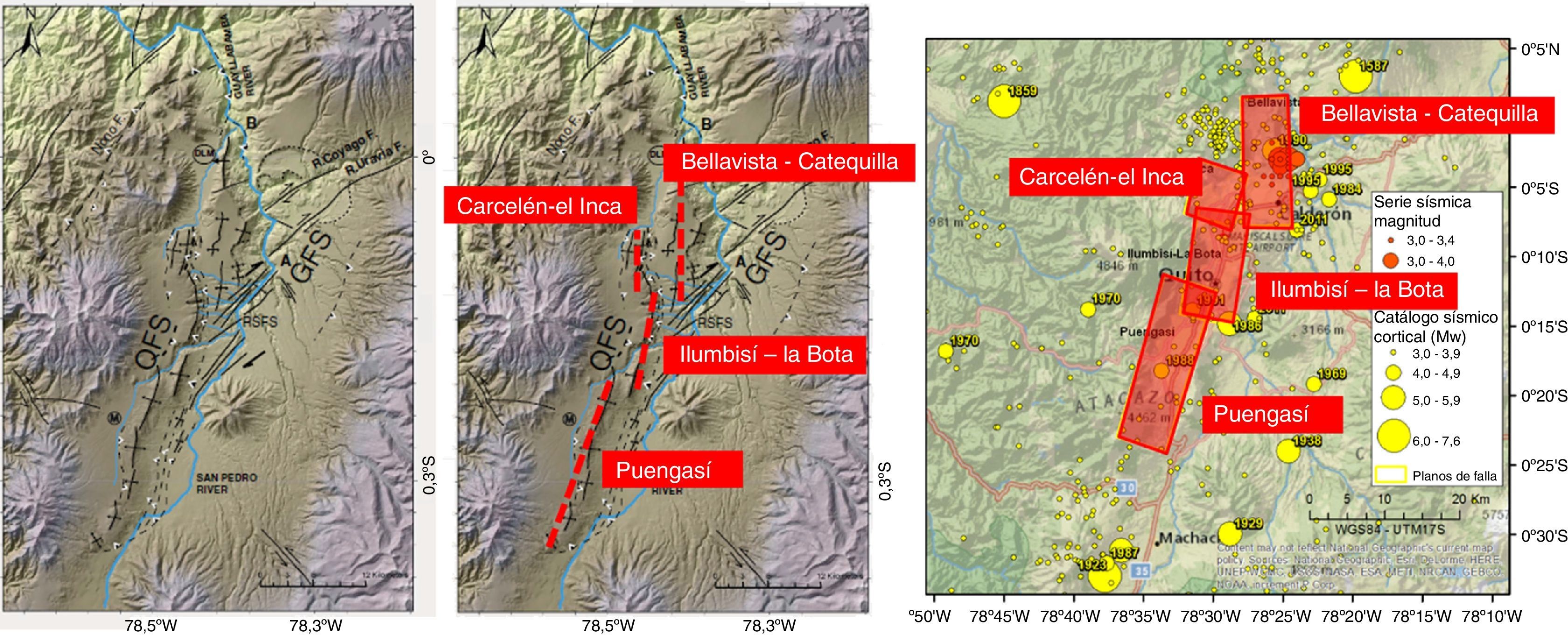
Una buena parte de la ciudad se halla sobre las fallas ciegas inversas de Quito y el resto de la urbe se halla muy cerca de las mismas. Cuatro segmentos han sido ya definidos y son de sur a norte los siguientes: Puengasí, Ilumbisí la Bota, Carcelén el Inca y Bellavista-Catequilla; hay un quinto segmento que se encuentra fuera de la zona norte de la ciudad pero que no va a afectar tanto la peligrosidad sísmica como los otros segmentos, debido a la cercanía a la falla. En la figura 1 se indican estas fallas con el plano de ruptura que podría producirse en caso de un sismo que rompa todo un segmento de las fallas.

Figura 1.

Fallas ciegas de Quito [2].

Por otra parte, se han obtenido espectros de control en forma determinista considerando sismos que se podrían generar en cada segmento de falla y tomando en cuenta el tipo de suelo de la ciudad. [5–7] Para la determinación de los espectros que se han denominado de control, se utilizaron los modelos de movimientos fuertes de Campbell y Borzognia [8], de Abrahanson [9] y de Chiou y Youngs [10] y se hallaron espectros para 50% y 84% de nivel de confianza.

Las estructuras de Quito han sido y son diseñadas para los espectros de diseño antes mencionados y no se consideran (por desconocimiento) los espectros de control, los mismos que tienen ordenadas espectrales más altas, especialmente para las zonas de períodos cortos, si se considera un nivel de confianza del 84%, en la determinación de los espectros de control.

Ahora bien, muchas estructuras de Quito, fueron diseñadas hace más de 30 años, con la normativa sísmica de aquel tiempo y son muy vulnerables, razón por la cual deben ser reforzadas. Una forma de hacerlo es mediante la incorporación de disipadores de energía por plasticidad del material, como los ADAS (Added damping and Stiffness) o TADAS (Triangular plate added damping and stiffness), que se pueden colocar sobre diagonales de acero en forma de «V» invertida. Los disipadores TADAS tienen una forma triangular y los ADAS tienen la forma de un reloj de arena. La geometría de estos dispositivos garantiza que la plastificación se va a dar en toda la sección del elemento, los TADAS por curvatura simple y los ADAS por doble curvatura. [11,12].

En este artículo se analiza una estructura irregular de 5 pisos de hormigón armado la misma que ha sido diseñada con el espectro de diseño ERN (2012) [2], empleando el método de superposición modal. Una vez diseñada, se ha evaluado su comportamiento mediante un análisis no lineal aplicando método del espectro de capacidad, a partir de un pushover multimodal [13,14], en el que se utilizan modelos de plasticidad extendida para los elementos estructurales [15].

Se ha constatado que la estructura colapsa cuando se la somete al sismo de control para 84% de nivel de confianza por lo que se decidió reforzarla mediante la colocación de disipadores de energía ADAS sobre diagonales de acero en forma de «V» con lo que se logra que la estructura no colapse; sin embargo, dicha estructura sufre un daño considerable.

Todo el análisis sísmico se realizó utilizando la librería de programas del sistema de computación CEINCI-LAB[16,17].

2

Modelo para el análisis no lineal

2.1

Modelo con dovelas en vigas y columnas

Se presentan dos modelos de plasticidad extendida para ser aplicados en el pushover multimodal, en los elementos viga y columna de un marco de hormigón armado, dividiendo al elemento en dovelas de longitud variable de acuerdo con la longitud plástica que tienen en cada ciclo de carga.

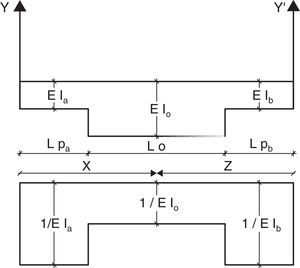
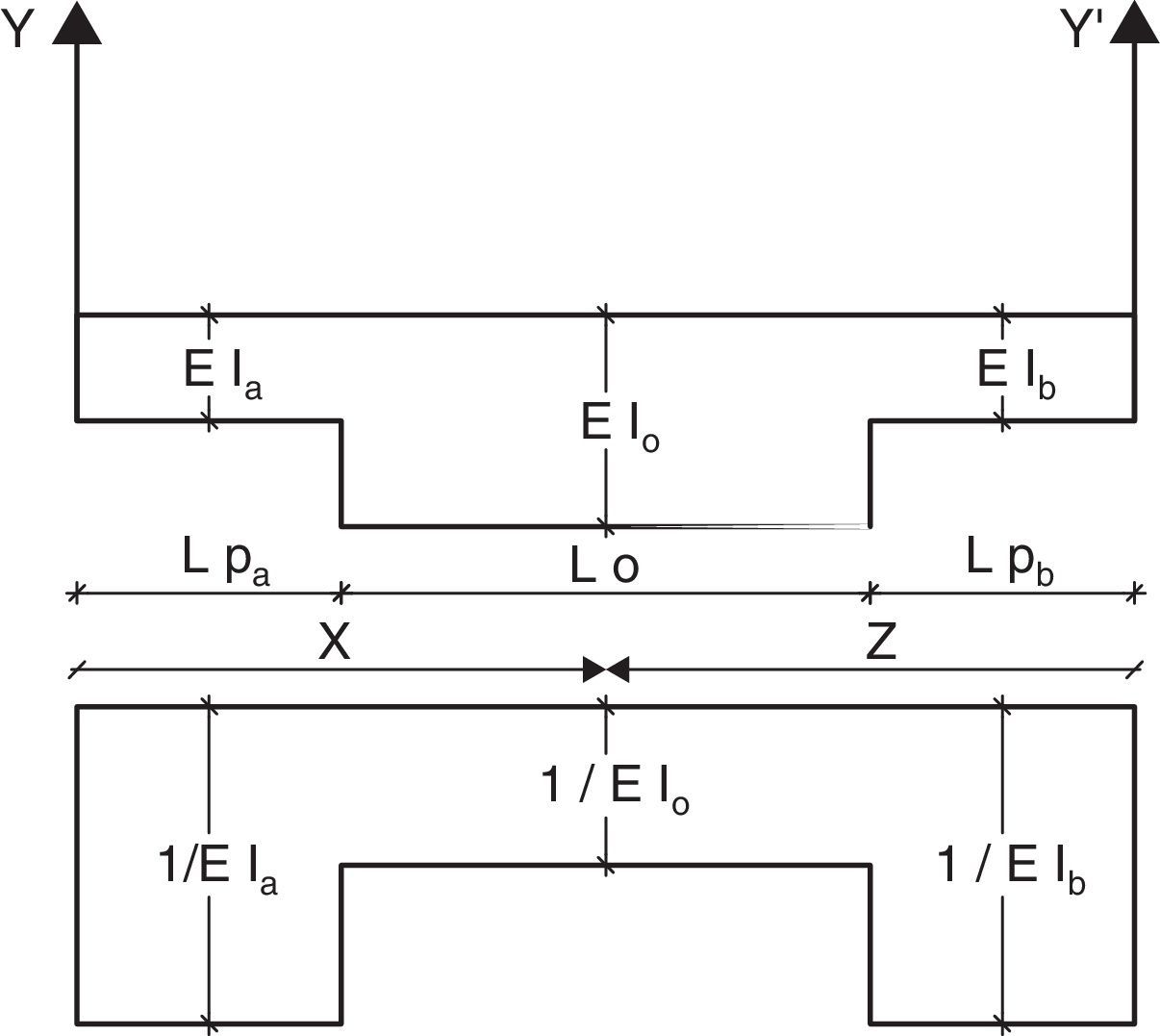
En el Modelo A, se consideran tres segmentos de longitudes L_pa, L₀, L_pb, y que tienen rigideces a flexión EI_a, EI₀, EI_b. Cuando el elemento se encuentra en el rango elástico, las longitudes plásticas L_pa, L_pb, en el nudo inicial y final son cero y se trabaja como un elemento de sección constante pero cuando ingresa al rango no lineal se tienen los tres segmentos que se indican en la parte superior de la figura 2[18]. En la parte inferior de dicha figura se presenta el diagrama de masas elásticas (1/EI) y la nomenclatura utilizada para hallar los momentos de inercia Iy,Iy′,Iyy′, con los cuales se halla la matriz de flexibilidad, f₁, en el sistema1 que no considera desplazamientos como cuerpo rígido, de tal manera que solo existe rotación (viga apoyada- apoyada)

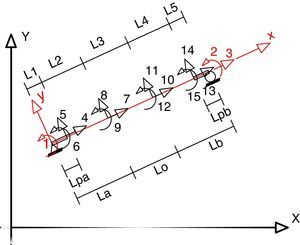
donde EIx es la rigidez a flexión en el punto x. Las restantes variables que intervienen en las integrales se indican en la figura 1.

Figura 2.

Modelo A: Rigidez escalonada y diagrama de masas elástica. (1/EI)

El Modelo B se indica en la figura 3; se observan las longitudes L_a, L₀, L_b, pensando en el armado de una viga que tiene diferente refuerzo con diferentes longitudes en el nudo inicial, centro de luz y nudo final. Posteriormente, y cuando uno de los extremos del elemento ingresa al rango no lineal, se determina la longitud plástica L_pa, L_pb, [19] de tal manera que la longitud de las dovelas va cambiando de acuerdo a los valores de L_pa y/o L_pb.

Figura 3.

Modelo 1. Dovelas en elementos viga y columna, para hallar matriz de rigidez en sistema 1, que no considera desplazamientos como cuerpo rígido.

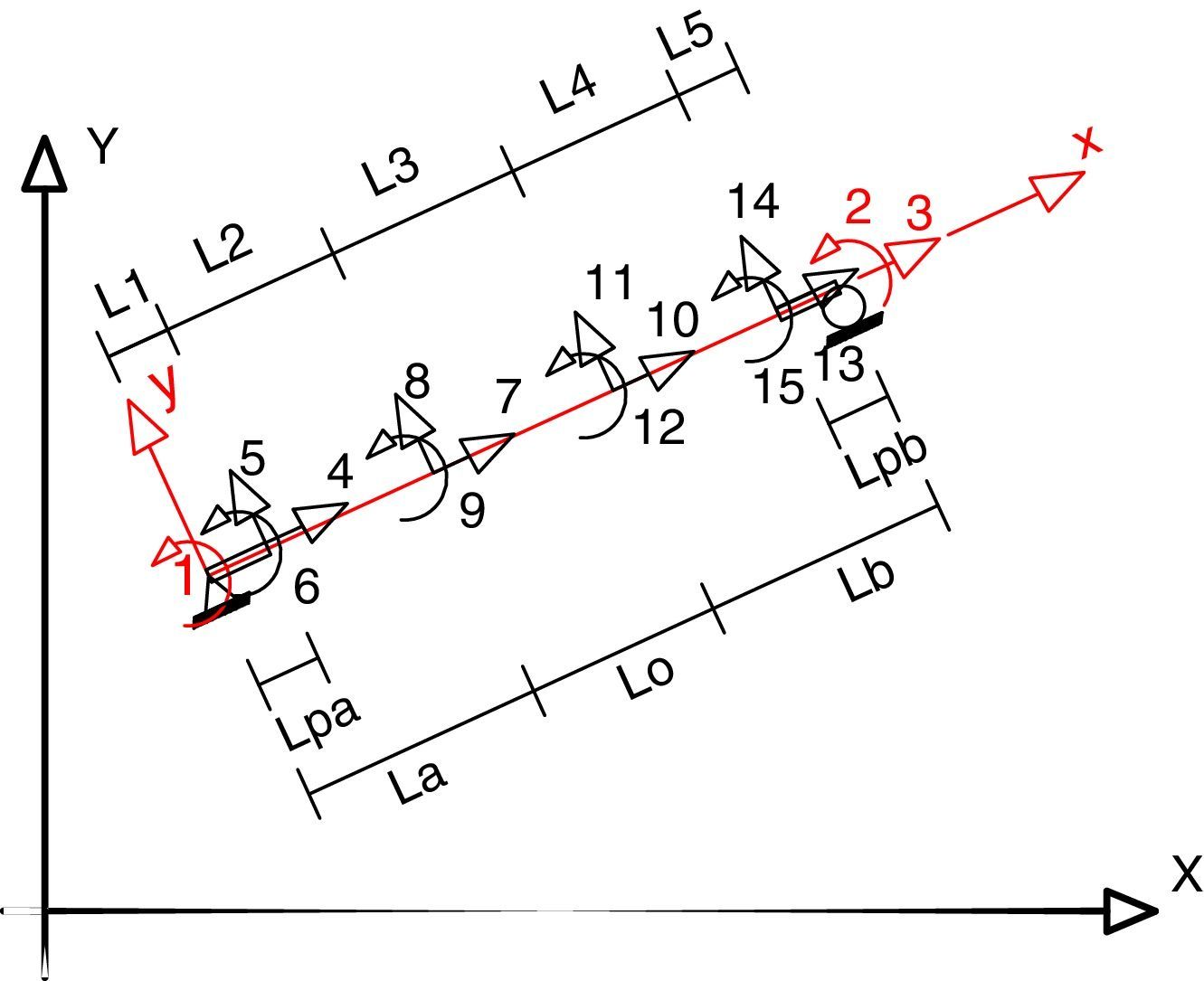
En la figura 3, las coordenadas principales son de la 1 a la 3 y están asociadas a un modelo articulado en el nudo inicial y rodillo en el nudo final, al cual se denomina modelo 1. Por medio de la matriz de transferencia T₁₋₂ se halla la matriz de rigidez en el sistema 2, en coordenadas locales y por medio de la matriz de rotación T₂₋₃ en el sistema 3, en coordenadas globales [17].

Los grados de libertad de los nudos interiores, son las coordenadas secundarias y van del 4 al 15. Se determina la matriz de rigidez por ensamblaje directo de 15/15; luego de lo cual se condensa a las coordenadas principales de 3/3.

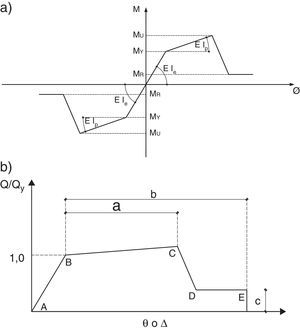
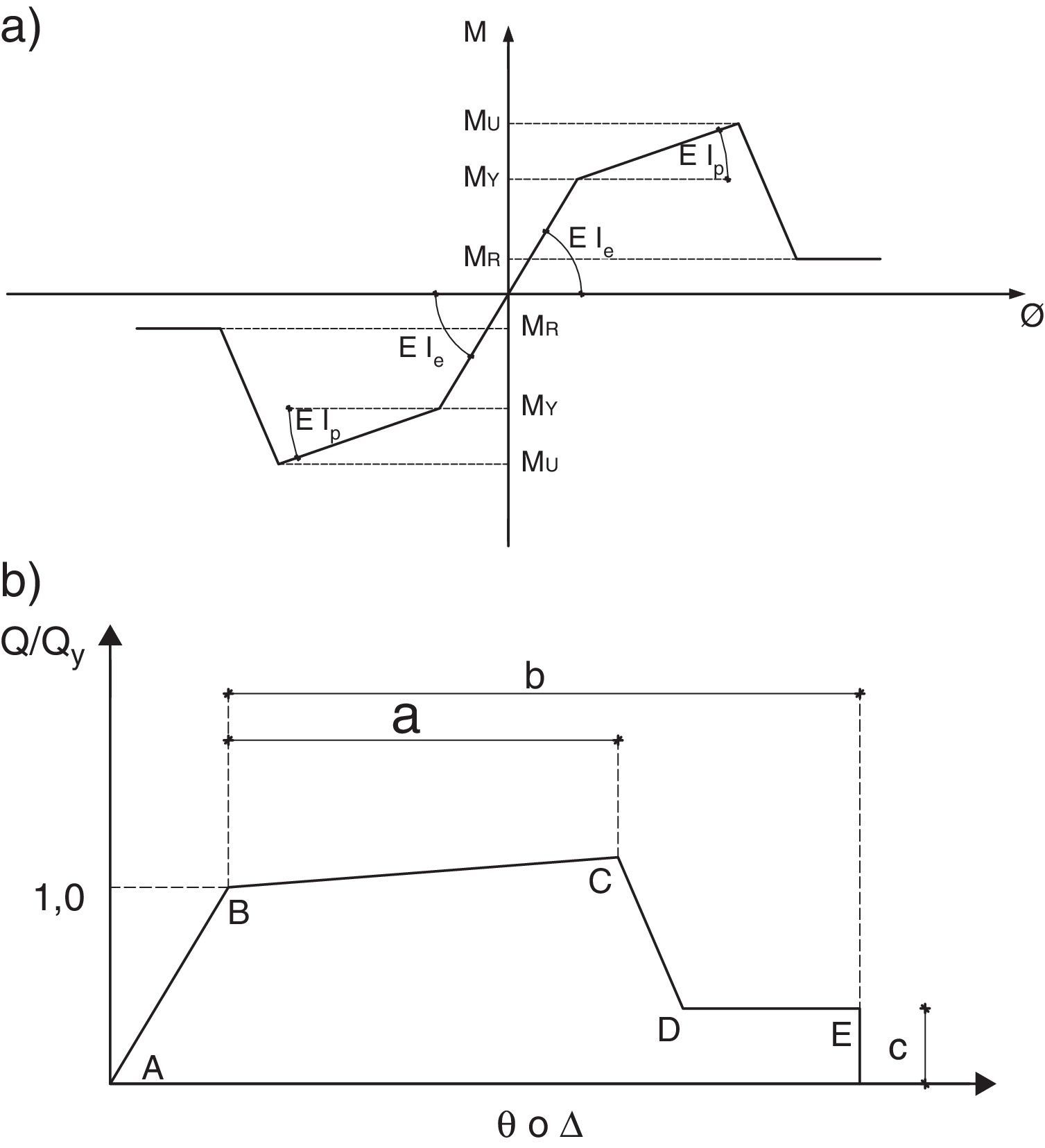
2.2

Modelo constitutivo

En la figura 4 a, se presenta el modelo constitutivo con el cual se halla la rigidez elástica EI_e, la de post plasticidad EI_p y la residual EI_r; para el caso de que la armadura a tracción sea la inferior (primer cuadrante) y para cuando la armadura a tracción sea la superior (tercer cuadrante). El cálculo del momento y curvatura en el punto de plasticidad M_y, ∅ _y, se realizó empleando las ecuaciones de Y. Park [20] que tiene un respaldo numérico y experimental de 400 ensayos en vigas y columna.

Figura 4.

a) Modelo del diagrama Momento- Curvatura; b) Relación momento curvatura y momento rotación, con modelo ASCE 41.

Para los restantes puntos del diagrama momento-curvatura, primero se halló el diagrama momento-rotación, empleando los criterios y tablas del ASCE 41 de 2011 [21], que se indica en la figura 4 b y en función de la longitud plástica se pasa al diagrama M− ∅ [16,19].

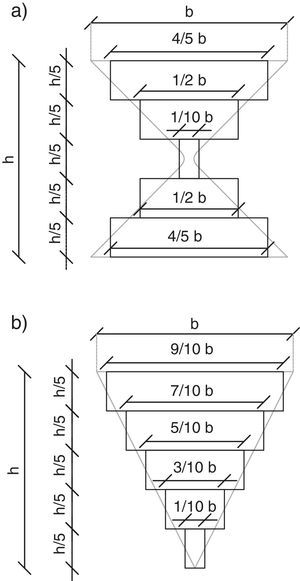
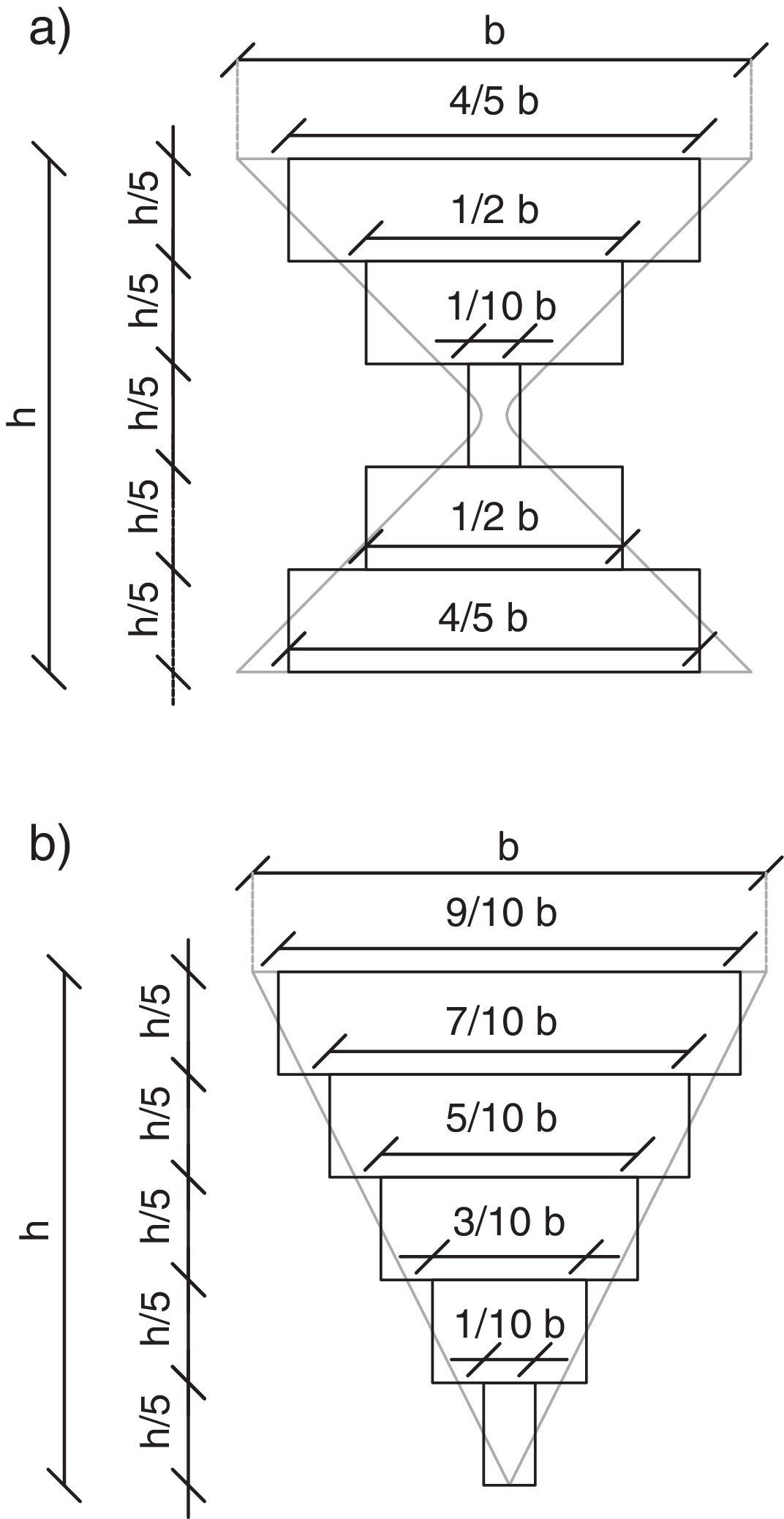
2.3

Elemento disipador

Existen soluciones analíticas, propuestas por Whitaker [11] y Tena [22] para encontrar la matriz de rigidez del elemento disipador sea éste TADAS o ADAS pero en éste artículo se prefiere calcular la matriz de rigidez, dividiendo al elemento en 5 dovelas, las mismas que se indican en la figura 5 a, para el disipador ADAS y en la 5 b, para el disipador TADAS.

Figura 5.

a) Dovelas consideradas en elemento disipador ADAS, b) Dovelas consideradas en elemento disipador TADAS.

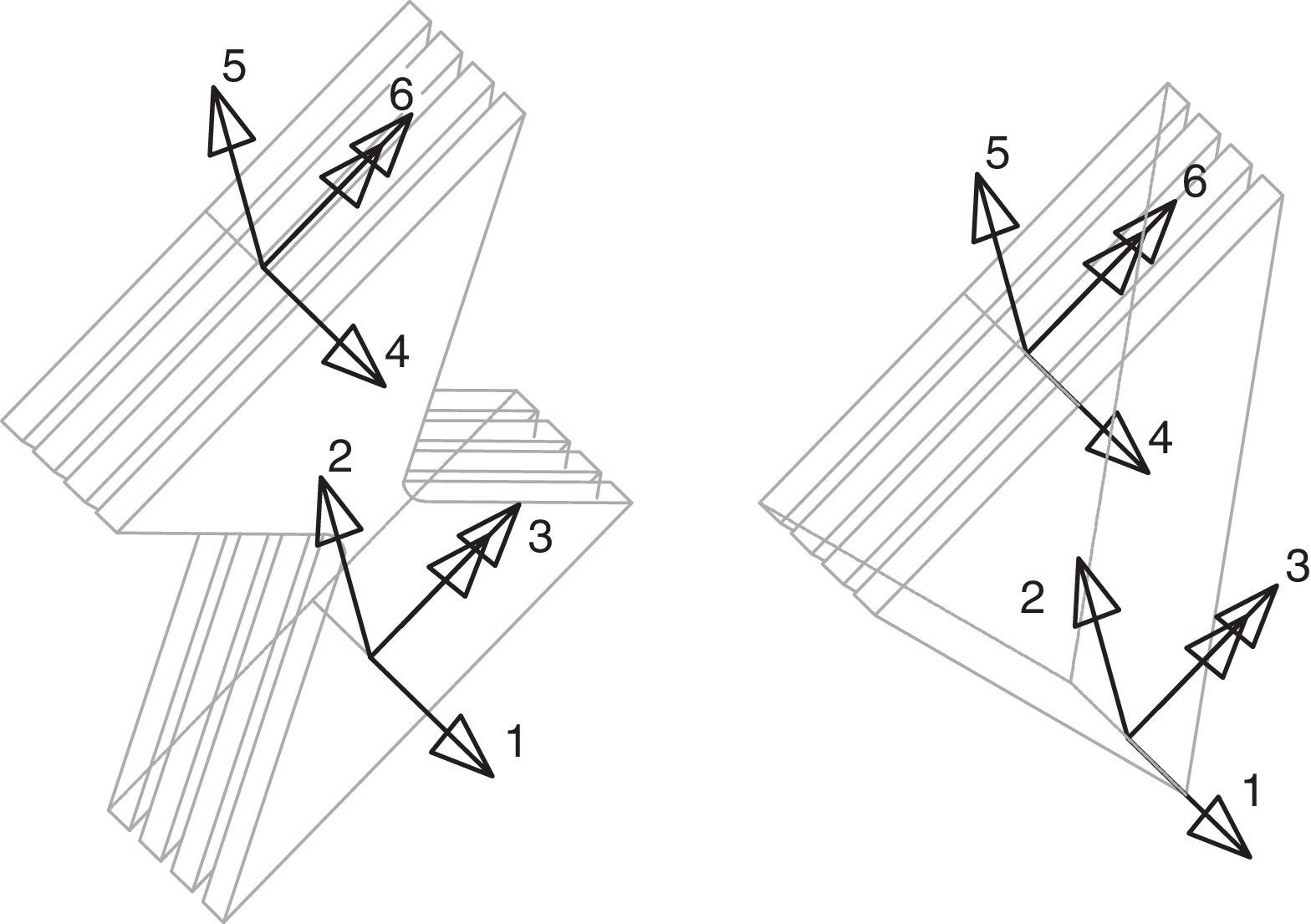
Cada una de las dovelas es de sección contante, cuya base está indicada en la figura 5 y la altura de la sección transversal es n t, siendo n el número de placas y t el espesor de cada placa. La longitud de cada dovela es h/5, donde h es la altura del disipador. Al ser de sección constante, el cálculo de la matriz de rigidez de cada dovela en coordenadas globales es directo [19]. En la figura 6 se presenta la numeración de los grados de libertad en coordenadas globales, a la que se llega luego de haber procedido en forma similar a la indicada en el sub apartado 2.1. La matriz de rigidez que se obtiene por ensamblaje directo es de 18/18 y luego se condensa a 6/6 [23].

Figura 6.

Coordenadas globales del elemento disipador ADAS y TADAS.

Para el modelo constitutivo del elemento disipador se determina primero el momento de plasticidad M_y en la cara superior, multiplicando el momento plástico z, por la tensión del material f_y

Para encontrar la curvatura de plasticidad ∅_y se halla la rigidez elástica EI_e, donde E es el módulo de elasticidad del material

La curvatura de plasticidad se la obtiene con la siguiente ecuación:

La curvatura última ∅_U se calcula en función de la ductilidad por curvatura μ_∅. Finalmente el momento último M_U se determina en función de α que es la relación entre la rigidez post plasticidad con respecto a la rigidez elástica

2.4

Elemento diagonal

La diagonal de acero del contraviento trabaja axialmente, de tal manera que la matriz de rigidez del elemento es de 4 por 4 [5]. Para el comportamiento no lineal, se tienen dos posibilidades, la una que la diagonal trabaje a compresión y la otra de que trabaje a tracción. La diferencia radica en la forma en que se obtiene el punto de plasticidad: cuando la diagonal trabaja a compresión, la fuerza del punto de plasticidad es el menor valor entre F_Y y F_Cr. Las fuerzas a nivel de plasticidad se obtienen multiplicando el área de la sección transversal por la tensión de plasticidad del material.

La carga crítica de pandeo es función de la relación Lr, donde r es el caso contrario.

Para hallar el desplazamiento de plasticidad, Δ_Y tanto a compresión como tracción se divide la fuerza de plasticidad para la rigidez axial EA. El desplazamiento último, Δ_U es igual a la ductilidad por el desplazamiento de plasticidad. Finalmente, la fuerza última, F_U, se halla en función de α que, en este caso, relaciona la rigidez axial post fluencia con la rigidez axial elástica.

3

Pushover multimodal y el Método de Espectro de Capacidad

La curva de capacidad sísmica resistente, que relaciona el cortante basal V con el desplazamiento lateral máximo de una estructura, D_t, se puede encontrar mediante un análisis pushover monotónico, cíclico o multimodal [24,25]. Esta última forma de cálculo es la que se presente en este apartado siguiendo las propuestas de Chopra y Goel [13,14,26].

La carga lateral, aplicada en cada uno de los pisos de la estructura, se obtiene con la siguiente ecuación:

donde Q_i,n es la fuerza lateral aplicada en el modo i, y en el piso n ; diagM es el vector de la diagonal de la matriz de masas de la estructura (si la matriz es diagonal); ϕ_i,n es el modo de vibración i, en el piso n; Γ_i es el factor de participación en el modo i; ΔV es el incremento del cortante basal que se considera para encontrar la curva de capacidad

donde M es la matriz de masas; b es el vector de incidencia de los grados de libertad en el movimiento del suelo. Se trabaja con el signo que tiene el factor de participación modal.

En el caso del pushover multimodal se hallan fuerzas laterales, en cada modo de vibración, cuyo factor de participación modal es diferente de cero en cada piso. Estas fuerzas tienen signo positivo o negativo. Para cada modo se encuentran la respuesta de la estructura igual que en el pushover monotónico y para hallar la respuesta total se aplica el criterio CQC (Complete Quadratic Combination) propuesto por Chopra [27]. En el CQC se consideró que el factor de amortiguamiento viene dado por la relación de Naoki [28] para el hormigón armado y es: ξ_i = 1.4 * ξ_i−1. Mora [19] presenta programas del sistema de computación CEINCI-LAB para encontrar el pushover multimodal.

En el Método del Espectro de Capacidad, MEC, el espectro de capacidad y los espectros de diseño se colocan en el formato desplazamiento-aceleración, utilizando las siguientes ecuaciones:

donde D_ti, V_i son las coordenadas de un punto de la curva de capacidad sísmica resistente para los cuales se determina el desplazamiento y aceleración espectral S_di, S_ai; M_T es la masa total de la estructura; α_i es el coeficiente de masa modal i; Γ_i es el factor de participación del modo i, en valor absoluto. En el MEC se determina el punto de demanda como aquel punto en el cual la ductilidad de demanda, μ, es igual a la ductilidad con la cual se halla el espectro inelástico [29–31].

El comportamiento de la estructura viene definido por un modelo bilineal. En este modelo se tiene:

donde E_D, E_S, son las energías disipada y elástica en un ciclo de histéresis; μ la demanda de ductilidad que relaciona el desplazamiento de demanda con el desplazamiento de plasticidad de la estructura; α relaciona la rigidez post plasticidad con la elástica del modelo bilineal.

Una vez encontrado el ξ_eq se halla el factor B por el cual se divide el espectro elástico de 5% de amortiguamiento para hallar el espectro inelástico asociado a ξ_eq

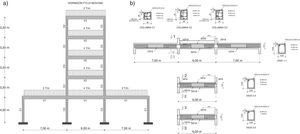
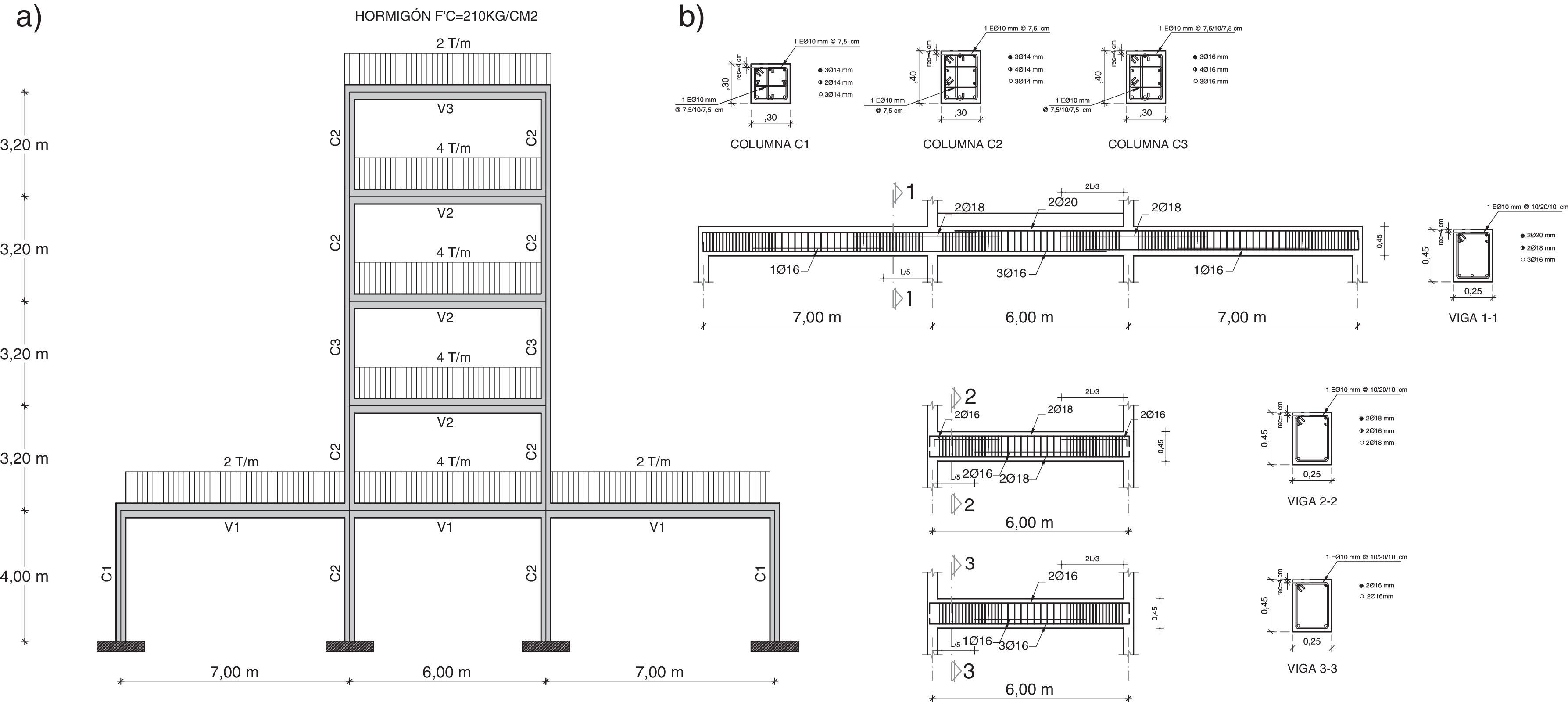
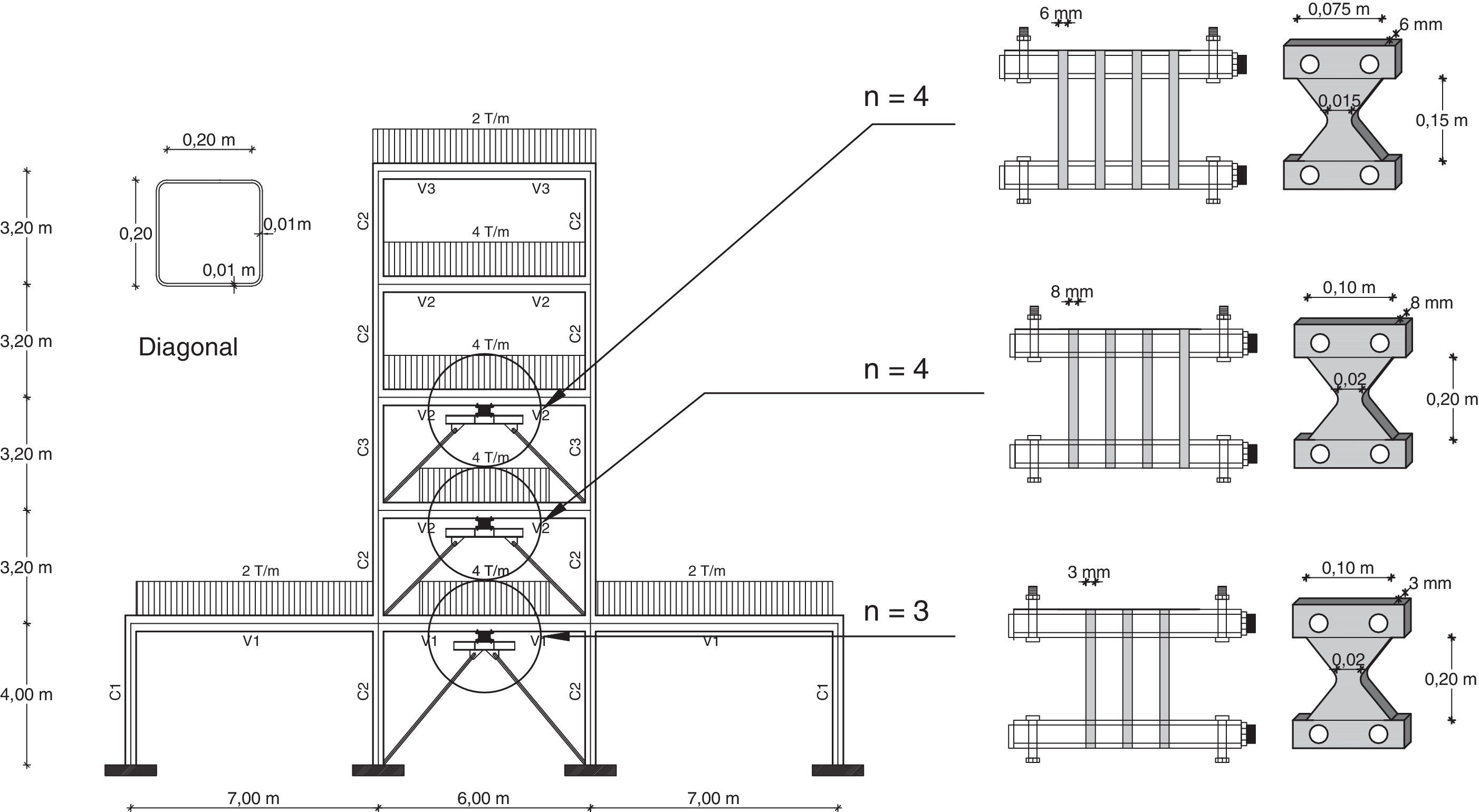
El punto de demanda se calcula en forma iterativa.

4

Estructura analizada

Se diseñó una estructura irregular de 5 pisos, ubicada en el Centro Norte de Quito, muy próxima a la falla Illumbisí- La Bota (ver figura 1). Los factores de sitio fueron obtenidos de la microzonificación de Quito [2] para el sector del antiguo Quito Tenis y tienen los siguientes valores, para la aceleración, desplazamiento y comportamiento no lineal de suelo: F_a = 1.267 ; F_d = 1.087 ; F_s = 1.22. El espectro inelástico se obtuvo para un factor de reducción R = 8; se utilizó el método espectral para el análisis sísmico y para el diseño se utilizó el ACI 318-14. En la figura 7 a se presenta la geometría de la estructura con sus cargas y en la figura 7 b se indica la estructura con la armadura longitudinal y transversal calculada.

Figura 7.

a) Geometría de la estructura sin disipadores de energía; b) Secciones de la estructura de hormigón armado.

El hormigón utilizado tiene una resistencia máxima a la compresión fc′=21   MPa y el acero de refuerzo un límite de plasticidad f_y = 420 MPa.

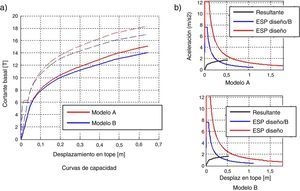
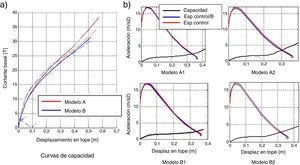
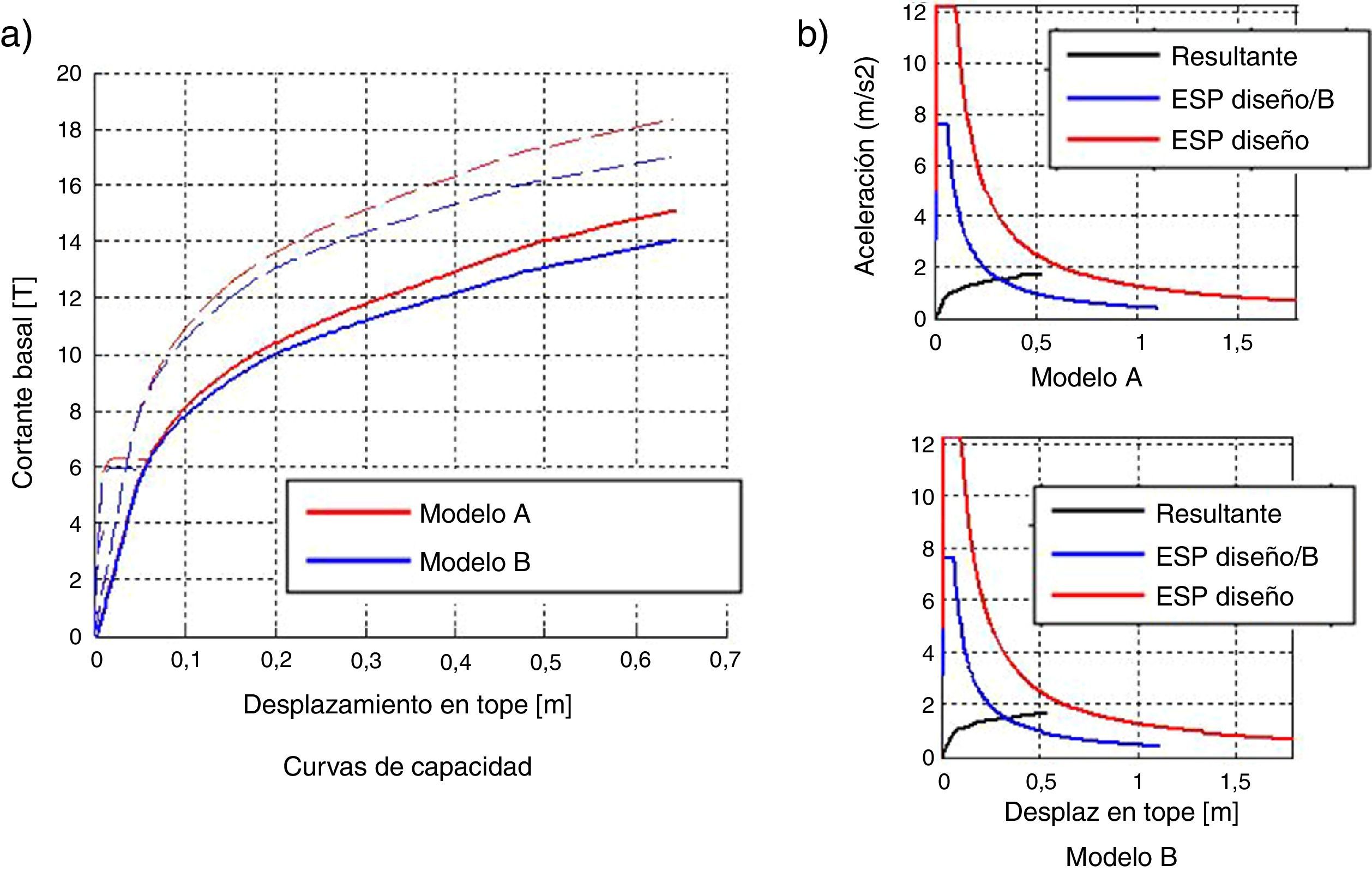
En la figura 8 a se indica la curva de capacidad sísmica resistente de la estructura sin reforzar, que fue obtenida mediante un pushover multimodal. Con líneas entrecortadas se presenta la contribución de cada uno de los modos; las curvas superiores corresponden a la respuesta del primer modo y en la parte inferior se muestra la contribución de los restantes modos. Se aprecia que los modos superiores contribuyen muy poco a la respuesta.

Figura 8.

a) Curvas de capacidad de la estructura sin reforzar. b) Método de espectro de capacidad para modelos: A, B sin reforzar para sismo de diseño.

Con línea continua se tiene la resultante que se halla al aplicar el criterio de combinación modal CQC en los desplazamientos y cargas que se hallan en cada incremento de fuerzas laterales. La línea roja corresponde al modelo A y la azul al modelo B, obtenida considerando el efecto de corte ∅. Se aprecia, en la figura 8 b que las curvas de capacidad halladas con los dos modelos son bastantes parecidas.

En la figura 8 b se presenta en cada grafica el espectro de diseño en el formato desplazamiento aceleración S_d − S_a; el espectro de diseño con el cual se obtiene el punto de demanda S_d − S_a/B y el espectro de capacidad hallado con el puhsover multimodal pero en el formato indicado. Para el modelo A, el punto de demanda (intersección de las dos curvas) es S_dem = 0.32 m y, para el modelo B, el punto de demanda es S_dem = 0.33 m. Los valores de los puntos de demanda prácticamente coinciden.

Para hallar el desplazamiento en la estructura de 5 pisos, a partir del punto de demanda, se utilizó la ecuación de Algan [32] que permite pasar de un sistema de 1 grado de libertad a múltiples grados de libertad; el desplazamiento en la cubierta del edificio viene dado por: D_t = C₀S_d

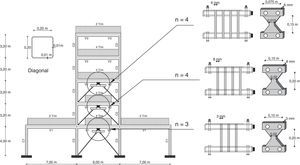
donde N el número de pisos. Con esto se halla que D_t = 0.44 m para el modelo A y la deriva global que se obtiene dividiendo el desplazamiento en la cubierta para la altura del edificio; para el estudio se halló que la deriva global es 2.6%; el valor obtenido es alto por lo que se decide reforzar la estructura con disipadores de energía [32–34].

5

Estructura reforzada

Para que la estructura tenga un mejor comportamiento sísmico se decidió colocar disipadores de energía tipo ADAS, de acero A36, con límite de plasticidad f_y = 253 MPa, en el vano central de los tres primeros pisos; sobre contravientos tubulares en forma de «V» invertida de 200/200/10 mm, de acero A36. En la figura 9 se indica la geometría de estos disipadores y el número de placas n en cada uno de ellos. La resistencia del hormigón y del acero es la misma que en la estructura sin disipadores.

Figura 9.

Reforzamiento de la estructura con disipadores de energía ADAS.

Con estos disipadores se logra tener derivas de piso menores al 2%, al aplicar el método espectral para el sismo de diseño ERN (2012) [2] que tiene un período de retorno de 475 años.

Ahora bien, en este apartado se presenta el desempeño de la estructura reforzada ante el sismo de control encontrado para la zona norte de Quito sobre un perfil de suelo «D», considerando que se registra un sismo de magnitud Mw=6.2, en la falla de Ilumbisí-La Bota, que es la más cercana al sitio del proyecto. El período de recurrencia de este sismo se encuentra entre 610 y 981 años [7].

Cuando se calcula la matriz de rigidez del elemento ADAS a partir de la solución analítica, se identifica como modelo 1 y cuando se encuentra a partir del método de las dovelas se denomina modelo 2. Con cada uno de estos modelos se tienen dos posibilidades de considerar la no linealidad de los elementos, las mismas que han sido ya identificadas como modelo A y modelo B.

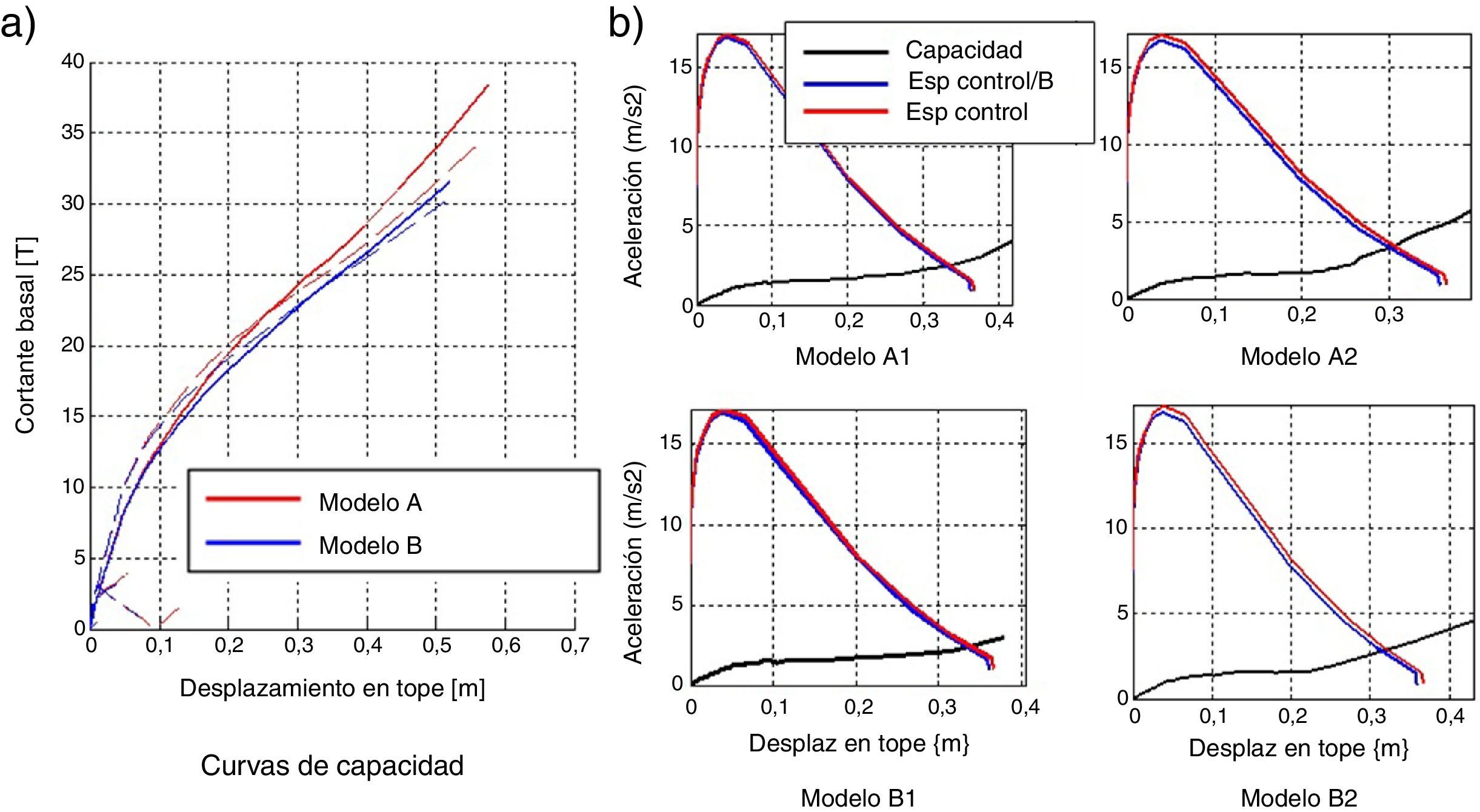
En la figura 10a, se muestra la curva de capacidad de la estructura reforzada con disipadores, calculada con el pushover multimodal (línea continua); con línea entrecortada se indica la contribución de cada uno de los modos de vibración (que es muy baja). Las curvas correspondientes a los casos con cortante en la base muy altos corresponden al primer modo y en la parte inferior se hallan de los restantes modos. Las curvas de capacidad de la estructura reforzada alcanzan cortantes que son aproximadamente el doble de la estructura sin reforzamiento (figura 8 a).

Figura 10.

a) Capacidad sísmica de la estructura reforzada; b) Método del espectro de capacidad para modelos: A, B.

Si bien es cierto, al colocar aisladores se confiere amortiguamiento a la estructura, no es menos cierto que las diagonales del contraviento confieren mayor rigidez. Por esta razón es que se tiene un incremento notable en el cortante basal de la curva de capacidad sísmica resistente.

En la figura 10b, se indica el espectro de control cuyas ordenadas espectrales máximas están alrededor de los 18 m/s2 en contraste con los 12 m/s2 del espectro de diseño (figura 8 b). Se presenta también el espectro de reducido por «B» con el cual se obtuvo el punto de capacidad y el espectro de capacidad. La identificación de cada gráfico está en de acuerdo a la nomenclatura de los modelos ya indicados; los resultados se resumen en la tabla 1.

Tabla 1.

Desplazamiento en punto de capacidad, en la cubierta del pórtico y deriva global en estructura reforzada ante sismo de control

Modelo Parámetro	A1	A2	B1	B2
Sd(m)	0.329	0.300	0.336	0.316
Dt(m)	0.453	0.428	0.485	0.462
γg(%)	2.70	2.55	2.89	2.75

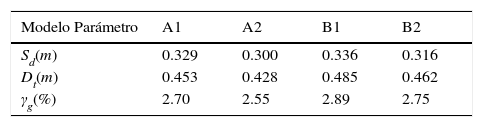
En la tabla 1 se observa que el desplazamiento en la cubierta está alrededor de 0.46 m, con este valor en la figura 10a se encuentra que el cortante basal es aproximadamente de 28 T., valor bastante alto, que implica daño en la estructura reforzada.

Se destacan dos aspectos de los resultados de la tabla 1: el primero que los resultados son bastante parecidos; y el segundo es que la estructura reforzada con disipadores va a tener un daño considerable ante el sismo de control que tiene un período de recurrencia entre 610 y 981 años. La estructura sin disipadores colapsa ante el sismo de control.

6

Conclusiones

Tres conclusiones importantes se han obtenido en este artículo. La primera tiene que ver con la necesidad de verificar el diseño de las estructuras de Quito con el sismo de control cuyo origen es en las fallas ciegas inversas sobre las que se asienta la ciudad. Esto se debe a que las ordenadas espectrales para la zona de períodos cortos, para un nivel de confiabilidad del 84%, son mayores que las que se obtienen al aplicar el espectro del NEC (2015) o ERN (2012).

La segunda conclusión es sobre la comparación de modelo de plasticidad (Modelo A) versus el modelo de método de las dovelas (Modelo B), existe una pequeña diferencia en los resultados de las curvas de capacidad, pero no es significativa al encontrar los puntos de capacidad.

El tercer tema tiene relación con el software del sistema computación libre CEINCI-LAB, esto son una serie de programas de código abierto, los cuales permiten estudiar o modificar procesos de cálculo según necesiten. Por esta razón es recomendable usarlo, para poder saber exactamente como se está trabajando.