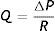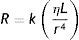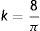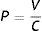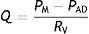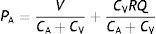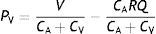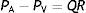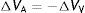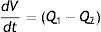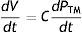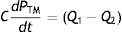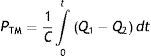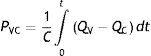El entendimiento convencional y abordaje actual de la dinámica de la circulación humana en la hemodinámica clínica recae sobre 4 modelos clásicos de la fisiología cardiovascular moderna, que conforman el marco conceptual dentro del cual los parámetros hemodinámicos mayormente relevantes en la práctica cotidiana son interpretados. Estos modelos son: Poiseuille, Krogh, Starling y Guyton; cada uno describe un aspecto fundamental del flujo a través de la circulación periférica, y de la función del corazón como bomba (Starling), complementándose entre sí.
Sin embargo, las interpretaciones prevalentes de aquellos experimentos clásicos son habitualmente confusas, y a veces hasta inconsistentes física y fisiológicamente. De este modo, es el propósito del presente trabajo proveer un marco conceptual realista para analizar la dinámica de la circulación sistémica, las variables hemodinámicas clásicas y la verdadera significación de los modelos mencionados y los parámetros relacionados. Finalmente, se presentará un modelo conceptual que integre dichas variables.
The conventional understanding and current approach to the dynamics of the human circulation in clinical hemodynamics moves between four classical models of modern cardiovascular physiology that make up the framework from which hemodynamic parameters relevant to everyday practice are interpreted. These are: Poiseuille; Krogh; Starling; and, Guyton; each one describes a fundamental feature of the flow through the peripheral circulation, and of heart's function (Starling), and, they also complement each other.
However, the prevailing interpretations of the classical experiments are often misleading, and sometimes present physical and physiological inconsistences. Thus, it is the purpose of this revision to provide a realistic framework through which analyze the dynamics of the systemic circulation, the classical hemodynamic variables, and the true significance of the classical models and the related hemodynamic parameters. Finally, a conceptual model that integrates these variables is presented.
A George L. Brengelmann
En señal de admiración y amistad No pueden satisfacernos significaciones que toman vida —cuando la toman— de intuiciones remotas, confusas, impropias. Debemos retroceder a las «cosas mismas». Edmund Husserl1
La circulación sistémica es inmediata y regularmente concebida como un circuito dirigido o «gobernado» por la presión (P), gran parte debido a una interpretación confusa del arreglo experimental sobre el cual Poiseuille derivó la ley que lleva su nombre, hacia mediados del siglo xix2, y que, en las palabras de Kim H. Parker «se ha convertido en el referente de comparación de cualquier tipo de flujo a través de tubos, quizás debido a su simplicidad»3.
El experimento consistió básicamente en generar una diferencia de presiones hidrostáticas (ΔP) entre 2 contenedores conectados por un segmento de tubuladura capilar de cristal, de radio (r) y longitud (L) conocidos. Así, la tasa de flujo volumétrico (Q) era medida luego de modificar cualquiera de las variables del sistema —especialmente el (ΔP)— para fluidos de diferente viscosidad η, obteniéndose una relación lineal entre ΔP y Q, e identificándose el primero como la variable independiente. Esto es, en este esquema enfrentamos la función: Q=f(P); lo que también es conocido como el «equivalente hidráulico» de la Ley de Ohm (es decir, de un circuito eléctrico homólogo «dirigido» por el voltaje).
Siendo la resistencia (R) proporcional a (ley de Hagen-Poiseuille):
Donde k es una constante igual a:
Este principio trasladado a la circulación conlleva a entender que el flujo sistémico o volumen minuto cardíaco (Q) obedece la misma relación que el circuito poiseuilliano, donde ΔP es identificado como la causa del Q; cuando en realidad, en ninguno de los 2 casos el ΔP de la ley de Poiseuille (el ΔP relacionado con el flujo) es la causa ni la consecuencia: ambos se generan simultáneamente al forzar un fluido viscoso a través de una resistencia. Es decir, que la pérdida o gradiente (función de la distancia, x) de presión (dP/dx) en cualquier circuito hidráulico en el flujo estacionario refleja la pérdida de energía por la resistencia viscosa del fluido al fluir4; de ningún modo el ΔP representa una fuente de energía mecánica en sí misma.
Poner un fluido en movimiento implica una transferencia de energía mecánica, que en el caso de Poiseuille era gravitacionala, esto es, la diferencia de energía potencial gravitacional entre los contenedores, manifestada en el ΔP. Este principio fue aplicado posteriormente en los viscosímetros gravimétricos, ya que la fuerza conductora (driving force) es la gravedad, y el flujo obtenido proporcional a η. La identificación del ΔP como «presión conductora» (driving pressure) solo es coherente en el contexto de un circuito como el poiseuilliano, donde el Q es minúsculo, afectando despreciablemente el volumen y la presión en los reservorios.
Esta aclaración pertinente al modelo y Ley de Poiseuille podría parecer trivial; y muchas veces se habla de la Ley de Poiseuille como siendo esta una «aproximación» al flujo a través del circuito cardiovascular, fundamentalmente porque las condiciones de flujo directo laminar no se cumplen en este sistema: el flujo es pulsátil, turbulento; el circuito es cerrado, global y heterogéneamente compliante, compuesto de resistencias y capacitancias no-lineales, ampliamente ramificado, y la sangre un fluido no-newtoniano, con propiedades reológicas específicas.
No obstante, la aproximación a la dinámica de la circulación mediante el modelo poiseuilliano es especiosa esencialmente porque introduce un circuito dirigido por la presión, confunde sobre la fuente de energía mecánica del flujo y omite un ingrediente fundamental en la hemodinámica: el efecto de la capacitancia vascular. Veremos a continuación cómo esta concepción ha influenciado el desarrollo y la perpetuación de uno de los modelos más influyentes de la hemodinámica clínica contemporánea.
Arthur C. Guyton y la cacería de la «presión media»Hacia mediados del siglo pasado un médico y fisiólogo de la Universidad de Mississippi, llamado Arthur C. Guyton, formado en cirugía, y con una gran vocación y afinidad por la ingeniería, la biofísica y la aplicación del análisis de circuitos electrónicos en la fisiología de los sistemas, lideró el desarrollo de un modelo de la circulación sistémica basado en la idea del «retorno venoso» (QV) —fenómeno que había comenzado a ser objeto de exhaustivas investigaciones por fisiólogos de comienzos del siglo xx—.
El modelo estaba centrando sobre una variable relativamente nueva en la historia de la fisiología circulatoria, la «presión media» (PM) del sistema, descubierta por Ernst H. Weber cerca de un siglo antes5, luego acuñada por Ernest H. Starling como «presión sistémica media»6, y finalmente cristalizada como «presión media de lleno circulatorio»b por Guyton7. La (PM) —o presión de «flujo cero»— simplemente representa la presión que ejerce el volumen sanguíneo (V) sobre la vasculatura cuando el perfil de presiones es homogéneo en todos los segmentos vasculares, y como tal es igual al cociente entre el volumen y la compliancia agregada (C) del sistema.
Guyton et al. diseñaron un modelo físico y matemático de la circulación sistémica compuesto por capacitancias y resistencias agrupadas (lumped) y dispuestas en serie, en el cual la PM cumpliría un rol efectivo sobre la regulación del gasto cardíaco, específicamente sobre el QV8. A través de una serie de experimentos sobre preparados caninos de derivación sistémico-pulmonarc demostraron la hipótesis de que la PM representaría nada menos que el cabezal de presión (pressure head) del flujo de retorno de la sangre desde la circulación periférica al corazón, o QV8,9. A su vez, dado que las mediciones de Guyton fueron realizadas en condiciones de flujo estacionario, la PM es por definición la «presión propulsora» del volumen minuto cardíaco, o Q.
Los registros de Guyton —datos pareados de Q y presión auricular derecha (PAD)— fueron trazados en el formato de las famosas «curvas del retorno venoso» (venous return curves), con su notación matemática, la «fórmula del retorno venoso»8:
En este análisis la PAD fue identificada como la variable independiente en el procedimiento experimental, e interpretada como una fuerza efectiva, o «contra-presión», que se opone al QV, y la PM como la fuente de energía mecánica del flujo —esto es, un circuito dirigido por la presión, como en el caso del circuito Poiseuilliano—. Entonces, habiendo sido aclarado que P y Q se generan simultáneamente en un circuito hidráulico, cabe la pregunta sobre cómo la PM genera el flujo y cuál es, en definitiva, el rol del corazón dentro de este esquema.
La PM representa en el modelo de Guyton la presión dentro de un compartimento de la vasculatura periférica, definido como el «compartimento venoso periférico», dado que allí reside la mayor parte de la volemia; esto a su vez implica que la PM persiste físicamente en un «locus» de la circulación aun en estados de flujo, independientemente de la actividad cardíaca —tal como lo había hipotetizado Starling durante una de sus trascendentales Lectures sobre insuficiencia cardíaca10—. Más aún, es la energía de retracción elástica (elastic recoil) almacenada en las paredes de la vasculatura a ese nivel la que impele el flujo en el sistema, siendo el rol de la bomba cardíaca meramente «permisivo»: disminuir la PAD favoreciendo el gradiente para el QV y, por lo tanto, el mismo11. ¿Es este razonamiento correcto?
Adherentes al modelo guytoniano muy influyentes en la hemodinámica clínica durante la segunda mitad del siglo xx, han llevado esta teoría un paso adelante planteando que solo parte del volumen sanguíneo contenido en el sistema así concebido es el responsable de generar la PM, conocido popularmente como «volumen sanguíneo estresado» (VS), mientras que la fracción de la volemia que solo «repleta» la vasculatura —volumen «no estresado» (V0)— sin generar presión transmural (PTM) solo contribuye a la circulación al ser «reclutado» a VS mediante, por ejemplo, la veno-constricción12. Es por ello que el VS es llamado también volumen hemodinámicamente «activo» o «efectivo», representando aproximadamente el 30% del volumen sanguíneo total13.
Sin embargo, la concepción intuitiva de «VSversus V0» solo es coherente (y a la vez respaldada) mediante una lectura abstracta de la curva de P-V —la elastancia— de un sistema compliante, como el vascular. Esto quiere decir que identificar los segmentos de aquella curva no-lineal con fracciones físicas del volumen total no tiene correlato físico real; dicho brevemente, es todo el volumen contenido en el sistema el que genera cualquier valor de PTM, en equilibrio con la tensión mural del continente. Así, todo el volumen sanguíneo contenido en aquellos compartimientos vasculares a PTM>0 está, por definición, «estresado» (en un punto determinado en la pendiente de la curva P-V); solo el volumen sanguíneo que atraviesa segmentos vasculares a PTM≤0 (como aquel alojado en el compartimento venoso central, según la acción de las fuerzas hidrostáticas circundantes) correspondería realmente a la categoría de V0, pero este volumen no es ni más ni menos «efectivo» hemodinámicamented. No es casualidad que este esquema que combina las variables derivadas del modelo de Guyton (PM, PAD, RV, QV, VS, V0) sea continuamente representado mediante modelos o análogos hidrostáticose (como el «análogo de la bañadera»13,14), claramente reminiscentes del preparado experimental de Poiseuille y el principio gravimétrico capilar, sugiriendo ideas inconsistentes con la física y la fisiología de la circulación15,16. También es predecible que especialistas e investigadores adherentes al modelo guytoniano hayan inaugurado una verdadera vertiente de la monitorización hemodinámica basada en la determinación de la PM y el VS por varios métodos en la cabecera del pacientef, así como el comienzo de una impensada controversia15.
Sin embargo, estas variables y terminología no serán desechadas. El modo en que la PM y el VS «se dan» realmente en la circulación intacta, y cómo son relevantes en la regulación del gasto cardíaco, será explicado a lo largo de las siguientes secciones y representado a través de un modelo idóneo.
Grodins y Levy: un circuito dirigido por el flujo y las «curvas de función vascular»Hacia fines de la década de 1950 —una década clave en las investigaciones y polémicas más intensas en fisiología cardiovascular— un nuevo punto de vista y metodología de análisis de la dinámica circulatoria fueron introducidos. Fred S. Grodins, fisiólogo y pionero de la bioingeniería, llevó a cabo un riguroso análisis y síntesis matemática del sistema circulatorio con el objetivo general de articular el sistema y sus componentes en el patrón general de un regulador por retroalimentación (feedback regulator), y dilucidar las leyes que gobiernan su dinámica17.
Para ello dispuso de la metodología del diagrama de bloques funcional —abordaje hasta entonces nunca utilizado para ese fin— en donde inequívocamente identificó al flujo como la entrada del circuito sistémico y las presiones venosas (PV) y arteriales (PA) como las salidas. Mientras que para el subsistema cardíaco la entrada corresponde a las presiones vasculares (como condiciones de carga), y el flujo (gasto cardíaco) la salida, el cual a su vez alimenta el circuito sistémico conformando el circuito o asa cerrada de retroalimentación negativa (closed negative-feedback loop), lo cual será ampliado en las secciones siguientes.
No solo la PMno cumple rol fisiológico alguno, sino que todas las presiones vasculares son determinadas por el flujo sistémico —inversamente a lo planteado en los modelos de Poiseuille y Guyton—. Así, Grodins escribe las ecuaciones básicas que operan en el circuito sistémico aislado para el flujo estacionariog:
Esta serie de ecuaciones resulta de la combinación de las ecuaciones (1) y (3), para ambos compartimentos vasculares, y resolviendo para las presiones, las cuales son función del flujo sistémico. A su vez, de las mismas se distingue que manteniendo V, CA, CV, y Q constantes, la PA aumenta y la PV disminuye en función lineal de R.
Al año siguiente, en 1960, Grodins conduce un estudio experimental sobre preparados de bypass derecho18, similares a los de Guyton, donde perfundiendo la circulación sistémica con una bomba extracorpórea registra los valores de PV (al nivel de la aurícula derecha) y PA (la cual había sido omitida en el experimento de Guyton, al estar centrado en el sistema venoso), sin dejar lugar a dudas de que el flujo es la variable independiente. Ambas curvas PA;V:Q siguen un trazado divergente a mayores tasas de Q, convergiendo hacia la PM lógicamente cuando Q=0.
El trabajo de Grodins es retomado 20 años después por el fisiólogo y cardiólogo Matthew N. Levy, quien reanaliza sus conceptos y diseño experimental (esta vez, un preparado de derivación cardiopulmonar total)19, en una época en la que el modelo de Guyton había comenzado a instaurarse en la esfera de la investigación y práctica clínica.
Utilizando el mismo procedimiento Levy sintetiza el diagrama de bloques del sistema cardiovascular, donde describe el gasto cardíaco de forma «dual»:
Esto es, la notación «ohmica» (7), en donde Q es la variable independiente; y como transferencia intercompartimental (veno-arterial) de volumen sanguíneo (8). A su vez, sustituyendo el V según la ecuación (3), y reordenando, obtenemos que:
Esto quiere decir simplemente que la transferencia veno-arterial de volumen sanguíneo (el gasto cardíaco) a través de la resistencia sistémica resulta en una razón de presiones absolutas, o gradiente de presión, dictado por la compliancia relativa de ambos compartimientos, para un valor de Q y R determinados.
Finalmente, Levy denomina a las curvas de la gráfica de Grodins «curvas de función vascular», donde la correspondiente al sistema venoso es nada menos que la curva de «retorno venoso» trazada con los ejes invertidos, esto es, el Q como la variable independiente (eje x).
En las secciones siguientes completaremos el análisis atendiendo a una consecuencia fundamental del flujo como variable independiente en un circuito compliante como el cardiovascular: la distribución del volumen sanguíneo (apartado August Krogh y el modelo bicompartimental. La relación flujo-presión-volumen) y la interacción de este fenómeno con la bomba cardíaca a través de la Ley de Starling (apartado: Starling; la «Ley del corazón», la presión venosa central y el resplandor de la hemodinámica funcional).
August Krogh y el modelo bicompartimental. La relación flujo-presión-volumenEn esta sección no trataremos específicamente con la obra de August Krogh —prolífico fisiólogo de principios del siglo xx, fundador de la fisiología comparativa—, sino con un abordaje a la dinámica de la circulación periférica, ideado por primera vez por el fisiólogo danés20, que hasta ahora no hemos contemplado, lo cual también servirá para analizar la dinámica del flujo transicional y el modo en que este interactúa con el gasto cardíaco.
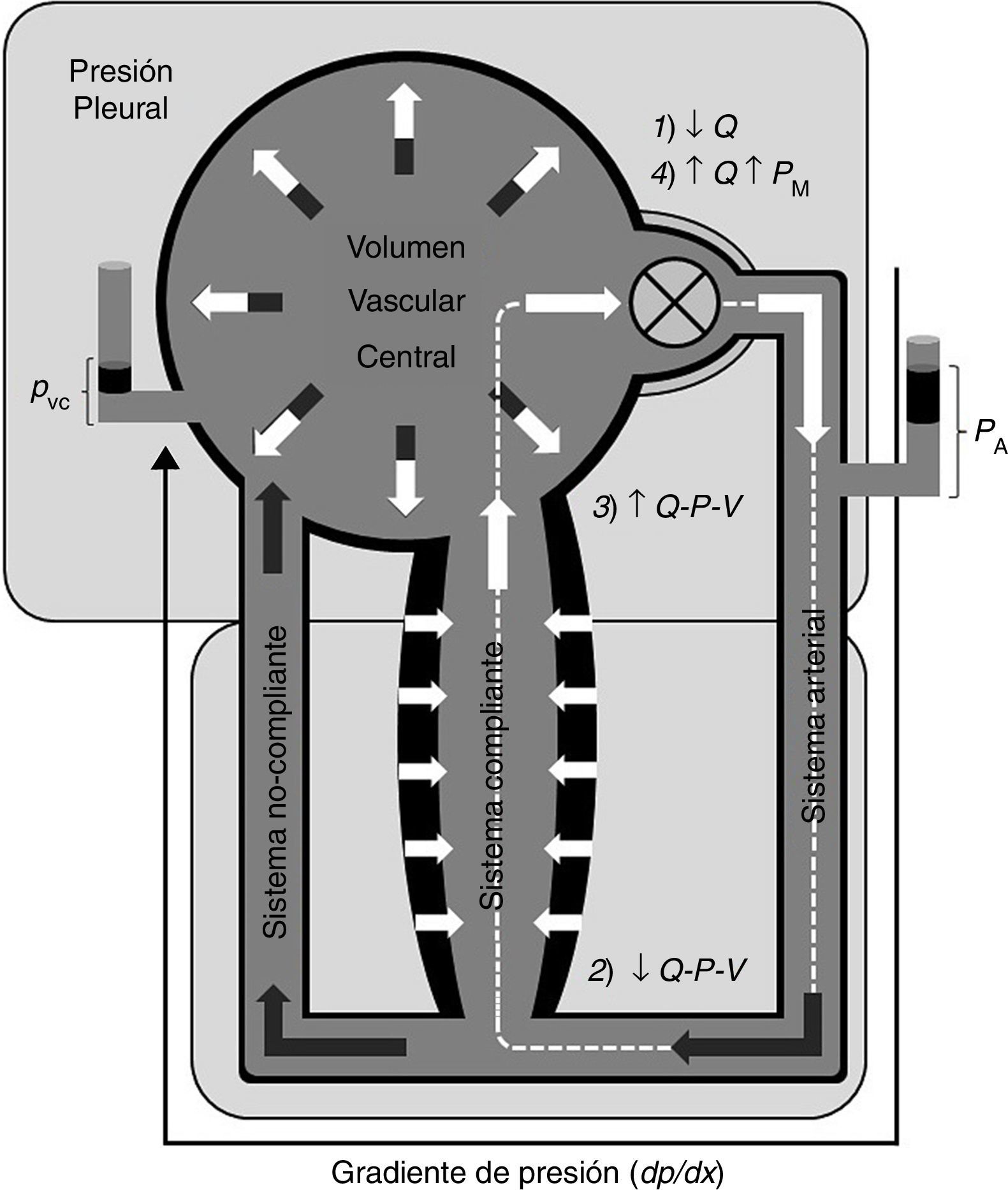
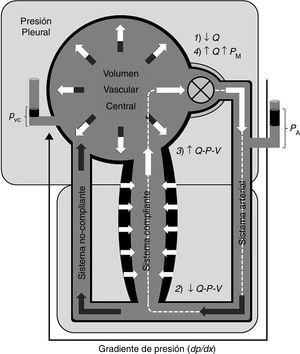
El modelo de Krogh consta básicamente de un circuito vascular compuesto de 2 canales (bicompartimental) dispuestos en paralelo y con diferente compliancia, siendo el prototipo del lecho vascular con elevada compliancia el cutáneo y esplácnico, y aquel de baja compliancia el muscular esquelético13. Ambos canales drenan en un reservorio central, desde donde el volumen sanguíneo es bombeado hacia el sistema arterial, el cual perfunde ambos lechos, de acuerdo a sus resistencias precapilares (fig. 1).
Modelo conceptual del circuito sistémico con la subdivisión vascular central (parte superior) y la periférica (parte inferior), la cual se compone de 2 canales o lechos vasculares de diferente compliancia, perfundidos por el sistema arterial.
Q−P−V: relación flujo-presión volumen (ver explicación en el texto).
Es especialmente distintivo de la dinámica de un circuito de estas características que los lechos de alta compliancia funcionen como reservorios periféricos de volumen sanguíneo amortiguando cualquier cambio en el flujo sistémico, así como cambios abruptos en la volemia21,22; del mismo modo, cambios activos en la capacitancia de aquellos segmentos vasculares afectan el flujo a su través, y también el flujo sistémico desde el corazón, ya que ambas subdivisiones del sistema intercambian volumen sanguíneo recíprocamente y están acoplados funcionalmente en términos de relación P-V21, como se verá en la sección siguiente.
De este modo, el reservorio vascular central es depletado a expensas de los lechos de alta compliancia, los cuales a su vez pueden transferir volumen sanguíneo hacia la circulación central al disminuir su capacitancia. Expresado esto cuantitativamente, tenemos que el volumen acumulado en el tiempo (t) en un segmento vascular es igual a la diferencia entre la tasa de influjo (Q1) y aflujo (Q2) a su través:
A su vez, este volumen acumulado es función de la presión transmural del sistema:
Sustituyendo en la ecuación (10):
Lo cual, por integración da:
Aquello que estas ecuaciones señalan es la interdependencia entre el volumen sanguíneo (o su derivada tempórea, el flujo), el flujo (o su integral tempórea, el volumen) y la presión transmural en un segmento vascular, lo que oportunamente puede llamarse «relación flujo-presión-volumen» (Q-P-V) de un sistema compliante.
Esta expresión quiere decir que el flujo determina el volumen, y los cambios de volumen (capacitancia) afectan el flujo, en proporción a cambios aparejados en la presión transmural del sistema. Al mismo tiempo, resulta particularmente útil para describir la dinámica del modelo bicompartimental de Krogh, ya que ambos canales guardan una relación Q-P-V opuesta en cuanto a la repercusión sobre el volumen vascular central, y por lo tanto el gasto cardíaco.
Esta dinámica es lo que groseramente refleja la pendiente lineal negativa entre las presiones venosas centrales y el flujo sistémico en los experimentos clásicos de Guyton, Grodins y Levy: la redistribución flujo-dependiente del volumen sanguíneo dentro del circuito23,24, la cual ha sido testada en la circulación humana intacta, bajo el efecto fisiológico del estrés térmico (temperatura corporal), hidrostático (posición corporal y presión atmosférica), y metabólico (ejercicio) en numerosos laboratorios de fisiología durante la segunda mitad del siglo xx.
Es decir, que la volemia fluye, pero a al mismo tiempo se «distribuye». Aun cuando Q=0, la presión en el sistema es homogénea PM≅7 mmHg, pero el perfil de volemia es heterogéneo: más volumen en el sistema venoso y menos en el arterial, según CV/CA; la volemia se distribuye en esta instancia de flujo (cero). Cuando el flujo estacionario es inaugurado la volemia se redistribuyeΔVA=−ΔVV, tornándose más empinado el perfil de presión en la vasculatura, según la relación PA/PV=−CV/CA.
A su vez, el flujo no es el único determinante de la distribución del volumen sanguíneo. Dado que el sistema es globalmente compliante, cualquier fuerza hidrostática que actúe sobre cualquier segmento vascular (presiones intratoracoabdominales, fundamentalmente13), o sobre la totalidad del mismo (la distribución de la presión hidrostática sobre la volemia, en la ortostasis, decúbito, inmersión corporal en líquidos), afectará su capacitancia, e indefectiblemente el gasto cardíaco, al menos en cierta medida.
A continuación, completaremos el análisis de la dinámica del circuito sistémico atendiendo específicamente al rol homeostático fundamental del mecanismo de Frank-Starling en la circulación, el significado de la «presión venosa central» y una cuestión relacionada con la aplicación del modelo de Starling en la hemodinámica clínica.
Starling; la «Ley del corazón», la presión venosa central y el resplandor de la hemodinámica funcionalNo es el objetivo aquí realizar una reseña sobre mecánica cardíaca, o de aquellos índices de rendimiento mecánico del músculo cardíaco aislado, que hacen al conocido mecanismo de Frank-Starling o «Ley de Starling» del corazón. Más bien, analizaremos brevemente la significación de este mecanismo en la circulación intacta a través de nuevos conceptos y abordajes que ayudarán a la vez a elucidar la relevancia de una variable particularmente controvertida en la hemodinámica clínica, la «presión venosa central» PVC, así como un aspecto especial de la rationale de la hemodinámica funcional basada en el análisis de la clásica curva de función ventricular de Starling.
Del análisis realizado en las secciones anteriores sobre la dinámica de la circulación periférica, puede notarse cómo la ley de Starling asegura la estabilidad del gasto cardíaco en cierto rango; es decir, que el gasto cardíaco no puede aumentar o disminuir ilimitadamente fuera de los límites impuestos por la pendiente de la curva PVC:Q, ya sea en el formato de Levy o de Guyton. Esta es la consecuencia predecible más importante de la presencia de una bomba cuyo volumen sistólico depende del volumen de fin de diástole, y constituye un mecanismo de autorregulación intrínseca del sistema.
Por otro lado, al considerar el subsistema cardíaco en la configuración de circuito o asa abierta (open-loop) —tal como en el experimento original de Paterson & Starling25—, la identificación de la PAD (y por extensión, la PVC) como variable independiente o causal genera comúnmente cierta confusión sobre la relevancia y el rol fisiológico de esta presión vascular en la regulación del volumen minuto cardíaco. Más específicamente esta confusión recae sobre cuál es la «señal de error»h(error signal)26 a ser corregida mediante el mecanismo de Frank-Starling. De la observación del experimento original podría concluirse que es la PAD misma la variable a ser regulada, dado que es lo que era medido; también podría sugerirse que es el influjo de volumen sanguíneo al corazón derecho (es decir, el QV) la variable clave, ya que los investigadores ajustaban la altura de un reservorio artificial desde el cual la sangre venosa desembocaba en la aurícula derecha del preparado.
Trasladados a la circulación intacta, estas 2 opciones generan aún mayor confusión al ser complementadas con el esquema ofrecido por la «Ley de Guyton», que rige para la vasculatura: ¿cómo puede la PAD al mismo tiempo disminuir e incrementar el gasto cardíaco, es decir, tener algo así como un rol «divergente»?; y en segundo lugar, considerado el QV como la variable conductora del experimento, tal suposición implicaría un mecanismo de retroalimentación positivo en el circuito, en el cual un aumento del QV produciría un aumento del gasto cardíaco QC, siendo esto claramente inconsistente fisiológicamente.
Pocos autores se han preocupado por estas inconsistencias o aparentes paradojas, y sus aportes atingentes a esta problemática serán someramente analizados aquí. Comenzando por la definición de lo que representa cualquier presión vascular, la PVCno es un caso especial; según la ecuación (13):
La PVC representa la presión del volumen sanguíneo acumulado sobre el tracto de entrada del corazón, resultante de cualquier diferencia entre la tasa de influjo y aflujo QV−QC a través de la bomba26; como todo volumen vascular depende de la presión transmural, y por lo tanto de las fuerzas hidrostáticas circundantes, determinando el lleno del corazón derecho y el gasto cardíaco a través del mecanismo de Frank-Starling, resaltando el concepto de que el sistema venoso y el ventrículo derecho se acoplan funcionalmente en términos de la relación P-V21.
Por último, un tercer punto de vista puede alcanzarse como resultado de la conjunción de las leyes de Guyton y Starling; lo que muestra la superposición de ambas curvas en el diagrama de Guyton8 es el punto de equilibrio del sistema para los parámetros físico-fisiológicos de ambos subsistemas en un determinado instante, con la salvedad de que obligadamente una de las curvas será siempre graficada en sentido inverso (la variable independiente sobre el eje y)22.
En hemodinámica clínica una cuestión adicional relacionada con el modelo de Starling —particularmente con la curva de función ventricular— presenta una problemática fundamental: el concepto de la precarga-dependencia y la respuesta a fluidos (fluid responsiveness), que constituye la rationale del paradigma moderno de la hemodinámica funcional27. El principio de este método consiste en evaluar una variable dinámica, la variación del volumen sistólico ΔVS, comúnmente a través de parámetros subrogados (conocidos como «parámetros dinámicos»).
Este índice se relaciona efectivamente con la precarga ventricular, y es analizado a través de la curva de función ventricular de Starling como sustrato lógico, determinándose la «posición» en la curva —«pendiente» versus «meseta»— de acuerdo al valor de la ΔVS, y clasificando el estado volémico (volume status) del paciente en «respondedor» o «no-respondedor», respectivamente. Asimismo, esta metodología permite no solamente evaluar la respuesta a fluidos, sino también predecirla a través de la evaluación de la ΔVS y ΔQ luego de maniobras como la elevación pasiva de las piernas, por ejemplo.
No obstante, esta metodología no contempla no solo el hecho de que la decisión terapéutica (la carga de fluidos) basada en los parámetros dinámicos recae sobre una variable no conocida (el volumen sanguíneo), sino que además no tiene en cuenta la propiedad amortiguadora (buffer) que poseen los lechos vasculares de alta compliancia, mediante cambios en su capacitancia21. Un bolo de fluidos puede ser o no amortiguado por la vasculatura, y su efecto no transmitirse al sistema cardíaco en la forma de un aumento de la precarga; y del mismo modo, cambios súbitos del tono vasomotor redistribuirán volumen sanguíneo a veces en una magnitud tal que afecte la precarga ventricular, y por lo tanto la ΔVS y el gasto cardíaco.
Esto quiere decir, en conclusión, que la posición en la curva de Starling depende de la distribución del volumen sanguíneo, y por lo tanto, la rationale de la respuesta a fluidos está basada en una interpretación aislada de la curva de Starling, aislada en el sentido de concebir la precarga ventricular como desvinculada de la capacitancia vascular —principio opuesto al acoplamiento veno-ventricular—21.
Sin embargo, este aspecto esencial ha sido tratado solo en pocas ocaciones28,29, prevaleciendo en la literatura biomédica la discusión relativa a los aspectos técnico-metodológicos y epidemiológicos del empleo de los distintos parámetros dinámicos —tal como en el caso del empleo de la PVC— hasta el extremo de llegarse a plantear la no necesidad de evaluar el gasto cardíaco como variable hemodinámica al ser este efectivamente remplazado por subrogados de la ΔVS30.
Esta crítica no pretende descalificar la esencia de la hemodinámica funcional; si la misma ha implicado un progreso en la práctica clínica, lo ha sido al considerar el gasto cardíaco no ya como variable absoluta y aislada, sino en cuanto a su efectividad y optimización31.
Conclusión: un modelo conceptualEl modelo de la figura 1 muestra un esquema simplificado del circuito sistémico, con la subdivisión central de baja presión (reservorio venoso central —no se muestra la circulación pulmonar—) y alta presión (bomba y aorta proximal), y la circulación periférica, compuesta del sistema arterial y 2 lechos vasculares de diferente compliancia (modelo bicompartimental de Krogh). El circuito es cerrado, global y heterogéneamente compliante.
Una bomba precarga-sensible conduce el flujo de volumen sanguíneo (superficie de color claro), determinando un gradiente de presión en el circuito dP/dx proporcional a la resistencia viscosa de la sangre en el estado estacionario, en el cual solo se manifiesta el componente resistivo del sistema; es decir, en este estado no hay cambios en la relación P-V en ningún segmento vascular, por lo que el flujo puede ser descrito según la notación: PA−PVC=QR.
No hay volumen sanguíneo «no-estresado», ya que toda la volemia se encuentra, por definición, «estresada» (en un punto de la pendiente de la curva P-V), mayormente del lado arterial, y en menor medida del lado venoso. Del mismo modo, la PM no se asocia con un compartimento vascular determinado, corriente arriba a una resistencia determinada, así como tampoco representa el cabezal de presión del flujo en ningún punto del sistema.
El asa rectangular (línea discontinua) señala un ciclo de flujo transicional, en donde una alteración del estado estacionario es producida, en este caso, por una caída del flujo desde la bomba ↓Q; como consecuencia, en una primera instancia la PA disminuye y la PVC aumenta, ya que ΔVA=−ΔVV ha disminuido. Dado que Q a través de la circulación periférica disminuye, V y P en los lechos de alta compliancia descienden pasivamente, ya que la tasa de influjo hacia aquel segmento es menor que el aflujo, según la ecuación (8)↓dV/dt=Q1
La PTM del volumen vascular central (PVC) está en equilibrio con la PTM de la bomba, determinando su volumen de lleno y volumen sistólico (acoplamiento veno-ventricular y ley de Starling). Entonces, la relación P-V aumentada en el reservorio venoso central aumenta el volumen de fin de diástole ventricular (precarga), reclutando el mecanismo de Frank-Starling, restableciendo el gasto cardíaco.
Este ciclo acontece durante una serie de sístoles, durante la cual el volumen sanguíneo desplazado del sistema de alta compliancia es derivado o redistribuido hacia el resto del sistema (área color oscuro). Esto significa que, como consecuencia, la totalidad de la volemia se encuentra ahora a una PM mayor, o mayormente «estresada», respecto al estado previo. En otras palabras, el patrón de distribución de la volemia, y las presiones vasculares, depende del patrón de distribución del flujo.
Conflicto de interesesNinguno.
El autor extiende su agradecimiento a George L. Brengelmann, PhD, del Departamento de Fisiología y Biofísica de la Universidad de Washington; este trabajo no hubiese sido posible sin su ayuda, enseñanzas, inspiración y estimulación. A Sean M. Carroll, PhD, del Departamento de Física del Instituto de Tecnología de California; su devoción y compromiso en la búsqueda y la divulgación de la verdad a través de la ciencia y las leyes fundamentales de la física han sido de mayor inspiración personal. Finalmente, al Dr. Rubén D. Allori, Dr. Gustavo A. Elena y Dr. Carlos D. Romero, por haber apoyado la publicación de este trabajo.
Esto no quiere decir que la gravitación, como fuerza hidrostática, no tenga efecto sobre la circulación. Como será comentado en la sección August Krogh y el modelo bicomparimiental. La relación flujo-presion-volumen, la gravedad afecta la distribución del volumen sanguíneo, la precarga ventricular, y el flujo a través de ciertos lechos vasculares especiales (encefálico, pulmonar funcional y cutáneo), básicamente porque la vasculatura es compliante y colapsable. El énfasis en este parágrafo es sobre el hecho de que la fuerza gravitacional no propulsa un fluido dentro de un sistema cerrado4.
Título inspirado en The big picture. On the origins of life, meaning, and the Universe itself, por Sean M. Carroll.
En su artículo de 1954, Guyton define la «presión media de lleno circulatorio» (mean circulatory filling pressure) como la media de las presiones de todos los segmentos infinitesimales en que puede considerarse dividida la vasculatura, aun en condiciones de flujo.
Para obtener una explicación clara y completa sobre el procedimiento original de Guyton y sobre el equívoco en su interpretación convencional, así como el significado de las «curvas de retorno venoso», y la manipulación algebraica detrás de la ecuación de Guyton, consultar a Brengelmann22.
Simplemente: es el resultado de la redistribución flujo-dependiente del volumen sanguíneo, en su interacción con las propiedades físicas del sistema y la acción otras fuerzas hidrostáticas (ver el apartado August Krogh y el modelo bicomparimiental. La relación flujo-presión-volumen)
Los «análogos hidrostáticos» son modelos conceptuales del retorno venoso guytoniano. Existen varias versiones, siendo la más conocida el «análogo de la bañadera» (bathtub analog), ideada por Magder en 1998. El lector podrá encontrar una descripción concisa de las inconsistencias de este tipo de modelo en Brengelmann15 y Brengelmann16.
La determinación clínica de la PM fue inaugurada por Pinsky y Versprille, separadamente, hacia mediados de 1980, a través de un método conocido como «maniobra de la pausa inspiratoria» (inspiratory-hold manouver). Actualmente existen 5 métodos para estimar la PM en la cabecera del paciente, incluyendo el paro circulatorio. En su rationale, todos los autores coinciden en que la PM es el cabezal de presión del retorno venoso sistémico.
Por practicidad, el análisis del flujo transicional será realizado en el apartado siguiente.
En Teoría del control de sistemas dinámicos la «señal de error» representa la diferencia entre la entrada deseada y la obtenida o medida.