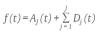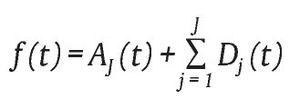Introduction
The study of heart rate variability (HRV) offers a unique view, a window into the complex mind-body connection that exists behind the regulation of life processes, such as blood circulation and breathing. However, the intrinsic properties of the complex autonomic regulation of cardiovascular function are difficult to measure, since, even at rest, it may be affected by emotions and mental loading.
The Soto Zen Buddhist meditation has a targeted approach to the state known as mindfulness. Differently than simple rest or sleeping, during mindfulness meditation the mental contents are observed with emotional detachment, creating a delicate state of consciousness that involves both an extraordinarily attention and deep relaxation. This state is characterized by a sustained awareness of the present moment1,2. Everything arising in the field of perception is contemplated, yet, nothing is preselected, neither analyzed.
An inconsistency in the available studies on meditation lies in what the authors conceive as «experienced practitioners». Some authors refer to experienced meditators subjects with five years of experience, when the psychophysiological response of a subject with 20 years of practice may be essentially different. Bogart3 alerted that «we must note that different effects may be associated with different stages of meditative practice». Therefore, for this work we recruited subjects with varying degrees of expertise.
Methods
Subjects
A total of 37 time series from 13 Zen meditators were analyzed in this study. The constancy and the minimum period of five years of Zen practice were the first criterion for inclusion in the sample. Five years of practice was required in order to select only mindfulness meditators (novice Zen practitioners usually focus the attention on the breath, which often induce voluntary changes in the natural breathing pattern). Exclusion criteria included the presence of cardiovascular disease or any other disease that affect the autonomic balance and the use of any drugs that might influence the results. Participants were between 37 and 50 years of age and between 5 and 20 years of experience in meditation (5 females and 8 males). An informed written consent was obtained from each subject after explaining the experimental procedure. This study was conducted according to guidelines of the Declaration of Helsinki adopted by the World Medical Association for research involving human subjects.
Data collection
Data were collected 2-4 times in each subject in the meditation rooms of Luz Serena Temple (Valencia, Spain) and of Dojo Zanmai San (Tenerife, Spain), which follow the same tradition and are systemically integrated. Subjects were asked to withhold food during the two hours that preceded the recording of data and not to take any stimulant drink in the prior 24 hours.
RR intervals (the time-interval between each heart beat) were measured using the heart rate monitor Polar S810i (Polar Electro Oy, Kempele, Finland). After placing the device, participants were instructed to seat quietly for 10 minutes, in the position they customarily adopt to meditate (cross-legged on a cushion, with the hands held together in front of the navel and the eyes opened) for baseline measurements; then, without moving, they start meditating for 30 minutes. A chime signalled the beginning and end of meditation.
Data management
Data obtained by the Polar S810i, with a sampling rate of 1,000 Hz, were transferred to the Polar Precision Performance Software by means of an interface with an infrared device for signal emission. Data were then edited using UltraEdit text editor (IDM Computer Solutions, USA) and furthered processed using specific programs written in our laboratory in the platform of MATLAB (The Math Works, USA). The measurement errors and ectopic heart beats were visually checked and eliminated manually. The series were interpolated linearly and normalized by subtracting the mean and dividing by the standard deviation.
Data analysis
Multiresolution analysis
In the discrete wavelet transform (DWT) the data sequence is filtered to obtain the wavelet coefficients at different levels: the signal is decomposed into both approximation (cAj) and detail (cDj) coefficients by the use of two quadrature mirror filters. Thus, the DWT analysis can be seen as a filtering operation where the high frequency (highpass) component appears in the detail coefficients cDj and the low frequency (lowpass) component in the approximation coefficients cAj. The detail coefficients are not further decomposed, and at each scale, the detail signal is stored and the decomposition continues filtering the approximate signal which will be taken as the input signal for the next scale. At each decomposition or reference level J, the approximation coefficients cAj and detailed coefficients cD1, cD2, ..., cDj are obtained, and we can reconstruct the approximation signal Aj(t) and the details signal Dj(t), j = 1... J. Therefore, the signal f(t) may be expressed as the sum of a smooth part plus details,
Where each details Dj is associated with changes at physical scale of sj = 2j-1; j = 1... J and the approximations Aj represent variations over scales 2J and higher4.
The properties of a time series at different scales can be summarized by the discrete wavelet variance, which decomposes the variance of a time series in a scale-by-scale basis. However, the number of wavelet coefficients at each scale, obtained by the DWT, decreases by a factor of 2 for each increasing level of the transform, limiting the ability to carry out statistical analyses on the coefficients. This limitation can be overcome if the downsampling in the DWT is avoided by using the maximal overlap discrete wavelet transform (MODWT). Therefore, the MODWT yields an estimator of the variance of the wavelet coefficients for each scale that is statistically more efficient than the corresponding estimator based on the DWT4.
The wavelet variance over scales sj = 2j-1; j= 1... J constitutes a wavelet spectrum, with large values of j corresponding to low frequencies and small values of j corresponding to high frequencies. Equivalent to the spectral density function that decomposes variance across frequencies, the discrete wavelet variance decomposes variance across scales.
In this paper the wavelet variance was estimated from the level J = 6 MODWT using the Daubechies (db6) wavelet filter5. For a better interpretation of the results we defined the scale index, where: the scale corresponding to the approximation coefficient 2J+1 is the scale index 1; 2J, the index 2; and then successively till 21, which is the scale index J+1. Then, each scale index was compared to the standard frequency intervals defined by the Task Force of the European Society of Cardiology and the North American Society of Pacing and Electrophysiology6. Thus, for J = 6, the wavelet coefficients at levels 2 and 4 (scale index 7 and 6) correspond approximately to the HF range (0.15-0.4 Hz); wavelet coefficients at levels 8 and 16 (scale index 5 and 4) correspond to the LF range (0.04- 0.15 Hz); and, finally, wavelet coefficients at levels 32, 64 and 128 (scale index 3, 2 and 1) correspond to the VLF range (≤= 0.04 Hz). The frequency intervals determined by the geometric mean between each two scales may vary depending on the sample interval of each time series.
Principal components analysis
We used an exploratory principal component analysis (PCA) (MATLAB Statistics Toolbox, The Math Works, USA) to analyze the underlying structure of the data, by means of its discrete wavelet variance distribution. The PCA identifies the largest variations in the data through a smaller number of latent variables or principal components (PCs), which present the so called factor loadings or the correlation coefficients with the original variables. The first PC accounts for as much of the variability in the data as possible, and each succeeding component accounts for as much of the remaining variability as possible. A low dimensional representation of a dataset is obtained by projecting the data on a small number of PCs. Each data point in the coordinate system defined by the PCs corresponds to one sample or observation and can be reconstructed by a suitable linear combination (scores) of the PCs.
The PCA was conducted on the correlation matrix of HRV indices defined by the scales indexes. We extracted the normalized wavelet variance in each scale using the MODWT for all HRV time series collected during meditation.
Results
The first important outcome reveals that the rhythmic pattern of cardiac oscillations presented by each subject during meditation is largely reproducible in all sessions recorded. Nevertheless, as expected, we found different results among subjects, though the PCA clearly distinguished the less experienced practitioners from the others, and also revealed subgroups within practitioners with longer time-practice. The dataset distribution when using a scatter plot of the first two PCs reveals three apparent cluster structures (fig. 1). Note that the different observations of each subject were arranged within the same cluster.
Fig. 1. Distribution of data over the two-dimensional space defined by the first two PCs, which account for more than 70% of the overall variance. The samples in black and grey correspond to meditators with more than 10 years of practice, including five Zen instructors and a Zen master. Samples without color correspond to meditators who have between 5 and 10 years of practice.
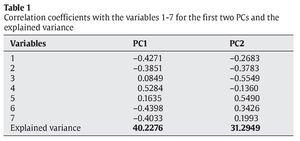
Table 1 shows the correlation coefficients (loadings) for the first two PCs corresponding to the scale indexes (original variables) 1-7 and the explained variance (the proportion to which each PC accounts for the variability in the data).
As shown, the first PC is marked by high positive loading on scale 4, corresponding to LF cardiac oscillations, and negative loadings on scales 1, 2, 6 and 7, corresponding to VLF and HF oscillations. The appearance of a unique high positive loading in the PC1 indicates that this component separates samples which present the variance centered in only one frequency range (LF).
The variables with lower coefficients in the first PC (3 and 5) in turn have high loadings in the PC2; the scale 3 with negative sign and the scale 5 with positive sign. As it can be appreciated in figure 1, all samples represented with grey color share a common pattern of cardiac oscillations characterized by great variability in the scale 3, which corresponds to a higher range of the VLF band. Other samples represented with black color have, in this case, high positive scores in the second PC. These samples also seem to present the variance centered in a specific frequency interval, since the unique high and positive loadings in the PC2 correspond to the neighboring scales 5 (higher loading) and 6.
Figure 2 shows the medians of the variance in each scale for the three clusters. Note the variance centered in the LF range (scales 4 and 5) for the samples in black. It is clear that the more experienced practitioners (black and grey) decrease variability in the HF range (scales 6 and 7), though not all of them share the pattern of predominant LF oscillations.
Fig. 2. The medians of the variance in each scale for the three clusters identified in figure 1.
Figure 3 shows the spectral analysis of RR interval time series corresponding to practitioners with different time-practice. It seems that the HF oscillations gradually shifts to the lower frequency ranges with the pass of the years of meditation.
Fig. 3. Spectral analysis (Welch's periodogram with a Hamming window of length 512) of RR interval time series, in normalized units, corresponding to practitioners with 5 (top left), 10 (top right), 14 (bottom left) and 19 (bottom right) years of meditation practice.
Figure 4 shows the spectral analysis of RR interval time series corresponding to three meditations recorded of the Zen master. The spectral power is narrowly distributed around 0.08 Hz in two of them, though all meditations «produce» almost exclusively LF oscillations.
Fig. 4. Spectral analysis (Welch's periodogram with a Hamming window of length 512) of RR interval time series, in normalized units, corresponding to three meditations of the Zen master.
Discussion
A strong coupling between the HF oscillator, which correspond to respiratory modulation of the heart rhythm known as respiratory sinus arrhythmia (RSA), and the LF oscillations, as a result of a decreased breathing frequency, produces a powerful resonance phenomenon that entrains all rhythms embedded in the heart rate time series to oscillate at the same frequency band. This phenomenon generally occurs in the LF range, around the natural resonant frequency at 0.1 Hz. In this study, we found that practitioners who present a resonance effect may have a lower (scale 4) or higher (scale 5) resonance; however, in any case, they present similar dynamics. The variables which have negative loadings in the first component (1, 2, 6 and 7) behave like oscillating systems that do not fall into resonance, suggesting that different rhythmic processes operate independently of each other and, therefore, VLF, LF and HF oscillations will be present. This is particularly true for the less experienced practitioners (circles with no color) who have higher negative scores in the first component. Less experienced practitioners who have lower scores in the PC1 (values close to zero) present some frequencies interaction due to a decreasing frequency of the RSA that starts to overlap the LF oscillations.
It is clear that the more experienced practitioners (black and grey) decrease variability in the HF range, though not all of them share the pattern of predominant LF oscillations. This result suggests that for some of those long-term meditators there is a weak respiratory modulation (low RSA) in the LF range, causing a decrease in the extent of synchronization between the RSA and the LF oscillations. The intriguing question is why those very advanced practitioners (6 samples within the group represented in grey color are from Zen instructors) do present this kind of dynamics? The most likely explanation is that it might be related to the activity of the «emotional brain», the limbic system, which could affect the parasympathetic outflow and reduce the extent of RSA. It is possible that some kind of «emotional attachment» to the mental content could be preventing a deeper relaxation state.
According to the exposed, it seems that the RSA gradually shifts to the lower frequency ranges with the pass of the years of meditation, probably as a result of a natural decreasing breathing frequency, till it matches and synchronize with the processes underlying slower rhythms. However, why the system evolves this way?
Entrainment between the RSA and the LF oscillations imply in a «low cost mode of functioning» that probably favors the meditation practice. We suggest that a decreased respiration rate and entrainment among cardiovascular rhythms during mindfulness meditation featured by experienced practitioners may reflect a natural physiologic adaptation of the cardiovascular autonomic regulation to this practice. Lehrer et al7 and Cysarz and Büssing8 also found synchronization between the oscillators during Zen meditation, in experienced practitioners.
The Zen master (in two of his meditations) exhibits a narrower resonant peak than the rest of practitioners that present resonance. Resonance within a smaller range of frequencies probably is more difficult to reach, however it is certainly more stable. A well defined resonant peak probably appears among long-term practitioners when the effect of mental oscillations on the breathing pattern is strongly reduced, which may represent a very equable meditation practice.
Conclusion
The present findings suggest the existence of gradual autonomic and cardiovascular adaptations that practitioners experience along several years in order to ascend on deeper meditative states. We found evidences that different stages in the practice of Zen meditation can be characterized by specific patterns of cardiac variability that tend to evolve to a «low cost mode of functioning», characterized by the appearance of resonance phenomena between cardiovascular rhythms, that probably favors the meditation practice.
Regarding the methodology, the scale-based approach inherent to the discrete wavelet methodology allowed a scale-by-scale comparison of the signals and provided an improved estimation of the lower frequencies content. Beyond that, the MODWT demonstrated to be an efficient methodology to use as a pre-treatment step before doing principal components analysis.
Limitations of the study
Sample size: the sample was selected based on availability. Our intention was to find only devoted practitioners, which have always followed the same tradition. Inclusion and exclusion criteria were highly delimiting when selecting the sample. Even so, the fact that we have measured twice or more each meditator gave rise to more reliable results though cannot be extrapolated. In addition, the gender effects cannot be discarded; however, we showed synchronization processes and interactions between physiological oscillators, which probably do not depend on gender.
Acknowledgments
The authors acknowledge Zen Masters Dokushô Villalba and Denkô Mesa Sensei for their guidance and facilitation in this work; and also the community of Luz Serena Temple and Dojo Zanmai San for their sincere collaboration.
Correspondence:
C. Peressutti.
Departamento de Educación Física.
Facultad de Ciencias de la Actividad Física y el Deporte.
Universidad de Las Palmas de Gran Canaria. 35017 Canary Islands. Spain.
E-mail: caroldailha@gmail.com (C. Peressutti).
History of the article:
Received September 17, 2010
Accepted January 8, 2011