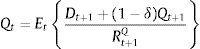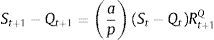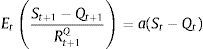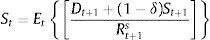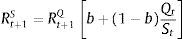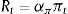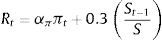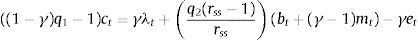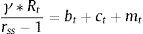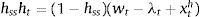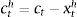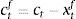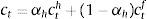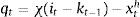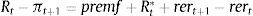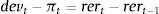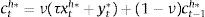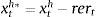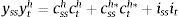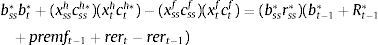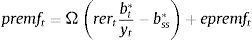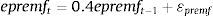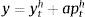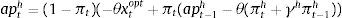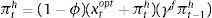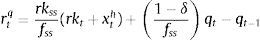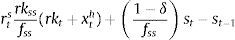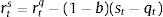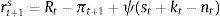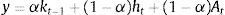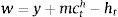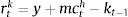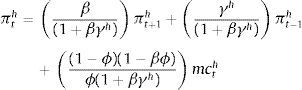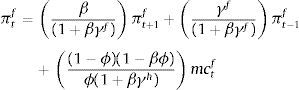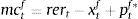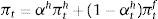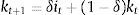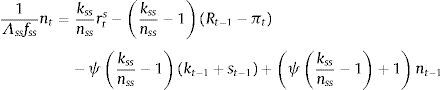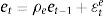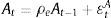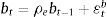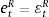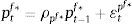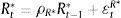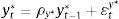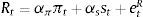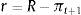Asset price bubbles and monetary policy in a small open economy

Abstract

In this paper we expanded the closed economy model by Bernanke and Gertler (1999) in order to account for the macroeconomic effects of an asset price bubble in the context of a small open economy model. During the nineties emerging market economies opened their financial accounts to foreign investment but generated growing macroeconomic imbalances in these economies. Our goal in this paper is twofold: first we want to analyze if the conclusions of Bernanke and Gertler (1999) remain in the case of a small open economy. And second, we want to compare the results in terms of macroeconomic volatility of the model for a closed economy versus the model for a small open economy. Our results show that the conclusion about the fact that the Central Bank should not react to asset price remains as in the case of a closed economy model, and that small open economies are more vulnerable to asset prices bubbles due to capital inflows and the exchange rate mechanism of the monetary policy. Therefore in small open economies the business cycle is deeper. Finally, in the face of a boom followed by a bust in an asset price bubble, macroeconomic volatility would be dampened if the monetary authority focuses only on inflation.

Resumen

En el presente ensayo ampliamos el modelo de economía cerrada de Bernarke y Gertler (1999) con el fin de tener en cuenta los efectos macroeconómicos de la burbuja de precios de los activos en el contexto de un modelo de economía pequeña y abierta. Durante los noventa, las economías emergentes abrieron sus cuentas financieras a las inversiones extranjeras, pero esto generó un desequilibro macroeconómico creciente en estas economías. Nuestro objetivo con este estudio es doble: en primer lugar, queremos analizar si las conclusiones de Bernarke y Gertler (1999) se mantienen en el caso de una economía abierta y pequeña. En segundo lugar, queremos comparar los resultados en el ámbito de la volatilidad macroeconómica del modelo en una economía cerrada frente al modelo de de una economía abierta y pequeña. Nuestros resultados demuestran que la conclusión acerca de que el Banco Central no debería reaccionar ante los precios de los activos se mantiene como en el caso del modelo económico cerrado, y que las economías abiertas pequeñas son más vulnerables a las burbujas de precios de los activos debido a la afluencia de capital y al mecanismo de tipos de cambio de la política monetaria. Por lo tanto, el ciclo económico está más acentuado en las economías abiertas pequeñas. Por último, ante un rápido incremento seguido de una caída repentina de la burbuja de precios de los activos la volatilidad macroeconómica se vería amortiguada en caso de que la autoridad monetaria se centrase únicamente en la inflación.

1

Introduction

Asset price bubbles are of major concern for scholars and policy makers because of the devastating consequences on the real economy if the bubble bursts. During the nineties emerging market economies opened their financial accounts to foreign investment but it generated growing macroeconomic unbalances in these economies.

The liberalization of financial markets and the globalization of capital markets have improved the provision of financial services and the allocation of resources, but they are also related to more pronounced financial cycles. The deepness of these cycles has usually come hand-in-hand with strong movements in asset prices, amplifying the business cycle and sometimes ending in banking and exchange market crises. Although industrial and emerging market economies had been affected, emerging markets like the ones in Latin America and Asia, had incurred the heaviest costs (Collyns & Senhadji, 2003).

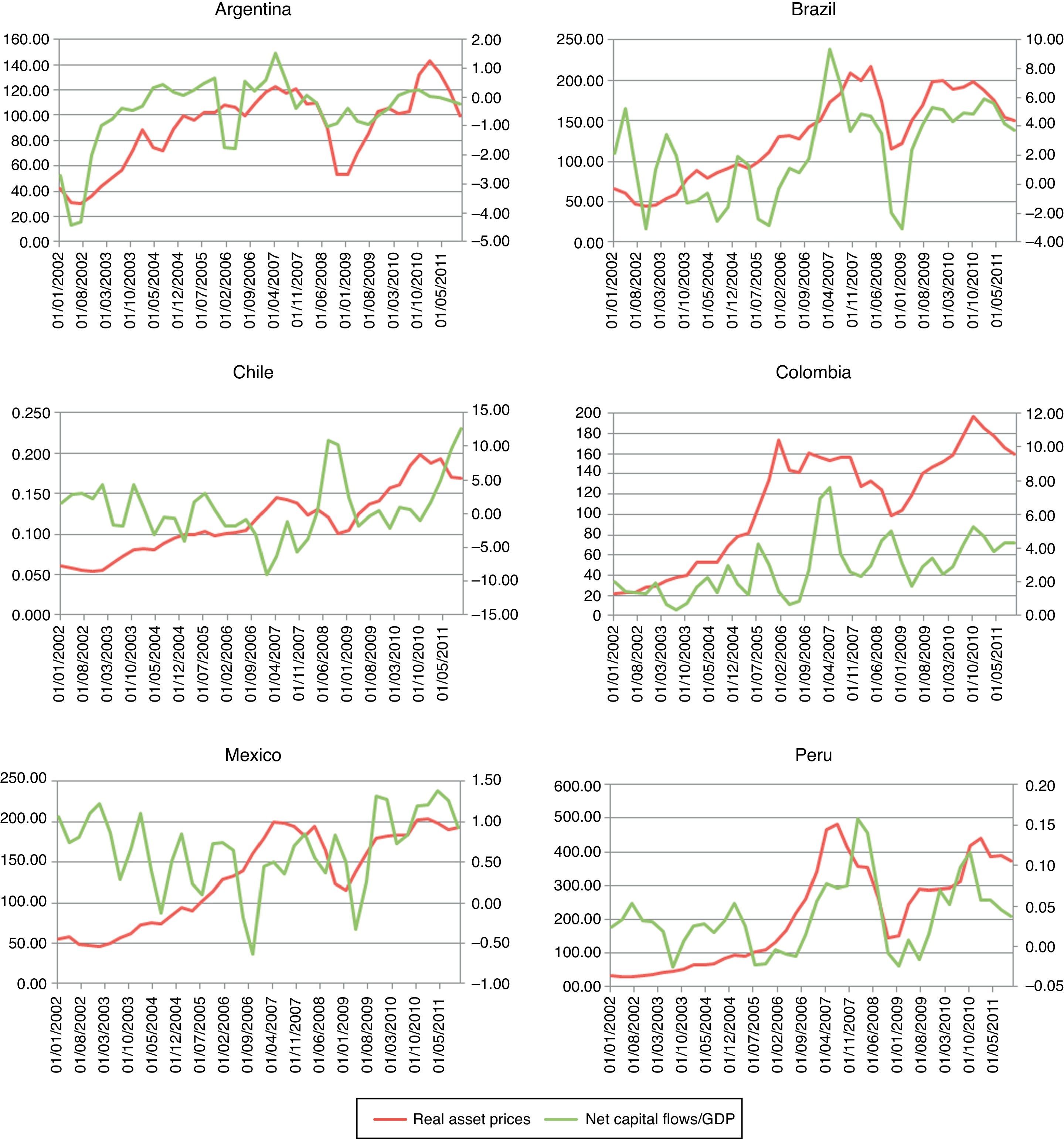
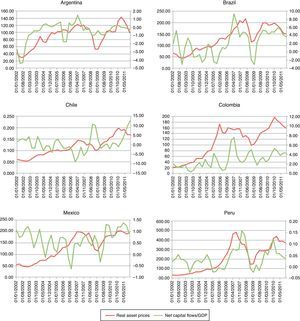
During the 2000s the emerging market economies introduced some regulatory measures to prevent crises like the ones presented at the end of the 1990s. However, capital inflows continue to be a major concern for these economies as they present strong correlation with asset prices overvaluations. As we can observe in Fig. 1, the surge of capital inflows during the 2000s in some Latin American countries has been related with strong movements in asset prices, especially since 2004.

Fig. 1.

Asset prices and Net capital inflows in some countries of Latin America.

As Herrera and Perry (2003) document, the determinants of bubbles in Latin America are not only common external factors (like the degree of overvaluation in U.S. asset prices and the spread between 10-year bonds and three month Treasury-bills) but also some country specific factors like capital flows and terms of trade shocks.

Similarly, during the 1990s, countries like Indonesia, Philippines, Thailand and Korea experienced an extreme capital and asset prices cycle. “Key features of the build up included heady belief in an “East Asian Miracle” capable of delivering rapid economic growth over an extended period; capital account and financial market liberalization that contributed to heavy capital inflows intermediated in considerable part through the banking system; and high rates of investment and rapid increase in asset prices. Subsequently, economic growth suffered set backs, asset markets reversed, and both financial and corporate balance sheets deteriorated” (Collyns & Senhadji, 2003).

In the case of Asian countries, the initial 2007s cracks in the financial system of the West had relatively limited impact. In part, the Asian banking model reflected the relatively conservative regulatory regime developed in the 2000s, in light of the lessons learned during the Asian financial crisis of the late 1990s. Regulators took a relatively conservative approach toward financial stability issues and risk management, Filardo (2011). Additionally, fiscal authorities strengthened their policy in the 2000s generating important fiscal surpluses. Finally, the region had accumulated massive quantities of foreign reserves throughout the decade. However, despite the strong fundamentals of the region, it was finally hit by the international financial crisis in 2008. Research by Kim, Loretan and Remolona (2010) found that most of the sharp increase in the sovereign CDS spreads in the region was due to changes in risk appetite. Along with a rapid reversal of commodity prices it was present a massive wave of investor pessimism that led to an abrupt swing in the mispricing of risk: from a large underpricing of risk before the crisis to a significant overpricing of risks after it. The severe disruption in international, especially U.S.-dollar-denominated, money and capital markets was a major characteristic of the international financial crisis. One lesson from the crisis was that those economies most vulnerable to a shock to external demand suffered heavily, Filardo (2011). Cross-border capital outflows aggravated the situation in countries like Korea which is an economy with fairly liquid and open equity markets.

But asset price volatility is also of major concern for policy makers in industrialized countries. Even though Central Banks have inflation under control, financial instability is one of the major concerns, of which one important dimension is the increased volatility of asset prices, especially since the 1990s. However, as pointed out by Bernanke (2010), even though capital inflows from emerging markets to industrial countries can help to explain asset price appreciation in the countries receiving the funds, we can say that the main source of this financial instability are not the capital inflows but that for example in the recent financial crisis of the United States in the late 2000s, the availability of alternative mortgage products prove to be quite important in the building up of the housing bubble.

Turning now to the study of the proper reaction of the monetary authorities to the presence of bubbles, in their seminal paper of 1999, Bernanke and Gertler address the question of how central banks ought to respond to asset price volatility in an overall strategy for monetary policy. In doing so, they set up a closed economy model, which we will describe below, and they ask the question if the Central Bank, with its nominal interest rate, should react not only to the inflation rate but also to asset prices in the face of an asset price bubble. Their conclusion, as we will replicate it below, is that no, it should not react to asset prices.

In this paper, we extended their model to account for capital inflows and real exchange rate appreciation in the context of a small open economy model. Our goal in this paper is twofold: first we want to analyze if the conclusions of Bernanke and Gertler (1999) remain in the case of a small open economy. And second, we want to compare the results in terms of macroeconomic volatility of the model for a closed economy versus the model for a small open economy.

Our results show that the conclusions about the fact that the Central Bank should not react to asset prices remains as in the case of a closed economy model, and that small open economies are more vulnerable to asset prices bubbles due to the exchange rate mechanism of the monetary policy. Therefore in small open economies the business cycle is deeper. Finally, in the face of a boom followed by a bust in an asset price bubble, macroeconomic volatility would be dampened if the monetary authority focuses only on inflation.

The paper is organized as follows: the first section is this introduction; the second section describes the Bernanke and Gertler (1999) closed economy model; the third section presents our small open economy model and its simulations; the four section concludes.

2

The Bernanke–Gertler model: closed economy model

In their seminal paper, Bernanke and Gertler (1999, 2001) present a closed economy model (CEM) based on the model of financial accelerator by Bernanke, Gertler and Gilchrist (1999) (BGG from now on) but adding an exogenous bubble. The model is a dynamic new Keynesian framework with financial frictions. The agents in the economy are a household sector, a business sector and a government that manages fiscal and monetary authority. Households are infinitely lived and decide labor supply, consumption and savings. The firms are divided into two groups: one that is the group of entrepreneurs who produce wholesale goods and make the investment decisions related with the financing of acquisition of capital; the other group of firms is the retailers that differentiate the wholesale good and make the price setting in the economy à la Calvo (1983).

The flow of funds in the economy is between households and entrepreneurs. Households demand bonds issued by entrepreneurs to finance their investment. Entrepreneurs finance purchases of capital partly with their own net worth and partly by issuing debt. In this setting, the existence of credit-market frictions, that is, problems of information, incentives, and enforcement in credit relationships give rise to an external finance premium (the difference between the lending and the safe interest rate) that depends on the financial condition of potential borrowers: firms with higher equity can offer more collateral to borrowers.

The external finance premium depends on the leverage ratio of firms. This in turn depends on the evolution of net worth, and asset prices. In a standard new Keynesian model, a monetary policy shock will have an impact on consumption, investment and output by the direct interest rate mechanism. In a BGG setting, the shock will have a multiplier effect through the additional effects of asset prices and net worth that will impact further aggregate spending. For example, an increase in the monetary policy interest rate will have a first round effect on the lending rate that will decrease investment but at the same time it will decrease asset prices (discounted value of dividends) and net worth that in turn will negatively affect financial conditions of firms and therefore will increase the external finance premium which worsen the initial reduction in investment: a financial accelerator mechanism.

As pointed out by Bernanke and Gertler (1999) “The BGG model assumes that only fundamentals drive asset prices, so that the financial accelerator serves to amplify only fundamental shocks, such as a shock to productivity or spending”. Their extension to the BGG model is to allow for the possibility that nonfundamental factors affect asset prices.

2.1

Adding exogenous asset price bubbles

Bernanke and Gertler (1999) add exogenous bubbles to the BGG model as follows. Investment is related to the fundamental value of capital, Qt. The fundamental value of capital is the present value of dividends the capital is expected to generate.

where δ is the physical depreciation of capital, Dt+1 are dividends, and Rt+1Q is the relevant stochastic gross discount rate at t for dividends received at t+1.

However, observed price of capital, St, may temporarily differ from fundamental value because of bubbles for example. A bubble exists whenever St−Qt≠0. It is assumed that a if a bubble exists at date t, it persists with probability p and grows as follows:

and pq is close to one, this bubble specification can be made arbitrarily close to a rational bubble. Given that a/p>1, the bubble will grow until such a time when it bursts. The expected part of the bubble follows the process:

Because the parameter is restricted to be less than unity, the discounted value of the bubble converges to zero over time.

It is possible to derive an expression for the evolution of the market price of capital inclusive of the bubble using expressions (1) and (3):

where the return on capital stock, Rt+1S, is related to the fundamental return on capital, Rt+1Q, by:

and b≡a(1−δ).

When there is a positive bubble, St>Qt, therefore the expected return on market price will be below the fundamental return, Rt+1S

A market price of capital higher than its fundamental value will affect real activity in two ways. First, the external finance premium is assumed to depend on the market value of capital. So whenever it is higher than the fundamental value, the financial conditions of firms improve and they will be able to obtain funds at a lower financial premium. Second, there is a wealth effect on consumption.

It is important to notice that “Although bubbles in the stock market affect balance sheets and, thus, the cost of capital, we continue to assume that firms make their investment based on fundamental considerations, such as net present value, rather than on valuations of capital including the bubble. This assumption rules out the arbitrage of building new capital and selling it at the market price cum bubble” (Bernanke & Gertler, 1999).

2.2

Macroeconomic responses under alternative monetary policy rules: the closed economy model

The closed economy model (CEM) presented above has a modification only in the functional form of the utility function which depends on consumption, money and leisure, to resemble the model for the Colombian economy but in a closed economy context. The model is calibrated with some parameters of the Colombian economy in order to do simulations and to compare them later on with the case of the open economy model. The model is closed with two alternative monetary policy rules. The goal of this exercise is twofold: first, we want to replicate the results obtained by Bernanke and Gertler (1999) regarding what type of policy rules are best at moderating the disruptive effects of asset market disturbances. Second, we will compare the results with those obtained with a model for a small open economy presented in section three.

The baseline policy rule is a Taylor rule that responds to inflation:

The alternative monetary policy rule is a rule that also responds to changes in stock prices. Specifically, we assume that the instrument rate responds the once-lagged log level of the stock price, relative to its steady-state value:

2.2.1

Asset price bubbles with response only to inflation: CEM

In order to conduct the simulation experiments we parameterize the equation that governs the bubble process, Eq. (3), so that the non-fundamental component of the stock price increases in the first quarter and the bubble is assumed to last one period and then burst. The panic is unanticipated by investors before it happens, that is, agents know the ex ante stochastic process for the bubble and not the time it will burst.

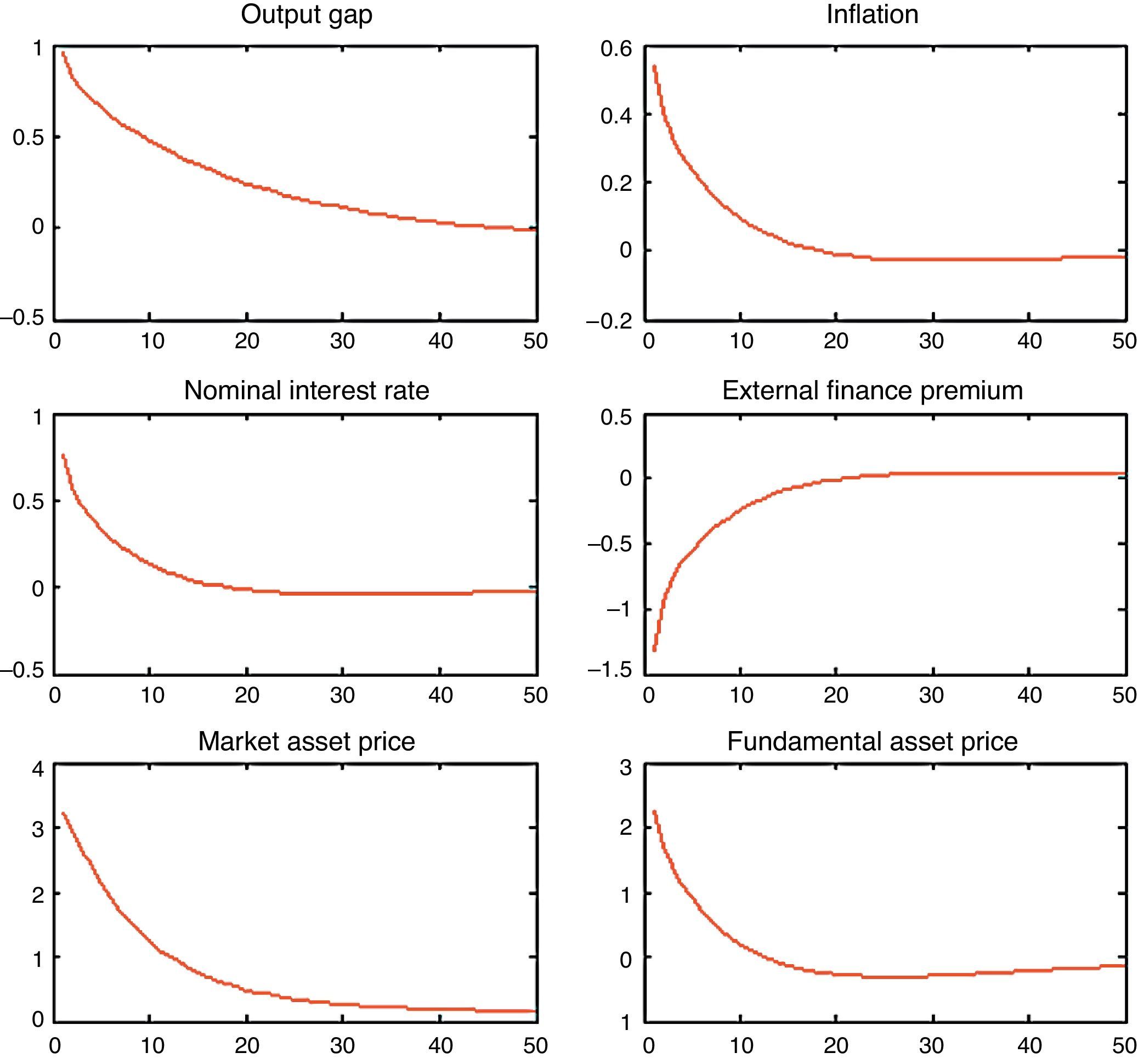
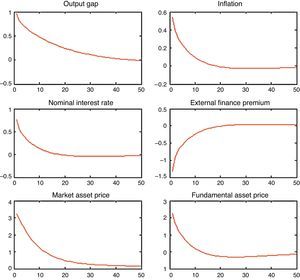
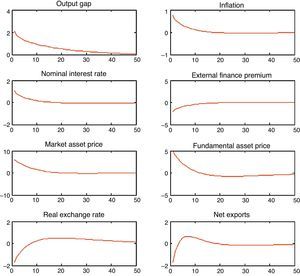
Fig. 2 shows the impulse responses of some macroeconomic variables to a bubble shock. We use a monetary policy accommodative with respect to inflation by setting απ=1.4. As it can be observed, as the market price of capital increases, net worth also increases giving place to the collateral effects described earlier: the financial conditions of firms improve lowering the risk premium, which allows firms to borrow more and finance more investment. This collateral effects stimulate spending. As can be seen, the fundamental value of capital is also positive because of the increase in discounted expected dividends. This stimulates even further investment by the q-theory of investment. When the bubble bursts, there is a corresponding collapse in firm's net worth. The later increases the external finance premium (the spread between firm's borrowing rates and the safe rate) and a rapid fall in output takes place.

Fig. 2.

Effects of an asset bubble when monetary policy responds only to inflation: closed economy model.

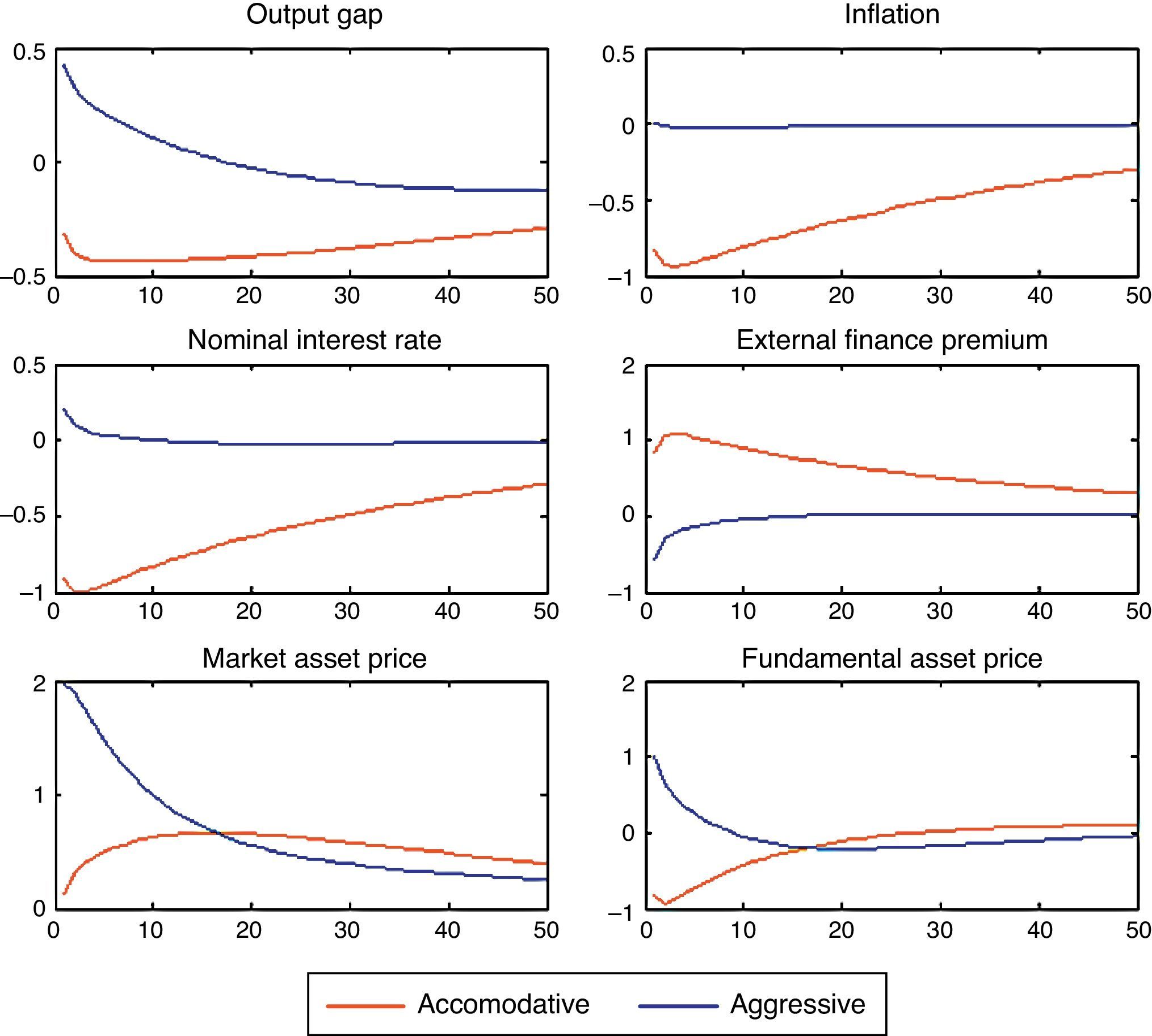
2.2.2

Asset bubbles with a policy response to stock prices: CEM

Fig. 3 shows the macroeconomic effects of the monetary policy when the Central Bank decides to react to asset prices as well as to inflation. In a setting where the monetary policy is assumed to be accommodating with respect to inflation απ=1.4 the monetary policy produces a perverse outcome. Notice that in this case the fundamental price of capital falls and in turn investment and output “The expectation by the public that rates will rise in the wake of the bubble pushes down the fundamental component of stock prices, even though overall stock prices (inclusive the bubble) rise” Bernanke and Gertler (1999). On the contrary, if monetary policy is aggressive in fighting inflation relative to asset prices απ=3, we are again in a result where investment and output increase.

Fig. 3.

Effects of an asset bubble when monetary policy responds to both asset prices and inflation closed economy model.

In this sense, Bernanke and Gertler (1999) conclude that it can be very dangerous for policy simultaneously to respond to stock prices and to accommodate inflation.

3

The small open economy model: SOEM

In this section we briefly describe the additional characteristics of the small open economy model (SOEM). This model was setup and estimated with Bayesian techniques by Lopez, Prada, and Rodriguez (2009) for the Colombian economy. The model is based on BGG and Gertler, Gilchrist and Natalucci (2007). Therefore, the model takes into account both financial market imperfections and also the macroeconomic effects of the exchange rate in a small open economy.

In our setup, households demand not only domestic bonds from entrepreneurs but also foreign bonds from abroad, with their corresponding foreign interest rate and country external finance premium. The country external finance premium depends on the net foreign indebtedness in the economy. Thus, following Schmitt-Grohe and Uribe (2003) we introduce a small friction in the world capital market. The first order condition for the foreign bonds along with the one for domestic bonds results in an uncovered interest parity condition that determines the real exchange rate depreciation.

The consumption bundle of households is composed of domestic and foreign goods. In the foreign sector, we distinguish between the wholesale (import) price of foreign goods and the retail price in the domestic market by allowing for imperfect competition and pricing-to-market in the local economy. At the wholesale level the law of one price holds. Both foreign nominal interest rate and nominal price of foreign goods are taken as exogenous. We assume that foreign demand for the home tradable good depends on international prices and external real output gap.

Finally, as in BGG, at the domestic level, the entrepreneurial sector makes the investment decisions related with the financing of purchases of capital, which are financed with their own net worth and by issuing domestic debt. The marginal cost of funds depends on financial conditions where an agency problem makes uncollaterized external finance more expensive than internal finance (giving place to the external finance premium). This firm produces the wholesale goods. At the retail level, firms set prices à la Calvo (1983). Households consume, work and save. A summary of the log-linearized model is presented in Appendix A.

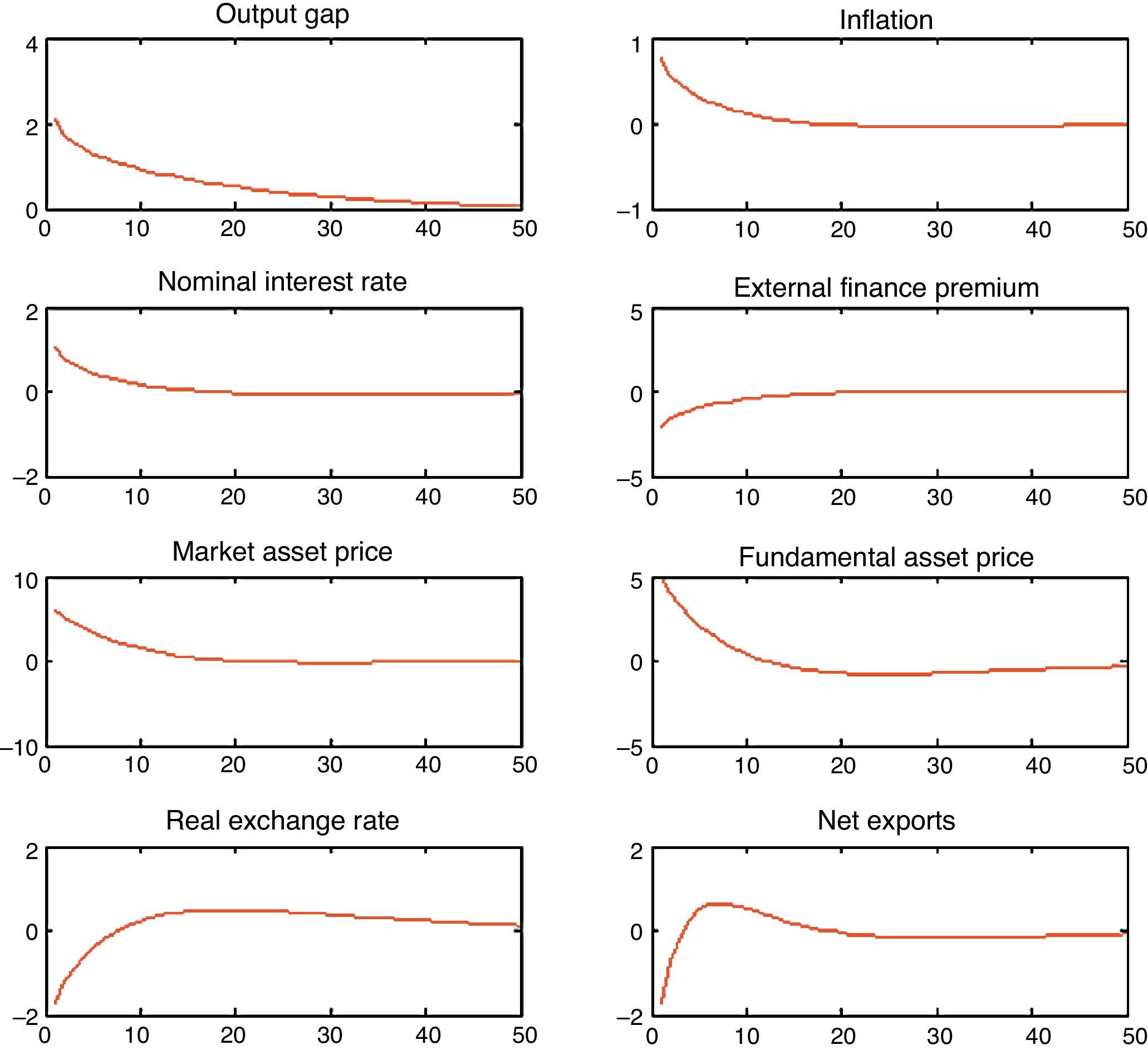
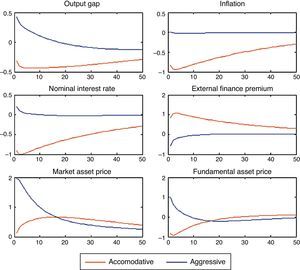
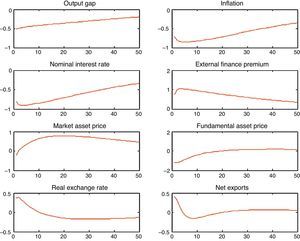
3.1

Asset price bubbles with response only to inflation: SOEM

Fig. 4 presents our simulation results. As in the case of the closed economy, both the fundamental component and the market price of capital rise when the monetary authority targets only inflation. The increase in net worth caused by the increase in the market price of capital pushes up aggregate spending stimulating the rise in the fundamental price of capital and therefore investment. As domestic interest rate responds to inflation, capital inflows appreciate the real exchange rate and we observe an initial net export deficit. One important factor to take into account is that the size of the increase in aggregate spending is higher than in the case of the closed economy model, which is in line with the empirical observations that emerging economies are more vulnerable than closed economies due to capital inflows (see Fig. 2 compared with Fig. 4). This occurs because given the appreciation of the real exchange rate, the market price of assets (which in an open economy depends on the relative price of domestic goods and the household consumption index) is higher than in the closed economy which allows higher collateral effects. This is reflected in the important decrease in the external finance premium relative to the one in the close economy. As a result, the fundamental asset price increases, busting investment, output and inflation rate. The appreciation of the real exchange rate is the result of the increase in the nominal interest rate. In addition, there is a fall in net exports that in the aggregate is compensated by the increase in investment.

Fig. 4.

Effects of an asset bubble when monetary policy responds only to inflation: Open economy model.

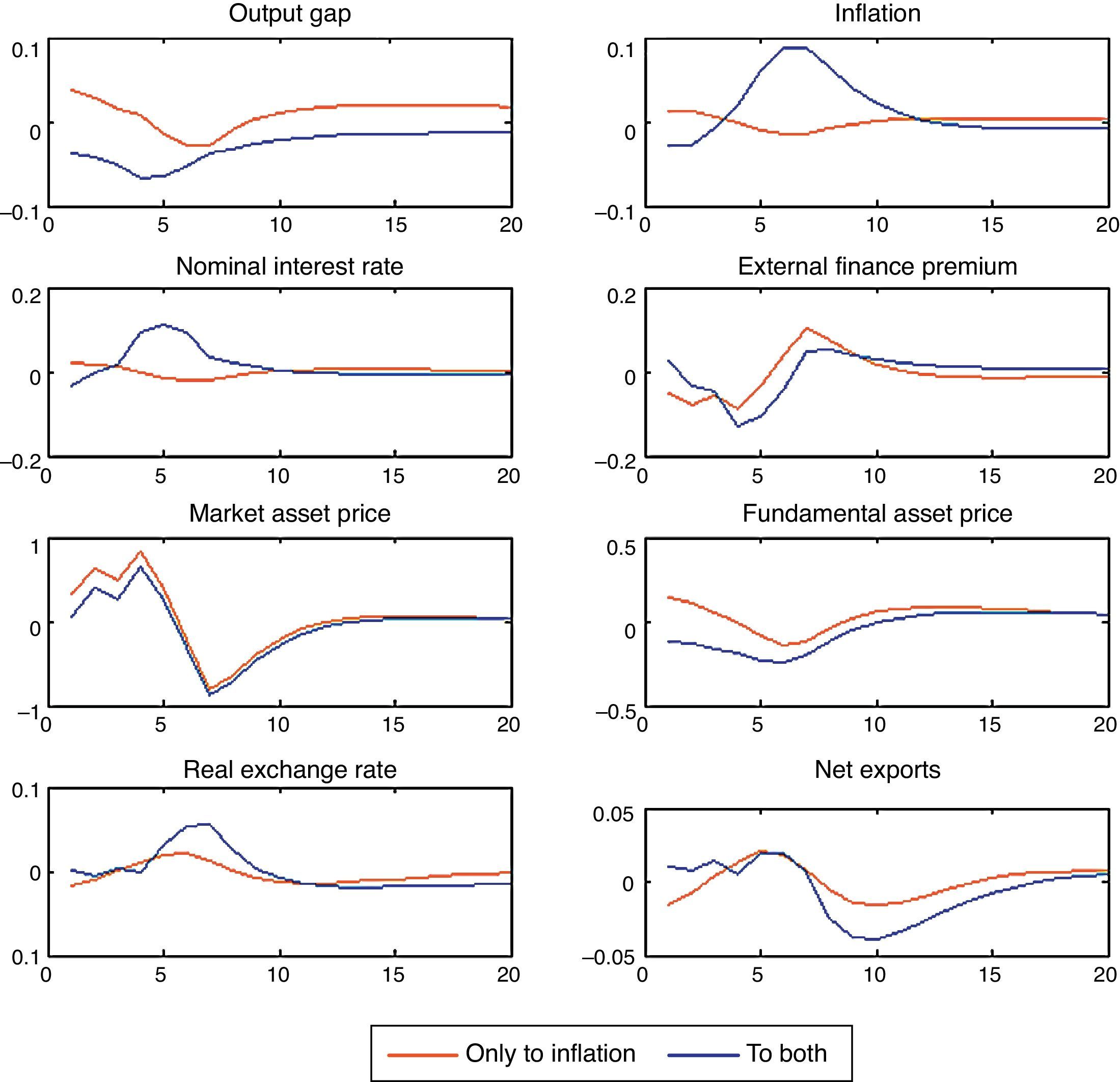
3.2

Asset bubbles with a policy response to stock prices: SOEM

Fig. 5 shows the macroeconomic effects when the Central Bank reacts to both, inflation and asset prices in a small open economy. The results showed here correspond to a monetary authority that accommodates inflation απ=1.4. As in the case of a closed economy, the effect is a fall in output. The monetary authority may generate the recession it pretended to prevent. The transmission mechanism is the same as in the closed economy. Given that agents are rational and they know the Central Bank is going to react to asset prices, they know that the rise in the nominal interest rate will be higher and that this may burst the bubble and future dividends. The fundamental asset price is the discounted value of future dividends and both forces are forcing it to fall (the interest rate and future dividends). As fundamental asset price falls, investment and output fall. With an increase of asset bubble of 1%, the fall in output is higher −0.5% (in the open economy) versus −0.4% (in the closed economy) on impact. This result is due the fact that as the exchange rate depreciates, the market price of assets is lower (relative to the closed economy) and therefore the balance sheet effects are mitigated.

Fig. 5.

Effects of an asset bubble when monetary policy responds to both inflation and asset prices: Open economy model.

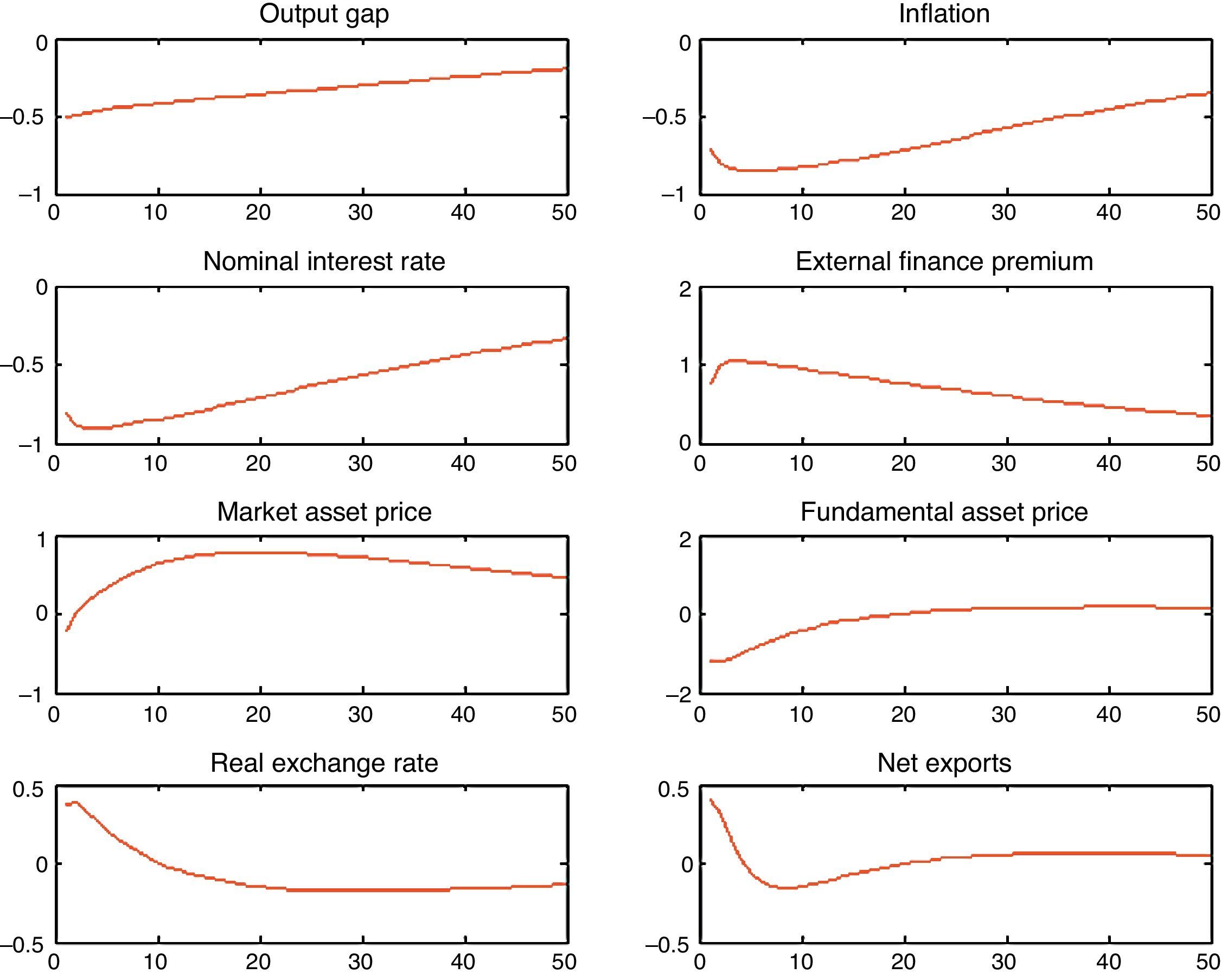
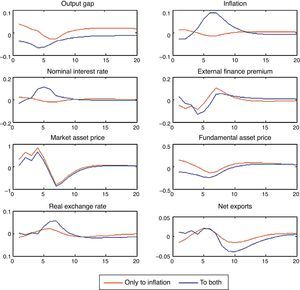
3.3

Asset bubble followed by an asset bust: SOEM

A scenario, which is of at most interest for the monetary authorities given the major consequences for the economy, is one where we analyze what would happen if the bubble bursts generating a negative bubble in stock prices that is exactly symmetric with the positive bubble that preceded it. In this case, we parameterize the equation that governs the bubble process so that the non-fundamental component of the stock price roughly doubles each period, as long as the bubble persists. The bubble is assumed to last three periods and then it is assumed that the crash of the bubble sets off a negative bubble in stock prices that also last three periods. The panic is unanticipated by investors before it happens.

Regarding this possibility, we run two scenarios: one where the monetary authority does not respond to asset prices but only to inflation with an accommodative policy rule, and the other where the monetary authority responds also to asset prices. The results are plotted in Fig. 6. As can be observed in the graph for the market price of assets, the bubble grows until it bursts to generate a negative bubble in the third quarter. In the first case, if the monetary authority focuses only in targeting inflation, the macroeconomic volatility in the economy is not as high as in the second scenario. Macroeconomic volatility is very strong if the Central Bank responds to asset prices. The fall in output is considerable and the inflation rate is very high when the bubble bursts, because due to the depreciation of the real exchange rate the inflation of imported goods increases considerably. The fall in output in the second scenario is the result of the strong initial fall in the fundamental asset price that affects investment. There are two forces acting in this scenario: first, the fundamental asset price falls because forward looking agents know that the monetary authority is going to react to market asset prices and therefore is going to decrease the expected value of dividends. Second, when the bubble bursts, the fundamental asset price falls even more; comparing the fall in this case with the one in the case when the bubble does not burst, Fig. 5, we can see that the fall in the fundamental asset price last until quarter two while if the bubble bursts it falls until quarter six.

Fig. 6.

Effects of an asset boom followed by an asset bust: Open economy model.

4

Concluding remarks

In this paper we expanded the closed economy model by Bernanke and Gertler (1999) in order to account for the macroeconomic effects of an asset price bubble in the context of a small open economy model. In both models balance sheet effects are one of the mechanisms of transmission of monetary policy, but in the later, additional exchange rate mechanisms are in place.

Empirical evidence, addressed in the literature regarding the subject, shows that in emerging market economies capital inflows are one of the most important determinants of asset price bubbles.

The main findings of our model are that when the monetary authority responds only to inflation the surge of an asset price bubble in an emerging market economy faced with capital inflows causes strongest output fluctuations compared to a closed economy. The presence of capital inflows causes an appreciation of the real exchange rate that causes a higher response of market asset prices relative to a closed economy. This results in strongest collateral effects that cause a higher fundamental asset price busting investment and output even further. Similar effects are present if the monetary authority responds to asset prices but in opposite direction. Moreover, if the asset bubble is followed by a crash in asset prices generating a negative asset price bubble, the response of the monetary authority to asset prices generates very strong macroeconomic volatility and output losses.

A similar result has been modeled by Jeanne and Korinek (2010) and Korinek (2011) in a context of a model where there are externalities associated with financial crises because individual participants do not internalize their contributions to aggregate financial instability decisions. Models like ours and the one just cited call for the introduction of capital controls imposed for prudential reasons. These capital controls have been implemented recently in countries like Brazil in October 24, 2009 after experiencing a 36% appreciation of its currency, and countries like Taiwan in November and similarly in Colombia in May of 2007, Vargas and Varela (2008).

Finally, one of the directions in which this research can move is by relaxing the assumption of perfect information to allow for endogenous bubbles. For example Branch (2012) shows that under this setting, a permanent decrease in the supply of safe assets can lead to a substantial over-shooting of the asset prices from its fundamental value and that when asset prices include a liquidity premium there can be recurrent bubbles and crashes that arise as endogenous responses to economic shocks. Therefore, under this environment it would be fruitful to investigate the “proper” response of monetary policy to asset prices. In a similar setting, Lim and McNelis (2007) try to answer this question but in a context of a model where monetary authorities learn about the laws of motion for inflation rate and Q-growth. They find that under imperfect information it would be optimal to respond to both, but under perfect information it would be not.

Conflict of interest

The authors declare no conflict of interest.