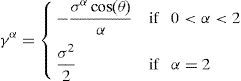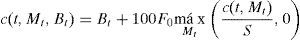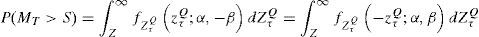Pricing of a structured product on the SX5E when the uncertainty of returns is modeled as a log-stable process

Abstract

This work presents the participation factor and the valuation of a first-generation structured product with European call options on the Eurostoxx, when the uncertainty of the yields is modeled through log-stable processes. The basic statistics of the index yields are also exposed, the α-stable parameters are estimated, and the valuation of the of the structured models is compared through the log-stable and log-Gaussian models using inputs from the bond markets; concluding that investors obtain higher yields than those of the bond market through both models, and that the differences of the yields depend on the participation factor and on the value of the index at the time of liquidation.

Resumen

Se presenta el factor de participación y la valuación de un producto estructurado de primera generación con opciones europeas de compra sobre el Eurostoxx cuando la incertidumbre de los rendimientos está modelada a través procesos log-estables, se presentan los estadísticos básicos de los rendimientos del índice, se estiman los parámetros α-estables y se compara la valuación de los productos estructurados a través de los modelos log-estable y log-gaussiano utilizando insumos de los mercados de deuda concluyendo que los inversionistas obtienen rendimientos superiores a los de los mercados de deuda a través de ambos modelos y que las diferencias de los rendimientos dependen del factor de participación y del valor del índice en la fecha de liquidación.

Introduction

Financial markets have evolved due to information technologies, global competence, and financial engineering, which has innovated the design of products to satisfy the coverage needs of investors and issuers. Structured products have been successful because they provide the possibility of investments with higher yields than those of debt securities when the interest rates are in decline. Structured products are combinations of debt securities and derived products, and are issued by institutions with an elevated credit quality and a low credit risk. They are attractive for investors due to the expected yields, the credit quality, the flexibility of the maturity structure, the design of the issuances, the use of assets, the access to global markets that are otherwise inaccessible, and the capacity for efficient risk management. The Bank of Mexico, the National Banking and Securities Commission (CNBV, for its acronym in Spanish), and the National Retirement Savings System (CONSAR, for its acronym in Spanish) are responsible for the regulation of the structured products in Mexico.

McCann and Cilia (1994) analyze the yields of structured products, concluding that they are superior to those of the market when the yields are on a decline. Lamothe Fernández and Pérez Somalo (2003) analyze the importance of structuring. Gómez Almaraz (2007) indicates that structure products allow investment companies, insurance companies, banks, and pension funds to obtain higher yields than those of the bond markets through the expectations and eventualities of the markets. Venegas-Martínez (2008) analyzes the valuation of the main structured notes. Castillo Miranda (2008) indicates the basic functioning of the structured products. Blümke (2009) encourages the use of structured products as investment instruments. Mascareñas (2010) shows that the issuers of structured products especially acquire the implicit risks, given that they transfer or share them through coverages using derived products. This allows designing products that satisfy the needs of investors who are exposed to credit risk and depend on the credit quality of the issuers. Ortiz-Ramírez, Venegas-Martínez, and López-Herrera (2011) indicate that the valuation of the structured products has a complexity that requires understanding the behavior of the market, knowing specialized theories, and having sophisticated knowledge to determine the prices of structured products which are complex in their design. Wallmeier (2011) indicates that there is concern because the complexity and diversity of the structured products are accompanied by low transparency; in practice, the information provided to the investors focuses on the payment diagrams. Therefore, it is important to improve the information and the understanding of the investors. The structured products are issued by banks, and are negotiated in an organized exchanged or with the issuing bank, who cites offer and demand prices during the validity of the product. The issuers design attractive structured products that have risk-yield profiles that are not easy to replicate by traditional financial instruments, and which provide access to types of assets to which the investors do not have direct access. The investors have difficulty in understanding the characteristics of complex products, and the assessment of just prices is not always available to the public. The empirical studies on the valuation of structured products in the primary market find premiums of 2–6% higher than the theoretical values, the surcharges are more pronounced in emerging markets and are positively related with the complexity of the products. The information suffers because it is focused on the payment profile and not on the probability of the payment profile. The preferences of the investors are characterized by the yield distribution moments: expected yield, volatility, asymmetry, and kurtosis. The yield distribution for structured products of guaranteed capital proposes low volatility, positive asymmetry, and average kurtosis. It concludes that structured products need to be analyzed as a diversified portfolio, and the risk-yield needs to be based on a market balance analysis because the asymmetry and kurtosis characteristics of the yield distribution can be included in the risk premiums. Cao and Rieger (2013) show that, theoretically, the expected yield of the structured products is unlimited, whereas the restriction to estimate the maximum expected loss through the risk value (VaR, for its acronym in Spanish) could be met. They indicate that structured products are a type of financial products that combine financial instruments such as assets and derivatives to achieve specific investment purposes. Guaranteed capital structured products allow investors to participate in the potential benefits of the underlying price, while being protected against potential losses; these products can be created combining a call option and a fixed interest investment. Since the 2008 financial crisis and the payment default of structured products, the understanding of the risk is a crucial factor and a complicated task for investors because knowledge on payment structure is insufficient, and knowledge of the estimation of risks is even more so. In order to attract investors, issuers design structured products that maximize the expected yield and satisfy the VaR restriction, thus reaching any yield profile. They define a risk-yield measure that depends on the gains, losses, and the market parameters in such a way that the risk depends only on the product losses; it is strictly monotonous regarding the losses, it is strictly monotonous regarding the gains, and for a level of risk, the yield is limited, thus it does not allow the investors to only search for a yield with a level of risk and to be deceived. The measure is applied on guaranteed capital structured products, and the risk and yield profiles change when the level of guarantee changes: the lower level of guaranteed capital, the higher the level of risk and a greater measure of yield is obtained. It is concluded that the risk could be “swept under the rug” and structured products can be designed with high expected yields, while investors that follow a strategy to maximize the yields with a given level of risk are deceived to take greater risks. Climent-Hernández and Venegas-Martínez (2013) present a range of α-stable distributions to model financial and economic series. They analyze the orthogonal log-stable model for the valuation of European options, and estimate the distribution parameters of the yields of the peso-dollar exchange through the following models: maximum verisimilitude, tabulation per quantiles of the α-stable distributions, and regression on the characteristic function of the sample. Furthermore, the authors carry out a qualitative analysis to demonstrate the quality of fit of the distribution, and a quantitative analysis to choose the best fit for the distribution. They compare the log-stable model with the log-Gaussian model and a price vector from MexDer. They also show that the log-stable model presents advantages over the log-Gaussian model in the quantification of risk factors such as kurtosis and asymmetry, adequately modeling the dynamic of the yields that present clusters of elevated volatility and extreme events that have a financial and economic impact of amounts above what is indicated by the log-Gaussian distribution. The authors present a comparative analysis assessing European options through the log-stable and log-Gaussian models, showing the differences in the prices of the contingent payments; however, the differences between the log-stable and log-Gaussian valuations are reversed due to a technical error in Eqs. (27) and (28). Therefore, the log-stable valuation is lower for the valuation of options in a close interval to in the money, and higher when the valuation is out of the money. Aguilar-Juárez and Venegas-Martínez (2014) develop an investment strategy with a portfolio of structured notes that guarantee a predictable cash flow upon maturity, and a structured note that begins its validity at the maturity of the portfolio, offering the possibility of obtaining a greater yield than the market with a low level of risk. The authors indicate that in the structured notes markets, investors are averse to risk and take advantage of opportunities with lower risk and a greater yield with guaranteed initial capital or at least a proportional part. They define a structured product as a portfolio with a fixed or variable debt instrument and derived products, which in some cases are options, and state that the most used and negotiated are the structured notes with debt securities and derived products where the options are European, standard, or exotic. They conclude that risk management is growing more complex and requires strategies that allow investors to satisfy their needs for guarantee on investment and greater yields. To reduce the risk of an investment, it is possible to develop strategies by combining both traditional financial products and derived products into a single product. Hens and Rieger (2014) demonstrate that for rational investors with correct and constant risk aversion beliefs, the gains of the structured products over a portfolio with risk-free asset and the market portfolio are lower than the market rates; the result is equal if the investors continuously operate the risk-free asset and the market portfolio without cost or if they purchase the assets and keep them until the maturity of the structured product. Considering the prospective theory, or investors with erroneous beliefs, the gains of the payments can be considerable. The authors also indicate that structured products include financial derivatives and the payment at maturity depends on one or more assets. These products are issued by banks and are directed to retail investors. The optimal structured product is calculated and it is evaluated if there is a significant increase in the utility. It is concluded that the increase in the utility of the better structured products is of 10 base points, and said increase is small compared to the 200 base points paid by structured products over a risk-free asset and the market portfolio, without considering compensation for the counterpart risk of the investor. There is no evidence that the Neumann–Morgenstern's expected utility model can explain the demand, but the utilities of the prospective theory with non-rational beliefs could be greater. Ilin, Koposov, and Levina (2014) propose using structured products as an investment portfolio management strategy combining options, assets, bonds and swaps. The authors develop a model that allows outlining the strategy to build and manage the portfolio with a regulated level of risk. Furthermore, they indicate that the structured products offer exposure to markets with different characteristics and structures that provide precision to the investors for specific investment strategies, they can combine characteristics from the capital market (possibility of unlimited gains), bond market (fixed income) or bank deposits (limited risk); this allows establishing the risk and the yield is lower than that of the underlying investment. The buyers are private investors and investment funds. The market of structured products increases during the growth of volatility. The structured products are directed to maximize the value of the assets of the investors, the benefits are comprised by the yields of the risk-free assets and the yields of the options; if the options are not exercised, the value of the assets is reduced. The risk-free interest rate must be the minimum limit of the yield. The disadvantages are: First, the investment strategy cannot be planned in full, that is, there is a risk of making erroneous decisions; second, a significant part of the assets must be invested in risk-free instruments with low returns; they are a progressive approach to the management of capital. The authors conclude that the issuers take advantage of the campaign promotion opportunities to offer unusual investments. Schroff, Meyer, and Burghof (2015) study the impact of the demand for information by the investors regarding the negotiation of investment issued by banks using structured products that are designed for retail investors. They indicate that the demand for information positively predicts the speculative negotiation activity. Furthermore, they find a positive relation between the demand for information of the market and speculation when investing. The demand for information does not encourage investors to take long or short stands, which entails a low efficiency. The authors indicate that the hypothesis that the financial markets are informative efficient rests on the assumption that the prices immediately answer to the information; however, the incorporation of information to the prices requires the investors to have access to all the information and to pay attention to said information for it to be considered in the decision-making process. When retail investors are interested in investing on a company, it is likely that they obtain information through search engines; institutional investors are more prone to using sources of information from financial data providers such as Bloomberg. The structured products market can be divided into long-term investments with conservative payment characteristics and speculative investments designed for short-term strategies. The design allows the investors to obtain benefits from the increase or drop in the underlying prices. Investment structured products are for long-term investment strategies and are used by retail investors in saving plans. The authors conclude that there is a positive effect in the demand for information in speculative negotiation and that there is no relation in the long-term investment activity, therefore, the information efficiency of the structured products market is limited.

The objective is to evaluate a structured product that includes a bond and a European call option on the Eurostoxx. The proposal is to use the options valuation theory and, given that the yields present leptokurtosis and asymmetry, it is suggested that the valuation of the options is done using the model presented in the research by Climent-Hernández and Venegas-Martínez (2013), innovating in the valuation of first-generation guaranteed capital structured products. This innovation is done using log-stable distributions to adequately model the dynamic of the yields (leptokurtosis, asymmetry, fluctuations distant from the mode or extreme values, property of stability, or persistence) with clusters of elevated volatility. It considers improbable extreme events in the context of the Gaussian distribution that have superior frequencies and a financial and economic impact of greater amounts in the markets, which allows comparing the valuation of the structured products through the log-stable and log-Gaussian models, as is the limit case of the log-stable model when α = 2. Thus, the log-stable applications are broader than the log-Gaussian application.

This work is organized as follows: In Section ‘The purchase structured product’, the guaranteed capital structured product referenced in index SX5E, the calculation of the capital invested in the bond, and the calculation of the participation factor for call options on the index are described; Section ‘Valuation of the purchase structured product’ shows the valuation of the bond using an instantaneous interest rate equivalent to the simple interest rate and the valuation of the log-Gaussian and log-stable options; Section ‘Analysis of the Eurostoxx yields’ presents the analysis of the index yields, the estimation of the basic statistics, the estimation of the α-stable parameters, the goodness of fit tests, the index performance, and the performance of the volatilities; Section ‘Valuation of the structured call product on the Eurostoxx’ presents the estimation of the implicit scale parameter, the performance of the volatilities and historical scales, the performance of the log-Gaussian and log-stable options, the performance of the bond, the calculation for the monetization of the options, and the performance of the log-Gaussian and log-stable products; Section ‘Conclusions’ presents the conclusions of the research paper, and the bibliography is presented at the end.

The purchase structured product

The structured product object of this study is a portfolio comprised by a bond and the long position of European call options on the SX5E index, issued on September 4th, 2014, with a maturity of August 28th, 2017 (fixing date), and with a liquidation date of August 31st, 2017 (validity period of 1092 days for the maturity of the bond). The guaranteed capital structured product is known as the purchased structured banking bond without loss of capital at maturity. And, indexed to the Eurostoxx, it has a refundable percentage of the initial amount at 100% maturity, in pesos, when there is a drop in the SX5E index; that is, it has a maximum loss of 0%. The structured product must invest in the bond in the following quantity:

where B_T is the nominal value of the bond, T is the maturity time of the bond, τ=T−t is the remaining time of the bond, and i is the instantaneous interest rate equivalent to the simple interest rate i_s; so that i=365τ ln1+isτ360 is the applied rate in the structuring. The remaining capital for the long option in European call options on the Eurostoxx is:

thus, the participation factor is obtained through the quotient:

where c (0, M₀) is the European call option value on the Eurostoxx on the date of issuance.

The guaranteed capital call note protects the nominal value of the investment one-hundred percent; so, the future yield is at risk, since the worst-case scenario has a null value for the payoff of the option, whereas the payoff of the bond is B_T. Thus, the investor at least receives the invested capital plus the interests; if Eurostoxx increases its value, the payment of the option increases the value of the call note. The call note c(t,Mt,Bt) on an option issued on Eurostoxx is a debt instrument with an implicit yield variable (zero coupon) equivalent to the bond market value (fixed income), which is paid off in a single payment, in pesos, at the maturity of the structured product plus the yield value (variable income) of the participation factor of the c(t,Mt) option. The payoff for this last option is also made in a single payment, in pesos, at the maturity of the structured product. The objectives of the investors in this case are to speculate, while taking advantage of the expectations for the rise of Eurostoxx, obtaining a coverage for existing risks in the investment portfolio or obtaining an investment in a market to which they do not have direct access. The structured call note on Eurostoxx is of first-generation given that the options are not exotic, there is only one yield rate, the maturity date for the bond coincides with the payoff date of the options, and the yield rate is the LIBOR-EURO rate because the options on the index are issued by a European institution and the investor is the issuer that monetizes, in pesos, the gains for the options. This structured product is successful due to the understanding of it by investors and issuers, where the investors wait for the index value to increase and the issuers must transfer the price risk through derived products. In September 2014, the amount in pesos of the call notes increased to 35.3465% of the negotiated amount, taking first place.

Valuation of the purchase structured product

The call note on Eurostoxx is a portfolio comprised by a bond and the participation factor in European call options on Eurostoxx, thus, it is necessary to appraise the bond and the options with market inputs. The price providers in charge of giving certainty to the market calculate the theoretical value of the European options on the index, the theoretical price of the bond, and publish the theoretical value of the structured product. The evidence that the underlying yields present leptokurtosis and asymmetry as observed in the works of Dostoglou and Rachev (1999), Čížek, Härdle, and Weron (2005), and Climent-Hernández and Venegas-Martínez (2013) lead to the proposal that the valuation of the options should be carried out through the model suggested in the research work of Climent-Hernández and Venegas-Martínez (2013) using log-stable distributions that adequately model the leptokurtosis, asymmetry, fluctuations distant from the mode (extreme values), and the stability property (persistence) of the yields. This is because they are an effective alternative to modeling financial and economic series with clusters of elevated volatility, extreme values with frequencies superior to the log-Gaussian distribution, and which have a financial and economic impact of greater amounts. Furthermore, they satisfy the central limit theorem because the yields are within the attraction domain of a log-stable law in which the log-Gaussian distribution is the limit case of the log-stable model when α=2, and it has been shown that it is not efficient to adequately model the leptokurtosis, asymmetry, the events distant to the localization parameter, and the stability property observed in the yields of the financial and economic series. On the other hand, the log-stable yields satisfy the stability property that allows modeling the empirical series by optimizing the performance of the system, thus, the applications of the log-stable distributions are broader than the applications of the log-Gaussian distribution that consider extreme and improbable high impact events that are more frequent for the α-stable distributions. This allows comparing the valuation of the structured products through the log-stable and log-Gaussian models. The valuation of the bond is done with the following equation.

where the instance t∈[0,T]. The valuation of the European call options is done using the log-Gaussian model:

where

Using the assumption that the yields have a log-Gaussian distribution where M_t is the index value, S is the payoff price (3172.63 points), r is the rate of dividends of the index, and σ is the volatility of the index yields. The valuation of the call options is done using the log-stable model:

where

Using the model proposed by Climent-Hernández and Venegas-Martínez (2013) where β is the asymmetry parameter, γ is the scale parameter, and α is the stability parameter of the α-stable distributions.

Analysis of the Eurostoxx yields

The SX5E is the underlying asset used in this research, which is a stock index comprised of the fifty most liquid assets in the Euro zone. The performance of the Eurostoxx during the period of January 4th, 2010, to September 3rd, 2014, is shown in Fig. 1.

Fig. 1.

Performance of the Eurostoxx.

Source: Own elaboration using a spreadsheet.

Fig. 1 shows the performance of Eurostoxx up to the immediate business day prior to the issuance of the structured banking call bond without loss of capital at maturity and referenced to Eurostoxx with 1201 observations that present a minimum of 1995.01 and a maximum of 3314.80 points.

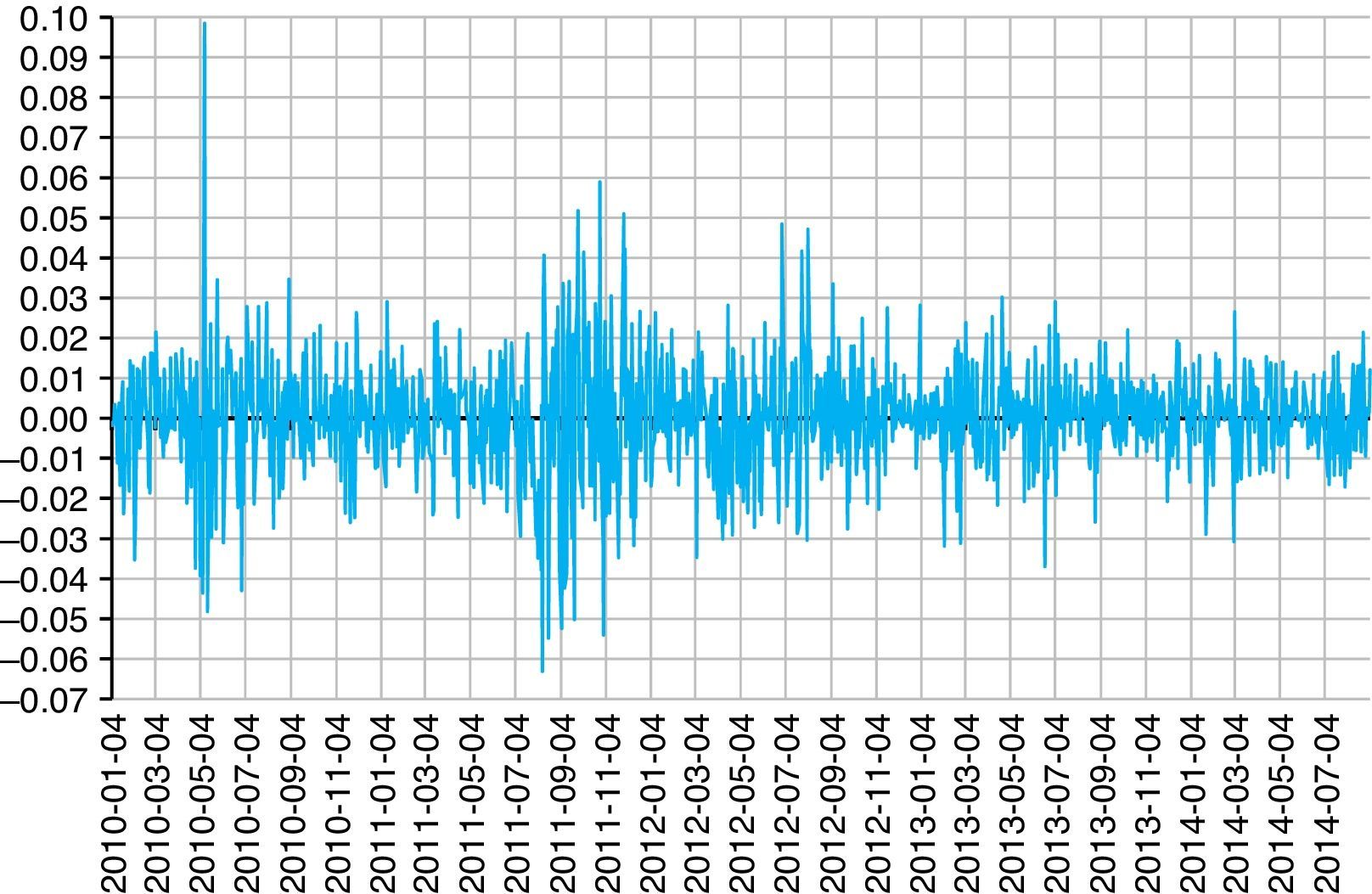
Estimation of the basic statistics of the Eurostoxx yields

The period utilized to estimate the α-stable distribution parameters of the Eurostoxx yields is January 4th, 2010, to September 3rd, 2014, a period which comprises 1201 observations for the index and 1200 observations for the logarithmic yields. The daily yields for Eurostoxx are shown in Fig. 2.

Fig. 2.

Performance of the Eurostoxx yields.

Source: Own elaboration using a spreadsheet.

Fig. 2 shows the performance of the daily Eurostoxx yields that present a minimum of −6.3182 and a maximum of 9.8466%. The performance of annual historical volatilities of Eurostoxx is shown in Fig. 3.

Fig. 3.

Performance of the annual historical volatilities of Eurostoxx.

Source: Own elaboration using a spreadsheet.

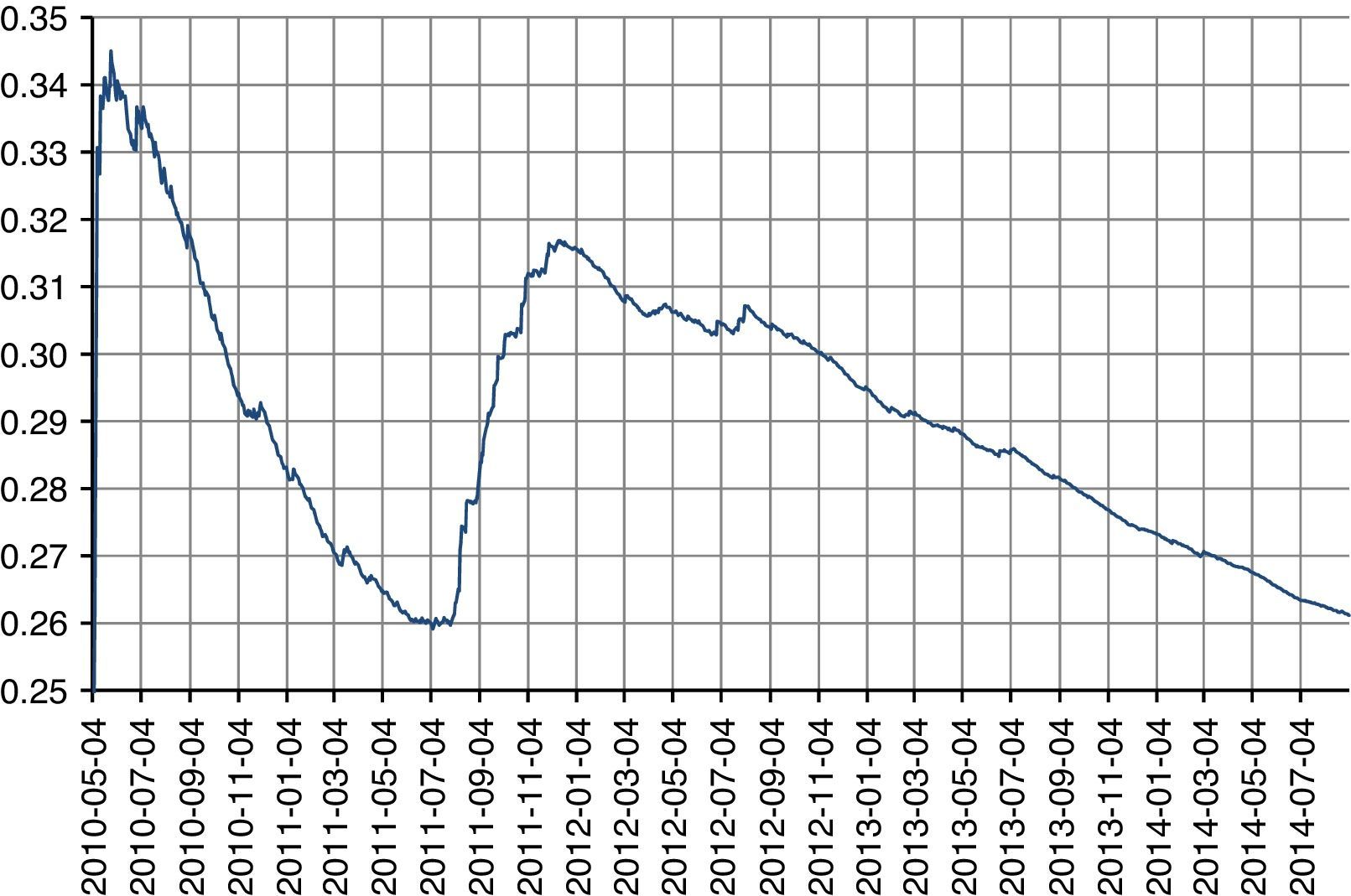
Fig. 3 shows the performance of the annual historical volatilities which present a minimum of 1.08% and a maximum of 34.51%. The annual historical volatilities present a declining tendency since December 11, 2011, and up to the business day prior to the issuance of the structured product. The estimation of the basic statistics of the daily Eurostoxx yields is shown in Table 1.

Table 1.

Estimation of the basic statistics of the daily Eurostoxx yields.

Underlying asset	Minimum	Maximum	Average	Deviation	Asymmetry	Kurtosis
Eurostoxx	−0.063182	0.098466	0.000054	0.013671	0.088444	4.055143

Source: Own elaboration with data from MexDer using a spreadsheet.

In Table 1, the average indicates that the Eurostoxx yields are observable. The positive asymmetry coefficient indicates that the yields have a distribution that extends toward positive values with greater frequency than they do toward the negative values. The Kurtosis coefficient indicates that distribution of the yields is leptokurtic with regard to the Gaussian distribution. Therefore, the Eurostoxx yields have an asymmetric and leptokurtic distribution.

Estimation of the α-stable parameters of the Eurostoxx yields

The characteristics of the Eurostoxx yields indicate that the distribution is asymmetric and leptokurtic. In order to model the yields, the α-stable parameters are estimated using the maximum verisimilitude estimation method, which are the values that maximize the verisimilitude function ℓ(α,β,γ,δX1,…,Xn)=∑k=1nlog(Xkα,β,γ,δ) and which is the most asymptotically efficient estimator. This estimator is given by the Fisher information matrix; and the density function can be expressed in terms of Meijer G functions, a representation that is not practical in evaluating α-stable density functions according to the research by Nolan (2001). The estimation of α-stable parameters at 95% confidence is shown in Table 2.

Table 2.

Estimation of the α-stable parameters of the Eurostoxx yields.

Underlying asset	α	β	γ	δ
Eurostoxx	1.6945 ± 0.0858	−0.1707 ± 0.2349	0.007851 ± 0.000427312	−0.000138 ± 0.000784006

Source: Own elaboration with data from MexDer and the STABLE.EXE program.

The stability and asymmetry parameters of the Eurostoxx yields presented in Table 2 are consistent with the results of the research by Dostoglou and Rachev (1999), Čížek et al. (2005), Scalas and Kim (2006), Contreras Piedragil and Venegas-Martínez (2011), and Climent-Hernández and Venegas-Martínez (2013). The stability parameter with a 95% confidence interval is between the values of 1.6087≤α≤1.7803 and indicates that the distribution of the yields is leptokurtic; the asymmetry parameter with a 95% confidence interval is between the values of −0.4056≤β≤0.0642 and indicates that the distribution extends toward the left extreme with greater frequency than toward the right extreme. These results indicate that the Eurostoxx yields show negative leptokurtosis and asymmetry.

Kolmogorov–Smirnov goodness of fit test

The quantitative analysis to prove the null hypothesis H₀ which indicates that the Eurostoxx yields show an α-stable distribution against the alternative hypothesis H₁ which states that the yields do not show an α-stable distribution, is done using the Kolmogorov–Smirnov statistic shown in Table 3.

Table 3.

Results of the Kolmogorov–Smirnov test.

Distribution	D	D0.90	D0.95	D0.99	Result
Gaussian	0.06187	0.02210	0.02415	0.02792	Reject H0
α-Stable	0.03066	0.03292	0.03653	0.04379	Do not reject H0

Source: Own elaboration using a spreadsheet.

Based on Table 3 and with significance levels of 10%, 5% and 1%, we conclude that the null hypothesis indicating that the Eurostoxx yields present a Gaussian distribution must be rejected, and the null hypothesis indicating that the Eurostoxx yields present an α-stable distribution must not be rejected.

Anderson–Darling goodness of fit test

Another test for the null hypothesis H₀ which states that the yields present an α-stable distribution against the alternative hypothesis H₁ which indicates that the yields do not present an α-stable distribution is done using the Anderson–Darling goodness of fit statistic shown in Table 4.

Table 4.

Results of the Anderson–Darling test.

Distribution	A2	A0.902	A0.952	A0.992	Result
Gaussian	10.27164	0.63235	0.75241	1.03557	Reject H0
α-Stable	1.18344	1.93406	2.49336	2.85856	Do not reject H0

Source: Own elaboration using a spreadsheet.

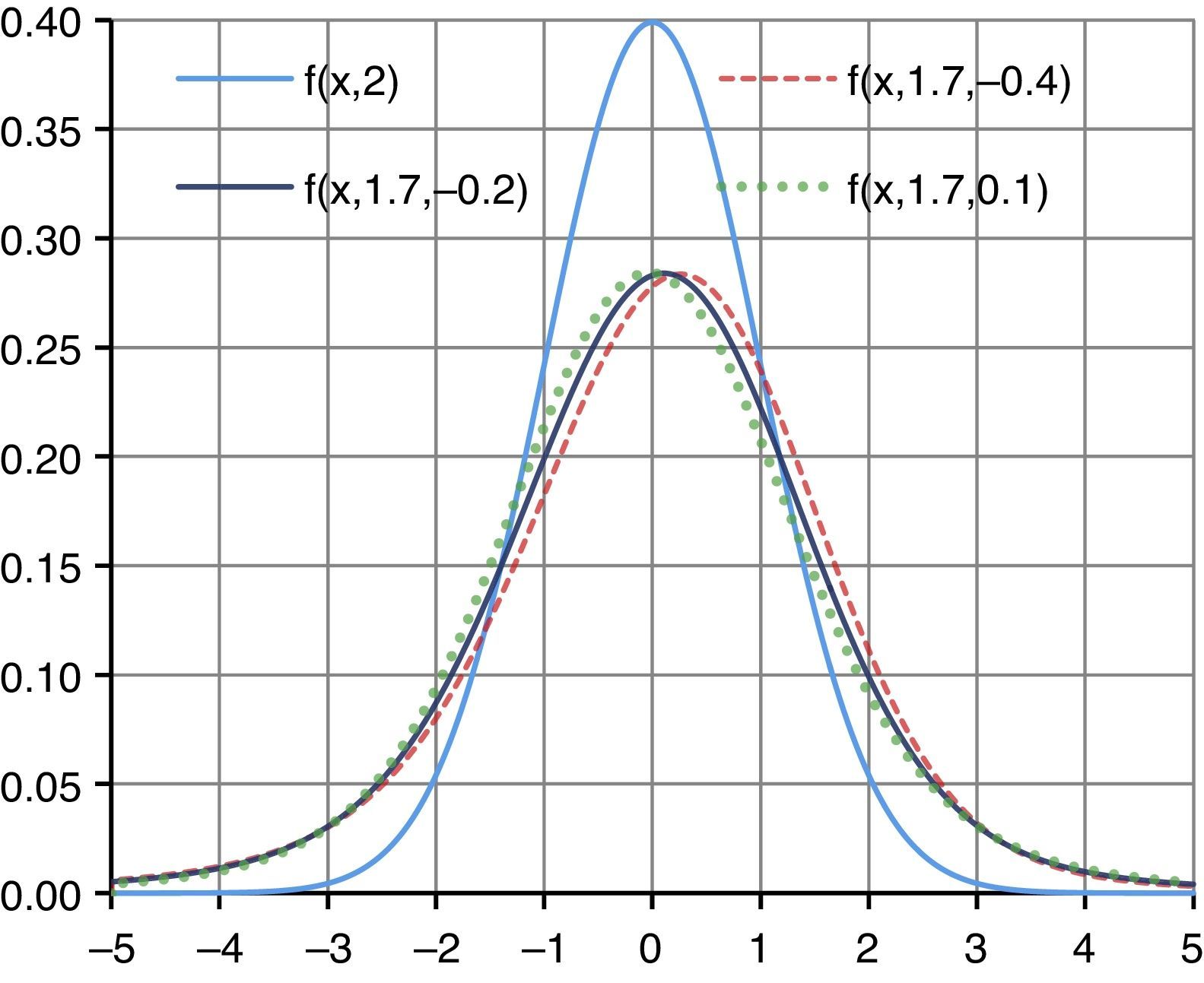
Based on the results shown in Table 4 and with significance levels of 10%, 5% and 1%, we conclude that the null hypothesis indicating that the Eurostoxx yields present a Gaussian distribution must be rejected; and the null hypothesis indicating that the Eurostoxx yields present a standard α-stable distribution fX(x,1.6945,−0.1707) in a fractional probability space must not be rejected. The log-Gaussian distribution and the log-stable distributions with α=1.6945 and the three asymmetry parameters are shown in Fig. 4.

Fig. 4.

Log-Gaussian distribution and log-stable distributions.

Source: Own elaboration using a spreadsheet.

Fig. 4 shows the standard log-Gaussian distribution fX(x,2) with the sky-blue line; the standard log-stable distribution fX(x,1.694,−0.406) with the discontinuous red line shows negative asymmetry, indicating that the mode is located to the right of the mean, mode and median of the log-Gaussian distribution; the standard log-stable distribution fX(x,1.694,−0.171) with the navy blue line shows negative asymmetry, indicating that the mode is located to the right of the mean, mode and median of the log-Gaussian and the standard log-stable distribution fX(x,1.694,0.064) with the dotted green line showing positive asymmetry, indicating that the mode is located to the left of the mean, mode and median of the log-Gaussian distribution (origin). The log-Gaussian distribution indicates that events close to the origin occur with lower frequency than with the Eurostoxx yields, therefore, it can be observed that the log-Gaussian distribution overestimates low financial and economic impact events when −1.53Fig. 5.

Fig. 5.

Log-Gaussian distribution and log-stable distributions.

Source: Own elaboration using a spreadsheet.

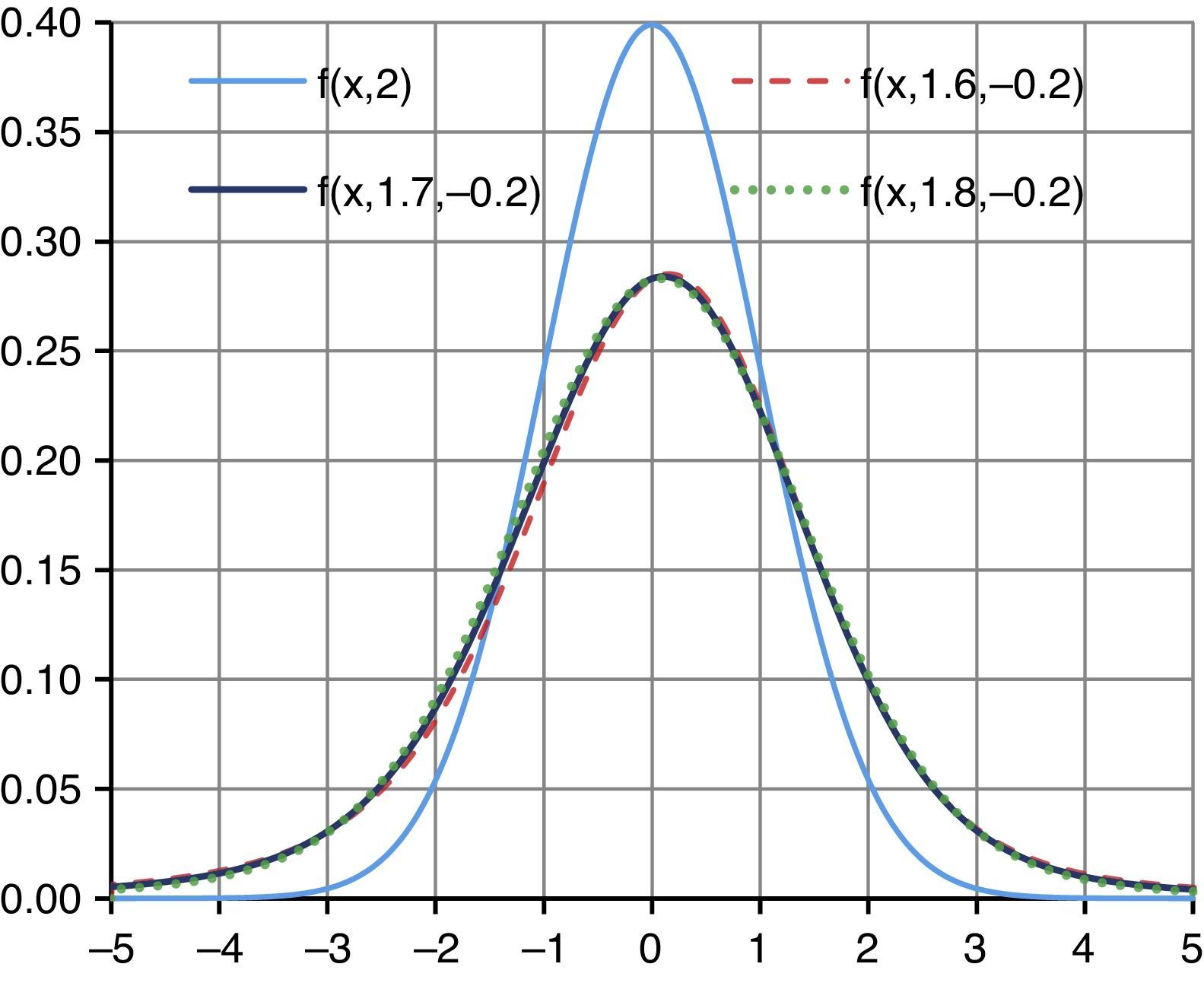
Fig. 5 shows that the log-Gaussian distribution also overestimates low financial and economic impact events for the following distributions: fX(x,1.609) discontinuous red line; fX(x,1.694) navy blue line; and fX(x,1.780) discontinuous green line. It also underestimates high financial and economic impact events for the following distributions: fX(x,1.609) discontinuous red line; fX(x,1.694) navy blue line; and fX(x,1.780) discontinuous green line, where the lowest overestimation is for distribution fX(x,1.609,−0.406) and the highest overestimation is for fX(x,1.780,−0.406), the lowest underestimation is for fX(x,1.780,−0.406) and the highest underestimation is for fX(x,1.609,−0.406). Therefore, we can conclude that leptokurtosis and the bias of the distribution of the Eurostoxx yields provokes that lower financial and economic impact events are overestimated by the log-Gaussian distribution, while the greater financial and economic impact events are underestimated by the log-Gaussian distribution, benefitting the issuers and affecting the investors when the payoff is at an interval close to the market price at the time of negotiation. The performance of the Eurostoxx during the validity period (09-04-2014 to 05-04-2015) of the structured product is shown in Fig. 6.

Fig. 6.

Performance of the Eurostoxx during the valuation period.

Source: Own elaboration using a spreadsheet.

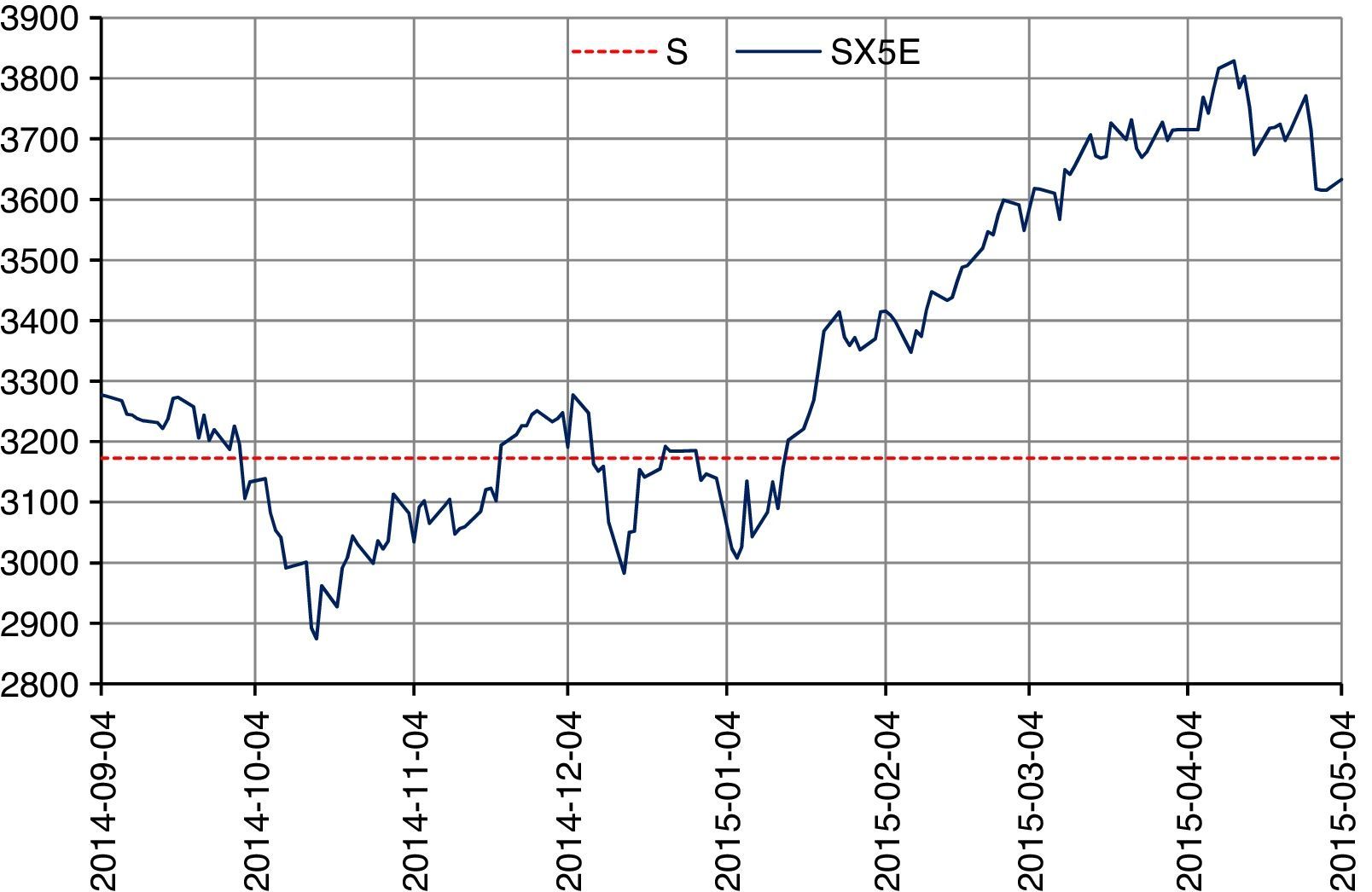
Fig. 6 shows the performance of the Eurostoxx (navy blue line) during the valuation period with 170 observations that present a minimum of 2874.65 points and a maximum of 3828.78 points, the gains are shown due to the value of the SX5E index, beginning on January 16th, 2015, and reaching a maximum on April 13th, 2015. The guaranteed capital structured product has a value referenced to the Eurostoxx that grants gains to the investors when the index goes above the payoff price S = 3172.63 points (discontinuous red line) and has a guaranteed value that reaches $100.00 (one hundred pesos 00/100 MXN). The state of the results for the structured product presents a behavior similar to the long position of a European call option on the Eurostoxx equivalent to a strategy in which the investors speculate on the score of the index waiting for it to surpass 3172.63 points on the date of maturity, generating gains for the investors. On the other hand, when the Eurostoxx does not surpass the 3172.63 points on the date of maturity, the investors receive the nominal value of the banking bond for the amount of one hundred pesos. The state of the results of the purchase strategy is shown in Fig. 7.

Fig. 7.

State of the results of the structured product on the payoff date.

Source: Own elaboration using a spreadsheet.

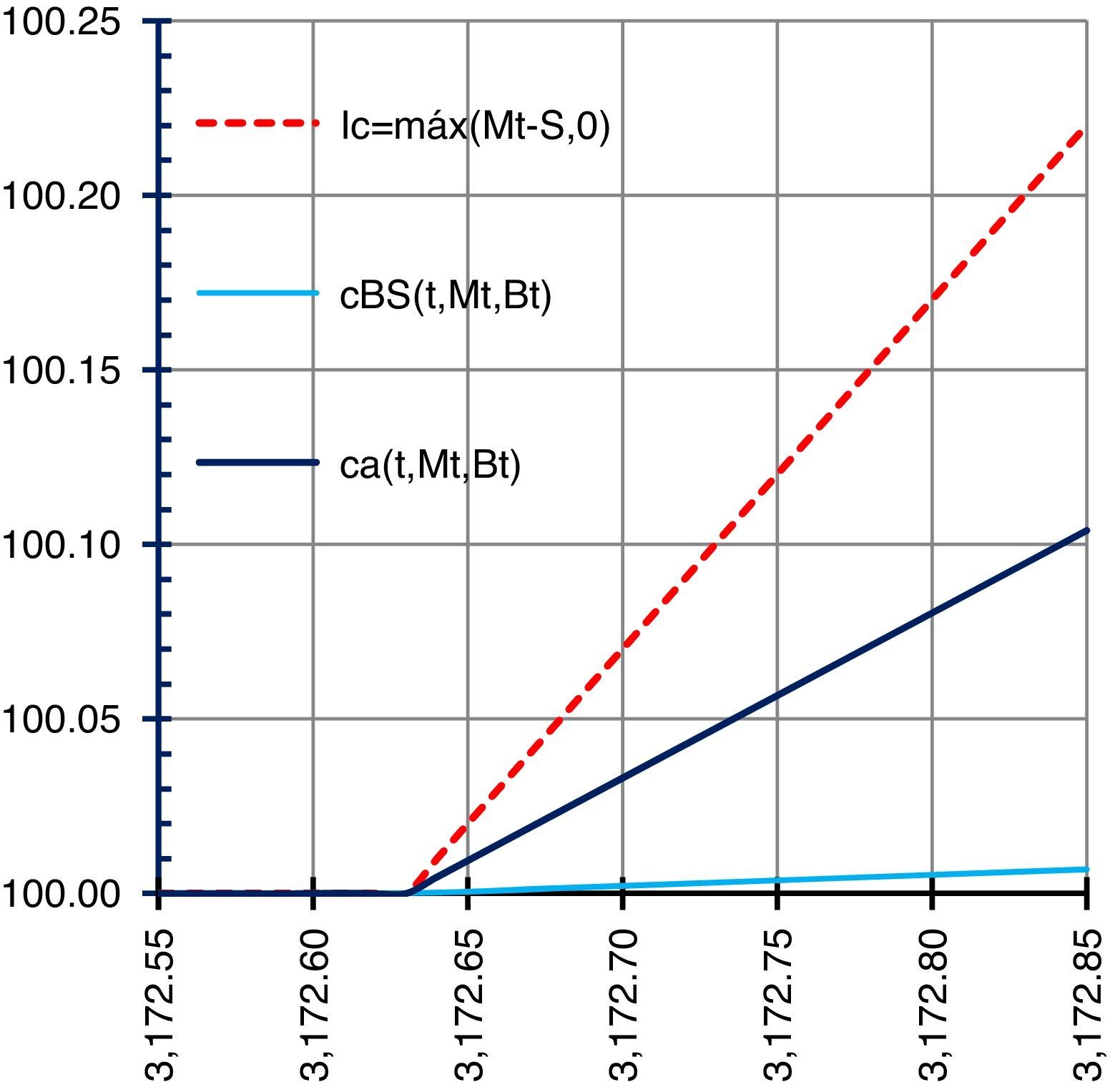
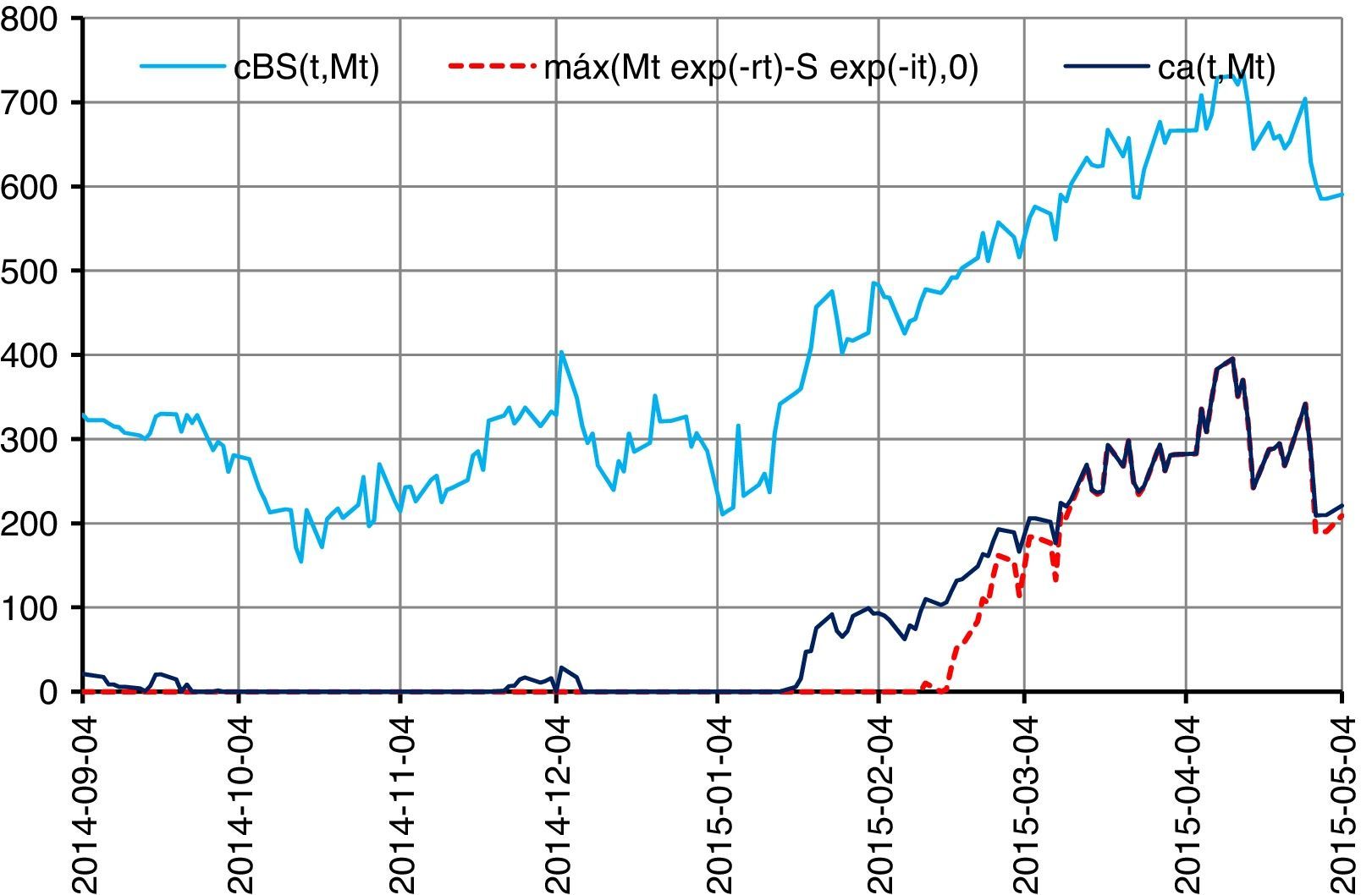
Fig. 7 shows that the gains of the guaranteed capital structured products come from the Eurostoxx value and when this surpasses 3172.63 points on the date of maturity, the gains increase proportionally to the increase of the index. The discontinuous red line represents the intrinsic value of the call options, which is the maximum value of the difference of the market price and the payoff price, or it is zero:

The navy-blue line represents the gain of the log-stable structured product considering the participation factor F₀ and the monetization of the options, which is one hundred times the maximum value of the quotient of the value of the options on the Eurostoxx at the date of maturity and the payoff price or zero:

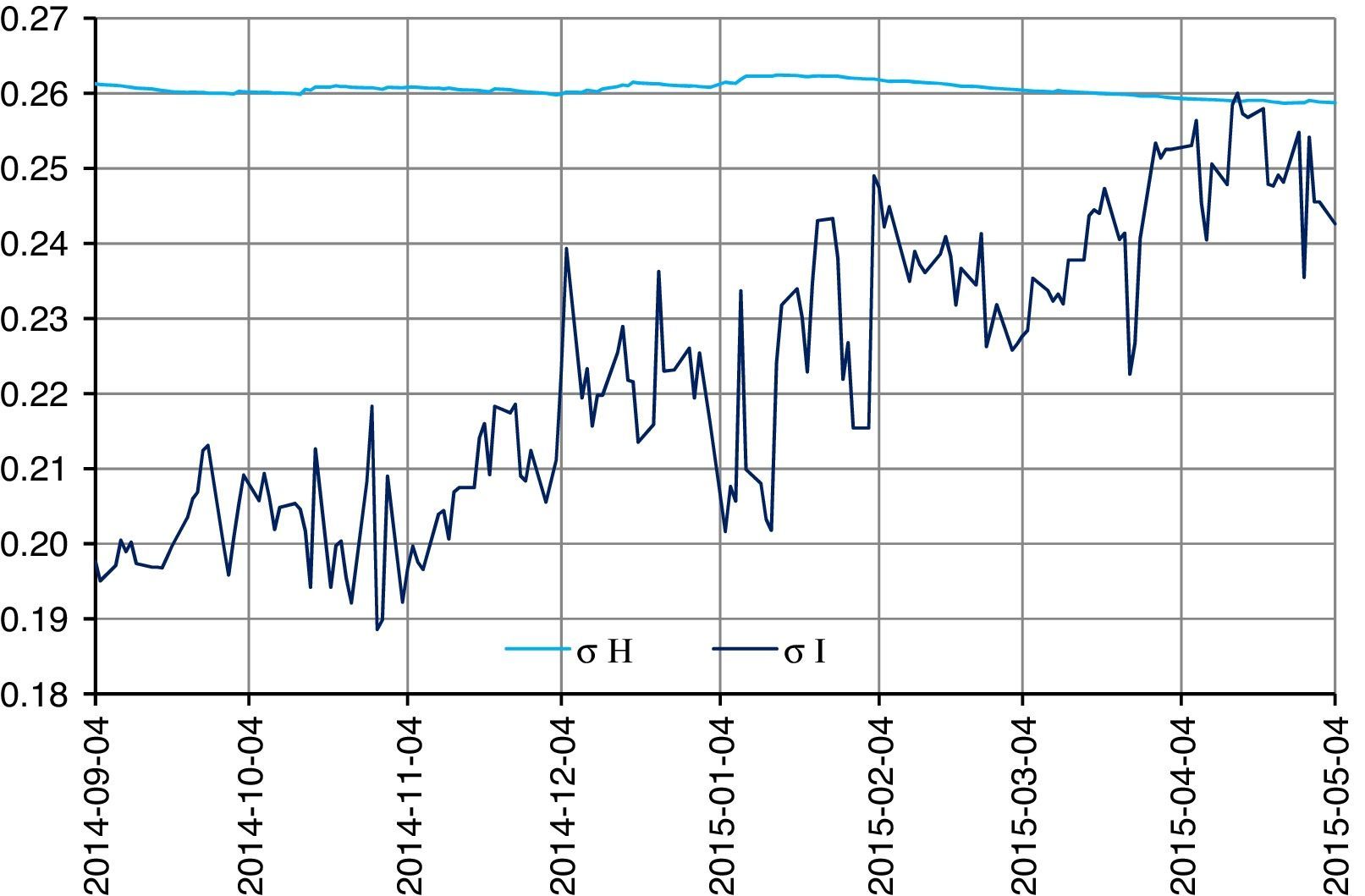
where the value of the options on the date of maturity is:

and represents the additional gains for the investment in the log-stable options. The sky-blue line represents the gain of the log-Gaussian structured product, considering the participation factor and the monetization of the log-Gaussian option. As can be observed, the utilities on the date of maturity of the log-stable structured product are superior to the log-Gaussian when the index value surpasses the payoff price at maturity. This is due to the participation factor which, in the log-stable case, includes in the portfolio structure 15 options, and only one option in the log-Gaussian portfolio – promoting the gains of the log-stable portfolio through the payment at maturity of the option. The comparison of annual historical and implicit volatilities during the valuation period is shown in Fig. 8.

Fig. 8.

Comparison of the annual historical and implicit volatilities.

Source: Own elaboration using a spreadsheet.

Fig. 8 shows the comparison of the annual historical (sky-blue line) and implicit (navy blue line) volatilities during the valuation period. The implicit volatilities present a minimum of 18.8544% and a maximum of 25.9993% with a differential of 715 percentage points, while the historical volatilities present a minimum of 25.8675% and a maximum of 26.2418% with a differential of 38 percentage points. It can be observed that April 15th (2015) is the only day in which the implicit volatility is greater than the historical, which means that the European call options on the Eurostoxx are undervalued except on April 15, 2015, because the implicit volatility is used in the valuation.

Valuation of the structured call product on the Eurostoxx

The valuation of the structured product depends on inputs such as the Eurostoxx, the implicit volatility on the options on the Eurostoxx, the LIBOR-EURO interest rate, the interest rate of the index dividends, the payoff price, the time remaining for the valuation of the European call options through the log-Gaussian model, and the zero-coupon rate for the valuation of the bond. There is no implicit scale parameter available for the log-stable model; therefore, it is proposed to carry out the calculation using the following theoretical relation:

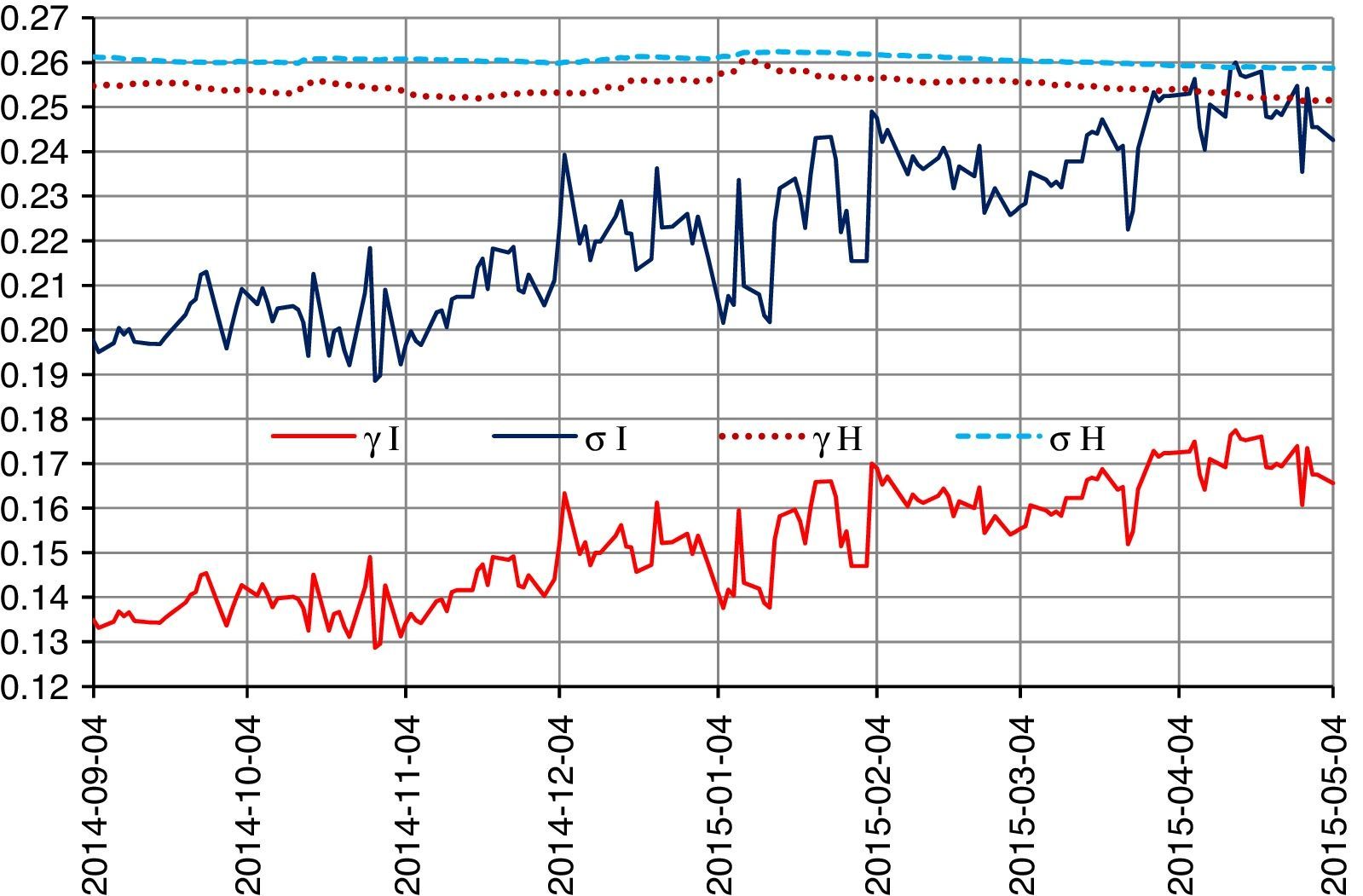
where σ is the annual implicit volatility.

Using Eq. (9), the annual implicit scales are calculated for the valuation of the European call options of the log-stable model using the same endogenous factors: the index, the LIBOR-EURO interest rate, the index dividends rate, and the same exogeneous factors: the payoff price and the remaining time, and also the same zero-coupon rate for the valuation of the bond. The comparison of the yearly scales during the valuation period is shown in Fig. 9.

Fig. 9.

Comparison of the annual historical and implicit volatilities and scales.

Source: Own elaboration using a spreadsheet.

Fig. 9 shows the comparison of historical volatilities (discontinuous sky-blue line), implicit volatilities (navy blue line), implicit scales (red line), and historical scales (dotted purple line). Implicit scales present a minimum of 12.8685% and a maximum of 17.7450% with a differential of 488 percentage points. On the other hand, historical scales present a minimum of 25.1359% and a maximum of 26.0497% with a differential of 92 percentage points. It can be observed that the implicit scales are always lower than the historical scales. The limits for the valuation of European options are:

The prices of the call options must be positive and must be greater than the difference between the present value of the price underlying the rate of index dividends and the present value of the payoff price to the domestic rate, and they must be lower than the price of the underlying asset to avoid arbitrage opportunities. The valuation of the European call options through the log-Gaussian and log-stable models is shown in Fig. 10.

Fig. 10.

Valuation of European call options.

Source: Own elaboration using a spreadsheet.

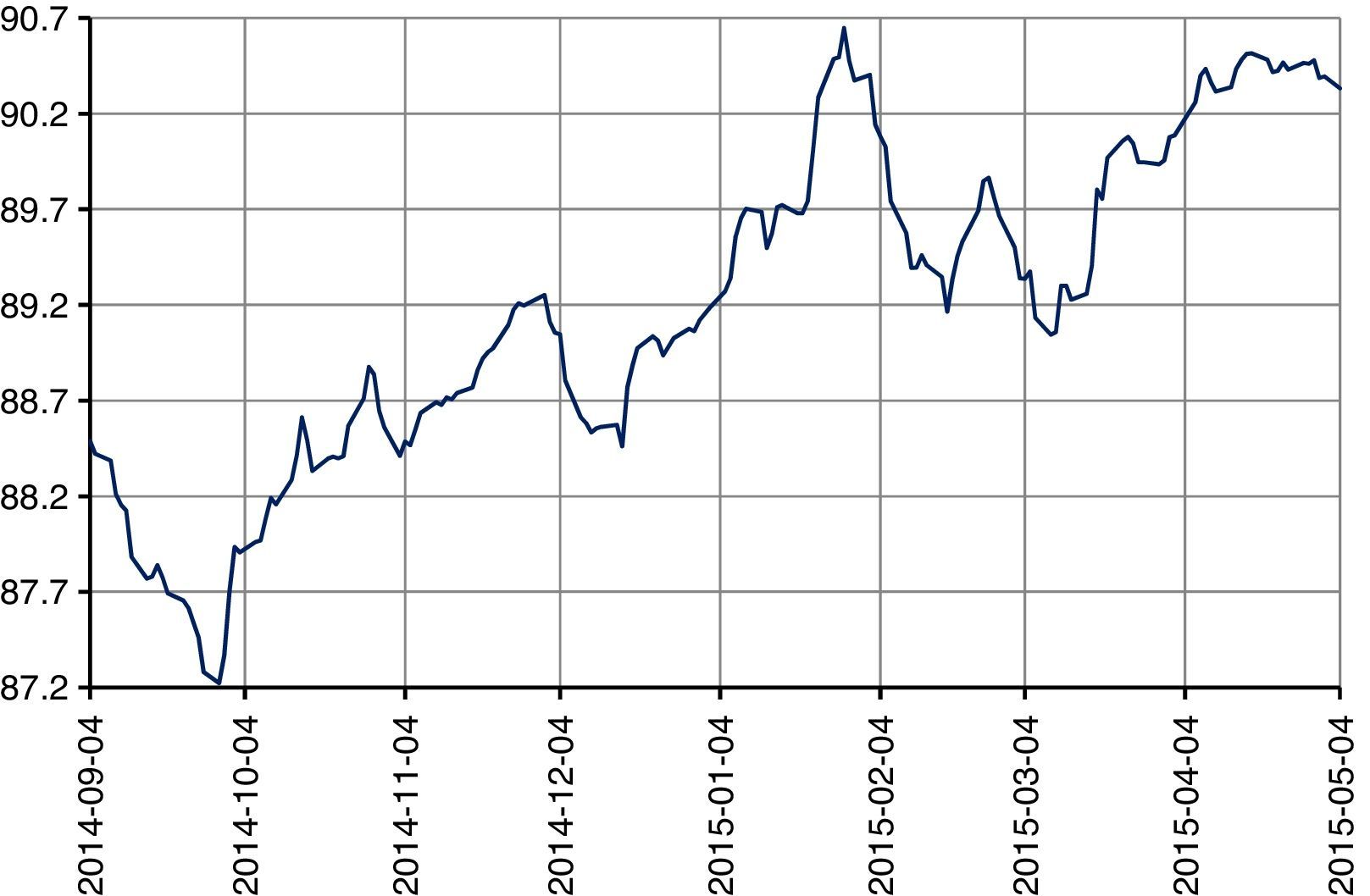
Fig. 10 shows the valuations of the European call options using the log-Gaussian model (sky-blue line), the valuations of the European call options using the log-stable model (navy blue line), and the lower limits for the valuations of the European call options (discontinuous red line). The log-Gaussian valuations present a minimum of $154.5342 and a maximum of $736.8478 with a differential of $582.3136, whereas the log-stable valuations present a minimum of $0.00 and a maximum of $395.1987 with a differential of $395.1987. The minimum difference between the valuations of the utilized models during the valuation period was of $154.5342 on October 16th, 2014, and the maximum difference was of $402.6041 on April 17th, 2015. It can be observed that the log-Gaussian valuations are greater than the log-stable valuations, confirming that the log-Gaussian model overestimates the low financial and economic impact events. The log-stable valuations approximate the log-Gaussian valuations when the Eurostoxx increases or decreases and the other factors remain constant, the maximum difference is of $482.9548 and it becomes present when the index reaches 4180 points — when increasing or decreasing, the difference is decreasing. The valuation of the bond is shown in Fig. 11.

Fig. 11.

Valuation of the bond.

Source: Own elaboration using a spreadsheet.

Fig. 11 shows the valuations of the bond with regard to the structure of the zero-coupon interest rates. The valuations present a minimum of $87.2236 and a maximum of $90.6480 with a differential of $3.4244. In the prospect of the structured banking bond referenced to the SX5E index it is indicated that the following amount is the payment, in pesos:

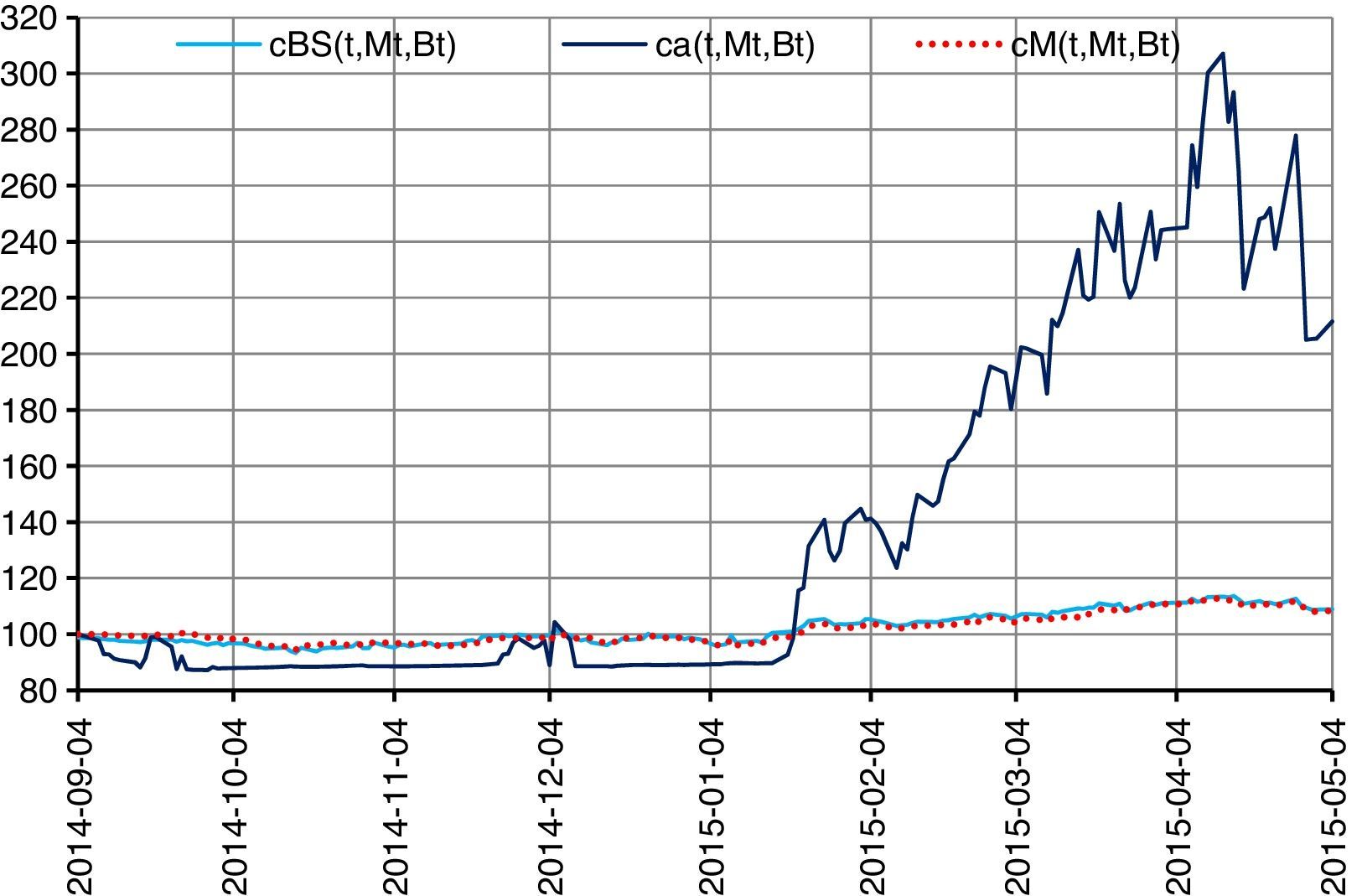
where the product of one-hundred times the participation factor and the maximum value of the quotient divided by the valuation of the option on the Eurostoxx and the payoff price or zero is the monetization of the options and represents the additional gains, in pesos, that the investors could obtain with the structured product. On the date of issue, the bond has a value of $88.4874, the remaining capital for the long position in European call options on the Eurostoxx is of $11.5126, therefore, the participation factor for the log-Gaussian model is of only one option, because the price of the European option is of $328.9045, the monetization is of $10.3669, and the issuer obtains a commission of $1.1457 for each structured model for an issue price of $100.00. The participation factor for the log-stable model is of 15 options due to the price of the options rising to $20.9925, the monetization is of $0.6617, and the issuer receives a commission of $1.5875 for each structured product for an issue price of $100.00. The valuations of the structured products through the log-Gaussian and log-stable models are shown in Fig. 12.

Fig. 12.

Valuation of the guaranteed capital structured product.

Source: Own elaboration using a spreadsheet.

Fig. 12 shows the valuations of the guaranteed capital structured product using the log-Gaussian model (sky-blue line), the valuations of the structured product using the log-stable model (navy blue line), and the market prices (dotted red line), which are similar to the log-Gaussian valuations. The log-Gaussian valuations present a minimum of $93.3655 and a maximum of $113.7071 with a differential of $20.3416, whereas the log-stable valuations present a minimum of $87.2237 and a maximum of $277.1856 with a differential of $189.9619, and the market prices present a minimum of $94.1255 and a maximum of $112.8350 with a differential of $18.7095. The log-Gaussian valuations are greater than the log-stable valuations until January 20th, 2015. From January 21st, 2015, the log-stable valuations are superior to the log-Gaussian, confirming that the log-Gaussian model overestimates low financial and economic impact events and underestimates high financial and economic impact events. The log-stable valuations more adequately quantify the market risk, and the gains are reflected when the index value increases and the valuation of the log-stable options also increase. Furthermore, the participation factor multiplies the gains of the structured note. The log-stable model allows for greater commissions for each structured product for the issuers, and allows obtaining greater gains for the investors. The valuations of the structured products of the log-Gaussian model and the market price are shown in Fig. 13.

Fig. 13.

Valuation of the structured product and the market prices.

Source: Own elaboration using a spreadsheet.

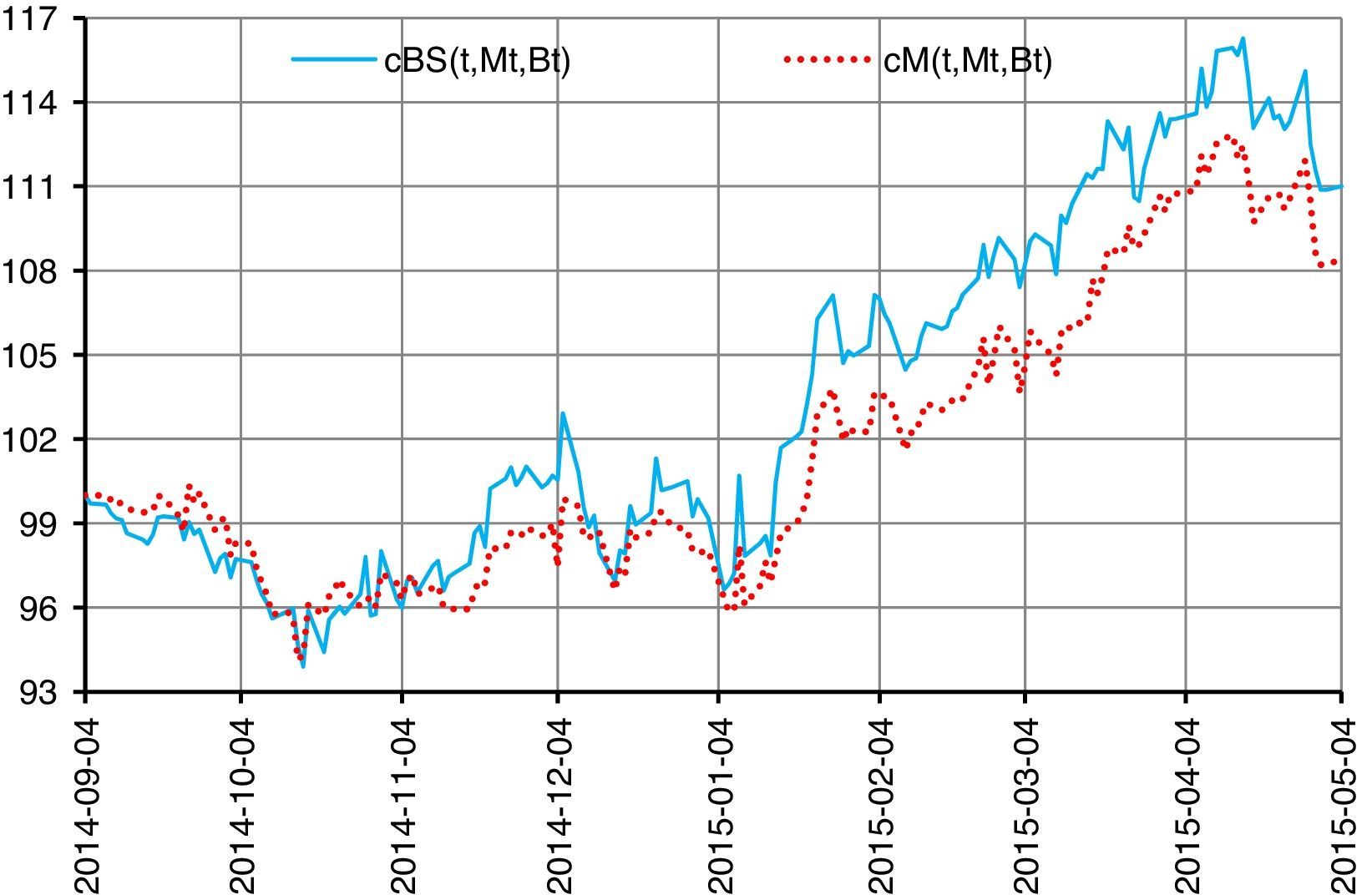
Fig. 13 shows the log-Gaussian structured product values (sky-blue line) and the market prices (dotted red line). The maximum difference of the log-Gaussian structured product and the market price is of $3.1012 presented on March 16th, 2015, representing a difference of 2.9221%, and the minimum is of $0.0089 presented on December 18th, 2014, representing a difference of 0.0089%. It can be observed that on the most recent dates, the market value is lower than the theoretical price of the log-Gaussian model, which decreases the gains of the investors. The prices of the options in accordance with the underlying asset and of the stability parameter are shown in Fig. 14.

Fig. 14.

Prices of the options in accordance with the underlying asset and the stability parameter.

Source: Own elaboration using a spreadsheet.

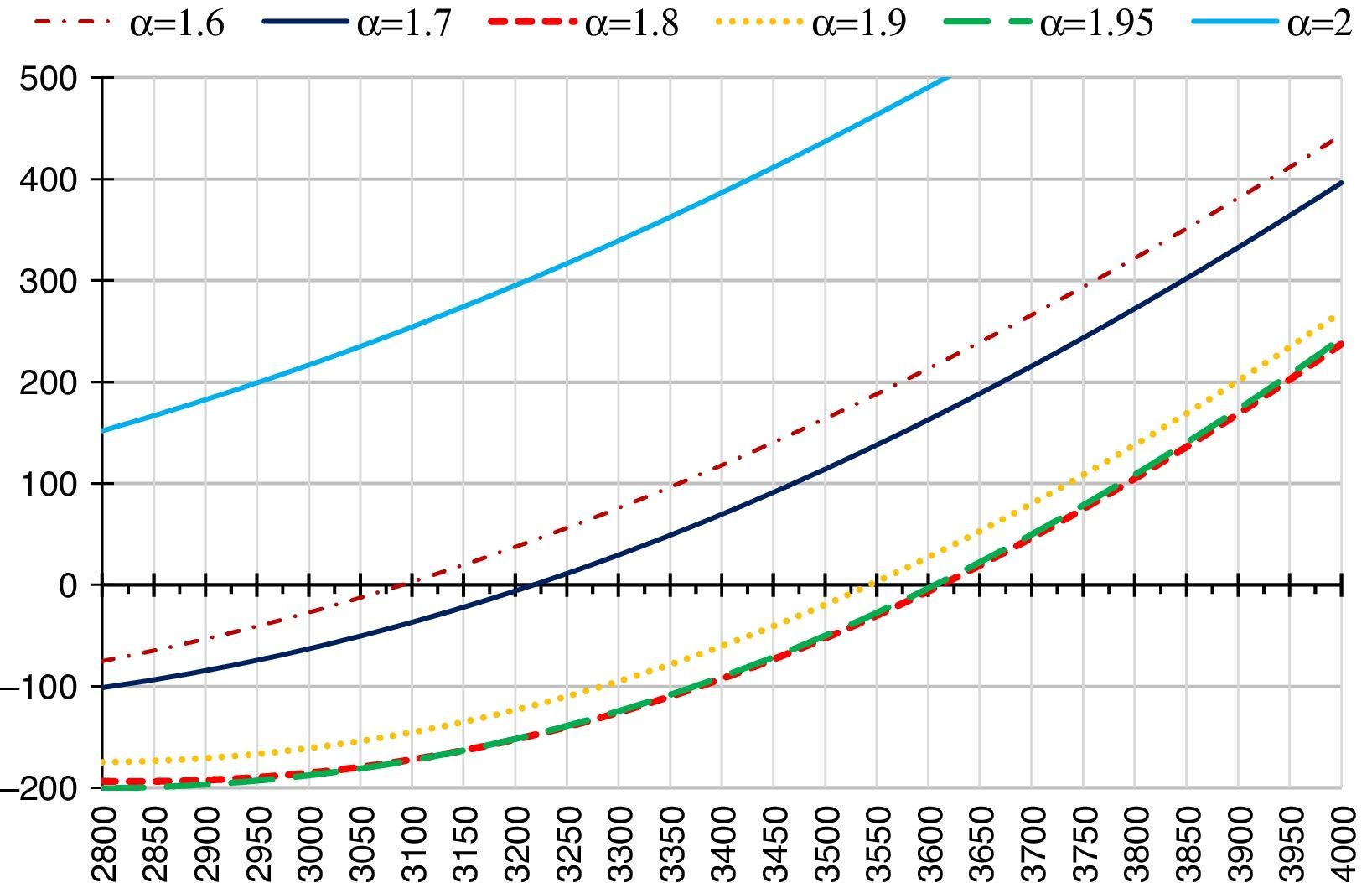
Fig. 14 shows the prices of the log-Gaussian option (sky-blue line) and the prices of the log-stable options in accordance with the value of the underlying asset (including the minimum 2874 points and the maximum 3828 points during the valuation period), of the stability parameter (navy blue line 1.6945, discontinuous and dotted purple line 1.6, discontinuous red line 1.8, dotted yellow line 1.9, and discontinuous green line 1.95), without considering the lower limit in the value of the options. On the valuation date, the index showed a value of 3277.25 points; the theoretical value of the log-Gaussian option, and the theoretical values of the log-stable options, which are in the money, were positive at $328.9045 and $20.9925, respectively. It can be observed that the valuation of the log-Gaussian option overestimates the valuations of the log-stable options with different stability parameters. Additionally, the participation factor of the log-stable model is superior to the factor of the log-Gaussian model, multiplying by 15 times the gains of the log-stable investors for the estimated distribution fX(x,1.6945,−0.1707) when the index surpassed 3245 points on January 21st, 2015. Therefore, the participation factor is the multiplier that allows the log-stable investors to obtain greater gains when the index increases its value, given that it multiplies the gains by the payment of the options in the money, and if the options out of the money do not obtain gains, then the investors only receive the nominal value of the bond on the date of maturity. It can also be observed that the log-stable prices are lower to the log-Gaussian prices that are in a position close to the options in the money. This behavior is explained by the log-Gaussian density function presenting a greater probability mass on values adjacent to the payoff, and the log-stable density functions present a probability mass on the extremes of the distribution. Furthermore, given that most of the options are valuated with payoff prices adjacent to the forward price or future pricing of the underlying asset as a fair price considering the market inputs on the date of negotiation, the options are thus valuated in an adjacent interval when they are in the money, a little out of the money or a little in the money, but not too out of the money or too in the money, which is when the log-stable options increase their value and could gain lower participation factors than the log-Gaussian options.

The market price of the guaranteed capital structured product is similar to the theoretical price. However, the market price is not available to the general public, and because of this, the characteristics of the product are described, and the market inputs are used for the valuation, innovating by modeling the kurtosis and asymmetry through the log-stable distributions, which none of the cited works has done as they have used the log-Gaussian distribution. The attractiveness of the structured guaranteed capital note is that the payment diagram indicates that the yield expected by the investors can theoretically be unlimited. For this reason, a confidence interval is calculated for the Eurostoxx through:

The underlying price on the date of issuance is M0=3277.25, the annual historical scale parameter is γ=0.25470617, and the distribution of the Eurostoxx yields is Z∼S1(1.6945,−0.1707). Using Eq. (12), the 95% confidence interval is calculated for the 170 business days in which the structured product has been valuated, this being 1556.93≤MT≤6297.03, including the confidence interval when Z∼S1(2) which is 2318.08≤MT≤4662.78. The index values prior to the valuation date are of 1995.01 as a minimum and 3828.78 as a maximum, period during which no high financial or economic impact events were observed. The confidence interval indicates that the value of the index tends to drop with greater frequency than to increase, and this is unknown by the investors. The 95% confidence interval during the validity period of the structured product for the underlying price on the date of maturity is of 1556.93≤MT≤6297.03, including the confidence interval when Z∼S1(2), which is 2169.73≤MT≤4995.23. The probability of obtaining gains on the date of maturity is calculated as follows:

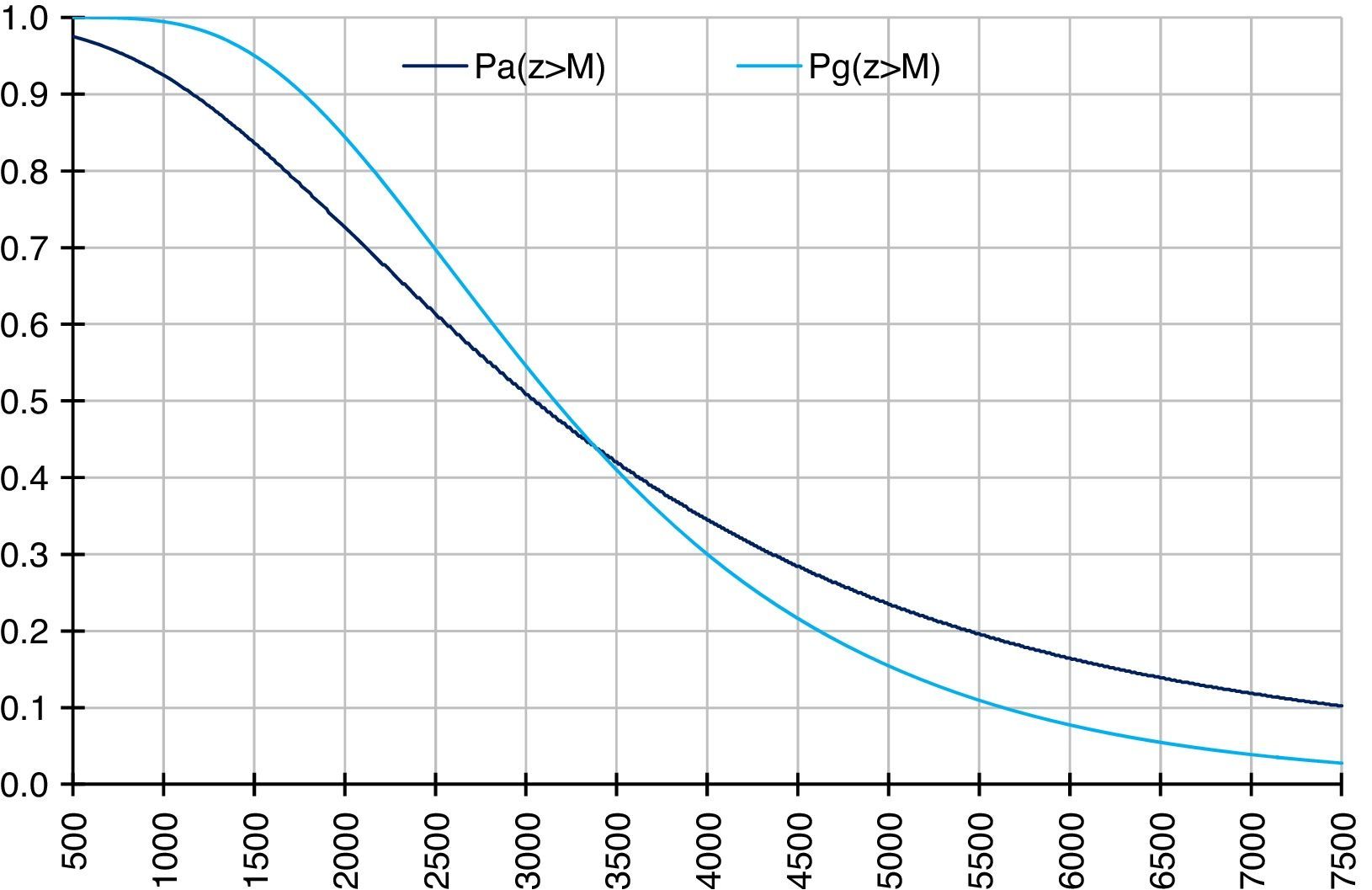
where

The probabilities according to the index value are shown in Fig. 15.

Fig. 15.

Probabilities according to the index value.

Source: Own elaboration using a spreadsheet.

Fig. 15 shows the probabilities that variable Z (index value) surpasses the value indicated in the horizontal axis on the date of maturity and how it can be observed that the log-Gaussian probabilities (sky-blue line) are superior to the log-stable probabilities (navy blue line) until the index value surpasses the 3390 points and both probabilities are in decline; that is, the probabilities of obtaining greater gains are monotonous decreasing. For example, the probability that the log-stable options are in the money is 47.69%, and the probability that log-Gaussian options are in the money is 49.60% when the index value surpasses the 3172.63 points; whereas the probabilities that the index value surpasses 4000 points are 34.45% and 30.03% for the log-stable and log-Gaussian options, respectively. The logarithm of the underlying yield frequency is shown in Fig. 16.

Fig. 16.

Logarithm of the underlying yields frequency.

Source: Own elaboration using a spreadsheet.

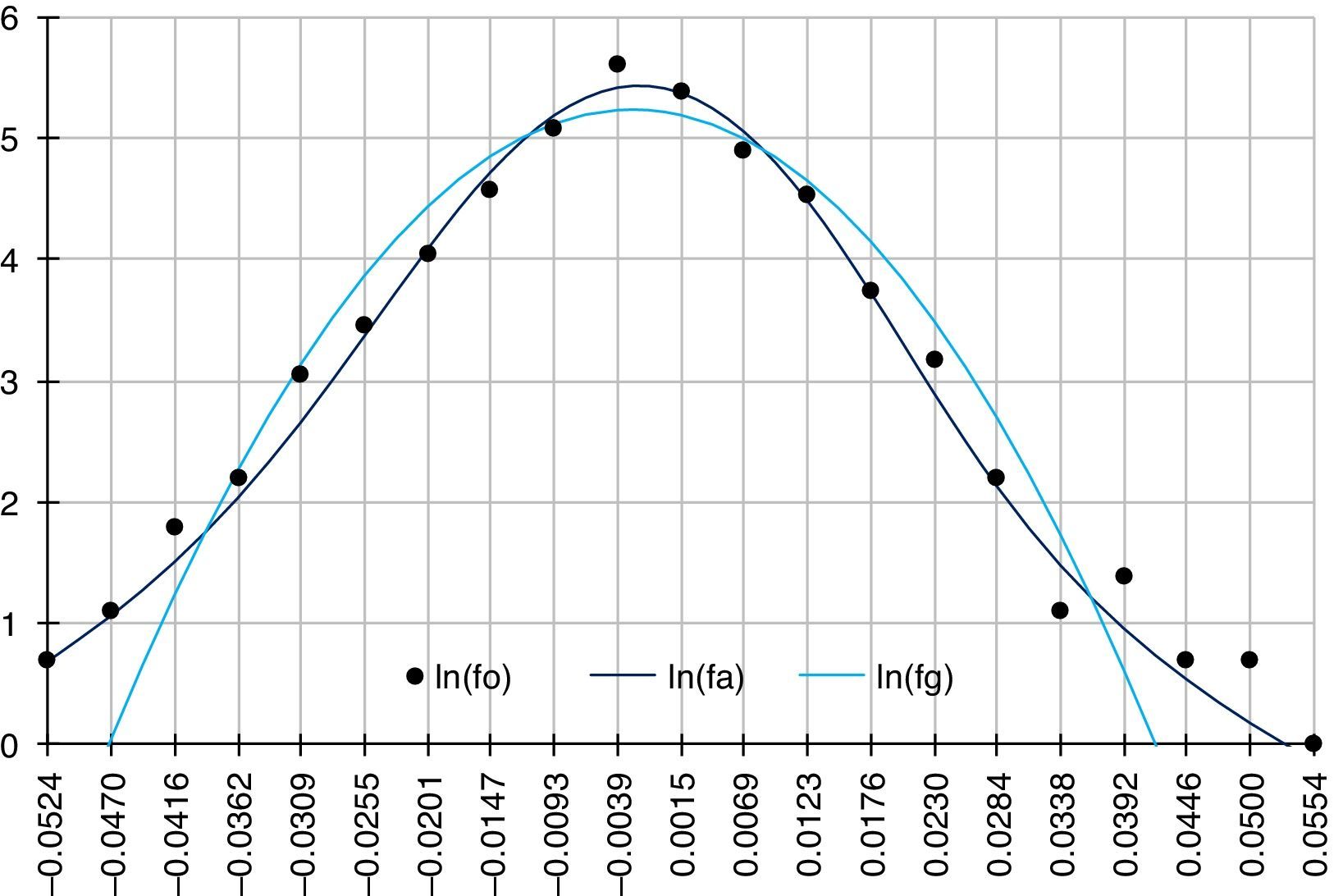
Fig. 16 shows that the estimation of the yields is more adequate using the log-stable distribution (navy blue line), given that it more adequately models the kurtosis and asymmetry of the observed yields (black points) compared to the log-Gaussian distribution (sky-blue line). Therefore, the log-stable model better quantifies the loss and gain frequencies of low financial and economic impact by the investment in Eurostoxx, the options on Eurostoxx, and the guaranteed capital structured products valuated in this work when compared to the log-Gaussian model.

Financial markets are not complete because perfect coverage does not exist, and in incomplete markets it is not possible to transfer risks in full. Assuming that the markets are complete, there is an unreal vision of the neutral measure of the risk when valuating options. Incomplete markets are more efficient because the risk coverages can be quantified to minimize risks; the lack of completeness of the financial markets is caused by the commercialization levels in relation to the risks that need to be covered, by the ignorance of the appropriate model to model the yields and, mainly, by the discontinuities of the prices. The equivalent Martingale of the incomplete markets allow valuating options in different manners, and these probabilities must be interpreted as the value that the investors bet on the event. The stability parameter provides information on the behavior of the process; when α approximates to two, the process shows a large quantity of fluctuations of low financial impact (yields close to zero) between the high financial impact jumps (yields that generate moderate losses or gains). When α approximates to the unit (Lévy process), the prices of the options change due to the jumps that generate high losses or gains, and the presence of stability periods between the jumps. This can be observed in Figs. 1–6, which are more adequately captured by the log-stable processes given that they capture the low financial impact fluctuations through the Wiener process and the high financial impact jumps that generate losses or gains through the Poisson process. The log-stable processes model the yields more adequately than the log-Gaussian process because the latter is a particular case (symmetric) of the log-stable processes, which capture the kurtosis and asymmetry of the market yields as can be observed in Figs. 4, 5, 15 and 16. Furthermore, they satisfy the properties that the options values with positive payments (in the money) must be positive, therefore, the call options with null payments (out of the money) must be less valuable than the call options in the money, as can be observed in Fig. 14, being possible to have negative values that would provide arbitrage opportunities. The qualitative tests that show that the log-stable processes surpass the log-Gaussian process can be observed in Fig. 16, and the quantitative tests are confirmed in Tables 2–4. Thus, the valuation of the log-stable contingent claims quantifies more adequately the market risk (price risk), which is an important characteristic in financial mathematics so that the prices of the options are fairer for the issuers and the investors (holders). This would in turn allow financial engineering to be more efficient in the valuation process, providing the issuers and investors with more adequate tools that adhere to reality in order to generate investment instruments that adapt to the needs and realities of the markets.

Conclusions

The valuations of the log-Gaussian options are greater than the log-stable valuations, confirming that the log-Gaussian model overestimates the low financial impact events using the same endogenous and exogenous factors available. The log-stable valuations approximate the log-Gaussian valuations when the Eurostoxx increases or decreases, while the inputs remain constant, indicating that the log-stable contingent payments are better quantified than the log-Gaussian contingent payments because the latter underestimate the high financial impact events, which translate into significant gains or losses that are not adequately considered by the log-Gaussian insurances and that are quantitatively sustained by the goodness of fit statistics.

The comparisons of the log-stable and log-Gaussian structured products show that the log-Gaussian valuations are greater than the log-stable valuations, provided that the index value is less than 3269.18 points. When the index value surpasses 3269.18 points, the log-stable valuations are superior to the log-Gaussian valuations, confirming the overestimation of low financial impact events when the index is close to the payoff price and to the underestimation of high financial impact events that generate greater gains for the log-stable investors, because they quantify the price risk more adequately. The gains occur when the index surpasses 3269.18 points and the log-stable valuations increases with regard to the log-Gaussian. The log-stable participation factor enhances gains because it includes 15 options that multiply the payment on the payoff date, whereas the log-Gaussian participation factor includes a single option for the same payment. The log-stable model grants bigger commissions to the issuers for each structured product and grants greater gains to the investors due to the difference in the participation factor and the fact that it depends on the adequate valuation of the options at the time of negotiation.

The valuation of structured products depends on the correct quantification of the price risk. The log-stable processes have shown to be superior to the log-Gaussian process in adequately modeling the kurtosis and asymmetry, enabling the valuation of the options to be carried out more closely tied to reality with the available inputs. The estimation of the distribution of the yields and the quantitative validation allow observing that the log-Gaussian process overestimates the events that do not generate significant losses or gains, and underestimates the events that generate significant losses or gains and those found at the extremes of the distribution. Using the stability parameter, the log-stable processes more adequately capture the events distant to the mode to better valuate the significant losses or gains and; whereas, using the asymmetry parameter, the options in the money show superior valuations to the options out of the money.

A different type of structured products on forward or future contracts, swaps, or options on other underlying assets with other characteristics could be evaluated in future research, creating another type of coverage through log-stable distributions.