Este trabajo buscó analizar si las variables memoria de trabajo (MT) verbal, MT visoespacial, velocidad de procesamiento y habilidad verbal pueden predecir la habilidad de los niños para el cálculo mental durante la realización de problemas aritméticos simples. Se administraron los subtests Vocabulario y Span de Dígitos del WISC-III; el subtest Casita de Animales del WPPSI-R y una prueba de problemas aritméticos (ad hoc) a 70 niños de 6 años. Un análisis de regresión lineal con el método stepwise mostró que solo la MT visoespacial predijo la variabilidad en las puntuaciones de cálculo mental (t=4.72; p<0.001; β=0.50). Los resultados son contrarios a estudios realizados en adultos y niños mayores en los cuales el mayor peso recae sobre la MT verbal. Es posible que a medida que los niños crecen la automatización de ciertos procesos de conteo y el almacenamiento de hechos aritméticos en la memoria de largo plazo produzca que dependan en mayor medida de la MT verbal para la resolución de este tipo de cálculos.
This study aimed to analyze whether verbal working memory (WM), visual-spatial WM, processing speed, and verbal ability predicted children's ability to perform mental arithmetic. Five tests were administered to 70 6-years-old children: the Vocabulary and Digits Span subtests from the WISC-III Intelligence Scale, the Animal Pegs subtest from WPPSI-R, and an arithmetic test (ad hoc). A linear regression analysis showed that only visual-spatial WM predicted the variability in children's scores in the arithmetic test (t=4.72; P<.001; β=.50). These findings contradict studies carried out in adults and older children where verbal WM seemed to play a greater role in the subject's ability to conduct calculations without external aids. It is possible that as they grow older, the automation of certain counting processes, as well as the storage and recovery of arithmetic knowledge from long-term memory will cause them to rely primarily on verbal WM resources.
La fluencia en el cálculo, es decir, la resolución de problemas aritméticos de forma eficiente, ha sido considerada un logro básico y necesario sobre el que posteriormente pueden construirse conceptos matemáticos de mayor complejidad (Geary, Frensch y Wiley, 1993; Mazzocco, Devlin y McKenney, 2008; Price, Mazzocco y Ansari, 2013). Quienes estudiaron la capacidad para realizar estas operaciones identificaron como aspectos necesarios la codificación de la información que se presenta, la identificación y recuperación de los algoritmos adecuados desde la memoria de largo plazo, llevar a cabo el cálculo propiamente dicho y alcanzar una respuesta determinada (DeStefano y LeFevre, 2004; LeFevre y Bisanz, 1996). Estudios previos en niños describieron un pasaje del uso de estrategias explícitas, como el conteo en voz alta o con los dedos, a estrategias implícitas como el conteo silente y la recuperación automática, desde la memoria de largo plazo, de combinaciones numéricas sencillas (por ejemplo, 2+2=4) llamadas hechos aritméticos (Ashcraft, 1982; Kaufmann, 2002; Siegler y Shrager, 1984). El uso de estrategias implícitas permite a los niños realizar operaciones aritméticas mentalmente, es decir, sin utilizar recursos externos como papel y lápiz, conteo con dedos, o la presencia de los elementos para ser manipulados. Para realizar el cálculo efectivamente el niño debe sostener la información relevante, los algoritmos necesarios y resultados parciales en un sistema de memoria. Específicamente, estudios han vinculado la capacidad de los niños para realizar cálculos mentales con la memoria de trabajo (MT) (Berg, 2008; DeStefano y LeFevre, 2004; Geary, Hoard, Byrd-Craven y DeSoto, 2004).
Este sistema fue descripto originalmente por Baddeley y Hitch (1974; Baddeley, 2010). Se trata de un sistema de memoria activo que se encarga del almacenamiento temporal de información y el procesamiento concurrente de la misma. Según el modelo clásico planteado por los autores, está compuesto por un ejecutivo central, amodal y sin capacidad de almacenamiento propia, y dos subsistemas esclavos supervisados por este, el bucle fonológico y la agenda visoespacial, encargados de almacenar por breves períodos de tiempo una cantidad limitada de información verbal y visual, respectivamente. Se ha sugerido que la MT está involucrada en las etapas tempranas de las operaciones aritméticas, específicamente en el proceso de codificación visual o fonológica de la información y, a su vez, en el mantenimiento de dicha información para su procesamiento, así como el sostenimiento de resultados parciales para su integración subsecuente (Berg, 2008; DeStefano y LeFevre, 2004; Geary et al., 2004). Sin embargo, la evidencia respecto del rol de cada uno de los componentes de este sistema en el cálculo mental es escasa y, en ocasiones, contradictoria.
Ciertos estudios realizados mostraron que la interferencia del bucle fonológico por supresión articulatoria (por ejemplo, repetir la palabra «the» una vez por segundo durante la resolución de la operación) en adultos afectaba el rendimiento en la resolución mental de operaciones matemáticas de cifras de 2 o 3 dígitos. Ya que la supresión articulatoria evita el repaso subvocal de los operandos o los resultados parciales, los autores concluyeron que la MT verbal tiene un rol preponderante en la realización de cálculos mentales. Sin embargo, siendo que este efecto se observó solo cuando las operaciones se presentaron brevemente de forma visual, pero no cuando las cifras permanecían presentes, se infirió que los recursos de la MT verbal estarían involucrados en el sostenimiento de los números y los resultados parciales, y no en la recuperación o puesta en marcha de estrategias (Furst y Hitch, 2000; Logie, Gilhooly y Wynn, 1994). Noel, Desert, Aubrun y Seron (2001) encontraron resultados similares utilizando como medida de MT verbal una tarea Span de Dígitos (cantidad máxima de dígitos presentados oralmente que el participante puede retener y reproducir respetando el orden original), en ausencia de una asociación significativa entre la resolución de problemas aritméticos y la capacidad de la MT de sostener información visoespacial, la cual fue evaluada con una prueba de retención de patrones de cuadros en una matriz.
Otros estudios observaron, en niños escolarizados de 6 y 7 años, asociaciones entre la resolución mental de operaciones presentadas visualmente y la MT verbal, la cual fue evaluada con la tarea Span de Dígitos de la Escala de inteligencia para niños WISC-R (Wechsler, 1974) (Solan, 1987; Geary, Brown y Samaranayake, 1991). Estos autores reportaron que estrategias iniciales, como el conteo con dedos o el conteo verbal, imponen mayores demandas a la MT verbal que la recuperación de hechos aritméticos desde la memoria de largo plazo. De ser así, sería esperable que la asociación entre la realización de operaciones aritméticas y la MT verbal disminuyera con la edad.
Investigaciones recientes enfatizaron la importancia de la MT visoespacial para habilidades matemáticas tempranas, como el conteo (Kyttälä, Aunio, Lehto, van Luit y Hautamaki, 2003; Holmes y Adams, 2006). McKenzie, Bull y Gray (2003) encontraron que la disrupción del bucle fonológico por supresión articulatoria afectó la capacidad de niños de 8 y 9 años para resolver mentalmente operaciones aritméticas de un solo dígito presentadas verbalmente, teniendo poco efecto en niños más pequeños (6-7 años). Mientras que encontraron el patrón opuesto al interferir con la MT visoespacial, donde observaron un mayor efecto en el rendimiento en cálculo mental en los niños más pequeños. Además, los autores encontraron asociaciones positivas significativas entre el puntaje en una tarea de Span de Dígitos y la resolución de operaciones mentalmente en los niños mayores, y no en los menores. Los hallazgos sugieren que los niños más pequeños utilizaron la MT visoespacial, la pizarra mental descripta por Baddeley y Loggie (1999), para mantener activa y manipular la información de la operación aritmética. Estos autores concluyeron, al contrario de los trabajos mencionados previamente, que en edades tempranas la capacidad de repaso subvocal no es suficiente para que los niños recurran a estrategias verbales cuando se encuentran frente a este tipo de problemas, pero que a los 8 y 9 años las estrategias verbales se vuelven dominantes. Estudios en niños de 7 a 14 años con dificultades para la realización de operaciones matemáticas, por otro lado, encontraron que su rendimiento en tareas de MT visoespacial también era inferior al observado en niños sin alteración, esto en ausencia de una dificultad de la MT verbal (Bull, Espy y Wiebe, 2008; Jarvis y Gathercole, 2003; McLean y Hitch, 1999).Otra variable que ha sido vinculada a la efectividad con que se realizan cálculos mentales es la velocidad de procesamiento. Se trata de una característica general que informa acerca del tiempo que insume a un participante la codificación, transformación y recuperación de información, por ejemplo, durante la realización de una tarea (Jensen, 1993; Salthouse, 1996; Conway, Cowan, Bunting, Therriault y Minkoff, 2002). Se ha sugerido que influye sobre la velocidad con que se recuperan hechos aritméticos y se ponen en marcha algoritmos de cómputo (Ackerman, Anhalt y Dykman, 1986; Bull y Johnston, 1997; Fuchs, Compton, Fuchs, Paulsen, Bryant y Hamlett, 2005; Fuchs et al., 2006). Bull y Johnston (1997) mostraron que la velocidad de procesamiento, evaluada a través del pasaje de clavijas de un tablero a otro y una tarea de cancelación, resultó un predictor de la habilidad de los participantes para resolver mentalmente problemas de adición simple. Berg (2008) sugirió que cuanto más veloz es el participante, mayor cantidad de información puede procesar en cada unidad de tiempo, lo cual puede impactar en la eficiencia de la MT liberando los recursos disponibles más rápidamente. Es posible que el procesamiento lento pueda dar lugar a que las representaciones en la MT de las cifras involucradas en cualquier operación aritmética decaigan antes de alcanzar el resultado final, disminuyendo la efectividad del niño en este tipo de tareas y, a su vez, reduciendo la probabilidad de que los operandos y la respuesta se asocien en la memoria a largo plazo en forma de hecho aritmético (Bull y Johnston, 1997).Finalmente, se ha observado que las habilidades verbales en edades tempranas predicen el rendimiento posterior en la resolución de problemas aritméticos, la recuperación de hechos aritméticos y algoritmos de cálculo (Cirino, Tolar, Fuchs y Huston-Warren, 2016; Fuchs et al., 2005; Fuchs et al., 2006; Hecht, Torgesen, Wagner y Rashotte, 2001). La habilidad verbal de un niño refiere a su capacidad para activar desde la memoria de largo plazo conocimientos semánticos y vocabulario en el momento en que lo requiere (Baddeley, 2010) y, a su vez, a su capacidad para generar conceptos verbales enfocándose en las características relevantes de los objetos e ignorando las accesorias (Bourne, 1986). Bull et al. (2008) plantearon que al encontrarse frente a un problema aritmético presentado verbalmente se activan representaciones almacenadas en la memoria de largo plazo sobre el significado de las palabras en general, así como términos específicos que permiten seleccionar los algoritmos necesarios para resolver la operación. Durand, Hulme, Larkin y Snowling (2005) observaron que el vocabulario, el razonamiento verbal y la comprensión desde una entrada verbal auditiva se asocian a la resolución de operaciones aritméticas de forma escrita, y que la habilidad verbal en general predice la capacidad de resolución de este tipo de operaciones. A su vez, Fuchs et al. (2006) encontraron asociaciones significativas entre el nivel de lenguaje y formación de conceptos y la capacidad para resolver problemas aritméticos. Finalmente, se ha encontrado que la habilidad lingüística de niños, medida a través de un test de vocabulario en que los niños debían definir las palabras que se les presentaban, se asoció de forma significativa a su capacidad para recuperar hechos aritméticos y algoritmos de cálculo, por lo que se la relacionó con la eficiencia del cálculo mental (Cirino et al., 2016; Hecht et al., 2001).
La literatura al respecto de las diferentes habilidades cognitivas vinculadas al cálculo mental es escasa, particularmente a nivel local, y en ciertos casos contradictoria. La mayoría de los trabajos se centran en una de las variables descriptas previamente, de forma que es dificultoso comparar el peso que cada una tiene en esta particular habilidad. Por otro lado, la mayoría de los estudios utilizan operaciones de adición o resta simples presentadas visualmente, por lo que la resolución depende en gran medida del conocimiento que el niño posea de los numerales arábigos incluidos en la operación. Knudsen, Fischer, Henning y Aschersleben (2015) encontraron que los niños aprenden a identificar las cantidades asociadas con las palabras número (e.g. /siete/) y a reconocer los nombres de los arábigos primero, y que el vínculo entre estos últimos y las cantidades que representan se consolida más tardíamente, hacia los primeros años de primaria. Siendo que el cálculo mental ha sido identificado como un predictor del rendimiento posterior del niño en habilidades matemáticas más complejas (Geary, 1993; Ostad, 1998; Price et al., 2013), conocer las habilidades cognitivas que influyen sobre este en edades tempranas permitirá identificar indicadores tempranos de dificultad en las matemáticas y abordar de forma integral su intervención, ya que déficits en dichas habilidades cognitivas pueden acarrear problemas en la adquisición y ejecución de habilidades matemáticas. Es por ello que el presente trabajo tiene como objetivo estudiar si las variables MT verbal, MT visoespacial, velocidad de procesamiento y habilidad verbal predicen la habilidad de niños de 6 años de la Ciudad Autónoma de Buenos Aires para resolver problemas aritméticos presentados verbalmente (sin utilizar su representación arábiga) a través del cálculo mental, y en qué medida cada una de ellas influye en esta habilidad. Se espera que las 4 variables propuestas predigan el rendimiento de estos niños en cálculo mental, pero que la velocidad de procesamiento y la MT visoespacial sean las que tengan un rol preponderante en esta edad.
MétodoSe trató de un estudio de tipo descriptivo-correlacional de corte transversal (Hernández Sampieri, Fernández Collado y Baptista Lucio, 2008).
ParticipantesLa muestra estuvo conformada por 70 niños de 6 años [media de edad en meses=76.80; DE=3.76; 16 mujeres (53.30%) y 14 varones], alumnos de 2 escuelas de la Ciudad Autónoma de Buenos Aires, Argentina, divididos en 5 salones de clase. El muestreo fue de tipo intencional no probabilístico, de participantes voluntarios. Los niños participaron con el consentimiento escrito de los padres y los datos recabados fueron tratados de manera anónima y confidencial. Además del consentimiento de los padres, fue un requerimiento que los niños participaran de forma voluntaria. La administración fue cancelada en los casos en que el participante manifestó no querer realizar la tarea y los datos fueron desechados en el caso de los niños que realizaron parte de las tareas y luego no quisieron continuar. Fueron excluidos del estudio niños con trastornos auditivos o del lenguaje, alteraciones neurológicas, psiquiátricas o con un CI inferior a 80. El CI fue estimado utilizando una versión abreviada de la Escala de inteligencia WISC-III (Wechsler, 1994), a través del procedimiento descripto por Tellegen y Briggs (1967) para obtener los cocientes de desviacion estimados de la escala total, administrando las pruebas Diseño con Cubos y Vocabulario. Los resultados obtenidos con esta versión abreviada mantienen una correlación alta con el CI obtenido mediante la administración de la escala completa (r=0.911), y un alto coeficiente de fiabilidad test-retest (r=0.911). (El desarrollo del método completo, con las fórmulas pertinentes, puede encontrarse en el manual Evaluación infantil de Jerome Sattler [1996]).
MaterialesPara cada participante se obtuvieron medidas de MT verbal, MT visoespacial, velocidad de procesamiento, habilidad verbal y cálculo mental. Las tareas diseñadas o adaptadas para este estudio fueron validadas en una muestra de 233 niños de 4, 5 y 6 años, alumnos de escuelas de la Ciudad Autónoma de Buenos Aires. Los índices de fiabilidad de cada prueba son reportados junto con la descripción de las mismas.
Cálculo mentalSe evaluó a través de la resolución de problemas aritméticos de suma y resta presentados verbalmente. El instrumento incluyó 4 ítems de entrenamiento y 12 ítems de la prueba de dificultad creciente. Los ítems de entrenamiento incluyeron cantidades pequeñas (1+1, 1+2, 1–1, 2–1) para corroborar que el niño comprendiera la tarea, más allá de si podía operar o no con cantidades mayores. Respecto de la estructura de los ítems, cada uno de ellos incluía un máximo de 3 proposiciones, y las operaciones se realizaban sobre elementos del mismo tipo (añadiendo manzanas a manzanas, lápices a lápices), evitando la mayor cantidad posible de información irrelevante, como puede ser nombres o lugares. El objetivo fue facilitar tanto como fuese posible la construcción de la representación mental del texto. Siguiendo la clasificación de Kintsch y Greeno (1985), solo se utilizaron problemas de tipo Cambio con resultado desconocido («Si tenés seis globos pero dos se vuelan, ¿cuántos globos te quedan?») y Combinación con conjunto mayor desconocido («Si hay tres galletitas en la lata azul y dos galletitas en la lata roja, ¿cuántas galletitas hay en total?»). Tanto para las sumas como para las restas la cantidad mayor con que se trabajó fue de 12 elementos, y los sets a combinar son 2 o 3, dependiendo del nivel de dificultad del ítem. Cuenta con un índice de fiabilidad por consistencia interna de α=0.89 (alfa de Cronbach). Se incentivó a los niños a realizar cada ejercicio mentalmente, ya sea por conteo verbal silente o por recuperación de hechos aritméticos, pidiéndoles que mantuvieran las manos cerradas, sobre el regazo, y a la vista del investigador, de forma que este pudiese corroborar que no los movieran o levantaran. En los casos en que el niño no acató la consigna inicial, o en aquellos casos en que no logró alcanzar el resultado correcto operando mentalmente, se le permitió utilizar los dedos para resolver la tarea, pero esto no sumó al puntaje de la tarea. Para cada participante se sumó la cantidad de respuestas correctas teniendo en cuenta lo mencionado previamente.
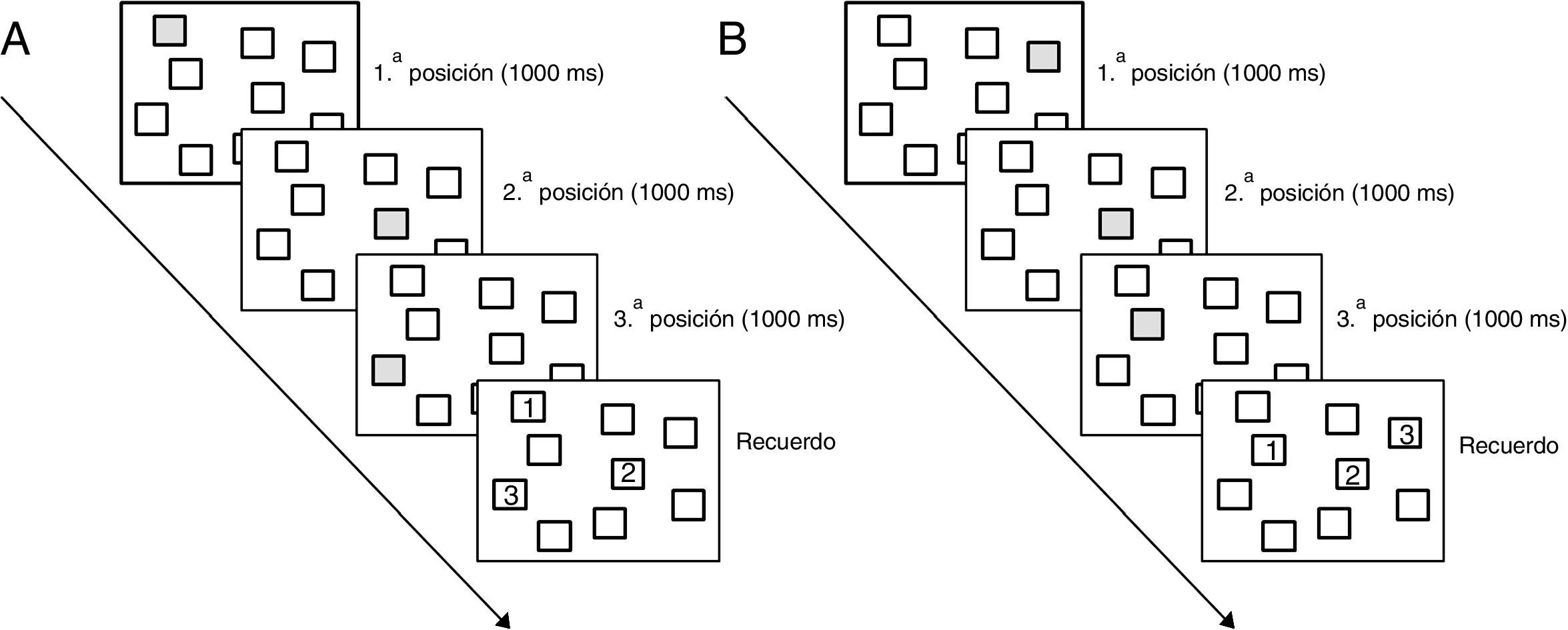
Memoria de trabajo visoespacialEste componente fue evaluado a través de una versión computarizada de la prueba Bloques de Corsi (Corsi, 1972). En este caso, se presentaron en la pantalla de una computadora de 15” 9 bloques blancos posicionados de forma irregular, respetando su ubicación en el test original, que cambiaban de color de a uno por vez generando una secuencia. Los participantes debieron registrar los cubos que cambiaron de color y el orden particular en que lo hicieron, para luego reproducirlo en una matriz igual a la original. La tarea incluyó 2 ítems de entrenamiento y 6 niveles de 3 ensayos cada uno. Cada niño debió realizar correctamente un mínimo de 2 ensayos para pasar al nivel subsiguiente.
Se administraron una versión directa, en la cual el niño debía reproducir la secuencia manteniendo el orden exacto en que le fue presentada, y una versión inversa, en la cual el niño debía repetir la secuencia observada en el orden opuesto, comenzando por el último bloque que hubiese cambiado de color. De esta forma se evaluó la capacidad de almacenamiento y la manipulación de información visoespacial de la MT (ver fig. 1A y B). Para cada participante se obtuvo un total de respuestas correctas. Esta versión de la prueba cuenta con un índice de fiabilidad por consistencia interna de α=0.78 (alfa de Cronbach).
Memoria de trabajo verbalEste componente se evaluó utilizando la prueba Span de Dígitos de la Escala de inteligencia para niños y adolescentes WISC-III (Wechsler, 1994). Se administraron las versiones directa e inversa. En ambas el examinador leía en voz alta una secuencia de dígitos, formada por cifras del 1 al 9, que el niño debía retener y reproducir.
En la versión directa el participante debía repetir los dígitos en el orden en que le fueron leídos por el examinador, mientras que en la versión inversa el niño debía repetirlos en el orden opuesto, comenzando por la última cifra mencionada por el examinador. Ambas versiones contaban con 2 ítems de entrenamiento cada una, los cuales no se computaron en el puntaje final. Además, cada versión incluyó 6 niveles de 2 ensayos cada uno. Luego de 2 errores simultáneos en el mismo nivel se discontinuaba la administración.
Para cada participante se obtuvo un total de respuestas correctas. El índice de fiabilidad por consistencia interna de este test puede encontrarse en el manual de la adaptación argentina de la Escala de inteligencia para niños WISC-III (Wechsler, 1994).
Velocidad de procesamientoLa velocidad de procesamiento se evaluó a través de la prueba Casita de Animales de la Escala de inteligencia para prescolares de Wechsler WPPSI-R (Wechsler, 1998), una tarea cronometrada de emparejamiento visual análoga a al subtest Búsqueda de Símbolos de la escala de adultos (Wechsler, 1998).
La tarea incluyó un tablero con dibujos de 4 animales (perro, gallina, pez, gato), los cuales se repetían 6 veces cada uno de forma aleatoria alcanzando un total de 24 elementos. Las imágenes se distribuían en hileras, con un espacio debajo de cada una para insertar una clavija. Se ofrecían a los niños 28 clavijas de 4 colores diferentes, cada uno asociado a un animal determinado. En la primera hilera el examinador ubicaba una clavija de un color particular debajo de cada animal (perro-negro, gallina-blanco, pez-azul, gato-amarillo). La consigna pedía al niño que colocara las clavijas restantes debajo de cada animal siguiendo el patrón de la primera hilera. Cada niño debió realizarlo lo más rápido posible, de izquierda a derecha y de arriba a abajo (el examinador previamente señaló la dirección e hizo hincapié en que debía respetarse ese orden), sin saltear ningún animal. El niño contó con un tiempo límite de 5min para llevar a cabo la tarea. Se registran tanto el tiempo de resolución en cantidad de segundos como los errores en la elección de color y las omisiones. El índice de fiabilidad por consistencia interna de este test puede encontrarse en el manual de la adaptación argentina de la Escala de inteligencia para prescolares WPPSI-R (Wechsler, 1998).
Habilidad verbalLa habilidad verbal fue evaluada a través del subtest Vocabulario del WISC-III (Wechsler, 1994). Su resolución requiere que el niño acceda al conocimiento verbal cristalizado que posee y genere conceptos verbales, por lo que mide tanto la riqueza de conocimientos almacenados en la memoria de largo plazo como el grado de desarrollo lingüístico. El índice de fiabilidad por consistencia interna de este test puede encontrarse en el manual de la adaptación argentina de la Escala de inteligencia para niños WISC-III (Wechsler, 1994).
ProcedimientoLas tareas fueron administradas en única sesión individual de 40min aproximadamente, en un ambiente libre de ruidos y distracciones dentro de la institución escolar. Las tareas fueron presentadas en el siguiente orden: Casita de Animales, Span de Dígitos, Bloques de Corsi, Vocabulario y la resolución de problemas aritméticos.
ResultadosEn la tabla 1 se presentan los estadísticos descriptivos de las variables incluidas en el estudio: Media de las puntuaciones, desvío estándar, máximos y mínimos, percentiles 25 y 75, valores de asimetría y curtosis, y del estadístico Kolmogorov-Smirnov.
Estadísticos descriptivos de las variables
| M | DE | Min | Max | As | Ku | P25 | P75 | K-S70 | |
|---|---|---|---|---|---|---|---|---|---|
| Cálculo mental | 6.71 | 3.10 | 0 | 12 | –0.22 | –0.99 | 4.00 | 9.00 | 0.14* |
| MT verbal | 9.23 | 2.01 | 7 | 15 | –0.72 | –0.28 | 8.00 | 11.00 | 0.23** |
| MT visoespacial | 14.1 | 4.11 | 7 | 26 | –0.85 | –0.71 | 11.00 | 17.00 | 0.15* |
| V de procesamiento | 77.43 | 19.64 | 46 | 133 | –0.64 | –0.12 | 61.00 | 89.25 | 0.11 |
| Habilidad verbal | 21.41 | 4.15 | 11 | 31 | –0.14 | –0.07 | 19.00 | 24.25 | 0.10 |
As: asimetría; DE: desvío estándar; K-S: Kolmogorov-Smirnov; Ku: curtosis; M: media; Max: valor máximo; Min: valor mínimo; MT: memoria de trabajo; P25: percentil 25; P75: percentil 75; V: velocidad.
Nota. Nivel de significación: * p < .05, ** p < .01.
Si bien la prueba Kolmogorov-Smirnov resultó significativa para las puntuaciones de cálculo mental, MT verbal y MT visoespacial, los valores de asimetría y curtosis en todos los casos se encontraron entre –1.5 y 1.5, lo cual permitió asumir la normalidad de la distribución de las puntuaciones (Field, 2009; Gravetter y Wallnau, 2014; Tabachnick y Fidell, 2013; Trochim y Donnelly, 2006).
Para alcanzar el objetivo de este estudio se realizó una regresión múltiple por el método stepwise o pasos sucesivos, en la cual se incluyó al cálculo mental como variable dependiente y a las variables MT verbal, MT visoespacial, velocidad de procesamiento y habilidad verbal como variables independientes. El análisis mostró que, de las variables incluidas, solo las puntuaciones en la tarea de MT visoespacial predijeron significativamente el rendimiento en cálculo mental (F(1,68)=22.25; p<0.001, β=0.50; t=4.72; p<0.001) con un R2 de 0.25, indicando que aproximadamente el 25% de la varianza en cálculo mental puede explicarse por la capacidad de MT visoespacial. La ecuación de la regresión para la predicción de las puntuaciones de cálculo mental es la siguiente: cálculo mental=1.44+0.37×MT visoespacial.
DiscusiónResolver cálculos mentalmente es una actividad cognitiva compleja que implica la codificación y el almacenamiento temporal de la información con la que se va a operar, la identificación y recuperación de los algoritmos y procedimientos pertinentes desde un almacén de largo plazo, llevar a cabo los pasos necesarios, sostener resultados parciales y alcanzar la respuesta correspondiente (DeStefano y LeFevre, 2004; Geary, 1993; LeFevre y Bisanz, 1996; Mazzocco et al., 2008; Price et al., 2013). Se ha sugerido que la MT está vinculada a la capacidad para realizar cálculos mentales, en tanto interviene en el proceso de codificación visual (MT visoespacial) o fonológica (MT verbal) de la información, el mantenimiento de la misma para su procesamiento, y el sostenimiento de resultados parciales (Berg, 2008; DeStefano y LeFevre, 2004; Geary et al., 2004). A su vez, se ha sugerido que el cálculo mental depende de la velocidad de procesamiento (Bull y Johnston, 1997; Zentall, 1990) y la habilidad verbal del participante (Cirino et al., 2016; Durand et al., 2005; Hecht et al., 2001), los cuales se asocian a la facilidad para recuperar hechos aritméticos y algoritmos de cómputo desde un almacén de largo plazo.
El presente estudio se propuso analizar si las variables MT verbal, MT visoespacial, velocidad de procesamiento y habilidad verbal predicen la capacidad de niños de 6 años para resolver problemas aritméticos mediante cálculo mental. Para ello se trabajó con 70 niños de 6 años a los cuales se administraron pruebas destinadas a evaluar dichas variables. Los resultados obtenidos del análisis mostraron que, de las variables propuestas, solo la MT visoespacial predice el rendimiento en cálculo mental. Si bien esto se contrapone a los resultados obtenidos por Solan (1987) y Geary et al. (1991), es consistente con los obtenidos por McKenzie et al. (2003) con operaciones aritméticas presentadas visualmente (en lugar de verbalmente, al igual que en el presente estudio), tanto a través de la interferencia del bucle fonológico por supresión articulatoria durante la realización de la tarea como al evaluar la asociación entre puntuaciones de MT verbal (Span de Dígitos) y la resolución de este tipo de operaciones. Aun cuando la presentación de la información a retener en la MT en el presente estudio fue de naturaleza auditiva y, por lo tanto, involucra el bucle fonológico para la codificación de dicha información, los resultados obtenidos sugieren que se activan simultáneamente representaciones visuales cuyo almacenamiento temporal depende de la agenda visoespacial.
Muchos de los estudios que asignaron a la MT verbal el rol preponderante en la resolución mental de cálculos trabajaron con participantes adultos (Furst y Hitch, 2000; Noel et al., 2001). Incluso McKenzie et al. (2003) encontraron que en el caso de niños de 8 años la MT verbal tiene mayor peso que la MT visoespacial en el cálculo mental, siendo esta asociación inversa en niños de 6 años. Al respecto, Baddeley, Gathercole y Pagano (1998) observaron que la estructura de la MT en niños muestra una disociación en rendimiento entre MT verbal y MT visoespacial con un mejor rendimiento en esta última hasta los 8 años, la cual tiende a desaparecer hacia los 9 años de edad. En el caso de la lectura se ha encontrado que a esta última edad (9 años) aproximadamente la misma comienza a depender más fuertemente de habilidades fonéticas que visuales; en la medida en que los niños aprenden a traducir códigos gráficos en asociaciones auditivas el procesamiento visoespacial que media la lectura empieza a apuntalarse en lo verbal (Fastenau, Conant y Lauer, 1998). Es posible que un proceso similar ocurra en el cálculo mental, y así los niños más pequeños puedan resolver las tareas, por ejemplo, activando y sosteniendo una representación visual de la cantidad de objetos a combinar, y que posteriormente su habilidad dependa en mayor medida de la recuperación y sostenimiento de hechos aritméticos almacenados como representaciones verbales.
Al respecto, Palmer (2000) encontró, en una tarea de memorización de imágenes, que los niños más pequeños utilizaban procesos visoespaciales, ya que no se veían afectados por la interferencia fonológica concurrente, pero su desempeño disminuía significativamente con una interferencia visoespacial. Los niños mayores, en cambio, se vieron afectados por ambos tipos de interferencia, aunque la visoespacial tuvo un menor efecto que en los niños menores. El autor concluyó que los niños pequeños, alrededor de los 5 o 6 años, pasan del uso de estrategias estrictamente visuales a una etapa de uso de estrategias duales (visuales y verbales), y finalmente al uso preponderante de estrategias verbales hacia los 8 o 9 años. Para este autor, la etapa de estrategias duales da tiempo al ejecutivo central para madurar y encargarse de la recodificación del material presentado visualmente a una representación fonológica. También da tiempo al perfeccionamiento del repaso subvocal vinculado al bucle fonológico. En conjunto, los resultados mencionados sugieren que el pasaje de estrategias visuales a verbales es general para cualquier tarea que haga uso de recursos de MT, incluyendo la resolución de problemas aritméticos a través del cálculo mental.
Es importante tener en cuenta que este estudio midió la eficiencia en cálculo mental registrando solo las respuestas correctas. No fue considerado el tipo de error o la distancia entre el error y el blanco, ni se preguntó al niño la forma en que resolvió la tarea. Un análisis de este tipo podría aportar información acerca del tipo de estrategia utilizada, e incluso acerca de los recursos de MT involucrados. Resultaría de interés analizar la existencia de una asociación diferenciada entre MT visoespacial y cálculo mental en niños más pequeños, según la resolución de los problemas se alcance a través del conteo verbal silente o la recuperación de hechos aritméticos. Sin embargo, debido al diseño de la tarea utilizada en este trabajo para evaluar el cálculo mental no es posible diferenciar ambos métodos.
Adicionalmente, las conclusiones a las que se llegó plantean la necesidad de nuevos estudios longitudinales que evalúen, ya sea la asociación entre los distintos componentes de la MT y el cálculo mental, o los diferentes efectos de la interferencia verbal o visoespacial sobre el cálculo mental, sobre todo abarcando un rango etario más amplio que los mencionados previamente. Estudios de este estilo permitirían confirmar o refutar los hallazgos descriptos hasta el momento. Estas limitaciones plantean posibles puntos de partida para futuras líneas de investigación.
FinanciaciónEl estudio presentado en este manuscrito se realizó en el marco de una beca doctoral financiada por la Universidad de Buenos Aires.
Conflicto de interesesLos autores declaran no tener ningún conflicto de intereses.
La revisión por pares es responsabilidad de la Universidad Nacional Autónoma de México.