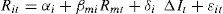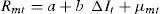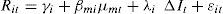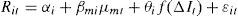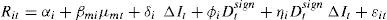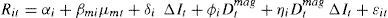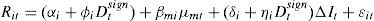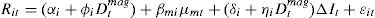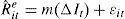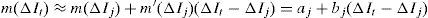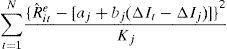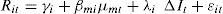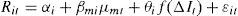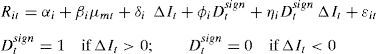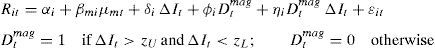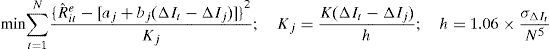Interest rate risk is one of the major financial risks faced by banks due to the very nature of the banking business. The most common approach in the literature has been to estimate the impact of interest rate risk on banks using a simple linear regression model. However, the relationship between interest rate changes and bank stock returns does not need to be exclusively linear. This article provides a comprehensive analysis of the interest rate exposure of the Spanish banking industry employing both parametric and non-parametric estimation methods. Its main contribution is to use, for the first time in the context of banks’ interest rate risk, a nonparametric regression technique that avoids the assumption of a specific functional form.
On the one hand, it is found that the Spanish banking sector exhibits a remarkable degree of interest rate exposure, although the impact of interest rate changes on bank, stock returns have significantly declined following the introduction of the euro. Further, a pattern of positive exposure emerges during the post-euro period. On the other hand, the results corresponding to the nonparametric model support the expansion of the conventional linear model in an attempt to gain a greater insight into the actual degree of exposure.
Interest rate risk (IRR, hereafter) is acknowledged as one of the major financial risks borne by companies. This is due to the fact that changes in interest rates affect both a firm's expected cash flows and the discount rates used to value them. Moreover, the high volatility in interest rates in recent years along with the significant level of financial leverage for most companies has also contributed to the growing relevance of interest rate exposure.
Much of the research on corporate exposure to IRR has concentrated on financial institutions because of the particularly interest rate sensitive nature of the banking business. Indeed, financial assets and liabilities represent a substantial portion of the balance sheet of banks and there exists generally a maturity mismatch between them. The asset-liability maturity mismatch has been usually identified as the key factor responsible for the high interest rate sensitivity of banking firms. The most common approach in the literature has consisted of measuring interest rate exposure by estimating the sensitivity of the value of the bank, proxied by the bank's stock return, to movements in interest rates using a simple linear regression model. There are, however, several reasons to suspect that the relationship between interest rates and market value of banks may be of nonlinear nature. On the one hand, since bank stock prices depend on interest rates both through the discount factor and the effect of interest rate changes on expected net interest income, it seems reasonable to expect that the impact of IRR is not exclusively linear. On the other hand, the risk management policy followed by banks, typically focused on the use of instruments with linear payoff profiles, favors the presence of nonlinearities in the interest rate exposure. In addition, the response of bank stock returns to interest rate shocks may depend upon the sign or the magnitude of the shock, thus generating an asymmetric exposure to IRR. In particular, interest rate rises and falls may affect bank value differently (sign asymmetry). Similarly, larger interest rate fluctuations may have a differential effect on bank value than smaller interest rate changes (size or magnitude asymmetry).
The aim of this paper is to provide a comprehensive analysis of the impact of IRR on the Spanish banking industry at the portfolio level. To this end, the degree of interest rate exposure is assessed not only using the standard linear model but also examining the existence of nonlinearities through parametric and nonparametric techniques. The primary contribution of the paper lies in the fact that it constitutes, to the best of our knowledge, the first attempt to quantify interest rate exposure through nonparametric regression methods. As a matter of fact, the only two studies that have employed a nonparametric approach in the context of corporate exposure to risk have focused on exchange rate exposure (Guo and Wu, 1998; Aysun and Guldi, 2009).
Nonparametric estimation techniques provide a flexible framework to model the relationship between variables. Unlike parametric regression, nonparametric analysis does not require any prior assumptions about the functional form of the model and the distribution of the error terms. The comparison of the results of the different methods allows us to evaluate to what extent the assumptions concerning the functional relationship between interest rates and bank stock prices can affect the results about the level of interest rate exposure.
The Spanish financial system can be classified as a bank-based system in which banking institutions play a central role in mobilizing savings and allocating resources. Spanish banks follow a universal banking model with a marked focus on retail banking. The Spanish banking sector has undergone a dramatic transformation over the past two decades largely due to an intensive process of deregulation, liberalization and consolidation during the run-up to the European Economic and Monetary Union. As a result, the major Spanish banking conglomerates, Santander and BBVA, rank currently among the top twenty largest banks in the world based on market capitalization, with a strong presence in Latin America and Europe. Therefore, the Spanish banking industry provides an excellent setting to investigate whether the adoption of the euro as a single currency in January 1999, with its implications in terms of greater financial stability induced by a common monetary policy and deepening and broadening of capital markets, has changed the nature and magnitude of banks’ interest rate exposure.
This study reveals some interesting results. First, the Spanish banking sector exhibits a remarkable interest rate exposure, even though the extent of IRR faced by Spanish banks has noticeably decreased after the launch of the euro. Second, a pattern of positive exposure seems to emerge during the post-euro period, reflecting a sharp change in the nature of the impact of IRR on bank stocks. Third, the superior performance of the nonparametric model supports the expansion of the traditional linear model in order to gain a better insight into the actual degree of exposure to IRR of banking institutions.
The evidence of a lower exposure to interest rate changes in the more stable environment associated to the European Monetary Union could be a relevant piece of information for other economies whose banking industry is currently involved in a process of modernization just like the one occurred in Spain. This is the case, for example, of the Central and Eastern European countries which have joined the European Union and have adopted the euro recently or are expected to do so in the following years.
The knowledge of the effect of interest rate fluctuations on bank equity values is crucial not only for purposes of IRR management, but also for other areas of finance such as asset allocation, portfolio management, asset pricing, and banking regulation.
The remainder of the paper is organized as follows. Section 2 provides an overview of previous literature regarding banks’ exposure to IRR. Section 3 details the data employed in this study. Section 4 describes the different model specifications employed. Section 5 reports the major empirical findings. Finally, Section 6 concludes.
2Review of literatureA large number of empirical studies have examined the impact of IRR on the value of banking institutions since the early 1980s. Most of this research, focused on a few highly developed countries, especially the US and only more recently Germany, Australia, Japan, or the UK, has adopted a capital market approach within the framework of the two-index linear model postulated by Stone (1974). The Stone's model includes an interest rate change factor in addition to the traditional market index for explaining bank stock returns.1 Three main results emerge from this body of work. First, a significantly negative effect of movements in interest rates on banking firms’ stock returns is generally documented, and it has been commonly attributed to the maturity mismatch between banks’ assets and liabilities (Flannery and James, 1984; Elyasiani and Mansur, 1998; Au Yong and Faff, 2008; Czaja et al., 2009, 2010). This finding corresponds to the traditional view of banks as financial intermediaries borrowing short-term from savers and lending long-term to investors (positive duration gap). Accordingly, a rise in interest rates would adversely affect a bank's market value (the present value of its assets would fall more than the present value of its liabilities) and net interest income (the cost of its liabilities would increase more rapidly than the yield on its assets). Second, bank stock returns tend to exhibit more sensitivity to changes in long-term interest rates than to changes in short-term rates (Elyasiani and Mansur, 1998; Bartram, 2002; Saporoschenko, 2002; Czaja et al., 2009). Third, the interest rate sensitivity of stock returns of banks has declined over time mainly due to the increased availability of more advanced tools for measuring and managing IRR (Faff and Howard, 1999; Benink and Wolff, 2000; Ryan and Worthington, 2004; Joseph and Vezos, 2006).
Even though the literature on corporate exposure to IRR in the Spanish case has received a considerable boost in recent years, this field has not been fully explored. Yet, it is possible to distinguish two lines of research. The first concerns the interest rate exposure of Spanish corporations at the industry level, including both bank and non-bank firms (Jareño, 2006, 2008; Ferrer et al., 2008, 2010; Jareño and Navarro, 2010). These studies demonstrate the high interest rate sensitivity of various sectors such as construction, real estate, electrical, and banking. The second line consists of a few studies that specifically focus on the impact of IRR on the stock market performance of the Spanish banking industry (Fernández and García, 1992; López, 2002; Ballester et al., 2009). Nevertheless, this body of work provides mixed evidence concerning the importance of interest rate exposure of Spanish banks, probably due to differences in the sample periods, interest rate variables used and/or methodologies applied.
It is worth noting that the implicit assumption underlying almost all the literature is that interest rate exposure is linear. Consequently, much less attention has been paid to other possible IRR patterns. In fact, the great majority of studies about corporate exposure to macroeconomic risks (e.g., exchange rate risk, IRR, or inflation risk) that investigate the presence of nonlinear or asymmetric exposure components have focused on exchange rate risk (Koutmos and Martin, 2003; Bartram, 2004; Tai, 2005; Priestley and Odegaard, 2007).
Despite the above mentioned, there are some empirical papers that explore the possibility of a profile of exposure more complex than the linear one. The seminal work in this field was done by Chen and Chan (1989), who investigate for potential asymmetry of interest rate sensitivity of U.S. financial institutions around interest rate cycles. A significant asymmetry is found during up and down cycles of interest rates, suggesting that the sensitivities of bank stock returns are highly sample-dependent. In the same vein, Hallerbach (1994) documents that the sensitivity of the Dutch stock market to changes in interest rates is not constant over time, showing a clear pattern of asymmetry to interest rate fluctuations of different sign. He points out that the specification of a nonlinear model could partly explain the asymmetry between sensitivities to interest rate rises and falls. More recently, Verma and Jackson (2008) utilize a multivariate EGARCH (exponential generalized autoregressive conditional heteroskedastic) model to evaluate the presence of spillover effects and asymmetries between short- and long-term interest rates and portfolios of US bank stocks. Their results provide evidence of response asymmetries for the portfolios of money center and other large banks, indicating that these banks are more sensitive to negative than positive interest rate changes.
In a very interesting paper, Bartram (2002) analyzes the impact of IRR on a large sample of German nonfinancial corporations at the industry level. His results support the existence of significant linear and nonlinear exposures with respect to changes in several interest rate variables. Ferrer et al. (2010) perform a similar study for Spain at the industry level, including both financial and nonfinancial firms. A significant linear and nonlinear interest rate exposure is found for the construction, real estate, electrical, utility and banking industries, although the traditional linear exposure pattern is economically more important than the nonlinear one. Using smooth transition regression models, Arango et al. (2002) also report some evidence of a nonlinear and inverse relationship between the share prices of the Colombian stock market and several interbank loan interest rates.
3DataThe sample consists of commercial banks listed on the Spanish Stock Exchange over the period from January 1993 to December 2008 whose stocks traded publicly for at least a year (a total of 23 banking institutions). Due to factors such as mergers and acquisitions and IPOs, the number of firms included in the sample varies over time. This sample selection procedure uses all the bank data available at the end of each year, hence minimizing the survivor bias and improving the efficiency of the estimation.
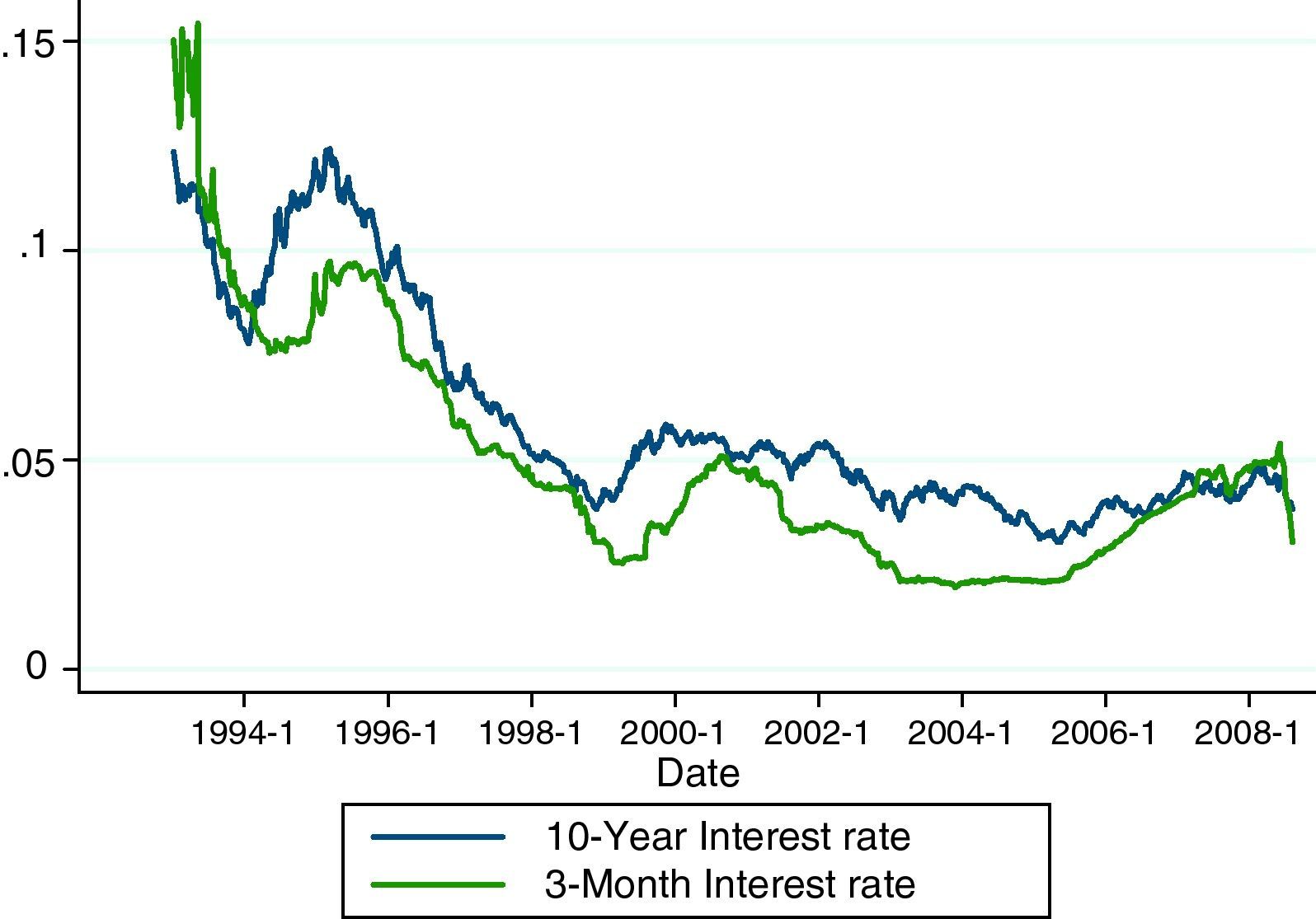
The period of study allows us to investigate whether the introduction of the euro in January 1999 did induce a significant alteration in the pattern of interest rate exposure of Spanish commercial banks. To this end, the total sample period is split into two subsamples, the pre-euro period, from January 1993 to December 1998, and the post-euro period, from January 1999 to December 2008. The adoption of the euro as a common European currency is a major historical event in international financial markets. Thus, it is likely to have a significant impact on the risks incurred by European banks in their activity. The euro may affect interest rate exposure of banks through two main channels. First, since the launch of the common currency Eurozone interest rates are set by the European Central Bank, which implements a single monetary policy for the euro area as a whole, with no national bias. Thus, the environment of more stable and historically low interest rates and greater transparency in monetary policy brought about by the European Monetary Union is expected to reduce the extent of IRR faced by European banking institutions.2 Second, the broadening and deepening of European corporate bond and interest rate derivative markets associated with the euro have greatly increased the availability of liquid instruments to implement a more effective IRR management, with the consequent negative effect on banks’ interest rate exposure.3
Following a usual practice in the literature (Flannery and James, 1984; Hirtle, 1997; Benink and Wolff, 2000; Soto et al., 2005; Ferrer et al., 2010), weekly stock returns, adjusted for dividends and stock splits, are employed. The weekly returns are calculated from Wednesday to Wednesday using closing stock prices in order to prevent the possible bias associated to the weekend effect. Weekly rather than daily data are utilized because sometimes the market takes a while to understand and reflect the effects of interest rate changes on asset prices. Thus, the use of very short (daily) horizon returns can make it much more difficult to properly assess a firm's interest rate exposure. In addition, weekly data are preferred over monthly data because of the availability of a much larger number of observations that allows us to obtain more precise results. The market portfolio is proxied by the Indice General de la Bolsa de Madrid, the widest Spanish value-weighted market index. Equity market data are obtained from the Madrid Stock Exchange database.
The 10-year Spanish government bond yield and the 3-month interbank rate are used as proxies for Spanish long- and short-term interest rates, respectively. The choice of the yield on 10-year government bonds to measure banks’ IRR has become a standard in the literature (Hirtle, 1997; Elyasiani and Mansur, 1998; Oertmann et al., 2000; Faff et al., 2005). Long-term interest rates are those that further incorporate expectations about future prospects for the economy and determine to a greater extent the cost of borrowed funds. Therefore, it seems reasonable to assume that long-term rates have a greater influence on corporate investment decisions and the expected future profitability of firms. In addition, 3-month interbank rates may also play a critical role as the money market has become increasingly important for Spanish banks in recent years due to two main reasons. First, interbank rates are widely used as reference rates for a great variety of variable-rate products, both on the asset and the liability side of the balance sheet. Second, banking institutions have relied heavily on the interbank market to finance the extraordinary credit expansion within the framework of the Spanish housing boom. All interest rate data are extracted from the Bank of Spain's database.
Along the lines followed by, among others, Elyasiani and Mansur (1998), Faff et al. (2005), Verma and Jackson (2008) and Czaja et al. (2009, 2010), portfolio data rather than individual firm data are used to examine banks’ interest rate exposure. The advantage of forming portfolios is twofold. First, it provides an efficient way for condensing a substantial amount of information about stock return behaviour. Second, it helps to smooth out the noisiness in the data due to transitory shocks to individual banks, hence producing more reliable results. The portfolio analysis may, however, mask the potential dissimilarities among individual firms within each portfolio. The sample is disaggregated by size into three equally weighted portfolios (large banks, medium banks and small banks). The large banks portfolio is made up of banks with total assets exceeding €60 billion, leading to the inclusion therein of the two big Spanish banking groups (Banco Santander and BBVA). The medium banks portfolio is formed by those institutions with total assets ranging from €7 billion to €60 billion. A total of seven banking institutions, representative of the Spanish mid-size banks, are included within this category. Lastly, the small banks portfolio is comprised of the twelve smallest banks (with total assets less than €7 billion).
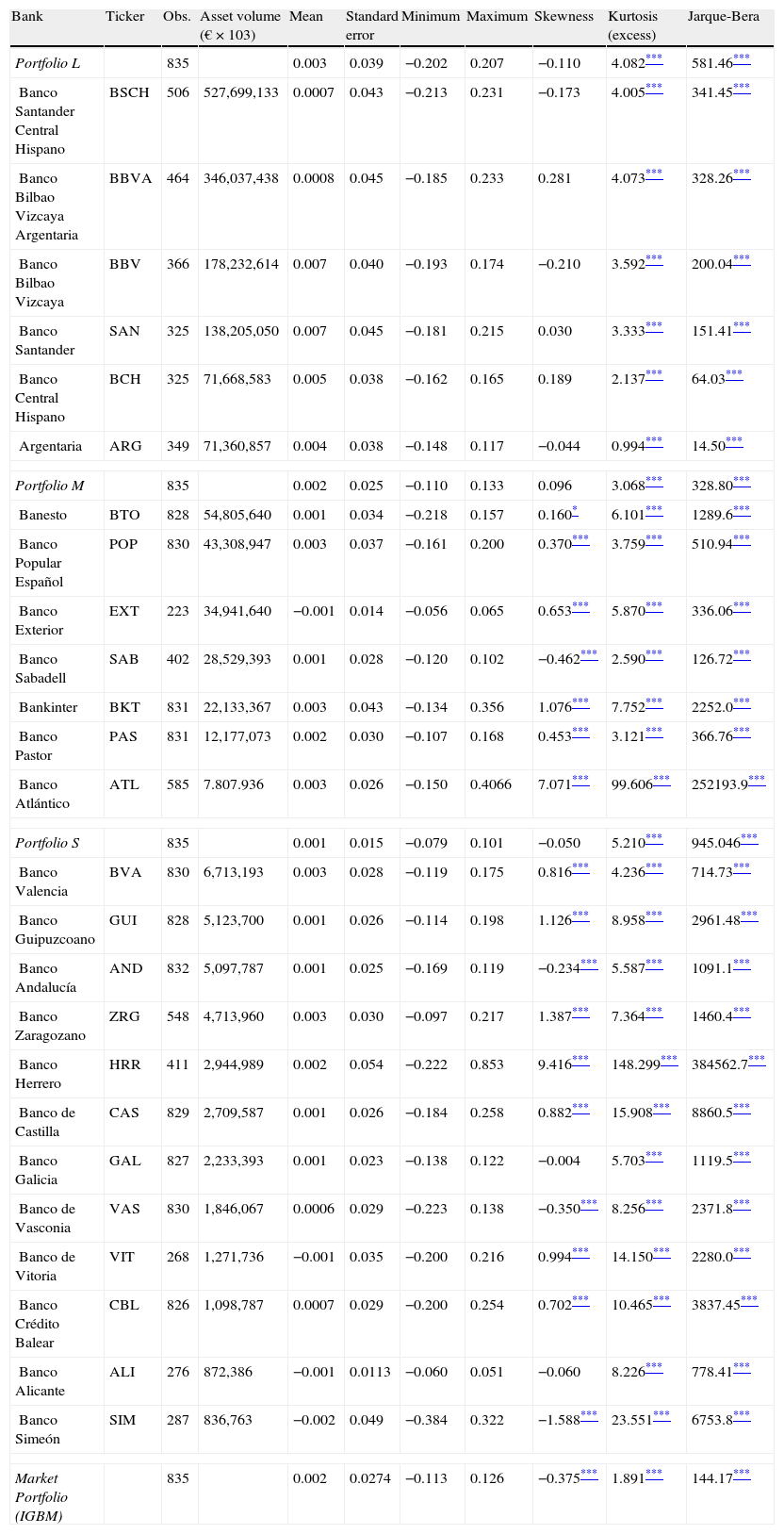
Table 1 lists the individual banks included in the analysis and their allocation among the three portfolios, along with their respective stock ticker symbol, number of observations, and average amount of total assets. Some descriptive statistics for the returns on individual banks and size-based portfolios are also reported.4 The vast majority of return series exhibit statistically significant skewness and kurtosis at the conventional levels. Hence, the null hypothesis of normality of returns is clearly rejected in all cases.
Composition of bank portfolios and descriptive statistics of individual and portfolio weekly returns Entire sample period (1993–2008).
| Bank | Ticker | Obs. | Asset volume (€×103) | Mean | Standard error | Minimum | Maximum | Skewness | Kurtosis (excess) | Jarque-Bera |
| Portfolio L | 835 | 0.003 | 0.039 | −0.202 | 0.207 | −0.110 | 4.082*** | 581.46*** | ||
| Banco Santander Central Hispano | BSCH | 506 | 527,699,133 | 0.0007 | 0.043 | −0.213 | 0.231 | −0.173 | 4.005*** | 341.45*** |
| Banco Bilbao Vizcaya Argentaria | BBVA | 464 | 346,037,438 | 0.0008 | 0.045 | −0.185 | 0.233 | 0.281 | 4.073*** | 328.26*** |
| Banco Bilbao Vizcaya | BBV | 366 | 178,232,614 | 0.007 | 0.040 | −0.193 | 0.174 | −0.210 | 3.592*** | 200.04*** |
| Banco Santander | SAN | 325 | 138,205,050 | 0.007 | 0.045 | −0.181 | 0.215 | 0.030 | 3.333*** | 151.41*** |
| Banco Central Hispano | BCH | 325 | 71,668,583 | 0.005 | 0.038 | −0.162 | 0.165 | 0.189 | 2.137*** | 64.03*** |
| Argentaria | ARG | 349 | 71,360,857 | 0.004 | 0.038 | −0.148 | 0.117 | −0.044 | 0.994*** | 14.50*** |
| Portfolio M | 835 | 0.002 | 0.025 | −0.110 | 0.133 | 0.096 | 3.068*** | 328.80*** | ||
| Banesto | BTO | 828 | 54,805,640 | 0.001 | 0.034 | −0.218 | 0.157 | 0.160* | 6.101*** | 1289.6*** |
| Banco Popular Español | POP | 830 | 43,308,947 | 0.003 | 0.037 | −0.161 | 0.200 | 0.370*** | 3.759*** | 510.94*** |
| Banco Exterior | EXT | 223 | 34,941,640 | −0.001 | 0.014 | −0.056 | 0.065 | 0.653*** | 5.870*** | 336.06*** |
| Banco Sabadell | SAB | 402 | 28,529,393 | 0.001 | 0.028 | −0.120 | 0.102 | −0.462*** | 2.590*** | 126.72*** |
| Bankinter | BKT | 831 | 22,133,367 | 0.003 | 0.043 | −0.134 | 0.356 | 1.076*** | 7.752*** | 2252.0*** |
| Banco Pastor | PAS | 831 | 12,177,073 | 0.002 | 0.030 | −0.107 | 0.168 | 0.453*** | 3.121*** | 366.76*** |
| Banco Atlántico | ATL | 585 | 7.807.936 | 0.003 | 0.026 | −0.150 | 0.4066 | 7.071*** | 99.606*** | 252193.9*** |
| Portfolio S | 835 | 0.001 | 0.015 | −0.079 | 0.101 | −0.050 | 5.210*** | 945.046*** | ||
| Banco Valencia | BVA | 830 | 6,713,193 | 0.003 | 0.028 | −0.119 | 0.175 | 0.816*** | 4.236*** | 714.73*** |
| Banco Guipuzcoano | GUI | 828 | 5,123,700 | 0.001 | 0.026 | −0.114 | 0.198 | 1.126*** | 8.958*** | 2961.48*** |
| Banco Andalucía | AND | 832 | 5,097,787 | 0.001 | 0.025 | −0.169 | 0.119 | −0.234*** | 5.587*** | 1091.1*** |
| Banco Zaragozano | ZRG | 548 | 4,713,960 | 0.003 | 0.030 | −0.097 | 0.217 | 1.387*** | 7.364*** | 1460.4*** |
| Banco Herrero | HRR | 411 | 2,944,989 | 0.002 | 0.054 | −0.222 | 0.853 | 9.416*** | 148.299*** | 384562.7*** |
| Banco de Castilla | CAS | 829 | 2,709,587 | 0.001 | 0.026 | −0.184 | 0.258 | 0.882*** | 15.908*** | 8860.5*** |
| Banco Galicia | GAL | 827 | 2,233,393 | 0.001 | 0.023 | −0.138 | 0.122 | −0.004 | 5.703*** | 1119.5*** |
| Banco de Vasconia | VAS | 830 | 1,846,067 | 0.0006 | 0.029 | −0.223 | 0.138 | −0.350*** | 8.256*** | 2371.8*** |
| Banco de Vitoria | VIT | 268 | 1,271,736 | −0.001 | 0.035 | −0.200 | 0.216 | 0.994*** | 14.150*** | 2280.0*** |
| Banco Crédito Balear | CBL | 826 | 1,098,787 | 0.0007 | 0.029 | −0.200 | 0.254 | 0.702*** | 10.465*** | 3837.45*** |
| Banco Alicante | ALI | 276 | 872,386 | −0.001 | 0.0113 | −0.060 | 0.051 | −0.060 | 8.226*** | 778.41*** |
| Banco Simeón | SIM | 287 | 836,763 | −0.002 | 0.049 | −0.384 | 0.322 | −1.588*** | 23.551*** | 6753.8*** |
| Market Portfolio (IGBM) | 835 | 0.002 | 0.0274 | −0.113 | 0.126 | −0.375*** | 1.891*** | 144.17*** | ||
This table lists the Spanish individual commercial banks considered in this study and their grouping into three portfolios based on their size: large banks portfolio (portfolio L), medium banks portfolio (portfolio M) and small banks portfolio (portfolio S). The stock ticker symbol, number of observations and average volume of total assets for each individual bank are also reported. Descriptive statistics associated with individual and portfolio weekly returns are presented as well.
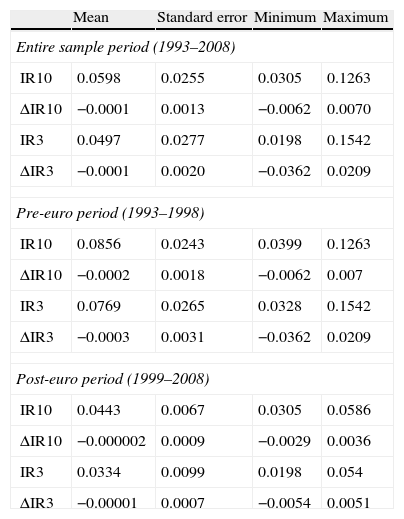
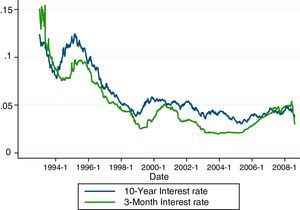
Table 2 contains summary information on the interest rate series. For both the full sample period and the two sub-periods the average yield on 10-year government bond yields is higher than the average 3-month interbank rate. It should be also noted that the average 10-year and 3-month rates take substantially lower values in the post-euro era. Further, the 10-year yield series has the lowest standard deviation regardless of the sample period considered, consistent with the idea that volatility of interest rates usually decreases as maturity increases. As expected, interest rate volatility has significantly declined following the introduction of the euro, confirming the greater stability in interest rates during the post-euro period.5Fig. 1 illustrates the evolution over time of the series of interest rates, which exhibit a clear downward trend during most of the sample period.
Descriptive statistics of the interest rate series.
| Mean | Standard error | Minimum | Maximum | |
| Entire sample period (1993–2008) | ||||
| IR10 | 0.0598 | 0.0255 | 0.0305 | 0.1263 |
| ΔIR10 | −0.0001 | 0.0013 | −0.0062 | 0.0070 |
| IR3 | 0.0497 | 0.0277 | 0.0198 | 0.1542 |
| ΔIR3 | −0.0001 | 0.0020 | −0.0362 | 0.0209 |
| Pre-euro period (1993–1998) | ||||
| IR10 | 0.0856 | 0.0243 | 0.0399 | 0.1263 |
| ΔIR10 | −0.0002 | 0.0018 | −0.0062 | 0.007 |
| IR3 | 0.0769 | 0.0265 | 0.0328 | 0.1542 |
| ΔIR3 | −0.0003 | 0.0031 | −0.0362 | 0.0209 |
| Post-euro period (1999–2008) | ||||
| IR10 | 0.0443 | 0.0067 | 0.0305 | 0.0586 |
| ΔIR10 | −0.000002 | 0.0009 | −0.0029 | 0.0036 |
| IR3 | 0.0334 | 0.0099 | 0.0198 | 0.054 |
| ΔIR3 | −0.00001 | 0.0007 | −0.0054 | 0.0051 |
This table contains descriptive statistics for the series of interest rates considered in this study. Summary statistics are presented for the full sample period and the pre- and post-euro periods. IR10 denotes the series of yields on 10-year Spanish government bonds and IR3 the series of 3-month interbank rates. Δ is the first difference operator.
This section provides a brief description of the model specifications employed. The linear regression model traditionally used in prior research on banks’ IRR is presented first, followed by several nonlinear parametric and nonparametric approaches.
4.1Parametric models4.1.1Linear modelThe two-index linear regression model proposed by Stone (1974) is the benchmark model in the literature to quantify the degree of bank interest rate exposure. This model takes the following form:
where Rit denotes the return on asset i in period t, Rmt the return on the market portfolio, ΔIt the change in the interest rate, and ¿it an error term.The coefficient on the market portfolio return, βmi, reflects the sensitivity of the return on asset i to general market fluctuations and is, therefore, a measure of market risk. The inclusion of a market index is designed to control for market-wide factors, mitigating the omitted variable bias and improving the efficiency of the estimation. The coefficient on the interest rate change term, δi, represents the sensitivity of the return on asset i to movements in interest rates, controlling for changes in the return on the market. Hence, it can be interpreted as a measure of exposure to IRR. Note that a negative interest rate exposure coefficient corresponds to the traditional view of banks as borrowing short-term and lending long-term.
Since movements in interest rates also affect the market return and, through that channel, bank stock returns, the impact of IRR on asset i is partly captured by the coefficient of market risk βmi and, hence, the interest rate coefficient δi only represents a partial indicator of IRR. In order to obtain a measure of the total interest rate exposure of asset i, an orthogonalization procedure is implemented.6 Considering that the main focus of this study is to evaluate the impact of IRR on the value of banks, an orthogonalization scheme where the market factor is orthogonalized with respect to the interest rate change factor is adopted. The same strategy has been followed by, among others, Hirtle (1997), Fraser et al. (2002), Soto et al. (2005) and Czaja et al. (2009, 2010), to avoid any estimation bias due to multicollinearity between independent variables. Thus, the auxiliary regression run is:
where a and b are parameters to be estimated and μmt denotes the residuals of the regression. This residual series is usually called the residual market factor and represents the part of the market returns that cannot be explained by changes in interest rates. Obviously, the residual market factor is uncorrelated with interest rate fluctuations by construction.Then, the original market return is replaced by the residual market factor estimated from Eq. (2), so that Eq. (3) is obtained as follows:
where γi=αi+aβmi and λi=δi+bβmi. In contrast, the market beta coefficient βmi remains the same than in Eq. (1). Residuals also coincide implying the same R2 in the empirical estimations of models in Eqs. (1) and (3).The main advantage of using the specification in Eq. (3) is that it allows us to obtain a total measure of interest rate exposure. The coefficient λi reflects both the direct and indirect (via the market return) effects on interest rate variations on bank equity values. As pointed out by Czaja et al. (2009), the resulting λi is identical to the coefficient from a simple univariate regression of bank asset returns on changes in interest rates, just with more precision in the estimates. In turn, βmi reflects the pure sensitivity to general market movements uncontaminated by interest rate effects. Moreover, the same orthogonalization approach is used in all the other models described below.
4.1.2Nonlinear modelEarly empirical studies of corporate exposure to IRR focused almost exclusively on linear exposure. Nevertheless, as noted by Bartram (2002), the value of a firm, defined as the present value of all its expected cash flows, may depend in a very complex way on interest rates since movements in interest rates affect both discount rates and expectations about future cash flows. Further, most companies typically employ risk management instruments with linear payoffs (e.g., forward rate agreements, futures or swaps), thus only hedging against linear exposure. In contrast, nonlinear exposure is much less taken into account by firms when designing their hedging strategies. This implies a higher chance of finding empirically a significant nonlinear exposure, which in turn could be hedged using instruments with nonlinear payoff schedules such as interest rate options. Therefore, in order to gain a better understanding of the nature of IRR borne by firms it is interesting to examine the presence of nonlinear effects in their interest rate exposure.
Even so, it is very difficult to impose a specific functional form a priori to characterize the nonlinear exposure as the shape of the exposure may not be uniform across companies. In fact, the exact form of nonlinearity may be a complex function of different firm characteristics such as financial leverage, profitability, size, liquidity or risk management practices. This study represents a first attempt to assess the presence of nonlinear exposure, to be completed later on with the nonparametric model. Therefore, a simplifying approach, which is based on the assumption that some generic nonlinear functions are enough to accurately capture the nonlinearities, is used. Thus, a regression equation with a general nonlinear component can be written as:
where f(·) denotes a nonlinear function of the changes in interest rates and the parameter θi measures the effect of nonlinear movements in interest rates on the returns of asset i. A nonlinear specification implies that the interest rate sensitivity depends on the size of the interest rate shock.Relevant nonlinear functions in this context can be classified as concave and convex functions. Concave functions (e.g., cubic root function or inverse hyperbolic sine function) assume a relatively higher sensitivity of stock returns to small movements in interest rates than to large interest rate changes. Accordingly, these functional forms do not seem very appropriate to provide a realistic measure of the impact of interest rate changes on bank equity prices. In contrast, convex functions (e.g., cubic function or hyperbolic sine function) reflect a comparatively more aggressive response of stock returns to larger interest rate fluctuations, so that they are better suited to inefficiencies in capital markets. In particular, convex functions are consistent with the idea that small changes in interest rates are probably dominated by other price relevant information and have less or even no effect on stock prices, while large interest rate shocks have a greater impact on stock prices. Consequently, convex functions appear to be more appropriate to model a nonlinear relationship between interest rate fluctuations and stock returns.
In any case, there is no consensus about the most convenient convex function to be used in order to estimate a nonlinear interest rate exposure. In this sense, one of the simplest ways to introduce nonlinearity is to use a cubic function of the form f(x)=a+bx+cx2+dx3, where the quadratic and cubic terms permit this function to take different shapes depending on the sign and magnitude of the parameters c and d. Further, this function is sign-sensitive, allowing us to distinguish between the effect of interest rate rises and that of interest rate falls. Therefore, the cubic function will be used in this study. Additionally, it is worth to point out that the parametric models are estimated for each bank portfolio applying OLS with the Newey-West procedure to correct standard errors for autocorrelation and heteroscedasticity.
4.1.3Sign and size asymmetric modelsAn alternative way of detecting nonlinear effects is to examine the presence of asymmetries in the response of bank asset returns to interest rate changes of different sign and/or size. On the one hand, bank asset returns may react differently to interest rate rises and falls (sign asymmetry). On the other hand, large and small interest rate shocks (size or magnitude asymmetry) may impact differently on bank asset returns. To allow for these asymmetries, the basic model in Eq. (1) is extended. Specifically, the sign asymmetry can be analyzed using the following model:
The dummy variable Dtsign is equal to 1 if ΔIt>0 and zero otherwise. For a given value of the market portfolio, the response of bank stock returns will be δi when ΔIt<0, and δi+ηi when ΔIt>0.
Analogously, the size or magnitude asymmetry can be assessed through the following model:
The dummy variable Dtmag is equal to 1 if ΔIt≥zU or ΔIt≥zL where zU and zL indicate the upper and lower threshold levels, respectively, that discriminate between small and large interest rate movements, and Dtmag=0 otherwise. The threshold values zL are calculated as ΔIt¯+2σΔIt and ΔIt¯+2σΔIt, respectively. Thus, the response of bank stock returns will be equal to δi+ηi when ΔIt≥zU or ΔIt<zL, and δi in the remaining cases.
Both models can be used to estimate the coefficients associated to interest rate fluctuations of different sign or size, but they do not offer a direct test of asymmetry. Thus, in order to directly test the asymmetry hypothesis Eqs. (5) and (6) can be rewritten as follows:
As Koutmos and Martin (2003) point out, a test for asymmetry is equivalent to testing that ηi is statistically significant irrespective of the sign of the coefficient.
4.2Nonparametric modelAll the model specifications discussed above require a specific functional form and assume that it does not change during the sample period. In this section, however, the measurement of banks’ interest rate exposure is tackled from a completely different perspective, using nonparametric estimation techniques. The primary advantage of this method is its flexibility, as it allows estimating the relationship between movements in interest rates and bank stock returns without adhering to a particular function. Specifically, the local linear regression developed by Stone (1977) is employed to avoid the well-known problem of misspecification in the functional form inherent to traditional parametric models. The basic idea behind the local linear approach is to fit a linear regression locally around a neighbourhood of each data point in the sample, giving a greater weight to closer neighbours. This procedure has a higher asymptotic efficiency and allows for faster convergence at boundary points compared to other nonparametric methods (Fan and Gijbels, 1996).
Under this framework, it is assumed that the relationship between bank asset returns and interest rate changes is given by the following generic model:
where Rˆite is the abnormal return on asset i in period t, calculated as Rˆite=Rit−βˆiμmt, i.e., eliminating the impact of market-wide factors on individual asset returns. μmt denotes the orthogonalized market portfolio return and the parameter βˆi is estimated using the classical market model. In turn, m(ΔIt) represents an unknown smooth function and ¿it is a random error term.The unknown function m(ΔIt) can be approximated through a Taylor series expansion around a given point ΔIj, such that:
where m′(ΔIj) is the partial derivative of m(ΔIt) with respect to ΔI, also called marginal effect or response and it is similar in interpretation to the regression coefficient (slope) in a linear regression model.The local linear regression is equivalent to finding aj and bj to minimize the following weighted objective function:
where Kj=K(ΔIt−ΔIj)/h is a kernel function and h denotes the bandwidth parameter of the kernel, respectively. The kernel function assigns weights to the data points improving the system of local averaging. This function assigns more importance, and so weight, to a point closer to the point of interest than to one further away. Therefore, the kernel determines the weight that the observation ΔIt receives in estimating the value of Rˆite at target point ΔIj. The Gaussian kernel, which is one of the most popular kernel functions in financial applications, is used in this study. The bandwidth indicates how much “local” the estimator is. For every point ΔIj, the bandwidth dictates the width of the neighbourhood on which the estimation of m(ΔIj) is based. As Fan and Gijbels (1996) indicate, the choice of the bandwidth parameter may have crucial repercussions on the results of nonparametric regressions. Following a usual practice in the literature, when the standard Gaussian kernel is employed the optimal bandwidth is computed according to the Silverman's rule of thumb. This value is given by the formula h=1.06⋅σΔIt/N5, where σΔIt is the sample standard deviation of the interest rate change series and N the number of observations. Notice that this local regression uses only observations close to the point ΔIj to minimize the sum of squared residuals, so that the estimates of a and b are not longer constants but functions of ΔIj.After estimating the coefficient bj for every point in the sample, the sample mean of these pointwise estimates can be used in the same way as the estimated coefficient of the parametric regression model. Rilstone (1991) shows that this estimator is consistent and asymptotically normally distributed and its standard errors are comparable to those from traditional parametric estimation. As a result, hypothesis tests can be easily conducted to compare the nonparametric estimates with their parametric counterparts.
5Empirical resultsTable 3 presents the interest rate exposure coefficients from the different models. The first four columns report the coefficient estimates of the parametric specifications, and the fifth column shows the estimates of the nonparametric approach. Panel A provides the exposure estimates for the entire sample period, and Panels B and C for the pre-euro and post-euro sub-periods, respectively.
Exposure of bank portfolios to interest rate risk.
| Linear model (3) | Nonlinear model (4) | Sign asymmetric model (5) | Size asymmetric model (6) | Nonparametric model (11) | |||
| λi | θi | δi | (δi+ηi) | δi | (δi+ηi) | bˆ¯j | |
| Panel A: Entire sample period (1993–2008) | |||||||
| 10-Year interest rate changes | |||||||
| Portfolio L | −2.305** | −102670.3*** | −3.705** | −1.982 | −1.789 | −2.842*** | −2.234*** |
| (0.905) | (31031.8) | (1.706) | (1.419) | (1.357) | (0.935) | (0.054) | |
| R2 (%) | 47.66 | 47.51 | 47.61 | 47.56 | 48.36 | ||
| Portfolio M | −3.090*** | −97596.8*** | −2.728** | −3.043** | −3.509*** | −2.656*** | −3.118*** |
| (0.628) | (22497.3) | (1.108) | (1.094) | (0.912) | (0.718) | (0.006) | |
| R2 (%) | 28.03 | 26.46 | 27.86 | 27.90 | 29.08 | ||
| Portfolio S | −1.640*** | −62855.2*** | −0.738 | −2.306*** | −1.448** | −1.810*** | −1.613*** |
| (0.405) | (14172.3) | (0.813) | (0.748) | (0.612) | (0.493) | (0.045) | |
| R2 (%) | 7.60 | 6.77 | 7.60 | 7.86 | 8.00 | ||
| 3-Month interest rate changes | |||||||
| Portfolio L | −1.590*** | −1285.64*** | −1.845*** | −1.316 | 0.404 | −1.749*** | −1.677** |
| (0.488) | (141.48) | (0.675) | (0.460) | (1.726) | (0.410) | (0.059) | |
| R2 (%) | 47.64 | 47.28 | 47.54 | 48.11 | 48.45 | ||
| Portfolio M | −1.073*** | −514.66*** | −1.178** | −0.448 | −0.532 | −0.963** | −1.510** |
| (0.377) | (124.10) | (0.582) | (0.276) | (1.050) | (0.403) | (0.111) | |
| R2 (%) | 27.28 | 26.70 | 27.21 | 27.73 | 28.27 | ||
| Portfolio S | −0.412** | −358.04*** | −0.458* | −0.274 | 0.395 | −0.5020 | −0.326 |
| (0.205) | (110.26) | (0.265) | (0.402) | (0.754) | (0.212) | (0.024) | |
| R2 (%) | 6.66 | 6.47 | 6.38 | 6.82 | 6.95 | ||
| Panel B: Pre-euro period (1993–1998) | |||||||
| 10-Year interest rate changes | |||||||
| Portfolio L | −6.037*** | −231892.3*** | −7.433*** | −7.970*** | −5.287*** | −7.168*** | −5.875*** |
| (0.540) | (30679.4) | (1.125) | (1.025) | (0.813) | (0.589) | (0.032) | |
| R2 (%) | 72.19 | 69.91 | 72.59 | 72.26 | 89.39 | ||
| Portfolio M | −4.963*** | −155293.6*** | −5.835*** | −3.787*** | −5.163*** | −4.890*** | −5.008*** |
| (0.508) | (24062.3) | (1.033) | (1.129) | (0.697) | (0.658) | (0.054) | |
| R2 (%) | 56.73 | 51.46 | 56.67 | 56.78 | 66.45 | ||
| Portfolio S | −1.904*** | −73900.7*** | −1.603* | −2.353** | −1.576*** | −2.390*** | −1.869*** |
| (0.330) | (12159.8) | (0.888) | (0.684) | (0.487) | (0.441) | (0.014) | |
| R2 (%) | 17.51 | 16.63 | 17.04 | 17.15 | 18.77 | ||
| 3-Month interest rate changes | |||||||
| Portfolio L | −1.647*** | −1730.74*** | −1.951*** | −1.952*** | 0.516 | −2.046*** | −1.216** |
| (0.268) | (192.01) | (0.259) | (0.234) | (1.054) | (0.111) | (0.061) | |
| R2 (%) | 74.17 | 71.09 | 71.69 | 72.14 | 77.35 | ||
| Portfolio M | −1.250*** | −857.64*** | −1.170*** | −0.655 | −0.488 | −1.333*** | −1.454*** |
| (0.251) | (172.16) | (0.352) | (0.301) | (0.741) | (0.374) | (0.093) | |
| R2 (%) | 58.33 | 55.44 | 56.87 | 57.25 | 60.28 | ||
| Portfolio S | −0.548*** | −474.05*** | −0.673*** | −0.504 | −0.116 | −0.606* | −0.475*** |
| (0.150) | (131.46) | (0.200) | (0.408) | (0.540) | (0.203) | (0.019) | |
| R2 (%) | 5.88 | 17.04 | 17.07 | 17.38 | 18.44 | ||
| Panel C: Post-euro period (1999–2008) | |||||||
| 10-Year interest rate changes | |||||||
| Portfolio L | 7.086** | 1039059.2 | 1.309 | 11.011*** | 8.624*** | 3.352 | 7.352*** |
| (2.873) | (909703.6) | (7.871) | (4.659) | (2.164) | (7.749) | (0.696) | |
| R2 (%) | 38.46 | 37.03 | 38.66 | 38.79 | 40.68 | ||
| Portfolio M | 1.655 | 16315.34 | 3.327 | -0.930 | 2.972** | -0.568 | 1.967* |
| (1.828) | (573103.6) | (4.6523) | (3.299) | (1.484) | (4.993) | (0.252) | |
| R2 (%) | 14.14 | 13.78 | 14.05 | 14.28 | 14.68 | ||
| Portfolio S | −0.950 | −459916.1 | 0.619 | −3.173* | 0.045 | −2.357* | −0.731 |
| (1.132) | (343701.6) | (3.0016) | (2.288) | (0.837) | (2.907) | (0.151) | |
| R2 (%) | 2.98 | 3.98 | 3.10 | 3.72 | 3.69 | ||
| 3-Month interest rate changes | |||||||
| Portfolio L | −1.443 | −450821.4 | −4.552 | 1.134 | 1.198 | −3.535 | 2.329 |
| (4.896) | (492240.6) | (7.891) | (6.516) | (4.345) | (6.596) | (0.853) | |
| R2 (%) | 39.28 | 35.87 | 39.33 | 39.44 | 44.45 | ||
| Portfolio M | 0.834 | −191386.3 | 0.002 | 0.909 | 3.192 | −1.003 | 3.209** |
| (2.706) | (263543.5) | (4.584) | (1.830) | (2.881) | (3.389) | (0.463) | |
| R2 (%) | 14.03 | 12.02 | 13.76 | 14.56 | 17.34 | ||
| Portfolio S | 1.056 | −13032.9 | 2.131 | 0.129 | −1.446 | 1.7622 | 1.290 |
| (1.762) | (161982.8) | (3.189) | (2.012) | (2.092) | (2.305) | (0.190) | |
| R2 (%) | 2.15 | 1.59 | 2.01 | 2.38 | 2.99 | ||
This table contains the interest rate exposure coefficients from estimating the parametric and nonparametric models considered for the three bank portfolios over the entire sample, pre- and post-euro periods. The 10-year Spanish government bond yield and 3-month interbank rate are used as proxies of market interest rates. Parametric models in Eq. (3)–(6) are estimated applying OLS. The cubic function is used for the estimation of the nonlinear model. Nonparametric model in Eq. (11) is estimated using the local linear regression method proposed by Stone (1977). The last column of this table reports the average nonparametric estimates. Standard errors are shown in parentheses. In the particular case of the nonparametric model, the statistical significance of the coefficients is given by the estimation output of the NP package (and not the standard t test).
The exposure coefficients from the two-index linear model in Eq. (1) are negative and statistically significant at the conventional levels for the whole sample regardless of the portfolio and interest rate proxy used. This implies that Spanish banks are, on average, adversely impacted by rises in interest rates. The inverse relationship between movements in interest rates and bank stock returns is consistent with the typical bank balance sheet maturity structure, where long-term assets are funded with short-term liabilities (positive duration gap). This negative link is also in accordance with most of the existing literature on bank IRR (e.g., Elyasiani and Mansur, 1998; Au Yong and Faff, 2008; Czaja et al., 2009, 2010). The interest rate sensitivity of banking firms varies depending on the interest rate variable chosen. Thus, the exposure coefficients associated with changes in 10-year government bond yields are larger in absolute value that those estimated with 3-month interbank rates. Further, the small banks portfolio shows the lowest coefficients in absolute values and R2, suggesting that smaller banks are the least vulnerable to linear IRR. This is consistent with the idea that Spanish small banks have a stock market behaviour hardly influenced by interest rate fluctuations, but rather dependent on idiosyncratic risk factors.
5.2Nonlinear interest rate exposureThe results of the nonlinear specification broadly corroborate the findings of the linear model. As is shown in the second column of Table 3, the cubic function permits to identify an important extent of nonlinear exposure to IRR during the entire sample period. In particular, all bank portfolios exhibit a significant nonlinear exposure irrespective of the interest rate variable under consideration. The sign of the nonlinear coefficients is negative in all cases, confirming that decreases in interest rates have a positive effect on Spanish banking firms. This result reinforces the widespread view that banks tend to maintain a positive mismatch between the maturity of their assets and liabilities. As in the linear model, the exposure coefficients are larger in absolute value when movements in 10-year government bond yields are used and the lowest coefficients and R2 are observed for the small banks portfolio.
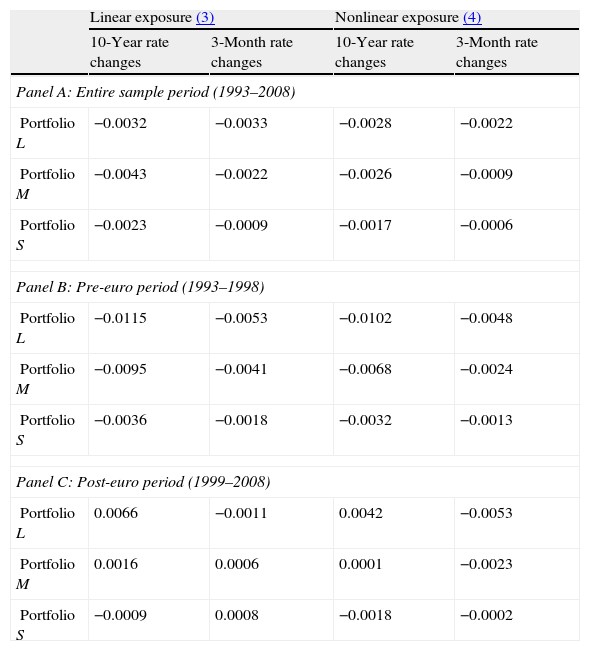
Since the independent variables in the linear and nonlinear models are different, in order to compare the economic importance of both types of exposure the product of the estimated exposure coefficient with one standard deviation of the interest rate proxy is computed for all portfolios exhibiting both significant linear and nonlinear exposure. As argued by Bartram (2002), this procedure makes the coefficients comparable as it standardizes the variables across regression specifications. The results displayed in Table 4 indicate that the linear exposure coefficients are always greater, in absolute value, than nonlinear coefficients during the entire sample period. This implies that, in general, the linear interest rate exposure of Spanish banks is economically more important than the nonlinear exposure measured using a cubic function. This finding coincides with that reported by Ferrer et al. (2010) for the banking sector in an analysis of the interest rate exposure of Spanish firms carried out at the industry level.
Economic significance of linear and nonlinear exposures.
| Linear exposure (3) | Nonlinear exposure (4) | |||
| 10-Year rate changes | 3-Month rate changes | 10-Year rate changes | 3-Month rate changes | |
| Panel A: Entire sample period (1993–2008) | ||||
| Portfolio L | −0.0032 | −0.0033 | −0.0028 | −0.0022 |
| Portfolio M | −0.0043 | −0.0022 | −0.0026 | −0.0009 |
| Portfolio S | −0.0023 | −0.0009 | −0.0017 | −0.0006 |
| Panel B: Pre-euro period (1993–1998) | ||||
| Portfolio L | −0.0115 | −0.0053 | −0.0102 | −0.0048 |
| Portfolio M | −0.0095 | −0.0041 | −0.0068 | −0.0024 |
| Portfolio S | −0.0036 | −0.0018 | −0.0032 | −0.0013 |
| Panel C: Post-euro period (1999–2008) | ||||
| Portfolio L | 0.0066 | −0.0011 | 0.0042 | −0.0053 |
| Portfolio M | 0.0016 | 0.0006 | 0.0001 | −0.0023 |
| Portfolio S | −0.0009 | 0.0008 | −0.0018 | −0.0002 |
This table reports the interest rate exposure coefficients multiplied by one standard error of the interest rate proxy for the three bank portfolios. Panel A refers to the whole sample period and Panels B and C to the pre- and post-euro periods, respectively. The exposures are estimated by regressing the portfolio returns on the market return and the interest rate variable. Nonlinear exposure is estimated using the cubic function.
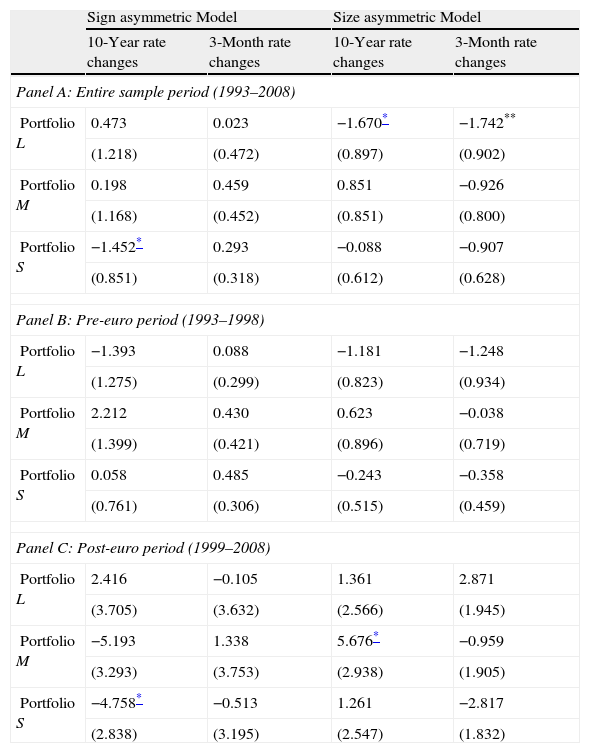
In line with the previous specifications, the findings of the estimation of the sign and size asymmetric models, also reported in Table 3, show the prevalence of negative exposure for the whole sample. With regard to the sign asymmetry, bank portfolio returns seem, in general, more sensitive to falling than to rising interest rates, especially for movements in 3-month interbank rates. Concerning the size or magnitude asymmetry, larger interest rate fluctuations appear to have a greater impact on portfolio returns than smaller interest rate changes. Once again, the lowest explanatory power of the asymmetric models is observed for the small banks portfolio. However, the results of the direct tests of sign and magnitude asymmetry presented in Table 5 do not support the existence of significant asymmetries in interest rate exposure for the full sample period, principally for the medium and small banks portfolios. As can be seen, the coefficient of asymmetry ηi is not statistically different from zero in the vast majority of cases.
Asymmetries in interest rate exposure.
| Sign asymmetric Model | Size asymmetric Model | |||
| 10-Year rate changes | 3-Month rate changes | 10-Year rate changes | 3-Month rate changes | |
| Panel A: Entire sample period (1993–2008) | ||||
| Portfolio L | 0.473 | 0.023 | −1.670* | −1.742** |
| (1.218) | (0.472) | (0.897) | (0.902) | |
| Portfolio M | 0.198 | 0.459 | 0.851 | −0.926 |
| (1.168) | (0.452) | (0.851) | (0.800) | |
| Portfolio S | −1.452* | 0.293 | −0.088 | −0.907 |
| (0.851) | (0.318) | (0.612) | (0.628) | |
| Panel B: Pre-euro period (1993–1998) | ||||
| Portfolio L | −1.393 | 0.088 | −1.181 | −1.248 |
| (1.275) | (0.299) | (0.823) | (0.934) | |
| Portfolio M | 2.212 | 0.430 | 0.623 | −0.038 |
| (1.399) | (0.421) | (0.896) | (0.719) | |
| Portfolio S | 0.058 | 0.485 | −0.243 | −0.358 |
| (0.761) | (0.306) | (0.515) | (0.459) | |
| Panel C: Post-euro period (1999–2008) | ||||
| Portfolio L | 2.416 | −0.105 | 1.361 | 2.871 |
| (3.705) | (3.632) | (2.566) | (1.945) | |
| Portfolio M | −5.193 | 1.338 | 5.676* | −0.959 |
| (3.293) | (3.753) | (2.938) | (1.905) | |
| Portfolio S | −4.758* | −0.513 | 1.261 | −2.817 |
| (2.838) | (3.195) | (2.547) | (1.832) | |
This table shows the results of the direct tests for sign and size or magnitude asymmetry in interest rate exposure using Eqs. (7) and (8), respectively. Panel A refers to the full sample period and Panels B and C to the pre- and post-euro periods, respectively. The test for asymmetry is equivalent to testing whether the coefficient ηi is statistically significant irrespective of the sign of the coefficient. Numbers in parentheses are standard errors.
The interpretation of nonparametric estimates is more complicated than that of linear parametric estimates. This is because the simple linear model assumes that the response of the dependent variable to changes in any explanatory variable is constant regardless of the level of the explanatory variable, while the nonparametric methods do not place such restrictions on the data. The estimation output of a nonparametric regression model consists of an estimate of the regression function and the marginal effect or response coefficient (for each regressor) at every point in the sample. Accordingly, this output can be difficult to interpret, being instructive its graphical representation.
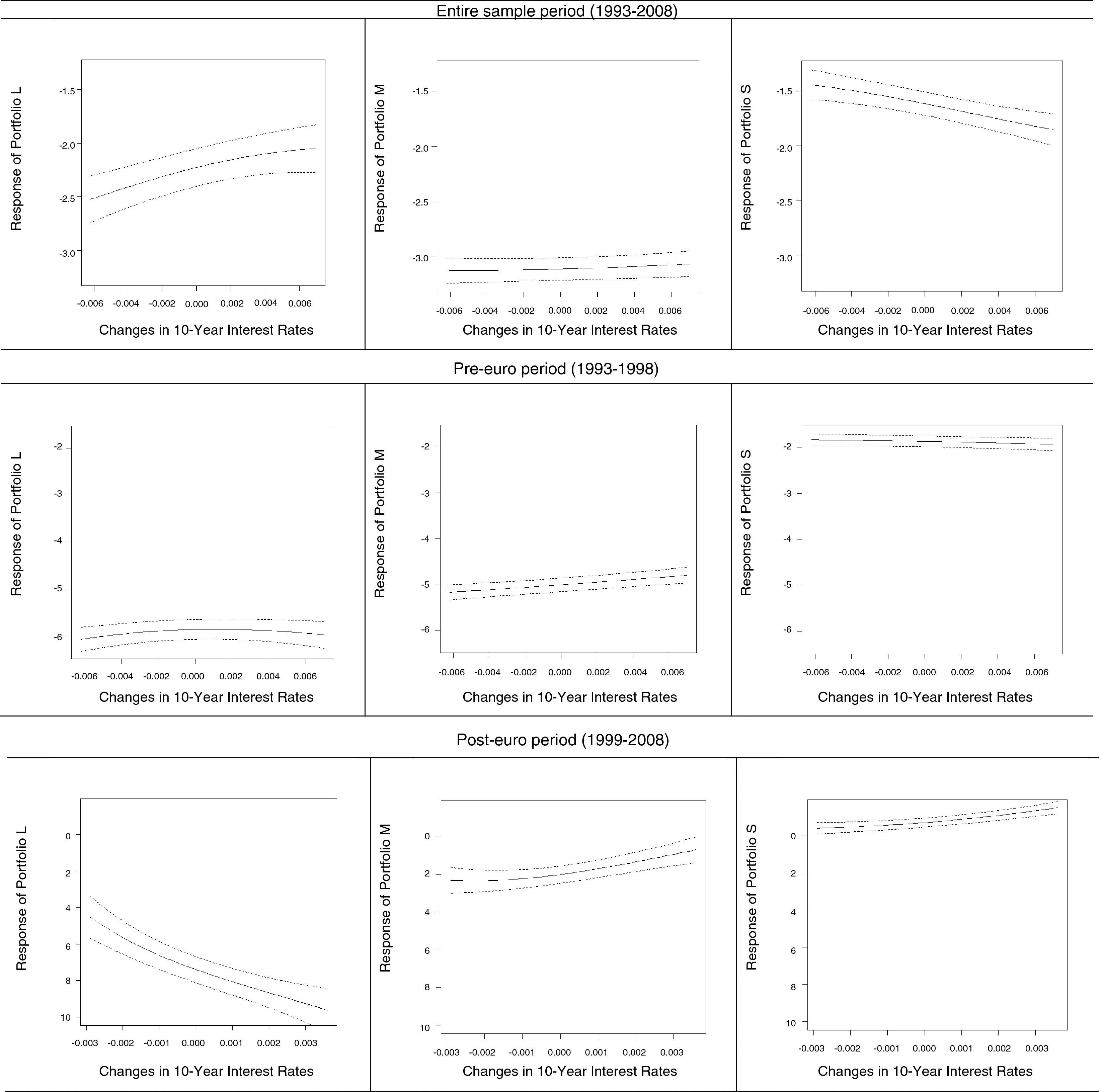
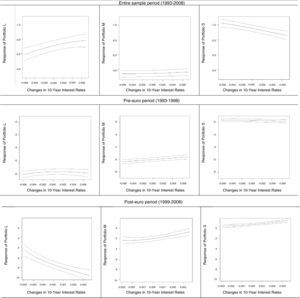
The nonparametric estimates of the response coefficients of bank portfolio returns to changes in interest rates and their associated 95% confidence bands are displayed in Fig. 2.7 The pointwise estimates show that the marginal effect of movements in interest rates on bank portfolios is not constant and negative at all levels of interest rate fluctuations during the full sample period irrespective of the portfolio and interest rate variable under consideration, in line with the inverse relationship found in the parametric specifications.
In order to facilitate comparisons with the parametric models, the fifth column of Table 3 presents the average estimates, computed as the sample mean of the pointwise estimates, of the interest rate sensitivity of each portfolio and their associated standard errors obtained with the nonparametric analysis. As it can be seen, the mean nonparametric estimates are very similar, both in absolute value and statistical significance, to the linear estimates. Thus, the nonparametric approach supports the results of the parametric estimations in terms of the negative influence of interest rate fluctuations, the higher sensitivity to changes in 10-year government bond yields, and the lower vulnerability of smaller banks to IRR. Interestingly, the regression standard errors are much lower for nonparametric estimates than for their parametric counterparts, indicating that more reliable and precise results are obtained by using the nonparametric analysis. It is also important to note that the nonparametric model produces higher R2 than the different parametric specifications considered. These findings seem to suggest than the nonparametric approach is better able to model the impact of IRR on Spanish banks than the parametric models.
5.5Sub-period analysisThe analysis by sub-periods reveals a sharp reduction in interest rate exposure during the post-euro era for all the model specifications, portfolios and interest rate variables. This seems to indicate that the relative importance of IRR in explaining bank stock return variability has declined since the launch of the euro. A possible explanation for this finding is closely related to the smaller variability of interest rates during the post-euro period in an environment of historically low interest rates along with the greater availability of more advanced IRR management tools. In this regard, banking institutions may have benefited from the large-scale use of interest rate derivatives and the increasing depth and breadth of European corporate bond markets with the advent of the euro to improve their management of IRR.
In the pre-euro period all the significant exposure coefficients have negative sign irrespective of the model considered. Further, there seems to be a size effect as the large banks portfolio always exhibits the highest interest rate exposure. In turn, 10-year government bond yields are found to exert the highest influence in absolute value on the stock performance of Spanish banks. Also, the absolute values of the pre-euro exposure coefficients are greater than those corresponding to the entire sample period.
The post-euro period shows, however, very different results. The number of significant exposure coefficients is considerably lower than that obtained in the pre-euro era regardless. Moreover, the few significant coefficients are almost all positive, suggesting that for this period decreases in interest rates would adversely affect Spanish banks. This result is in conflict with the negative relationship between bank stock returns and interest rate fluctuations typically documented in the literature (e.g., Flannery and James, 1984; Madura and Zarruk, 1995; Elyasiani and Mansur, 1998; Czaja et al., 2009, 2010). Nevertheless, this evidence is in line with the results of Ferrer et al. (2010), who find a positive interest rate exposure for the Spanish banking industry after the introduction of the euro.
Two key reasons may help to explain this apparently anomalous finding (positive exposure). First, the substantial reduction in banks’ asset-liability maturity mismatch over the last years due to the confluence of several new banking trends. On the one hand, the massive use of adjustable rate products tied to interbank rates since the mid-1990s, mainly in the mortgage segment. On the other hand, the extraordinary expansion of asset securitization along with the increased use of interest rate derivatives for hedging purposes may also have played a crucial role in this context.8 Second, the positive exposure may reflect serious difficulties of banks to maintain their margins at reasonable levels in a falling interest rate scenario. Thus, when interest rates are very low banking firms face to a narrowing of the lending-deposit rate spread since a positive interest rate on their deposit accounts is required by customers. This argument is consistent with the gradual compression in bank margins within an environment of pronounced decline in interest rates and fierce competition as the occurred in the Spanish banking industry over the past decade.
The response plots of bank portfolio returns to changes in interest rates under the nonparametric approach presented in Fig. 2 confirm the change from negative to positive response from the pre- to the post-euro period for all the portfolios. Furthermore, it is worth noting a substantial increase in the standard errors of the estimates for the post-euro period regardless of the model under consideration. This loss of precision implies that more caution in the interpretation of the results for the post-euro era is required. In addition, the R2 are much higher for the first sub-period irrespective of the model specification, interest rate proxy, and bank portfolio considered, so indicating a better model fit. These findings suggest that both the parametric and nonparametric models work reasonably well in the pre-euro period, but not equally well in the post-euro period, supporting, therefore, the notion that the degree of interest rate exposure faced by Spanish banks has significantly been reduced after the adoption of the euro. Lastly, the tests of asymmetry in Table 5 show the almost total absence of significant sign and size asymmetries in interest rate exposure during the pre- and post-euro periods.
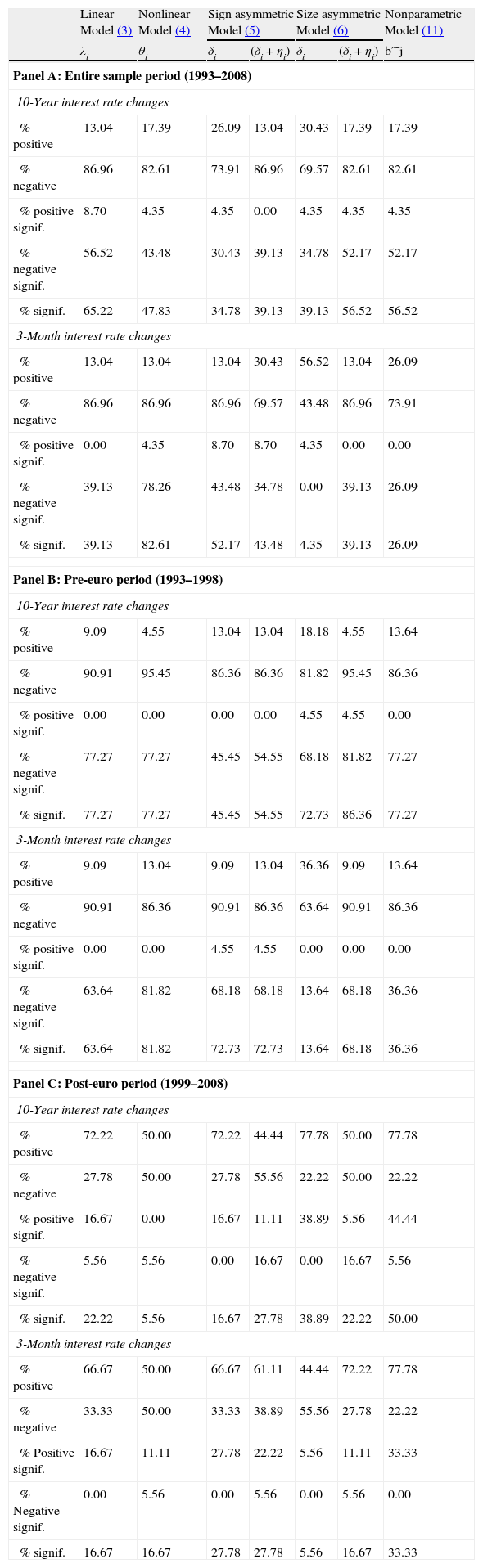
5.6Robustness analysisTo check the robustness of the results, the analysis at the portfolio level is complemented with a firm-level analysis. Overall, the findings at the individual bank level, reported in Table 6, are broadly consistent with those from the portfolios. Thus, the negative interest rate exposure prevails for individual banks during the whole sample and pre-euro periods irrespective of the model under consideration. In contrast, the post-euro period exhibits a substantially lower degree of exposure and the impact of IRR is predominantly positive, indicating that banking firms now would take advantage from rises in interest rates. Further, the results of this robustness analysis confirm that changes in 10-year government bond yields have a larger influence on the stock market performance of Spanish banks than movements in 3-month interbank rates.
Percentage of individual banks with significant interest rate exposure.
| Linear Model (3) | Nonlinear Model (4) | Sign asymmetric Model (5) | Size asymmetric Model (6) | Nonparametric Model (11) | |||
| λi | θi | δi | (δi+ηi) | δi | (δi+ηi) | bˆ¯j | |
| Panel A: Entire sample period (1993–2008) | |||||||
| 10-Year interest rate changes | |||||||
| % positive | 13.04 | 17.39 | 26.09 | 13.04 | 30.43 | 17.39 | 17.39 |
| % negative | 86.96 | 82.61 | 73.91 | 86.96 | 69.57 | 82.61 | 82.61 |
| % positive signif. | 8.70 | 4.35 | 4.35 | 0.00 | 4.35 | 4.35 | 4.35 |
| % negative signif. | 56.52 | 43.48 | 30.43 | 39.13 | 34.78 | 52.17 | 52.17 |
| % signif. | 65.22 | 47.83 | 34.78 | 39.13 | 39.13 | 56.52 | 56.52 |
| 3-Month interest rate changes | |||||||
| % positive | 13.04 | 13.04 | 13.04 | 30.43 | 56.52 | 13.04 | 26.09 |
| % negative | 86.96 | 86.96 | 86.96 | 69.57 | 43.48 | 86.96 | 73.91 |
| % positive signif. | 0.00 | 4.35 | 8.70 | 8.70 | 4.35 | 0.00 | 0.00 |
| % negative signif. | 39.13 | 78.26 | 43.48 | 34.78 | 0.00 | 39.13 | 26.09 |
| % signif. | 39.13 | 82.61 | 52.17 | 43.48 | 4.35 | 39.13 | 26.09 |
| Panel B: Pre-euro period (1993–1998) | |||||||
| 10-Year interest rate changes | |||||||
| % positive | 9.09 | 4.55 | 13.04 | 13.04 | 18.18 | 4.55 | 13.64 |
| % negative | 90.91 | 95.45 | 86.36 | 86.36 | 81.82 | 95.45 | 86.36 |
| % positive signif. | 0.00 | 0.00 | 0.00 | 0.00 | 4.55 | 4.55 | 0.00 |
| % negative signif. | 77.27 | 77.27 | 45.45 | 54.55 | 68.18 | 81.82 | 77.27 |
| % signif. | 77.27 | 77.27 | 45.45 | 54.55 | 72.73 | 86.36 | 77.27 |
| 3-Month interest rate changes | |||||||
| % positive | 9.09 | 13.04 | 9.09 | 13.04 | 36.36 | 9.09 | 13.64 |
| % negative | 90.91 | 86.36 | 90.91 | 86.36 | 63.64 | 90.91 | 86.36 |
| % positive signif. | 0.00 | 0.00 | 4.55 | 4.55 | 0.00 | 0.00 | 0.00 |
| % negative signif. | 63.64 | 81.82 | 68.18 | 68.18 | 13.64 | 68.18 | 36.36 |
| % signif. | 63.64 | 81.82 | 72.73 | 72.73 | 13.64 | 68.18 | 36.36 |
| Panel C: Post-euro period (1999–2008) | |||||||
| 10-Year interest rate changes | |||||||
| % positive | 72.22 | 50.00 | 72.22 | 44.44 | 77.78 | 50.00 | 77.78 |
| % negative | 27.78 | 50.00 | 27.78 | 55.56 | 22.22 | 50.00 | 22.22 |
| % positive signif. | 16.67 | 0.00 | 16.67 | 11.11 | 38.89 | 5.56 | 44.44 |
| % negative signif. | 5.56 | 5.56 | 0.00 | 16.67 | 0.00 | 16.67 | 5.56 |
| % signif. | 22.22 | 5.56 | 16.67 | 27.78 | 38.89 | 22.22 | 50.00 |
| 3-Month interest rate changes | |||||||
| % positive | 66.67 | 50.00 | 66.67 | 61.11 | 44.44 | 72.22 | 77.78 |
| % negative | 33.33 | 50.00 | 33.33 | 38.89 | 55.56 | 27.78 | 22.22 |
| % Positive signif. | 16.67 | 11.11 | 27.78 | 22.22 | 5.56 | 11.11 | 33.33 |
| % Negative signif. | 0.00 | 5.56 | 0.00 | 5.56 | 0.00 | 5.56 | 0.00 |
| % signif. | 16.67 | 16.67 | 27.78 | 27.78 | 5.56 | 16.67 | 33.33 |
% positive denotes the percentage of positive exposure coefficients to the total number of commercial banks listed on the Spanish Stock Exchange in each period. Conversely, % negative indicates the percentage of negative exposure coefficients. % positive (negative) signif. indicates the percentage of positive (negative) exposure coefficients significantly exposed to interest rate risk. Lastly, % signif. refers to the percentage of significant exposure coefficients to the total number of banks. The significance level used to consider an individual bank as significantly exposed to interest rate risk is 5%.
This paper presents a comprehensive analysis of the interest rate exposure of the Spanish banking industry employing both parametric and nonparametric estimation methods. Its main contribution is to use, for the first time in the field of the measurement of IRR faced by banks, a nonparametric regression model that avoids the prior specification of a specific functional form.
The empirical analysis sheds light on several important issues. Overall, the Spanish banking sector shows a significant degree of interest rate exposure, although the introduction of the euro has led to a substantial decline of the impact of interest rate changes on bank stock returns. This lower interest rate sensitivity during the post-euro period may be a result of factors such as the remarkable stability in interest rates in the historically low interest rate environment associated with the European monetary union, or the increased availability of improved tools for managing IRR in recent years. Contrary to the evidence typically documented in the literature, a pattern of positive exposure seems to emerge in the post-euro era, which can be attributed to two main reasons. First, the dramatic reduction in the maturity mismatch between banks’ assets and liabilities caused by the combination of several recent banking trends such as the overwhelming predominance of adjustable rate products, the explosive growth of asset securitization, or the rapid proliferation of derivative securities. Second, the positive exposure may also reflect the downward pressure on bank margins arising from increased competition in a scenario of marked downward trend in interest rates in force over the last years. A significant nonlinear exposure to IRR, measured through a cubic function, is also found, but the traditional linear exposure profile prevails in terms of economic magnitude over the nonlinear one. Further, there is no evidence of significant sign and size asymmetries during the full sample period and the pre- and post-euro periods.
The results of the nonparametric estimation in terms of both absolute value and statistical significance of exposure coefficients are similar to those from the parametric specifications. However, the standard errors of the nonparametric estimates are much lower, and the nonparametric model has greater explanatory power than the parametric models. These findings support the reliability of the nonparametric approach to assess the extent of IRR faced by Spanish banks. The better performance of the nonparametric model may be attributed to its high flexibility to capture nonlinear effects in the link between bank stock returns and interest rate fluctuations, and supports the expansion of the conventional linear model to gain a better insight into the degree of exposure to IRR. Moreover, the results by sub-periods indicate that the fit of the models is substantially better in the pre-euro period. Another interesting result is that the lowest interest rate sensitivity is observed for the small banks portfolio regardless of the model under consideration, suggesting that Spanish smaller banks, because of their idiosyncratic nature, have a market stock performance less vulnerable to IRR.
Laura Ballester would like to express her gratitude for the funding received from the JCCM, proyecto PEII11-0031-6939. The authors would like to thank Alfonso Novales, Juan Nave, Ángeles Fernández, Paz Jordá, Miguel Ángel Martínez, Joaquín Maudos, and Eliseo Navarro for their valuable comments and suggestions. The authors are also grateful to the two anonymous referees for their comments that have contributed to improve this paper.