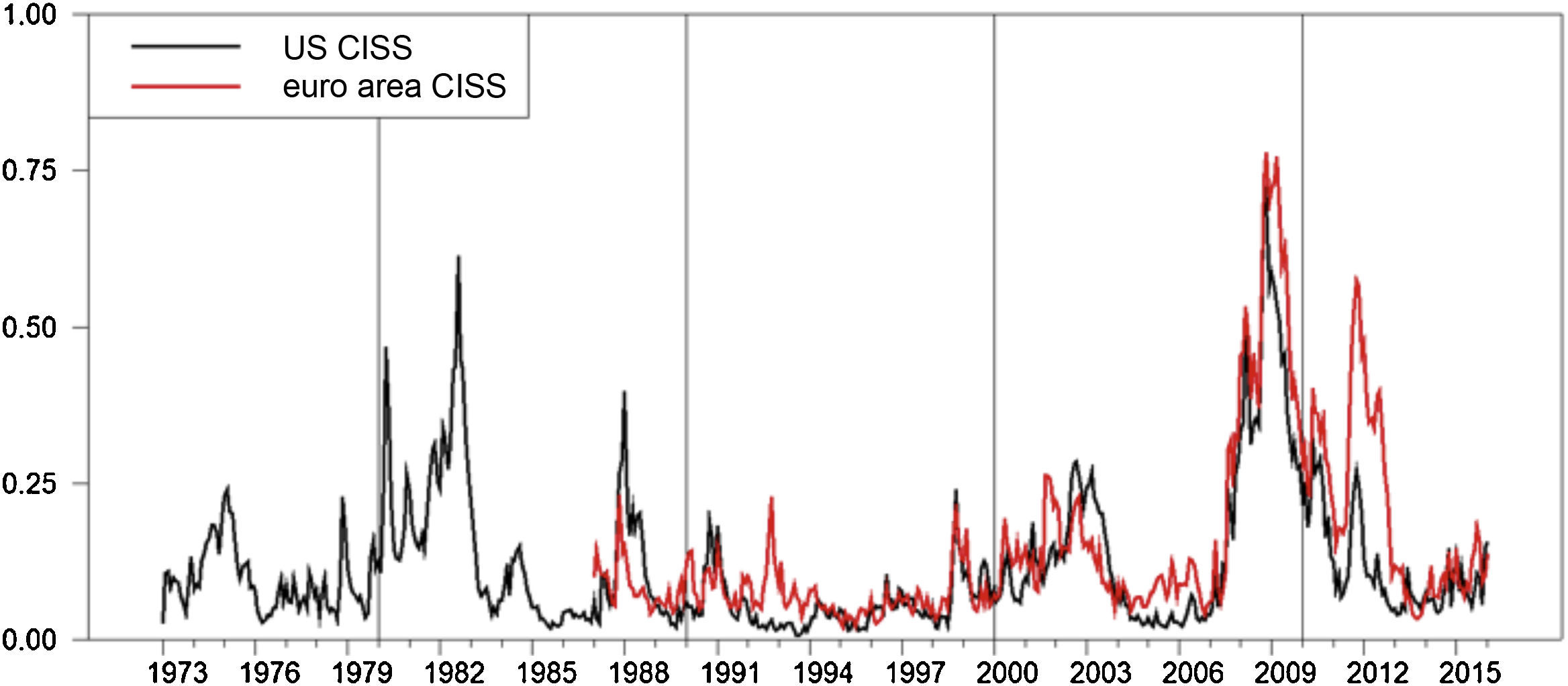
It has become conventional wisdom that financial development is critically important for economic growth (see Levine, 2005). Hence, finance is not just a pure veil under which real transactions are shrouded. Rather, a well-developed and smoothly operating financial system performs essential functions enabling the real economy to prosper. Finance helps overcome frictions in the real sector arising from a variety of imperfections such as information and transaction costs, thereby influencing economic agents’ savings and investment behaviour, and therefore long-term economic growth (Beck, 2014). However, the causal relationship between finance and growth—which actually can run both ways—holds true for good and bad times alike. As recent events vividly reminded us, financial development may also become the root cause of a deep financial and economic crisis. This ambiguous role of finance reflects the fact that the financial sector itself is prone to market failures resulting, in particular, from informational frictions. When such financial frictions become dominant and widespread, as is the case in a systemic crisis, they tend to have severe repercussions for the real economy. Against this background, policy makers have a particular interest in measuring, ideally in real time, the overall stress level in the financial system caused by financial frictions in order to assess its imminent macroeconomic risks, and to consider appropriate timely counteractions. There exist a great variety of standard indicators measuring the level of stress in individual market segments, each capturing certain symptoms of the underlying financial friction (see Holló et al., 2012). For instance, option-implied volatilities provide information about market participants’ degree of risk aversion and uncertainty (Bekaert and Hoerova, 2014); they can be computed for the prices of many important assets such as government bonds, interest rate derivatives, interbank deposits, equities, foreign exchange and many more. The VIX1 has received particular attention in this context, since the financial press often refers to it as investors’ “fear gauge” (Carr and Lee, 2009). Other stress indicators are, for instance, (1) credit default swap spreads and other credit risk premia, (2) liquidity measures such as bid-ask spreads, (3) cumulative equity valuation losses, (4) quantity-based indicators measuring activity in certain primary and secondary markets. Such indicators have long been used by policy institutions engaged in financial stability surveillance, such as the IMF, the BIS, central banks and other national supervisory authorities. These standard indicators form the backbone of any financial stability report produced by any of these institutions. While all of these individual indicators provide useful partial information, the sheer amount of existing stress measures complicates the task of inferring whether stress observed in one particular market segment is either of a more idiosyncratic nature or, instead, a more widespread and thus systemic phenomenon. Sometimes you “can’t see the wood for the trees.” One way to synthesise the information contained in many individual indicators is to build a composite indicator of financial stress, or “financial stress index” as it has become known in the literature. Financial stress indices quantify the current stress level in the financial system by compressing a certain number of individual stress indicators into a single statistic. Despite the fact that composite indicators have been used for other purposes for a long time (e.g., monetary and financial conditions indices), financial stress indices have become a popular tool only in recent years, spurred by the financial crisis. This special issue of the Spanish Review of Financial Economics is dedicated to three new variants of a financial stress index. Before briefly summarising the three papers introducing these new indicators, I first present and discuss the ECB's financial stress index, which I developed together with two colleagues (Holló et al., 2012). This may help better understand some features of the three indices since all of them build, at least to some extent, on our indicator concept. We have called our index the Composite Indicator of Systemic Stress, abbreviated CISS (pronounced /kis/), whereby the term “systemic stress” is understood as systemic risk that has materialised. The indicator's distinctive design emphasises the systemic dimension of financial stress by applying basic portfolio-theoretic principles to the aggregation of individual stress indicators into the composite indicator. Analogous to the computation of the risk of an asset portfolio—where portfolio risk is generally not just the simple weighted average of individual asset risks, but also depends on the assets’ return correlations—the CISS aggregates the information from its constituent individual stress indicators by taking into account the time-varying (rank) correlations between them. In doing so, the CISS puts a larger weight on situations in which stress prevails in several market segments at the same time, capturing the idea that financial stress is more systemic, and hence more hazardous for the real economy if instability spreads more widely across the whole financial system. Apart from the portfolio-theoretic aggregation scheme, the CISS is also characterised by the application of the probability integral transform to homogenise its individual raw stress components in terms of scale and, more importantly, in terms of distributional properties. After transformation, all input series are approximately standard uniform distributed. By contrast, “conventional” standardisation—i.e., subtracting the mean and dividing by the standard deviation—only rescales the indicators, but leaves their basic distribution unaffected. Accordingly, after such standardisation, the set of input series remain very heterogeneously distributed, which may give rise to unintended dynamics of the composite indicator. While the CISS is not the first financial stress index that proposes to transform its input series based on their empirical cumulative distribution function, it is the first that does so explicitly on grounds of distributional homogeneity, and the stronger robustness of the transformed indicators against outliers. Since financial crises are by definition times in which many if not all input series approach extreme values, such robustness features may become important if the financial stress index is to be used and updated on a real time basis. If the statistical framework of a composite index is not robust, the addition of a string of extreme observations can render previously published historical values of the index meaningless, giving rise to the so-called event re-classification problem. Composite indicators which apply conventional standardisation to their individual input series are particularly susceptible to outliers, and more so the smaller the available data sample. The application of principal components analysis (PCA) or other factor models may exacerbate the robustness problems if combined with conventionally standardised input series, since PCA itself is sensitive to outliers as it minimises squared distances from the multidimensional mean. In my view, robustness is an important property of a financial stress index if that index is to be used for regular financial stability monitoring, and so far one which has not yet received sufficient attention in the literature. Let me add a few words on the way the time-varying cross-correlations are computed. We apply the exponential smoother, i.e. exponentially weighted moving averages (EWMA), to estimate them. EWMA is a common procedure to estimate arbitrarily large variance-covariance (or correlation) matrices. It is widely used both in the financial industry and in academia.2 We set the smoothing parameter to a value similar to what practitioners often use. This approach has several advantages. First of all, EWMA is computationally very simple and quick. Since the smoothing parameter is identical for all correlation pairs, it ensures positive-definiteness of the correlation matrix, a crucial condition to be met when estimating higher-dimensional correlation matrices.3 In addition, since the smoothing parameter can be estimated from an Integrated-GARCH model specification, it can be tailored to the specific data set at hand and, therefore, does not need to be fixed arbitrarily, even if the I-GARCH model is not re-estimated every time, but only once for the initial index specification as we did for the CISS. In addition, since the I-GARCH model assumes the transformed indicators and their cross-correlations to follow integrated processes, it may better accommodate all kinds of potential structural breaks which may happen to change the cross-correlations on a permanent basis. However, when fixing the smoothing parameter without prior estimation, one should not forget to properly account for the data frequency. For instance, if the CISS were to be computed on the basis of monthly instead of weekly data, standard smoothing parameter values for weekly data would have to be raised to the power of four.4 The euro area CISS was first published in 2010 (ECB, 2010). Since then the indicator has become a widely known and used financial stress index. We have made weekly updates of the euro area CISS available via the ECB's Statistical Data Warehouse (SDW); via this route, the CISS also feeds into Bloomberg, Thomson Financial Datastream and Haver Analytics.5 I am particularly happy that several central banks and other financial authorities have also adopted the CISS concept for the construction of the financial stress indices for their respective countries (see, e.g., Johansson and Bonthron, 2013; Banco de España, 2013; Braga et al., 2014; Huotari, 2015). Let us now take a look at some real data. Fig. 1 displays two different CISS series measuring system stress for the financial system as a whole —one for the euro area and one for the United States. The euro area CISS starts in January 1987. It has been back-dated for the pre-EMU period based on either synthetic aggregate euro area series, or a few sufficiently representative individual country indicators. The US CISS series starts in January 1973.6 It is composed of a set of indicators similar to its euro area counterpart. Visual inspection reveals two facts. On the one hand, both time series display a rather high degree of co-movement in general, and in episodes of heightened financial stress in particular. This suggests to me that periods with elevated levels of systemic stress are in most cases global phenomena. Global stress episodes can be brought about by either common exposure to the same set of shocks, or via spillover effects which transmit stress in one country to the financial systems of other countries. On the other hand, there also exist a few episodes in which financial stress has more of an idiosyncratic nature. The 1992–93 exchange rate crisis in the European Monetary System is a clear case in point. In addition, at its height, the sovereign debt crisis in the Eurozone in 2011 and 2012 affected the US financial system only to a limited extent compared with the market noise it created in Europe.
In general one can say that for both economies the CISS peaks at all well-known financial stress events since 1973 and 1987, respectively.7 In this regard, the recent financial and economic crisis—the Great Recession—clearly stands out as the episode with the severest levels of systemic stress observed in both economic areas in the respective sample periods. The levels of stress experienced in both economies during the recent crisis are probably second only to what happened during the Great Depression in the late 1920s and early 1930s. Overall, it seems that the CISS may indeed serve as a useful gauge of financial stress in the euro area financial system as a whole. The CISS has often been shown in presentations by ECB officials, and in ECB publications such as the Financial Stability Review, with the aim of providing the audience with a snapshot of current financial stability conditions. In this capacity, the index also appears as the first chart in the Risk Dashboard published by the European Systemic Risk Board (ESRB).8 For similar purposes, the CISS has also been used by the financial press.9 But the CISS has also been increasingly applied in empirical academic research. Just to cite a few examples, the CISS has proved useful in the evaluation of a set of indicators that were used to calibrate the release of counter-cyclical capital buffers in Europe (see Detken et al., 2014). In a recent paper I demonstrate that the CISS possesses substantial and robust explanatory power for standard macroeconomic variables like inflation, real GDP growth and monetary policy interest rates in the euro area, where the predictive power is particularly strong for economic activity (Kremer, 2016).10 The strong macroeconomic predictive power of the CISS has also been confirmed by the recent inclusion of the index as one of the eight components of the Conference Board's Leading Economic Index (LEI) for the euro area.11Bekaert and Hoerova (2014) demonstrate that when the VIX is decomposed into the conditional stock market variance and the variance premium, both components significantly explain variations in the CISS, which the authors interpret as a measure of financial instability. In fact, I regard the application of financial stress indices in empirical research as one important way to evaluate the general quality and usefulness of such indicators. This notwithstanding, I am rather sceptical that the relative performance in predictive “horse races” can help assess whether one financial stress index is generally superior or inferior to another. My scepticism owes to the fact that financial instability is an elusive concept and, thus, hard to measure. In addition, financial crises are (fortunately) rare events, which severely restrict the statistical degrees of freedom available in such predictive competitions. Let me now briefly address the three papers included in this special issue. The paper entitled “A Spanish Financial Market Stress Index (FMSI)” by Isabel Carbón and Leticia Estévez introduces an index that measures the general level of systemic stress in the Spanish financial system as a whole. Its design follows rather closely that of the euro area CISS. The paper demonstrates, among other things that the FMSI is remarkably robust when computed over different sample periods. As I mentioned before, this stability is essential for a financial stress index to be monitored and updated on a regular basis. The paper “Measuring market liquidity in US fixed income markets: A new synthetic indicator” by Carmen Broto and Matías Lamas proposes an index that focusses more narrowly on measuring systemic liquidity stress in US fixed income markets. The authors collect 17 different liquidity measures for sovereign and corporate fixed-income securities issued in the US market. The input series are transformed on the basis of the probability integral transform (or the empirical CDF) as in Holló et al. (2012). This ensures robustness to outliers when updating the indicator on a regular basis. In contrast to the CISS concept, the transformed liquidity indicators are then aggregated into the composite index by means of the first four principal components which represents a popular statistical tool to emphasise the commonality in the movements of a set of economic indicators. I am curious to see some applications of the index in future work. The paper “Systemic liquidity risk and portfolio theory: An application to the Italian financial markets” by Stefano Nobili and Eleonora Iachini also introduces a composite indicator of liquidity stress, but for Italian securities markets. The authors aggregate ten different liquidity measures for assets traded in the Italian equity, corporate bond, government bond and money markets—grouped into three market segments—into a composite index. The composite index is designed along the lines of the CISS concept, where the cross-correlations are estimated on the basis of a multivariate GARCH model. The indicator fits very well—within a probit regression framework—a set of dummy variables which capture well-known liquidity crisis events in the Italian market, as identified in an expert survey. I very much hope that the collection of papers published in this special issue help further popularise financial stress indices among academics and practitioners alike. I am convinced that financial stress indices offer the basis of a promising, broad and rich research agenda that is very likely to produce tangible results feeding into the practice of monetary and macro-prudential policy making.
The VIX is the Volatility Index of the Chicago Board of Options Exchange, constructed from a portfolio of options on the S&P 500 index.
See, e.g., Engle (2002) and Koop and Korobilis (2013).
For instance, in my application of the CISS concept to the computation of a stress index for the euro area sovereign market (the “SovCISS”), I compute a 66×66 dimensional correlation matrix.
For instance, Louzis and Vouldis (2012) compare time-varying correlations computed using the BEKK specification of a multivariate GARCH model with those computed as EWMAs. However, the authors obtain much smoother and, thus, less reactive correlations with EWMA since they use monthly data with a standard smoothing parameter for daily or weekly data.
The US CISS will also be published soon in the ECB's SDW as part of the CISS index family.
The only other sort of financial stress index for the US available for such a long data sample is the National Financial Conditions Index (NFCI) published by the Federal Reserve Bank of Chicago.
See Holló et al. (2012) for a more detailed description of relevant financial crisis events in the euro area.
Similar results are obtained by, e.g., Boeckx et al. (2014) and Silvestrinia and Zaghini (2015).