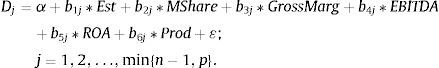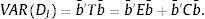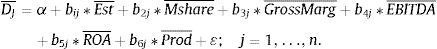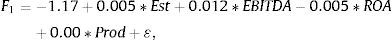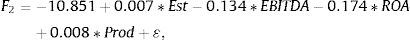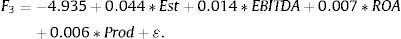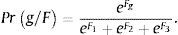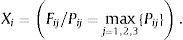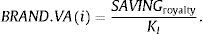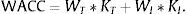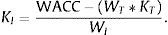The aim of this paper is to introduce a statistical procedure to value a brand by means of which firms may be able to determine the level of implicit royalty that they would charge for the use of their brand, applying multivariate techniques from market references. The study has been based on a statistical contrast of the royalties paid in Spanish franchises belonging to three different industries: food, health and beauty and fashion. Each industry has been segmented using cluster techniques, and then, through linear discriminating analysis, a model is proposed to explain the royalty paid according to certain economic figures of the companies. The implicit impartiality in the development of the model means that it could be generally accepted by analysts, consultants and companies who need to determine the value of a brand.
In the last three decades some authors, such as Lev (1989, 2000, 2001, 2005), have shown the gradual increase between firms’ market value and their book value. Other authors, such as Brown, Lo, and Lys (1999), or Dantoh, Radhakrishnan, and Ronen (2004) also warn about how equity and profits have lost relevance for explaining the market value of American companies. In the Spanish case Sánchez and Espinosa (2005) introduce a measure of the intangible value not explained by financial economic magnitudes of the firms, but paid in the prices of business transactions (around 50%). Rubio, Rodríguez, and Maroto (2013) find for the pharmaceutical and biotechnology sectors that these quantities paid and unexplained are higher than 69%. All these works suggest a change in the business model: this has moved from a system based on industrial production to another one in which firms base their success on knowledge.
Despite the fact that International Accounting Standard: IAS 38 (2008) forbids the recognition of internally generated intangible assets, in business combinations the International Financial Reporting Standard 3 (2008) states that the purchasing company will have the obligation to identify and measure each one of the assets and liabilities deriving from the operation performed, including even tangible and intangible assets.
Such assets will be quantified by their fair value (IAS 38, 2008; IFRS 3, 2008), which is defined in the IFRS 13 (2011), “Fair Value Measurement”, as the amount for which each asset can be exchanged or a liability canceled between the concerned parties properly informed. The transaction must be performed on mutual independence terms, including market expectation and, at the same time, excluding the synergies for a particular buyer.
There is a wide typology of academic and professional intangibles and brand valuation proposals, as well as their contribution to the value creation process for the company, from different areas of expertise. In marketing and management: Kapferer (1992, 2004), Park and Srinivasan (1994), Aaker David (1996, 2000), Ratnatunga and Ewing (2008) and Jourdan (2001), and in finance: Smith (1997), Damodaran (2002), Reilly (1999), Lev (2001) are outstanding among others. For its part, the accounting standards, and the guidelines of the International Valuation Standard Council, impose a specific hierarchy in the valuation criteria: market and income methodology. If none of these could be used, then the replacement cost methodology would be applied. So the most important business consulting agencies in the world apply this hierarchy.
The royalty relief is based on the measurement of the license payments, from a market database, which has been saved as a consequence of having the ownership of the asset. The interest of this method is that it can be considered as a market-income methodology. Therefore, the accounting standards place it as the most important compared to the other methods, but there is no such academic methodology that supports its use.
The goal of this paper is dual: on the one hand, applying multivariate techniques from market references, to check whether in the Spanish franchising market the royalties paid are efficient in reflecting enterprises’ performance. Then, they could be an important tool for assessing brand. On the other hand, we introduce a statistical procedure adapted to the international standards of accounting and valuation of intangible assets, by means of which any firm could obtain the level of the corresponding implicit royalty from market references and the fair value for the brand.
This paper is organized as follows: after the Introduction, in the second section the theoretical framework and hypothesis, as well as the importance and the problems involved in the calculation of the royalty relief are analyzed. In section three the data and the statistic model are developed. In section four we deal with the applications and results of the model and, finally, the article ends with the conclusions and final remarks.
Theoretical framework and hypothesis: the importance and the problems involved in the calculation of the royalty reliefDespite the efforts that have been made, there is still a large heterogeneity present among all the methodologies developed (Cerviño, Martínez, de la Tajada, & Orosa, 2005; Salinas, 2007). Specifically, market methodologies involve the use of multiples, which will depend on prices paid in previous transactions. Nevertheless, one problem of this method is the absence of a database about prices paid for individual intangible assets.
Likewise, income methodologies have had greater academic and professional growth. A royalty-saving method is one of the most common typologies, especially used to assess brands and patents, and it is the one that has been introduced in different ways by consultant agencies such as Brand Finance (2000), Whitwell (2013), Intangible Business and AUS Consultants or Consor (Salinas, 2007).
Other income methods frequently employed for intangible assessment are: the multiple periods earning excess of return, incremental cash flow and real options. The first one is built on operating cash flows of the enterprise, and from these, the charges of the other contributory assets (tangibles and intangibles) will be deducted in order to determine the cash flow arising from the excess of return. Authors such as Smith (1997) or Lev (2001) and consulting agencies like Brand Economics (2002) base their proposal on this technique.
Concerning the incremental cash flow method, its main goal is the measurement of the increase of these cash flows due to a price premium in goods and services sold by companies or savings that come from the ownership of the intangible asset. Some academics, such as Damodaran (2002), Reilly (1999) or Fernández (2007) have developed this methodology. Consulting agencies such as Interbrand1 or BBDO (2001, 2002), through the division Brand Equity, also have used it in many modalities. Alternatively, the real options method includes uncertainty and risk as variables in the valuation of the assets depending on companies’ management capacity. Among the authors who have proposed this technique in diverse variations Myers (1977), Amram and Kulatilaka (2000), Schwartz (2003) and Rubio and Lamothe (2010) are worthy of mention.
The great problem when valuing brands among all the methodologies shown above is to properly delimit the corresponding flow. Brands also include psychological aspects or symbolic constructions in the users’ minds on the basis of which future expectations about their functioning will be generated, which is very difficult to measure and capture objectively.
We can define brand value as the incremental utility or added value to the product by brand name (Bigné, Borredá, & Miquel, 2013; Kamakura & Russell, 1993; Park & Srinivasan, 1994). In this sense, Kapferer (1992) proposes a hexagonal brand identity prism reflecting internal aspects: brand physique, personality, culture, and other external ones: relationship, reflection and self-image. Aaker David (1996) concluded a brand measure, called “The Brand Equity Ten”, based on aspects such as loyalty, perceived quality, association or differentiation measures, awareness, but also, the behavior on market measures that represent information obtained from market-based information rather than directly from customers: price and distribution indices and market share.
Many times the so called brand strength is used to summarize all the qualitative brand aspects, a score of 0–10 that places a particular brand against the competitors. The strength of the brand is used in model valuation, at the same time being a multiple of the profit corresponding to the brand, such as the Interbrand proposal or, in other cases, it also serves to assign an implicit royalty, like that proposed by Intangible Business Ltd. (Salinas, 2007).
Bello Acebrón, Gómez Arias, and Cervantes Blanco (1994) defines the brand image as “the set of partnerships developed in the imaginative power of the consumer, enabling the brand to reach a higher sales volume than if you do not have a brand name”. In this line, some authors have explored the relationship between brand affiliation and firm performance (Park & Srinivasan, 1994), between prices and higher quality brands (Cerviño, 2004; Sivakumar & Raj, 1997), others, in terms of competitiveness (Fernández, 2011), and finally between important brands and shareholder value (Cerviño, 2004; Doyle, 2001). So, it is clear there is a relationship between qualitative brand attributes, and quantitative variables such as prices, market share, and higher profits, then, quantitative variables could also explain the brand value in an impartial form.
For its part accounting standards, specifically the IFRS 13 (2011) explains that “a fair value measurement requires that the valuation technique(s) used should maximize the use of relevant observable inputs and minimize unobservable inputs”. It establishes a fair value hierarchy that is categorized into three levels of inputs; level 1 inputs are quoted prices in active markets for identical assets, level 2 are inputs other than quoted prices included within level 1 that are observable for the asset, either directly or indirectly. Level 3 inputs are unobservable inputs for the asset or liability, but these inputs will have to be used to measure fair value whenever relevant observable inputs are not available.
In general, to have an active market for intangible assets is very uncommon. Therefore, since there is not an active market relative to purchase and sale of brands, the accounting standard puts the royalty relief method as the most important compared to the other methods listed above, especially in business combinations, since the valued assets must meet the requirements of the accounting standard.
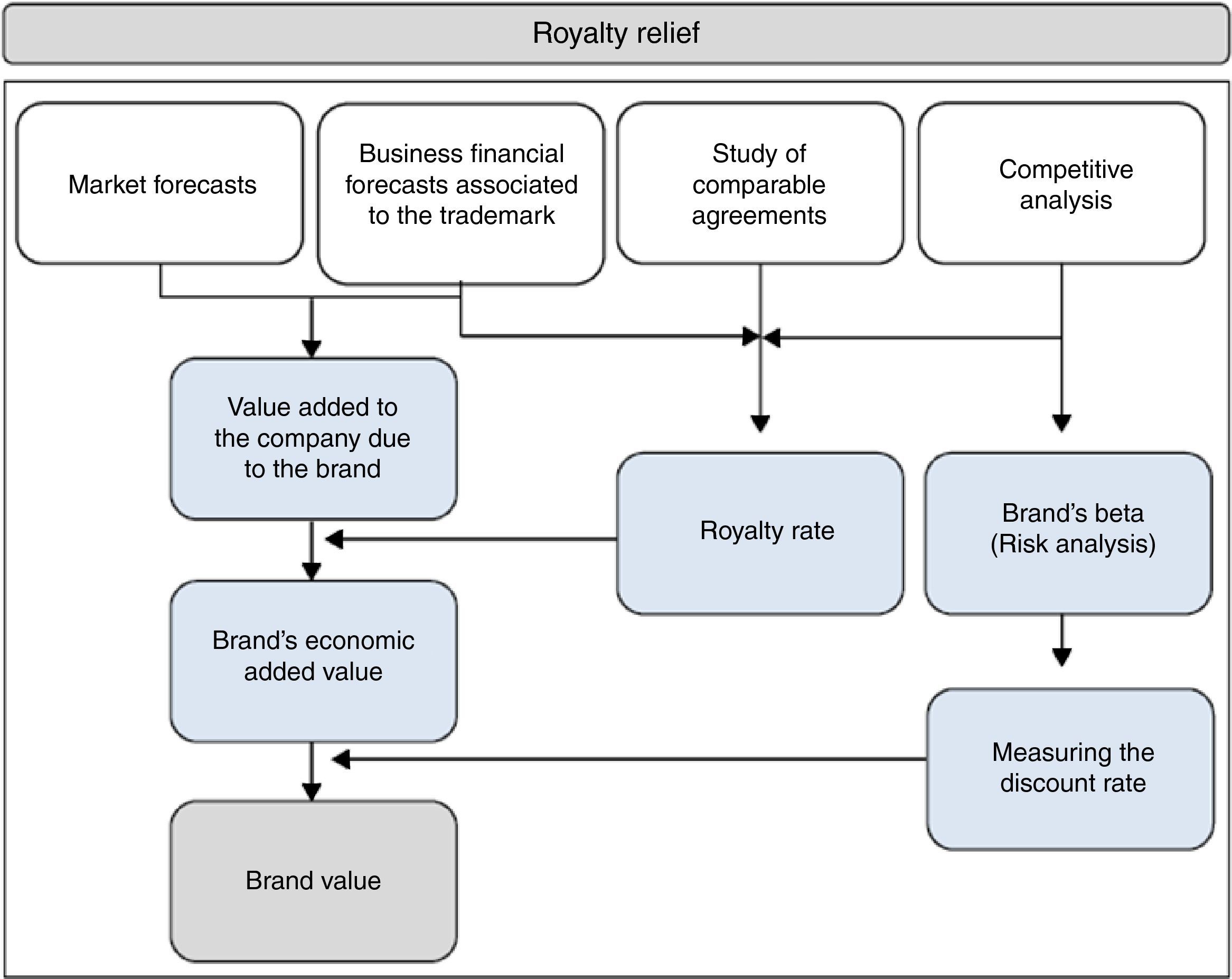
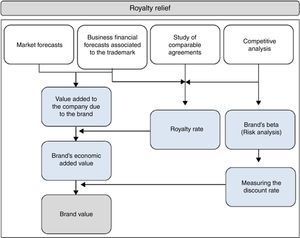
The royalty relief, as detailed in the following image (Fig. 1) consists first of a long run estimation of the company’ sales. Second, it is necessary to determine the royalty rate which would correspond to that sales forecast from market databases. Then this rate would be multiplied by the forecast sales and so we find the cash flow corresponding to the brand. Third, it is necessary to determine a proper discount rate which must include the risk associated with the valued asset and, finally, it would suffice to update the cash flows and find the sum of the updated assets whose result would correspond to the brand's value.
Licensing agreements for similar assets generally provide the best basis for determining an appropriate royalty rate. However, the proposed models developed to calculate the proper royalty do not seem to include the impartiality and accuracy required.2 For instance, according to Salinas (2007), Consor consulting is developing a model based on the licenses of other similar brands. To do this, they start by valuing the brand strength according to 20 determining factors, among which the following are included: profit margins, the state of the brand's life cycle, transferability and its international protection.
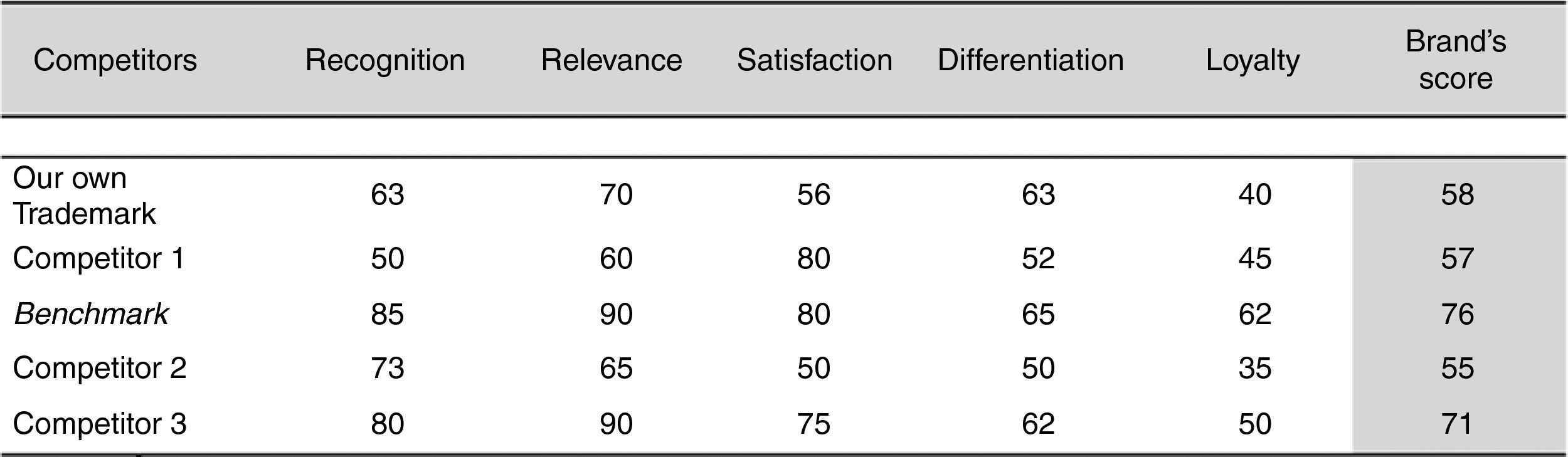
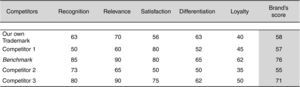
For its part, the proposal of Intangible Business Ltd. (Salinas, 2007) also determines the brand strength against competitors through the variables that are shown in Fig. 2. This figure also contains measures related with the strength of the different trademarks that participate in the market.
In this figure the reference competitor, Benchmark, collects an explicit royalty, the market's maximum, and from this the score of the valued brand is obtained. If the score obtained by the valued company is 58 and the market's maximum is 76, with a royalty of 5%, a rule of thumb would suffice to find that the royalty that would correspond to a score of 58 is 3.82%.
As shown in Fig. 2, the variables that nurture the brand strength are not the same in the two models (Consor Consulting and Intangible Business), and the process seems to lead to the inclusion of large doses of discretion. This is of particular concern when determining their weights, with both lacking an aforementioned mathematical and statistical contrast. The factors or variables could be redundant or even correlated with each other. Thereby the whole process leads to the calculation of a royalty which is probably biased. Finally, the methods assume that the factors and their weights are the same for all industrial sectors, regions or categories, when in fact they may vary.
Nevertheless, statistical techniques have been used in academic brand value analyses; for instance, Punj and Stewart (1983) explained issues and problems related to the use and validation of cluster analysis in marketing research. Perreault, Behrman, and Armstrong (1979) show, across discriminatory analysis, a better understanding of how some groups of customers or items differ as a consequence of some set of explanatory metric variables, such as a set of attributes or performance ratings. Sivakumar and Raj (1997) have proved that higher quality brands are generally less affected by a rise in prices than lower quality brands. Other remarkable researches are those regarding the application of joint analysis,3 such as Kamakura and Russell (1993), Swait, Erdem, Louviere, and Dubelaar (1993), or the ones about logit regression techniques, as in Green and Srinivasan (1990), Park and Srinivasan (1994) or Jourdan (2001). More recently Chung and Rao (2012) presents a general consumer preference model when it is not easy to consider some qualitative attributes of a product or when there are too many attributes. These papers do not make up an overall and quantitative measure of the brand; although they show unequivocally that brand is a differentiating factor that generates and increases utility and consumer loyalty. These aspects allow the enterprise at the same time to increase its prices, market shares, and performance.
With the aim of producing convergence between the academic and the professional environment, a process is proposed that incorporates enough statistical tools to obtain higher accuracy and objectivity in the royalty relief methodology. With this study, the following hypotheses and proposals are analyzed:
- I.
The royalties paid can be classified depending on measures about performance of companies: market position, economic profit and the capacity to generate wealth in terms of factors of production employed.
At the beginning of the article several studies (Brown et al., 1999; Dantoh et al., 2004; or Lev, 2000) have been discussed showing the inability of accounting variables to explain the values of intangible assets. We have used cluster technique to discover distinct groups in the enterprises’ database depending on performance items mentioned above, and we have checked as to whether groups of cluster match royalties paid.
- II.
There is a significant, II (a), and positive, II (b), statistical relationship between the different indicated firms’ performance variables and the clusters of royalties collected in each industry.
Many authors (Aaker David, 1996; Park & Srinivasan, 1994), among others, ensured that brand value attributes allow increased sales volume (higher prices or market share), and this is transformed into different measures of enterprise performance. So, it is necessary to know more precisely the way in which performance variables generate value to the royalties groups. Finally, we have checked if:
- III.
The behavior of the performance variables of Spanish franchisors is the same or changes for different industries. This fact will reveal whether the royalty model relief is the same or changes for each sector.
We have used linear discriminant analysis (LDA) to evaluate the relationship between the economic variables and the royalties collected across different industries, and to check hypotheses II (a), II (b) and III.
Having contrasted the above hypotheses we have checked the results of following questions: firstly, the capacity of methodology for predicting what would be the corresponding royalty to a new company of the industry.
Secondly, we examine whether on the basis of the scores generated by the model, the strength of a brand can also be considered compared to the other competitors on the market regardless of the group it belongs to. Finally, we propose a process of brand value, in accordance with Fig. 1, based on the implicit royalty found.
Data and statistic methodologyThe Spanish franchising firms, the explicit royalty, and the number of establishments in each one, have been obtained through specialized web pages4 (the franchisors are listed in annex 1) from year 2012. In addition, the economic variables: employees, assets, sales, EBITDA (earnings before interest, taxes, amortization and depreciation) and EBIT (earnings before interest and taxes) have been obtained from the System Analysis of Iberian Balances (SABI) data base and represent the average value of each enterprise from three previous years (2009–2011). We have selected three sectors heterogeneous enough among each other to test whether the model works in the same way in each of them: food, health and beauty, and fashion.
The number of enterprises with information about royalties in the web pages was 149 for food, 105 for health and beauty, and 67 for fashion. Of these, all required economic and financial data were provided by only 73 for food, 74 for health and beauty, and 57 for fashion. This represents a cover of 68.18%.
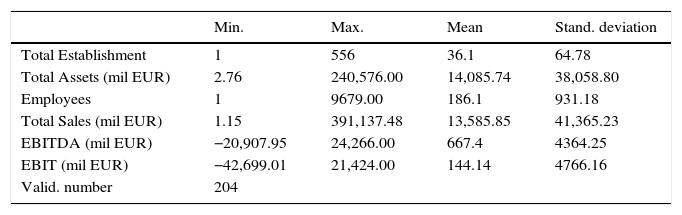
The geographical area is diverse but the major concentration is in Madrid, 26.2%, and in Barcelona with 20.6% with respect to the rest of Spanish provinces. The variables used to build the exogenous items are presented in Table 1. We can appreciate a great heterogeneity in the magnitudes of the Spanish franchise sample.
Main descriptive statistics.
| Min. | Max. | Mean | Stand. deviation | |
|---|---|---|---|---|
| Total Establishment | 1 | 556 | 36.1 | 64.78 |
| Total Assets (mil EUR) | 2.76 | 240,576.00 | 14,085.74 | 38,058.80 |
| Employees | 1 | 9679.00 | 186.1 | 931.18 |
| Total Sales (mil EUR) | 1.15 | 391,137.48 | 13,585.85 | 41,365.23 |
| EBITDA (mil EUR) | −20,907.95 | 24,266.00 | 667.4 | 4364.25 |
| EBIT (mil EUR) | −42,699.01 | 21,424.00 | 144.14 | 4766.16 |
| Valid. number | 204 |
The exogenous variables are a good representation of the value drivers or performance of firms from the most important points of view suggested in previous studies (Aaker David, 1996; Bello Acebrón et al., 1994; Cerviño, 2004; Park & Srinivasan, 1994; Sivakumar & Raj, 1997): first, market position measured by total establishments, and market share variables, secondly, the ability to generate economic profit from different levels: Gross Operating Margin, and EBITDA Margin. Finally, we have added other criteria regarding the capacity to generate wealth in terms of factors of production employed, as a consequence of scale economies and better competitiveness (Doyle, 2001; Fernández, 2011): Return on Assets,5 and Employee Productivity:
- 1.
Total Establishment, including those that are operated by own firm or by third-parties.
- 2.
Market Share, measured from the result of dividing the turnover of each franchise among the total incomes that each industry generates.
- 3.
Gross Operating Margin, i.e. the quotient obtained from dividing gross profit (which is at the same time the difference of the sales and the cost of the same) and the turnover obtained for each company.
- 4.
EBITDA Margin, i.e. the quotient between the earnings before interest, taxes, depreciation and amortization (EBITDA) and the figure regarding revenues.
- 5.
Return on Assets or ROA, known as the quotient between EBITDA and the net book value of the asset.
- 6.
Employee Productivity (EBIT/Employee), measured as the ratio among the earnings before interest and taxes (EBIT) and the number of employees.
In order to contrast hypothesis I, following Punj and Stewart (1983), a K-means clustering analysis, through an SPSS statistical program, has been made to obtain a group classification for each industry, according to clearly defined features that exogenous variables show. In this way, every one of these records the elements of the sample that, on the whole, achieve the maximum distance of its means, also known as centroids.
Once the different groups for each industry have been obtained, to check hypotheses II (a), II (b) and III, in line with Perreault et al. (1979), a linear discriminating analysis has been performed. The linear discriminating analysis can be considered as a regression technique that establishes linear relationships, where the endogenous variable is a categorical one (determines the groups) and the exogenous variables, being continuous, will help to predict the belonging group. Following Dillon, Goldstein, and Schiffman (1978): “if the assumptions of normality and identical covariance matrices are satisfied, then there is no reason to examine alternatives to Fisher's LDF (discriminatory functions)6”.
To achieve this mathematically, series of canonical equations are going to be generated (the minimum {n−1,p}, n being the number of classification groups and p being the exogenous variables one) with the aim of discriminating between or separating all the groups as much as possible:
For Est=Total establishments; MShare=Market Share; GrossMarg=Gross Margin; EBITDA=EBITDA Margin; ROA=Return of Assets; Prod=Employees Productivity.
These linear combinations of the six variables used must maximize the variance between the groups and, at the same time, should minimize it within groups:
In Eq. (2), b¯, is the vector of coefficients; T, the matrix of total variances and covariance; E, the matrix of variances and covariance among the groups and C, the covariance within groups. The vector of coefficients b¯ must maximize the relationship of the variance among the groups regarding the variance within the groups.
Nevertheless, it is necessary also to know the value of the centroids by using the following equation. In the LDA each canonical function explains the relationship between two centroids D¯J whose distances are maximized:
The goodness of fit of the methodology for predicting the corresponding royalty for a new company, purpose one, has been proved across a confusion matrix. This matrix compares the real classification, which was elaborated using cluster technique, and the one obtained by the linear discriminating function, using this way to check the number of goals that were achieved in each one of the analyzed industries. The mechanism of classification for each individual location depends on the odds of Bayes’ Theorem.7
Fisher equations are another way of measuring allocation scores. This classification coincides exactly with the one previously obtained using all the canonical functions and the Bayes rule. To calculate the strength of a brand, purpose two, we propose a Fisher score vector which is the result of the scores generated by maximizing the probability of each company pertaining to the most likely cluster. The cumulative probability of these scores F(x) will represent the brand strength.
ResultsThe heterogeneity on firm's data in each industry has allowed the distinguishing different groups to apply cluster technique. The best classification found is the one corresponding to three groups, called: high, medium and low royalty.
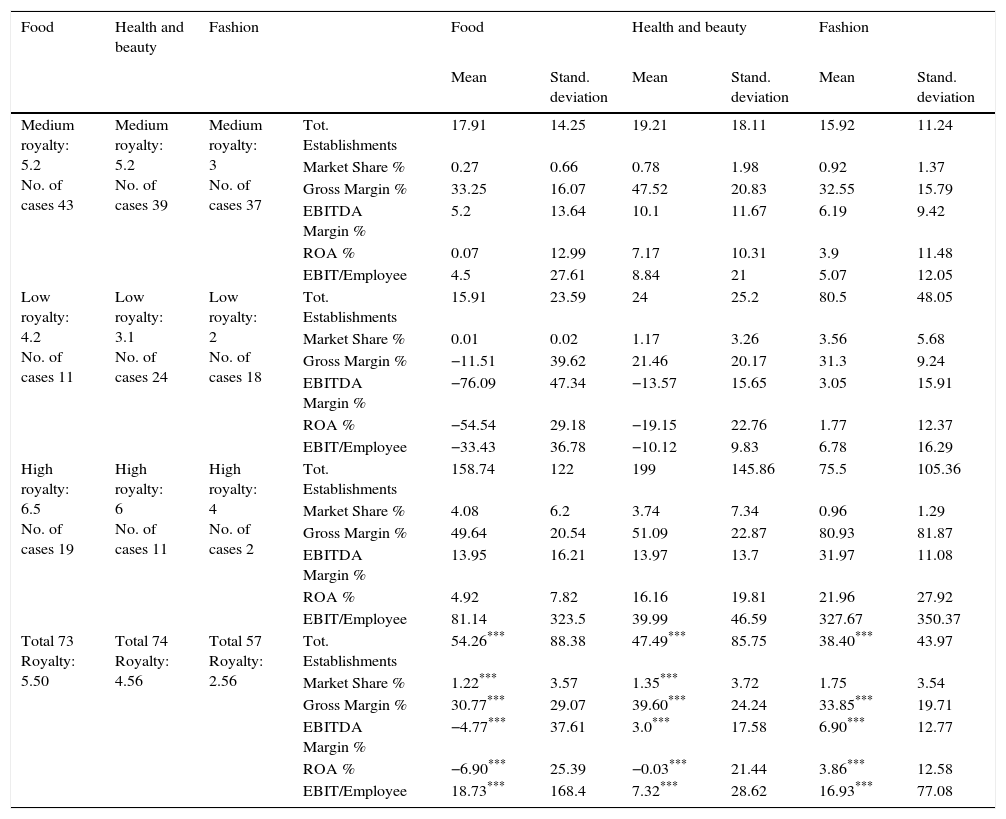
We can highlight in Table 2 the presence of remarkable differences over all magnitudes used, among the cluster of each industry. Specifically, the average royalty collected by the food industry is 5.5% larger in comparison with the health and beauty, and fashion industries, which are 4.56% and 2.56%, respectively. On the other hand, high variability among the means of the groups can be seen: the high royalty group generates exogenous variable values greater than the medium and low range in each sector. In this form the variables, after ANOVA test, show a p-value lower than 0.01, except for Market Share in the case of the fashion industry. Nevertheless, despite the fact that variables are significant individually in cluster it does not imply that they will be significant in the proposed model.
Classification from K-means cluster.
| Food | Health and beauty | Fashion | Food | Health and beauty | Fashion | ||||
|---|---|---|---|---|---|---|---|---|---|
| Mean | Stand. deviation | Mean | Stand. deviation | Mean | Stand. deviation | ||||
| Medium royalty: 5.2 No. of cases 43 | Medium royalty: 5.2 No. of cases 39 | Medium royalty: 3 No. of cases 37 | Tot. Establishments | 17.91 | 14.25 | 19.21 | 18.11 | 15.92 | 11.24 |
| Market Share % | 0.27 | 0.66 | 0.78 | 1.98 | 0.92 | 1.37 | |||
| Gross Margin % | 33.25 | 16.07 | 47.52 | 20.83 | 32.55 | 15.79 | |||
| EBITDA Margin % | 5.2 | 13.64 | 10.1 | 11.67 | 6.19 | 9.42 | |||
| ROA % | 0.07 | 12.99 | 7.17 | 10.31 | 3.9 | 11.48 | |||
| EBIT/Employee | 4.5 | 27.61 | 8.84 | 21 | 5.07 | 12.05 | |||
| Low royalty: 4.2 No. of cases 11 | Low royalty: 3.1 No. of cases 24 | Low royalty: 2 No. of cases 18 | Tot. Establishments | 15.91 | 23.59 | 24 | 25.2 | 80.5 | 48.05 |
| Market Share % | 0.01 | 0.02 | 1.17 | 3.26 | 3.56 | 5.68 | |||
| Gross Margin % | −11.51 | 39.62 | 21.46 | 20.17 | 31.3 | 9.24 | |||
| EBITDA Margin % | −76.09 | 47.34 | −13.57 | 15.65 | 3.05 | 15.91 | |||
| ROA % | −54.54 | 29.18 | −19.15 | 22.76 | 1.77 | 12.37 | |||
| EBIT/Employee | −33.43 | 36.78 | −10.12 | 9.83 | 6.78 | 16.29 | |||
| High royalty: 6.5 No. of cases 19 | High royalty: 6 No. of cases 11 | High royalty: 4 No. of cases 2 | Tot. Establishments | 158.74 | 122 | 199 | 145.86 | 75.5 | 105.36 |
| Market Share % | 4.08 | 6.2 | 3.74 | 7.34 | 0.96 | 1.29 | |||
| Gross Margin % | 49.64 | 20.54 | 51.09 | 22.87 | 80.93 | 81.87 | |||
| EBITDA Margin % | 13.95 | 16.21 | 13.97 | 13.7 | 31.97 | 11.08 | |||
| ROA % | 4.92 | 7.82 | 16.16 | 19.81 | 21.96 | 27.92 | |||
| EBIT/Employee | 81.14 | 323.5 | 39.99 | 46.59 | 327.67 | 350.37 | |||
| Total 73 Royalty: 5.50 | Total 74 Royalty: 4.56 | Total 57 Royalty: 2.56 | Tot. Establishments | 54.26*** | 88.38 | 47.49*** | 85.75 | 38.40*** | 43.97 |
| Market Share % | 1.22*** | 3.57 | 1.35*** | 3.72 | 1.75 | 3.54 | |||
| Gross Margin % | 30.77*** | 29.07 | 39.60*** | 24.24 | 33.85*** | 19.71 | |||
| EBITDA Margin % | −4.77*** | 37.61 | 3.0*** | 17.58 | 6.90*** | 12.77 | |||
| ROA % | −6.90*** | 25.39 | −0.03*** | 21.44 | 3.86*** | 12.58 | |||
| EBIT/Employee | 18.73*** | 168.4 | 7.32*** | 28.62 | 16.93*** | 77.08 | |||
* Prob≤0.10.
** Prob≤0.05.
The groups resulting from the clusters, Table 1, basically match those that come from manually classified companies based only on their royalty, which shows that the market is efficient and there is a clear relationship between groups of prices paid and economic characteristics of the enterprises, so hypothesis I is confirmed.
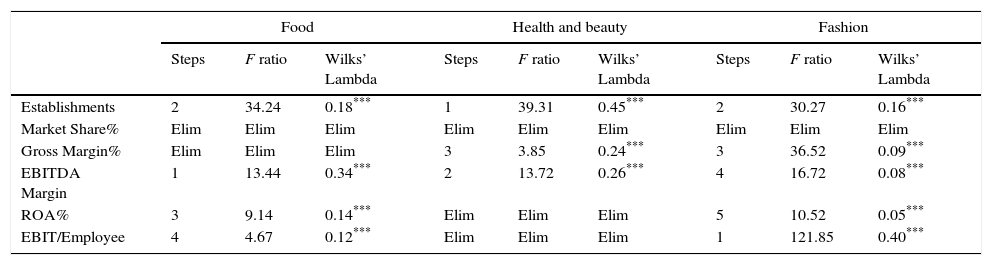
To evaluate the importance that each variable possesses specifically in Eq. (1) and to check the hypothesis II (a), we have employed the forward stepwise method in SPSS (Table 3), which consists of elaborating sequential models in which an additional variable is included time after time until they stop providing significance and so, the procedure ends. It should be mentioned that the predictors included are continuously re-evaluated, so that if a variable has not enough discriminating power or is explained by others it is deleted. The method chooses firstly the variable that has the best abilities for explaining the group differences. Afterwards, through the step by which the variable has been selected we can ascertain its importance. This is done by using the global Wilks’ Lambda8 and the F statistic.9 As a consequence of the introduction of each exogenous variable (all of them with a p-value less than 0.01) the Lambda goes down, which means that the discriminating power is improved among the groups.
Results of the variables selection to the stepwise method.
| Food | Health and beauty | Fashion | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Steps | F ratio | Wilks’ Lambda | Steps | F ratio | Wilks’ Lambda | Steps | F ratio | Wilks’ Lambda | |
| Establishments | 2 | 34.24 | 0.18*** | 1 | 39.31 | 0.45*** | 2 | 30.27 | 0.16*** |
| Market Share% | Elim | Elim | Elim | Elim | Elim | Elim | Elim | Elim | Elim |
| Gross Margin% | Elim | Elim | Elim | 3 | 3.85 | 0.24*** | 3 | 36.52 | 0.09*** |
| EBITDA Margin | 1 | 13.44 | 0.34*** | 2 | 13.72 | 0.26*** | 4 | 16.72 | 0.08*** |
| ROA% | 3 | 9.14 | 0.14*** | Elim | Elim | Elim | 5 | 10.52 | 0.05*** |
| EBIT/Employee | 4 | 4.67 | 0.12*** | Elim | Elim | Elim | 1 | 121.85 | 0.40*** |
* Prob≤0.10.
** Prob≤0.05.
In the table above it is observable that included-excluded variables change for each industry. For example Market Share is dropped from all the sectors. However, in the case of the food industry the Gross Margin is also eliminated.
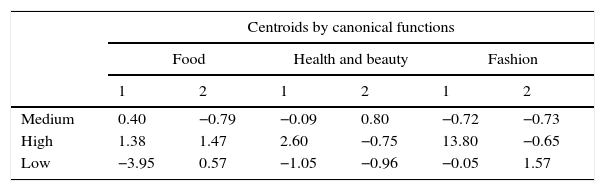
With this method, as in our analysis we have created three groups by industry, we use two canonical functions. Each one of them explains the differences in the behavior of each pair of groups. The canonical correlation in Table 4 measures the association between the discriminating score and the set of exogenous variables. It is very high in all cases: in food D1 has 0.87 and D2 0.71, health and beauty 0.77 and 0.65, and in fashion 0.94 and 0.74 respectively. In this table the test of Wilks’ Lambda also compares hierarchically the significance of the two functions obtained. Null hypothesis10 is rejected to a probability of 100%, so both, D1 and D2, distinguish significantly between groups. Correlations and p-value confirm that there is a significant relationship between exogenous variables selected by stepwise method and the groups of royalties, as we indicated in hypothesis II (a).
Centroids by canonical functions, standardized coefficients and significance.
| Centroids by canonical functions | ||||||
|---|---|---|---|---|---|---|
| Food | Health and beauty | Fashion | ||||
| 1 | 2 | 1 | 2 | 1 | 2 | |
| Medium | 0.40 | −0.79 | −0.09 | 0.80 | −0.72 | −0.73 |
| High | 1.38 | 1.47 | 2.60 | −0.75 | 13.80 | −0.65 |
| Low | −3.95 | 0.57 | −1.05 | −0.96 | −0.05 | 1.57 |
| Standardized coefficients of the canonical functions | ||||||
|---|---|---|---|---|---|---|
| Food | Health and beauty | Fashion | ||||
| D1 | D2 | D1 | D2 | D1 | D2 | |
| Tot. Establishment | 0.27 | 0.98 | 0.82 | −0.59 | 0.23 | 1.19 |
| Market Share % | – | – | – | – | – | – |
| Gross Margin % | – | – | 0.28 | 0.37 | 1.31 | −0.69 |
| EBITDA Margin% | 0.67 | −0.27 | 0.38 | 0.71 | 1.56 | 0.82 |
| ROA% | 0.55 | −0.15 | – | – | 1.06 | −0.39 |
| EBIT/Employee | −0.14 | 0.52 | – | – | 1.90 | −0.22 |
| Wilks’ Lambda=0.12 | Wilks’ Lambda=0.49 | Wilks’ Lambda=0.24 | Wilks’ Lambda=0.57 | Wilks’ Lambda=0.05 | Wilks’ Lambda=0.46 | |
| Chi2(8)=144.115 | Chi2(3)=48.14 | Chi2(6)=101.02 | Chi2(2)=39.20 | Chi2(10)=151.68 | Chi2(4)=40.98 | |
| Prob>Chi2=0.000 | Prob>Chi2=0.000 | Prob>Chi2=0.000 | Prob>Chi2=0.000 | Prob>Chi2=0.000 | Prob>Chi2=0.000 | |
| Correlation=0.87 | Correlation=0.71 | Correlation=0.77 | Correlation=0.65 | Correlation=0.94 | Correlation=0.74 | |
It is observable that in the food industry, the centroid of the high royalty group is located in D1 at the positive extreme, whereas the mean of enterprises with medium royalty is in the center of the interval and finally the sign of a low royalty is negative. In this way we can interpret the rest of the values of centroids by canonical functions in the other sectors. So, in Table 4, the first function (D1) explains the differences between the high versus low royalty for food, health and beauty, while the second function, (D2) shows the relationship between the medium and high royalty for food, and it compares the score of a medium value relative to a low one for health and beauty. For its part, in fashion, (D1) accounts for the behavior of the high versus medium royalty, while (D2) shows the behavior of the medium versus low royalty.
In general terms there is a positive relationship between the variables and the royalties paid. For example, in the function D1, we can see in Table 4 that the food industry shows positive in the following coefficients: total Establishments, EBITDA Margin and ROA. In Health and beauty we can observe a positive sign in Total Establishments, Gross Margin and EBITDA Margin, and in fashion also in Employee Productivity. When each one of these variables increases it raises the probability of the enterprise belonging to the high royalty group. However, there are exceptions: Employee Productivity, in D1 for food, or Total Establishments, in D2 for health and beauty, and also for fashion. So we can only partially confirm hypothesis II (b).
EBITDA Margin and Total Establishment are the variables which explain the differences between the groups in all sectors, and they have the highest coefficients in absolute terms in food and health and beauty. Nevertheless we can check that variables concerning productivity: Return on Assets and Employee Productivity are only relevant in food and fashion. This fact indicates that each franchise sector collects structural differences and capabilities to create value in the companies.
Then, although it is obvious that in all sectors when the level of royalty rises productivity variables also increases, see Table 2, in the case of health and beauty, this contribution is not as relevant or seems to be explained by other variables. So, in this model it is not possible to use the same quantitative variables and their corresponding weights for different sectors, confirming hypothesis III.
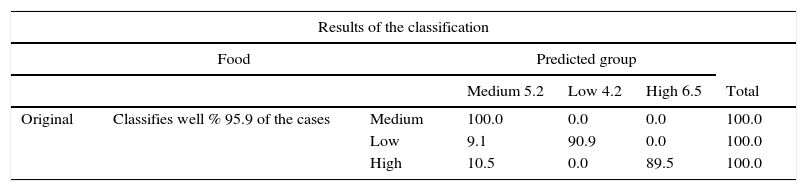
In this research, a confusion matrix has been used in order to determine the model's goodness of fit, purpose one. The number of well classified cases is very high (Table 5) because it is up to 95% for the case of the food industry, 89.2% for the health and beauty industry and, finally 96.5% for the fashion industry. As an illustration, in the beauty and health sector, over all enterprises classified in origin as royalty medium (vertical axis), the proposed model (horizontal axis) has classified the 92.3% in this level, while the rest, 7.7%, in the low royalty.
Results of the classification: confusion matrix.
| Results of the classification | ||||||
|---|---|---|---|---|---|---|
| Food | Predicted group | |||||
| Medium 5.2 | Low 4.2 | High 6.5 | Total | |||
| Original | Classifies well % 95.9 of the cases | Medium | 100.0 | 0.0 | 0.0 | 100.0 |
| Low | 9.1 | 90.9 | 0.0 | 100.0 | ||
| High | 10.5 | 0.0 | 89.5 | 100.0 | ||
| Beauty and health | Predicted group | |||||
|---|---|---|---|---|---|---|
| Medium 5.2 | High 6 | Low 3.1 | Total | |||
| Original | Classifies well % 89.2 of the cases | Medium | 92.3 | 0.0 | 7.7 | 100.0 |
| Low | 8.3 | 0.0 | 91.7 | 100.0 | ||
| High | 18.2 | 72.7 | 9.1 | 100.0 | ||
| Fashion | Predicted group | |||||
|---|---|---|---|---|---|---|
| Low 2 | High 4 | Medium 3 | Total | |||
| Original | Classifies well % 96.5 of the cases | Medium | 0.0 | 0.0 | 100.0 | 100.0 |
| Low | 88.9 | 0.0 | 11.1 | 100.0 | ||
| High | 0.0 | 100.0 | 0.0 | 100.0 | ||
Below, we illustrate by an example the process to calculate the strength and the value of a brand for the food industry, purpose two.
The Fisher equations are: F1 which represents the medium royalty, F2 for the low royalty and F3 explains the higher royalty:
From the above equations, a Pr(g/F) probability can be calculated, in other words, if a company obtains a discriminating score F, then it will belong to g group. From Uriel (1996) the following formula (the result of which coincides with Bayes’ rule considering the priori probabilities of groups as equal), may be applied:
Therefore, if a company i has, for example, 201 Establishments, an EBIT/Employee equal to 17.04 (in thousands of monetary units), ROA equal to 14.03%, an EBITDA Margin of 18.48%, then F1=−0.24, F2=−9.38 and F3=3.95. Consequently, applying (7), Pr(1/F)=0.015, Pr(2/F)=0, Pr(3/F)=0.985. Then it could be predicted that this company belongs to the third group, or high royalty, because this is most likely, and we obtain at the same time a score F3=3.95, the largest of the three expressed above.
In this way, a shortlist of three values Pij=(Pi1,Pi2,Pi3) would be assigned for each company, Pij being the probability of a company i belonging to the group j, thus Xi is the solution of the discriminating score (Eq. (8)):
For each sector, we obtain X, the Fisher discriminating score vector, a set of solutions (one for each enterprise) resulting from the probability of pertaining to the most likely cluster. In order to determine the companies’ brand strength, purpose two, the previous vector must be divided into deciles. The fifth and tenth decile corresponds to the low royalty cluster. The twentieth decile contains two elements which have obtained the highest score in the low royalty group and the rest are those that have obtained the lowest scores in the medium royalty cluster. For its part, the 13th, 15th and 17th deciles include the remaining companies of the medium cluster with successively larger scores and finally, the eightieth, ninetieth and 95th deciles have been set up using these companies that have been classified as high royalty.
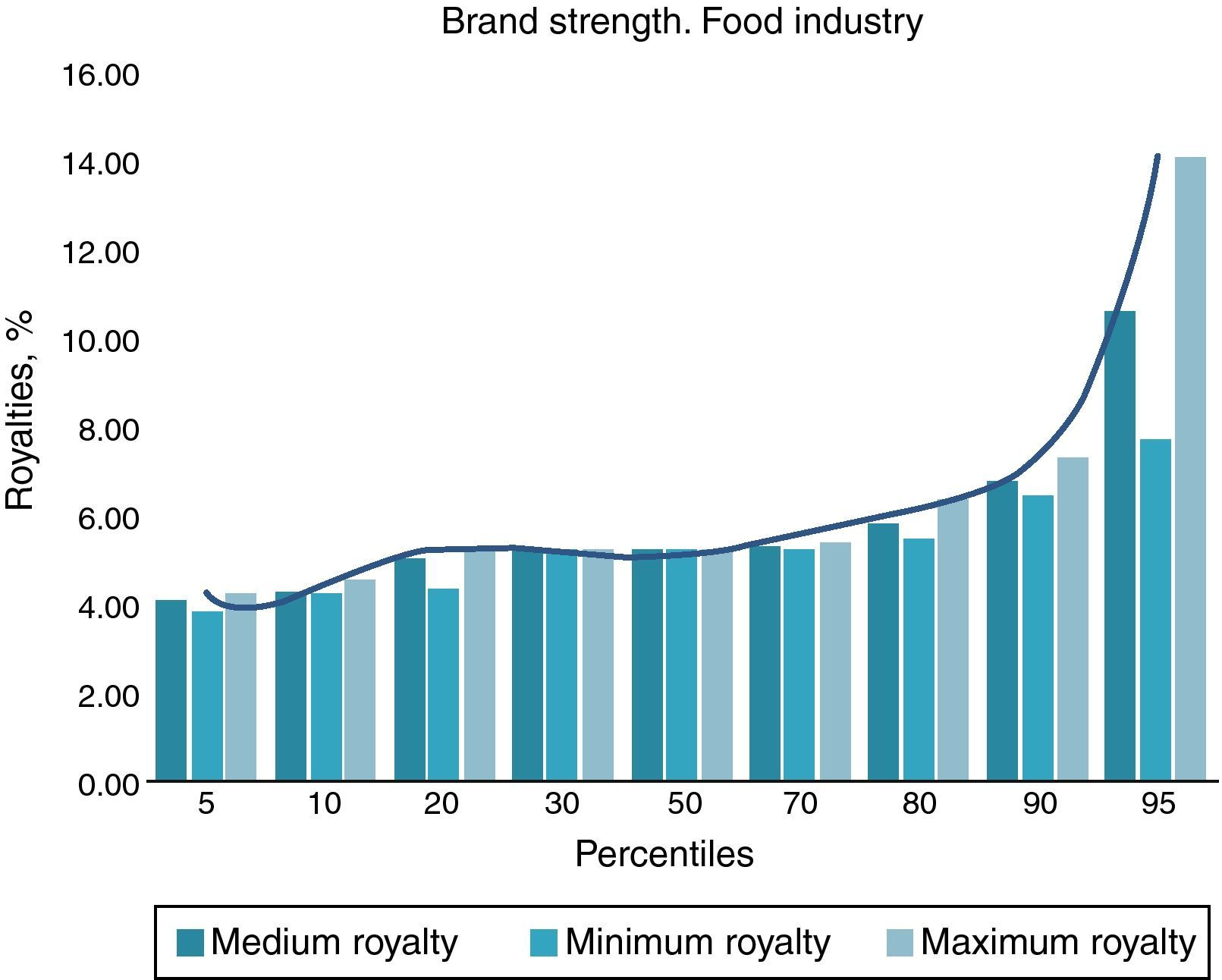
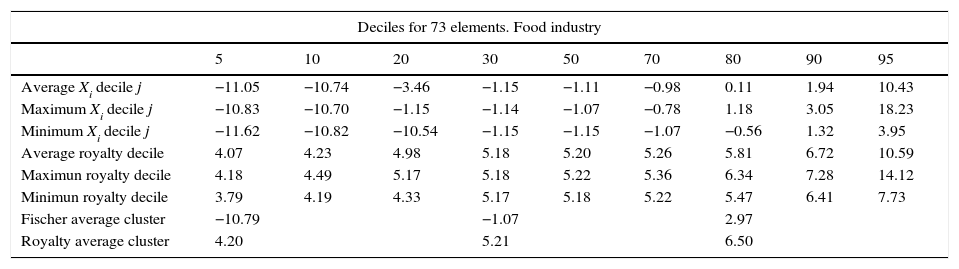
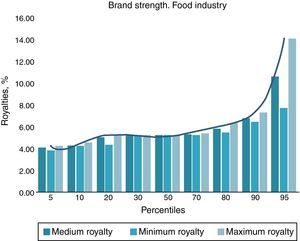
Each decile, F(x), represents the cumulative probability of these scores or brand strength. It will record, through a score from 0 to 100, the level or strength with which the attributes of any company in the sector add value with respect to the whole sample. Brand strength is represented in Table 6 and Fig. 3 for the food sector, in which for each percentile the medium, minimum and maximum corresponding discriminating score and market royalty is shown.
Brand strength expressed as a function of deciles.
| Deciles for 73 elements. Food industry | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 5 | 10 | 20 | 30 | 50 | 70 | 80 | 90 | 95 | |
| Average Xi decile j | −11.05 | −10.74 | −3.46 | −1.15 | −1.11 | −0.98 | 0.11 | 1.94 | 10.43 |
| Maximum Xi decile j | −10.83 | −10.70 | −1.15 | −1.14 | −1.07 | −0.78 | 1.18 | 3.05 | 18.23 |
| Minimum Xi decile j | −11.62 | −10.82 | −10.54 | −1.15 | −1.15 | −1.07 | −0.56 | 1.32 | 3.95 |
| Average royalty decile | 4.07 | 4.23 | 4.98 | 5.18 | 5.20 | 5.26 | 5.81 | 6.72 | 10.59 |
| Maximun royalty decile | 4.18 | 4.49 | 5.17 | 5.18 | 5.22 | 5.36 | 6.34 | 7.28 | 14.12 |
| Minimun royalty decile | 3.79 | 4.19 | 4.33 | 5.17 | 5.18 | 5.22 | 5.47 | 6.41 | 7.73 |
| Fischer average cluster | −10.79 | −1.07 | 2.97 | ||||||
| Royalty average cluster | 4.20 | 5.21 | 6.50 | ||||||
In our example, in addition to putting the new company i within the high royalty cluster, as was indicated before, the strength of its brand against other competitors would be between 90 maximum and 95 minimum deciles because its score (Xi) was 3.95. Based on the strengths the royalty rate would be between the maximum decile 90, 7.28% and minimum decile 95, 7.73%.
Once the range of implicit royalty is enclosed the value of the brand may be determined. First, we can calculate the cash-flow corresponding to the brand, or saving royalty (SAVINGroyalty), multiplying sales planned for that product or brand by its implicit royalty. If the projected sales i are 10 (MM €), the saving royalty would be 728–773 (thousand €). Finally, the financial value of the brand incorporates other parameters, such as the lifetime and the required return of the specific intangible asset for the financial structure (KI). Given that the IAS 36 (2004) provides an indefinite life for brands, it is possible to calculate its value from the present value of an income of infinite term, see Eq. (9):
To determine KI, the starting point is always the WACC or weighted average cost of capital. This concept also is the mean rate at which the economic structure rewards the financial structure. Therefore the entity could have added a risk premium to the WACC that is estimated to be appropriate based on the economic characteristics of the intangible asset11:
From the market remuneration of the tangible elements, we can easily isolate the WACC of the intangible part solving Eq. (10):
For example, if enterprise i has a WACC equal 11%, an enterprise value (EV) equal 17 (thousand €), of which tangible structure (WT) represents 10 (MM €), 58.82%, and the market remuneration (KT), 6%, the intangible rate discount (KI), from (11), give a value equal 18.14%. If the projected sales are 10,000 (thousand €) and the adjusted discount rate is 18.14%, then, applying Eq. (9) the confidence interval corresponding to the value of the brand would be 4012.60–4260.63 (thousand €).
Conclusions and final remarksFrom the described statistical methods: cluster technique and LDA, we have developed a model to determine the implicit royalty for buying or using a brand. Other statistical techniques, such as cluster, discriminating and multinomial logit models, have been widely analyzed in marketing studies, as in Punj and Stewart (1983), Perreault et al. (1979), Kamakura and Russell (1993) or Swait et al. (1993), but only from the point of view of the analysis that certain features confer to the product or to the buyers in order to achieve the best position in the market. However, the suitability of the cluster and LDA for this purpose has never been proved, despite authors like Nomen (2005) or Torres Coronas (2002) warning of the flaws of the royalty methodology and the necessity of including statistical techniques.
After being implemented, we have contrasted all the hypotheses and proposals. Firstly, although authors like Lev (1989, 2000, 2005), Brown et al. (1999), Dantoh et al. (2004) demonstrate the ineffectiveness of accounting variables to explain the value of intangibles, cluster technique proves to be useful for segmenting the companies according to the performance variables used (see Table 2), and, this classification coincides with that made by the market, so we conclude that the market is efficient in assigning royalties based on the variables proposed, hypotheses I.
Secondly, in line with Park and Srinivasan (1994), Bello Acebrón et al. (1994), Aaker David (1996) or Cerviño (2004), between others, we have proved (based on statistical tests) that the exogenous economic variables used generate enough discriminating power to explain the different groups of royalties which are collected in the three industries, hypothesis II (a) (see Tables 3 and 4), so it is clear that qualitative variables, which make up the brand value: leadership, stability, support or image, among others, when creating a value must be expressed in terms of improvements of companies’ income statements, and those affecting the level of royalty.
Specifically, we have found that higher royalties paid depend positively on the market position and the economic profit, measured by number of establishments and EBITDA margin, confirming in part hypotheses II (b). Nevertheless, in the Food and Fashion sector also the royalties paid are explained positively by other productivity variables, employee productivity and ROA. So, the behavior and the relevance of the exogenous variables are different depending on the industry, hypotheses III and Table 3, and then it is not possible to use the same model for all sectors.
Finally, the discriminating technique suitably predicts the group to which a new company belongs for all the mentioned industries (Table 5) and, using the scores obtained with the equations of Fisher (Table 6), a ranking of the companies can be created to determine the brand strengths, which is confirmed by their market position with respect to other competitors.
The implications of this research are very important for practitioners and researchers. For consulting firms, the proposed model allows us to determine the flow corresponding to a certain brand, of any non-franchising company, in order to ascertain its value with the rigor and demands that the accounting standard requires. This is particularly the case of IAS 38, IFRS 3 and 13, for example in a business combination. On the other hand, it is important for companies which want to expand through franchises and they need to calculate the level to charge by royalty in line with the market. Finally, from a strategic point of view, the model allows them to calculate the companies’ brand strength. This shows the market position of a specific franchisor vis-á-vis the competitors across their economic value drivers, and this would help the companies to carry out strategic plans to increase their brand's value.
This proposal could also be complemented in future research lines with other models which try to find an internal and qualitative perspective of the brand value generation. In fact, it remains a challenge to find the map with the corresponding relationships between qualitative and quantitative variables, thus to achieve a complete knowledge of value brand generation.
| AKRA FRÍO, S.L. |
| ALADA 1850, S.L. |
| ALMA DE CACAO |
| ARROCERÍAS DE ALICANTE, S.L.U. |
| ARROCERÍAS DE ALICANTE, S.L.U. |
| AZEITE E VINAGRE, LDA. |
| BAÑOS GARRE, S.L. |
| BEER & FOOD GRUPO DE RESTAURACIÓN |
| BEIRUT KING S.L. |
| BIERWINKEL, S.L. |
| BODEGAS GALIANA ALIMENTACIÓN, S.L. |
| BRASERÍA LOS DUENDES S.L. |
| BRUSTERS RESTAURANTES 2010, SL |
| BURGER KING ESPAÑA, S.L.U |
| BURGER RICKY |
| CAFÉ DEL MERCADO FRANQUICIAS, S.L. |
| CAFÉS CANDELAS SL |
| CENTRAL DE FRANQUICIAS PANTAIBERIC |
| CHOCOLATES VALOR, S.A. |
| CIA. DALLAS RIB'S, S.A. |
| COFFEE & FOODS |
| COMESS GROUP DE RESTAURACIÓN |
| COMESS GROUP DE RESTAURACIÓN, S.L. |
| COMESS GROUP DE RESTAURACIÓN, S.L. |
| COMESS GROUP DE RESTAURACIÓN, S.L. |
| COREN GRILL, S.A |
| DEHESA SANTA MARIA FRANQUICIAS S.L. |
| DIABLITO FRANCHISING, S.L. |
| DISTRIB. ALIMENT. SURESTE SAU |
| DON ULPIANO FRANQUICIAS S.L |
| DOOPIES & COFFEE, SL |
| DRUNKEN DUCK FOOD, S.L. |
| DUNKIN ESPAÑOLA S.A |
| EL MOLÍ VELL |
| EURO TAPASBAR, S.A. |
| EXPANSIÓN DE FRANQUICIAS, S.L. |
| EXPANSIÓN DE FRANQUICIAS, S.L. |
| FABORIT COFFEE SHOP, S.L. |
| FOOD SERVICE PROJECT, S.L. |
| FRANCHISINGS KURZ & GUT, S.L |
| FRANQUICIAS LA PIEMONTESA SLU |
| FRANQUIPAN, S.L. |
| FRIENDS & MOJITOS S.L |
| GINOS FRANCHISING, S.L. |
| GRAN PALADAR SL |
| GREEN DEVELOPPEMENT |
| GRUPO ALASKA |
| GRUPO RESTALIA |
| GRUPO ZENA DE RESTAURACIÓN, S.A. |
| GRUPO ZENA DE RESTAURANTES S.A. |
| HOSTELOESTE, S.L.U. |
| ILOPEZHIDALGOA |
| INVERSIONES VENESPOR, S.A. |
| INVESANVEL, SL |
| JUNIO 1972 RESTAURACIÓN, S.L. |
| KANIKAMA PROJECT, SL |
| KRUNCH FRANCHISING, S.L. |
| L.N.F. FRANCHISING S.L.U. |
| LA BOHEME |
| LA CUEVA 1900 |
| LA SUREÑA |
| LACREM, S.A. |
| LLOGUECATA, S.L. |
| LOS BODEGONES |
| MAC PAPAS, S.L. |
| MATERASTURIAS, S.L. |
| MIGUEL SANCHO S.L |
| MY CREPE, SL |
| O REI DAS TARTAS |
| ODRE Y HOGAZA, S.L. |
| OPEN 25 |
| OVERPANI FRANQUICIAS, S.L |
| PANA-ROM S.L |
| PANSFOOD, S.A. (THE EAT OUT GROUP, S. L.) |
| PARSIN'S, S.L |
| PASTIFICIO SERVICE, S.L. |
| PECADITOS |
| PIZZA LEGGERA WORLDWIDE |
| PIZZA MARZANO, S.A. |
| POLLO CAPORAL FRANQUICIAS, S.L. |
| RAMÓN Y VIDAL, S.L. |
| RECREATIVOS TORNAJUELO |
| RESENDE, S.L. |
| RESTAURANTES BRUNO, S.L |
| RIGARUSSO ASOCIADOS, S.L. |
| RODILLA SÁNCHEZ, S.L. |
| SAFO MEDITERRÁNEA, S.A. |
| SAMORVARTE Y CAFÉ, S.L. |
| SDAR SRL |
| SERVIFRUIT GOMAB S.L. |
| SPORTS FRANCHISING, S.L. |
| STICKHOYSE BCN, SL |
| TELEPIZZA, S.A |
| TERRA VITAE, SL |
| THE EAT OUT GROUP, S.L. (BOCATTA 2000, S.L) |
| UNIDE |
| URBAN LIFE FOOD COURT |
| VINUS BRINDIS S.L. |
| YUM RESTAURANTS ESPAÑA |
| ZUMO BAR CANARIAS S.L. |
| ABANOLIA |
| ACORDE PLUS, S.L |
| ACR WAX COSMETICS, S.L. |
| ACR WAXCOSMETICS, S.L. |
| ACTUAL STHETIC, SL |
| ALDABE S.A. |
| ALDABE, S.A. |
| ALDABE, S.A. |
| ALTA ESTÉTICA SL |
| ASOCIADOS LLONGUERAS |
| BE STHETIC |
| BEN&SULY S.L |
| BENESSERE FITNESS PILATES NUTRICIÓN. |
| BENZAQUEN2, S.L |
| BODY FACTORY FRANQUICIAS, S.L. |
| BYE BYE PELOS, SL |
| C&C CASANOVA S.A. |
| CEBADO, S.A |
| CEFOGA 2000, S.L. |
| CELLULEM BLOCK |
| CENTROS DESESTRES, S.A |
| CENTROS PULSAZIONE INTERNACIONAL, SL |
| CLÍNICA SACHER–MEDICINA ESTÉTICA. |
| CLÍNICAS CAREDENT, S.L. |
| CLÍNICAS CETA S.L. |
| CLINICAS PODOLOGICAS |
| CLÍNICAS VIRGEN DE LA PAZ S.L |
| COMPAÑÍA DE SERVICIOS MÉDICOS AMENTA S.L. |
| CONTIFARMA, S.L. |
| CONTOURS EXPRESS IBÉRICA S.L |
| COVALDROPER GRUPO |
| CUERPOS FITT |
| CURVES INTERNATIONAL OF SPAIN, S.A. |
| D ELITE EVENT PLANNERS SL |
| DENTALIS |
| DEPICOOL |
| DEPILINE WAX & COSMETICS S.L. |
| DORSIA CENTRAL DE COMPRAS, SL |
| ECOLOGIC BY LINDA NICOLAU, S.L. |
| ELIMINA EL VELLO |
| EPILAE NORTE, S.L. |
| ESTETICA Y SALUD MASCULINA S.L. |
| ESTETICBODY |
| ETHIA CENTROS MÉDICO ESTÉTICOS |
| EXTENSIONMANIA |
| FITNESS19 |
| FK ESTETICA INFANTIL S.L. |
| FRANCK PROVOST |
| GIRÓN & NAVARRO INTERNACIONAL |
| GLOMONT S.L |
| GRUPO ACTUAL ESTHETIC - BIOTHECARE ESTETIKA |
| ARZANO, S.L. |
| CALDERÓN FRANQUICIAS, S.L. |
| CÁLLATE LA BOCA |
| CHAQUE S.A. |
| CHICCO ESPAÑOLA, S.A. |
| CITY FINANCE 2011, SL |
| CRYSANNA COLLECTION, S.L |
| CUPPERTON DEVELOPS S.L. |
| DISTRIBUCIONES INTERNACIONALES M.ERCILLA, S.L |
| DIVINA PROVIDENCIA |
| DM2 ESTILO MODA S.L. |
| EIGHTEEN OCTOBER 2001, S.L. |
| EMERGENCIA PERMANENTE, S.L. |
| EMERGENCIA PERMANENTE, S.L. |
| EMPORIO FRANCHISING |
| EVA ALFARO |
| FERNANDEZ-MATAMOROS MAS-SARDA JOSÉ MARÍA S.L.N.E |
| FRANDESIM, S.L. |
| FRANQUICIA LAS LILAS S.L. |
| GLOBAL DE PRODUCTOS ONLINE S.L |
| GOLD SYSTEM MERCADO, SL |
| GROUPE ZANNIER ESPAÑA S.A |
| GRUPO LOVE STORE, S.A. |
| GRUPO OSBORNE S.A. |
| GRUPO ROSA CLARÁ |
| GUBESA CO, S.L |
| IKKS SPORTSWEAR SPAIN |
| INDUSTRIA FRANCO ESPAÑOLA DE MODA, S.A |
| INTERMALLA, S.L. |
| JONAS 3000,S.L |
| JORDI ANGUERA ESPAI I COSTURA SL |
| JULIO MAESTRE, S.L. |
| KARPI CONFECCIÓN, S.L. |
| KIABI ESPAÑA - KSCE, S.A. |
| LA COMPAGNIE DES PETITS |
| LA NÁUTICA SERVICIOS NÁUTICOS, SL |
| LA POUNTY S.L. |
| LA TIENDA DE LOLÍN FRANQUICIAS, S.L. |
| LAPEGAL ARTE LEÓN S.L. BULKA |
| LOURIDO Y REAL S.L. |
| LUXENTER SHOPS |
| MACSONSA |
| MARFA TESSILE, S.L. |
| MEIGALLO |
| MIROGLIO ESPAÑA, S.A.U. |
| NECK CHILD S.A |
| OPI PRENDAS INFANTILES ORCHESTRA S.L. |
| PASARELA CLM S.L. |
| PATRIC SPORT, S.L. |
| PATRICKS S.A |
| PIEL DE TORO |
| PILI CARRERA, S.A. |
| PLATAX ORFEBRES, S.L. |
| POETE S.L. |
| RECSTORE |
| SELCONET, S.A. |
| STAR TEXTIL, SA |
| SUPERDRY |
| SUX TRIT, S.L. |
| TEXTIL TEXTURA, S.L. |
| THIS WEEK |
| VARLION ESPAÑA S.L. |
| WOLFORD ESPAÑA, S.L. |
Technique described in Motameni and Shahrokh (1998) and in Ratnatunga and Ewing (2008).
The analyzed consulting firms do not indicate that their procedures contain any statistical technique. However, given the opacity of their procedures this fact cannot be ensured.
It is basically a statistical technique that allows us to measure the relative value of each feature of a product, with which we can determine the combination of these features to maximize the probability of their being chosen by the consumer. Its application to marketing was conceived in 1974 by Paul Green, professor in The Warton School.
Others returns measures like ROE (return on equity) are not included because companies in this database are unlisted, so they don’t have the market data of equity.
In many marketing analyses explanatory variables are usually qualitative, in the sense that each variable takes on a small number of values and the Fisher's LDF method can introduce distortions. However, in our analysis the explanatory variables are quantitative and tend to fulfill a normal distribution and equal covariance matrices according to The Box's M test.
The probability of belonging to a group given a specific discriminating score P(di/gk)=((p(v)∗P(gk))/(∑i=1gP(di/gk)∗P(gk))); P(gk) is the prior probability of each group and P(di/gkc)is the probability that a score di belongs to a group gk.
Lambda is equal to the quotient between the sum of the square of each group (squared deviations of each data point concerning the mean of the groups or centroid) and the total square sum (squared deviations of each data point concerning the mean of the whole points). The result shows the percentage of the variance is not explained by group differences.
This criteria works in the following way, if the value of F is higher than 3.84 (the critical 0.05 significance), the variable will be included, if not, it will be deleted. However, finally, a minimum output value which must be at least 2.71 is required. The F statistic as a function of Wilks’ Lambda is measured by the following formula: (n−g−p)/(g−1)[(1−λp+1/λp)/(λp+1/λp)] where n is the number of elements of the sample, g is the number of groups and p is the number of exogenous variables. The result gathers the change in the value of λ after the incorporation of every variable in the model. Forward stepwise procedure can introduce those variables which fulfill the requirements of the F statistic and also have the lowest value of the Wilks’ Lambda statistic. However, if finally it is a minimum level of tolerance, which is defined as 1−r2, r2 being the determination coefficient of the multiple linear regression, in which the dependent variable is the one that has entered in the final stage and the explanatory ones are those that have entered in previous steps. In this paper the level of tolerance by default using SPSS is 0.001.
Ho implies the model does not distinguish the group means.
Smith and Parr (2005) assume that the weighted average return on the different assets within the company (denominated WARA) equals the WACC. The required return on intangible assets can be deduced from this equation if we know the rest of the terms. This method has been widely accepted in the process of purchase price allocation in business combination.