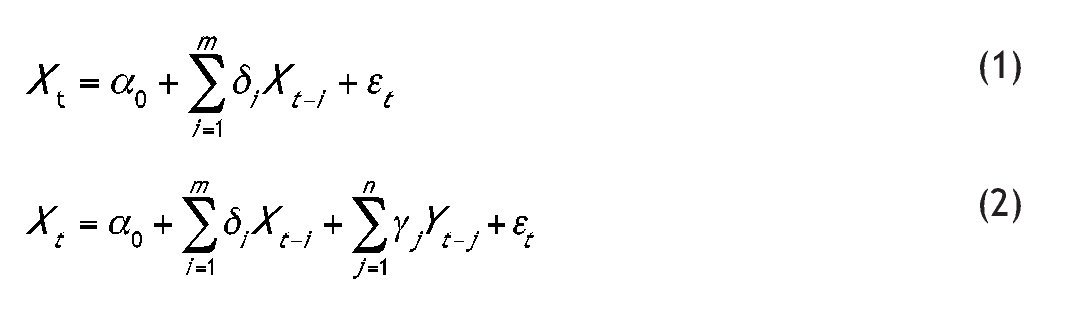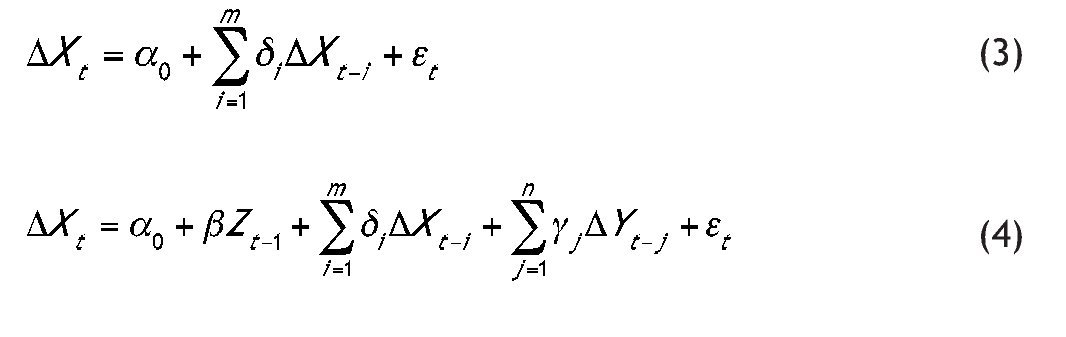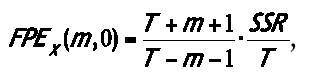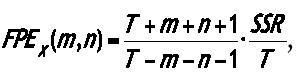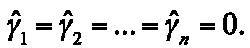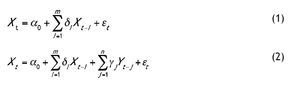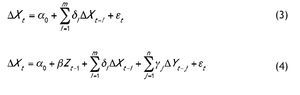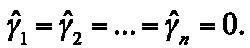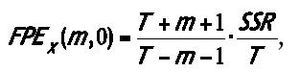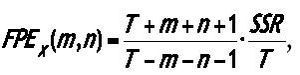This paper tests for causality between the US dollar-euro exchange rate and US-EMU bond yield differentials. To that end, we apply Hsiao's (1981) sequential procedure to daily data covering the 1999¿2011 period. Our results suggest the existence of statistically significant Granger causality running one-way from bond yield differentials to the exchange rate, but not the other way round. The results do not change when using short-term interest rate differentials or when we examine the Japanese yen-euro exchange rate. Nevertheless, we detect bi-directional Granger causality between the pound sterling-euro exchange rate and the short-term interest rate differential between UK and EMU.
Este trabajo realiza un contraste de causalidad entre el tipo de cambio dólar estadounidense-euro y el diferencial de rendimiento de los bonos entre Estados Unidos y la Zona Euro. Para ello, se aplica el procedimiento secuencial de Hsiao (1981) a datos diarios para el período 1999-2011. Nuestros resultados sugieren la existencia de causalidad en el sentido de Granger estadísticamente significativa desde el diferencial de rendimiento de los bonos hacia el tipo de cambio, pero no a la inversa. Los resultados no cambian cuando se usan diferenciales de tipos de interés a corto plazo o cuando se analiza el tipo de cambio yen japonés¿euro, sin embargo, detectamos causalidad bidireccional de Granger entre el tipo de cambio libra esterlina-euro y el diferencial del tipo de interés a corto plazo entre el Reino Unido y la Zona Euro.
1. Introduction
Since the beginning of the European Economic and Monetary Union (EMU), the US dollar¿euro exchange rate has fluctuated considerably. The ups and downs of the exchange rate have coincided with varying interest rate differentials between the USA and EMU.
Interest rates have long been considered key determinants of exchange rate movements despite the empirical failure of the uncovered interest rate parity (UIP) (see Engel, 1996, or Chinn, 2005, for a survey). Bekaert et al. (2007) conclude that evidence against UIP is mixed and currency, not horizon, dependent. The academic literature lists time-varying risk premia and forecasting errors concerning rational expectations and heterogeneous expectations as causes of the low empirical support for the UIP.
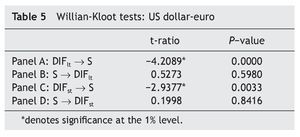
In the majority of cases, tests of UIP have been based on short-term interest rates. Nevertheless, in recent years, there is growing evidence supporting a relatively robust fundamental relationship between long-term interest rates and exchange rates (see, for example, Flood & Taylor, 1996; Alexius, 2001; Chinn & Meredith, 2004).
The diverging results could be related to the fact that movements in short¿term interest rates are largely a reflection of the impact of monetary policy measures, whereas changes in long-term interest rates also reflect long-run growth and inflation expectations.
Given the limited number of studies and diverging results, a consensus view on the effects of using long-term interest rates rather than short-term interest rates in tests of UIP has yet to be reached.
The aim of this paper is to provide some additional evidence on the relationship between long-term interest rates and exchange rates. To that end, we apply time series techniques to determine the appropriate Granger causality relations between nominal long-term interest rates and the nominal exchange rate using US and EMU data. Applying Hsiao's (1981) sequential procedure, we find that the long-term interest rate differential between USA and EMU Granger causes the US dollar-euro exchange rate, but not the other way round.
This paper is laid out as follows: Section 2 explains our econometric methodology. Section 3 considers the data used in this study, and presents and interprets our empirical results. Section 4 explores the robustness of our results for different countries and short-term interest rates. This paper ends with Section 5 that summarizes our findings.
2. Econometric methodology
Granger's (1969) causality test is widely used to test for the relationship between two variables. However, the causality tests are sensitive to lag length and, therefore, it is important to select the appropriate lengths. Otherwise, the estimated model will be inconsistent and, therefore, it is likely that we draw misleading inferences (see, for example, Thornton & Batten, 1985).
Although there are alternative methods in the empirical literature (such as that proposed by Toda & Yamamoto, 1995), Hsiao's (1981) sequential procedure ensures efficiency in testing Granger-causality a bi-variable setting, since it delivers a congruent and encompassing representation of the data generating process (Hendry & Mizon, 1999). Hsiao's (1981) procedure is a generalization of the Granger notion of causality, which combines the Akaike's (1969) final predictive error (FPE, from now on) and the definition of Granger causality. Basically, the FPE criterion trades off bias that arises from under-parameterisation of a model against a loss in efficiency that results from over¿parameterization of the model.
Consider the following models,
where Xt and Yt are stationary variables [i.e., they are I(0) variables]. The following steps are used to apply Hsiao's procedure for testing causality:
(i) Treat Xt as a one-dimensional autoregressive process (1), and compute its FPE with the order of lags m varying from 1 to m.1 Choose the order which yields the smallest FPE, say m, and denote the corresponding FPE as FPEX (m, 0).
(ii) Treat Xt as a controlled variable with m number of lags, and treat Yt as a manipulated variable as in (2). Compute again the FPE of (2) by changing the order of lags of Yt from 1 to n, and determine the order which gives the smallest FPE, say n, and denote the corresponding FPE as FPEX (m,n).2
(iii) Compare FPEX (m, 0) with FPEX (m,n) [i.e., compare the smallest FPE in step (i) with the smallest FPE in step (ii)]. If FPEX (m,0) > FPEX (m,n), then Yt is said to Granger-cause Xt. If FPEX (m,0) < FPEX (m,n), then Xt is an independent process.
(iv) Repeat steps (i) to (iii) for the Yt variable, treating Xt as the manipulated variable.
When Xt and Yt are not stationary variables, but they are first¿difference stationary [i.e., they are I(1) variables] and they are co-integrated (see, among others, Dolado et al., 1990), it is possible to investigate the causal relationships from ΔXt to ΔYt and from ΔYt to ΔXt, using the following error correction models:
where Zt is the OLS residual of the co-integrating regression Xt = μ + λYt. Note that, if Xt and Yt are I (1) variables, but they are not co-integrated, then β in (4) is assumed to be equal to zero.
In both cases [i.e., Xt and Yt are I(1) variables, and they are or they are not co-integrated], we can use Hsiao's sequential procedure substituting Xt with ΔXt and Yt withΔYt in steps (i) to (iv), as well as substituting expressions (1) and (2) with equations (3) and (4).
3. Data and empirical results
3.1. Data
We use daily data of US dollar-euro exchange rate taking from the European Central Bank's Statistical Data Warehouse. Regarding the US long-term interest rate, we use ten-year Treasury Constant Maturity Rate taking from the Board of Governors of the Federal Reserve System. As for the EMU long-term interest rates, we use as a proxy the JPM EMU Government Bond Index, taking from J. P. Morgan. Our database covers the period January 1999 to January 2011.
To avoid using index and row data, we construct indices for both the US dollar-euro exchange rate and the US long-term interest rates using the same base year as the JPM EMU Government Bond Index. Once these indices are constructed, we compute the long-turn interest rate differentials between the USA and EMU.
3.2. Preliminary results
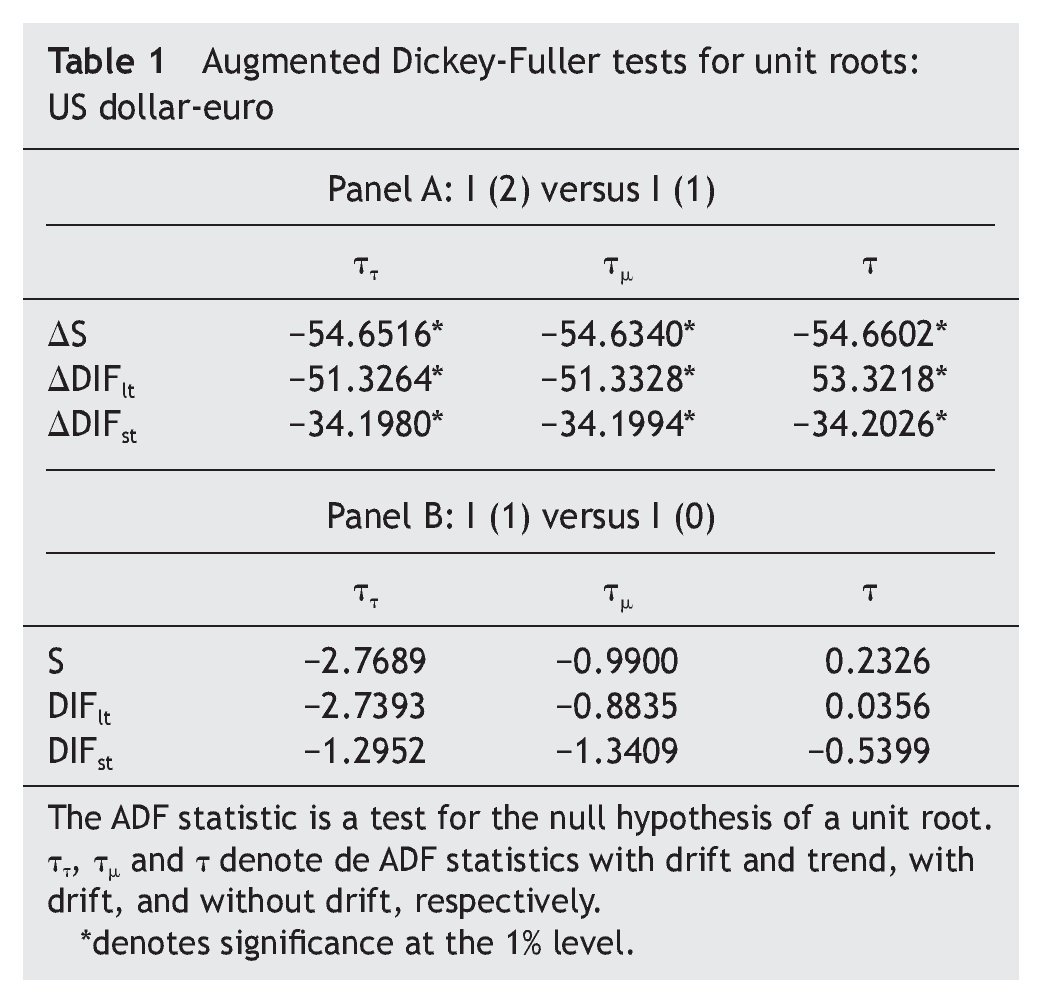
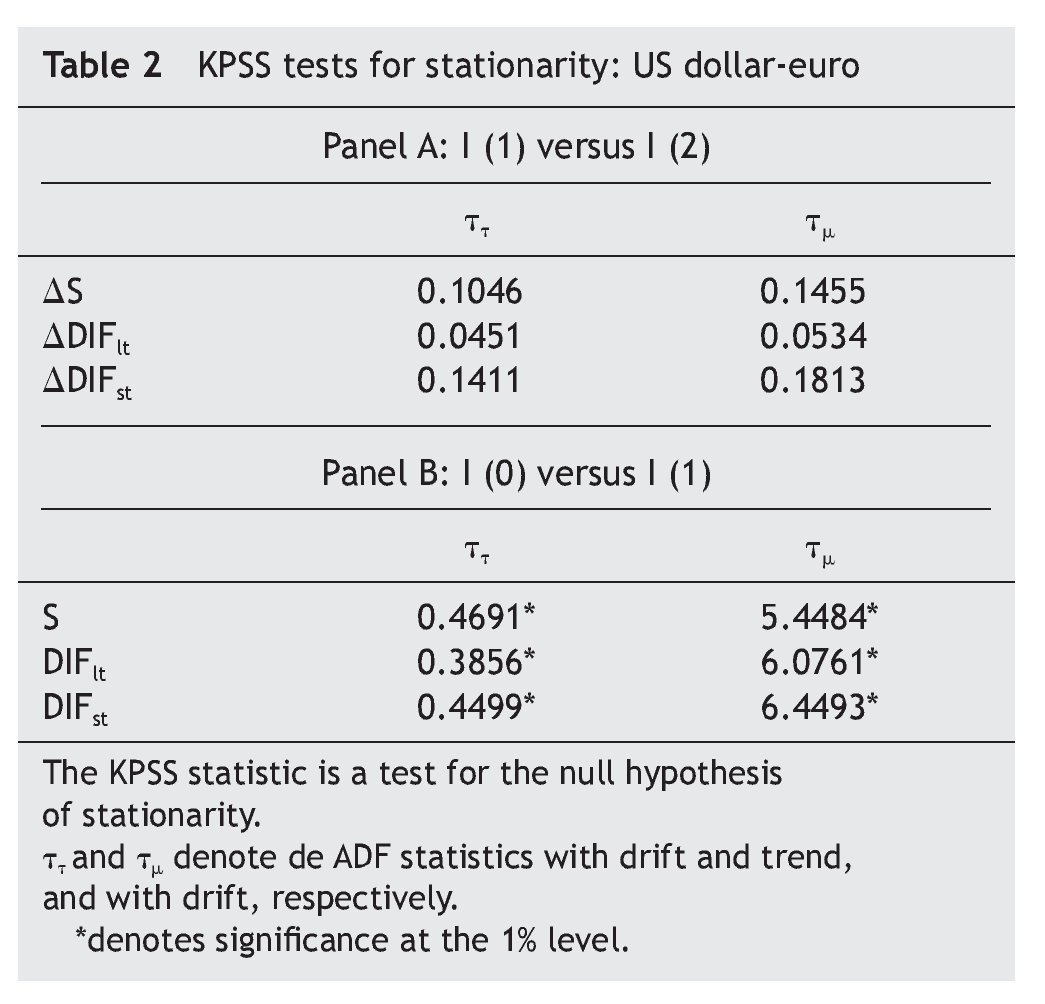
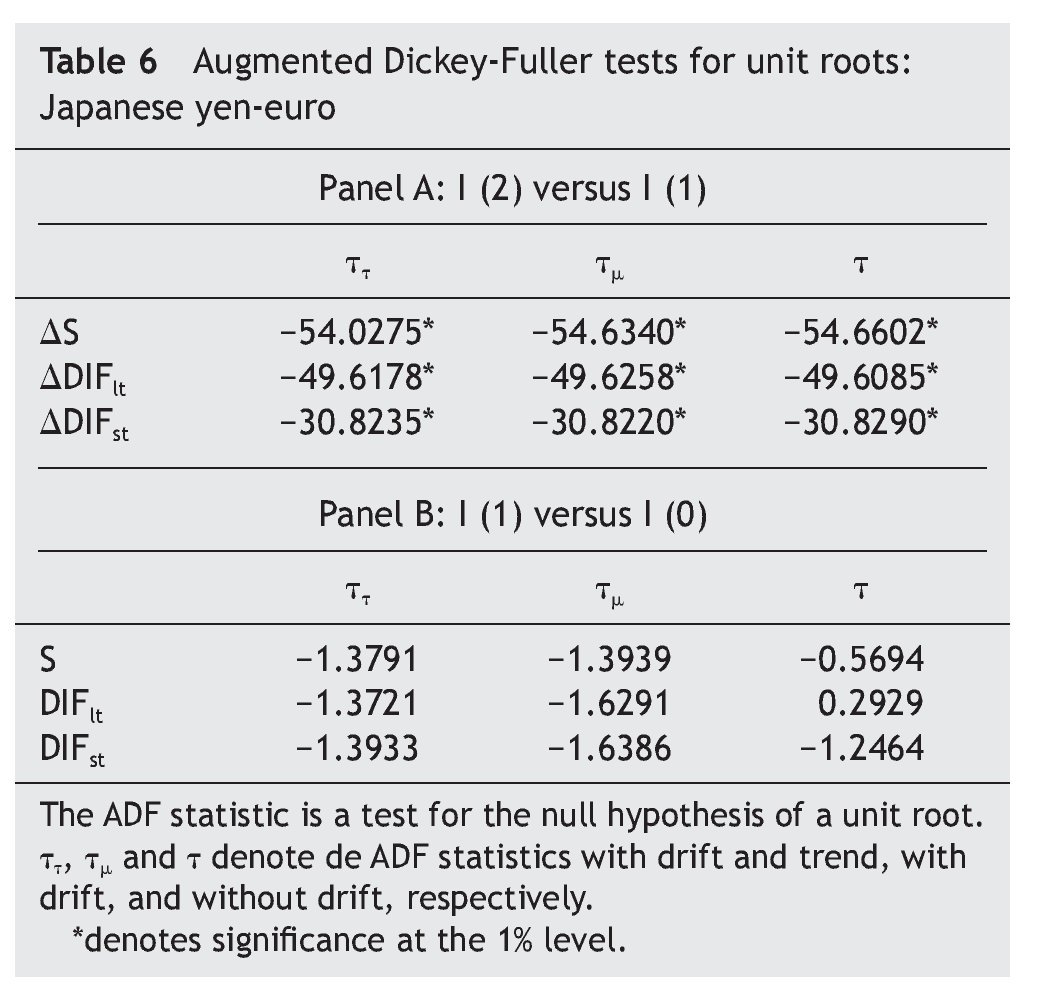
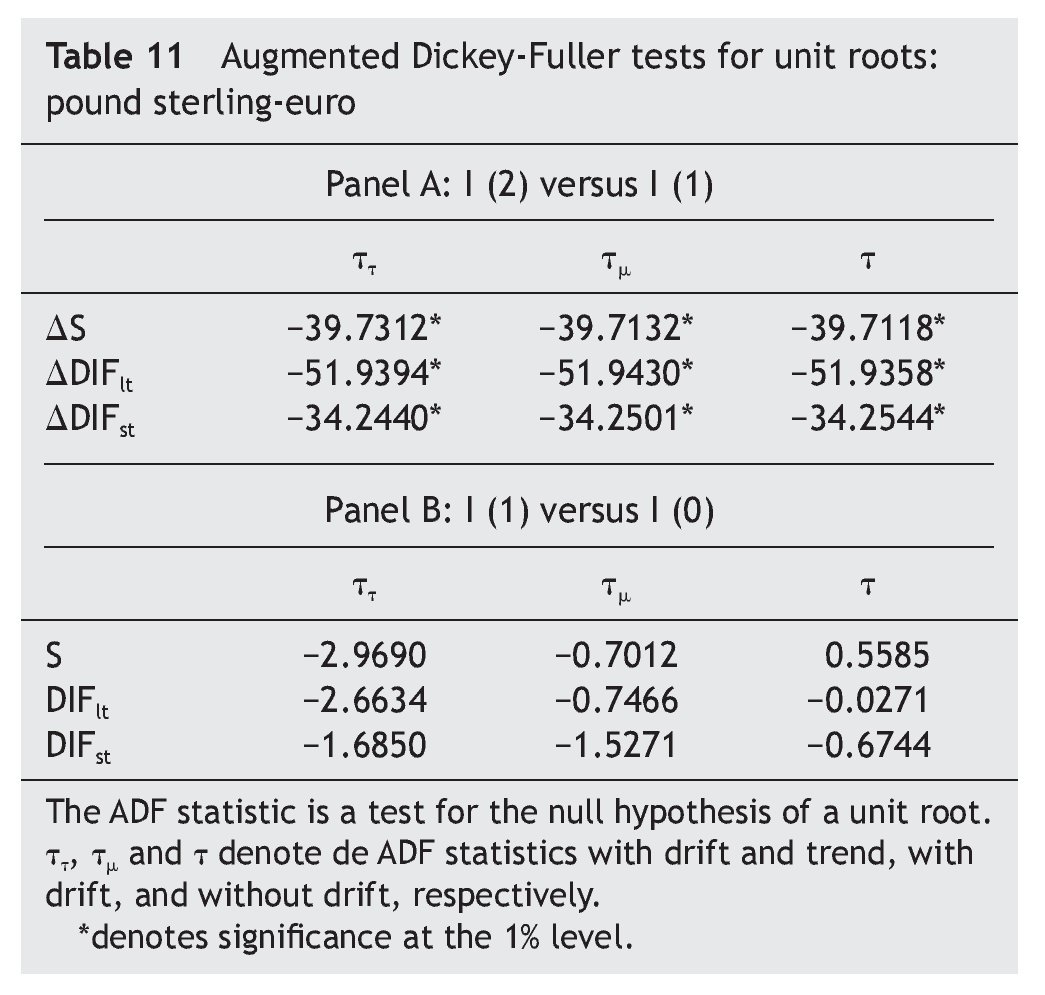
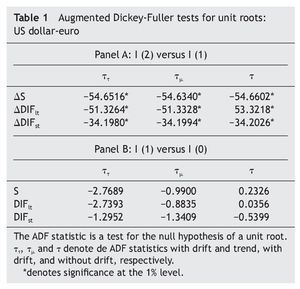
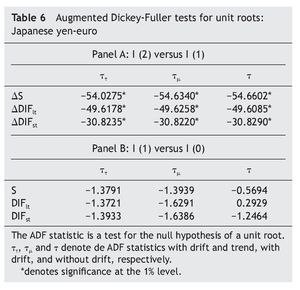
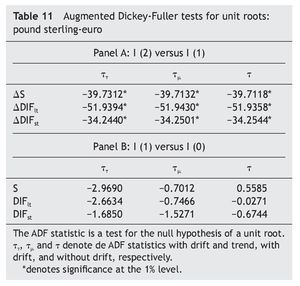
As a first step, we tested for the order of integration of the US dollar-euro exchange rate (that we denote S) and the USA-EMU long-term interest rate differential (that we denote DIFlt) by means of the Augmented Dickey-Fuller (ADF) tests. The results, shown in Table 1, decisively reject the null hypothesis of non-stationarity, suggesting that both variables could be treated as first¿difference stationary.
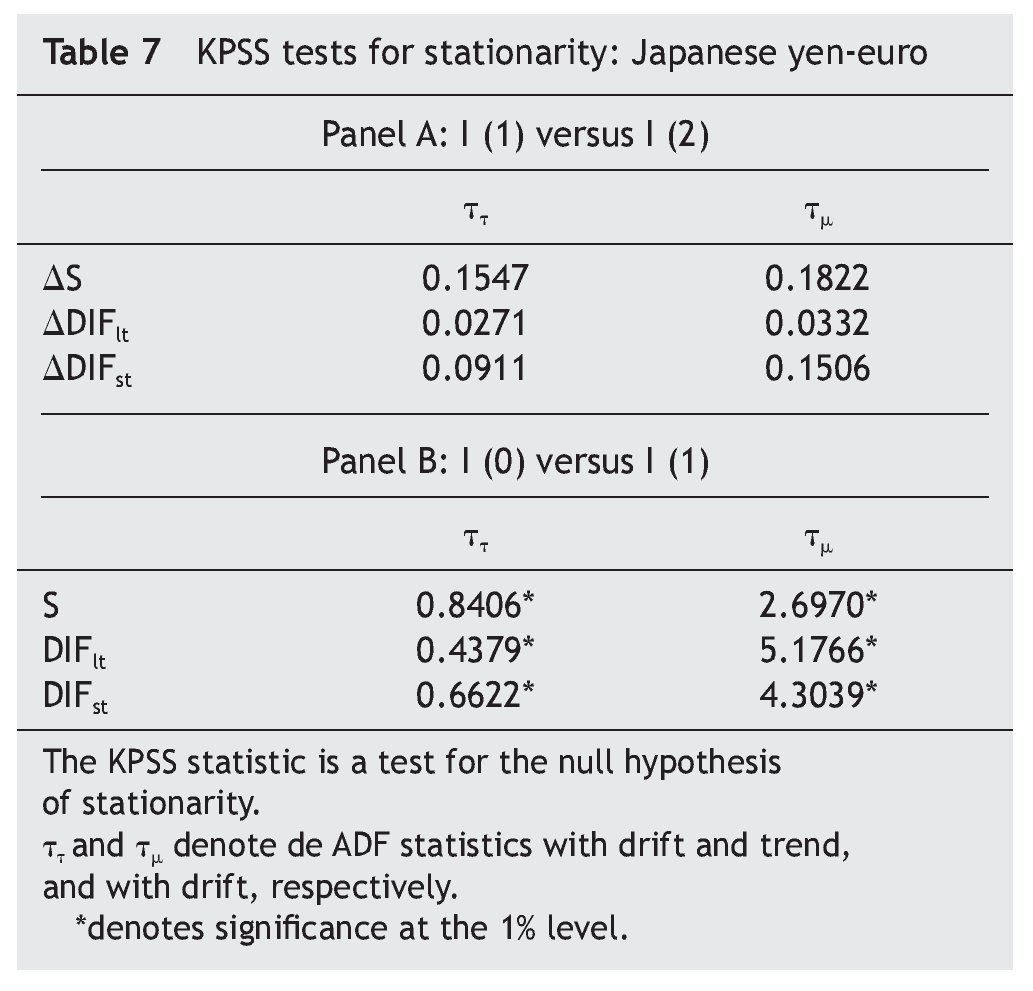
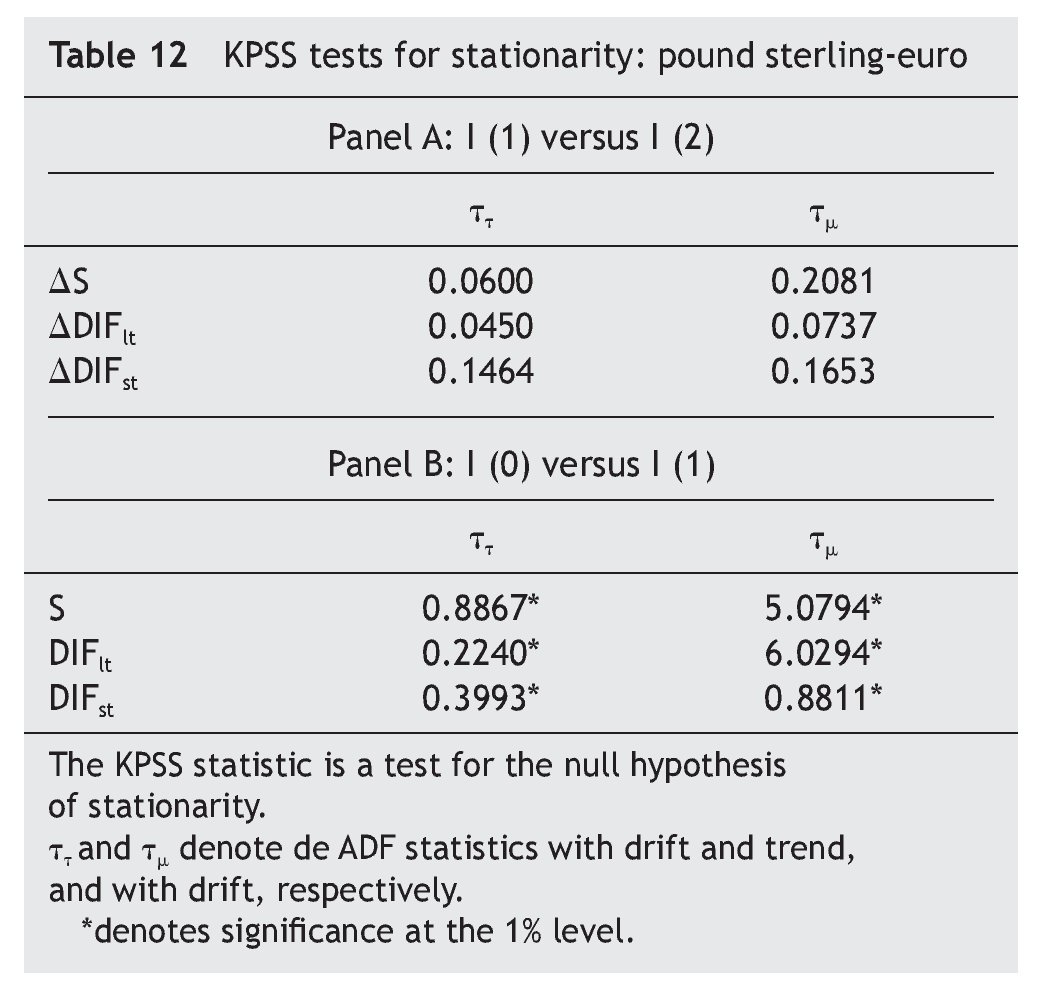
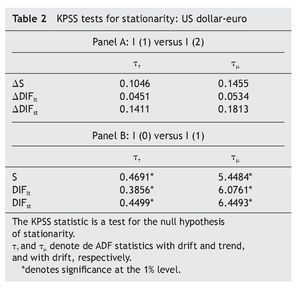
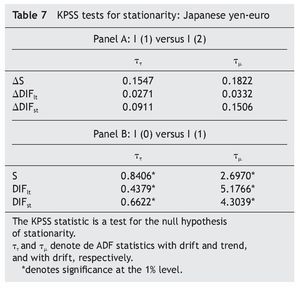
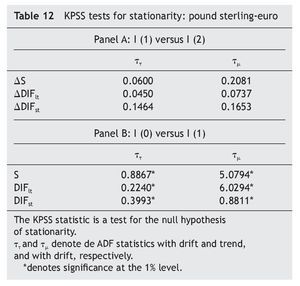
Following Carrión-i-Silvestre et al.´s suggestion (2001), we confirm this result using the Kwiatkowski et al. (1992) (KPSS) tests, where the null is a stationary process against the alternative of a unit root. As can be seen in Table 2, the results fail to reject the null hypothesis of stationarity in first¿difference but strongly reject it in levels.
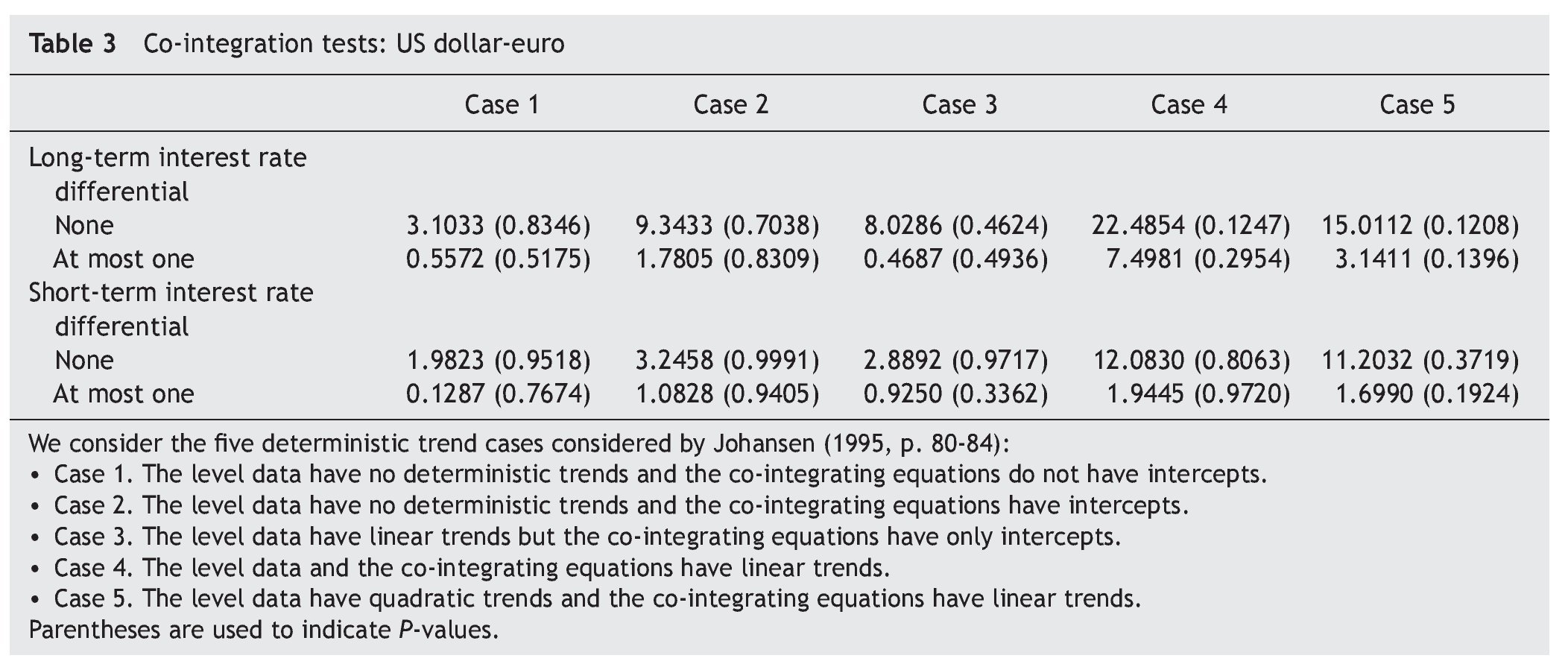
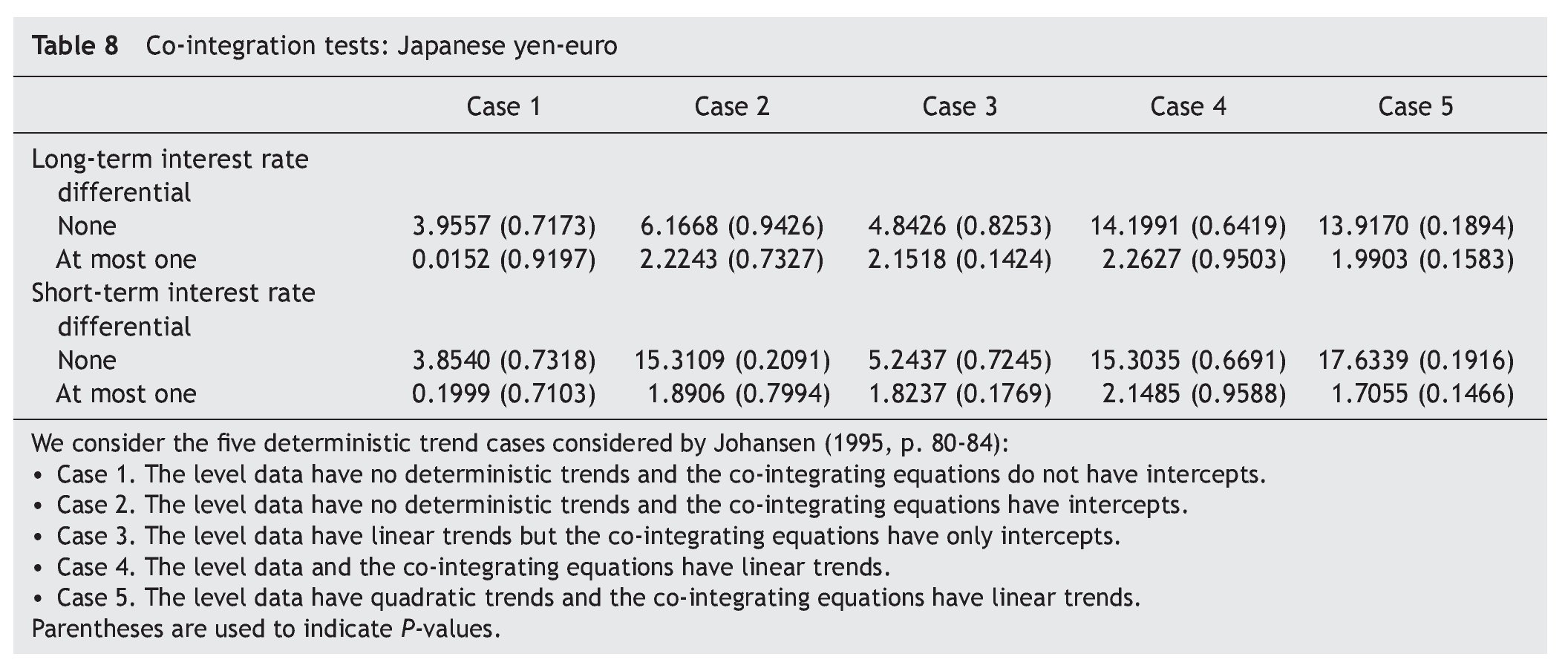
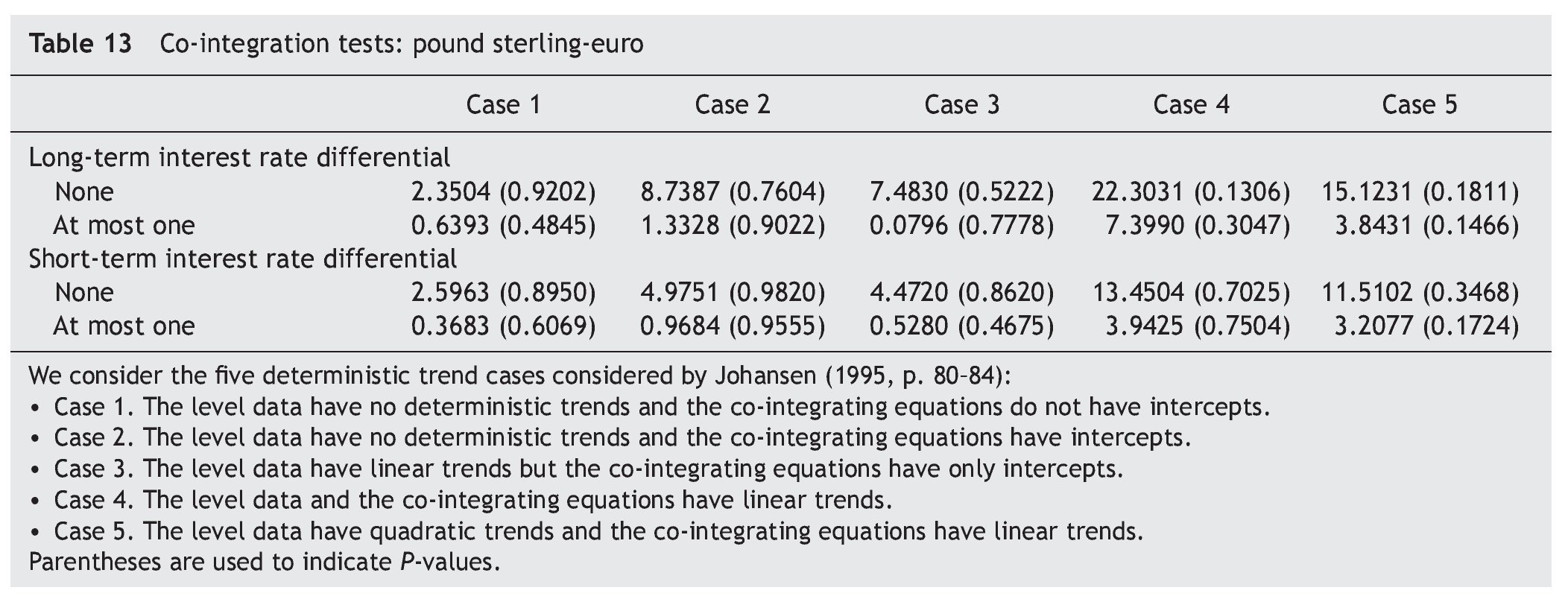
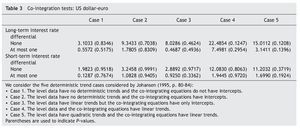
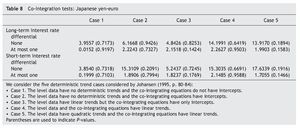
As a second step, we have tested for co-integration between exchange rate and the long-term interest rate differential. To that end, we use the Johansen's (1991, 1995) co-integration test. As shown in Table 3, the results of the trace test statistics indicate that the null hypothesis of no co¿integration is not rejected at the 1% significance level. Our results of no co-integration between exchange rate and long-term interest rate differentials agree with Campbell and Clarida (1987) and Meese and Rogoff (1988), who fail to find co¿integration between these variables. The absence of a co-integrating relation in our case could be related to the relative short sample used in this paper, imposed by the introduction of the euro on 1 January 1999. As Hakkio and Rush (1991) have shown, the power of co-integration tests depends on the data's span, rather than on its frequency. Even though we use 2975 daily observations, we only have long-run information for twelve years.
3.3. Causality results
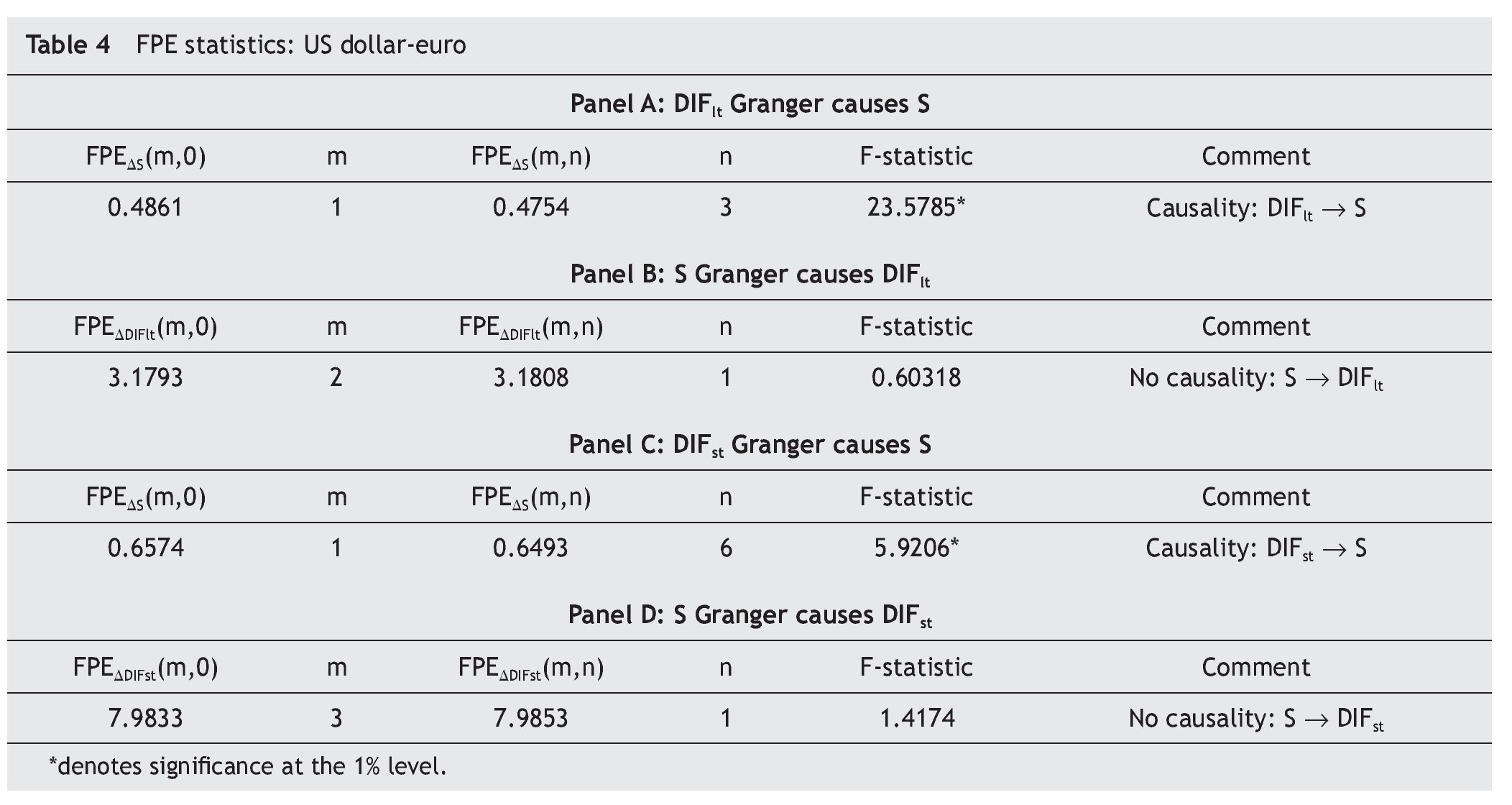
While the results from the co-integration tests deny a long-run relation between the exchange rate and the long-term interest rate differential, they do not rule out the possibility of a short-run relation. Therefore, we tested for causality in first differences of the variables, with no error-correction term added [i. e., equations (3) and (4), with β = 0]. Panels A and B in Table 4 show the optimum order of lags and the corresponding FPEs. The reported F¿statistics are the Wald statistics to test the joint hypothesis
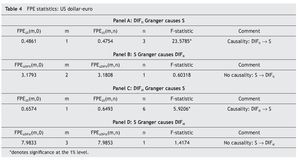
As can be seen, the optimum order lag m of ΔSt¿j (ΔDIFltt¿j) when ΔSt (ΔDIFltt) is regressed on its own past values and a constant only is one (two), while the optimum order lag n of ΔDIFltt¿j (ΔSt¿j) when ΔSt (ΔDIFltt) is regressed on its own past values (whose order of lags is fixed at m), the past values of ΔDIFltt¿j (ΔSt¿j) and a constant is three (one). On the other hand, FPEΔS(m,0)>FPEΔS(m,n) and FPEΔDIFlt(m, 0) ΔDIFlt(m, n), suggesting that Granger causality runs one-way from DIFlt to S and not the other way round. This conclusion is also reached using the F-statistics since it is significant at the 1 percent level when testing that all coefficients of the lagged ΔSt are zeros, but we cannot reject the null hypothesis that all coefficients of the laggedΔDIFltt are zeros at the usual levels.
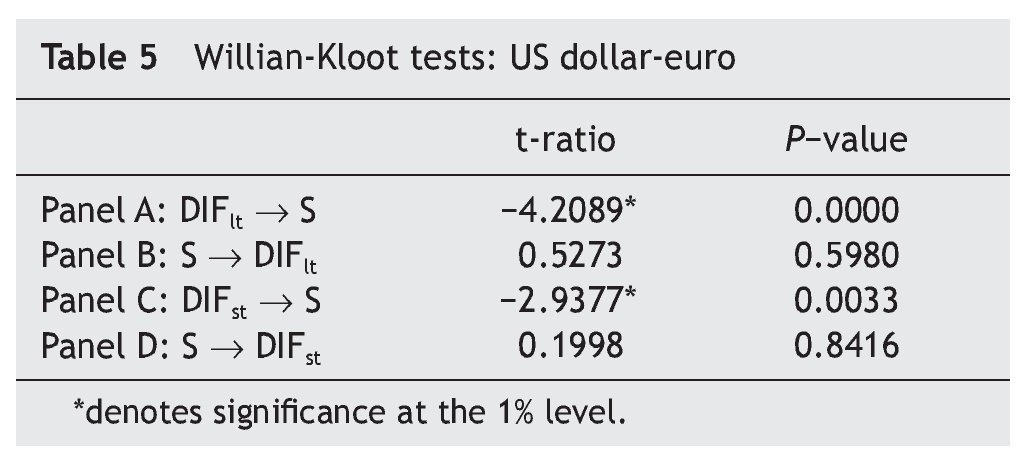
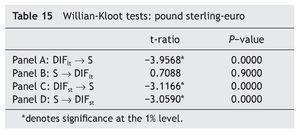
In order to further check our results, we have computed the Williams-Kloot test for forecasting accuracy described in Williams (1959). Let ƒ1 and ƒ2 denote alternative forecasts of the variable z, the Williams-Kloot test statistic is the t¿ratio for the hypothesis that the coefficient on ƒ1 - ƒ2 is zero in a regression of z -( ƒ1 + ƒ2)/2 on ƒ1 - ƒ2. A significantly negative value implies that ƒ2 is statistically superior to that of ƒ1 (and vice versa). Therefore, we generated forecasts for ΔS and ΔDIFlt both considering only past values of the forecasted variable and considering also, in addition, past values of the other variable. The results are shown in Panels A and B of Table 5. As can be seen, the Williams-Kloot test suggests that ΔSt can be better predicted by adding the information content of the ΔDIFltt, rather than by using past values of ΔSt¿j alone. On the other hand, forecasting accuracy for ΔDIFltt cannot be reached by considering also the information content of ΔSt¿j. Therefore, these results reinforce our earlier conclusion about from Table 4.
3.4. Rolling regressions
In order to assess the model's stability over time, we make use of rolling analysis to check for changes in Granger causality between the US dollar-euro exchange rate and the USA-EMU long-term interest rate differential over time. We report the results of estimates from a sequence of short rolling samples to track a possibly evolving relationship in the sense of time-varying. In particular, we carried out 2776 regressions using a window of 200 observations. In each estimation, we apply Hsiao's (1981) sequential procedure outlined in Section 2 to determine the optimum FPEΔS(m, 0), FPEΔS(m, n), FPEΔDIFlt(m, 0) and FPEΔDIFlt(m, n) statistics.
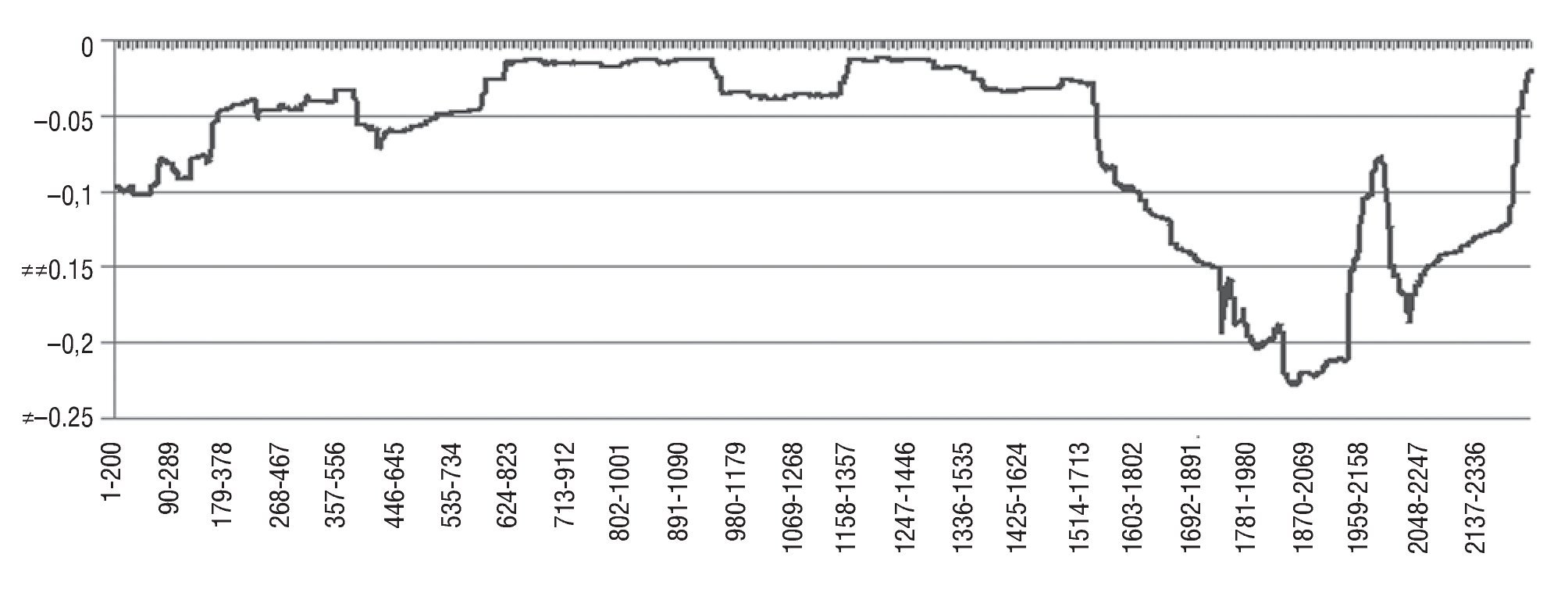
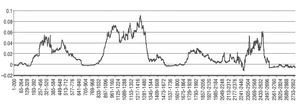
A graphical presentation of the evolution of the difference between FPEΔS(m, 0) and FPEΔS(m, n) statistics is shown in Figure 1. This figure provides us with a view of the time¿varying influence of DIFlt over S. As can be seen, most of the time the difference is positive, suggesting statistically significant Granger causality running from long¿term interest rate differential between US and EMU towards the exchange rate. Nevertheless, there are some episodes where a negative difference is found, indicating that both variables are independent processes: September 2001 - April 2001, January 2005 -September 2005 and March 2009 - January 2011. The first episode is associated with the increased risk aversion that followed the tragic events of 11 September and led to an appreciation of the euro against the US dollar, intensified as a result of existing market concerns about the proper enforcement of accounting standards by companies in that country, the widening of negative interest rate in the euro area, market concerns about the imbalance in the current account of the emergence of a budget deficit and uncertainty about future economic growth prospects. As for the second episode (January 2005 - September 2005), it could be related to the market perceptions of an improvement in US economic activity and a slower growth in the euro area, together with the rejection of the Treaty establishing a Constitution for Europe in referendums in France and the Netherlands in 2005. Finally, the last episode starting in March 2009 coincides with an appreciation of the euro in a climate of improving the situation of financial markets, a trend that was interrupted from December 2009 following the fiscal crisis in Greece, which led to episodes of instability, particularly severe in the second half of April and early May 2010, resulting in the euro exchange rate to depreciate against the US dollar.
Figure 1 Rolling regression results when testing causality from DIFlt to S: US dollar-euro. Difference between FPEΔS(m, 0) and FPEΔS(m, n) statistics for each rolling regression using a window of 200 observations.
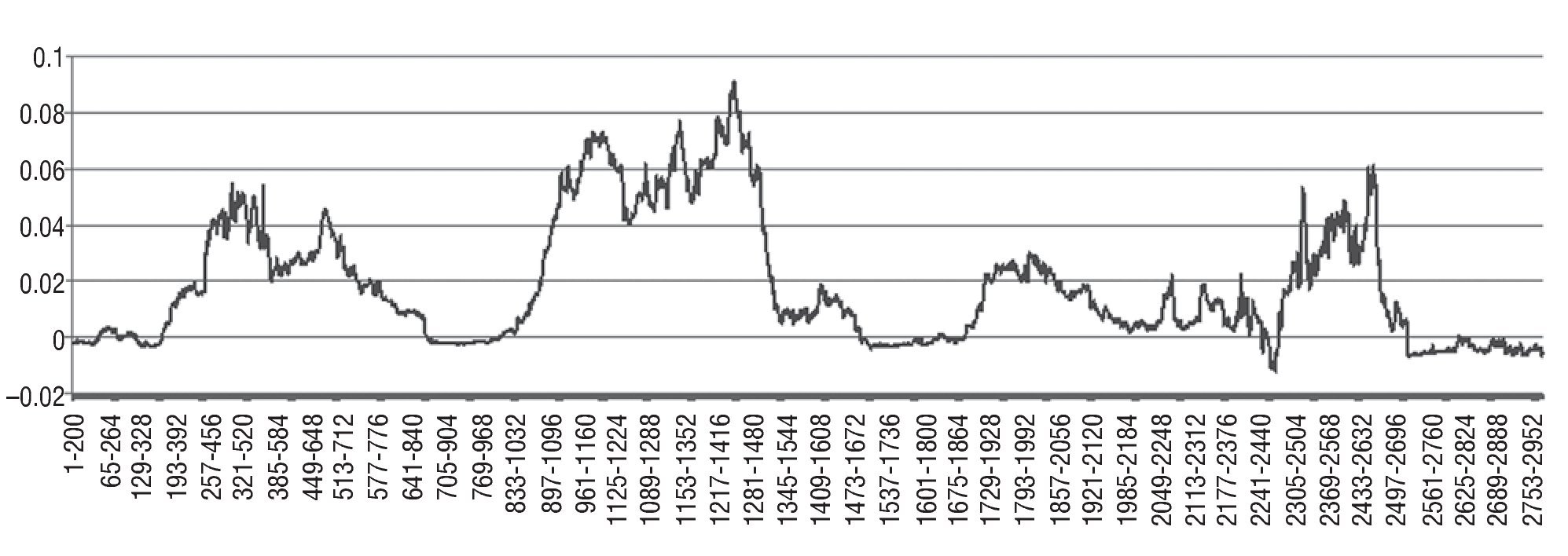
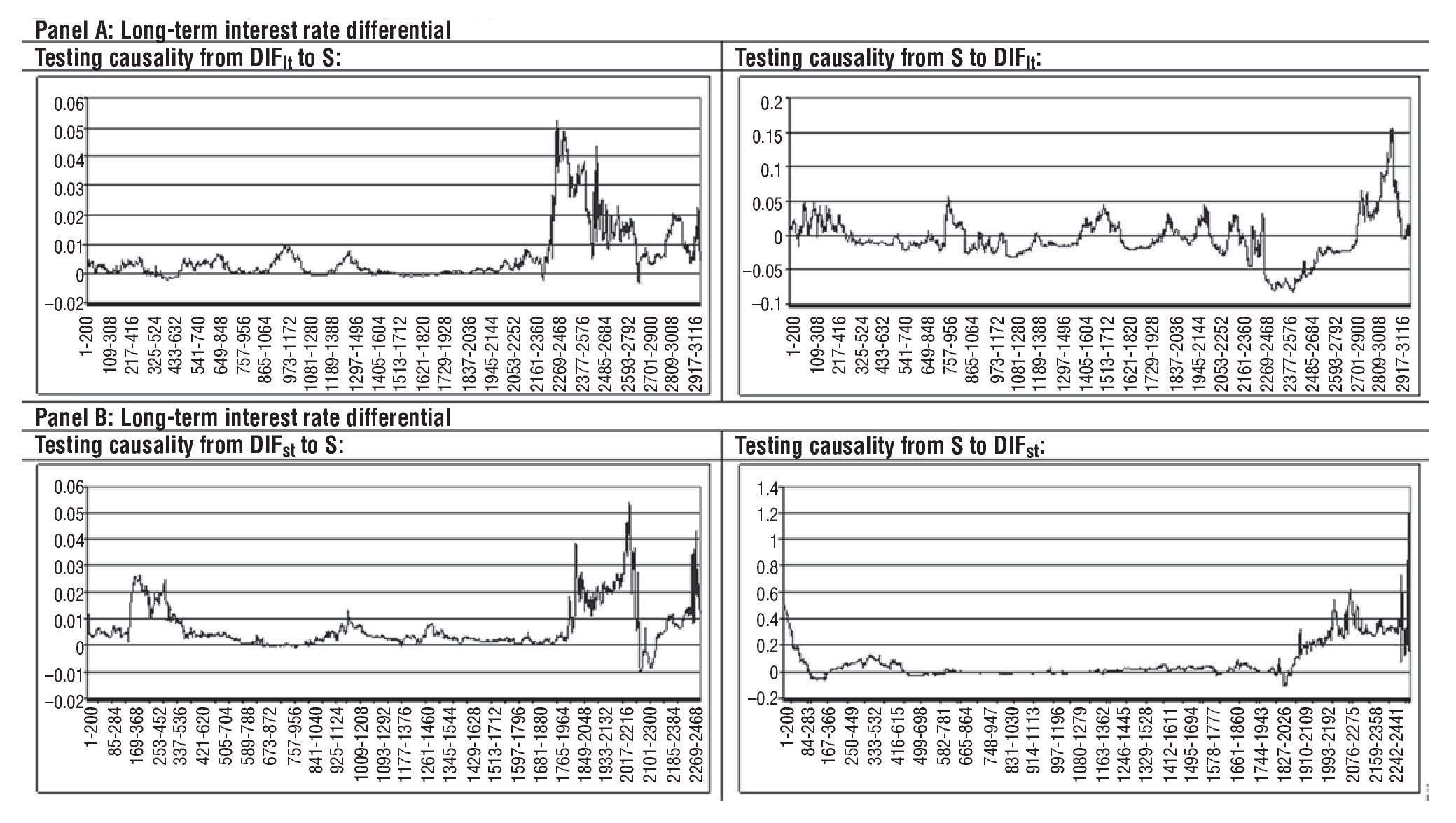
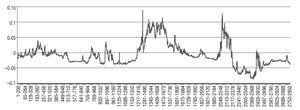
Regarding the results from the rolling regressions used to test Granger causality running from the US dollar-euro exchange rate towards the USA-EMU long-term interest rate differential, Figure 2 indicates that difference between FPEΔDIFlt(m, 0) and FPEΔDIFlt(m, n) statistics is negative most of the time. This pattern suggests that DIFlt can be predicted more accurately by using the only its own past than by using past values of DIFlt and S (i. e., S does not Granger cause DIFlt). Interestingly, there are several episodes where we do find evidence of causality: October 1999 - January 2000, December 2003 - December 2005, and May 2007 - October 2010. The first episode coincides with increasing concerns in financial markets that the US economy was growing at a rate that might lead to inflationary pressures in the economy, while in EMU, after the European Central Bank's decision to raise interest rates on 4 November, market participants revised their long¿run inflation expectations downwards and lowered the magnitude of the inflation risk premium required for holding euro-denominated bonds. As for the second episode (December 2003 - December 2005), it can be associated with the changing perceptions of market participants with regard to inflationary pressures after of the sharp rise in oil prices and the outlook for the euro area economy, perceptions which were in turn closely related to changes in global macroeconomic prospects throughout this period. This led to some decoupling of long-term bond yield movements reflecting diverging views among market participants about the macroeconomic prospects and short-term interest rate expectations in the two economies. Finally, the last episode (May 2007 - October 2010), the financial turmoil and the re¿pricing of risk registered in the second half of 2007 created favourable investment opportunities outside EMU, being stimulated by the strengthening of the euro exchange rate.
Figure 2 Rolling regression results when testing causality from S to DIFlt: US dollar-euro. Difference between FPEΔDIFlt(m, 0) and FPEΔDIFlt(m, n) statistics for each rolling regression using a window of 200 observations.
4. Robustness3
4.1. Short¿run interest rates
Since the aim of the paper is to provide additional evidence on the relationship between long-term interest rates and exchange rate, in this sub-section we compare our results with those obtained with short-term interest rate models.
We use three-month Treasury Bill Rates in the secondary market taking from the Board of Governors of the Federal Reserve System. As for the EMU short-run interest rate, we use three-month interbank lending rates taking from the Bank of Spain.
As in the previous section, the series cover the period January 1999 to January 2011, and we construct indices for both the US dollar-euro exchange rate and the US and EMU short-term interest rates. Once these indices are constructed, we compute the short-term interest rate differentials between the USA and EMU (DIFst).
As can be seen in Table 1 and Table 2, results from both the ADF tests and the KPSS tests suggest that the series are I(1). Regarding co-integration between exchange rate and the short-term interest rate differential, results in Table 3 indicates the absence of a long-run co-integrating relation between them, implying that we have to test for causality in first differences of the variables, with no error¿correction term added [i. e., equations (3) and (4), with β = 0].
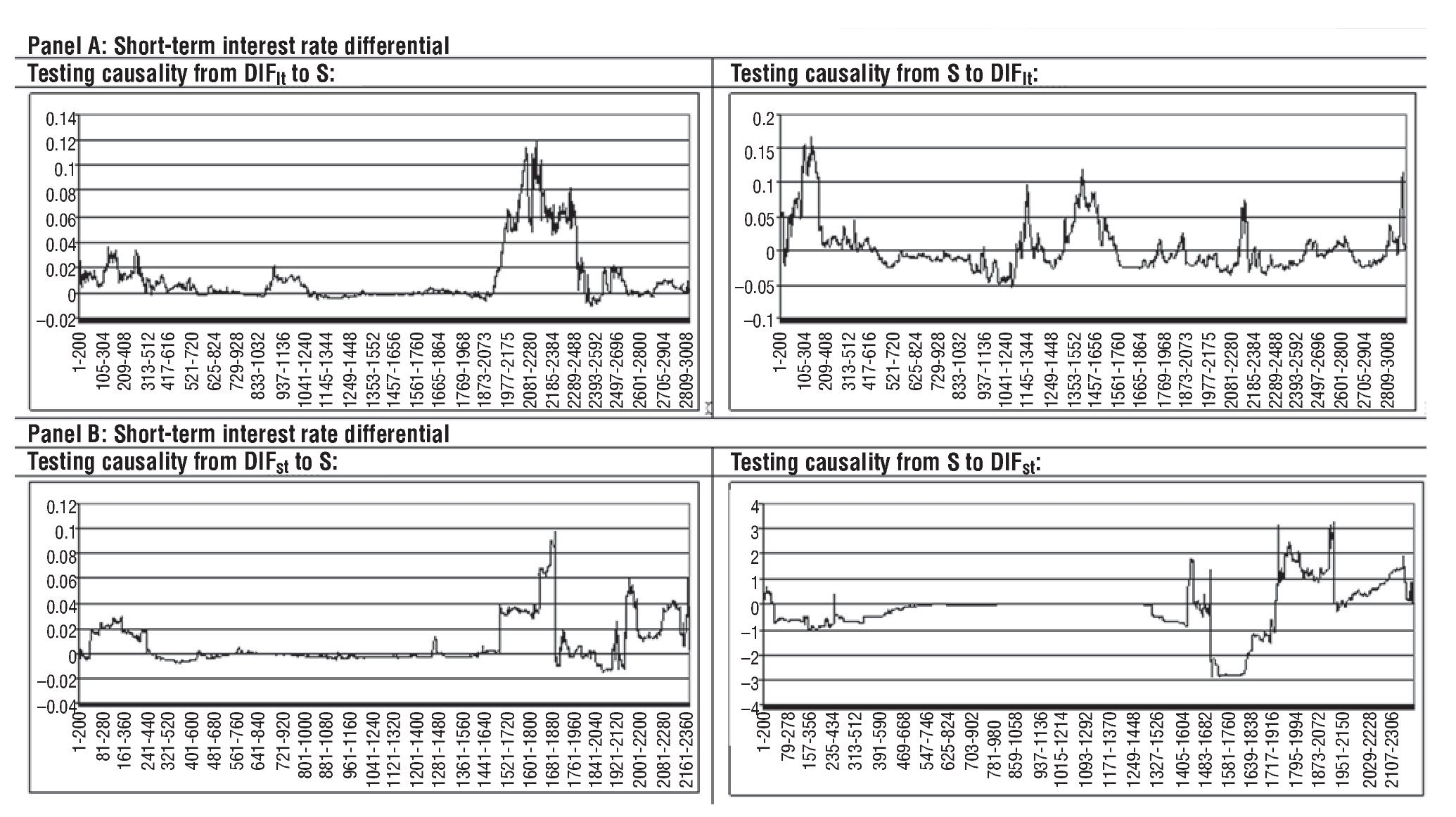
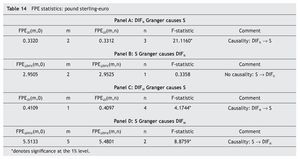
Panels C and D in Table 4 report the FPE statistics. As can be seen, the optimum order lag m of ΔSt¿j (ΔDIFstt¿j) when ΔSt (ΔDIFstt) is regressed on its own past values and a constant only is one (three) , while the optimum order lag n of ΔDIFstt¿j (ΔSt¿j) when ΔSt (ΔDIFstt) is regressed on its own past values (whose order of lags is fixed at m), the past values of ΔDIFstt¿j (ΔSt¿j) and a constant is six (one). Furthermore, FPEΔS(m, 0)>FPEΔS(m, n) and FPEΔDIFst(m, 0) ΔDIFst(m, n), suggesting, once again, that Granger causality runs one-way from DIFst to S and not the other way round. This conclusion is reinforced both when using the F¿statistics for testing the joint significance of all coefficients of the lagged ΔSt and that of all coefficients of the lagged ΔDIFstt (Panels C and D in Table 4) and when using the Williams-Kloot test (Panels C and D in Table 5).
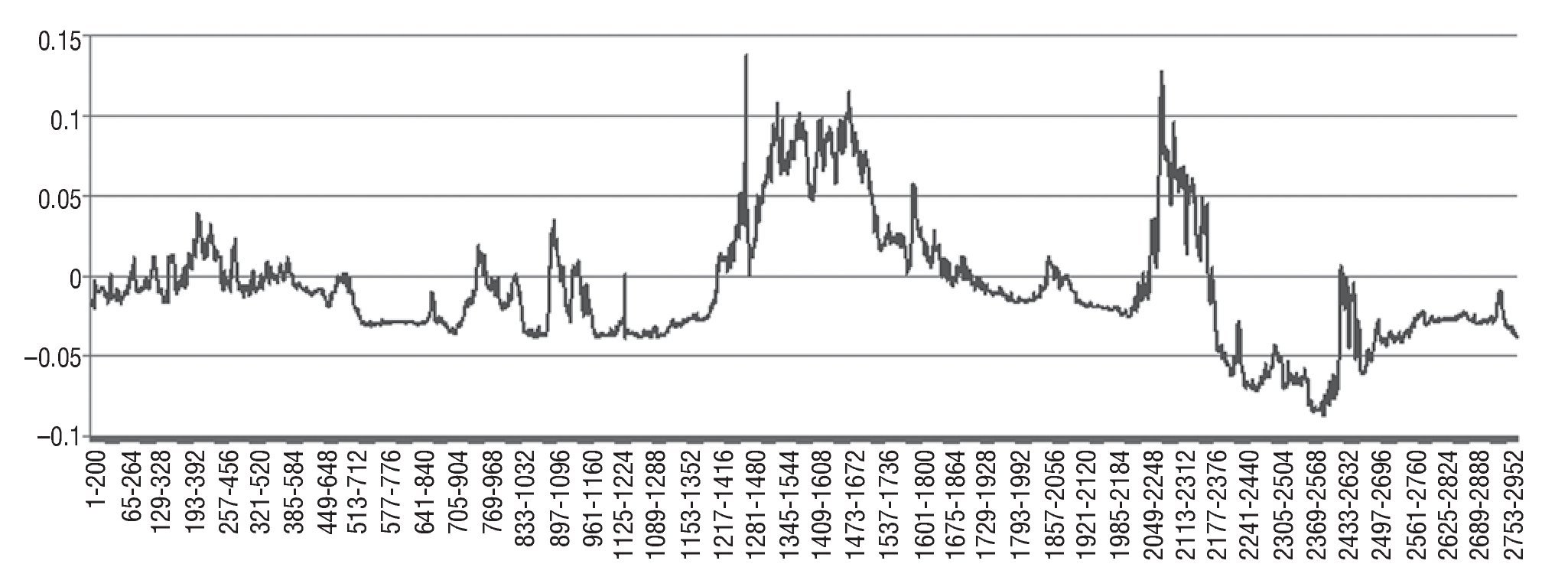
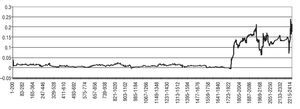
Figure 3 shows the results from the rolling regressions used to test Granger causality running from the USA-EMU short-term interest rate differential towards the US dollar-euro exchange rate, while Figure 4 presents the results for assessing the dynamic Granger-causality from the US dollar-euro exchange rate to the USA-EMU short-term interest rate differential. As can be seen in Figure 4, the difference between FPEΔDIFst(m, 0) and FPEΔDIFst(m, n) statistics is always negative, indicating, once again, that S does not Granger-cause DIFst. In contrast, the difference between FPEΔS(m, 0) and FPEΔS(m, n) statistics in Figure 3 is positive most of the time, giving further support for our previous finding of DIFst Granger¿causing S. The only two exceptions correspond with the subperiod immediately after the decision of increasing the key ECB interest rates by another 25 basis points taken by the Governing Council on 3 August 2006 and with the fluctuations registered in the US dollar¿euro exchange rate from May to mid August 2007, when market participants revised their assessment of the relative cyclical strength of the two economies.
Figure 3 Rolling regression results when testing causality from DIFst to S: US dollar-euro. Difference between FPEΔS(m, 0) and FPEΔS(m, n) statistics for each rolling regression using a window of 200 observations.
Figure 4 Rolling regression results when testing causality from S to DIFst: US dollar-euro. Difference between FPEΔDIFlt(m, 0) and FPEΔDIFlt(m, n) statistics for each rolling regression using a window of 200 observations.
4.2. Other exchange rates
In order to further assess robustness of our findings, we analyse here other country pairs. Given that the latest triennial survey by the Bank for International Settlements (2010) indicates that the four currencies most traded in foreign exchange markets in 2010 were, in this order, the US dollar (85% of total), euro (39%), Japanese yen (19%) and pound sterling (13%),4 we also examine the cases of the Japanese yen-euro and pound sterling-euro exchange rates, using both long-term and short-term interest rates.
The exchange rates are taken from the European Central Bank's Statistical Data Warehouse and the interest rates from the Japanese Ministry of Finance and the Bank of England. As before, we use three-month interbank lending rates as relevant short-term interest rates and yield from ten-year Government bonds as a proxy for long-term interest rates and construct indices that cover the period January 1999 to January 2011.
Regarding the Japan-EMU case, results in Table 6 and Table 7 suggest that the series are I(1). The results from the co-integration tests indicate that there is no evidence that variations in the Japanese yen-euro exchange rate over time are explained either by the long-term or the short-run interest rate differential between Japan and EMU (Table 8), leading us one more time to test for causality in first differences of the variables, with no error-correction term added [i. e., equations (3) and (4), with β = 0].
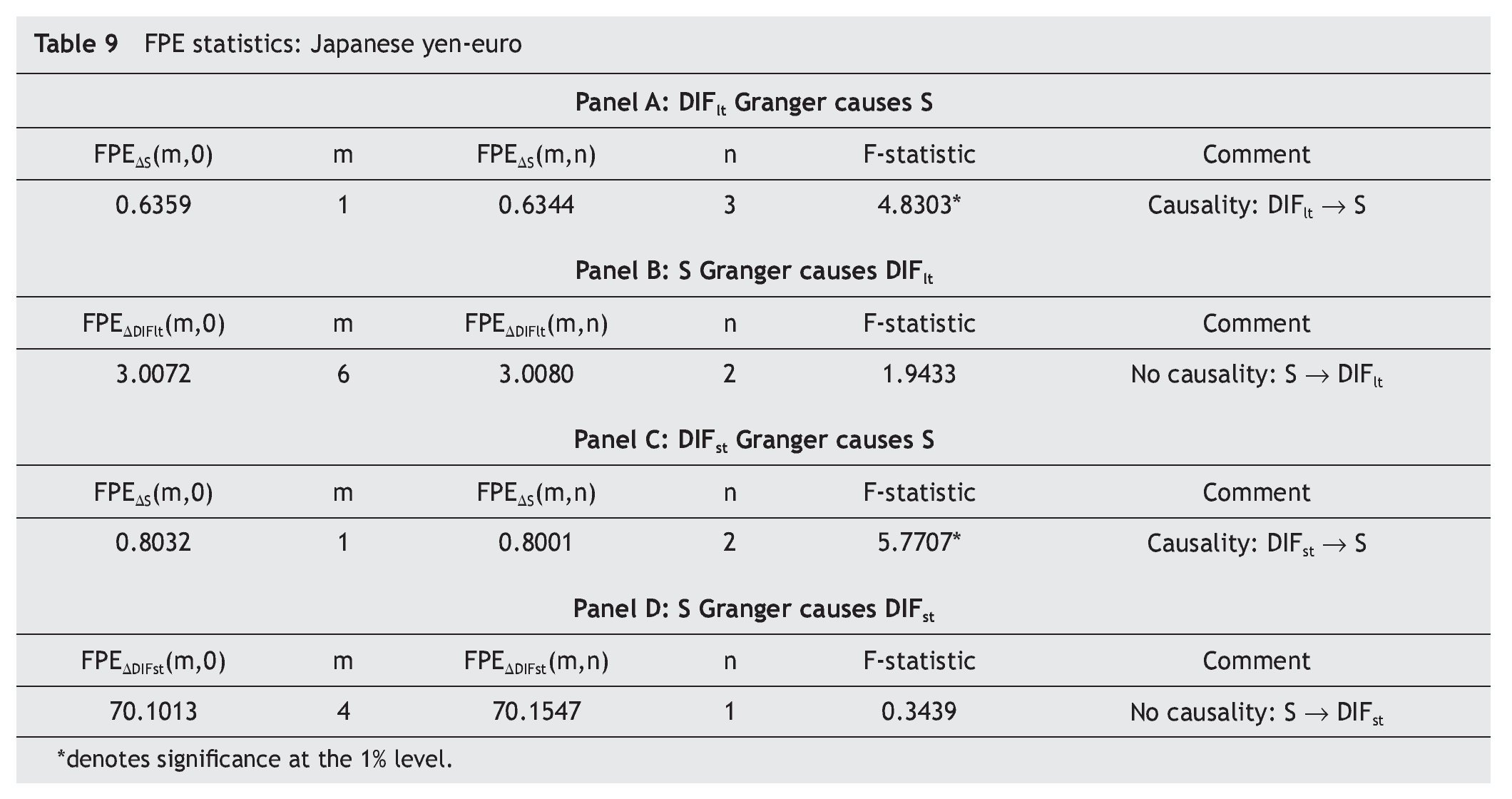
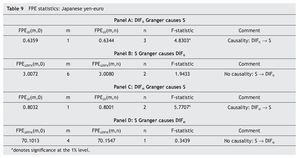
Table 9 presents the FPE statistics. As can be seen, once again we find unidirectional Granger causality running from the interest rate differential between Japan and EMU to the Japanese yen-euro exchange rate for both the long-term and the short-term interest rate differentials. This conclusion is further supported by both the F-statistics in Table 9 and the Williams-Kloot test in Table 10.
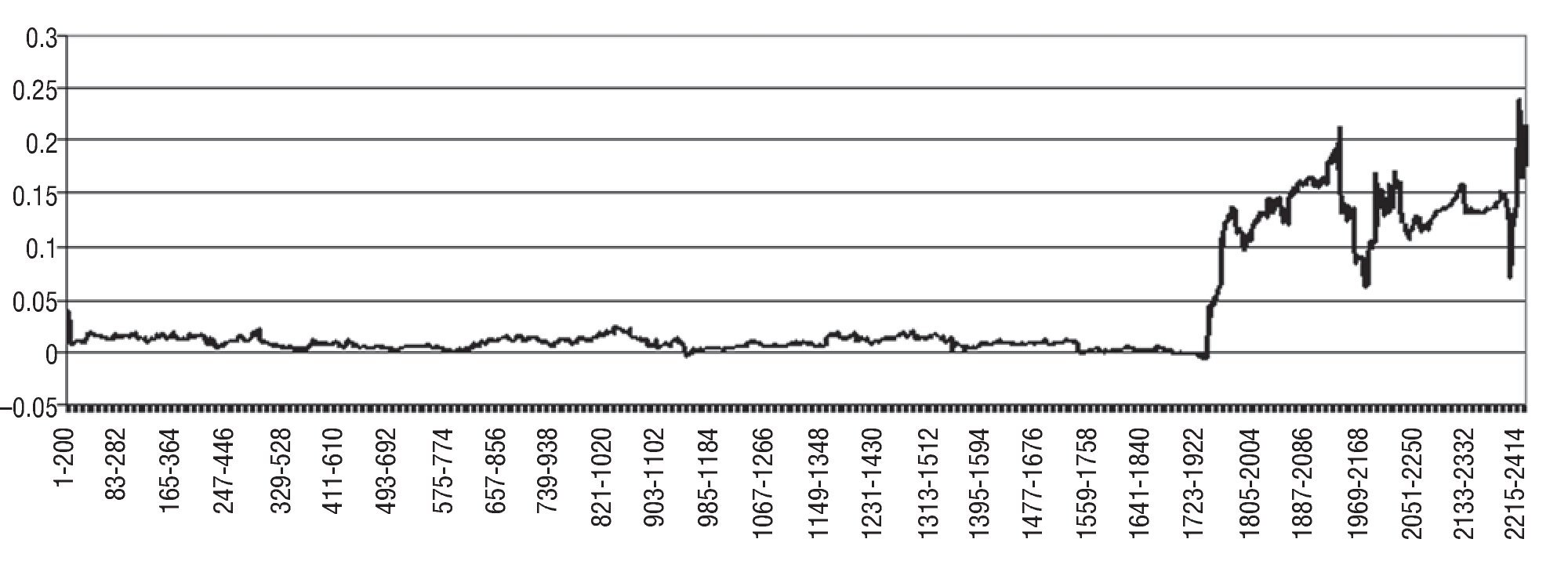
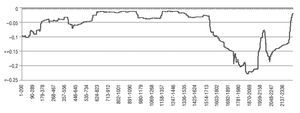
To analyse the possible time-varying nature of the Granger-causality relationships, Figure 5 shows the results from the rolling regressions, both for the long-term and short-term interest rate differentials between Japan and EMU. We obtain further support for our previous conclusion of Granger-causality running from both DIFlt and DIFst toward S, since most of the time the difference of the FPE statistics is positive. On the other hand, we detect subperiods in which there is evidence of transitory Granger-causality running from S to both DIFlt and DIFst.
Figure 5 Rolling regression results: Japanese yen-euro. FPE statistics for each rolling regression using a window of 200 observations.
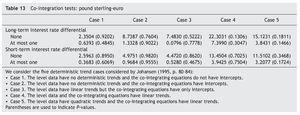
As for the UK-EMU case, results in Table 11 and Table 12 suggest that the series are I(1), while those in Table 13 indicate that there is no any co-integrating relation linking the pound sterling-euro exchange rate with either the long-term or the short-term interest rate differential between UK and EMU, imposing us, once again, the need to test for causality in first differences of the variables, with no error-correction term added [i. e., equations (3) and (4), with β = 0].
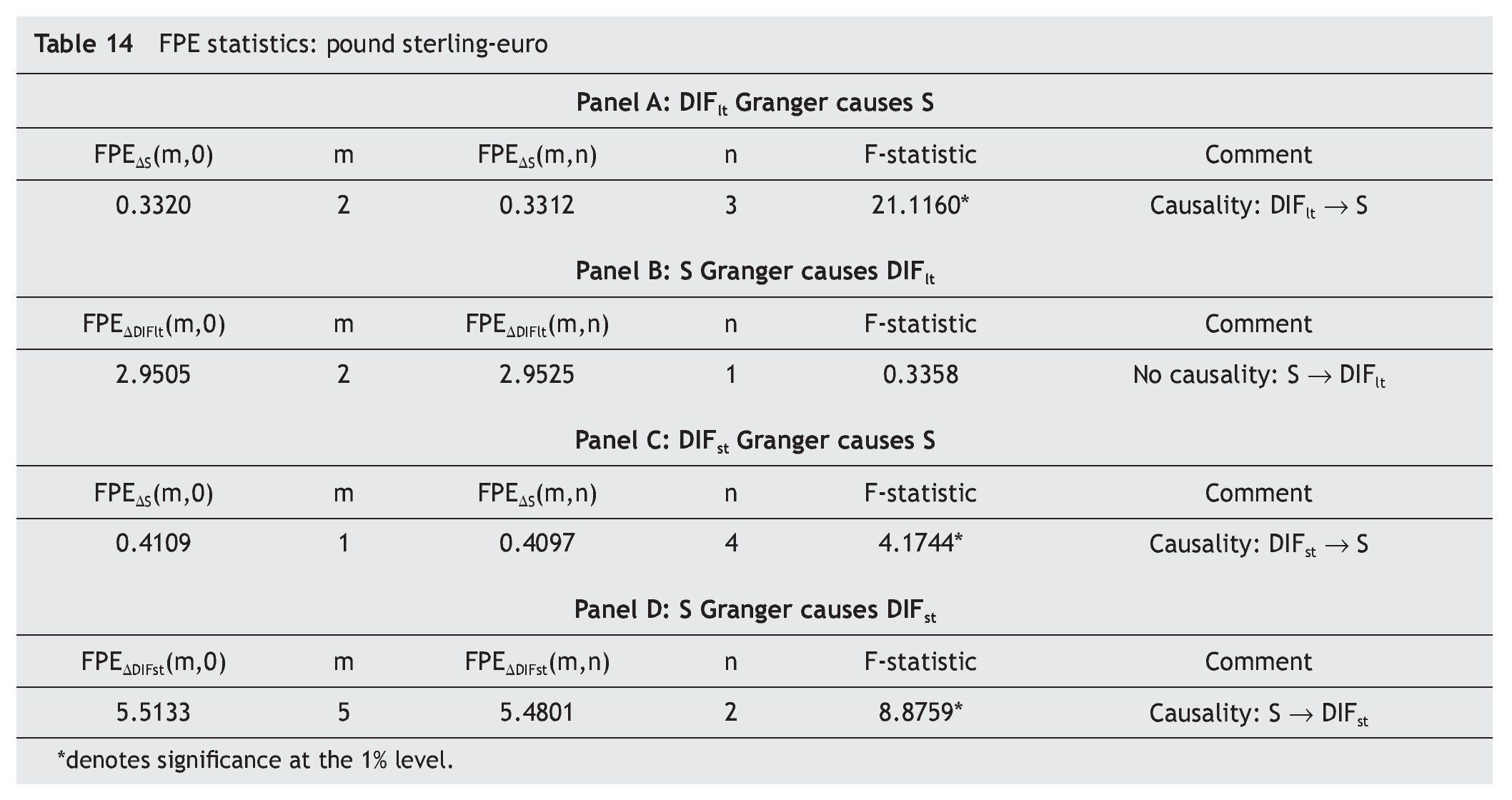
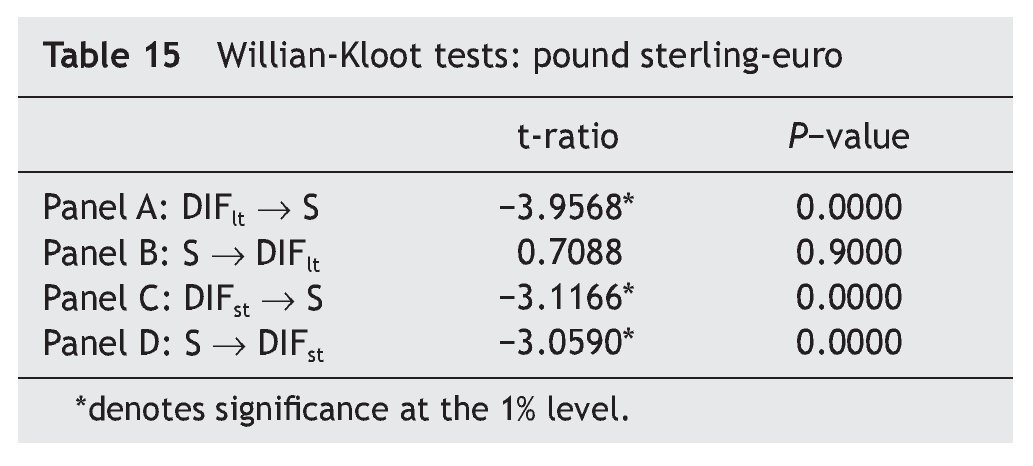
Table 14 shows the FPE statistics. While we obtain evidence Granger causality running from the long-term interest rate differential between UK and EMU to the pound sterling-euro exchange rate and not the other way round, we also find bi-directional Granger causality between the pound sterling-euro exchange rate and the short-term interest rate differential between UK and EMU. These conclusions are further supported by both the F-statistics reported in Table 14 and by the Williams-Kloot test shown in Table 15.
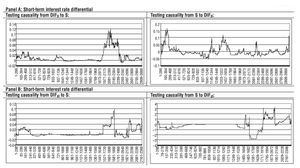
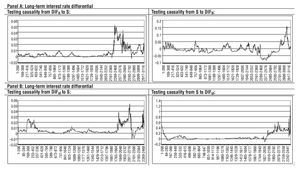
Finally, Figure 6 presents the results from the rolling regressions, both for the long-term and short-term interest rate differential between UK and EMU. The difference of the FPE statistics is positive when testing Granger-causality running from both DIFlt and DIFst toward S, giving further support to our previous finding, while the evidence of Granger-causality running from S to DIFst seems to be supported by the rolling regressions expect for some short episodes at the beginning and at the end of the sample.
Figure 6 Rolling regression results: pound sterling-euro. FPE statistics for each rolling regression using a window of 200 observations.
5. Concluding remarks
This paper represents an attempt to examine the causal relationship between exchange rates and long-term interest rates, contributing to the burgeoning literature on the empirical determinants of exchange rate movements. To that end, we initially analyse data for the US dollar-euro exchange rate and US-EMU ten-year bond yield differentials covering the period January 1999 to January 2011.
Rather than focusing on structural models of UIP, this paper considers the casual relationship between interest rates and exchange rate. We focus on causality because of its relevance in the econometric literature to ascertain the importance of the interaction between two series. To that end, we conduct a sequential procedure to characterize the empirical relationship between exchange rates and interest rate differentials. In particular, we use Hsiao's (1981) test for Granger causality to estimate if interest rates are informationally relevant to the evolution of exchange rates or whether the opposite is true.
Our results suggest that, despite the absence of any common long-run trend between both variables, Granger-causality tests revealed that short-run relationship among them does exist: the nominal US dollar-euro exchange rate appears Granger-caused by the long-term interest rate differential between USA and EMU, but not the other way round.
The findings are robust and consistent over different countries and interest rates. In particular, we obtain similar results for the US dollar-euro exchange rate and US-EMU short-run interest rate differential, for the Japanese yen-euro exchange rate and both the long-run and short-run differential between Japan and EMU, and for the pound sterling-euro exchange rate and the long-run differential between the UK and EMU. Nevertheless, we detect bi-directional Granger-causality between the pound sterling-euro exchange rate and the short-run interest rate differential between the UK and EMU.
Overall, our results are in line with those reported by Kohler (2010), who argues that interest rate differentials explain more of the exchange rate movements in current crisis than in the past. This probably reflects structural changes in the determinants of exchange rate dynamics such as the increased role of carry trade activity (involving borrowing funds in a low-interest currency and investing them in a high-interest currency) and worldwide restructuring of portfolios.5
Acknowledgements
The authors thank the editor, Nikolas Müller-Plantenberg, and two anonymous referees for useful comments and suggestions. We are also grateful for the financial support from the Spanish Ministry of Science and Innovation (ECO2011-23189). María del Carmen Ramos-Herrera also acknowledges her grant (F.P.U.) from the Spanish Ministry of Science and Innovation (Ref. AP2008-004015).
1. FPEX(m,0) is computed using the formula:
where T is the total number of observations and SSR is the sum of squared residuals of OLS regression (1).
2. FPEX(m,n) is computed using the formula:
where T is the total number of observations and SSR is the sum of squared residuals of OLS regression (2).
3. We are very grateful to a referee and the editor for suggesting us this section.
4. Because each transaction involves two currencies, the shares sum to 200%.
5. See King and Rime (2010) and Gyntelberg and Schrimpf (2011) for an analysis of the growing importance of automatic strategies in foreign exchange markets.
Received February 9, 2012; accepted May 31, 2012
* Corresponding author.
E¿mail address: sosvilla@ccee.ucm.es (S. Sosvilla-Rivero).
References
Akaike, H., 1969. Fitting autoregressive models for regression. Annals of the Institute of Statistical Mathematics 21, 243-247.
Alexius, A., 2001. Uncovered interest parity revisited. Review of International Economics 9, 505-517.
Bank for International Settlements, 2010. Triennial Central Bank Survey: Report on global foreign exchange market in 2010. Bank for International Settlements, Basel.
Bekaert, G., Wei M., Xing Y., 2007. Uncovered interest rate parity and the term structure. Journal of International Money and Finance 26, 1038-1069.
Campbell, J.Y., Clarida, R.M., 1987. The dollar and real interest rates. Carnegie-Rochester Conference Series on Public Policy 27, 103-140.
Carrión-i-Silvestre, J.L., Sansó-i-Roselló, A., Ortuño, M.A., 2001. Unit root and stationarity tests' wedding. Economics Letters 70, 1-8.
Chinn, M.D., 2005. The (partial) rehabilitation of interest rate parity in the floating rate era: longer horizons, alternative expectations, and emerging markets. Journal of International Money and Finance 25, 7-21.
Chinn, M., Meredith, G., 2004. Monetary policy and long-horizon uncovered interest parity. IMF Staff Papers 51, 409-430.
Dolado, J. J., Jenkinson, T., Sosvilla-Rivero, S., 1990. Cointegration and unit roots. Journal of Economic Surveys 4, 149-173.
Engel, C., 1996. The forward discount anomaly and the risk premium: a survey of recent evidence. Journal of Empirical Finance 3, 123-192.
Flood, R.P., Taylor, M.P., 1996. Exchange rate economics: what's wrong with the conventional macro approach? In: Frankel, J., Galli, G., Giovanni, A. (Eds.), The microstructure of foreign exchange markets. University of Chicago Press, Chicago, pp. 262-301.
Granger, C.W.J., 1969. Investigating causal relations by econometric models and cross-spectral methods. Econometrica 37, 24-36.
Gyntelberg, J., Schrimpf. A., 2011. FX strategies in periods of distress. BIS Quarterly Review, December, 29-40.
Hakkio, C.S., Rush, M., 1991. Cointegration: how short is the long run? Journal of International Money and Finance 10, 571-581.
Hendry, D.F., Mizon, G.E., 1999. The pervasiveness of Granger causality in econometrics. In: Engle, R.F., White, H. (Eds.), Cointegration, causality, and forecasting. A festsschrift in honour of Clive W. J. Granger. Oxford University Press, Oxford, pp. 102-134.
Hsiao, C., 1981. Autoregressive modelling and money-income causality detection. Journal of Monetary Economics 7, 85-106.
Johansen, S., 1991. Estimation and hypothesis testing of cointegration vectors in Gaussian vector autoregressive models. Econometrica 59, 1551-1580.
King, M.R., Rime, D., 2010. The $4 trillion question: what explains FX growth since the 2007 survey? BIS Quarterly Review 27-42 (December).
Johansen, S., 1995. Likelihood-based inference on cointegrated vectors autoregressive models. Oxford University Press, Oxford.
Kohler, M., 2010. Exchange rates during financial crises. Bank of International Settlements Quarterly Review, March, 39-50.
Kwiatkowski, D., Phillips, P.C.B., Schmidt, P., Shin, Y., 1992. Testing the null hypothesis of stationarity against the alternative of a unit root. Journal of Econometrics 54, 159-178.
Meese, R., Rogoff, K., 1988. Was it real? The exchange rate-interest differential relation over the modern floating-rate period. Journal of Finance 43, 933-948.
Thornton, D.L., Batten, D.S., 1985. Lag-length selection and tests of Granger causality between money and income. Journal of Money, Credit, and Banking 27, 164-178.
Toda, H.Y., Yamamoto, T., 1995. Statistical inference in vector autoregressions with possibly integrated processes. Journal of Econometrics 66, 225-250.
Williams, E.J., 1959. Regression analysis. Wiley, New York.