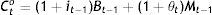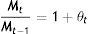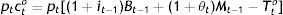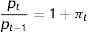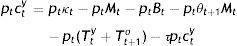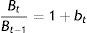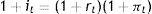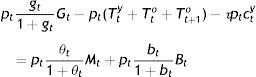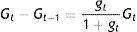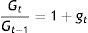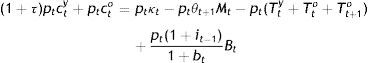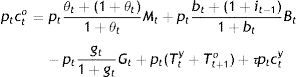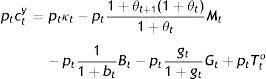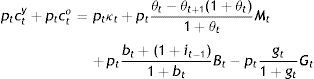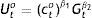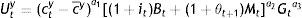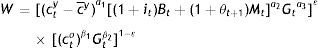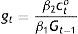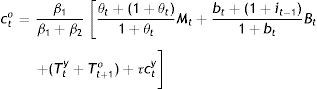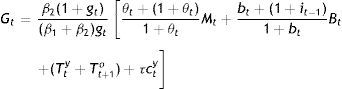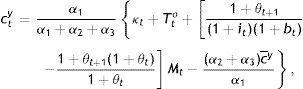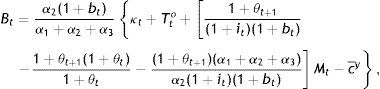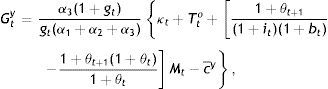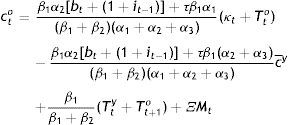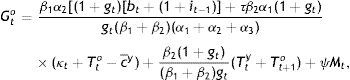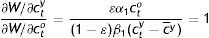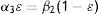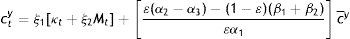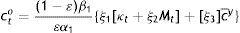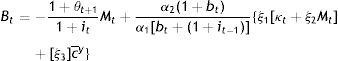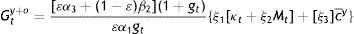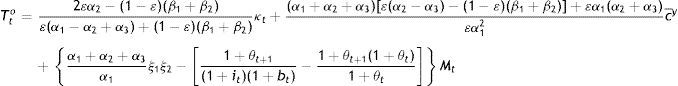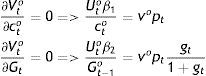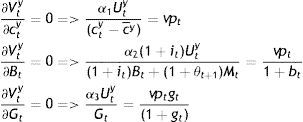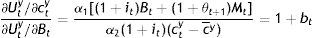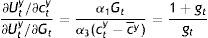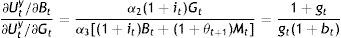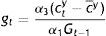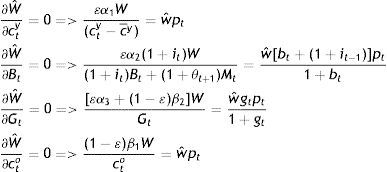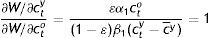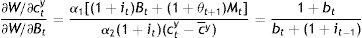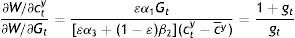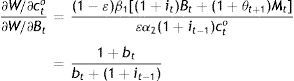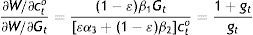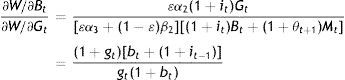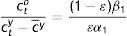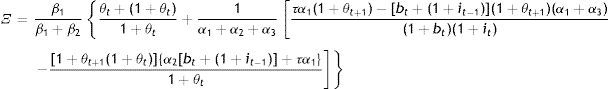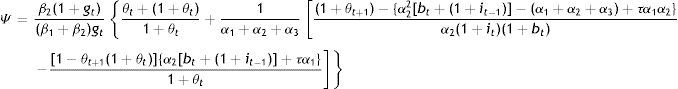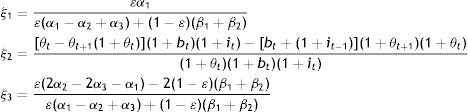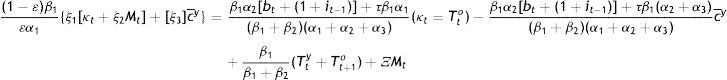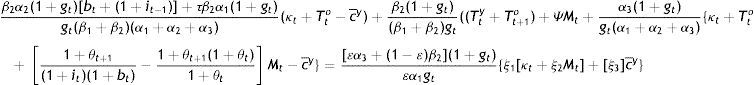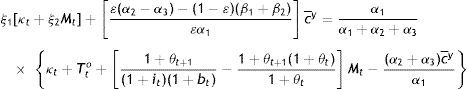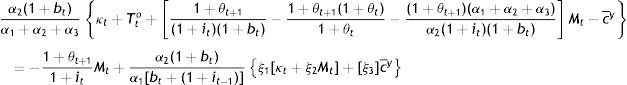Based on a Cobb–Douglas social welfare function in terms of the utilities of two concurrent generations, this paper derives a Pareto-efficient, envy-free, and equitable interest rate rule supported by a nonlinear-tax feedback rule in case of steady-state disturbance. The young are taxed to subsidize the elderly, expecting the same treatment when the young become old; hence, fiscal policy matters as much as the monetary policy does with regard to the “same”. The emphasis on monetary policy lies rather in the fact that once the equilibrium status quo of a policy accommodative of a given tax subsidy-cum-interest rate scheme is disturbed, the “interest-rate part” will continue being a sensible policy choice only by manipulating the “tax-subsidy part”. From the political economy view of tax nonlinearity, the tax policy under instability is expected to be both a self-confirming and a perfect insight majority rule equilibrium.
Basándose en una función de bienestar social de Cobb–Douglas en términos de las utilidades de 2 generaciones concurrentes, este documento extrae una norma sobre tipos de interés, que es eficiente conforme a Pareto, libre de conflictos, y equitativa, sustentada por una norma de retroalimentación de los impuestos no lineales en caso de alteración del equilibrio. La fiscalidad de los jóvenes se utiliza como subsidio para los mayores, esperándose este mismo tratamiento cuando dichos jóvenes envejezcan; por tanto, la política fiscal tiene tanta importancia como la política monetaria para «los mismos». El énfasis sobre la política monetaria radica más bien en el hecho de que una vez que se altera el statu quo de equilibrio de una política que se acomoda a un programa de tipos de interés unidos a subsidios fiscales, la «parte de tipos de interés» seguirá siendo una elección de política prudente solo si se manipula la «parte de subsidios fiscales». Desde la óptica de la economía política de la no linealidad fiscal, es probable que la política fiscal en condiciones de inestabilidad constituya tanto un equilibrio de la norma mayoritaria autoverificativo como de percepción perfecta.
“Fiscal policy and monetary policy are both beautiful; we need them both and we should treat them both lovingly.” Arthur M. Okun (1971, p. 51)
It is noteworthy that the debate on “rules vs. discretion” in economic policymaking has not managed to capitalize so far upon optimal control theory suggestions that if rules do work they can be improved if followed by feedback rules, too (see e.g. Kydland and Prescott, 1977). Actually, not much on this debate per se has been done save some studies documenting empirically the alleged tradeoff between rules and discretion, and other work examining theoretically the various aspects of it, by Friedman (2012), Taylor (2012), Amador et al. (2006), Albanesi et al. (2003), Canzoneri (1985), and Goldfeld (1982) among others. Lately, authors like Carluccio and Menegatti (2012), Arestis and Mihailov (2009), and Athey et al. (2005), appear to leave some room for limited compromise, but nowhere is to be found a discussion about complementarity from the viewpoint of having a monetary policy rule becoming operational just because it is accompanied by a fiscal policy feedback rule in a dynamic system.
Also, note that if the focus of such a system is to be the medium- and long-run, it should be having an intergenerational form, because aging changes the generation one is in. And, if aging alters quite plausibly preferences the particular intergenerational form should be the one of overlapping generations and not that of the infinitely lived individual. Now, it is noteworthy that the overlapping-generations cash-in-advance specification, which is adopted herein too, postulates a Diamond (1965) utility function of consumption when young and consumption when old; and it does so almost uniformly in the relevant literature (see e.g. Yanagihara and Lu, 2013; Gahvari, 2009; Smith, 2003; Crettez et al., 1999; Qi, 1994, and the subsequent literature). Nevertheless, policymaking should be approached under a social planner's viewpoint, and hence, based on a social welfare function incorporating explicitly the standard analytical parable of monetary overlapping-generations modeling according to which the young and the old are two different concurrent generations, with the former altering behavior as they age (see e.g. McCallum, 1983).
To tackle the issue of monetary and fiscal policy rules complementarity, this paper elaborates upon such a “social-planner overlapping-generations” approach through a stylized model of this sort. It is driven by the mere logical fact that there has to be some entity to be bridging the two generations for policy to exist. There has to be therefore a social planner taking subsequently into account the element of intergenerational equality without hurting individual preferences, in fostering at the same time monetary equilibrium. Put differently, this bridging raises the issues of intergenerational equality and envy beyond the matter of Pareto efficiency, and the planner's solution has to be not only as Pareto efficient as the solution desired by the individual but equitable and envy-free as well. A one-to-one treatment of the current with the future elderly in private consumption plus the respect of individual preferences with regard to the public good provided by the planner, is certainly equitable, and is the first of the results.
But, societal welfare would still be suboptimal without equilibrium in the market of the bonds that are issued by the planner toward its socioeconomic obligations, because equilibrium preservation in this market ensures that no intergenerational-envy driven disequilibria are prompted given that it is this market through which such envy would be channeled. And, precisely this is to what our second result of deriving an interest rate rule corroborated by a tax feedback rule amounts. Indeed, methodologically, policymaking is sensible at off equilibrium states, and should be based on a fiscal instrument monitoring and correcting for the deviations from equilibrium that incapacitate the monetary rule.
To put the modeling and its conclusions into further perspective with the relevant literature, complementarity of monetary and fiscal rules is found when disequilibrium is attributed to sticky prices too, as, for instance, Benigno and Woodford (2003) or Schmitt-Grohé and Uribe (2007) do. Disequilibrium emanates through a dynamic system, which is compatible with the Tinbergen (1952)–Theil (1958) tradition to optimal policymaking even if the dynamics were seen to be intergenerational, because simply they would be about an infinitely lived individual. And, indeed, an active role for fiscal policy beyond optimal monetary policy considerations can come up once additional tax instruments are introduced into the standard analytical framework of the literature on optimal monetary policy; the concern is the minimization of the consequences of nominal rigidities under the presumption that only lump-sum taxes are available.
Complementarity of policy rules is found to be the case here too, but because of liquidity disturbances, which are modeled as coming out of asynchronous intergenerational decisions, with the asynchronism being attributed to intergenerational equality-envy considerations rather than to random relocation (see e.g. Haslag and Martin, 2007). Within such a framework of envy and/or equality induced asymmetric intergenerational information with regard to intergenerational transfers, the policymaker assumes an additional, social-welfare maximizing role beyond the strictly economic Tinbergen–Theil one; it is the role of insurer against this asymmetric information that the banking system alone cannot assume as efficiently as in an Arrow–Debreu fashion (see e.g. Diamond and Dybvig, 1983; Qi, 1994).
It is from this point of view that the modeling in this paper is one of optimal monetary policy too, with results in the spirit of the literature on optimal fiscal policy as well in two respects. First, to the extent that monetary policy matters under flexible prices, (perfect competition in our case), and financial instability as is assumed by that literature. And, second and more importantly, in an overlapping-generations version of intergenerational modeling, like the one employed below, the young are taxed to subsidize the elderly, expecting the same treatment when the young become old; hence, fiscal policy matters as much as the monetary policy does with regard to the “same”. The emphasis on monetary policy lies rather in the fact that once the equilibrium status quo of a policy accommodative of a given tax subsidy-cum-interest rate scheme is disturbed, the “interest-rate part” will continue being a sensible policy choice only by manipulating the “tax-subsidy part”.
As a matter of fact, at steady state, no money at all would be needed to carry through intergenerational transfers if money was not useful in taking care the storage problems surrounding goods, fiscal policy would be equivalent to army quartermaster accounting, and the social planner would be the quartermaster officer. An intergenerational mediator armed with both, monetary and fiscal policy instruments, are needed only at off equilibrium states, in which case monetary policy serves like a compass pointer guided by the optimal social-welfare, which only the mediator can handle efficiently. In a non-overlapping generations context, no such issues can be raised ex hypothesi… Anyway, in what follows, the next section tackles all these issues formally by simply deriving Nash demands on the part of the young and the concurrent old, and finding them to differ from those under societal optimum when the time subscript is allowed to be making a difference. The paper concludes with still another section discussing the tax rule as such in the light of the relevant literature.
2The modelConsider a constant-population economy which is composed at time t of a young generation and of an old one, with agent types, y and o, respectively. Each of them maximizes utility U from consumption, c, and a public good, G, under the corresponding budget constraint. The planning horizon of the young extends to time t+1, when they will have become old, and when the current old will not “be around”, focusing thereby the latter exclusively on calculations for t. Each young generation receives a consumption bundle, κ, as manna from heaven, and is called for to handle with it its lifetime utility as well as the utility of its contemporary elderly under the following arrangement:
Consumption when old, co, consists of goods the old buy from the young on the basis of the liquidation of bonds, B, acquired when young, the money holdings M carried over from t to t+1, and a government subsidy of θ percent of these holdings so that before taxes:
where i is the nominal interest rate. The government exists for this precisely reason as well as because the young have agreed to be paying τ percent of c, when young, and a lump-sum of Tty, when young plus Tt+1o, when old, to a society-wide institution, and to be lending it by buying its bonds toward the provision of pure public good G beyond the subsidy of θM to the elderly.That is, at time t, the budget constraint of the current old is after taxes:
where pt is the time price of one unit of money from the viewpoint that discounting takes place at the rate of inflation, π, as described by:and bonds are issued in terms of the consumption good. The budget constraint for the young is:All money is held by the elderly and is directed to purchases of goods from the young while even more goods are sold by y to o in exchange of (1+it−1)Bt−1, who young buy also the new stock of B, i.e. Bt−(1+it−1)Bt−1, for old age, with:
where r is the real rate of interest on bonds under the Hicksian–Morishima view of being the price of illiquidity.In view of Eq. (5), Bt−(1+it−1)Bt−1=(bt−it−1)Bt−1: The new stock of B will be zero in real terms if bt=it−1, which is an important equilibrium relationship that will be interpreted later in the text.
Finally, the government would be restricted by its own current at t budget constraint, too:
whereis the change in the supply of the public good between the two periods, with:The future tax revenue Tt+1o enters into the current government budget constraint, because it is the one regarding the two generations at t and not only those living at t.
The government as a social planner would be restricted by the sum of the budget constraints of y and o too, which after some operations is:
In view of Eq. (8), the budget constraints Eqs. (3), (5), and (10) become:
given also Eqs. (2) and (5),andrespectively.Now, the old maximize the Cobb–Douglas utility function:
with respect to cto, and Gt subject to (3′), where the β’s are constants. The young maximize the Stone–Geary utility function:with respect to cty, Bt, and Gt, subject to Eq. (5′), where c¯y is some minimum consumption regardless t, the a's are constants, and in line with Eq. (1), ct+1o=(1+it)Bt+(1+θt+1)Mt, before taxes. The Stone–Geary specification simply reflects the fact that one has to secure some minimum consumption before starting creating a portfolio and that one cannot live on public goods alone. There is not such a minimum when old, because the elderly consume all which has not been determined to consume when they were young, in which case the Stone–Geary utility function coincides with the Cobb–Douglas one. In view of fixed for the elderly G, the maximization problem makes sense from the viewpoint that public and private goods are substitutes or complements in consumption (see e.g. Fiorito and Kollontzas, 2004). And, as a matter of fact, this relationship between the two types of goods can be critical for the effectiveness of policymaking (see e.g. Ganelli and Tervala, 2009).Finally, the government maximizes as a social planner some social welfare function in terms of the utilities of the two concurrent generations:
with respect to cty, ctoBt, and Gt, under the constraint given by Eq. (10′), where the constant ¿ captures the preferences of the planner over the two generations. The planner focuses on the maximization of the current welfare of the two concurrent generations at time t, plus the welfare of the elderly at t+1, so that Tt+1o only from its future tax revenue is included in the government budget constraint of time t.From the first-order conditions for the elderly (see Appendix), we obtain that the rate of substitution between co and G depends exclusively on the rate of growth of the public good:
which growth rate is the weighted by the β’s ratio of the consumption of the current old to last period's stock of G, since Eqs. (14) and (9) imply that:That's how at least the government should be providing the public good from the viewpoint of the elderly. Solving Eq. (14) for Eq. (3′), inserting the resulting expression in Eq. (3′), and solving for co, yields that:
which when inserted back in Eq. (14) gives:These are the demands for c and G by the elderly, and their steady-state values are simply those without the time subscript in Eqs. (15) and (16). They are the best response to whichever the choice of cty may be by the young.
Next, from the first-order conditions for the young (see Appendix), one obtains rates of substitution depending again on growth rates and producing the following solutions for c, B, and G:
andThese are the demands for c, B, and G by the young, and their steady-state values are simply those without the time subscript in Eqs. (17)–(19). Inserting Eqs. (17) and (18) in Eqs. (15) and (16) will produce the Nash-follower values of co and G of the elderly, which are complicated expressions and only that for co will be presented, as it is needed for comparison purposes below:
andwhere Ξ and Ψ are long sums of parameter ratios immaterial to our discussion here and therefore, presented in the Appendix.Let us instead proceed with the first-order conditions for the government (see Appendix). A couple of remarks should be made based on these rates of substitution before we proceed to the solution of cty,cto⋅⋅Bt, and Gt. Firstly, from Eq. (A5) in the Appendix:
it is clear that age discrimination in private affairs would be suboptimal for the society and for the government. From Eq. (A5), but also from Eqs. (A7) and (A9), one obtains:and concludes that what would be optimal for the government as a social planner is to discriminate between the two concurrent generations according to their preferences for the public good at time t (given that the preference structure of the current young need not be the same when they become old). Second, Eqs. (A6) and (A8) imply that it=it−1, i.e. that societal welfare is maximized when the nominal interest rate is kept constant as, for example, under Friedman's rule, which prescribes a zero such rate all the time. In view of Eq. (7), a constant i means that inflation and bond liquidity variations cancel out, and this can be the case only if bt=it−1 as noted at the outset.Setting bt=it−1, indicates that the planner finds it optimal to be matching the current bond growth rate with last period's nominal interest rate, or the same to be preserving bond market equilibrium by satisfying the change in the demand of bonds brought about by bond price changes last period, crystallized inversely by that period's nominal interest rate. These price changes are in response to changes in bond liquidity as decided by the young.
Assume, for instance, that when the young sell goods to the old, they decide to accept payment directly in bonds as they do with money. r, which is the price of bond liquidity, falls immediately to zero at the same time at which this decision of the young is equivalent to increased demand for bonds. This increased demand raises the price of the bond, which is the acquisition cost of a bond in terms of the consumption good. More of this good is offered by the young in exchange of the same amount of bonds. The purchasing power of bonds increases, raising the price level and thereby the nominal interest rate, ceteris paribus A policy of bt=it−1=it comes to restore equilibrium as a necessary but not sufficient condition as the following solution to the social planner's problem suggests:
where the ξ’s are as in the Appendix. Of course, Gty+o is the total amount of the public good for both generations including that which the current young think in line with their current preferences that they would like to consume when old.It is easily checked that under the same θ, all partial derivatives with respect to M are negative: Suppose, for instance, that the old get more than planned M to channel into purchases of c from the young. The government has simply printed more money to increase G. If θ and hence, θM are not expected to return back to “normal”, all, cy, co, and G, will have to be adjusted downwards in consumer plans, and finances will have to change at the expense of B in response to this crowding-out effect on the constant supply of κ from heaven… And, an interest rate rule can do nothing to deter or correct this government-induced distortion, this societally suboptimal equilibrium, because the derivatives with respect to M continue being negative even if bt=it−1=it. Unless θ is allowed to vary, since lowering it would simply tax away the “extra” M of the old the same way a direct tax increase on the old would. θ is a monetary as much as fiscal policy instrument and should be used discretionarily along with the rule bt=it−1=it in keeping the economy at the optimal societal equilibrium.
Technically, setting cty, cto, Bt, and Gty+o in Eqs. (24), (25), (26), and (27) equal to cty, cto, Bt, and Gty+Gyo in Eqs. (17), (20), (18), and (19)+(21), respectively, one obtains a system of four equations in the four tax variables, which when solved will give the tax structure needed to have coincidence between planner and individual optima. For example, equating Eq. (24) with Eq. (17) yields that:
which is the simplest expression for Tto, since another one may be obtained by equating B's. We have actually the two remaining equalities to be solved for the sum Tty+Tt+1o and τ, but it is clear that we are dealing with highly complicated non-linear expressions in terms of the (preference) parameters accompanying κt, Mt, and c¯y, plus the coefficient θt accompanying especially Mt. They would not help analytically, because taxes act no differently than θ. The solutions, the whole approach, actually suggest that we are really dealing with feedback tax rules, i.e. with a tax system neutralizing any disturbances from continuing following the interest rate rule off societal optimum.Indeed, from an intergenerational perspective, monetary rules and fiscal discretion are not mutually exclusive but complementary to each other in fostering the societally optimum equilibrium when taxation serves as a feedback rule. It is a policy mix which is Kydland–Prescott (1977) consistent and at the same time, Pollak (1968) optimal, because even if θ summarizes a time-invariant cash-in-advance constraint on the part of the policymaker, the combination of an interest rate rule with flexible taxation, does allow the policymaker at t+1 to contemplate on his policy effects given the expectations formed at t: In Tto above, (1+θt+1)Mt is the expectation about Mt+1 formed at t. The iterative process of the rule may be incorporating these expectations through their impact on a tax policy, which has been designed to serve as a feedback rule. The real issue for the public is not any steady state, but whether or not its government is acting as a social planner, having developed means of monitoring and materializing its wishes whenever the optimum is disturbed, incapacitating its rules; and, this means is the tax policy.
3Concluding remarksOur results are in the spirit of Wallace (1980) and Kareken and Wallace (1981) in that constant money-growth policy expectations may result in suboptimal societally and still, optimal in a Barro–Gordon (1983) sense equilibria, when in our case such expectations continue to be held off societal optimum. Also, based on the Helpman–Sadka (1979) shopping time approach to cash-in-advance and money-in-the-utility-function, our results are in the spirit of Bryant and Wallace (1980) and Sargent and Wallace (1981) in that the rich want to hold more bonds than the poor; the rich in our case being all agents before societal equilibrium disturbance, and the poor being all again agents at a societally suboptimal, Barro–Gordon like equilibrium.
Much more important, however, in understanding our results is their relationship with the thesis of Gahvari and Micheletto (2009, p. 1) that “the ability to levy nonlinear taxes can neutralize monetary policy only if the source of heterogeneity concerns earning abilities, as inda Costa and Werning (2008), but not if it concerns heterogeneity of the typeWilliamson (2008)has in mind.” This paper too, presumes such ability as well as earnings equilibrium-dependent heterogeneity upon reflection on that a suboptimal equilibrium would simply be fostered as an optimum one if the endowment κ of the young were less. It is a heterogeneity which is independent not only from age but also from variations in the ability to access financial institutions, which ability is what Williamson (2008) emphasizes. And, within such a framework, our nonlinear Mirrleesian taxes do neutralize a constant θ policy off societal optimum; but they do so shaped under the consequent monetary policy expectations, allowing thus the continuation of the operation of our interest rate rule.
From Romer's (1975) political economy view of tax nonlinearity, our taxes herein do constitute a Fudenberg–Levine (1993) majority rule equilibrium, because simply at disequilibrium, the consensus about the ordering of the alternatives “stability vs. instability” favors unanimously stability à laRoberts (1977); these are clearly the preferences crystallized in monetary policy expectations off equilibrium. Disequilibrium does upset plans but tax policy confirms expectations about the unanimous quest in words and practice for equilibrium restoration. This is the mentality under which tax policy is voted for in the first place. Of course, this is an “angelic” world since all policy turns out to be a Kranich (2002) perfect foresight majority rule equilibrium as well. It is a world in which the future policymaker need not worry about the political effects of the current tax policy and the subsequent incapacitation of rules.
Possibly because intergenerational conflicts of interest are alleviated by intrafamily intergenerational altruism: “It is well-known that macrodynamic models with finite-lived and selfish individuals are compatible with (dynamically) inefficient equilibria, while models with infinite-lived and dynastically altruistic individuals are not. This suggests that strong intergenerational altruism within the population and long life expectancy prevent the occurrence of inefficient equilibria”, (d’Albis and Decreuse, 2009, p. 1897). And, Wilhelm et al. (2008) show that parental generosity toward their children can be hereditary and remark that it can even take the place of government transfer policy in a Ricardian-equivalence fashion. Although these are quite plausible arguments made in connection with the steady state when as observed in the introductory section not even money would be necessary if not as a lubricant, it might equally plausibly claimed that at disequilibrium intergenerational altruism alleviates the business cycle, (leaving thereby much room for the presence of a social planner).
A formal treatment of such issues lies certainly beyond the scope of this paper. The same can be said about the disrupting effects from “frictions” stemming from the presence of an underground economy (see e.g. Snyder and Kramer, 1988) and tax collection problems (see e.g. Hindriks et al., 1999). Instead, there are two points on methodology that need to be stressed as an epilog to this paper: Firstly, the analytical usefulness of the employment of a social welfare function in the place of the usual “Diamond utility function” when tackling policymaking given that policy should be motivated by the three welfare desiderata of Pareto-efficiency, envy-freeness, and equitability. And, second, the persistence technically on time subscripts, invoking upon steady-state considerations only for insight as to the direction of policymaking, given that policy problems arise when steady-state is disturbed and the task is to turn the clock back to the future…. It is because our deliberation on the topic originated from such a perception of things that a highly stylized model managed to produce worthy of discussion propositions.
We are grateful to two anonymous reviewers for useful comments and suggestions. Any remaining errors and omissions are our own.
First-order conditions regarding the elderly (where Vto is the Lagrangean and υo is the Lagrange multiplier):
Their ratio gives Eq. (14) in the text, which given Eq. (9), becomes Eq. (14′).
First-order conditions regarding the young (where Vty denotes the Lagrangean function and v is the Lagrange multiplier):
It follows that:
From Eqs. (A2) and (9):
which will coincide with Eq. (14′) if:Solving Eq. (A1) for Bt and Eq. (A2) for Gt, inserting the subsequent relations in Eq. (5′), and solving for cty, yields Eq. (17), which when put back in the expressions for Bt and Gt found from Eqs. (A1) and (A2), respectively, will give Eqs. (18) and (19).
First-order conditions regarding the government (Wˆ is the Lagrangean and wˆ is the Lagrange multiplier):
It follows that:
From Eq. (A5), but also from Eqs. (A7) and (A9):
which in view of Eq. (A4) implies that:(1−ε)β1εα1=α3β1α1β2and this in turn, Eq. (23).Finally,
andNow, a solution for Tty+Tt+1o and τ only numerically may be approximated, since the equations involved are the following four: