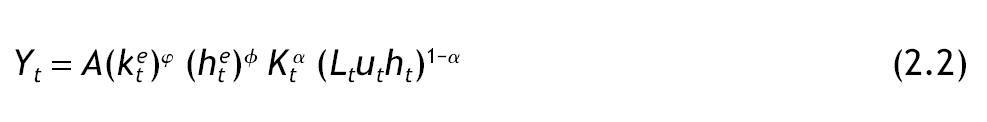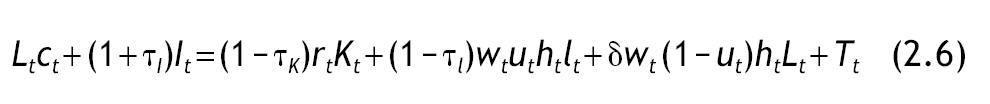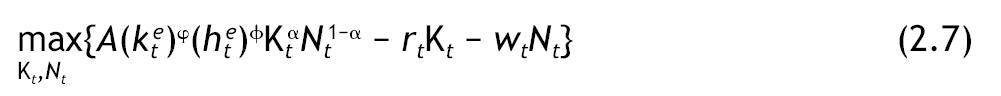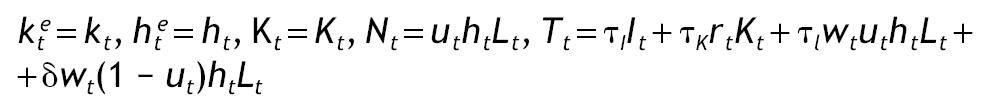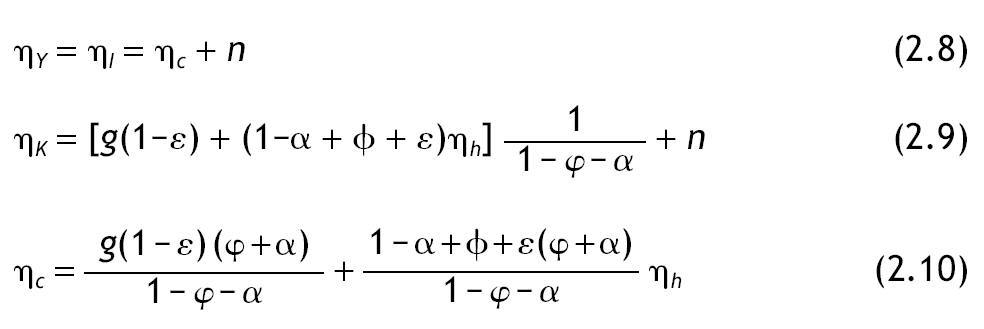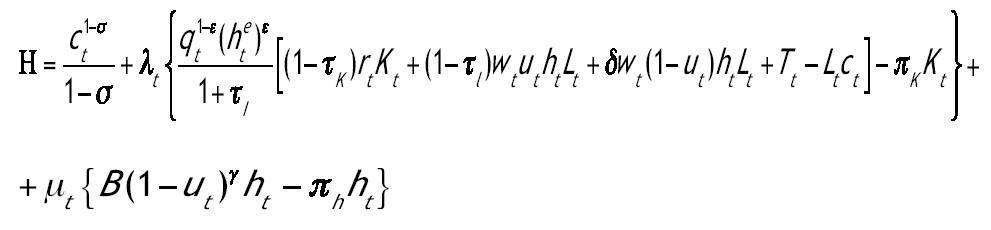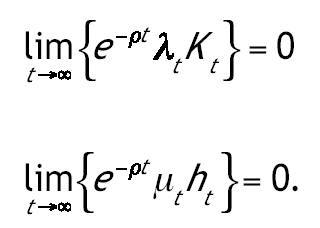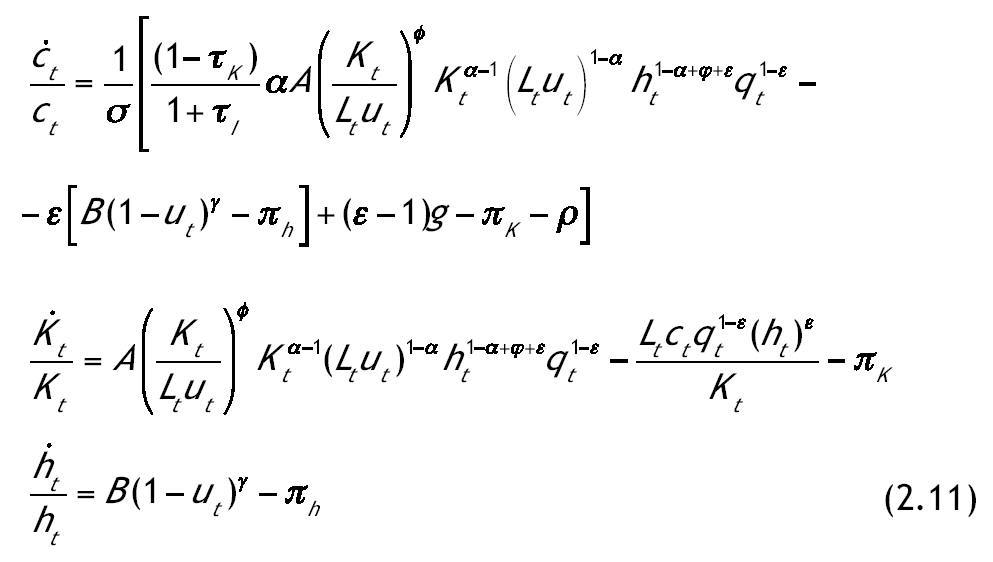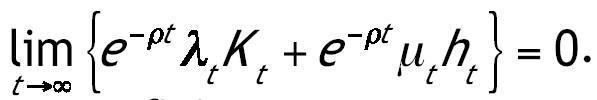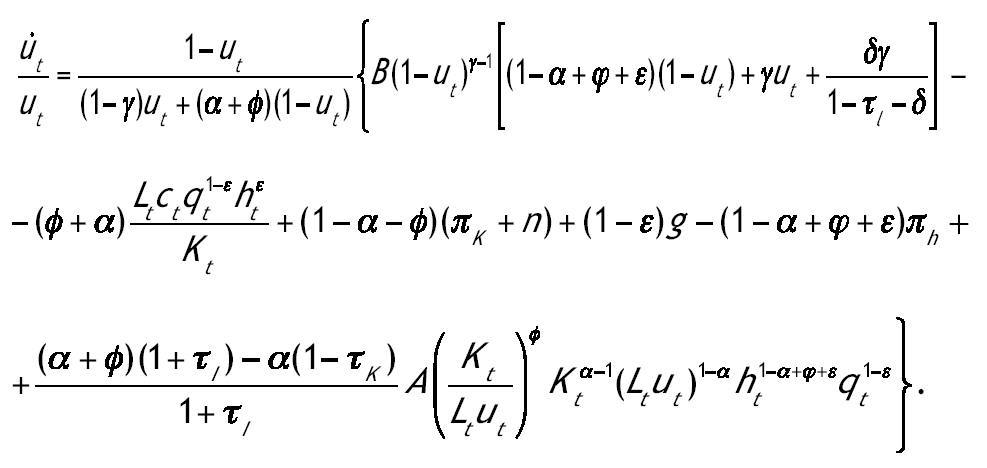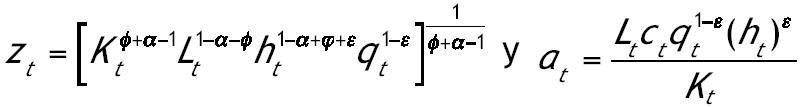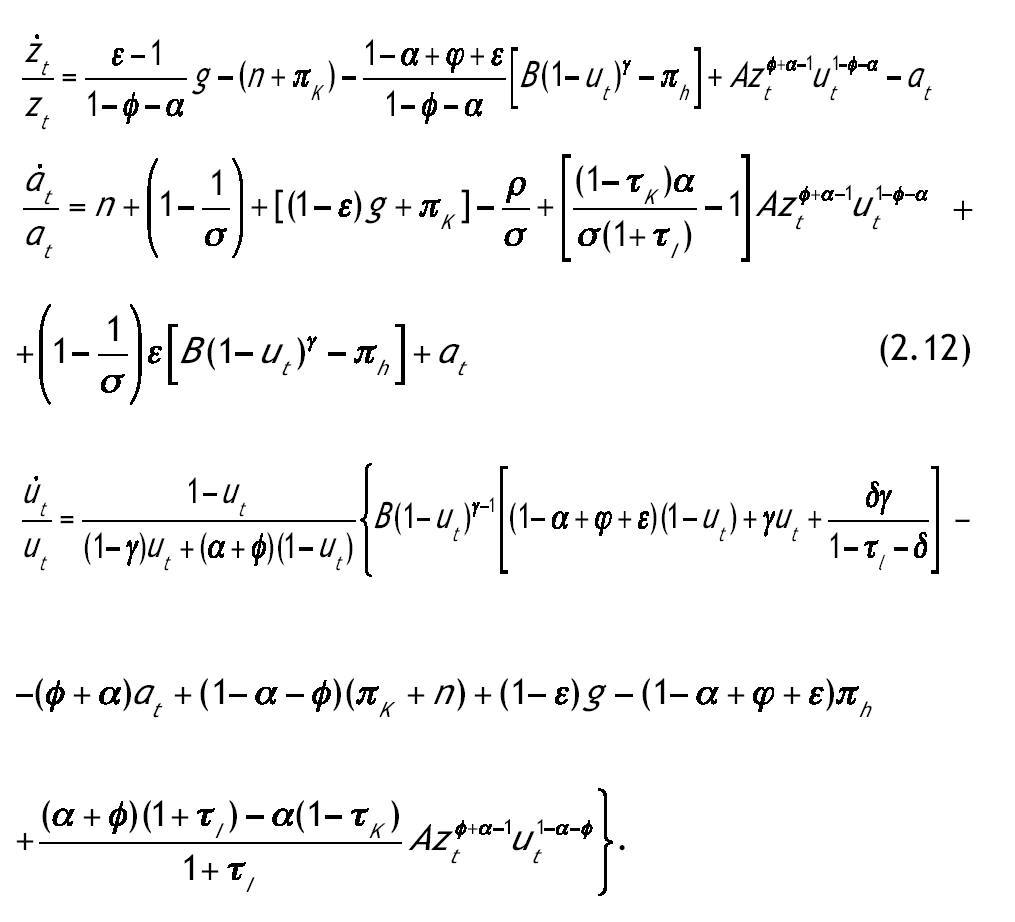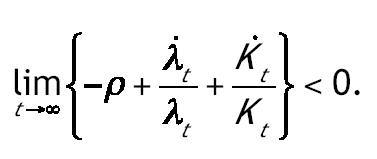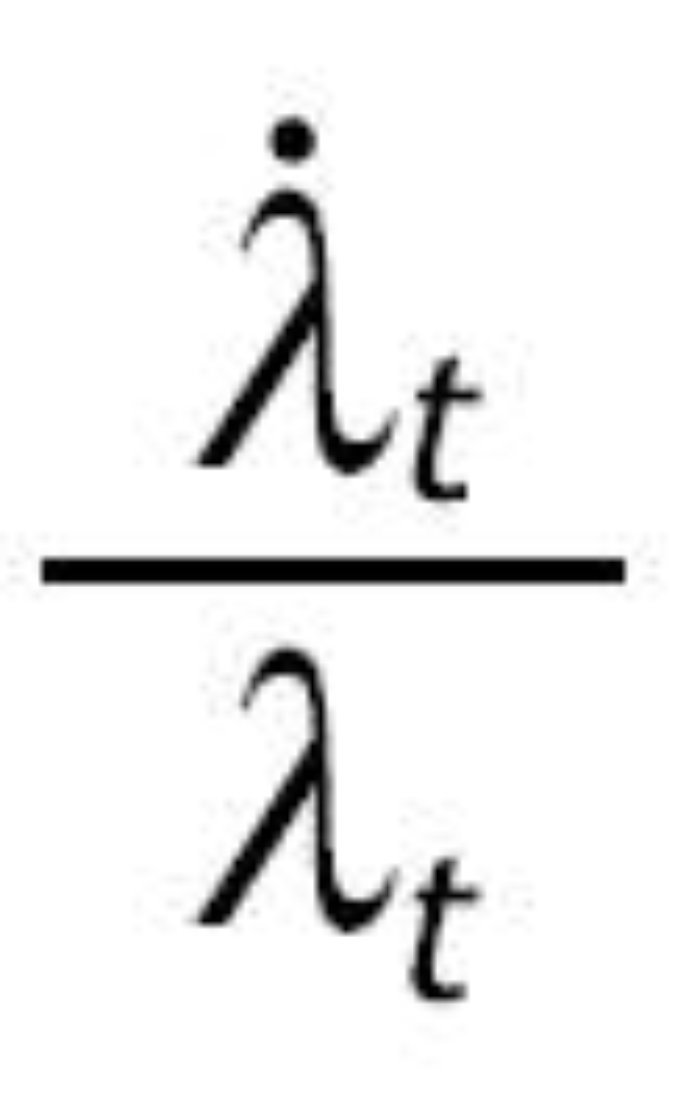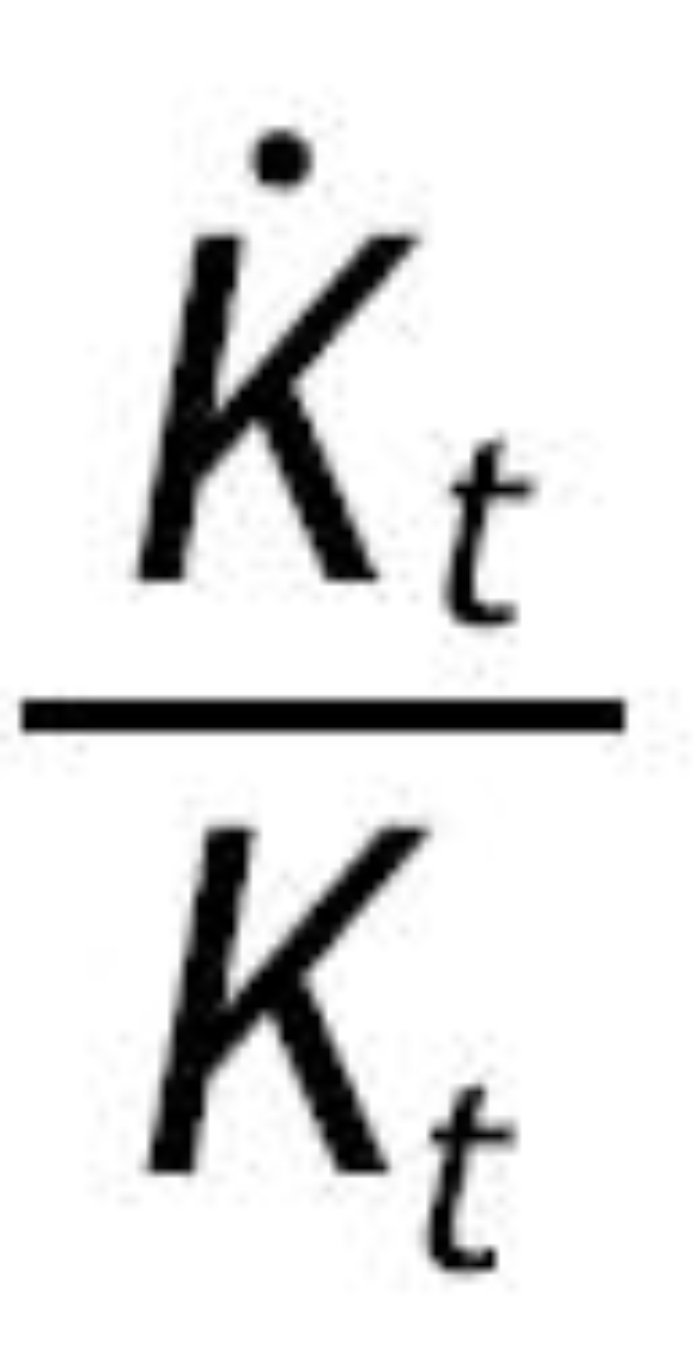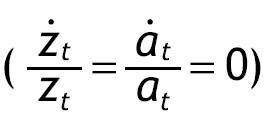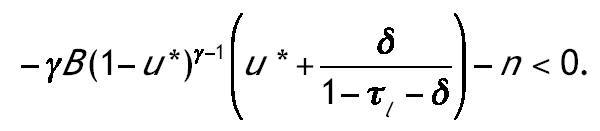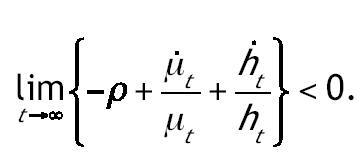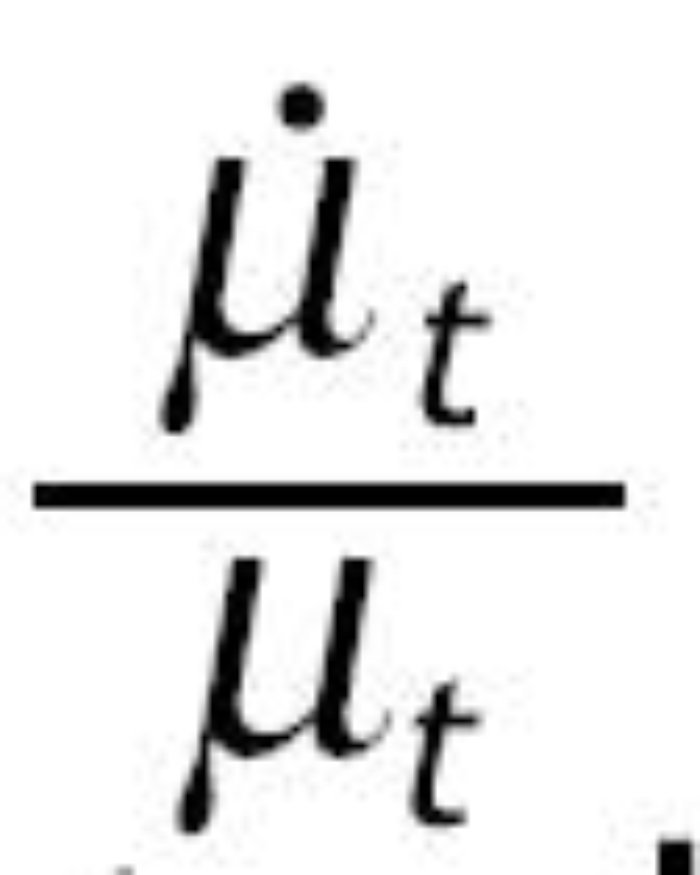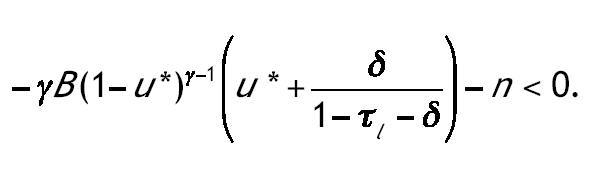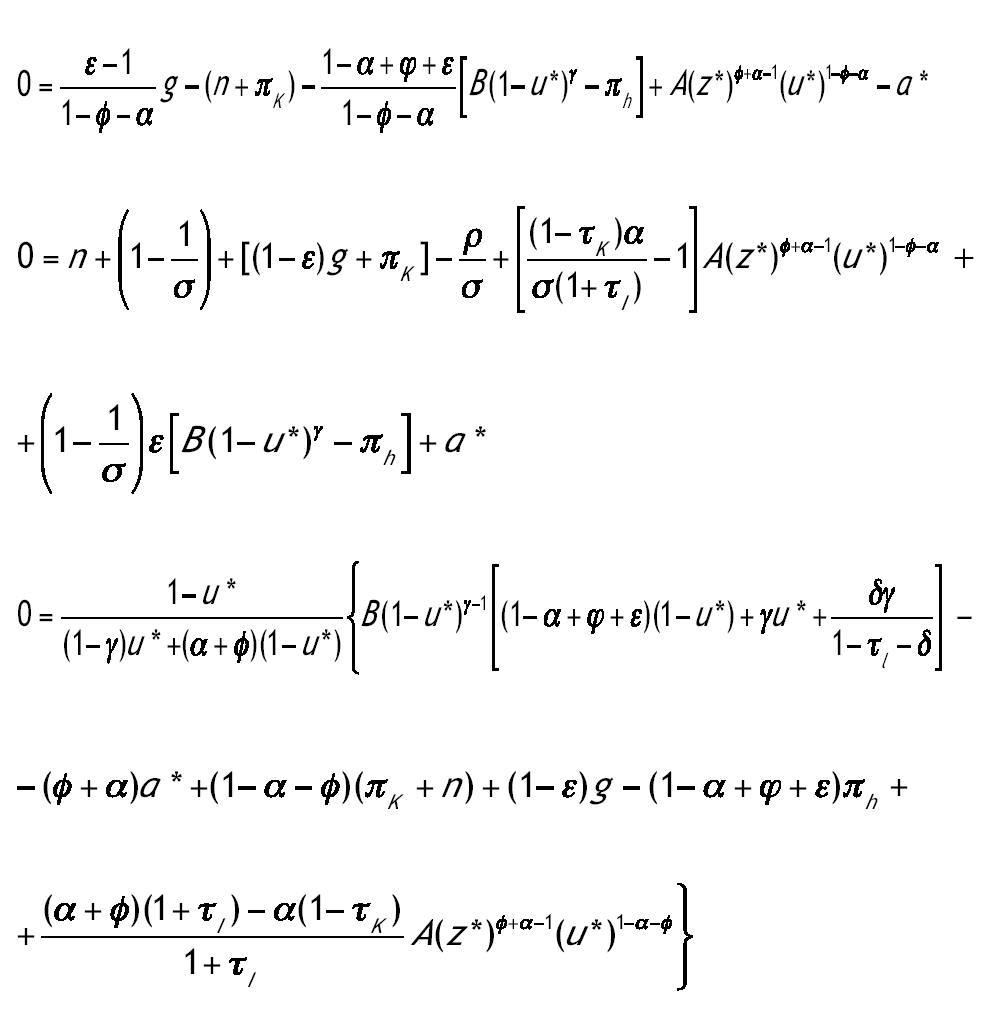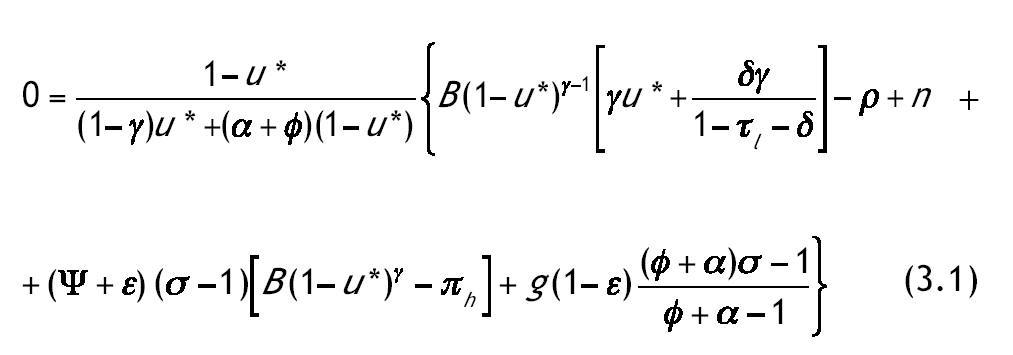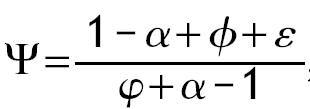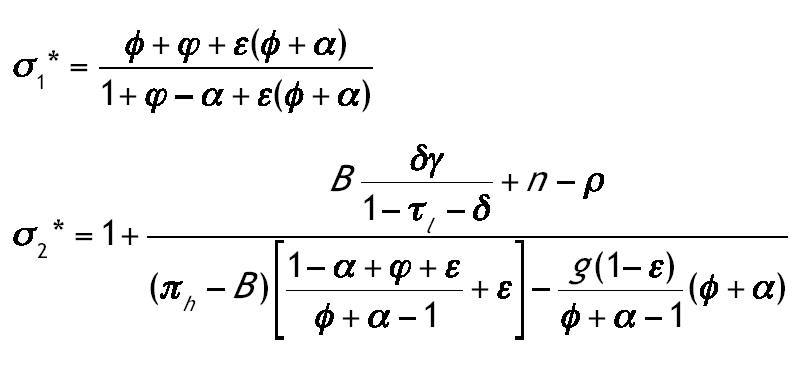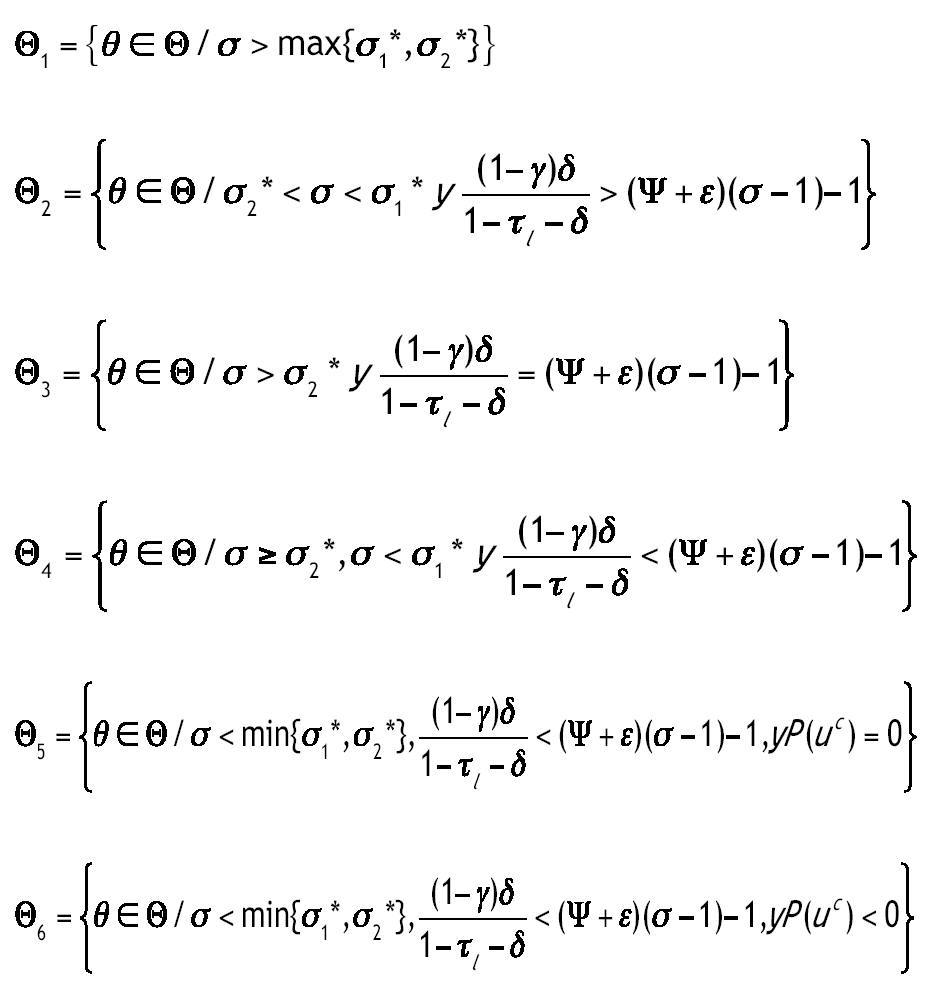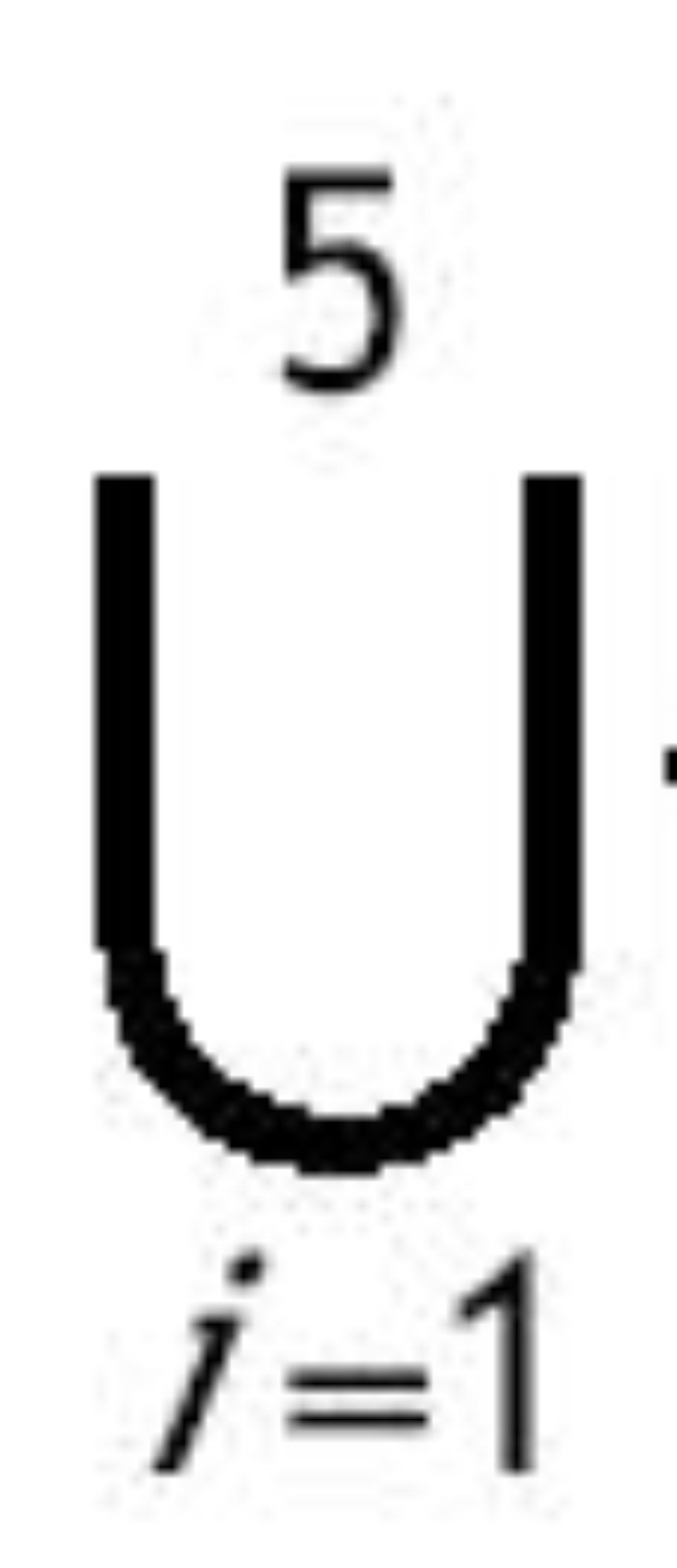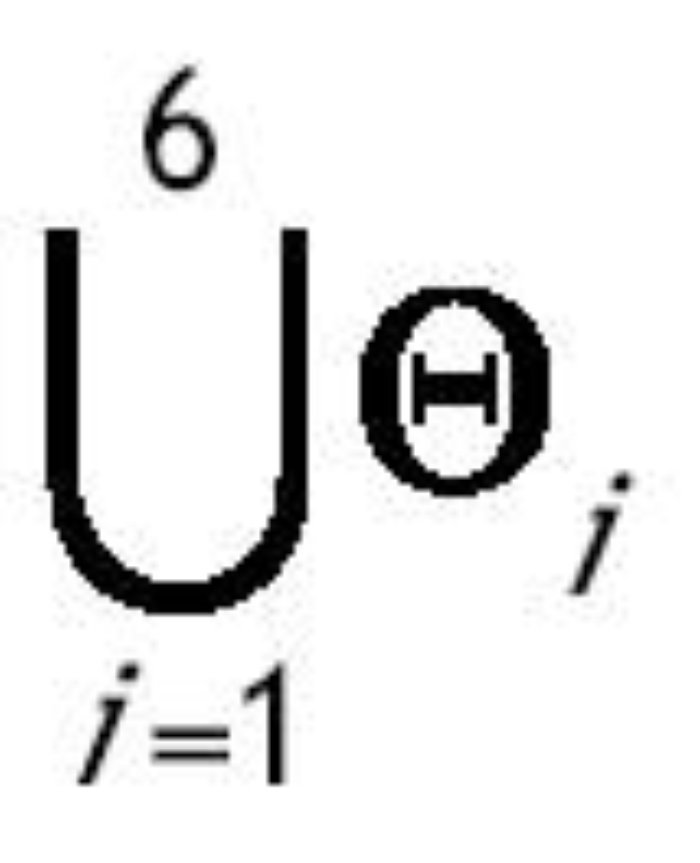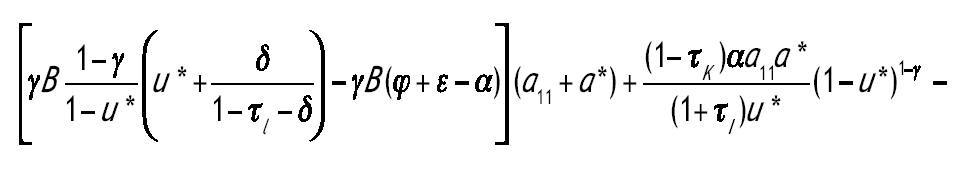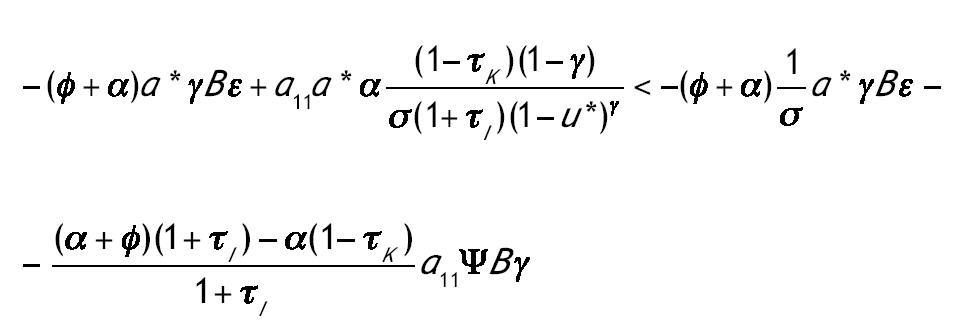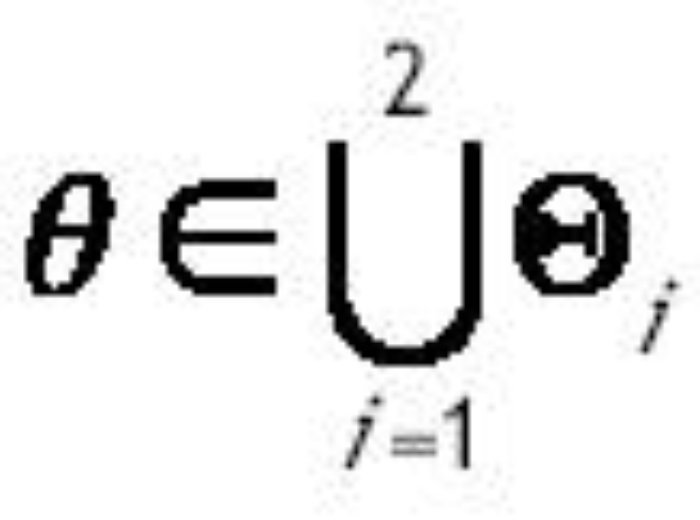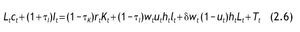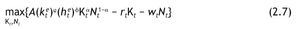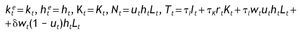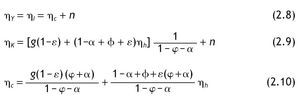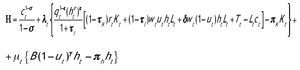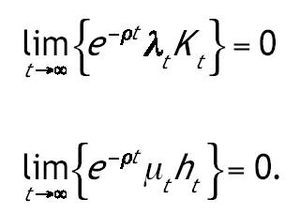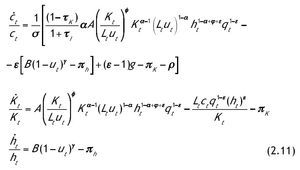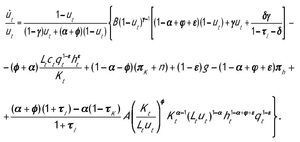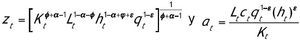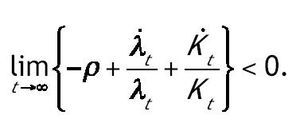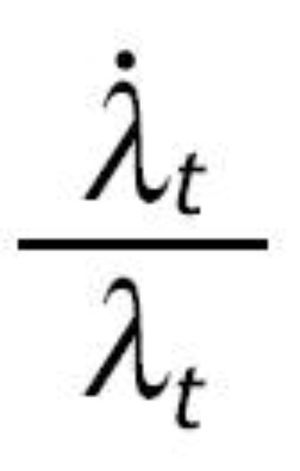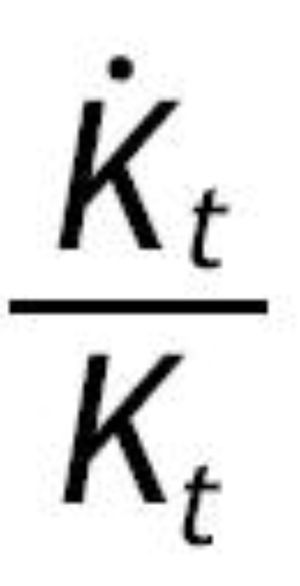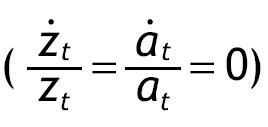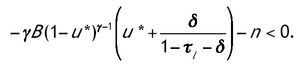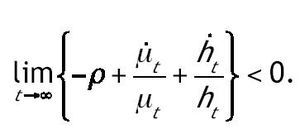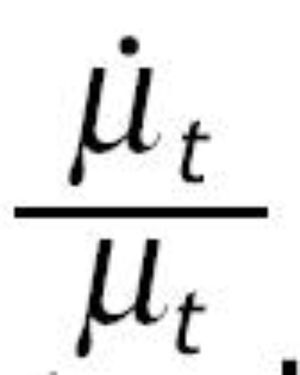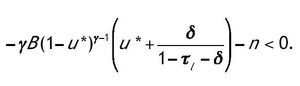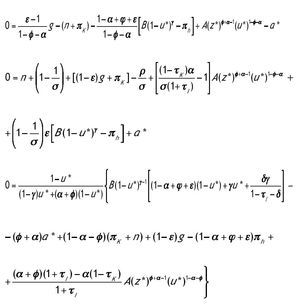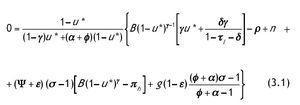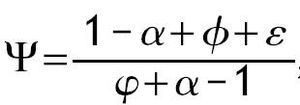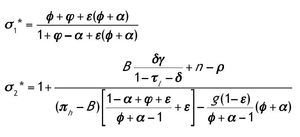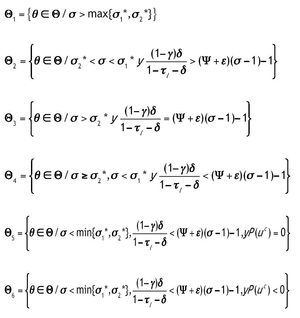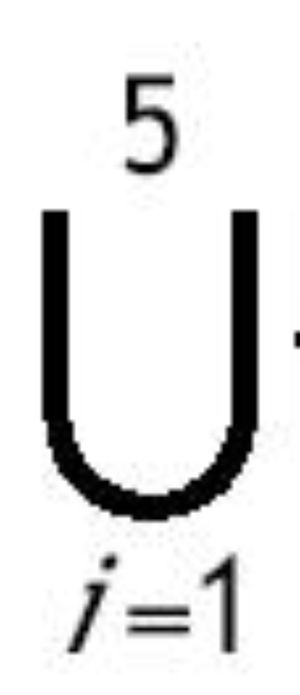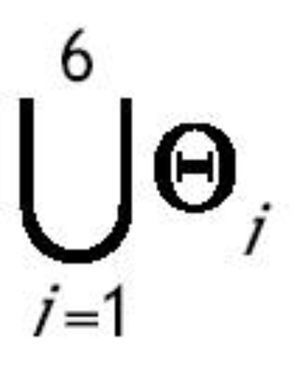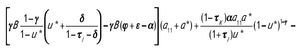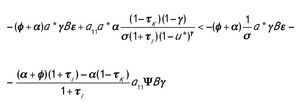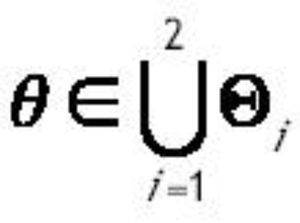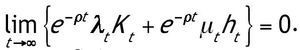En este artículo se estudia la dinámica de una amplia clase de modelos de crecimiento endógeno con dos sectores, externalidades agregadas e impuestos y subvenciones distorsionadores sobre el capital físico y el humano. El análisis incluye el estudio de la dinámica local evaluando la posibilidad de múltiples estados estacionarios y la estabilidad local de dichos estados estacionarios. Los resultados muestran que es posible la existencia de más de una solución estacionaria. También es posible la existencia de indeterminación en la senda de equilibrio, pero este caso es más probable cuando existen dos estados estacionarios.
In this article we study the dynamics of a broad class of two-sector endogenous growth models with external effects and distortionary taxes and subsidies on physical and human capital. In our analysis we focus on local dynamics, assessing the possibility of multiple steady states and their local stability. The results show that the existence of various stationary solutions is possible. The indeterminacy of the equilibrium path is also possible, although it is more likely when there are two steady states.
1. Introducción
Este trabajo estudia la dinámica de una clase de modelos macroeconómicos de crecimiento, centrándose en el estudio de los estados estacionarios, su estabilidad local y la influencia que sobre ellos ejercen distintos impuestos y subvenciones al capital físico y humano.
Numerosos trabajos han estudiado la existencia de múltiples estados estacionarios en modelos de crecimiento. En modelos con un sector sin ocio, la unicidad de la solución estacionaria está garantizada bajo rendimientos constantes a escala. Sin embargo, como demuestran Benhabib y Gali (1994), la existencia de externalidades y rendimientos crecientes puede dar lugar a la presencia de varios estados estacionarios. En modelos de crecimiento con dos sectores de economías óptimas [véase Caballé y Santos (1993)] existe un único continuo de estados estacionarios. Este resultado se mantiene en presencia de externalides provenientes del nivel medio de capital humano como demuestran Benhabib y Perli (1994). Sin embargo, en un modelo similar Alonso- Carrera (2001) prueba que la existencia de rendimientos decrecientes en el esfuerzo dedicado a la educación puede ocasionar la aparición de un segundo continuo de estados estacionarios. Por último, en modelos de dos sectores en los que está presente la decisión ocio-trabajo pueden aparecer múltiples soluciones estacionarias [véase Ladrón de Guevara et al. (1997) y (1999)].
El estudio de la dinámica de estos modelos se ha centrado en muchos casos en la aproximación lineal alrededor del estado estacionario. Los trabajos ya mencionados de Benhabib y Perli (1994) y de Alonso-Carrera (2001) determinan las condiciones bajo las que puede existir indeterminación de la senda de equilibrio mediante el estudio de los autovalores de la matriz del sistema lineal asociado. Sus resultados indican que el parámetro determinante para la existencia de indeterminación es la elasticidad intertemporal de sustitución.
El conocimiento de la dinámica de estos modelos a través del estudio local es limitado y es más interesante intentar comprender las leyes que rigen el modelo fuera del estado estacionario. Sin embargo, la dinámica global resulta más difícil de entender y la falta de soluciones analíticas en la mayoría de los casos obliga a la utilización de métodos de análisis más indirectos. Numerosos trabajos se han dedicado al estudio de la existencia de equilibrio Markoviano en modelos macroeconómicos. Desde el primer trabajo de Lucas y Prescott (1971) en economías de un sector, diversos estudios han ampliado las condiciones bajo las cuales se garantiza su existencia [véase Coleman (1991), Datta et al. (2002), Greenwood y Huffman (1995) y Lucas y Stokey (1987)]. Entre los trabajos con varios sectores destacan Caballé y Santos (1993), que utilizando las propiedades de la función de valor demuestran la continuidad y monotonicidad de la solución en un modelo con dos sectores óptimo. No obstante, estas propiedades no están presentes en todos los modelos con dos sectores. Ortigueira y Santos (2002) presentan una economía con dos sectores en la que la inestabilidad local del estado estacionario conlleva la existencia de ciclos.
En este artículo se estudia el número de estados estacionarios y su dinámica local en una clase de modelos macroeconómicos que incluyen externalidades y subvenciones e impuestos distorsionadores sobre el capital físico y humano. El conocimiento más profundo de los de los efectos de estas variables nos va a ayudar a evaluar diferentes políticas económicas desde un marco teórico.
En la sección 2 presentamos un modelo de dos sectores con acumulación de capital físico y humano. En este modelo existen subvenciones e impuestos distorsionadores sobre los rendimientos del trabajo y del capital físico. También se incluyen externalidades en la función de producción del bien físico, así como en la ley de movimiento del capital físico. En la sección 3 se analiza la dinámica local del modelo. Los resultados muestran que es posible la existencia de más de una solución estacionaria. También es posible la existencia de indeterminación en la senda de equilibrio, pero este caso es más probable cuando existen dos estados estacionarios. Por último la sección 4 presenta las conclusiones. En el anexo del capítulo se incluyen las demostraciones de las proposiciones.
2. El modelo
En esta sección se presenta el modelo objeto de estudio en este artículo. Nuestra economía está formada por una dinastía de agentes representativos cuyo número crece a una tasa exógena. Los individuos de dicha dinastía intentan maximizar la suma descontada de utilidad que se deriva del consumo del único bien físico en la economía y que está representada por:
La función de utilidad tiene elasticidad constante de sustitución y el inverso de la elasticidad intertemporal de sustitución está representado por el parámetro σ > 0, ct es el consumo per cápita en el periodo t y ρ es el factor de descuento. El número de individuos en la economía en el periodo t está representado por Lt y su ley de movimiento viene dada por el proceso exógeno Lt = L0ent con n ≥ 0.
En el proceso productivo del bien físico se emplean dos tipos de recursos: capital físico y trabajo. El factor trabajo está ajustado por el nivel de capital humano del individuo. El proceso productivo está representado por la siguiente función de producción:
El capital físico utilizado en la producción es Kt. La cantidad de trabajo utilizada en el proceso productivo es Ltutht, que se compone del número de individuos que trabajan Lt, del esfuerzo dedicado a las actividades productivas ut y del nivel de educación de los individuos que está representado por el capital humano medio en la economía ht. Cada individuo de esta economía posee una unidad de tiempo del cual puede dedicar una fracción ut a actividades productivas y otra 1 - ut a incrementar su nivel educativo. La participación del capital físico en la renta está representada por el parámetro αÎ(0,1) Esta función de producción incluye además dos efectos externos representados con el superíndice "e". El primero de ellos proviene del capital físico medio por trabajador kt = Kt/(Ltut) y el segundo del nivel medio de capital humano ht. El tamaño de estas externalidades es φ ≥ 0 para el capital físico y f ≥ 0 para el capital humano. El parámetro A representa el nivel de la tecnología.
La producción del bien físico en cada periodo t se puede dedicar a dos fines, o bien se consume o bien se invierte para aumentar el stock de capital físico en el periodo t + 1.
La cantidad de capital físico en la economía evoluciona de acuerdo a la siguiente ley de movimiento:
En esta ley de movimiento el capital físico aumenta debido a la incorporación de la parte de producción no consumida y disminuye por la depreciación, cuya tasa es πK. Sin embargo, la inversión no se incorpora al stock de capital de una forma homogénea. En esta incorporación interviene el proceso qt = q0egt. Este proceso representa el cambio tecnológico presente en los nuevos bienes de inversión y en nuestro modelo es de naturaleza exógena y crece a una tasa g ≥ 0. Como sugirieron Nelson y Phelps (1966) y más tarde Hulten (1992) y Greenwood et al. (1997) introducimos la idea de que las nuevas inversiones en capital son más productivas que las anteriores. De esta forma inversiones en capital de la misma cuantía tienen distinto efecto sobre el stock de capital si son hechas en periodos distintos. Además, el proceso tecnológico qt se incorpora de una manera más efectiva cuanto mayor sea el capital humano medio. Este último efecto está representado por la externalidad hte y el parámetro ε Î[0,1) indica su intensidad. En cuanto al capital humano, evoluciona de acuerdo a la siguiente ley de movimiento:
En esta ecuación el parámetro B > 0 nos indica el nivel tecnológico mientras que 1 - ut es la proporción de tiempo que el individuo dedica a incrementar su nivel educativo. Existe la posibilidad de rendimientos decrecientes a este esfuerzo representados en el parámetroγÎ(0,1]. Por último la tasa de depreciación es πh > 0. Hacemos dos supuestos sobre los valores de los parámetros que serán de utilidad en las dos secciones siguientes:
Supuesto 1: 1 - φ - α > 0
Supuesto 2: B - πh > 0
El primer supuesto implica que no puede haber rendimientos crecientes a escala en el capital físico. El segundo es una condición necesaria para que tasa de crecimiento del capital humano pueda ser positiva.
2.1. El equilibrio competitivo
En este apartado estudiamos el equilibrio competitivo de la economía descrita más arriba; para ello definimos el problema del agente representativo y la maximización a la que se enfrenta la única empresa presente en la economía.
Definición 1: En nuestra economía el problema del agente representativo consiste en elegir las sendas de consumo ct, inversión It y esfuerzo dedicado al trabajo ut en cada periodo que maximizan (2.1) sujeto a (2.2)¿(2.5) y sujeto también a la siguiente restricción presupuestaria:
La ecuación (2.6) implica que los gastos en consumo e inversión no pueden ser superiores a la suma de los ingresos totales. Los ingresos provienen de los impuestos sobre la inversión (1 +τj)It, de los rendimientos del capital después de impuestos (1 - τK)rtKt, de los rendimientos del trabajo después de impuestos δwt (1 - ut)htLt, de los subsidios a la educación δwt (1 - ut)htLt y de las transferencias provenientes del gobierno Tt · τI representa el tipo impositivo sobre la inversión si τI > 0, por el contrario si τI < 0 existe una subvención a la inversión. El parámetro τK representa la tasa impositiva sobre los rendimientos del capital rt Kt, mientras que τl representa la tasa impositiva sobre rendimientos del trabajo. El salario competitivo wt está definido en unidades eficientes de trabajo. La constante δ ≥ 0 representa los subsidios a la educación. En el siguiente supuesto restringimos los valores posibles de las tasas impositivas y los subsidios:
Supuesto 3: 1 - τI- δ > 0
Si el supuesto anterior no se satisface el individuo no tiene incentivos a trabajar y dedica todo su tiempo a la educación.
Definición 2: El problema de la empresa representativa en esta economía consiste en escoger la cantidad de capital Kt y de trabajo Nt que maximizan los beneficios en cada periodo t.
Una vez definidos los problemas del agente y de la empresa definimos el equilibrio competitivo de esta economía.
Definición 3: El equilibrio competitivo de esta economía es un conjunto de secuencias para las cantidades {ct, It,ut,Kt,ht,Tt}∞t=0 para los precios {rt,wt}∞t=0 y de tasas impo¿ sitivas y subsidios constantes τI, τK,τl y δ, tal que tomando los precios como dados y fijadas unas condiciones iniciales, el vector de cantidades cumple las siguientes condiciones:
1) El individuo representativo resuelve su problema.
2) La empresa resuelve su problema.
3) Se cumplen las siguientes condiciones de equilibrio en cada periodo t:
Definición 4: La senda de crecimiento equilibrado (SCE) para esta economía es un conjunto de secuencias de las variables {ct,It,ut,Kt,ht,Tt}∞t=0, de precios {rt,wt}∞=0 y de tasas impositivas y subsidios constantes τI, τK,τl y δ, que satisfacen la definición 3 y que, para unas condiciones iniciales dadas, las variables {ct,It,ut,Kt,ht,Tt} crecen a una tasa constante y ut permanece constante para todo periodo t.
Si definimos las constantes ηY,ηc,ηI,ηK y ηh como las tasas de crecimiento de la producción, el consumo, la inversión, el capital físico y el capital humano en la SCE, podemos deducir las siguientes relaciones utilizando las ecuaciones (2.2)-(2.4),
Para resolver el problema del agente representativo construimos el siguiente hamiltoniano:
Las variables de coestado están representadas por λt y μt. El principio del máximo nos proporciona unas condiciones necesarias que definen un conjunto de posibles soluciones al problema. Estas condiciones necesarias son las condiciones de primer orden del hamiltoniano más dos condiciones de transversalidad1:
Una condición suficiente para que las condiciones de primer orden resuelvan el problema es que el hamiltoniano sea cóncavo conjuntamente en las variables de estado después de sustituir en él las variables de control por sus valores maximizadores. Se puede comprobar fácilmente que este requisito se cumple acudiendo a las condiciones de primer orden de ct y ut. Una vez obtenidas las condiciones de primer orden y habiendo impuesto las condiciones de equilibrio kte = kt y hte = ht obtenemos un sistema de cuatro ecuaciones diferenciales con la ayuda de las leyes de movimiento (2.4)-(2.5):
En este sistema la única variable que es constante en la SCE es ut. De forma similar a Mulligan y Sala i Martin (1993) definimos dos ratios que son función de las variables anteriores y que son estacionarios en la SCE. Las nuevas variables
Se puede comprobar fácilmente utilizando (2.8)-(2.10) que ambos ratios permanecen constantes en la SCE. Para obtener las leyes de movimiento de estas dos nuevas variables tomamos logaritmos y diferenciamos en las definiciones anteriores. Con estas dos definiciones y el sistema (2.11) obtenemos un sistema equivalente reducido en una dimensión:
Por último comprobamos que se satisfacen las condiciones de transversalidad. Una condición suficiente para que se cumpla la del capital físico es:
Sustituimos el valor de
calculado en las condiciones de primer orden y el de
contenido en (2.11) en la expresión anterior. Una vez hecho esto imponemos la condición de estado estacionario
en las dos primeras ecuaciones de (2.12) y de esta forma obtenemos:
Donde u* es el valor en el estado estacionario. Una condición suficiente para la segunda condición de transversalidad es:
Sustituyendo el valor de
de las condiciones de primer orden y la ley de movimiento del capital humano resulta:
3. Dinámica local
Procedemos ahora al estudio de la dinámica local del modelo. De esta forma establecemos las condiciones bajo las cuales es posible la existencia de una, ninguna o más de una solución estacionaria. Además se caracteriza el espacio de parámetros en cuanto a la estabilidad local de dichos estados estacionarios. Para calcular los valores de las variables en la solución estacionaria imponemos que las derivadas de las variables sean iguales a cero en el sistema (2.12). De esta forma se obtiene el siguiente sistema de ecuaciones:
siendo z*, a* y u* los valores de las variables en la SCE. Sustituyendo las dos primeras ecuaciones en la tercera obtenemos una ecuación en la que sólo aparece la variable u*. El número de raíces de esta ecuación permite conocer el número de estados estacionarios interiores para los cuales las condiciones de primer orden son válidas.
Definimos
, de forma que |Ψ| >1 si f + ε > φ y que Ψ< 0. Nótese que no puede darse el caso de una solución estacionaria con u* = 0 ya que iría en contra de la maximización de la utilidad. La solución u* = 1 tampoco es posible paraγÎ(0,1). De ser así, el individuo dedicaría todo su tiempo a trabajar y la derivada de la función de producción de capital humano tendría pendiente igual a infinito. Esto implicaría que la condición en Ladron de Guevara, Ortigueira y Santos (1999) para la existencia de una solución esquina no se cumpliría.
Antes de pasar al estudio de las raíces de la ecuación (3.1) dividimos el espacio de parámetros en varios subconjuntos; para ello definimos antes dos valores de referencia de la elasticidad intertemporal de sustitución.
Bajo el supuesto 1, σ1*Î(0,1). Sea θ el vector que contiene todos los parámetros de nuestro modelo, θ = {σ, ρ, n, A, f, α, φ, ε, g, πK, πh, B, γ, τI, τK,τl, δ}, y sea Q el espacio que contiene todos los posibles valores de θ. Dividimos Q en los siguientes subconjuntos:
La función P(u) está definida por la expresión entre paréntesis en la ecuación (3.1) y uc es el valor de u que hace que la derivada de P(u) sea cero. La siguiente proposición determina la existencia y multiplicidad de los estados estacionarios del sistema para cada uno de los vectores de parámetros en Q.
Proposición 1: La existencia y unicidad de la SCE viene determinada por una de las tres siguientes posibilidades:
1) Si θ Î
Qi sólo existe una SCE y es interior.2) Siθ Î Q6 existen dos SCE interiores u1* < u2*.
3) Si θ Î Q - no existe ninguna SCE.
Demostración: Véase García-Belenguer (2007).
Los conjuntos Θ3, Θ5 y parte de Θ4 tienen igualdades en sus definiciones y prescindimos de su estudio por ser conjuntos de medida cero. Una vez conocidos los valores de los parámetros para los que existe una, dos o ninguna SCE pasamos al estudio de la estabilidad local de dicha solución estacionaria. El procedimiento seguido es similar al utilizado en Benhabib y Perli (1994) y Alonso-Carrera (2001), y consiste en el estudio de la matriz del sistema lineal asociado evaluada en el estado estacionario. Si la matriz posee un autovalor con parte real negativa y dos autovalores con parte real positiva el equilibrio es un punto de silla y la senda de equilibrio es única. Si hay dos autovalores con parte real negativa y uno con positiva existe un continuo de sendas que convergen al estado estacionario. Si los tres autovalores tienen partes reales negativas el estado estacionario es estable y por último si las tres son positivas es inestable. Definimos la matriz del sistema lineal asociado como J*. En la siguiente proposición se caracterizan los signos de los autovalores del sistema lineal correspondiente para los diferentes valores del espacio de parámetros. Las siguientes dos condiciones son utilizadas en dicha proposición.
Supuesto 4: Si ηh* es la tasa de crecimiento del capital humano en la SCE, entonces ηh* > 02.
Supuesto 5: Si la traza de J* es negativa entonces3:
Proposición 2: Bajo los Supuestos 1¿5 la estabilidad de los estados estacionarios viene determinada por una de las siguientes tres posibilidades:
1) Si hay dos autovalores con partes reales positivas y uno con negativa, por lo tanto el equilibrio es único.
2) Si θÎΘ4 pueden existir o bien tres autovalores con partes reales positivas o bien uno. En el primer caso el estado estacionario es inestable, en el segundo, existe un continuo de sendas de equilibrio.
3) Si θÎΘ6 la matriz del sistema lineal evaluada en u1* puede tener o bien tres autovalores con partes reales positivas o bien uno. La matriz evaluada en u2* tiene dos autovalores con partes reales positivas.
Demostración: Véase el anexo.
4. Conclusiones
En este trabajo se han estudiado los efectos de subvenciones e impuestos sobre el capital físico y humano en la dinámica de un modelo de crecimiento endógeno con externalidades en la función de producción y en las leyes de movimiento de los stocks de capital. En el estudio de la dinámica local, se ha caracterizado la existencia y el número de estados estacionarios así como su estabilidad local a través del estudio de la matriz del sistema lineal asociado. Los resultados muestran que es posible la existencia de más de una solución estacionaria y que también es posible la existencia de indeterminación en la senda de equilibrio. La existencia de dos SCE y trampas de pobreza es posible para valores suficientemente altos de la elasticidad intertemporal de sustitución, la concavidad de la función de producción de capital humano y los efectos externos. Además, los impuestos sobre el trabajo y los subsidios a la educación pueden determinar si la economía posee una, dos o ninguna solución estacionaria. También se demuestra que un equilibrio indeterminado es posible si hay dos SCE y trampas de pobreza.
Anexo
Recibido el 24 de noviembre de 2011; aceptado el 7 de marzo de 2012
Correo electrónico: fernando.garciabelenguer@uam.es
1. Sería suficiente escribir la condición de transversalidad como
Las dos condiciones expuestas arriba son suficientes para que se satisfaga esta última.
Bibliografía
Alonso-Carrera, J., 2001. More on dynamics in the endogenous growth model with human capital. Investigaciones Económicas 25(3), 561-583.
Benhabib, J., Gali, J., 1994. On growth and indeterminacy: Some theory and evidence. Carnegie-Rochester Conf. Ser. Public Policy 43, 163-212.
Benhabib, J., Perli, R., 1994. Uniqueness and indeterminacy: Transitional dynamics in a model of endogenous growth. Journal of Economic Theory 63, 113-142.
Caballé, J., Santos, M.S., 1993. On endogenous growth with physical and human capital. Journal of Political Economy 101, 1042-1068.
Coleman, W.J., 1991. Equlibrium in a production economy with an income tax. Econometrica 59,1091-1104.
Datta, M., Mirman, L.J., Reffett, K., 2002. Existence and uniqueness of equilibrium in distorted dynamic economies with capital and labor. Journal of Economic Theory 103, 377-410.
Gantmacher, F.R., 1960. The theory of matrices. Chelsea Pub. Co., Nueva York.
García-Belenguer, F., 2007. Stabiliy, global dynamics and Markov equilibrium in models of endogenous economic growth. Journal of Economic Theory 136, 392-416.
Greenwood, J., Hercowitz, Z., Krusell, P., 1997. Long run implications of investment-specific technological change. American Economic Review 87, 342-362.
Greenwood, J., Huffman, G., 1995. On the existence of non-optimal equilibria in dynamic stochastic economies. Journal of Economic Theory 65, 611-623.
Gordon, R., 1990. The measurement of durable goods prices. University of Chicago Press, Chicago.
Hulten, C.R., 1992. Growth accounting when technical change is embodied in capital. American Economic Review 82(4), 964-80.
Ladrón-de-Guevara, A., Ortigueira, S., Santos, M.S., 1997. Equilibrium dynamics in two-sector models of endogenous growth. Journal of Economic Dynamics and Control 21, 115-143.
Ladrón-de-Guevara, A., Ortigueira, S., Santos, M.S., 1999. A model of endogenous growth with leisure. The Review of Economic Studies 66, 609-632.
Lucas, R.E., 1988. On the mechanics of economic development. Journal of Monetary Economics 22, 3-42.
Lucas, R.E., Prescott, E.C., 1971. Investment under uncertainty. Econometrica 39, 659-681.
Lucas, R.E., Stokey, N.L., 1987. Money and interest in a cash-in-advance economy. Econometrica 55, 491-513.
Mulligan, C., Sala-i-Martin, X., 1993. Transitional dynamics in two-sector models of endogenous growth. Quarterly Journal of Economics 108, 739-775.
Nelson, R., Phelps E., 1966. Investment in humans, technological diffusion and economic growth. American Economic Review 56, 69-75.
Ortigueira S., Santos, M.S., 2002. Equilibrium dynamics in a two-sector model with taxes. Journal of Economic Theory 105, 99-119.
Santos, M.S., 2002. On non-existence of Markov equilibria in competitive-market economies. Journal of Economic Theory 105, 73-98.
Xie, D., 1994. Divergence in economic performance: Transitional dynamics with multiple equilibria. Journal of Economic Theory 63, 97-112.