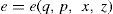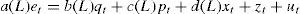Limitar el calentamiento global para evitar un cambio climático peligroso requiere una drástica reducción de las emisiones de gases de efecto invernadero y la transformación hacia una sociedad hipocarbónica. Los modelos económicos energético y climático, que sustentan la toma de decisiones políticas en la actualidad en el camino hacia una sociedad de cero emisiones netas, se perciben con creciente escepticismo en cuanto a su capacidad para pronosticar la evolución de sistemas socio-ecológicos altamente complejos y no lineales. Presentamos un revisión sistemática de la literatura de los últimos avances de los enfoques de modelización, centrándonos en su capacidad y limitaciones para desarrollar y evaluar las trayectorias hacia una sociedad hipocarbónica. Encontramos que los enfoques metodológicos existentes tienen algunas deficiencias fundamentales que limitan su potencial para entender las sutilezas de los procesos de descarbonización a largo plazo. Por tanto, un marco metodológico útil debe ir más allá de las actuales técnicas cumpliendo simultáneamente los siguientes requisitos: 1) representación de un análisis inherentemente dinámico, describiendo e investigando explícitamente las trayectorias entre los diferentes estados de las variables del sistema, 2) especificación de los detalles de la cascada energética, particularmente el papel central de las funcionalidades y servicios provistos por la interacción de flujos energéticos y las correspondientes variables de stock, 3) presentación de una clara distinción entre estructuras del sistema energético sociotécnico y los mecanismos socioeconómicos para desarrollarlo, y 4) capacidad para evaluar las trayectorias conjuntamente con criterios sociales. Para ello proponemos el desarrollo de un marco de modelización integrado versátil y multiobjetivo, partiendo de las fortalezas de los varios enfoques de modelización disponibles al mismo tiempo que excluyendo sus debilidades. Este estudio identifica las respectivas fortalezas y debilidades para guiar dicho desarrollo.
Limiting global warming to prevent dangerous climate change requires drastically reducing global greenhouse gases emissions and a transformation towards a low-carbon society. Existing energy- and climate-economic modeling approaches that are informing policy and decision makers in shaping the future net-zero emissions society are increasingly seen with skepticism regarding their ability to forecast the long-term evolution of highly complex, nonlinear social-ecological systems. We present a structured review of state-of-the-art modeling approaches, focusing on their ability and limitations to develop and assess pathways towards a low-carbon society. We find that existing methodological approaches have some fundamental deficiencies that limit their potential to understand the subtleties of long-term low-carbon transformation processes. We suggest that a useful methodological framework has to move beyond current state of the art techniques and has to simultaneously fulfill the following requirements: (1) representation of an inherent dynamic analysis, describing and investigating explicitly the path between different states of system variables, (2) specification of details in the energy cascade, in particular the central role of functionalities and services that are provided by the interaction of energy flows and corresponding stock variables, (3) reliance on a clear distinction between structures of the sociotechnical energy system and socioeconomic mechanisms to develop it and (4) ability to evaluate pathways along societal criteria. To that end we propose the development of a versatile multi-purpose integrated modeling framework, building on the specific strengths of the various modeling approaches available while at the same time omitting their weaknesses. This paper identifies respective strengths and weaknesses to guide such development.
The 2015 Paris Agreement showcased that the global society is stepping up to tackle dangerous climate change by aiming at limiting global average temperature increase to below 2 ºC, seeking 1.5 ºC (IPCC, 2014). The Fifth Assessment Report of the Intergovernmental Panel on Climate Change (IPCC, 2014) pointed out that to achieve this ambitious target with a likely chance, a transformation towards a net-zero carbon society has to be achieved by the end of the century, requiring large-scale changes in global as well as regional to local energy systems (IPCC, 2014). However, since global anthropogenic greenhouse gas (GHG) emissions have never been as high as today (Edenhofer et al., 2014), current incentive structures appear insufficient to catalyze such a transformation. Thus, additional policies are required to foster the necessary levels of investment into low-carbon technologies and behavioral change, and to stimulate technological as well as social innovation.
In developing these policies, climate- and energy-economic modeling is crucial for decision support. The number of such models has grown tremendously in recent years, fostered also by large and cheap computing capacities. At the same time existing energy- and climate-economic modeling approaches are being confronted with increasing skepticism with respect to their ability to forecast the long-term evolution of highly complex and nonlinear social-ecological systems such as the socioeconomic-climate-energy nexus considered in this paper, and to assess the transformation pathways leading to the desired low-carbon society (see e.g. Pindyck, 2013; Pindyck and Wang, 2013; Anderson, 2015; Stern, 2016). In particular, there is increasing concern – at least since the publication of the Stern Review (Stern, 2007) – regarding the applicability of the traditional neoclassical economic paradigm in long-term transformation analyses, as some major principles and implicit modeling mechanisms are questioned: the concept of economic equilibrium, the supremacy of market mechanisms, the relevance of relative prices as main endogenous driver of technological change, the implicit behavioral assumptions (profit- and utility maximizing rational agents), the incremental dynamics of technologies (based on exogenous assumptions for total factor productivity improvements), the emphasis on flows (GDP and consumption levels) over stocks (built and natural environment), and the critical role of the discount rate (cf. Barker, 2008). Moreover, the question arises whether it is feasible at all to predict the future evolution of social-ecological systems in the presence of deep or fundamental uncertainties (variations around expected system behavior that cannot be quantified) and (potentially non-stationary) catastrophic risks (Scrieciu et al., 2013).
The existing models to assess different energy- and climate-economic research questions vary considerably and the question arises which model is most appropriate for a certain purpose or situation. Therefore, in the following we seek to answer: What kind of modeling framework is most suitable for assessing the long-term transformation processes needed to drastically reduce global GHG emissions? The aim of this paper is to provide a structured review of state-of-the-art national and international energy- and climate-economic modeling approaches with respect to their ability and limitations to develop pathways for a low-carbon society (including its economy).
In a first step we suggest a set of relevant characteristics for the evaluation of different modeling approaches regarding their suitability for long-term transformation analyses. In a second step we identify specific methodological approaches that have been used in analyses of climate and energy policies in national and international contexts. In a third step, we evaluate these different climate- and energy-economic modeling approaches in terms of their strengths and weaknesses with respect to their ability of carrying out low-carbon transformation analyses and discuss their advantages and disadvantages to that end. The Appendix finally presents in more detail representative models and applications for each modeling approach.
2Characteristics for the evaluation of climateand energy-economic modeling approachesA general characteristic all models share is that a model is a purposeful and simplified representation of aspects of reality (Starfield et al., 1990). Purposeful since a model is always developed in order to answer a specific research question. Simplified because first, the just identified concrete purpose of a model already paves the way for a simplified representation of this specific aspect of reality only, and second, real world constraints, such as limited time and financial resources, also require simplifications.
Besides this general characteristic there are many individual characteristics which differ substantially between modeling approaches. Hence, it seems reasonable to assess existing climate- and energy-economic modeling approaches in order to allow for an identification of the most appropriate approach for the problem setting at hand – out of the multitude of existing models out there. While there have been some attempts in the literature to classify existing energy models (Grubb et al., 1993; Hourcade et al., 1996; van Beeck, 1999; Herbst et al., 2012), no systematic assessment of energy-economic models serving the purpose of analyzing transformation pathways towards a low-carbon society has been carried out so far. Hence, by relying on the existing literature on energy model classification, we identify the eight most important characteristics to evaluate existing energy-economic modeling techniques. We put special emphasis on certain (sub)characteristics, mainly linked to the model structure and modeled mechanisms, which are crucial for the models’ suitability for long-term transformation analyses. The eight characteristics include (cf. van Beeck, 1999):
- 1.
The general purpose and intended use.
- 2.
The analytical approach and conceptual framework (top-down, bottom-up, integrated assessment, hybrid energy-economy model).
- 3.
The model structure and exogenous assumptions: modeled mechanisms and assumptions (implicit/ endogenous and explicit/exogenous mechanisms/ assumptions; technological details). How an energy-economic model treats the following elements is crucial for its ability to carry out long-term transformation analyses.
- a.
Energy system: (disruptive/nonlinear) technological change; technological detail; detailed representation of the energy cascade, in particular of functionalities, defined as energy services (related to thermal, mechanical and specific electric tasks) that are provided by the interaction of energy flows and corresponding stock variables (Schleicher et al., 2016).
- b.
Economic system: international (trade) relations; price & market mechanisms; economic feedbacks and rebound effects; non-market mechanisms (such as non-market damages and climate feedbacks); equilibrium vs. out of equilibrium situations; financing/investment (e.g. energy efficiency measures); stocks vs. flows; structures vs. mechanisms – how do mechanisms influence structures?
- c.
Social system: behavioral mechanisms; governance and institutions; risk and uncertainty.
- a.
- 4.
The time horizon.
- 5.
The underlying methodology (Optimization, Sim-ulation, Econometric, Equilibrium etc.; statistical estimation vs. calibration).
- 6.
The treatment of path dynamics (Comparative Static vs. Dynamic (“path explicit”)) and the development of a baseline/reference scenario.
- 7.
Geographical and sectoral coverage.
- 8.
Data requirements.
The listing of these characteristics already follows an ordinal/hierarchical logic modelers could follow when setting out to identify the most appropriate approach for their very specific research questions. Modelers first have to be clear about the general and more specific purpose of the model. Next the analytical approach has to be chosen, i.e. whether the model should rather take a top-down or bottom-up or hybrid perspective. Closely related is the choice of the modeling structure which boils down to choosing what mechanisms should endogenously be determined within the model and what mechanisms should be based on exogenous assumptions. Before choosing the specific underlying methodology of the model, a modeler should also reflect on the time horizon his model should be able to operate in. After deciding on all these characteristics and choosing a specific method, the question of whether one wants to be path explicit needs to be answered. Finally, the geographical and sectoral coverage has to be decided, and the data requirements have to be assessed.
2.1Purpose and intended useModeling is a general kind of activity that follows certain principles independent on what is modeled and what technique is used. As mentioned above, a model is always a purposeful and simplified representation of an aspect of reality. Hence, models are usually developed to address specific research questions and are only applicable for the purpose they have been designed for. An application of a specific modeling technique for an inappropriate purpose may lead to significant misinterpretations of the problem at hand and eventually to misleading policy recommendations affecting real world social-ecological systems negatively. In the following we distinguish between general and more specific purposes of an energy-economic model.
2.1.1General purposeHourcade et al. (1996) define the general purpose of a model as the different ways how the future is addressed in a modeling framework and distinguish between three general purposes which are also applicable in the case of energy-economic models:
- 1.
Prediction or forecasting models. Many models are developed to try to “predict” the future and to estimate impacts of likely future events. This purpose imposes very strict methodological constraints on modelers as forecasting models require the establishment of a business as usual scenario against which future policy induced deviations from this best-guess future development can be assessed. This requires an endogenous representation of economic behavior and general growth patterns. Such models are based on the extrapolation of trends found in historical data and try to minimize the usage of exogenous parameters. Models built for a predictive purpose are most suitable for short term analyses, since a number of critical underlying parameters (such as elasticities of substitution) cannot reasonably be assumed to remain constant for longer time frames. Hence, this approach is mainly found in short term, econometrically driven economic analyses.
- 2.
Explorative scenario analyses models. Due to the inherent difficulties associated with the extrapolation of past trends in the long run, modelers might set out to “explore” rather than “predict” the future. An explorative purpose can be served by employing a scenario analysis approach. This requires the definition of different coherent visions of the future, determined by different values for key assumptions about economic behavior, economic growth, population growth, (natural) resource endowments, productivity growth, technological progress etc. A reference or nonintervention scenario is developed and then contrasted to different policy or intervention scenarios. It is important to note that these alternative scenarios only make sense in relation to the reference scenario and should therefore not be analyzed in isolation from it or in absolute terms. Furthermore, sensitivity analyses are crucial to provide information on the effects of changes in underlying assumptions.
- 3.
Backcasting models. The basic concept of backcasting models is to look back from desired futures, which are developed e.g. in expert stakeholder processes, to the present, and to develop pathways for actions that have to be taken in order to reach these desired futures. The backcasting methodology allows for the identification of major (technological) changes and discontinuities that might be required as well as institutional hurdles that need to be overcome to achieve a certain desirable state of the future.
More specific purposes are linked to the aspects of the economy, energy system, or the environment a model focuses on. With respect to energy-economic models one could distinguish between models that serve the purpose of modeling energy demand, energy supply, economic or environmental impacts from energy supply or conducting project appraisals (van Beeck, 1999). Historically there has been a strong focus on single-purpose models, contemporary models often pursue an integrated approach. Demand-supply matching models and impact-appraisal models are two examples of multi-purpose energy-economic model approaches.
2.2Analytical approach and the conceptual frameworkModels for the analysis of a low-carbon energy transformation can also be classified according to their degree of detail. On the one end of the spectrum there are bottom-up techno-micro-economic models, which are built to describe economic sectors or sub-sectors (e.g. the electricity sector). These models are rich in (technological) detail and are well suited to simulate market penetration and related cost changes of new (energy) technologies, to present detailed pictures of plausible energy futures and to evaluate sector- or technology-specific policies. However, this technological detail comes at the cost of a limited representation of macroeconomic implications. Bottom-up models typically do not capture feedback effects with other parts of the social-ecological system (e.g. other economic sectors, broader macro-economic relationships, users, the public sector, the environment, the climate system etc.).
On the other end of the spectrum there are “top-down” economic models with only limited explicit representation of alternative technologies using elasticities to implicitly reflect technological variability. They may even be more abstract and aggregated “integrated assessment models” (IAMs) or “hybrid energy-economic models”, which strive to close the loop between a specific economic activity and the surrounding environment. Within the class of IAMs one can further distinguish between “hard-linked” models which are built as one set of consistent (differential) equations, working within one closed model system, and “soft-linked” models which couple separate models and solve them sequentially using input/output exchange routines. In general, IAMs allow capturing feedback effects between aspects of the system under consideration (economy, climate system, society, other environment). However, both types of IAMs have shortcomings: Hard-linked models usually work on a very coarse level of detail by using (e.g. damage-) functions relating e.g. economic indices like a region’s GDP and global mean temperature changes. Such simplifications are problematic as effects within the economic system cannot be revealed and they can hardly be used to account for singular events, tipping points and catastrophic risks (Stern, 2016). Damage functions have often been calibrated based on limited expert judgment, which has implications for their validity (see the recent debate on Integrated Assessment Modeling and Social Costs of Carbon: e.g. Pindyck, 2013; Pindyck and Wang, 2013). Moreover, when it comes to climate change mitigation, IAMs struggle to adequately represent nonlinear developments in low-carbon energy technologies and the potential knowledge spillover into the wider economy (Stern, 2016). Soft- linked models on the other hand allow for more detail; however problems may arise in convergence and consistency among the models used.
In general, the distinction between top-down and bottom-up models is of substantial importance, as both approaches tend to deliver different – sometimes even opposite – outcomes. The difference in model outcomes of top-down and bottom-up modeling approaches arises from the distinct ways how these models treat technological change, the adoption of new technologies, the decision making of agents and how markets and institutions operate (Hourcade et al., 1996). Grubb et al. (1993) associates the top-down approach with a “pessimistic” economic paradigm and the bottom-up approach with a more “optimistic” engineering paradigm.
Purely economic top-down models and much more so IAMs often have no explicit representation of technologies. In many economic models technologies are regarded as a set of techniques by which a combination of inputs can be used to produce useful outputs, typically represented by production functions. Elasticities of substitution between different inputs in an aggregate technology production function are employed to implicitly reflect technological variety and in combination with an exogenous assumption of so-called “autonomous energy efficiency improvements” (i.e. efficiency improvements which happen w/o any explicitly modeled technological change) account for technological change in top-down economic models.
Engineering studies, on the other hand, start with a description of technologies, including their performances and direct costs, to identify options for technological improvements. From an engineering standpoint, the most energy efficient technologies have not been adopted so far and therefore an “efficiency gap” prevails, which could be closed by employing the most energy efficient technologies. The differences in outcomes eventually arise from the fact that the “optimistic” engineering bottom-up models tend to ignore existing constraints which hinder the actual adoption of most efficient technologies, such as hidden costs, transaction costs, implementation costs, market imperfections and macroeconomic relationships (Grubb et al., 1993).
A further distinction between bottom-up and top-down models can be drawn along the lines of data used in the different model analyses. While top-down economic models use aggregated data to examine interactions of different economic sectors as well as macroeconomic performance metrics, bottom-up models usually focus on one specific sector exclusively (e.g. the energy sector) and therefore use highly disaggregated data to describe energy technologies and end-use behavior in greater detail. Hourcade et al. (1996) summarizes (in the context of mitigation cost studies) that existing bottom-up and top-down modeling approaches are primarily meaningful at the margin of a given development pathway. Therefore their application is valid under the following conditions: (1) Top-down models are valid “as long as historical development patterns and relationships among key underlying variables hold constant for the projection period” (Hourcade et al., 1996) while (2) bottom-up models are valid “if there are no important feedbacks between the structural evolution of a particular sector in a mitigation strategy and the overall development pattern” (Hourcade et al., 1996).
While historically the distinction between bottom-up and top-down energy-economic models has provided the framework for the contemporary modeling debate, there have been first attempts to develop “hybrid” models, merging the benefits of both analytical approaches (Hourcade et al., 2006; Catenazzi, 2009; Jochem, 2009; Schade et al., 2009). For example a more detailed representation of different electricity generation technologies has been integrated in top-down economic models (Steininger and Voraberger, 2003; Böhringer and Rutherford, 2008).
2.3Model structure: endogenously modeled mechanisms and exogenous assumptionsDifferent research questions are addressed by different models, capturing only those mechanisms of the real world that are relevant to answer the stated question (i.e. to serve their purpose). Therefore another basis for the distinction of different modeling approaches is the nature of the model itself or, more precisely, the assumptions and mechanisms embedded in the mathematical structure of the model. Hourcarde et al. (1996) distinguish between four major dimensions to characterize structural differences of existing energy-economic models.
The first structural characteristic relates to the degree of endogenization, the extent to which behavioral assumptions and mechanisms are endogenized in the model equations so as to minimize the number of exogenous parameters. The more behavioral assumptions and mechanisms models endogenize, the better they are suited to predict actual outcomes. Those models that are treating most mechanisms as exogenous are, on the other hand, more suited to simulate the effects of changes in historical patterns (Hourcade et al., 1996).
The second structural characteristic describes the extent to which non-energy sector components of the economy or the environment are considered. The more detailed a model describes these mechanisms, the better it is suited for the analysis of wider economic effects of energy policy measures. A huge variety of models designed to serve different purposes can be found, which endogenize very different assumptions or mechanisms, such as economic, behavioral, engineering, geophysics or earth science mechanisms. There are also models capturing not only one of these mechanisms but a portfolio of them. The question of modeled mechanisms closely relates to the choice of the analytical framework, as for example IAMs aim to include as many mechanisms as possible, and – at least in their current state – are, however, subject to severe drawbacks as well (e.g. highly uncertain damage functions, inability to reflect catastrophic risk, arbitrary functional forms and parameter choice; see e.g. Pindyck, 2013, 2015; Pindyck and Wang, 2013; Stern, 2016).
Many state of the art economic models only capture a limited amount of economic and other mechanisms explicitly. In Computable General Equilibrium (CGE) models, for example, the sole mechanism that leads to the new equilibrium after an exogenous shock is the relative price mechanism. Many other mechanisms capturing behavioral, political, social, technological elements are neglected. Hence, the potential real world implications derived from results of such modeling exercises have to be critically reflected and complemented by other modeling techniques to eventually derive a more comprehensive and holistic picture. With respect to the analysis of long run low-carbon transformation pathways, there is increasing concern regarding the applicability of traditional economic models rooted in neoclassical economic theory, as some main modeling characteristics and implicit mechanisms are questioned: the relevance of prices, the implicit behavioral assumptions, the dynamics of technologies, the emphasis on flows over stocks.
The third and fourth structural characteristics refer to the extent of description of energy end uses and energy supply technologies, respectively. Models that describe end uses in more detail are more suitable for the analysis of energy efficiency measures, while models that focus on endogenizing energy supply technologies are more suitable for the analysis of technological potentials (Hourcade et al., 1996).
Moreover, the various model specifications have to be checked whether they are able to separate the description of the structure – e.g. the elements of an energy system – from the mechanisms that are generating these structures. This is a major problem with neoclassical specifications since they intimately link structures and mechanisms. Similar problems might occur with system dynamic (SD) and agent based modeling (ABM) type specifications.
Every type of model is relying on exogenously given parameter values and assumptions regarding interdependencies within the scope of parameters and variables which are in turn triggering endogenous responses within the model. A crucial task in modeling is to decide whether a model element is determined endogenously or exogenously, depending on the underlying question to be answered. In CGE models, for example, modelers have to choose between certain variants of economic model “closures” (savings-investment, government budget, external balance). Furthermore, while some economic models such as CGE or Input-Output (IO) models assume certain behavioral characteristics of agents (e.g. utility and profit maximization, representative agents) other approaches (ABM or SD) set out to endogenously derive behavioral details related to the emergence of complex phenomena.
2.4Time horizonModelers have to be clear about the time horizon underlying their analyses, as different economic, social and environmental processes may behave differently or become relevant at different time scales. Hence the time horizon eventually affects the choice of the specific modeling methodology (see the following section), as long run analyses may assume economic equilibrium in which all markets clear and all resources are fully allocated, while short-run models need to incorporate transformation dynamics and situations of disequilibrium (at least in some markets e.g. unemployment). With respect to the definition of different time horizons, no standard procedure exists. However, in model-based energy economic assessments short term is often assumed to reflect periods of five years or less, the medium term to range between 3 and 15 years and the long term to start at 10 years and beyond.
2.5Underlying methodologyFor energy and climate change related socioeconomic analyses the following methodological approaches have been employed, and are thus discussed in detail in Section 3 below:
- •
Econometric Models
- •
Macroeconomic (Post-Keynesian) Input-Output Models
- •
Neoclassical Economic Equilibrium Models
- •
System Dynamics and Simulation Models
- •
Backcasting Models
- •
Optimization Models
- •
Partial Equilibrium Models
- •
Multi agent or Agent Based Models (ABM)
One aspect relevant across the above methodological approaches is the issue of optimization versus simulation. Building a model aims to serve a general purpose (prediction, exploration, backcasting) and to answer a more specific question of interest, all within a specific time horizon. The character of this stated question then determines the methodology eventually employed in the modeling exercise. Basically there are two different kinds of questions which are commonly stated by economic modelers: The first one is about the right choice in certain situations of interest; this demands optimization models. The second question scientists often ask is “what if…?”; this demands simulation models.
For example, CGE analysis is a mix of both: Mathematically, a CGE model solves an optimization problem; however, by changing input parameters the optimization routine gives different outcomes which can also be interpreted as simulations. Other types of models, such as ABM and SD models do not optimize target functions with respect to certain constraints but simulate in a dynamic way the actions and interactions of either multiple autonomous agents or more aggregated system elements in an attempt to re-create and/or predict the appearance of complex phenomena.
For our field of analysis, i.e. in the context of transformations and a very-long run perspective, however, optimization per se is highly questionable for many reasons, among them ethical concerns (e.g. regarding the discount rate), and uncertainty about catastrophic climate-related risks and technological developments.
2.6Treatment of path dynamicsAnalyzing the long-term transformation process to a low-carbon society can be based on different modeling frameworks that differ with respect to their treatment of time and their explicit representation of transformation paths. Comparative static models compare different states of system variables without taking into account the development between these states (for example GDP before and after policy interventions). Many economic models, such as static Input-Output and static Computable General Equilibrium (CGE) models are characterized like this. When developments over time are analyzed with this kind of models, modelers often interpolate between different points in time to generate a hypothetical development path, however whether the development really follows this interpolated trajectory is not at the core of interest of such modeling approaches.
The counterpart to comparative static analysis is dynamic analysis, describing and investigating explicitly the path between different states of system variables. In the context of models that are rooted in neoclassical theory, development over time can be analyzed either by discretely taking over values of system variables from one point in time to the next (e.g. “recursive dynamic” models, optimizing only within each period, but thereby implicitly also determining the intertemporal development), or by continuously (“fully dynamic”) optimizing intertemporal functions; for example maximizing discounted utility over the full time horizon at any point in time. Both versions of dynamic economic models have their drawbacks. Discrete dynamic models are nothing more than static models solved iteratively and their results dependent on exogenous assumptions (e.g. the discount rate), fully dynamic CGE models assume perfect foresight and perfectly informed decision makers – assumptions that are not readily comparable with real world behavior of economic agents.
To take into account dynamic actions and interactions of different autonomous agents and their emergent effects on the system as a whole in the context of a transformation to a low-carbon society, the employment of ABMs or SD models might be suitable. While ABMs focus on individual behavior, actions and interactions, SD models try to give an understanding of the behavior of complex systems over time at a more aggregate level (i.e. by not explicitly distinguishing between autonomous individuals). The merit and main difference of SD models from other models studying the dynamic behavior of complex systems over time is its use of internal feedback loops, the stocks and flows concept, and time delays that affect the behavior of the entire system. Furthermore, ABMs and SD models – as well as any other non-stochastic model specification – allow for the introduction of randomness, uncertainty and emergent characteristics by e.g. using Monte Carlo Methods.
2.7Regional and sectorial coverage, data requirementsThe regional/geographical and the sectorial coverage reflect the level of detail of the analysis. The level of detail is an important factor linked to the structure of the model, as it determines which economic mechanisms and elements are endogenized in the model and which are treated as exogenous assumptions. Models at a global scale set out to explicitly model the global economy characterized by explicit market relationships. Regional models, most often referring to international regions such as the European Union or Southeast Asia, and local models focusing on subnational regions (such as Styria in an Austrian context), treat world market conditions as exogenous assumptions.
Similar to the geographical scope of a modeling framework, energy-economic models differ with respect to the explicit representation of individual economic sectors. Encompassing a high number of sectors within a country – or focusing on the most relevant, major economic sectors – allows for a comprehensive analysis of the most important cross-sectoral feedback effects and interrelations.
3Methodological approachesIn this section we identify specific methodological approaches that have been used in analyses of climate and energy policies in various national and international contexts. While we keep the review here rather general and focused on the methodological approaches, the Appendix presents in more detail specific representative models and applications for each approach.
3.1Econometric methods in energy modelingEnergy systems are undergoing fundamental changes, driven by disruptions in technologies, markets and policy designs. Econometric methods have a long tradition in accompanying modeling and analyses of energy systems (see for example the model by Cambridge Econometrics (2016) which is discussed in more detail in the Appendix). We evaluate econometric practices with respect to their adequacy in dealing with long-term transformations of energy systems.
3.1.1The methodMainstream approaches to determining the demand for an energy flow e typically postulate the relationship
with the causal variables q for an economic activity, p for a (real) energy price, x for other variables (e.g. a weather variable) and z for an autonomous technical change.
Assuming a sample of time series, a general econometric specification of this relationship might be the following linear relationship
which exhibits lag distributions, a linear trend component and a stochastic error term ut. Typically the variables are transformed into logarithms, thus obtaining elasticities for the estimated parameters.
This modeling approach faces a number of limits. The number of parameters to be estimated, in particular those for the lag distributions, require a long sample range which in turn may violate the underlying model specification of an invariant structure. Furthermore this model specification is not able to deal with interfuel substitution, i.e. switching the energy mix.
These limits lead to extended model specifications which include on the one hand additional data by using also cross-section information (panel data) and on the other hand additional restrictions on the parameters of the general specification (2).
Dealing with inter-fuel substitutionDemand for energy obviously needs to be considered in the context of an energy mix which in turn stimulates research for explaining the causalities for the composition of the bundle of energy consumed by households or needed in the production of goods. For modeling this interfuel substitution basically two approaches have emerged.
The Almost Ideal Demand Systems (AIDS) results from a consumer demand model that partition total expenditures (i.e. for energy) for a bundle of goods (i.e. different fuels) according to the prices of the individual goods (i.e. fuel prices).
A production-based approach explains energy as the output of several factors (i.e. fuels). A further extension includes non-energy inputs, such as the capital, labor and materials in a KLEM model. In a so-called translog specification the main drivers for these models are relative energy and relative factor prices.
The econometric implementation of these modeling approaches suffer most often from rather unreliable time series on factor prices and energy prices, a deficiency that is echoed in the rather weak significance of estimated direct and cross price elasticities.
Modeling integration, co-integration and Granger causalityA very different modeling paradigm has emerged over the last three decades in the context of non-stationary stochastic processes. Accordingly economic variables as GDP and energy are investigated with respect to their individual long-term behavior (typically exponential trends before the economic crisis that started in 2008) and thus classified by what is called the degree of integration. In a next step joint relationships of variables are investigated under the heading of co-integration. Finally statements are made, if one variable improves the prediction of another variable and this is termed Granger causality.
It seems to be fair to say that these modeling approaches just reflect the application of econometric methodology that has become available to energy data without reflecting if this methodology is adequate to the issue to be dealt with. The exponential trends of the past seem to be gone, a fixed long-term relationship, even of a stochastic type, is rather not desirable if we postulate this for an energy flow and an economic activity. Finally predictability should not be prematurely mixed with causality in the sense of cause and impact.
3.1.2Some conclusions for long-term transformation analysesIn view of the usability of econometric models for obtaining a better understanding of the long-term transformation options in an energy system, the conclusions are rather sobering. Almost all econometric specifications include market driven behavioral assumptions, visible in the role of energy prices in the model specifications. The specifications are therefore hardly able to deal with non-price determined mechanisms that are representative in particular in the context of innovation policies. The estimated elasticities for prices and activities have very limited credibility because of the inherent conflict between the required long time series from a statistical point of view and the accompanying structural changes that violate the statistical model assumption of structural invariance. Most econometric analyses of the energy system just ignore this issue by not reporting the sensitivity of their estimates with respect to variations in the sample size and in the specifications.
Other deficiencies are even more fundamental, as the almost complete absence of details in the energy cascade, in particular the central role of functionalities that are provided by the interaction of energy flows and corresponding stock variables. This extended view of an energy system emerges, however, as a prerequisite for understanding the subtleties of long-term transformation processes.
3.2Dynamic new Keynesian input-output models3.2.1The methodNew Keynesian models are developed in the tradition of general equilibrium models in the sense that their long run equilibrium results from market clearing prices (see for example the model by Kratena and Sommer (2014) which is discussed in more detail in the Appendix). As CGE models and many macro econometric models, New Keynesian Models build on an input output structure displaying the inter-linkages between sectors. In the short run, institutional rigidities and constraints, such as wage bargaining or liquidity constraints, imply a deviation from the long run equilibrium path.
New Keynesian models are inter alia applied to address the critical role of environmental and resource constraints for economic development (Jackson et al., 2014). The model structure and the underlying assumptions are suited to illustrate the impacts of the demand for goods and services on energy and resource use or on emissions.
Typical building blocks of a New Keynesian ModelThe typical building blocks of a New Keynesian model comprise the household sector, the production sector, labor market and the government sector. In the short run the demand driven model shows deviations from the long run equilibrium stemming from liquidity constraints or other rigidities. The adjustment paths to the long run equilibrium solutions can be modeled in different level of detail for the different building blocks of the model. In the long run, adjustments in the wage rate determine the full employment equilibrium in the labor market, which in turn determines household income and respectively consumption.
Models that integrate environmental aspects typically treat energy demand as a separate category of non-durable commodities, differentiating between different fuel types. In the long run, demand for different fuel types is determined by (equilibrium) income, autonomous technical change and fuel prices.
3.2.2Some conclusions for long-term transformation analysesWith respect to gaining insights into long-term transformation processes a number of fundamental uncertainties with respect to the development of economic activities and prices and the convergence to an equilibrium solution remain. The model solutions depend strongly on the development of (relative) prices that drives changes in the economy.
As in most economic model classes, New Keynesian Models implement long run development as an extrapolation of trends observed in the past. Technological change is modeled as incremental technical change; radical technological change cannot be captured in such models. When used for policy evaluation it is the underlying set of uncertain assumptions in the reference case that mainly determines the effects of policy shocks. The decisive role of prices for model solutions typically constrains the simulation of policy alternatives to price instruments like taxes.
3.3Optimization models3.3.1The methodAn optimization approach aims for the minimization (e.g. costs, CO2-emissions) or maximization (e.g. profits) of an objective function (see for example the model by ETSAP (2016) which is discussed in more detail in the Appendix). The results of such models are solutions found by a solver algorithm which are considered as optimal (or close to the optimum) with respect to the objective (or target) function. Therefore optimization models are prescriptive rather than descriptive. This means that this approach can rather be used for “how to” instead of “what if” research questions.
Optimization models usually comprise at least two parts: The first part is the modeling environment used for the model formulation and model building. Most optimization models are written in high-level, functional programming language in a declarative way. The computation is then done by evaluating the mathematical expressions. Commonly used optimization program languages are GAMS, MPL, AMPL, AIMMS or MOSL. In a subsequent step, the modeling environment translates the source code into an equation system. The solver software forms the second part of the model, which derives the solution by solving the equation system and thus by evaluating the optimality of solutions simultaneously. For several widely applied (bottom-up) optimization models (e.g. MARKAL, TIMES, MESSAGE, OSeMOSYS) a third component, the model-builder-toolbox using a graphical user interface (GUI) exists (e.g. Excel-file in case of the OSeMOSYS). This has the advantage that model-building can be done more easily as the developer doesn’t need to write source-code. However it is also limited to the model capabilities as defined by the GUI.
Optimization approaches are used for top-down models (e.g. CGE [e.g. GEM-E3 model]) or partial equilibrium models (e.g. [MARKAL-] MACRO) as well as bottom-up (technology explicit) models (e.g. MARKAL, MESSAGE or TIMES model) (see the Appendix).
The mathematical approach for solvingVan Beeck’s (2009) fifth dimension, the mathematical approach, defines how optimization models solve the problem. Most energy-related bottom-up optimization models use common mathematical methods such as Mixed Integer Linear Programming (MILP), partly Multi-Objective Linear Programming (MOLP). If the model optimizes the path from an existing system towards the optimal system state, also Dynamic Programming (DP) methods are to derive their solutions. Top-down optimization models and some (bottom-up) energy models use more advanced methods such as Nonlinear Programming (NLP), Mixed Integer Nonlinear Programming (MINLP), and (Multi-Objective) Fuzzy (Linear) Programming ((MO)F(L)P). The fuzzy logic approach (or Fuzzy Programming, FP) constitutes an improvement with respect to penny switching behavior. Similar (in a non-mathematical definition) to the logit model and other probability approaches commonly used in discrete choice analysis, Fuzzy logic allows that a variable is “partly true” and defines “how much” a variable is a member of a set. Thus, fuzzy logic approaches are more suitable to find realistic solutions for decentralised optimization problems with a medium or high degree of uncertainty than conventional approaches (Jana and Chattopadhyay, 2004).
3.3.2Some conclusions for long-term transformation analysesThe main strength of optimization models is their ability to identify a unique optimal solution (according to the objective function’s output variable e.g. minimal costs) while at the same time ruling out less preferable solutions. This capability is of great value for solving tactical and operational microeconomic questions in situations where strong constraints (e.g. budget) apply.
For transformation analysis in nonlinear complex systems however, optimization models face severe methodological difficulties in capturing real-world behavior. The solver-software, responsible for finding the (close-to-)optimal solutions needs to evaluate a large number of system states with respect to the objective function and the model constraints. Therefore such models are limited to a restricted complexity and/or simplifications have to be made in order to find a (close-to-)optimal solution within a reasonable time. With respect to complexity and simplifications, linear models (linear programming) define one end of the spectrum. Modern computers are easily able to solve systems with millions of equations, however the restriction to linear systems makes this kind of model formulation basically unusable for real-life research questions. A less restricted formulation are MILPs that allow variables not just to be an element of rational numbers but also of a restricted set of integers. Again such models can be solved for a very large number of equations and variables within a reasonable time if the model is defined carefully. Yet, integrating e.g. load behavior into such a structure already requires substantial modeling efforts in order to keep the model (easily) solvable. Most bottom-up energy-system models apply the MILP approach. On the other end of the spectrum range NLPs, MINLPs are much harder to solve. This is especially the case for models with positive feedback loops (concave models). NLP or MINLP therefore require that the defined model has a low degree of complexity.
Another disadvantage of (commonly solved) optimization models is their behavior with respect to inferior technologies. Usually the degree to which a given technology is part of the solution depends only on superior technologies and their restrictions as well as their own restrictions, while it is independent from inferior technologies (penny switching behavior). This is probably the main reason for the commonly held position that conventional optimization techniques are not particularly suited to analyze systems where many individual decision-makers decide on many rather small subjects. This “penny switching behavior” is not necessarily given and could be avoided in principal – at the cost of increased computational time. Yet most applied energy systems optimization models accept such a behavior in order to keep the model reasonably solvable.
Optimization models are well suited and widely applied to describe solutions for a “technological-optimal” hypothetical target system in a distant future as well as the “technologically optimal” pathway towards such a system. They are however less suited to evaluate realistic forecasts for system stages which are far from the optimal solution, as defined by the objective function, which is usually the case for real-life systems. They are furthermore not particularly apt to evaluate the real-life effects of policy measures or other framework conditions of complex energy-economic systems.
3.4Neoclassical computable general equilibrium (CGE) models (top-down optimization)3.4.1The methodTypically, a CGE model depicts the economy as a closed system of monetary flows across production sectors and demand agents on a yearly basis. These flows are based on real-world national input output tables as well as additional accounting data and are combined with the general equilibrium structure developed by Arrow and Debreu. Accordingly, CGE models solve numerically to find a combination of supply and demand quantities as well as (relative) prices in order to clear all of the specified commodity and factor markets simultaneously (Walras’ law) (see for example the model by Capros et al. (2013a) which is discussed in more detail in the Appendix).
The basic underlying mechanisms are that producers minimize their production costs (or maximize profits) subject to technological constraints (production functions), whereas consumers maximize their consumption (or “welfare”) subject to given resource and budget constraints (factor endowments and consumption functions).
Once the model is calibrated to a “benchmark” equilibrium of a certain base year it is shocked exogenously, triggering adjustments in supplied and demanded quantities and thus relative prices until all markets are in equilibrium again. The emerging new equilibrium depicts the state of the economy after the shock (i.e. shows how the economy would look like, if a certain policy had been introduced) and is compared to the benchmark equilibrium to analyze changes in endogenous variables such as activity levels of sectors and consumption, relative prices or welfare.
Mathematically CGE models are optimization problems since producers and consumers maximize/ minimize their objective functions; however the use of CGE models is more of simulation character, as typically different counterfactuals are used in economic impact analysis, leading to different solutions of the models’ optimizations routine, which then are interpreted as different results of simulation scenarios.
3.4.2Some conclusions for long-term transformation analysesThe main advantage of CGE models is their ability to capture interlinkages across all economic sectors and agents. This means that “indirect” or “knock-on” effects of e.g. the introduction of an energy tax can be quantified, giving a broader picture than an isolated sectoral analysis. Since the effects to the whole economy are captured by CGE models, the effects on typical macro indicators, such as GDP, national consumption or welfare and tax income, can be analyzed.
Next to these strengths of the CGE approach there are also limitations and weaknesses1. A first conclusion to be drawn for long-term transformation analysis using CGE models is that the underlying fundamental mechanism of optimization of producers and consumers – assuming perfect information and rational behavior solely based on prices – is unrealistic, leading to unrealistic results. Many other factors than just prices determine the actual behavior of agents, hence in that regard CGE models are too short sighted. Moreover, only annual monetary flows are modeled explicitly. Capital stocks, such as buildings or power plants, are not captured, despite their importance in energy-transformation modeling.
Another potential drawback of CGE models is that they can be too aggregate and coarse with respect to technological detail. Many CGE models use sector aggregates such as the energy sector, which includes generation and distribution of all kinds of energy. The supply side of these aggregates is typically modeled as constant elasticity of substitution (CES) production functions, which combines different production inputs such as primary factors (capital, labor, resources) and intermediate inputs (material and services) to generate output. Since the different inputs are partly allowed to substitute each other, elasticities of substitution are necessary. These elasticities usually stem from regression analysis based on historical time series, leading to the problem that there is no guarantee that they will not change in the future (Grubb et al., 2002).
With regard to climate change mitigation, the basic emission reduction mechanisms in CGE models are the following (cf. Capros et al., 2014): (i) substitution processes between fossil fuel inputs and non-fossil inputs, (ii) emission reductions due to a decline in economic (sectoral) activity and (iii) purchasing abatement equipment. However, CGE models do not allow for radical endogenous changes in the energy system (bifurcation points) which are necessary for deep decarbonization. Even if different technologies are modeled separately in CGE models (such as in top-down bottom-up hybrid models as in Fortes et al., 2014) the problem remains that no radical changes are possible endogenously within the model framework since the production functions are determined ex-ante and do not change over time. Technological change thus only happens at the margin via price induced factor substitution (endogenously), productivity growth and autonomous energy efficiency improvements (both exogenously) (cf. Böhringer and Löschel, 2004). Radical changes or the emergence of fundamentally new technologies are not possible.
Next to supply side issues, there are also weaknesses regarding the demand side. More precisely, substitution possibilities in final and intermediate demand are of crucial importance, requiring again elasticities of substitution. Analogous to production functions, also consumption functions in CGE models are determined ex-ante and do not change over time, thus limiting the representation of transformational behavioral changes of consumers.
Despite these drawbacks CGE modeling may offer also opportunities to capture the indirect effects of certain policy interventions or technological change can be provided to shock the model exogenously (on the premises of having enough data on possible future developments regarding energy technologies and energy demand available). These indirect effects are of crucial importance, as sectoral models which do not take into account a macro-economic embedding may under- or overestimate effects.
3.5Partial equilibrium models (bottom-up optimization3.5.1The methodThe basic concept of equilibrium models is to determine the state where demand and supply of different commodities are equal (equilibrium price) and thus market clearance is achieved (see for example the model by E3MLab and ICCS (2014) which is discussed in more detail in the Appendix). Partial equilibrium models only consider a specific market or sector where the economic equilibrium is determined independently from prices, supply and demand from other markets. Therefore other markets and sectors are considered to be fixed, not considering possible interrelations. Thus all parameters not incorporated directly within the model have to be provided exogenously.
The advantage of partial equilibrium modes is that they are capable of describing specific markets more detailed and disaggregated. This is also beneficial for analysing the effects of different policies.
3.5.2Some conclusions for long-term transformation analysesSome models like PRIMES have been extensively used to describe long-term transformations (Capros et al., 2013b). A possible drawback is that those models rely on exogenous parameters (e.g. world market prices for fossil fuels, CO2 permit prices) and neither provide direct feedback nor consider interrelationship to the sectors and markets exogenously provided. This may have considerable drawbacks on the long run, as e.g. significant changes in energy markets may have a considerable impact on the overall economy.
3.6System dynamics and simulation models3.6.1The methodThe concepts of system dynamics was developed by Jay W. Forrester in the late fifties with the aim to asses and improve industrial processes. System dynamics models allow in a very intuitive way to model, simulate and analyze complex dynamic problems. Hence, SD models, in contrast to optimization models, are well equipped to answer ‘what if’ research questions.
The basis of a system dynamics model is a system of differential equations which are numerically solved in a sequence of time steps. Characteristic to system dynamics is the incorporation of complex feedback structures within the different system variables. Thus they are simulation but not optimization models (see for example the model by Teufel et al. (2013) which is discussed in more detail in the Appendix).
The two central concepts of system dynamics are the interrelation of stocks and flows and the resulting complex feedback loops, which result either in reinforcement or in balancing (Dykes, 2010). Besides the possibility to simulate the effects of the different interrelationships within the model, SD models also provide a convenient way to analyze the driving forces within the system. In addition to the capability to describe dynamic and complex problems, SD models are increasingly combined with other methods like generic algorithms, iterative algorithms and game theoretical approaches. Also stochastic approaches, like Monte Carlo simulation, may be implemented in SD frameworks (Teufel et al., 2013).
3.6.2Some conclusions for long-term transformation analysesGiven their capability of representing stock-flow relationships and complex feedback processes, SD models hold a great potential for adequately describing real-world behavior of energy-economic systems, including long-term transformation processes. However, as this approach is a simulation and not an optimization method, SD modeling may be appropriate to simulate complex problems but it lacks the possibility to find techno-economic optimal pathways (e.g. least costs) for the transformation. Regarding this aspect the combination with other methods (e.g. optimization) could be a possible approach.
3.7Backcasting models3.7.1The methodThe backcasting2 approach was developed in the 1970s by Amory Lovins for the analysis of energy systems. Backcasting is seen as an alternative to conventional energy forecasting approaches that estimate a continuous and substantial increase in energy demand. Since the 1970s the approach has been frequently applied in energy studies as well as in studies dealing with sustainable development in general.
In contrast to forecasting models that are usually based on past trends, backcasting approaches start from a normative vision for a desirable future, such as a low-carbon society with a reduction of GHG emissions by 80-90% by mid-century compared to 1990. From that vision of the future, a development path is traced back to the current situation. Backcasting is hence well suited for modeling complex issues such as a transformation towards sustainable consumption and production patterns. Furthermore, the approach allows for modeling structural breaks that cannot be captured with traditional forecasting approaches. This is a valuable feature for modeling the very long-run, as a mere continuation of past trends over the next decades is very unlikely (see for example the model by Köppl and Schleicher (2014) which is discussed in more detail in the Appendix).
Backcasting is frequently used for (more or less) qualitative descriptions of the future (see e.g. Wächter et al., 2012 for Austria). In their energy perspectives for Austria, Köppl and Schleicher (2014) use the quantitative backcasting model sGAIN for analyzing low-carbon energy structures in Austria for 2030 and 2050.
3.7.2Some conclusions for long-term transformation analysesRelevant for long run transformations is the ability to capture structural breaks that are necessary for a fundamental transformation of existing energy systems. This applies also to a clearer depiction of specific technologies and thus comes closer to include more radical technological change. Backcasting requires the definition of explicit target values that need to be thoroughly chosen and argued. The same holds true for modeling of the paths between the future vision and the current situation.
3.8Multi agent or agent based models (ABM)3.8.1The methodThe ABM approach a very general one as it can be used to model nearly any system in dependency of the purpose of the model (see for example the model by Richstein et al. (2014) which is discussed in more detail in the Appendix). The variety of application ranges from physical over biological to social systems, while the approach is often seen in contrast to Equation Based Modeling (EBM) or SD, which have a similar general applicability. In a strict technical perspective, there is no difference between ABM and EBM as any ABM can be also expressed by an explicit set of mathematical formulas used by EBM (Epstein, 2006). However, in practice this set of formulas would be of hardly manageable size and complexity. The specifics of ABM, constituting a manageable modeling framework and distinguishing them from other modeling approaches, refer to three crucial points.
- 1.
The subjects of modeling are the system’s individual components and their behavior. The behavior of the modeled agents depends on the local interaction with other system elements and individual optimization based on each agent’s particular characteristic (as e.g. endowment, location or size).
- 2.
The possibility of (geographical) spatial representation of system elements. Agents do usually not interact with all possible system elements but only with those in their neighborhood. This specification can capture particularities for interaction including topological circumstance, transfer of information and network structures.
- 3.
The stochastic process of simulation. Other than deterministic approaches, in which the outcome of a model is fully determined by the parameter setting and the initial conditions, stochastic approaches as ABM bear an inherent randomness. Therefore one individual model simulation with a specific parameter setting and initial conditions can show only one possible outcome out of a well defined function space, but not a general solution (Epstein, 2006, p.29).
As an implication of the first specific, a system behavior may arise, which cannot be predicted from the behavior of the individual agents, as it emerges from the adaptive interaction between the agents and their environment. In that way ABMs are a bottom-up approach in which the autonomous behavior of the agents determines the state of the system instead of a top-down approach (like in System Dynamics or CGE models) in which the state of the system is described only by variables. Further, an analysis of an ABM can be made not only on the aggregate system output but also on the agent level. However, an empirical ABM approach usually needs not only other/ unconventional sources of data but also relies more heavily on more comprehensive data, specifying the multiple agents’ particular characteristics.
Concerning the second specific, a large range of modeling possibilities becomes relative easily accessible. Models of social or economic systems in an agent based framework are only seldom restricted to homo economicus decision rules and can relax certain stringent conditions from neoclassical models, like perfect information, location or size of agents, while still yielding a fruitful analysis (cf. Epstein, 2006, p.xvif).
The third specific of a stochastic simulation is closer to processes in the natural world because of its inherent randomness. However, this has the price of stark increasing complexity of the model, demanding a comprehensive way of simulating and analyzing the model. On the other hand, stochastics determine discrete decisions of agents and simulation in discrete time steps.
3.8.2Some conclusions for long-term transformation analysesWith ABMs questions of emergence can be treated as the systems behavior results of the interaction of its components. ABMs can merge the micro with the macro perspective in that sense that well studied individual behavior (as e.g. of plants, animals, people…) can be modeled in one framework with changing system conditions – the state of system changes because of the individual behavior and at the same time the individuals adapt their behavior to the changes of the system. Within the approach of ABM uncertainties can be addressed because of the stochastic modeling character. ABMs can also handle “non-equilibrium dynamics” – if equilibrium exists but is not attainable (e.g. on acceptable time scale) (cf. Epstein, 2006).
Additionally to mathematical and statistical modeling abilities, as necessary in other approaches (e.g. econometrics), also further modeling as well as programming and simulation skills are needed. This contains on the one hand the inclusion of different concepts as adaptive behavior, interaction and emergence. And on the other hand, stochastics affords an iterative way for testing and analyzing models. As already mentioned, data mining for empirical modeling with ABMs in social sciences is a big issue, as mostly micro data on an individual base for a large number of agents would be often required.
The explicit consideration of interrelations between individual actors brought together in the socio-economic-climate-energy nexus may be an advantage for describing long run transformation processes. In combination with a stochastic modeling approach the bottom-up nature of ABMs is more closely reflecting the emergent behavior and inherent randomness of real world circumstances. Moreover, the explicit spatial representation of system elements allows for a more realistic representation of social-ecological interactions, including topological circumstance, transfer of information, and network structures. Despite these potential strengths of the ABM modeling approach, the highly detailed model structure comes at the price of substantial empirical data requirements in order to properly characterize the different agents’ particular characteristics and behaviors.
4Discussion and conclusionsExisting energy- and climate-economic modeling approaches are increasingly seen with skepticism regarding their ability to forecast the long-term ev olution of social-ecological systems. The socio-economic-climate-energy nexus is a highly complex nonlinear social-ecological system, its subtleties so far most often only poorly dealt with when developing and assessing transformation pathways leading to a societally desirable low-carbon future. This paper reports a structured review of state-of-the-art national and international climate- and energy-economic modeling approaches, focusing on their respective abilities and limitations to develop and assess pathways towards a low-carbon society.
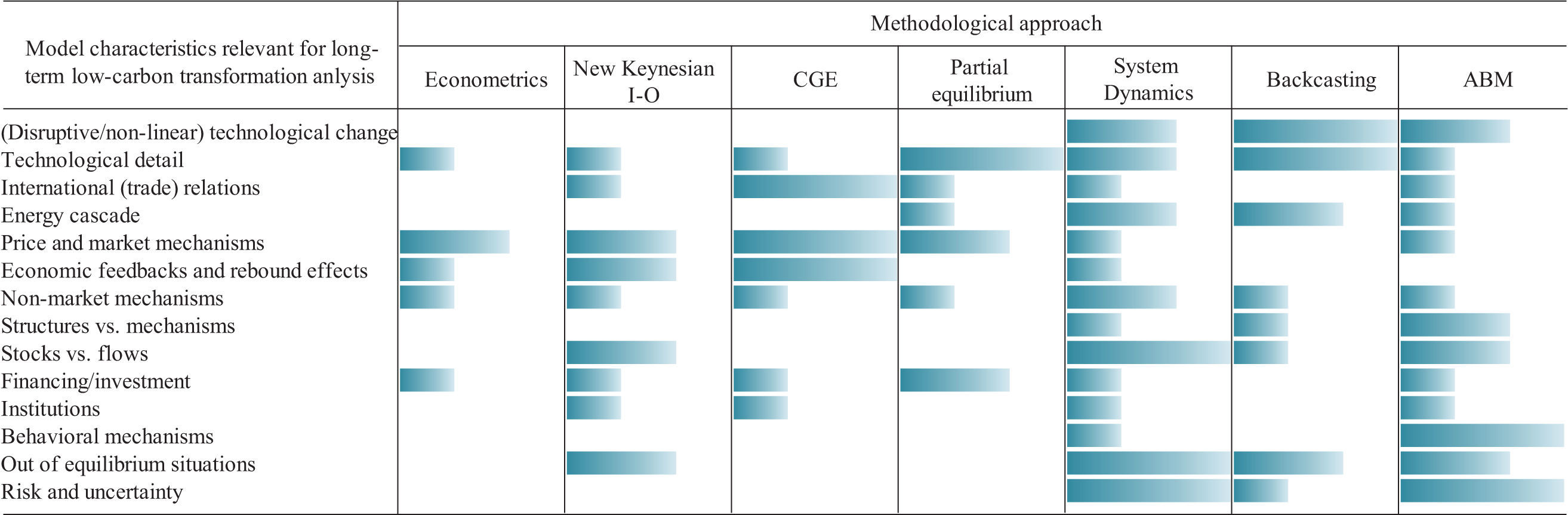
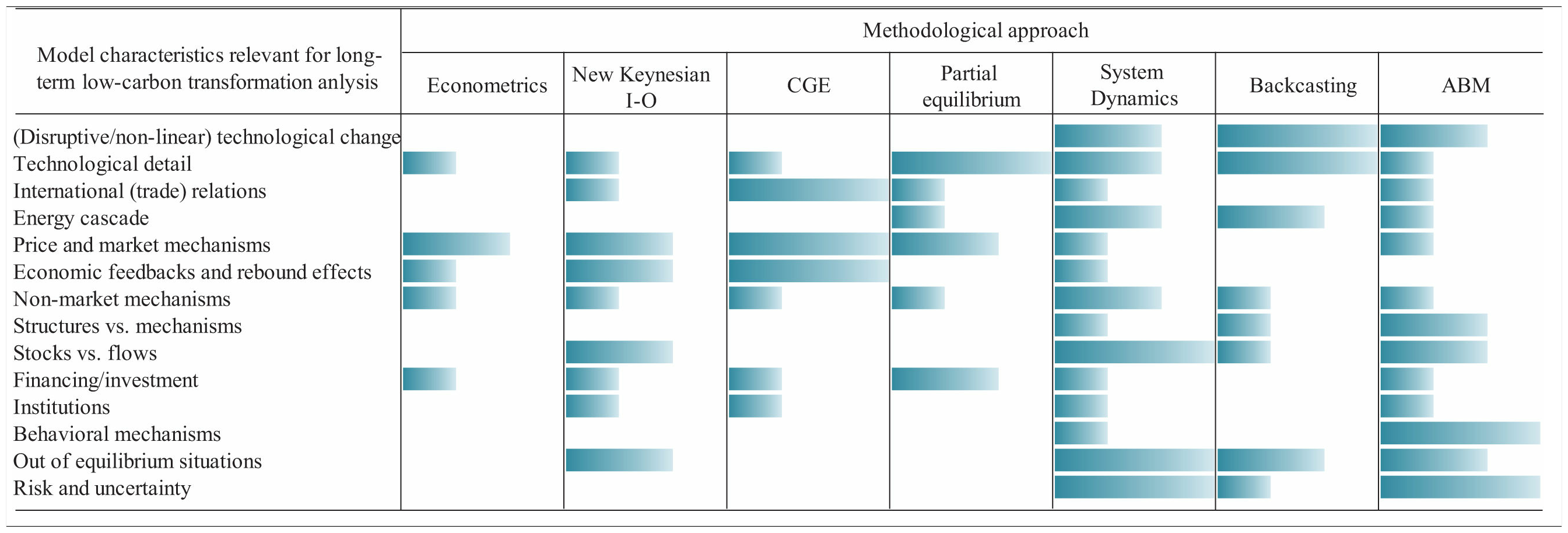
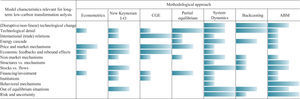
We find that existing methodological approaches have some fundamental deficiencies that limit their potential to understand the subtleties of long-term low-carbon transformation processes. Table I depicts a qualitative scoreboard for different methodological approaches’ capability of representing real-world aspects relevant for long-term energy transformation analysis. It is important to note here that this scoreboard is only a first qualitative mapping based on a systematic review of relevant literature. Most modeling approaches that were analyzed (specifically econometrics, CGE, and New Keynesian approaches) are characterized by an almost complete absence of details of the energy cascade. In particular they lack to model the central role of functionalities or services that are provided by the interaction of energy flows and corresponding stock variables. Further they are not well equipped for analyzing radical technological changes. Model results often depend on only a single mechanism depicted by the respective modeling approach e.g. for CGE models, partial equilibrium models or New Keynesian models (relative) price changes are the key drivers. Reversely, top-down integrated assessment models aim to include as many mechanisms as possible and are hence capable of capturing feedback effects between sub-elements (economy, climate system, society, other environment) of the social-ecological system under consideration, but this comes at the cost of either (a) working on a very coarse level of detail, with e.g. only limited explicit representation of alternative technologies and using highly uncertain functions for relating system variables to each other (hard-linked IAMs) or (b) experiencing problems in convergence and consistency among the models used (soft-linked IAMs).
Bottom-up, partial equilibrium optimization models investigating energy systems are capable of depicting a rich technological detail and of identifying techno-economically optimal solutions (as defined by an objective function), while ruling out inferior solutions. However, due to high computing requirements these models are limited to restricted complexity (e.g. convexity and missing macroeconomic feedbacks) and are therefore less well suited to evaluate realistic forecasts of energy-economic system states which are far from the optimal solution as defined by the objective function, which is usually the case for real-life systems. Moreover, partial equilibrium optimization models are only able to capture certain techno-economic aspects of the overall social-ecological system and thus cannot track important feedback effects with e.g. the climate or social system.
Comparatively novel methodological approaches such as SD models or ABMs do allow for representing stock-flow relationships and dynamic, disruptive transformation processes as well as system emergence but lack the possibility to find techno-economic optimal pathways (e.g. least cost, minimizing energy demand, minimizing emissions) and tend to be highly resource intensive regarding empirical data input, which is, however, critical for deriving real-world relevant results. Moreover for SD models and ABMs, just as for more traditional approaches such as CGE approaches, problems might occur regarding the separation of the structure – e.g. the elements of an energy system – from the mechanisms that are generating these structures. What is true for all modeling techniques mentioned so far is that the respective results are heavily driven by exogenous input (parameter) assumptions (e.g. price elasticities, perfect information, rational behavior of agents, model closures) which are in turn triggering endogenous responses within the model.
Based on this review we suggest that a methodological framework for analyzing long-run low-carbon energy transformations has to move beyond current state of the art techniques and simultaneously fulfill the following requirements: (1) representation of an inherent dynamic analysis, describing and investigating explicitly the path between different states of system variables, (2) specification of details in the energy cascade, in particular the central role of functionalities and services that are provided by the interaction of energy flows and corresponding stock variables, (3) reliance on a clear distinction between structures of the sociotechnical energy system and socioeconomic mechanisms to develop it and (4) ability to evaluate pathways along societal criteria (e.g. least cost, minimizing GHG emissions, minimizing local air pollution). Furthermore, a crucial task in modeling is to specify explicitly whether a model element is determined endogenously or exogenously, ideally governed by the demands of the underlying question to be answered.
Given the specific strengths and weaknesses of all energy-economic modeling approaches available we propose the development of a versatile multi-purpose integrated modeling framework for moving forward the meaningful analysis of a transformation towards a low-carbon society. A model constructed as a modular package would allow for the selection of the most promising building blocks from different existing modeling frameworks to serve the more general purpose and enable the user to select only those (sub)modules that are relevant for answering specific questions. This paper identified respective strengths and weaknesses to guide such development. Further research is necessary to first establish conceptual frameworks of modular modeling packages and then to foster their operationalization in the context of long-term low-carbon transformation analysis. A first conceptual attempt how this could be done is indicated in Schleicher et al. (2016), where within the approach of deepened structural modeling the functionalities of an energy system are determined via (a) the corresponding energy flows but also (b) the relevant application and transformation technologies, with feedbacks on the socioeconomic system.
This research was supported by the Austrian Climate and Energy Fund, project ClimTrans 2050 within the Austrian Climate Research Programme (ACRP). We thank for contributions by Thomas Gallauner, Claudia Kettner, Angela Köppl, Andreas Müller, Stefan Nabernegg and Ilse Schindler, and benefitted from discussions within the whole research team.
For each of the model classes distinguished in Section 3 by their underlying methodology, in the following we select representative “prototypical” models for further investigation. As a “prototypical” model we define a model which is prominently used in the analyses of energy-economic research questions either by the research community or by policy makers (such as the EU).
A typical representative model with a global coverage is E3ME, a macro-econometric E3 (Energy-Environment-Economy) model. Models like E3ME claim as a distinctive feature their treatment of resource use, including energy, and the related greenhouse gas emissions embedded into sectoral economic framework (Cambridge Econometrics, 2016).
Despite the merits of such an integration many deficiencies as to the treatment of energy remain that are crucial for obtaining a better understanding of long-run transformation processes. These shortcomings concern the rather simplistic treatment of technological progress, the overstated role of prices as drivers for structural changes, and the limited treatment of the cascade structure of the energy system.
The DYNK model by WIFO (Kratena and Sommer, 2014) treats energy use in a detailed way. In the household sector, an innovative approach for modeling energy demand is used: Starting point is energy service demand which is the result of the energy efficiency of the capital stock and final energy demand by fuel type. This approach explicitly illustrates the role of stock-flow interactions in the provision and demand of energy services. Household energy service demand is determined by the energy service price, as a function of the energy price and the energy efficiency parameter. In the short run, liquidity constraints and a fixed capital stock – reflected in a given efficiency parameter – imply that energy service demand is determined by changes in the energy price. In the long run, changes in energy prices induce adjustments of the capital stock that can result in changes in the energy efficiency parameter and thereby affect the energy service price.
In the production sector, the input factors capital (K), labor (L), energy (E), imported non-energy materials (Mm) and domestic non-energy materials (Md) are differentiated. The shares of the different input factors in production are determined using a translog specification based on factor prices. In a second step, the shares of the different fuel types are estimated, also based on a translog function. Technological change is modeled via autonomous technological change, for the different input factors as well as in form of total factor productivity.
The merit of the WIFO DYNK model is that it illustrates the interaction of stocks and flows for energy services. What drives the demand for energy services, however, is exclusively driven by prices.
The MARKAL (MARKet ALlocation) model, its successor the TIMES (Model) model, the MESSAGE model (Model), and the OSeMOSYS (Model) are well-known and widely applied energy system optimization models.
MARKAL and TIMES are dynamic (path dependent) bottom-up optimization modeling toolboxes developed by the International Energy Agency (IEA) within the Energy Technology Systems Analysis Programme (ETSAP). MARKAL was developed in the mid-90s, TIMES in the early to mid-2000s. According to the MARKAL homepage it is now applied by more than 70 institutions in more than 35 countries (ETSAP, 2016).
MARKAL focuses on the energy sector only, the main purpose of MARKAL models is to identify and evaluate “target-oriented integrated energy analysis and planning” using a least cost approach. The MARKAL toolbox has been superseded by the TIMES (ModeltoolboxmodelThe main advantage of TIMES compared to MARKAL is its flexibility. It allows several interacting regions and to sub-divide the year into several user-defined time periods. Both toolboxes contain a partially equilibrium models for the energy sector (considering supply curves of and demand curves for energy carriers and the subsequently derived energy prices).
One of the main advantages of MARKAL and TIMES is that they are widely used in the energy system planning community and easy-to-use model building (less steep learning curve). A disadvantage is the still rather rigid structure. Furthermore, they do not optimize the electricity supply for medium- to long-term energy system planning, energy policy analysis, and scenario development with a large share of intermittent energy sources (e.g. wind and PV).
The Greenhouse gas Air pollution Interaction and Synergies (GAINS) model is an integrated assessment model which is based on a technology specific bottom-up approach. It derives on the basis of emission factors and abatement effects the anthropogenic emissions, the resulting atmospheric pollution and impacts on human health and environment (Amann, 2012).
The GAINS model can be operated in a ‘scenario analysis’ and an ‘optimisation’ mode. In the ‘scenario analysis’ mode it analyses the pathway from the emitting source to the impact and allows therefore to assess the costs and benefits of different emission abatement strategies. In the ‘optimisation’ mode it derives the techno-economic optimal combination of different abatement and mitigation options which achieve the best overall benefit at minimum costs.
To be able to calculate the emissions of different pollutants on the basis of activity data the GAINS model incorporates around 1000 types of emission sources which are specific regarding economic sector and country (Capros et al., 2013a).
In order to describe the different mitigation options and pathways GAINS considers around 1,500 end-of-pipe measures to assess the abatement of a wide range of different air pollutants including greenhouse gases. The different mitigation effects are derived on country and sector specific implementation costs. This allows a detailed assessment of the environmental impact of different policies and measures (Amann, 2012).
Since the different activity levels are exogenous the different costs of the abatement measures generate no feedback regarding the underlying economic models.
Typical CGE models which focus on energy-economy-environment interaction are the GEME3 model (General Equilibrium Model for Energy-Economy-Environment interactions) for the European Union (Capros et al, 2013b) and PACE (Policy Analysis based on Computable Equilibrium; Löschel, 2015).
GEM-E3 focuses on the European Union and is of recursive dynamic type, solving in 5-year steps until 2050. It is mainly used to assess climate and environmental policy, hence including primary energy sources and energy technologies. PACE is a similar model, however static comparative.
The GEM-E3 model (General Equilibrium Model for Energy-Economy-Environment interactions) for the European Union has been applied for various climate and energy policy simulations to support decision makers within the European Commission. The main features are as follows (c.f. Capros et al, 2013b): (i) the model is of multi-country type with specific representation of all EU-15 member states, which are linked through endogenous bilateral trade, (ii) in every country multiple sectors and agents exist, allowing to analyze distributional effects and (iii) GEM-E3 is of recursive dynamic type, solving for general equilibrium in a specific year and then passing data on to the next year, for which a new equilibrium is solved. Furthermore the model includes taxes, subsidies and public spending (including deficit financing).
GEM-E3 is mainly used to assess climate and environmental policy (e.g. by Jansen and Klaassen, 2000; Pan, 2005; Mayeres and van Regemorter, 2008; Saveyn et al., 2011) and therefore special focus lies on the competition between the main power generation technologies (coal, oil, gas, nuclear, wind, biomass, solar, hydro, CCS coal and CCS gas) with the respective greenhouse gas emissions (see Capros et al., 2014 for more details). Recently, the model was also deployed to analyze macroeconomic climate change impacts (e.g. by Ciscar et al., 2012).
Regarding low-carbon transformation and pathway analysis GEM-E3 was linked to various bot-tom-up optimization model such as TIMES (e.g. by Fortes et al. (2013), 2014) to overcome the caveat of poor technological detail of the CGE model, but being able to quantify the macroeconomic implications of low-carbon (policy) scenarios. Similar modeling practice was carried out by Koopmans and te Velde (2001), Kumbaroglu and Madlener (2003), Messner and Schrattenholzer (2000), Scaramucci et al. (2006) and Wing (2006). Such studies (integrating bottom-up and top-down models) may serve as a good starting point for a holistic integrated assessment of energy-economic low-carbon transformation analysis for Austria.
Since partial equilibrium models are only capable of a single (or limited amount) market or sector they consider specific problems. Prominent examples for partial equilibrium models are PRIMES and CAPRI. PRIMES is an energy model to calculate developments on the energy market (E3MLab and ICCS, 2014). CAPRI is a model for the agricultural sector used for the assessment of agricultural and trade policies with a focus on the EU (CAPRI, 2015). Both models are extensively used be the European Commission.
The Model (PRIMES) is an energy system model to calculate projections of energy markets for the analysis of energy and climate policies in Europe. The model simulates the development of energy demand, energy supply and technology on the basis of market equilibrium (E3MLab and ICCS, 2014). Hence, PRIMES is a partial equilibrium model for the European energy system. Furthermore the model aims to represent agent behavior within the multiple markets. This is achieved by a modular approach where each module represents a specific agent, either a demander or supplier of energy. The behavior of the agents is modeled through a microeconomic foundation which maximizes the benefit (profit, utility, etc.) of each representative agent. To combine the sub-models equilibrium prices in different markets and equilibrium volumes considering balancing and constraints are determined.
PRIMES provides detailed energy balances in line with Eurostat statistics including sectoral demand by fuel as well as the structure of the power system and other fuel supplies. Moreover, energy prices and costs can be obtained such as costs per sector, investment costs, overall costs and consumer prices.
Since the economic development is modeled outside PRIMES there is no feedback generated by developments in the energy market. For the power system, daily and seasonal variations are modeled at an hourly resolution taking into account typical intra-day power load, wind velocity and solar irradiance. Despite this and detailed coverage of interconnecting capacities of electricity and gas flows, the model lacks information and representation at below-country levels such as retail infrastructure. This may be a particular concern if more volatile and decentralised production of electricity exceeds local grid capacities at short. Nevertheless, PRIMES should be well capable of simulating long-term energy system transformation and restructuring up to 2050, both in the demand and the supply sides.
Regarding the energy market a number of system dynamics models have been developed and successfully applied (Teufel et al., 2013). An example would be the model Kraftsim (Vogstad 2004) used for investigating the Nordic electricity market and simulating the effects on greenhouse gases caused by different policies. A more comprehensive overview can be found in Teufel et al. (2013).
The POLES (Prospective Outlook on Long-term Energy Systems) model is a global energy supply, energy demand and energy prices forecasting model, developed within the VENSIM system-dynamics software package (Enerdata, 2016). It has been developed by Enerdata and the CNRS National Center for Scientific Research.
It simulates the energy supply and demand (energy balances) of 15 economic sectors and of more than 57 countries and world regions within a partial equilibrium framework and explicitly considers about 50 energy supply technologies. The demand is modeled taking “into account the combination of price and revenue effects, techno-economic constraints and technological trends.” The simulation is done on a yearly basis (Enerdata, 2016).
POLES is a proprietary model, analyses with this model are rather provided as service by Enerdata; it is not (off-the-shelf) foreseen to hand-out the model to customers. Furthermore the included technologies are fixed and cannot be altered (by customers).
sGAIN by WIFO represents a detailed bottom up model of the energy system. In Köppl and Schleicher (2014) the model is used for backcasting, using the EU 2050 Roadmap as normative vision for 2050. The modeling framework puts energy services into the center of the analysis of energy structures that are compatible with long-term low-carbon targets. Data for energy services are typically not available. Information from useful energy balances are used to demonstrate quantity and quality of energy used for the provision of energy services. The model structure details useful energy categories by sector and energy source and puts a strong emphasis on innovation and energy productivity at all levels of the energy chain including the supply side. Various combinations of changes in the demand for energy services and energy productivity that achieve the same output in terms of energy flows and emissions are displayed.
The EMLab-Generation model (Richstein et al., 2014) mimics the behavior of electricity generation companies (i.e. the agents) which aim to optimize their profits by deciding upon short-term bidding, the procurement of fuels and CO2 as well as investments. The agents are heterogeneous and interact with each other, but act under incomplete knowledge regarding the future. More precisely each agent takes into account it’s surrounding and estimates future market developments (e.g. the expected merit order and the resulting electricity and CO2-prices) based on its current state and developments from the past. The outcome of the model is an endogenously determined development of the electricity mix over time. Since the agents act under incomplete information the outcome is sub-optimal as expectations and reality do not perfectly match; a characteristic which we can observe in reality very often. By introducing different energy and climate policies, the model can be used to derive the long-term effects of policies on the electricity mix and the corresponding emissions, CO2-price but also security of supply and affordability. One application of the model can be found in Richstein et al. (2014) where the authors analyze the effects of CO2 price floors and ceilings on investors’ decisions.
In general the underlying neoclassical theory of general equilibrium is subject to heavy critique. However, the aim of the underlying paper is to analyze the ability of different methodological approaches in the specific context of energy-transition, hence we do not further address this very general discussion of general equilibrium theory.
The term ‘backcasting’ was introduced by Robinson (1982), while Lovins initially used the term ‘backwards-looking analysis’ (Quist, 2007).