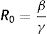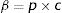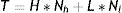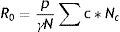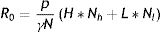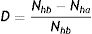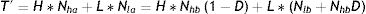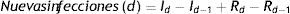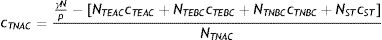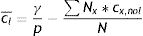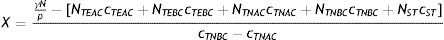Si bien se han realizado múltiples intentos de modelar matemáticamente la pandemia de la enfermedad por coronavirus 2019 (COVID-19), causada por SARS-CoV-2, pocos modelos han sido pensados como herramientas interactivas accesibles para usuarios de distintos ámbitos. El objetivo de este trabajo fue desarrollar un modelo que tuviera en cuenta la heterogeneidad de las tasas de contacto de la población e implementarlo en una aplicación accesible, que permitiera estimar el impacto de posibles intervenciones a partir de información disponible. Se desarrolló una versión ampliada del modelo susceptible-expuesto-infectado-resistente (SEIR), denominada SEIR-HL, que asume una población dividida en dos subpoblaciones, con tasas de contacto diferentes. Asimismo, se desarrolló una fórmula para calcular el número básico de reproducción (R0) para una población dividida en n subpoblaciones, discriminando las tasas de contacto de cada subpoblación según el tipo o contexto de contacto. Se compararon las predicciones del SEIR-HL con las del SEIR y se demostró que la heterogeneidad en las tasas de contacto puede afectar drásticamente la dinámica de las simulaciones, aun partiendo de las mismas condiciones iniciales y los mismos parámetros. Se empleó el SEIR-HL para mostrar el efecto sobre la evolución de la pandemia del desplazamiento de individuos desde posiciones de alto contacto hacia posiciones de bajo contacto. Finalmente, a modo de ejemplo, se aplicó el SEIR-HL al análisis de la pandemia de COVID-19 en Argentina; también se desarrolló un ejemplo de uso de la fórmula del R0. Tanto el SEIR-HL como una calculadora del R0 fueron implementados informáticamente y puestos a disposición de la comunidad.
Although multiple attempts have been made to mathematically model the current epidemic of SARS-CoV-2, the causative agent of coronavirus disease 2019 (COVID-19), few models have been conceived as accessible interactive tools for users from various backgrounds. The goal of this study was to develop a model that took into account the heterogeneity in contact rates within the population and to implement it in an accessible application allowing to estimate the impact of possible interventions based on available information. An extended version of the Susceptible-Exposed-Infected-Resistant (SEIR) model, named SEIR-HL, was developed, assuming a population divided into two subpopulations, with different contact rates. Additionally, a formula for the calculation of the basic reproduction number (R0) for a population divided into n subpopulations was proposed, where the contact rates for each subpopulation can be distinguished according to contact type or context. The predictions made by SEIR-HL were compared to those of SEIR, showing that the heterogeneity in contact rates can dramatically affect the dynamics of simulations, even when run from the same initial conditions and with the same parameters. SEIR-HL was used to predict the effect on the epidemic evolution of the displacement of individuals from high-contact positions to low-contact positions. Lastly, by way of example, SEIR-HL was applied to the analysis of the SARS-CoV-2 epidemic in Argentina and an example of the application of the R0 formula was also developed. Both the SEIR-HL model and an R0 calculator were computerized and made available to the community.
En diciembre de 2019 se registró en la ciudad de Wuhan, provincia de Hubei, China, un brote de neumonía de etiología desconocida. Rápidamente se logró identificar como el agente causal a un nuevo betacoronavirus, posteriormente nombrado SARS-CoV-247, en tanto la enfermedad causada por este nuevo virus se denominó COVID-19. Hasta el 6 de diciembre de 2020, se han reportado 66.818.756 casos de COVID-19 y 1.533.018 muertes por COVID-19 en 191 países y territorios. En Argentina se han reportado 1.459.832 casos y 39.632 muertes por COVID-196.
El SARS-CoV-2 está estrechamente emparentado con los virus responsables de la epidemia de SARS (síndrome respiratorio agudo severo), ocurrida en los años 2002-2004, y la epidemia de MERS (síndrome respiratorio del Medio Oriente), reportada por primera vez en Arabia Saudita en 20127,23,44,46. Los síntomas y signos más comunes de COVID-19 al inicio de la enfermedad son fiebre, tos seca, fatiga, mialgia, anosmia y ageusia; otros síntomas menos comunes incluyen disnea, producción de esputo, cefalea, hemoptisis y diarrea. El síndrome de dificultad respiratoria aguda constituye la complicación más común3,8,15,40. Se estima que alrededor del 80% de los casos presentan enfermedad leve, si bien la tasa de letalidad general es del 2,3%, esta asciende al 8% en individuos de 70 a 79 años y al 14,8% en mayores de 80 años43.
Los países de ingresos medios y bajos son particularmente vulnerables frente a la pandemia de COVID-19, debido a los desafíos económicos y logísticos que supone aumentar la capacidad del sistema de salud39. Es por esto que muchos de estos países han recurrido a medidas de distanciamiento social en gran escala, con el objetivo de reducir la morbilidad causada por COVID-19 y la consecuente demanda de recursos sanitarios, y de darle tiempo al sistema de salud para adaptarse32.
Se han realizado numerosos intentos de modelar la evolución de la pandemia de COVID-19. La mayoría de estos esfuerzos estuvieron dirigidos al desarrollo de un modelo matemático, al ajuste de los parámetros del modelo utilizando datos reales recolectados a nivel nacional, regional o global durante un período de tiempo determinado (a partir de reportes de número de casos confirmados, número de fallecimientos, información de movilidad a partir de datos de teléfonos móviles, etc.) y, sobre la base de dicha información, intentar predecir cualitativamente el curso de la pandemia y el efecto sobre esta de distintos tipos de intervenciones1,12,31,38. Si bien estos modelos proveen información muy útil, suelen estar diseñados para propósitos muy acotados temporal y geográficamente. Por otro lado, su uso puede ser engorroso para personas sin conocimiento técnico complejo.
Rainisch et al.32 notaron esta deficiencia y desarrollaron una herramienta más amigable para estimar el impacto futuro de la pandemia de COVID-19 sobre la demanda de recursos sanitarios en jurisdicciones de interés y para examinar los costos y beneficios de diferentes estrategias de intervención. Dicha herramienta se basó en el modelo SEIR, separando el compartimento R (removidos) en individuos recuperados y fallecidos, y utilizando dos tasas de letalidad, una menor cuando el sistema de salud tiene la capacidad de tratar a todos los infectados, y una mayor cuando el número de infectados activos supera esta capacidad. El programa considera cinco estrategias de intervención, desde el simple aislamiento de casos hasta la cuarentena total; el efecto de cada estrategia sobre la evolución de la pandemia es introducido en el modelo mediante la reducción del valor del número básico de reproducción (R0), según porcentajes basados en reportes previos. Para cada escenario (que puede incluir la combinación secuencial de las distintas estrategias), la herramienta estima el número de infectados y hospitalizados, y la demanda de camas comunes, camas de terapia intensiva y de ventiladores, entre otros factores, a distintos tiempos. Si bien se trata de una herramienta valiosa, presenta dos limitaciones: la simpleza del modelo en que se basa y el número limitado de intervenciones que permite modelar.
El objetivo de este trabajo fue desarrollar una herramienta accesible que permita estimar y comparar el efecto de distintas intervenciones dirigidas a limitar la propagación del SARS-CoV-2 en poblaciones determinadas. Entendemos el término «intervención» como cualquier medida o indicación de salud pública tendiente a modificar el curso natural de la pandemia. Al igual que Rainisch et al.32, partimos de un modelo SEIR modificado, al cual denominamos SEIR-HL. Sin embargo, nuestro modelo presenta ciertas ventajas por sobre el de los autores citados. En primer lugar, a diferencia de la mayoría de los modelos propuestos hasta el momento, con unas pocas excepciones22,31,34, nuestro modelo no asume mezcla homogénea y permite clasificar a los individuos en subpoblaciones según sus tasas de contacto, pues considera que el concepto de mezcla homogénea es poco aplicable a poblaciones que se encuentran bajo diversas medidas de distanciamiento social. Por otro lado, la herramienta que se ofrece aquí no limita el número o tipo de intervenciones que se pueden simular, ya que le permite al usuario implementar las intervenciones que desee mediante la manipulación del número de individuos dentro de una subpoblación o de la tasa de contactos de una subpoblación. Finalmente, esta aplicación permite, además, estimar el R0, considerando no solo la presencia de varias subpoblaciones con distintas tasas de contacto, sino también la discriminación de estas tasas de contacto según distintos tipos o contextos de contagio, a fin de proveer una herramienta práctica al momento de optar entre distintas intervenciones posibles.
Se ha demostrado que la intensidad de interacciones entre personas determina la transmisibilidad de enfermedades infecciosas y, en consecuencia, la efectividad de muchas intervenciones sanitarias. El conocimiento de la heterogeneidad en redes de contactos puede determinar si un patógeno se vuelve epidémico o endémico, ejercer presión selectiva para disminuir la virulencia del patógeno o determinar qué intervenciones pueden conducir a su mitigación o eliminación. Si bien los modelos que asumen mezcla homogénea son aptos para responder ciertos interrogantes, la incorporación de datos de contactos es necesaria para determinar la eficiencia de las intervenciones que tienen como blanco específico ciertas redes sociales14,28. En particular, en el caso del SARS-CoV-2, se ha demostrado la relación entre ocupaciones con distintos grados de exposición y probabilidad de contagio2,11,20. Dado esto, el modelo epidemiológico y la aplicación presentados aquí pueden ser de utilidad para la toma de decisiones en el contexto de la pandemia de COVID-19.
MetodologíaAntecedentesUno de los modelos matemáticos más utilizados para representar epidemias se conoce como SIR18. Se trata de un modelo compartimental, ya que divide a la población en tres compartimentos homogéneos: S (susceptibles), I (infectados) y R (resistentes), de manera que el tamaño de la población es N=S+I+R. La tabla 1 muestra el flujo entre estos compartimentos. Se asume que se trata de una población sin demografía, es decir, sin natalidad ni mortalidad basal, y que no hay movimiento de individuos hacia fuera ni hacia dentro de la población, por lo que el tamaño poblacional se mantiene constante.
Diagramas de flujo y sistemas de ecuaciones diferenciales ordinarias para los modelos matemático-epidemiológicos SIR, SEIR y SEIR-HL
S: susceptibles; E: expuestos; I: infectados; R: resistentes; Sh: susceptibles con alto contacto; Sl: susceptibles con bajo contacto; Eh: expuestos con alto contacto; El: expuestos con bajo contacto; Ih: infectados con alto contacto; Il: infectados con bajo contacto; Rh: resistentes alto contacto; Rl: resistentes bajo contacto; p: riesgo de transmisión por contacto; T: total de contactos en la población por unidad de tiempo.
Según el modelo SIR, un individuo solo puede pasar de un estado susceptible (no infectado, capaz de infectarse) a un estado infectado-infeccioso, y de un estado infectado-infeccioso a uno resistente (no infectado, incapaz de infectarse). La categoría de «resistente» incluye a aquellos individuos que están inmunizados contra la infección y, según el uso que se desee hacer del modelo, puede incluir también a los individuos fallecidos (en este caso, se suele hablar de individuos «removidos» del sistema, ya que los individuos inmunizados, recuperados y fallecidos no contribuirían a la diseminación de la infección).
Como se muestra en la tabla 1, el modelo SIR se expresa mediante tres ecuaciones diferenciales ordinarias que muestran cómo varían S, I y R en el tiempo. En este modelo, el número de infectados crece por contacto entre personas infectadas y susceptibles. El número de individuos dentro de cada compartimento es una variable dinámica, es decir que varía con el tiempo, y, por lo tanto, estas variables pueden expresarse como funciones del tiempo: S(t), I(t), R(t). Sin embargo, a fin de facilitar la lectura, se ha simplificado la notación: S, I, R.
En el modelo SIR hay dos parámetros a considerar: la tasa de contactos efectivos (β), que representa el número promedio de contactos en los que hay transmisión efectiva de la enfermedad, por unidad de tiempo; y la tasa de recuperación (γ), de manera que el período medio de recuperación es 1/γ. Esta «tasa de recuperación» contempla tanto la recuperación como la mortalidad.
Un desarrollo posterior del modelo SIR incluye un estadio adicional que corresponde a la categoría de expuesto (E), y se refiere a individuos que ya han estado en contacto efectivo con infectados, pero aún no tienen la capacidad de infectar a un individuo susceptible. Este modelo es conocido como SEIR y constituye la base del modelo empleado en este trabajo.
En este modelo, las categorías «expuesto» (E) e «infectado» (I) no se corresponden al uso habitual de estos términos. Los individuos de la categoría E ya son portadores del agente infeccioso y se transforman en infectados (I) cuando pueden infectar a sus contactos. En otras palabras, el compartimento E corresponde, en realidad, a individuos infectados, pero no infecciosos, mientras que los individuos del compartimento I son infectados e infecciosos. El número de infectados crece porque los expuestos adquieren luego de un cierto período de tiempo (el período de incubación) el carácter de infeccioso. Por lo tanto, además de la tasa de contactos efectivos y la tasa de recuperación, en el modelo SEIR hay un parámetro más a considerar: la tasa de incubación (σ), de forma que 1/σ es el período medio de incubación.
En el modelo SIR, la tasa de contactos efectivos y la tasa de recuperación permiten calcular el parámetro conocido como número básico de reproducción (R0) mediante la ecuación (1):
donde R0 representa el número promedio de nuevos infectados (infecciones secundarias) producidos por un infectado durante todo el periodo infectivo en una población totalmente susceptible. Se trata de uno de los indicadores más importantes en epidemiología: un R0 menor que 1 indica que la infección no será capaz de generar una epidemia en la población en cuestión, mientras que un valor mayor que 1 indica que sí lo será (en este caso, se considera que la epidemia será más difícil de controlar mientras mayor sea el valor de R0). El número básico de reproducción no depende exclusivamente del patógeno, sino que refleja también características de la población en estudio. Estas características incluyen, entre otras, el grado de mezcla o interacción entre los individuos que conforman la población. La ecuación (1) también puede aplicarse al modelo SEIR de manera aproximada, siempre y cuando se asuma que el período de incubación es mucho menor que la expectativa de vida media17.
El número de reproducción efectiva (Rt o Rt), esto es, el número de infecciones secundarias que genera cada individuo infeccioso en un tiempo determinado, puede estimarse como R0 multiplicado por la fracción de individuos susceptibles (S/N)33.
Desarrollo del modelo epidemiológicoEn los modelos previamente desarrollados no se consideran diferencias entre los individuos según su capacidad de contactarse con otros, es decir, se asume que todos los individuos tienen una tasa promedio de contactos similar. Esta suposición se aleja de la situación real bajo un contexto de cuarentena, aislamiento o distanciamiento social, como el impuesto en Argentina desde el 20 de marzo de 2020 hasta la actualidad (23 de julio de 2020), así como en otros países. El modelo aquí propuesto, SEIR-HL, busca una mejor aproximación a la situación real actual considerando la existencia de una población con dos tipos de individuos: los que tienen una gran cantidad de contactos y los que tienen una cantidad pequeña de contactos. Este modelo puede emplearse para representar una variedad de situaciones: individuos en aislamiento social, preventivo y obligatorio vs. individuos que trabajan en actividades y servicios esenciales4, individuos que se desempeñan en atención al público vs. individuos que no lo hacen, usuarios de transporte público vs. no usuarios de transporte público, etc.
A fin de simplificar el análisis se supuso que existen solo dos tipos de ocupaciones: aquellas que implican un alto número de contactos (H) y aquellas que implican un bajo número de contactos (L), siendo H y L las tasas de contacto, es decir, el número promedio de contactos por individuo por unidad de tiempo.
Como muestra la tabla 1, se divide a cada compartimento original del modelo SEIR en dos subpoblaciones: una con una tasa de contacto H (Sh, Eh, Ih, Rh) y otra con una tasa de contacto L (Sl, El, Il, Rl), con H mayor que L. Se asume que cada individuo mantiene la misma tasa de contactos durante todo el período analizado, es decir que un individuo de la subpoblación H no puede pasar a la subpoblación L, ni viceversa. Sin embargo, un individuo susceptible de cualquier subpoblación (Sh o Sl) puede interactuar con un individuo infectado de cualquier subpoblación (Ih o Il).
Las constantes asociadas a la tasa de recuperación (γ) y la tasa de incubación (σ) son las mismas para las subpoblaciones H y L. Sin embargo, la tasa de contactos efectivos (β) es distinta. Esta puede expresarse como el riesgo de transmisión por contacto (p), es decir, la probabilidad de que un contacto entre un individuo infectado y un individuo susceptible derive en una transmisión efectiva, multiplicada por la tasa de contacto (c)10:
Dado que en el modelo SEIR-HL hay un conjunto de la población para el cual c=H y otro para el cual c=L, con el mismo riesgo de transmisión por contacto, β será mayor para el primer conjunto que para el segundo.
El número total de contactos en la población por unidad de tiempo será:
donde Nh es el número de individuos con una tasa de contacto H, y Nl es el número de individuos con una tasa de contacto L, de forma que N=Nh+Nl. Dado que se parte de la suposición de que cada individuo mantiene siempre la misma tasa de contacto, Nh y Nl deberían ser constantes.
Tomando en cuenta estas consideraciones se genera una serie de seis ecuaciones diferenciales similares a las de SEIR, pero donde se discriminan los grupos de individuos según la tasa de contacto (tabla 1).
El número básico de reproducción R0 también puede ser expresado en términos del riesgo de transmisión y la tasa de contacto. Para el caso general de una población con una distribución no trivial de tasas de contacto, puede expresarse mediante la ecuación (4):
donde Nc representa el número de individuos que tienen una tasa de contacto c (si en una subpoblación hay individuos resistentes, se considera que estos tienen una tasa de contacto igual a 0).
En el caso del modelo SEIR-HL, la ecuación (4) puede reducirse a:
El modelo SEIR-HL fue concebido con el fin de evaluar el efecto de intervenciones tendientes a reducir la tasa promedio de contactos de la población, ya sea reduciendo la tasa de contactos efectivos de aquellas personas en posiciones o situaciones de alto contacto, o, lo que es equivalente matemáticamente, reduciendo el número de personas que ocupan dichas posiciones. En función de esto, se define una tasa de desplazamiento (D), la cual representa la proporción de la población en posiciones de alto contacto que es desplazada hacia posiciones de bajo contacto mediante una intervención, respecto de una situación inicial con una cierta distribución de la población entre ambos tipos de posiciones. Su expresión matemática es:
donde Nhb representa el número de individuos en ocupaciones de alto contacto antes de la intervención y Nha representa el número de individuos en ocupaciones de alto contacto luego de la intervención. Se plantea un único desplazamiento antes del comienzo de la simulación, luego del cual todos los individuos (desplazados y no desplazados) permanecen en sus respectivas subpoblaciones. De esta definición se desprende que el valor de D varía entre 0 y 1, dependiendo de la medida de la intervención. También puede ampliarse la definición de D para incluir el desplazamiento de individuos en el sentido opuesto, es decir, desde posiciones de bajo contacto a posiciones de alto contacto (por ejemplo, en el contexto de una relajación de la cuarentena o las medidas de distanciamiento social), en cuyo caso D también podría tomar valores negativos entre 0 y −1.
Si se consigue desplazar con una tasa D a individuos en ocupaciones con alto número de contactos hacia ocupaciones con bajo número de contactos, el nuevo número de contactos totales será:
donde Nlb y Nla representan el número de individuos en ocupaciones de bajo contacto antes y después de la intervención, respectivamente.
El cociente entre T′ y T se define como Q y es usado más tarde para estimar el β después de producir el desplazamiento. Q será menor de uno para cualquier D entre 0 y 1, lo que implica que el número de contactos después del desplazamiento va a ser siempre menor que el número de contactos inicial.
ResultadosImplementación del modelo epidemiológicoSe implementó el modelo SEIR-HL en Python 3.8, usando la biblioteca odeint (https://docs.scipy.org/doc/scipy/reference/generated/scipy.integrate.odeint.html)37 para resolver el sistema de ecuaciones diferenciales ordinarias. Por otro lado, se desarrolló una aplicación para el cálculo automatizado del R0 a partir de la ecuación (4), para una población dividida en hasta 10 subpoblaciones, con la posibilidad de discriminar las tasas de contacto de cada subpoblación según el tipo o contexto de contacto en hasta seis categorías. Se determinaron los parámetros más adecuados con el fin de modelar la evolución de la pandemia de COVID-19 en Argentina a partir de lo que informa la bibliografía16,21,37,42: Tagliazucchi et al. estimaron el valor de β (0,22) aplicando un modelo SEIR a los datos de Argentina, y los valores de p (0, 06), σ (0, 2) y γ (1/14) fueron tomados de reportes epidemiológicos.
Con el fin de comparar las predicciones del modelo SEIR-HL con las del modelo SEIR, se realizaron simulaciones con ambos modelos para una población hipotética de 1.000.000 de individuos, con 100 infectados iniciales, β=0, 22, p=0, 06, σ=0, 2, γ=0, 0714. En el caso de las simulaciones con SEIR-HL, se ensayaron distintas combinaciones de H y L (H=10, 33 y L=2, H=14, 33 y L=1, H=16, 33 y L=0, 5), de manera que la diferencia entre las tasas de contacto varíe, pero manteniendo en todos los casos una tasa de contacto promedio de 3,67 (y, por lo tanto, un β=0, 22). Las simulaciones con SEIR-HL se realizaron para una población dividida en una subpoblación de 200.000 individuos con tasa de contacto mayor (H) y 20 infectados iniciales, y otra de 800.000 individuos con tasa de contacto menor (L) y 80 infectados iniciales.
Posteriormente se usó el SEIR-HL para evaluar el efecto de distintas tasas de desplazamiento: se compararon para los distintos valores de D, el tiempo en que se alcanza el máximo en la curva de infectados, el número de infectados en dicho máximo y el número total de infectados al final de la pandemia. Para esto se realizaron simulaciones para una población hipotética de 1.000.000 de individuos, con 100 infectados iniciales, p=0, 06, σ=0, 2, γ=0, 0714, ensayando distintas combinaciones de H y L (H=10 y L=10, H=18 y L=8, H=30 y L=5, H=46 y L=1), de manera que la diferencia entre las tasas de contacto varíe, pero manteniendo en todos los casos una tasa de contacto promedio de 10. En todas las simulaciones, la población estaba dividida inicialmente (a D=0) en una subpoblación de 200.000 individuos con tasa de contacto mayor (H) y 20 infectados iniciales, y otra de 800.000 individuos con tasa de contacto menor (L) y 80 infectados iniciales. Se asumió que al desplazar individuos de la subpoblación H a la L, los individuos son tomados al azar, por lo que cada individuo infectado tiene la misma probabilidad de ser desplazado que un individuo susceptible. Usando la calculadora de R0 se analizó también el efecto de la medida de desplazamiento sobre el R0 para distintos valores de β y tasas de contacto (H y L).
Finalmente, se desarrollaron ejemplos de aplicación del modelo SEIR-HL y de la calculadora de R0. Por un lado, se realizó un ajuste del modelo a los datos de la pandemia de COVID-19 en Argentina mediante el método de mínimos cuadrados. Los datos de nuevas infecciones por día en función de la fecha de inicio de los síntomas para el período 9 de marzo a 22 de junio de 2020 fueron obtenidos de la Sala de Situación Coronavirus Online del Ministerio de Salud de la República Argentina (https://www.argentina.gob.ar/salud/coronavirus-COVID-19/sala-situacion)25. A partir de los números de individuos predichos para cada compartimento, se calculó para cada día d el número de nuevas infecciones como:
Con el modelo ajustado, se realizó una estimación del número máximo de infectados por día, el número total de infectados y el número total de fallecidos, comparando estos valores con la situación contrafáctica en la que no se hubiera implementado la cuarentena y demás medidas de distanciamiento social, y con un escenario donde la cuarentena se hubiera mantenido igual de estricta que al principio. Se asumió que el 25% de la población argentina seguía circulando durante la cuarentena a partir de un comunicado del Ministerio de Transporte de la República Argentina (https://www.argentina.gob.ar/noticias/la-circulacion-de-pasajeros-en-transporte-publico-en-amba-promedia-el-25)26. Se consideraron tres períodos para ajustar los datos de nuevas infecciones por día en Argentina: 9 de marzo a 19 de marzo (P1), 20 de marzo a 10 de mayo (P2) y 11 de mayo a 22 de junio (P3). Se realizaron tres ajustes: un primer ajuste («cuarentena + relajamiento»), donde se ajustó en P1 para una población única con el mismo número de contactos, y en P2 y P3 para dos subpoblaciones (el 75% de los individuos aislados y el 25% no aislados), un segundo ajuste («cuarentena»), donde se ajustó en P1 y P2 de la misma manera, pero para P3 se realizó una extrapolación a partir del ajuste de P2, y un tercer ajuste («sin cuarentena»), donde se ajustó en P1 de la misma manera que en los otros ajustes, pero para P2 y P3 se realizó una extrapolación a partir del ajuste de P1.
Por otro lado, se empleó la calculadora de R0 para estimar el efecto de una intervención particular sobre el R0 en una situación hipotética donde se desea modificar el número y/o las tasas de contacto de distintos tipos de trabajadores: trabajadores esenciales de alto contacto, trabajadores esenciales de bajo contacto, trabajadores no esenciales de alto contacto, trabajadores no esenciales de bajo contacto y personas sin trabajo. Se consideraron cuatro tipos de contacto: contacto domiciliario, contacto vecinal, contacto en transporte y contacto laboral. También se dedujeron los valores que debían tomar ciertas variables para que el R0 llegara a 1: se analizó la tasa de contacto de un grupo particular (trabajadores no esenciales de alto contacto), un tipo de tasa de contacto particular (contacto laboral) y el desplazamiento de individuos de un grupo a otro (de trabajadores esenciales de alto contacto a trabajadores esenciales de bajo contacto).
En la página web27https://ecm.famaf.unc.edu.ar/ se encuentran disponibles en línea una aplicación interactiva con la implementación del modelo SEIR-HL, una versión expandida del SEIR-HL para más de dos subpoblaciones, otros modelos y la calculadora de R0. Dicha página incluye, además, varios ejemplos de uso de la aplicación. El software es de código abierto bajo licencia GNU GPLv3.
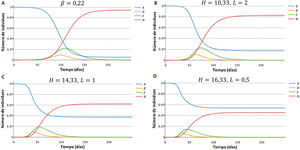
Comparación entre SEIR y SEIR-HLPara comparar ambos modelos se llevaron a cabo simulaciones con el SEIR y el SEIR-HL, empleando para este último tres combinaciones de H y L con diferencia creciente: H=10, 33, L=2 (combinación 1); H=14, 33, L=1 (combinación 2); H=16, 33, L=0, 5 (combinación 3). Estas simulaciones divergen en varios aspectos: i) el número de infectados en el pico es menor para los valores más divergentes entre H y L (fig. 1A,B,C,D); ii) el tiempo hasta alcanzar el pico de la infección disminuye a medida que aumenta la divergencia entre H y L, y fue de 117 días para el SEIR y de 74, 54 y 45 días para las combinaciones 1, 2 y 3 del SEIR-HL, respectivamente, y iii) el número de susceptibles al final de la simulación, es decir, el número de personas que no se han infectado, para el SEIR alcanza un valor de 54.249, mientras que para las distintas combinaciones del SEIR-HL, los valores ascienden a 175.053, 376.329 y 542.078 (fig. 1A,B,C,D).
Simulación de susceptibles, expuestos, infecciosos y recuperados en función del tiempo, generadas para una población de 1 millón con 100 infectados iniciales, una tasa de contactos promedio de 3,67, σ=0, 2, γ=0, 0714, usando el modelo SEIR (A) y el modelo SEIR-HL (B-D). (A) Modelo SEIR,. (B) Modelo SEIR-HL, H=10, 33, L=2. (C) Modelo SEIR-HL, H=14, 33,. (D) Modelo SEIR-HL, ,. Las simulaciones con SEIR-HL se realizaron para una población dividida en una subpoblación de 200.000 con tasa de contactos mayor y 20 infectados iniciales, y otra de 800.000 con tasa de contactos menor y 80 infectados iniciales (p=0, 06). Los valores de H y L fueron elegidos de manera que se mantenga la misma tasa de contacto promedio (3,67) y el mismo valor de (0,22) en todas las simulaciones.
Por otro lado, la proporción de infectados es mayor en las subpoblaciones de mayor contacto: en el caso de las simulaciones de la figura 1, la subpoblación H termina infectándose en todos los casos en más del 99,9%, mientras que el porcentaje de infectados totales de la población L fue del 78,1, 53 y 32,3% para las combinaciones 1, 2 y 3, respectivamente, lo que muestra que a mayor divergencia entre L y H, mayor es la probabilidad de que individuos de la subpoblación con menor contacto permanezcan sin infectarse a lo largo de la pandemia. Se observa, además, que la subpoblación H, a pesar de ser minoritaria (20%), contribuye más a la transmisión durante el período inicial de la pandemia y es responsable de la mayoría de los contactos infecciosos diarios (fig. S1). Sin embargo, hacia el final de la pandemia, a medida que estos individuos se infectan y pasan al compartimento R, los contactos producidos por la subpoblación L se vuelven relativamente más importantes, excepto en el caso donde hay mayor disparidad entre tasas de contacto (fig. S1F).
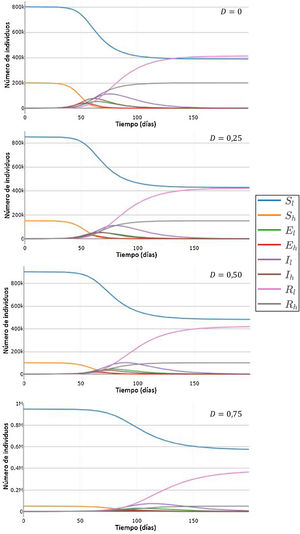
Efecto del desplazamiento de individuos de la población de mayor número de contactos sobre las curvas de los compartimentos S, E, I y RPara estudiar el efecto que producirían distintos valores de la tasa de desplazamiento de individuos de la población H a L en los valores de los compartimentos S, E, I y R, se llevaron a cabo simulaciones utilizando el SEIR-HL con tasas de desplazamiento crecientes. La figura 2 muestra un ejemplo de la forma en que varían las curvas de S, E, IyR para las subpoblaciones H a L a medida que aumenta la proporción de individuos H que son desplazados a la subpoblación L. Cada simulación se inicia (tiempo 0) con los valores de Nl y Nh obtenidos después del desplazamiento. Se puede observar que a mayores valores de D, ocurren tres fenómenos: el máximo de las curvas de infectados se alcanza más tarde y tiene valores menores, el número de susceptibles tiende a valores mayores, y el número de resistentes, que provienen de aquellos que han superado la infección, tiende a valores menores. En conjunto, los resultados muestran que el desplazamiento retrasaría la evolución de la pandemia y puede llegar a disminuir el número total de infectados.
Simulación de curvas H y L de susceptibles, expuestos, infecciosos y recuperados en función del tiempo, para distintos valores de la tasa de desplazamiento D, para una población de 1 millón con 100 infectados iniciales (inicialmente 20 en la subpoblación de menor contacto y 80 en la subpoblación de mayor contacto). Parámetros: H=10, L=1, , ,.
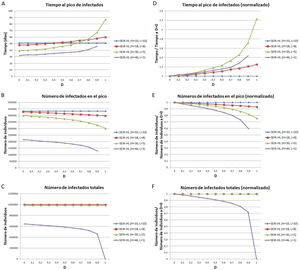
Para estudiar con más detalle el efecto del desplazamiento sobre las curvas considerando la divergencia entre los valores de H y L se utilizaron cuatro combinaciones progresivamente divergentes: H=10, L=10 (combinación 1); H=18, L=8 (combinación 2); H=30, L=5 (combinación 3); H=46, L=1 (combinación 4). Los valores de desplazamiento aplicados variaron entre 0 y 1, con un incremento gradual de 0,1. Para cada combinación y valor de D se realizó una simulación y se registró el tiempo hasta alcanzar el pico de infectados, la cantidad de infectados en el pico y el número de infectados totales.
En la figura 3, se representan el tiempo al pico de infectados (fig. 3A), el número de infectados en el pico (fig. 3B) y el número de infectados totales (fig. 3C). En concordancia con lo mostrado en la figura 2, a mayores valores de D, se observa un aumento del tiempo hasta alcanzar el pico de infectados (fig. 3A), una disminución en el número de infectados en dicho pico (fig. 3B) y una disminución en el número total de infectados al final de la pandemia (fig. 3C). Todos estos efectos se incrementan al aumentar la diferencia entre H y L. Por ejemplo, para la combinación 1, el número de infectados en el pico es igual para un D=9 que para un D=0 (sin desplazamiento), mientras que para las combinaciones 2, 3 y 4, el número de infectados en el pico con D=0, 9 representa una reducción respecto del valor para D=0 del 6,1%, 18,1% y 40,4%, respectivamente.
Tiempo en que se alcanza el pico de la curva de infectados (A, D), número de individuos infectados en el pico de la curva de infectados (B, E), número de individuos infectados totales (C, F), para distintos valores de la tasa de desplazamiento D, para poblaciones con la misma tasa de contactos promedio inicial pero distinta distribución de contactos. (A-C) Valores absolutos. (D-F) Valores normalizados, tomando como referencia los valores correspondientes a D igual a 0. Todas las simulaciones se realizaron para una población de 1 millón con 100 infectados iniciales. Previo al desplazamiento, la tasa de contactos promedio era igual a 10 para todas las poblaciones, y las mismas estaban divididas en una subpoblación de 200.000 con tasa de contactos mayor y 20 infectados iniciales, y otra de 800.000 con tasa de contactos menor y 80 infectados iniciales. Parámetros: , ,. Los valores de H y L fueron elegidos de manera que se mantenga la misma tasa de contacto promedio (10) en todas las simulaciones.
Si bien para las combinaciones de H y L menos divergentes (combinaciones 1, 2 y 3), el número total de infectados varía como máximo en un 0,3%, para la mayor diferencia evaluada (combinación 4), el número total de infectados resulta mucho más sensible al aumento de D (fig. 3C), constituyendo el valor para un D de 0,9 una reducción del 28% respecto del valor para D=0. Estos resultados muestran que la evolución de la pandemia depende de la divergencia entre las subpoblaciones.
Efecto del desplazamiento sobre la tasa básica de reproducciónEl valor de D también afecta al R0: a mayores tasas de desplazamiento, menor es la tasa básica de reproducción. Se observa que a mayor diferencia entre H y L, el efecto del desplazamiento sobre el R0 es mayor (fig. S2). Como β también se ve afectada por el número de contactos, el efecto del desplazamiento sobre R0 también depende del valor de β (fig. S3). Dado que con R0<1 la pandemia tiende a decrecer, se podría determinar cuál sería el valor de D necesario para controlar la pandemia si se contara con estimaciones confiables de β.
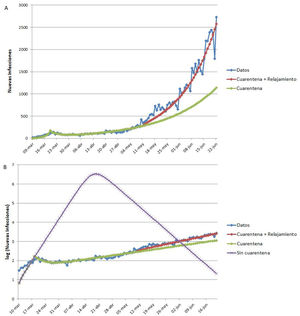
Ejemplo de aplicación del modelo SEIR-HL a la pandemia de COVID-19 en ArgentinaLa figura 4 muestra los datos reales de nuevas infecciones por SARS-CoV-2 por día reportadas en Argentina, así como los tres ajustes realizados con el modelo SEIR-HL: el ajuste a los datos completos entre el 9 de marzo y el 22 de junio («cuarentena + relajamiento»), la predicción para la situación en que la cuarentena se hubiera mantenido igual de estricta que al principio («cuarentena») (fig. 4A) y la predicción de la evolución de la pandemia en la situación en que la cuarentena no se hubiera aplicado («sin cuarentena») (fig. 4B). Según el modelo ajustado, la aplicación de la cuarentena ya sea estricta o con relajamiento posterior, habría reducido el número máximo de infectados por día, el número total de infectados y el número total de fallecidos en más del 99,8%, además de retrasar el pico de infectados por más de dos meses (cabe aclarar que en los escenarios con cuarentena no se alcanza el pico en el período analizado, por lo que el número máximo de infectados por día corresponde al último reporte). El modelo estima que, si la pandemia hubiera seguido evolucionando de la misma manera que lo hizo entre el inicio de la cuarentena y el 10 de mayo, se habría observado una reducción del número máximo de infectados por día del 55,8% y una reducción del número de infectados y fallecidos del 38%.
Ajuste del modelo SEIR-HL a los datos reportados de nuevas infecciones de COVID-19 en Argentina. (A) «Cuarentena + relajamiento»: modelo ajustado en tres secciones: 09/03/2020-19/03/2020 (una población, C=20), 20/03/2020-10/05/2020 (dos subpoblaciones: 75% con , 25% con ), 11/05/2020-22/06/2020 (dos subpoblaciones: 75% con L=2, 34, 25% con H=2, 85). «Cuarentena»: modelo ajustado en dos secciones: 09/03/2020-19/03/2020 (una población, ), 20/03/2020-10/05/2020 (dos subpoblaciones: 75% con L=0, 5, 25% con ), se extrapolaron las nuevas infecciones para el período del 11/05/2020-22/06/2020 suponiendo que la población mantenía los parámetros del segundo ajuste. (B) Se presentan los mismos modelos ajustados que en A, junto con el modelo «Sin cuarentena» (modelo ajustado para el período 09/03/2020-19/03/2020 (una población, ) y extrapolado para el período 20/03/2020-22/06/2020 suponiendo que la población mantenía los parámetros de este ajuste. Parámetros fijos: , y ). El eje vertical se muestra en escala logarítmica para facilitar la comparación.
Además de utilizar el concepto de dos subpoblaciones con distintas tasas de contacto para el desarrollo de un modelo matemático, también es posible emplear la definición general de R0 en función de las tasas de contacto (ecuación 4) para predecir el efecto de medidas sanitarias que tengan como blanco redes sociales específicas, para un número más amplio de subpoblaciones. Por ejemplo, suponiendo conocida la cantidad de trabajadores esenciales y no esenciales, con trabajos de alto o bajo contacto, y el número de desempleados, así como las tasas de contacto para cada grupo en diferentes contextos (contactos en la casa, en el trabajo, en el vecindario, en el transporte, etc.) para una situación preintervención, puede calcularse el R0 resultante del impacto de alguna intervención particular (tabla 2). También existe la posibilidad de determinar el grado de una intervención necesario para producir un R0=1. Esto puede hacerse ensayando distintos valores para número de individuos o tasa de contacto, o bien mediante un cálculo, igualando la ecuación (4) a 1 y despejando la variable de interés según la intervención. En la situación hipotética de la tabla 2, por ejemplo, podría calcularse el número máximo de contactos totales que debería tener la población de trabajadores no esenciales de alto contacto para que el R0 sea igual o menor que 1 a partir de la ecuación (9):
Ejemplo de aplicación del cálculo de R0 en función del número de contactos para predecir el efecto de una intervención
| Situación preintervención | ||||||
|---|---|---|---|---|---|---|
| Grupo | Población | Contacto domiciliario | Contacto vecinal | Contacto transporte | Contacto laboral | Contacto total |
| TEAC | 1.000 | 1 | 3 | 2 | 36 | 42 |
| TEBC | 1.000 | 2 | 3 | 2 | 9 | 16 |
| TNAC | 20.000 | 1 | 3 | 2 | 36 | 42 |
| TNBC | 3.000 | 2 | 3 | 2 | 9 | 16 |
| ST | 6.500 | 2 | 3 | 2 | 7 | 14 |
| R0=4, 70 | ||||||
| Situación posintervención | ||||||
| Grupo etario | Población | Contacto domiciliario | Contacto vecinal | Contacto transporte | Contacto laboral | Contacto total |
| TEAC | 1.000 | 1 | 0 | 1 | 15 | 17 |
| TEBC | 1.000 | 2 | 0 | 1 | 2 | 5 |
| TNAC | 20.000 | 1 | 0 | 0 | 0 | 1 |
| TNBC | 3.000 | 2 | 0 | 0 | 0 | 2 |
| ST | 6.500 | 2 | 0 | 0 | 0 | 2 |
| R0=0, 28 | ||||||
Se muestran los valores de R0 predichos para una situación anterior a la intervención, tomando como base la información sobre número de trabajadores y tasas de contacto, y luego de una intervención donde se mantiene a toda la población en casa, excepto a los trabajadores esenciales, y se minimizan los contactos en contextos de trabajo y transporte. Los cálculos fueron realizados asumiendo los siguientes valores para los parámetros epidemiológicos: p=0, 01, γ=0, 07.
TEAC: trabajador esencial, alto contacto; TEBC: trabajador esencial, bajo contacto; TNAC: trabajador no esencial, alto contacto; TNBC: trabajador no esencial, bajo contacto; ST: sin trabajo.
donde Nx y cx representan el número de individuos y la tasa de contactos correspondientes al grupo x (TEAC: trabajador esencial, alto contacto; TEBC: trabajador esencial, bajo contacto; TNAC: trabajador no esencial, alto contacto; TNBC: trabajador no esencial, bajo contacto; ST: sin trabajo). Haciendo uso de la ecuación (9), puede determinarse que para el ejemplo de la tabla 2, sería necesario que la tasa de contactos totales del grupo TNAC bajara a 1,18 para que el R0 disminuyera a 1, sin alterar las tasas de contacto de los demás grupos.
Alternativamente, también podría calcularse cuál debería ser la tasa media de contactos laborales que produciría un R0 igual a 1 a partir de la ecuación (10), también deducida a partir de la ecuación (4):
donde cl¯ es la tasa media de contactos laborales ponderada por grupo y cx,nol es la suma de las tasas de cada tipo de contacto, excepto los laborales, para el grupo x. En el caso del ejemplo de la tabla 2, la ecuación (10) permite concluir que sería necesario que la tasa media de contactos laborales se redujera a 0,67 para que el R0 bajara a 1, sin alterar las tasas de contacto en otros contextos.
Por último, podría calcularse el número X de individuos que deberían ser desplazados de un grupo a otro para que el R0 bajara a 1, a partir de la ecuación (11).
En el caso del ejemplo de la tabla 2, la ecuación (10) arroja un valor de X=31.404. Este valor es mayor que el número de trabajadores no esenciales de alto contacto (NTNAC=20.000), lo cual indica que no es posible llevar el R0 a 1 solamente desplazando a trabajadores no esenciales de alto contacto al grupo de trabajadores no esenciales de bajo contacto, por lo que esta medida debería combinarse con otra para alcanzar el objetivo deseado.
Otros ejemplos de aplicación del modelo y de la ecuación (4) similares a estos se pueden encontrar en el Material Suplementario (Ejemplos de Uso 1-5).
DiscusiónLos modelos matemáticos seleccionan los aspectos significativamente importantes de una situación real y generan predicciones utilizando el simbolismo y las ecuaciones matemáticas. Si bien estos modelos presentan ciertas limitaciones, aun así, pueden ser muy útiles para estudiar un proceso complejo, como es el caso de una pandemia y prever de manera semicuantitativa cómo la introducción de medidas concretas puede cambiar su evolución.
Los resultados muestran que el modelo SEIR-HL, que contempla la existencia de dos subpoblaciones con distintas tasas de contacto, conduce a conclusiones distintas respecto del SEIR. Las predicciones del SEIR-HL son, en general, más optimistas que las del SEIR, dado que, si bien el SEIR-HL predice un menor tiempo para alcanzar el pico de infectados activos que el SEIR, el valor del pico es menor en el SEIR-HL que en el SEIR y, lo que es más importante, el número total de infectados es menor con el SEIR-HL que con el SEIR.
Se observa, además, que la proporción de susceptibles al final de la simulación es mayor entre los que tienen un menor número de contactos. Por el contrario, la población con mayor número de contactos contribuye en mayor proporción al compartimento R. Este resultado es relevante, ya que, como se explicó antes, los individuos fallecidos forman parte del compartimento R. Si se consigue mantener a los individuos más vulnerables dentro de los que tienen menos contactos, disminuiría notablemente el número de fallecidos. Además, el retraso de la infección en los grupos más vulnerables permite que, de necesitarse hospitalización, esta se retrase dando tiempo a la preparación del sistema hospitalario. También en el caso de una epidemia por un nuevo agente, esta postergación permite el incremento del conocimiento médico-científico, lo que también repercute positivamente en la sobrevida de los infectados, aun en ausencia de una vacuna. Esto se vería más claramente en un modelo basado en Susceptible-Exposed-Infected-Recovered-Dead (SEIRD), donde se distingue entre la recuperación y la mortalidad, y donde se podrían asignar tasas de mortalidad diferenciales a la población según factores de riesgo.
Las simulaciones realizadas muestran que aquellos individuos que tienen alto número de contactos se infectan primero y que, al recuperarse, el número de contactos efectivos entre infectados y susceptibles (es decir, la cantidad de contactos capaces de dar la infección) disminuye. Este efecto es más notable cuanto mayor es la diferencia entre H y L. Según este desarrollo, la inmunidad de rebaño se conseguiría con una proporción relativamente pequeña de la población inmunizada. En concordancia con esto último, se está observando en distintos países del mundo que la pandemia de COVID-19 tiende a decrecer cuando solo un pequeño porcentaje de la población se torna resistente9. En ese sentido, el modelo SEIR-HL podría arrojar una explicación más adecuada de ese comportamiento, que se complementaría con los cambios en la conducta de las personas y el subdiagnóstico19.
Se ha visto en este y otros trabajos37 que la pendiente de la curva de infectados, la cual se correlaciona con el Rt, disminuye con el tiempo. El modelo SEIR-HL permite explicar esta disminución en la velocidad de expansión de la pandemia en términos de una caída del número de contactos debida a la depleción de individuos H susceptibles e infectados. Estos individuos H, ahora resistentes, actuarían como barrera entre susceptibles e infectados, ralentizando la propagación de la infección.
El modelo SEIR-HL también permitió estudiar las consecuencias de desplazar poblaciones de mayor número de contactos al grupo de menor número de contactos. Simulando distintas condiciones, se revela que un incremento de D disminuye el número total de infectados y retrasa la evolución de la pandemia, según se observa en las figuras 2 y 3. También se mostró cómo estas modificaciones llevan a un cambio en el R0 de la población. Este incremento de D que lleva a un menor número de contactos totales se puede obtener de varias maneras, por ejemplo, eliminando las tareas que impliquen contacto y no sean imprescindibles, o introduciendo dispositivos que eviten o minimicen el contacto en la ocupación (por ejemplo, que se le alcance al usuario de un servicio la mercancía o los elementos que requiere, sin acercarse al empleado), manteniendo la cuarentena para determinadas actividades (no exceptuados). Por otra parte, al ocurrir la infección, primero, entre los que tienen más contactos, puede estudiarse si estos individuos pueden servir como población centinela para detectar la introducción del virus.
Alternativamente, se puede recurrir a individuos inmunizados y que no porten el virus para ocupar estos puestos y derivar a los no protegidos a puestos internos, sin contacto con el público o usuarios. Estos individuos inmunizados pueden ser individuos selectivamente vacunados (suponiendo que se desarrolle una vacuna efectiva, pero que no sea posible vacunar a toda la población, al menos rápidamente) o bien individuos recuperados de COVID-19 (suponiendo que se demuestre que las personas curadas con títulos altos de anticuerpos son realmente inmunes a la reinfección). Esta idea ya ha sido propuesta por otros autores, pero acá se plantea considerando subpoblaciones41.
Es muy común el uso de R0 para estimar la evolución de la pandemia. Algunos autores objetan sobre su uso como medida segura en situaciones complejas5,33, sin embargo, en términos comparativos, el ascenso o el descenso de R0 al tomar ciertas medidas parece aceptable. Al estimar el R0 en función de subpoblaciones con distinto número y tipo de contactos, se cuenta con una herramienta para comparar distintas intervenciones; a su vez, se pueden estimar costos para obtener un beneficio equivalente con una u otra medida.
Aunque la utilidad del cálculo de R0 debe ser analizada con cuidado para el seguimiento de las epidemias32, aquí se utilizó la fórmula derivada del modelo SIR para una comparación sencilla de los efectos de determinados cambios en el manejo de la epidemia, considerando subpoblaciones con distinta cantidad y tipo de contactos.
Está en desarrollo la expansión del modelo mediante la consideración de más subpoblaciones de contactos, así como la inclusión de otros factores, como el tiempo de inmunidad, la posible reinfección (SEIRS), la mortalidad (SEIRD), la presencia de individuos contagiosos asintomáticos (SEIRA), entre otros.
Si bien ya se han propuesto otros modelos para SARS-CoV-2 basados en SEIR con estratificación de compartimentos, en la mayoría de los casos, los criterios de estratificación fueron la edad, el tipo de actividad en un determinado contexto (generalmente asociado a sectores) y la división en ciudades, regiones o países (modelos meta-poblacionales)13,24,29,30,36,45. El modelo presentado aquí utiliza la tasa de contacto como criterio único de estratificación. Los aportes originales de este estudio son la aplicación del modelo a datos de la pandemia de COVID-19 en Argentina, así como la consideración de una variable de desplazamiento de un grupo a otro (o variantes como vacunación selectiva, robotización o automatización de tareas para intentar controlar los contagios).
Es necesario señalar, también, las limitaciones del modelo desarrollado. Si bien el SEIR-HL incorpora la tasa de incubación, no se contempla en el modelo la posibilidad de que individuos infectados (preinfecciosos o infecciosos) sean detectados y aislados. De incorporarse esta información, es probable que el modelo prediga pandemias de menor magnitud y cinética que las presentadas en este trabajo. Asimismo, una estratificación por edad podría haber aportado información valiosa al modelo, pero dada la escasez de datos sobre tasas de contacto por grupo etario en Argentina, no fue posible incorporar este aspecto al modelo. Sin embargo, cabe resaltar que modelos más complejos no son, necesariamente, más confiables35. Por otra parte, el estudio de muchos parámetros necesarios para conocer mejor la pandemia (como la capacidad de contagio de asintomáticos, la distinta capacidad infectiva de contagio de variantes virales, la relevancia del contagio por aerosoles o la protección cruzada con otros coronavirus) está en plena evolución, lo que permitirá desarrollar modelos más ajustados en el futuro.
ConclusiónLas medidas tendientes a reducir el número de contactos en determinados puestos/ocupaciones pueden influir en la evolución de la pandemia; asimismo, determinar cuáles puestos/ocupaciones de mayor contacto tienen mayor peso en la propagación de la pandemia puede ayudar a dirigir los recursos de manera más eficaz. En ese sentido, el uso de modelos de simulación, como el presentado aquí, puede contribuir en la toma de decisiones.
Los modelos que consideran subpoblaciones con distinto número de contactos pueden dar resultados con diferencias relevantes a los tradicionales y sumar claridad a la hora de tomar medidas específicas.
FinanciaciónLa presente investigación no ha recibido ayudas específicas provenientes de agencias del sector público, sector comercial o entidades sin ánimo de lucro.
Conflicto de interesesLos autores declaran no tener ningún conflicto de intereses.
Al Dr. Nicolás Wolovick por facilitar el hosting del programa en el sitio web.
A la Dra. Mara Rosenzvit por sus aportes a la discusión de los resultados.